Bài viết này sẽ giúp bạn đọc tìm hiểu chi tiết vị trí tương đối của đường thẳng và đường tròn, từ đó ứng dụng các dạng bài về xác định vị trí và tiếp tuyến.
Tổng quan lý thuyết
[content_1]Vị trí tương đối của đường thẳng và đường tròn
Gọi d là khoảng cách từ tâm O của đường tròn (O; R) đến đường thẳng a, khi đó ta có:
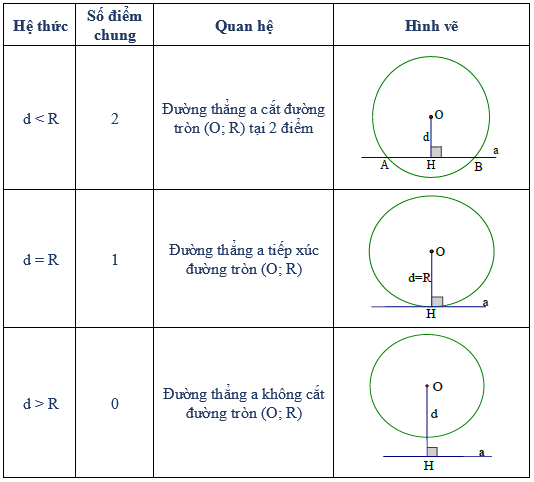
Định lý
Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
Phân dạng bài tập
Dạng 1. Xác định vị trí tương đối của đường thẳng và đường tròn và ngược lại
[content_2]Phương pháp giải
So sánh d và R dựa vào bảng vị trí tương đối của đường thẳng và đường tròn đã nêu trong lý thuyết
Bài tập vận dụng
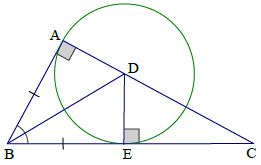
Bài 1. Cho ∆ABC vuông tại A có BD là đường phân giác. Xác định vị trí tương đối của đường thẳng BC và đường tròn tâm D bán kính DA.
Hướng dẫn giải
Vẽ DE ⊥ BC (E ∈ BC)
D thuộc tia phân giác ![\[\widehat {ABC}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-1.svg)
; DA ⊥ AB, DE ⊥ BC ⇒ DE = DA
Do đó đường thẳng BC và đường tròn tâm D bán kính DA tiếp xúc nhau.
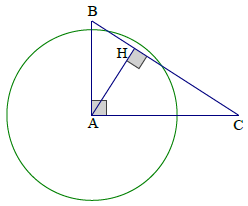
Bài 2. Cho ∆ABC vuông tại A có AB = 3 cm, AC = 4 cm. Vẽ đường tròn tâm A bán kính 2,8 cm. Xác định vị trí tương đối của đường thẳng BC và đường tròn tâm A bán kính 2,8 cm.
Hướng dẫn giải
Vẽ AH là đường cao của tam giác vuông ABC
Ta có: ![\[\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-2.svg)
⇒ AH = 2,4 cm < 2,8 cm (d < r)
Do đó đường thẳng BC và đường tròn (A; 2,8cm) cắt nhau
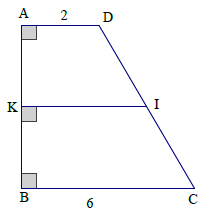
Bài 3. Cho hình thang vuông ABCD có ![\[\widehat A = \widehat B = 90^\circ \]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-3.svg)
, AD = 2 cm, BC = 6 cm, CD = 8 cm. Chứng minh rằng AB tiếp xúc với đường tròn đường kính CD
Hướng dẫn giải
Gọi I, K lần lượt là trung điểm của CD và AB
Ta có: IK là đường trung bình của hình thang ABCD
![\[ \Rightarrow IK = \frac{{AD + BC}}{2} = 4\left( {cm} \right)\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-4.svg)
Lại có: AD // IK, AD ⊥ AB
⇒ IK ⊥ AB; IK = ![\[\frac{1}{2}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-5.svg)
CD (= 4cm), IK ⊥ AB
Do đó AB tiếp xúc với đường tròn tâm I đường kính CD.
Dạng 2. Bài toán liên quan đến tính độ dài
[content_3]Phương pháp giải
Ta nối tâm với tiếp điểm để vận dụng định lý về tính chất của tiếp điểm và sử dụng định lý Py-ta-go.
Bài tập vận dụng
Bài 1. Cho đường tròn tâm O bán kính 6 cm và một điểm A cách O là 10 cm. Kẻ tiếp tuyến AB với đường tròn trong đó B là tiếp điểm. Tính độ dài đoạn AB.
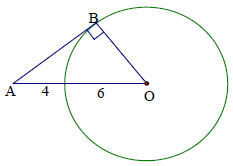
Hướng dẫn giải
Ta có: ∆ABC vuông tại B ⇒ AB = 8 cm
Bài 2. Cho đường tròn (O; R) và dây ![\[AB = \frac{8}{5}R\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-6.svg)
. Vẽ một tiếp tuyến song song với AB, cắt các tia OA, OB lần lượt tại M và N. Tính diện tích tam giác OMN
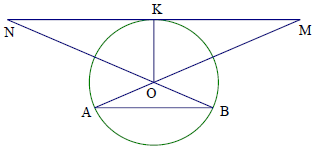
Hướng dẫn giải
Tiếp tuyến MN, tiếp điểm K. Vì AB // MN nên OK ⊥ AB
Ta tính được:
![\[OK = \frac{3}{5}R \Rightarrow KN = \frac{4}{3}R \Rightarrow {S_{OMN}} = \frac{4}{3}{R^2}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-7.svg)
Bài 3. Cho đường tròn (O; 2cm) và một điểm A chạy trên đường tròn đó. Từ A vẽ tiếp tuyến xy. Trên xy lấy một điểm M sao cho AM = ![\[2\sqrt 3 \]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-8.svg)
(cm). Hỏi điểm M di động trên đường nào khi A chạy trên (O).
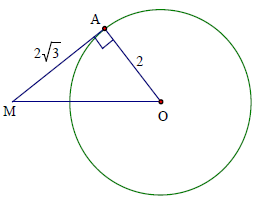
Hướng dẫn giải
Tính được OM = 4 ⇒ M di chuyển trên (O; 4cm).
Bài 4. Cho đường tròn (O; 2cm) và điểm A ngoài (O). Từ A kẻ cát tuyến với (O), cắt (O) tại B và C. Cho biết AB = BC và kẻ đường kính COD, tính độ dài đoạn thẳng AD.
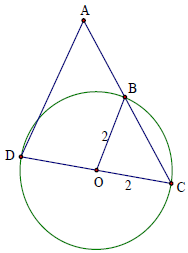
Hướng dẫn giải
Chứng minh được OB là đường trung bình của ∆CDA ⇒ AD = 4 cm.
Bài 5. Cho điểm M cách đường thẳng xy một khoảng 6 cm, vẽ đường tròn (M; 10cm)
a) Chứng minh rằng đường tròn tâm M và đường thẳng xy cắt nhau.
b) Gọi hai giao điểm là P và Q. Tính PQ.
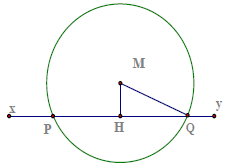
Hướng dẫn giải
a) Kẻ MH ⊥ xy = H ⇒ MH là khoảng cách từ M đến xy
⇒ ![\[\left\{ \begin{gathered} MH = 6cm \hfill \\ R = 10cm \hfill \\ \end{gathered} \right.\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-9.svg)
⇒ MH < R ⇒ xy cắt (O; 10cm) tại P và Q
b) Ta có: MH ⊥ PQ ⇒ HP = HQ = PQ (Quan hệ vuông góc đường kính và dây)
⇒ PQ = 2HQ
Xét ∆MHQ vuông tại H
⇒ HQ = 8 cm (HQ > 0) ⇒ PQ = 16 cm
Bài 6. Cho hình vuông ABCD, trên đường chéo BD lấy điểm I sao cho BI = BA. Đường thẳng kẻ qua I vuông góc với BD cắt AD ở E.
a) So sánh: AE, EI, ID
b) Xác định vị trí tương đối của đường thẳng BD với đường tròn (E ; EA)
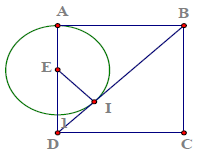
Hướng dẫn giải
a) Ta có: ∆AEB = ∆IEB (cạnh huyền – cạnh góc vuông) ⇒ AE = EI (1)
∆EID có: ![\[\widehat I = 90^\circ ,\widehat {{D_1}} = 45^\circ \]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-10.svg)
⇒ ∆EID vuông cân ⇒ IE = ID (2)
Từ (1), (2) ⇒ AE = EI = ID
b) Ta lại có: EI = EA ⇒ I ∈ (E; EA) ⇒ R = EI
Mặt khác: EI ⊥ BD ⇒ d = EI ⇒ d = R
⇒ Đường thẳng BD tiếp xúc với (E; EA)
Bài 7. Cho nửa đường tròn tâm O, đường kính AB, M là 1 điểm thuộc nửa đường tròn, qua M vẽ tiếp tuyến với nửa đường tròn. Gọi D và C theo thứ tự là các hình chiếu của A và B trên tiếp tuyến ấy
a) Chứng minh rằng M là trung điểm của CD
b) Chứng minh: AB = BC + AD
c) Giả sử: ![\[\widehat {AOM} > \widehat {BOM}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-11.svg)
, gọi E là giao điểm của AD với nửa đường tròn. Xác định dạng của tứ giác BDCE.
d) Xác định vị trí của điểm M trên nửa đường tròn sao cho tứ giác ABCD có diện tích lớn nhất. Tính diện tích đó theo bán kính của nửa đường tròn đã cho.
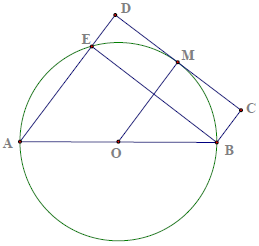
Hướng dẫn giải
a) Hình thang ABCD có AO = OB, OM // AD // BC
⇒ M là trung điểm của CD
b) Ta có: AB = 2OM = BC + AD
c) Tứ giác BDCE là hình chữ nhật vì có 3 góc vuông
d) SABCD = (AD + BC)⋅BE = OM⋅BE ≤ OM⋅AB = 2R2
⇒ max SABCD = 2R2 ⇒ OM ⊥ AB
Bài 8. Cho đoạn thẳng AB và trung điểm O của AB. Trên cùng một nửa mặt phẳng bờ AB vẽ tia Ax, By vuông góc với AB. Trên các tia Ax và By lấy theo thứ tự hai điểm C và D sao cho ![\[\widehat {COD} = 90^\circ \]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-12.svg)
, kẻ OH ⊥ CD
a) Chứng minh rằng H thuộc đường tròn tâm O đường kính AB
b) Xác định vị trí tương đối của CD với đường tròn (O)
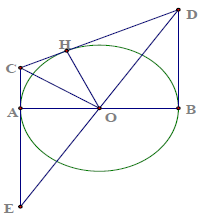
Hướng dẫn giải
a) Kéo dài DO cắt AC ở E, ta có:
∆AOE = ∆BOD (g.c.g)
⇒ ![\[\widehat E = \widehat D\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-13.svg)
; OD = OE
⇒ ∆OHD = ∆OAE (cạnh huyền – góc nhọn)
⇒ OH = OA = OB ⇒ H ∈ (O; AB)
b) Ta có: H thuộc đường tròn (O), CD ⊥ OH tại H
⇒ Khoảng cách từ O đến CD bằng bán kính của (O).
Vậy CD tiếp xúc với (O) tại H.
Bài 9. Cho điểm A cách đường thẳng xy một khoảng 12 cm
a) Chứng minh (A; 13cm) cắt đường thẳng xy tại hai điểm phân biệt.
b) Gọi hai giao điểm của (A; 13cm) với xy là B, C. Tính độ dài đoạn thẳng BC.
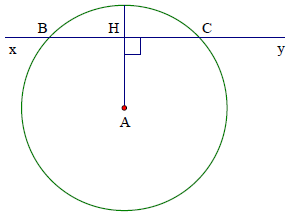
Hướng dẫn giải
a) Kẻ AH ⊥ xy ⇒ AH = 12 cm < R ⇒ (A) cắt xy tại hai điểm B và C
b) Tính được: BC = 2HC = 10 cm
Bài 10. Cho nửa đường tròn (O) đường kính AB. Lấy điểm C là điểm thuộc (O) và gọi d là tiếp tuyến qua C với với (O). Kẻ AE và BF cùng vuông góc với d; CH vuông góc với AB
a) Chứng minh: CE = CF và CH2 = AE⋅BF
b) Khi C di chuyển trên một nửa đường tròn, tìm vị trí của điểm C để EF có độ dài lớn nhất.
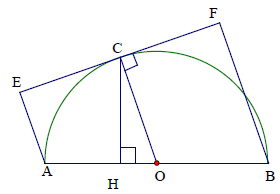
Hướng dẫn giải
a) Chứng minh được OC là đường trung bình của hình thang AEFB nên C là trung điểm của EF.
Chứng minh được: AE = AH, BH = BF
⇒ CH2 = HA⋅HB = AE⋅BF
b) Ta có: BF ∩ (O) = {H}
⇒ EF = AH ≤ AB ⇒ EFmax = AB
⇒ C là điểm chính giữa 
Dạng 3. Chứng minh tiếp tuyến của đường tròn
[content_4]Bài 1. Cho tam giác ABC đường cao AH. Chứng minh rằng BC là tiếp tuyến của đường tròn tâm A bán kính AH.
Hướng dẫn giải
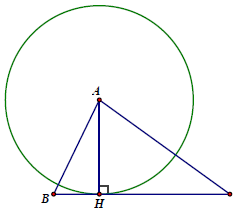
Cách 1: Sử dụng dấu hiệu về khoảng cách
Ta thấy khoảng cách từ tâm A của (A; AH) đến đường thẳng BC là AH
Suy ra BC là tiếp tuyến của (A; AH)
Cách 2: Sử dụng dấu hiệu vuông góc
Ta có: H là điểm chung của (A; AH) và BC
Lại có: BC ⊥ AH tại H. Suy ra BC là tiếp tuyến của (A; AH)
Bài 2. Cho hình thang vuông ABCD () có O là trung điểm của AB và góc . Chứng minh CD là tiếp tuyến của đường tròn đường kính
Hướng dẫn giải
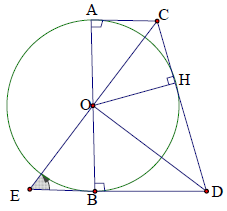
Kéo dài OC cắt BD tại E vì
Suy ra: ![\[\widehat {EOD} = 90^\circ \]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-17.svg)
Xét tam giác COD và ΔEOD ta có OD chung
![\[\frac{{OC}}{{OD}} = \frac{{OA}}{{OB}} = 1 \Rightarrow OC = OD\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-18.svg)
⇒ ΔCOD = ΔEOD.
Suy ra: DC = DE hay tam giác ECD cân tại D.
Kẻ OH ⊥ CD thì ΔOBD = ΔOHD ⇒ OH = OB
Mà OB = OA ⇒ OH = OB = OA hay A, H, B thuộc đường tròn (O).
Do đó CD là tiếp tuyến của đường tròn đường kính AB.
Bài 3. Cho hình vuông ABCD có cạnh bằng a. Gọi M, N là hai điểm trên các cạnh AB, AD sao cho chu vi tam giác AMN bằng 2a. Chứng minh đường thẳng MN luôn tiếp xúc với 1 đường tròn cố định.
Hướng dẫn giải
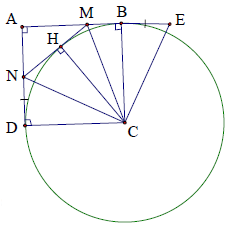
Trên tia đối của BA ta lấy điểm E sao cho BE = ND.
Ta có: ΔBCE = ΔDCN ⇒ CN = CE
Theo giả thiết ta có:
MN + AM + AN = AB + AD
= AM + MB + AN + DN
= AM + AN + MB + BE
Suy ra: MN = MB + BE = ME
Từ đó ta suy ra ΔMNC = ΔMEC
⇒ ![\[\widehat {CMN} = \widehat {CMB}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-19.svg)
Kẻ CH ⊥ MN ⇒ CH = CB = CD = a.
Vậy D, H, B thuộc đường tròn tâm C bán kính CB = a
Suy ra MN luôn tiếp xúc với đường tròn tâm C bán kính bằng a.
Bài 4. Cho tam giác ABC cân tại A đường cao BH. Trên nửa mặt phẳng chứa C bờ AB vẽ Bx ⊥ BA cắt đường tròn tâm B bán kính BH tại D. Chứng minh CD là tiếp tuyến của (B).
Hướng dẫn giải
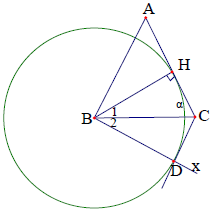
Vì tam giác ABC cân tại A nên ta có: ![\[\widehat B = \widehat C = \alpha \]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-20.svg)
Vì ![\[Bx{\text{ }} \bot {\text{ }}BA \Rightarrow \widehat {{B_2}} + \alpha = 90^\circ \]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-21.svg)
Mặt khác ta cũng có: ![\[\widehat {{B_1}} + \alpha = 90^\circ \Rightarrow \widehat {{B_1}} = \widehat {{B_2}}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-22.svg)
Hai tam giác ΔBHC và ΔBDC
Có BC chung, ![\[\widehat {{B_1}} = \widehat {{B_2}}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-23.svg)
, BH = BD = R
Suy ra ΔBHC và ΔBDC (c.g.c) suy ra ![\[\widehat {BHC} = \widehat {BDC} = 90^\circ \]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-24.svg)
Nói cách khác CD là tiếp tuyến của đường tròn (B).
Bài 5. Cho tam giác ABC vuông tại A (AB < AC) đường cao AH. Gọi E là điểm đối xứng với B qua H. Đường tròn tâm O đường kính EC cắt AC tại K. Chứng minh HK là tiếp tuyến của đường tròn (O).
Hướng dẫn giải
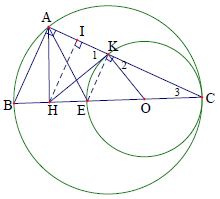
Vì tam giác EKC có một cạnh EC là đường kính của (O). Nên ![\[\widehat {EKC} = 90^\circ \]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-25.svg)
.
Kẻ HI ⊥ AC ⇒ BA // HI // EK
Suy ra AI = IK từ đó ta có tam giác AHK cân tại H.
Do đó: ![\[\widehat {{K_1}} = \widehat B\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-26.svg)
(cùng phụ với góc hai góc bằng nhau là ![\[\widehat {BAH},\widehat {IHK}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-27.svg)
).
Mặt khác ta cũng có: ![\[\widehat {{K_2}} = \widehat {{C_3}}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-28.svg)
(do tam giác KOC cân tại O).
Mà ![\[\widehat B + \widehat {{C_3}} = 90^\circ \Rightarrow \widehat {{K_1}} + \widehat {{K_2}} = 90^\circ \]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-29.svg)
Suy ra ![\[\widehat {HKO} = 90^\circ \]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-30.svg)
.
Hay HK là tiếp tuyến của (O).
Bài 6. Cho nửa đường tròn (O) đường kính AB. Qua điểm C thuộc nửa đường tròn, kẻ tiếp tuyến d của đường tròn. Gọi E và F lần lượt là chân các đường vuông góc kẻ từ A và B đến d. Gọi H là chân đường vuông góc kẻ từ C đến AB. Chứng minh:
a) CE = CF
b) AC là tia phân giác của góc ![\[\widehat {BAE}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-31.svg)
c) CH2 = AE⋅BF
Định hướng;
⋄ Tứ giác ABFE là hình thang và OC // AE // BF nên OC là đường trung bình của hình thang ABFE (vì O là trung điểm AB). Suy ra: CE = CF
⋄ Tam giác AOC cân tại O nên ![\[\widehat {CAO} = \widehat {OCA}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-32.svg)
và ![\[\widehat {CAE} = \widehat {ACO}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-33.svg)
do AE // OC. Suy ra: ![\[\widehat {CAE} = \widehat {CAB}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-34.svg)
⋄ Ta thấy: CH2 = AH⋅BH. Mà AE = AH, tương tự BF = BH. Suy ra: CH2 = AE⋅BF
Hướng dẫn giải
a) Ta có: AE ⊥ d, BF ⊥ d ⇒ AE // BF
Suy ra tứ giác AEFB là hình thang.
Lại có: O là trung điểm của AB và OC // AE // BF (vì OC ⊥ d).
⇒ C là trung điểm của EF ⇒ CE = CF
b) AE // OC ⇒ (2 góc so le trong) (1).
Mặt khác: OC = OA ⇒ ΔAOC cân tại O
⇒ (2)
Từ (1) và (2) suy ra ![\[\widehat {CAE} = \widehat {CAO}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-35.svg)
Suy ra AC là phân giác
c) Do C thuộc nửa đường tròn đường kính
⇒ OC = OA = OB = AB ⇒ ΔABC vuông tại C.
Áp dụng hệ thức lượng trong tam giác ABC vuông tại C, đường cao CH ta có: CH2 = AH⋅BH (3)
Xét ΔACE và ΔACH vuông ta có:
![\[\begin{gathered} \widehat {AEC} = \widehat {AHC} = 90^\circ \begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \widehat {CAE} = \widehat {CAH} \hfill \\ \end{gathered} \]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-36.svg)
Chung cạnh AC
⇒ ΔACE = ΔACH (cạnh huyền – góc nhọn)
Theo phần b ta có: ΔACE = ΔACH ⇒ AH = AE (4)
Tương tự ta có: BH = BF (5)
Từ (3), (4), (5) suy ra CH2 = AE⋅BF ⇒ đpcm
Bài 7. Cho ΔABC vuông tại A (AB < AC), đường cao AH. E là điểm đối xứng của B qua H. Vẽ đường tròn đường kính EC cắt AC tại K. Xác định vị trí tương đối của HK với đường tròn đường kính EC.
Hướng dẫn giải
Gọi I là tâm của đường tròn đường kính EC, I là trung điểm của EC.
Vì EC là đường kính của (I) và K thuộc (I) nên EK ⊥ KC.
Vì K ∈ AC ⇒ AC ⊥ EK
Mặt khác: ΔABC vuông tại A
⇒ AB ⊥ AC ⇒ AB // KE
Suy ra tứ giác ABEK là hình thang (dấu hiệu nhận biết hình thang).
Lấy M là trung điểm của AK. Vì E đối xứng với B qua H.
Suy ra: H là trung điểm của BE, suy ra HM là đường trung bình của hình thang ABEK
⇒ HM // EK mà EK ⊥ AC
⇒ HM ⊥ AC ⇒ HM ⊥ AK
HM vừa là đường cao vừa là đường trung tuyến của ΔAHK.
⇒ ΔAHK cân tại H
⇒ ![\[\widehat {HAK} = \widehat {AKH}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-37.svg)
(1)
Vì AK ⊥ EK, AH ⊥ BE ⇒ ![\[\widehat {HAK} = \widehat {KEI} = \widehat {EKI}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-38.svg)
Vì E và K thuộc (I) nên IK = IE
⇒ ΔKEI cân tại I
⇒ ![\[\widehat {KEI} = \widehat {EKI}\]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-39.svg)
(2)
Từ (1) và (2) ta có:
![\[\begin{gathered} \widehat {AKH} = \widehat {EKI}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \Rightarrow \widehat {HKI} = \widehat {HKE} + \widehat {EKI}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {}&{ = \widehat {AKH} + \widehat {HKE} = \widehat {AKE} = 90^\circ } \end{array}} \end{array}} \end{array} \hfill \\ \Rightarrow HK{\text{ }} \bot {\text{ }}IK\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \]](http://verbalearn.org/wp-content/uploads/2023/08/vi-tri-tuong-doi-cua-duong-thang-va-duong-tron-40.svg)
Vậy HK và đường tròn đường kính EC tiếp xúc với nhau.
