Tứ giác nội tiếp: Tổng quan lý thuyết và các dạng bài tập

Bài viết sau đây sẽ giúp bạn tìm hiểu định nghĩa, định lý và dấu hiệu nhận biết tứ giác nội tiếp. Ứng dụng giải các bài toán chứng minh góc bằng nhau, đoạn bằng nhau.

Tức giác nội tiếp — Định nghĩa, hệ quả và dấu hiệu nhận biết tứ giác nội tiếp

Lý thuyết tứ giác nội tiếp

[content_1]

Định nghĩa

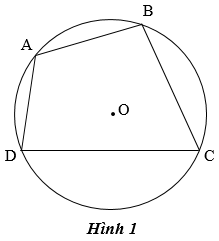
– Tứ giác nội tiếp đường tròn là tứ giác có bốn đỉnh nằm trên đường tròn đó.

– Trong Hình 1, tứ giác ABCD nội tiếp (O) và (O) ngoại tiếp tứ giác ABCD.

Định lí

– Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180°.

– Nếu một tứ giác có tổng số đo hai góc đổi diện bằng 180° thì tứ giác đó nội tiếp được đường tròn.

Dấu hiệu nhận biết tứ giác nội tiếp

– Tứ giác có tổng hai góc đổi bằng 180°.

– Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.

– Tứ giác có 4 đỉnh cách đều một điểm cố định (mà ta có thể xác định được). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác.

– Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc α.

Chú ý: Trong các hình đã học thì hình chữ nhật, hình vuông, hình thang cân nội tiếp được đường tròn.

Phân dạng bài tập

Dạng 1. Chứng minh tứ giác nội tiếp

[content_2]

Phương pháp giải

Để chứng minh tứ giác nội tiếp, ta có thể sử dụng một trong các cách sau:

Cách 1: Chứng minh tứ giác có tổng hai góc đôì bằng 180°.

Cách 2: Chứng minh tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc α.

Cách 3: Chứng minh tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.

Cách 4: Tìm được một điểm cách đều 4 đỉnh của tứ giác.

Bài tập vận dụng

Câu 1. Cho tam giác ABC nhọn, đường cao BM và CN cắt nhau tại H. Chứng minh các tứ giác AMHN và BNMC là những tứ giác nội tiếp.

Hướng dẫn giải

Xét tứ giác AMHN có:

$\widehat {AMH} + \widehat {ANH} = 90^\circ + 90^\circ = 180^\circ$

⇒ Đpcm

Xét tứ giác BNMC có:

$\widehat {BNC} = \widehat {BMC} = 90^\circ$

⇒ Đpcm

Câu 2. Cho tứ giác ABCD nội tiếp (O), M là điểm chính giữa của cung AB. Nối M với D, M với C cắt AB lần lượt ở E và P. Chứng minh PEDC là tứ giác nội tiếp.

Hướng dẫn giải

Ta có:

⇒ PEDC nội tiếp

Câu 3. Cho tam giác ABC nhọn nội tiếp đường tròn (O). M là điểm thuộc đường tròn. Vẽ MH vuông góc với BC tại H, vẽ MI vuông góc với AC. Chứng minh MIHC là tứ giác nội tiếp.

Hướng dẫn giải

Ta có: $\widehat {MIC} = \widehat {CHM} = 90^\circ$

⇒ MIHC nội tiếp (hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc vuông)

Dạng 2. Sử dụng tứ giác nội tiếp để chứng minh các góc bằng nhau, các đoạn thẳng bằng nhau, các đường thẳng song song hoặc đồng quy, các tam giác đồng dạng, …

[content_3]

Phương pháp giải

Sử dụng tính chất của tứ giác nội tiếp.

Bài tập vận dụng

Câu 1. Cho đường tròn (O) đường kính AB. Gọi H là điểm nằm giữa O và B. Kẻ dây CD vuông góc với AB tại H. Trên cung nhỏ AC lấy điểm E, kẻ CK ⊥ AE tại K. Đường thẳng DE cắt CK tại F. Chứng minh:

a) Tứ giác AHCK là tứ giác nội tiếp;

b) AH⋅AB = AD²;

c) Tam giác ACE là tam giác cân.

Hướng dẫn giải

a) Xét tứ giác AHCK có:

$\widehat {AHC} = \widehat {AKC} = 90^\circ$

⇒ AHCK là tứ giác nội tiếp

b) △ADB vuông tại D, có đường cao DH

⇒ AD² = AH⋅AB

(Tứ giác AKCH nội tiếp)

$\Rightarrow \widehat {EDC} = \widehat {KHC} \Rightarrow DF\parallel HK$ (H là trung điểm DC nên K là trung điểm FC)

⇒ Đpcm

Câu 2. Cho nửa (O) đường kính AB. Lấy M ∈ OA (M không trùng O và A). Qua M vẽ đường thẳng d vuông góc với AB. Trên d lấy N sao cho ON > R. Nối NB cắt (O) tại C. Kẻ tiếp tuyến NE với (O) (E là tiếp điểm, E và A cùng thuộc nửa mặt phẳng bờ d). Chứng minh:

a) Bốn điểm O, E, M, N cùng thuộc một đường tròn;

b) NE² = NC⋅NB;

c) $\widehat {NEH} = \widehat {NME}$ (H là giao điểm của AC và d);

d) NF là tiếp tuyến (O) với F là giao điểm của HE và (O).

Hướng dẫn giải

a) Ta có: $\widehat {OEN} = \widehat {NMO} = 90^\circ$

⇒ OMEN nội tiếp (hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc vuông)

⇒ Đpcm

⇒ △NEC ∼ △NBE (g.g)

⇒ Đpcm

c) △NCH ∼ △NMB (g.g)

⇒ NC⋅NB = NH⋅NM = NE²

⇒ △NEH ∼ △NME (c.g.c)

$\Rightarrow \widehat {NEH} = \widehat {EMN}$

d) $\widehat {EMN} = \widehat {EON}$ (tứ giác NEMO nội tiếp)

$\Rightarrow \widehat {NEH} = \widehat {NOE} \Rightarrow EH{\text{ }} \bot {\text{ }}NO$

⇒ △OEF cân tại O có ON là phân giác

$\Rightarrow \widehat {EON} = \widehat {NOF}$

⇒ △NEO = △NFO

Vậy $\widehat {NFO} = \widehat {NEO} = 90^\circ$

⇒ Đpcm

Câu 3. Cho đường tròn (O) đường kính AB, gọi I là trung điểm của OA, dây CD vuông góc với AB tại I. Lấy K tùy ý trên cung BC nhỏ, AK cắt CD tại H.

a) Chứng minh tứ giác BIHK là tứ giác nội tiếp.

b) Chứng minh AH⋅AK có giá trị không phụ thuộc vị trí điểm K.

c) Kẻ DN ⊥ CB, DM ⊥ Chứng minh các đường thẳng MN, AB, CD đồng quy.

Hướng dẫn giải

a) $\widehat {HIB} = \widehat {HKB} = 180^\circ$

⇒ Tứ giác BIHK nội tiếp

b) Chứng minh được: △AHI ∼ △ABK (g.g)

⇒ AH⋅AK = AI⋅AB = R² (không đổi)

c) Chứng minh được MCND là hình chữ nhật, từ đó ⇒ đpcm

Câu 4. Cho đường tròn (O; R) và điểm A cố định ngoài đường tròn. Qua A kẻ hai tiếp tuyến AM, AN với đường tròn (M, N là hai tiếp điểm). Một đường thẳng d đi qua A cắt đường tròn (O; R) tại B và C (AB < AC). Gọi I là trung điểm BC.

a) Chứng minh năm điểm A, M, N, O, I thuộc một đường tròn.

b) Chứng minh AM² = AB⋅

c) Đường thẳng qua B, song song với AM cắt MN tại E. Chúng minh IE song song MC.

d) Chứng minh khi d thay đổi quanh quanh điểm A thì trọng tâm G của tam giác MBC luôn nằm trên một đường tròn cố định.

Hướng dẫn giải

a) Chú ý: $\widehat {AMO} = \widehat {AIO} = \widehat {ANO} = 90^\circ$

⇒ △AMB ∼ △ACM (g.g)

⇒ Đpcm

c) AMIN nội tiếp

$\begin{gathered} \Rightarrow \widehat {AMN} = \widehat {AIN}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ BE\parallel AM \Rightarrow \widehat {AMN} = \widehat {BEN}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \Rightarrow \widehat {BEN} = \widehat {AIN}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered}$

⇒ Tứ giác BEIN nội tiếp

$\Rightarrow \widehat {BIE} = \widehat {BNM}$

Chứng minh được: $\widehat {BIE} = \widehat {BCM} \Rightarrow IE\parallel CM$

d) G là trọng tâm △MBC ⇒ G ∈ MI

Gọi K là trung điểm AO ⇒ MK = IK = $\frac{1}{2}$ AO

Từ G kẻ GG’ // IK (G’ ∈ MK)

$\Rightarrow \frac{{GG'}}{{IK}} = \frac{{MG}}{{MI}} = \frac{{MG'}}{{MK}} = \frac{2}{3}IK = \frac{1}{3}AO$ không đổi (1)

$MG' = \frac{2}{3}MK$ ⇒ G’ cố định (2)

Từ (1) và (2) có G thuộc $\left( {G';\frac{1}{3}AO} \right)$

Nâng cao phát triển tư duy

Câu 1. Cho hình hành ABCD có đỉnh D nằm trên đường tròn đường kính AB. Kẻ BN và DM cùng vuông góc với đường chéo AC. Chứng minh rằng:

a) Tứ giác CBMD là tứ giác nội tiếp.

b) Khi điểm D di động trên đường tròn thì $\widehat {BMD} + \widehat {BCD}$ không đổi.

c) DB⋅DC = DN⋅AC

Hướng dẫn giải

a) AB là đường kính đường tròn (O) $\Rightarrow \widehat {ADB} = 90^\circ$ mà $\widehat {ADB} = \widehat {DBC}$ (so le trong) $\Rightarrow \widehat {DBC} = 90^\circ$ .

Mặt khác: $\widehat {DMC} = 90$ suy ra: $\widehat {DMC} = \widehat {DBC} = 90^\circ$ do đó tứ giác CBMD nội tiếp đường tròn đường kính CD.

Nhận xét. Ngoài cách giải trên, chúng ta có thể giải theo hướng sau:

⋄ Ta có: $\widehat {MDB} = \widehat {DBN} = \widehat {DAN} = \widehat {MCB}$

Suy ra điều phải chứng minh.

⋄ Ta có: $\widehat {DMB} = \widehat {DNB};{\text{ }}\widehat {DAB} = \widehat {DCB}$

Mà: $\widehat {DAB} + \widehat {DNB} = 180^\circ$

Suy ra điều phải chứng minh.

b) Khi điểm D di động trên đường tròn (O) thì tứ giác CBMD luôn là tứ giác nội tiếp

Suy ra: $\widehat {BMD} + \widehat {BCD} = 180^\circ$ (điều phải chứng minh)

c) Do $\widehat {ANB} = 90^\circ$ thuộc (O)

Ta có: $\widehat {BDN} = \widehat {BAN}$ (góc nội tiếp) mà $\widehat {ACD} = \widehat {BAN}$ (so le trong)

$\Rightarrow \widehat {BDN} = \widehat {ACD}$

Mặt khác: $\widehat {DAC} = \widehat {DAN} = \widehat {DBN}$ (cùng chắn cung DN)

Suy ra: △ACD ∼ △BDN (g.g)

$\Rightarrow \frac{{AC}}{{BD}} = \frac{{CD}}{{DN}} \Rightarrow AC.DN = BD.CD$

Câu 2. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Các tiếp tuyến tại A của đường tròn (O) và (O’) cắt đường tròn (O’) và (O) theo thứ tự tại C và D. Gọi P và Q lần lượt là trung điểm của các dây AC và AD. Chứng minh rằng:

a) Hai tam giác ABD và CBA đồng dạng.

b) $\widehat {BQD} = \widehat {APB}$

c) Tứ giác APBQ nội tiếp.

Hướng dẫn giải

a) Áp dụng hệ quả góc tạo bởi tia tiếp tuyến và dây cung, ta có:

$\widehat {CAB} = \widehat {ADB};{\text{ }}\widehat {ACD} = \widehat {BAD}$

Suy ra: △ABD ∼ △CBA (g.g)

b) Vì △ABD ∼ △CBA, suy ra: $\frac{{AD}}{{CA}} = \frac{{BD}}{{BA}}$

Mà $DQ = \frac{{AD}}{2};AP = \frac{{AC}}{2}$

$\Rightarrow \frac{{BD}}{{BA}} = \frac{{DQ}}{{AP}}$

Lại có: $\widehat {QDB} = \widehat {PAB}$

Suy ra: △BQD ∼ △APB (c.g.c)

$\Rightarrow \widehat {BQD} = \widehat {APB}$

c) Ta có: $\widehat {AQB} + \widehat {BQD} = 180^\circ$

Mà $\widehat {BQD} = \widehat {APB} \Rightarrow \widehat {AQB} + \widehat {APB} = 180^\circ$

Suy ra tứ giác APBQ nội tiếp.

Câu 3. Cho hai vòng tròn (O₁) và (O₂) tiếp xúc ngoài nhau tại điểm T. Hai vòng tròn này nằm trong vòng tròn (O₃) và tiếp xúc với (O₃) tương ứng tại M và N. Tiếp tuyến chung tại T của (O₁) và (O₂) cắt (O₃) tại P. PM cắt vòng tròn (O₁) tại điểm thứ hai A và MN cắt (O₁) tại điểm thứ hai B. PN cắt vòng tròn (O₂) tại điểm thứ hai D và MN cắt (O₂) tại điểm thứ hai C.

a) Chứng minh rằng tứ giác ABCD là tứ giác nội tiếp.

b) Chứng minh rằng các đường thẳng AB, CD và PT đồng quy.

Hướng dẫn giải

a) Gọi O₁, T, O₂ thẳng hàng

Các tam giác cân O₁MB và O₃MN có chung góc M

Suy ra: △O₁MB ∼ △O₃MN

$\Rightarrow \frac{{MB}}{{MN}} = \frac{{M{O_1}}}{{M{O_3}}}$

Tương tự suy ra: △O₁MA ∼ △O₃MP

$\Rightarrow \frac{{MA}}{{MP}} = \frac{{M{O_1}}}{{M{O_3}}}$

Vậy $\frac{{MB}}{{MN}} = \frac{{MA}}{{MP}} \Rightarrow AB\parallel PN$

Tương tự ta có: CD // PM

Gọi E là giao điểm AB và CD

Tứ giác AEDP là hình bình hành

Ta có: $\widehat {EBC} = \widehat {PNM};{\text{ }}\widehat {ECB} = \widehat {PMN}$

Nên △EBC ∼ △PNM (g.g) (1)

$\Rightarrow \frac{{EB}}{{EC}} = \frac{{PN}}{{PM}}$

Ta có: $\widehat {PTA} = \widehat {PMT}$ và $\widehat {MPT}$ chung nên △PAT ∼ △PTM (g.g)

$\Rightarrow \frac{{PA}}{{PT}} = \frac{{PT}}{{PM}} \Rightarrow PD.PN = P{T^2}$

Tương tự ta có: PD⋅PN = PT²

⇒ PA⋅PM = PD⋅PN nên △PNM ∼ △PAD (c.g.c) (2)

Mà APDE là hình bình hành nên △EDA = △PAD (3)

Từ (1), (2), (3) suy ra: △EBC ∼ △EDA

$\Rightarrow \widehat {EBC} = \widehat {EDA}$

Do đó tứ giác ABCD nội tiếp

b) Gọi giao điểm của PT và AB là I. Tia IC cắt (O₂) tại D’

Ta có: IA⋅IB = IT² = IC⋅ID’ suy ra △IBC ∼ △ID’A

$\Rightarrow \widehat {IBC} = \widehat {ID'A}$

Do đó tứ giác ABCD’ nội tiếp, mà ABCD cũng nội tiếp

Nên D trùng D’

Vậy các đường thẳng AB, CD và PT đồng quy.

Câu 4. Từ điểm A nằm ngoài đường tròn tâm O kẻ hai tiếp tuyến AB và AC (B và C là các tiếp điểm). Gọi M là điểm bất kì trên cung nhỏ BC của đường tròn (O) (M khác B và C). Tiếp tuyến qua M cắt AB và AC tại E và F. Đường thẳng BC cắt OE và OF ở P và Q. Chứng minh rằng:

a) Tứ giác OBEQ, OCFP là các tứ giác nội tiếp.

b) Tứ giác PQFE là tứ giác nội tiếp.

c) Tỉ số $\frac{{PQ}}{{FE}}$ không đổi khi M di chuyển trên đường tròn.

Hướng dẫn giải

a) Ta có: EB, EM là tiếp tuyến nên $\widehat {EOM} = \frac{1}{2}\widehat {BOM}$

Ta có: FC, FM là tiếp tuyến nên

$\widehat {FOM} = \frac{1}{2}\widehat {COM} \Rightarrow \widehat {EOF} = \frac{1}{2}\widehat {BOC}$

Mặt khác: $\widehat {EOF} = \frac{1}{2}\widehat {BOC}$

Suy ra: $\widehat {EBQ} = \widehat {EOQ}$

Từ đó ta có O và B là hai đỉnh liên tiếp cùng nhìn EQ dưới một góc bằng nhau

Vậy OBEQ là tứ giác nội tiếp

Chứng minh tương tự ta có OCFP là tứ giác nội tiếp

b) OBEQ là tứ giác nội tiếp nên

$\begin{gathered} \widehat {OBE} + \widehat {OQE} = 180^\circ \hfill \\ \Rightarrow \widehat {OQE} = 90^\circ \Rightarrow \widehat {FQE} = 90^\circ \begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered}$

OCFP là tứ giác nội tiếp nên

$\begin{gathered} \widehat {OCF} + \widehat {OPF} = 180^\circ \hfill \\ \Rightarrow \widehat {OPF} = 90^\circ \Rightarrow \widehat {EPF} = 90^\circ \begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered}$

Suy ra: $\widehat {EPF} = \widehat {EQF} = 90^\circ$

Vậy tứ giác PQFE là tứ giác nội tiếp

c) Kẻ OH ⊥ BC

Ta có: PQFE là tứ giác nội tiếp

Suy ra: $\widehat {OPQ} = \widehat {EFO}$

Do đó: △OPQ ∼ △OFE (g.g)

$\Rightarrow \frac{{PQ}}{{EF}} = \frac{{OH}}{{OM}}$

Vì điểm A và (O) cố định nên OH và OM không đổi do đó tỉ số $\frac{{PQ}}{{FE}}$ không đổi khi M di chuyển trên đường tròn.

Câu 5. Cho tam giác ABC, D và E là các tiếp điểm của đường tròn nội tiếp với các cạnh AB và AC. Chứng minh đường phân giác trong của góc B, đường trung bình của tam giác song song với cạnh AB và đường thẳng DE đồng quy.

Hướng dẫn giải

Tứ giác ADOE nội tiếp $\Rightarrow \widehat {EAO} = \widehat {EDO}$

Gọi tia BO cắt tia DE tại H thì:

$\begin{gathered} \widehat {BHD} = 180^\circ - \widehat {HDB} - \widehat {HBD}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} = 180^\circ - 90^\circ - \frac{{\widehat A}}{2} - \frac{{\widehat B}}{2} = \frac{{\widehat C}}{2} \hfill \\ \hfill \\ \end{gathered} \end{array}} \end{array} \hfill \\ \end{gathered}$

Mặt khác: $\widehat {ACO} = \frac{{\widehat C}}{2}$ nên tứ giác EOCH nội tiếp

$\Rightarrow \widehat {OHC} = \widehat {OEC} = 90^\circ$

Hay BH vuông góc với CH

Gọi M là trung điểm của BC

Suy ra: MB = MC = MH ⇒ △BHM cân

$\Rightarrow \widehat {HBM} = \widehat {MHB} \Rightarrow \widehat {ABH} = \widehat {MHB}$

Suy ra: BH // AB

Suy ra điều phải chứng minh

Câu 6. Cho đường tròn (O; R) đường kính AB cố định và đường kính CD quay quanh điểm O. Các đường thẳng AC và AD cắt tiếp tuyến tại B của đường tròn theo thứ tự tại E và F.

a) Chứng minh rằng tứ giác CDFE nội tiếp đường tròn.

b) Gọi I là tâm đường tròn ngoại tiếp tứ giác CDFE. Chứng minh rằng điểm I di động trên đường thẳng cố định khi đường kính CD quay quanh điểm O.

Hướng dẫn giải

a) Ta có: $\widehat {ACD} = \widehat {ABD};{\text{ }}\widehat {ABD} = \widehat {AFB}$ nên $\widehat {ACD} = \widehat {AFB}$

Do đó tứ giác CDFE nội tiếp

b) Gọi I là tâm đường tròn ngoại tiếp tứ giác CDFE

Đường tròn (I) qua CD nên I thuộc trung trực của CD

Đường tròn (I) qua EF nên I thuộc trung trực của EF

Gọi H là trung điểm của EF

Do đó I là giao điểm hai đường trung trực của CD và EF

⇒ AO // HI hoặc trùng với HI (cùng vuông góc với EF) (1)

△AEF vuông có, AH là trung tuyến ứng với cạnh huyền nên HA = HE ⇒ △HAE cân tại H

$\Rightarrow \widehat {HAE} = \widehat {HEA} \Rightarrow \widehat {HAE} = \widehat {ADC}$

Mà $\widehat {ADC} + \widehat {ACD} = 90^\circ$

Nên $\widehat {HAE} + \widehat {ACD} = 90^\circ$

Suy ra: AH ⊥ CD

Mà OI ⊥ CD nên AH // OI (2)

Từ (1), (2) suy ra: tứ giác AOIH là hình bình hành

Do đó: IH = OA = R.

Suy ra: I cách EF một khoảng không đổi bằng R, nên I di động trên đường thẳng d song song với EF và cách EF một khoảng bằng R.

Câu 7. Cho tam giác ABC vuông tại A và D là một điểm trên cạnh AC (khác với A và C). Vẽ đường tròn tâm D tiếp xúc với BC tại E. Từ B kẻ tiếp tuyến thứ hai BF với đường tròn (D). Gọi M là trung điểm của BC, N là giao điểm của BF và AM. Chứng minh năm điểm A, B, E, D, F cùng nằm trên một đường tròn và AN = NF.

Hướng dẫn giải

Ta có: $\widehat {BFD} = \widehat {BED} = \widehat {BAD} = 90^\circ$

Do đó: B, E, D, A, F cùng thuộc một đường tròn đường kính BD

Trong △ABC vuông có AM là cạnh huyền nên MA = MC

⇒ △MAC cân tại M

$\Rightarrow \widehat {MAC} = \widehat {MCA}$

Xét đường tròn đi qua năm điểm A, B, E, D, F

Ta có: DE = DF nên

Xét $\widehat {NAF} = \widehat {MAC} + \widehat {DAF} = \widehat {MCA} + \widehat {DBF}$

$= \widehat {MCA} + \widehat {DBE} = \widehat {BDA} = \widehat {NFA}$

⇒ △NAF cân tại N ⇒ NF = NA

Câu 8. Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại hai điểm phân biệt A và B. Từ một điểm C thay đổi trên tia đối của tia AB, vẽ các tiếp tuyến CD, CE với đường tròn tâm O (D, E là các tiếp điểm và E nằm trong đường tròn tâm O’). Hai đường thẳng AD và AE cắt đường tròn tâm O’ lần lượt tại M và N (M, N khác với điểm). Đường thẳng DE cắt MN tại I. Chứng minh rằng:

a) MI⋅BE = BI⋅AE

b) Khi điểm C thay đổi thì đường DE luôn đi qua một điểm cố định.

Hướng dẫn giải

a) Ta có: $\widehat {BDE} = \widehat {BAE}$ (cùng chắn cung của đường tròn tâm O)

$\widehat {BDE} = \widehat {BMN}$ (cùng chắn cung của đường tròn tâm O’)

$\Rightarrow \widehat {BDE} = \widehat {BMN}$ hay $\widehat {BDI} = \widehat {BMN}$

⇒ Tứ giác BDMI nội tiếp

$\Rightarrow \widehat {MDI} = \widehat {MBI}$ (cùng chắn cung )

Mà $\widehat {MDI} = \widehat {ABE}$ (cùng chắn cung của đường tròn tâm O)

$\Rightarrow \widehat {ABE} = \widehat {MBI}$

Mặt khác: $\widehat {BMI} = \widehat {BAE}$

⇒ △MBI ∼ △ABE (g.g)

$\Rightarrow \frac{{MI}}{{AE}} = \frac{{BI}}{{BE}} \Rightarrow MI.BE = BI.AE$

b) Gọi Q là giao điểm của CO và DE

Ta có: OC ⊥ DE tại Q

⇒ △OCD vuông tại D, có đường cao là DQ nên OQ⋅OC = OD² = R² (1)

Gọi K là giao điểm của hai đường thẳng OO’ và DE, H là giao điểm của AB và OO’

Ta có: OO’ ⊥ AB tại H

Xét △KQO và △CHO, có:

$\left\{ \begin{gathered} \widehat O{\text{ }}chung \hfill \\ \widehat Q = \widehat H = 90^\circ \hfill \\ \end{gathered} \right.$

⇒ △KQO ∼ △CHO (g.g)

$\Rightarrow \frac{{KO}}{{CO}} = \frac{{OQ}}{{OH}} \Rightarrow OC \cdot OQ = KO \cdot OH{\text{ }}\left( 2 \right)$

Từ (1) và (2), suy ra: $KO \cdot OH = {R^2} \Rightarrow OK = \frac{{{R^2}}}{{OH}}$

Vì OH cố định và R không đổi nên OK không đổi. Do đó K cố định.

Câu 9. Cho đường tròn (O; R) và dây AB cố định, $AB = R\sqrt 2$ . Điểm P di động trên dây AB (P khác A và B). Gọi (C; R₁) là đường tròn đi qua P và tiếp xúc với đường tròn (O; R) tại A, (D; R₂) là đường tròn đi qua P và tiếp xúc với (O; R) tại B. Hai đường tròn (C; R₁) và (D; R₂) cắt nhau tại điểm thứ hai M.

a) Trong trường hợp P không trùng với trung điểm dây AB, chứng minh OM // CD và 4 điểm C, D, O, M cùng thuộc một đường tròn.

b) Chứng minh khi P di động trên dây AB thì điểm M di động trên đường tròn cố định và đường thẳng MP luôn đi qua một điểm cố định N.

c) Tìm vị trí của P để tích PM⋅PN lớn nhất? Diện tích tam giác AMB lớn nhất.

Hướng dẫn giải

a) Nối CP, PD

Ta có: A, C, O thẳng hàng; B, D, O thẳng hàng

Ta có: △ACP, △OAB lần lượt cân tại C, O nên

$\widehat {CPA} = \widehat {CAP} = \widehat {OBP}$

Do đó: CP // OD (1)

Tương tự ta có: OD // CP (2)

Từ (1) và (2) suy ra tứ giác ODPC là hình bình hành.

Gọi H là giao điểm của CD và MP, K là giao điểm của CD và OP.

Do đó K là trung điểm của OP.

Theo tính chất của hai đường tròn cắt nhau thì CD ⊥ MP

⇒ H là trung điểm của MP

Do đó: HK // OM ⇒ CD // OM

Giả sử: AP < BP

Vì tứ giác CDOM là hình bình hành nên OC = DP; DP = DM = R₂ nên tứ giác CDOM là hình thang cân.

Do đó 4 điểm C, D, O, M cùng thuộc một đường tròn

b) Ta có: OA² + OB² = 2R² = AB². Do đó △AOB vuông cân tại O.

Vì 4 điểm C, D, O, M cùng thuộc một đường tròn (kể cả M trùng O) nên $\widehat {COB} = \widehat {CMD}{\text{ }}\left( 1 \right)$

Ta có: $\widehat {MAB} = \widehat {MCD}$ (cùng bằng của đường tròn (C))

Vì $\widehat {MBP} = \widehat {MDC}$ (cùng bằng của đường tròn (D))

Do đó: △MAB ∼ △MCD (g.g)

$\Rightarrow \widehat {AMB} = \widehat {AOB} = 90^\circ$ mà $\widehat {CMD} = \widehat {COD}$ (tứ giác CDOM nối tiếp)

Do AB cố định nên điểm M thuộc đường tròn tâm I đường kính AB

Ta có: $\widehat {ACP} = \widehat {BDP} = \widehat {AOB} = 90^\circ$

$\Rightarrow \widehat {AMP} = \frac{1}{2}\widehat {ACP} = 45^\circ$ (góc nội tiếp và góc ở tâm của (C))

$\Rightarrow \widehat {BMP} = \frac{1}{2}\widehat {BCP} = 45^\circ$ (góc nội tiếp và góc ở tâm của (P))

Do đó: MP là tia phân giác của $\widehat {AMB}$

Mà $\widehat {AMB} = \widehat {AOB} = 90^\circ$ nên M thuộc đường tròn (I) ngoại tiếp tam giác AOB.

Giả sử MP cắt đường tròn (I) tại N và N là trung điểm cung không chứa điểm O nên N cố định.

c) Ta có: $\widehat {MPA} = \widehat {BPN};{\text{ }}\widehat {AMP} = \widehat {PBN}$ (góc nội tiếp cùng chắn một cung)

Do đó: △MAP ∼ △BNP (g.g)

$\begin{gathered} \Rightarrow \frac{{PA}}{{PN}} = \frac{{PM}}{{PB}} \Leftrightarrow PM \cdot PN = PA \cdot PB\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&\begin{gathered} \hfill \\ \hfill \\ \hfill \\ \end{gathered} \end{array} \leqslant {\left( {\frac{{PA + PB}}{2}} \right)^2} = \frac{{A{B^2}}}{4} = \frac{{{R^2}}}{2} \hfill \\ \end{gathered}$

Vậy PM⋅PN lớn nhất là $\frac{{{R^2}}}{2}$ khi PA = PB hay P là trung điểm của dây AB. Tam giác AMB vuông tại M nên:

${S_{AMB}} = \frac{1}{2}AM \cdot BM \leqslant \frac{1}{4}\left( {A{M^2} + B{M^2}} \right) = \frac{{A{B^2}}}{4} = \frac{{{R^2}}}{2}$

Vậy S_ABM lớn nhất là $\frac{{{R^2}}}{2}$ khi PA = PB hay P là trung điểm của dây AB.

Câu 10. Cho tam giác ABC (AB < AC) nội tiếp đường tròn (O) có AD là phân giác góc $\widehat {BAC}$ , tia AD cắt đường tròn tại điểm E (E khác A). Kẻ đường kính EF của đường tròn (O). Gọi P là một điểm nằm giữa A và D. Tia FP cắt đường tròn (O) tại Q khác F. Đường thẳng qua P vuông góc với AD cắt CA, AB lần lượt tại M, N.

a) Chứng minh rằng các tứ giác PQBN, PQCM là tứ giác nội tiếp.

b) Giả sử QN và PC cắt nhau tại một điểm thuộc đường tròn (O). Chứng minh rằng QM và PB cũng cắt nhau tại một điểm thuộc đường tròn (O).

Hướng dẫn giải

a) EF là đường kính nên $\widehat {EAF} = 90^\circ$

Mà AE ⊥ MN suy ra AF // MN

$\Rightarrow \widehat {QPN} = \widehat {QFA}$

Mà AFQB nội tiếp nên $\widehat {QFA} + \widehat {QBA} = 180^\circ$

$\Rightarrow \widehat {QPN} + \widehat {QBN} = 180^\circ$

Suy ra tứ giác PQBN nội tiếp

Lại có: $\widehat {QCA} = \widehat {QFA} \Rightarrow \widehat {QPN} = \widehat {QCM}$

Suy ra tứ giác PQCM nội tiếp

b) Giả sử QN và PC cắt nhau tại R thuộc (O)

Từ tứ giác PQBN nội tiếp suy ra:

$\widehat {NPB} = \widehat {NQB} = \widehat {BCP}$

Từ tứ giác PMCQ nội tiếp ta có:

$\begin{gathered} \widehat {PBC} = \widehat {RPB} - \widehat {PCB}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ \hfill \\ \end{gathered} \end{array} = \widehat {RPN} + \widehat {NPB} - \widehat {NPB} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ \hfill \\ \end{gathered} \end{array} = \widehat {RPN} = \widehat {MPC} = \widehat {MQC} \hfill \\ \end{gathered}$

Từ đó nếu QM cắt BP tại điểm S thì SBQC nội tiếp hay S thuộc đường tròn (O).

Câu 11. Cho tam giác ABC có 3 góc nhọn nội tiếp (O; R) có AB < AC. Vẽ 3 đường cao AD, BE, CF của tam giác ABC cắt nhau tại H, AD cắt (O) tại K và cắt EF tại I.

a) Chứng minh rằng: BC là trung trực của HK và IF⋅IE = IH⋅IA

b) Chứng minh rằng: Các tứ giác DHEC, BFIK nội tiếp được

c) Chứng minh rằng: $\frac{{KC}}{{AC}} + \frac{{BK}}{{BA}} = \frac{{EF}}{{AI}}$

d) Đường thẳng qua E song song với AD cắt BK tại M. Chứng minh rằng: 3 điểm F, D, M thẳng hàng.

Hướng dẫn giải

a) Ta có: $\widehat {BKA} = \widehat {ACB}$ (2 góc nội tiếp cùng chắn cung )

Mà $\widehat {ACB} = \widehat {BHK}$ (cùng phụ với góc $\widehat {EBC}$ )

$\Rightarrow \widehat {BKA} = \widehat {BHK}$

⇒ Tam giác BHK cân ⇒ BH = BK

Lập luận tương tự ta có: CH = CK

⇒ BC là trung trực của HK

Ta có: $\widehat {AEH} = \widehat {AFH} = 90^\circ$

⇒ Tứ giác AFHE nội tiếp

Xét tam giác AIE và tam giác FIH ta có:

$\widehat {AIE} = \widehat {FIH}$ (2 góc đối đỉnh)

$\widehat {IAE} = \widehat {IFH}$ (tứ giác AFHE nội tiếp)

⇒ △AIE ∼ △FIH (g.g)

$\Rightarrow \frac{{AI}}{{EI}} = \frac{{FI}}{{HI}} \Rightarrow AI \cdot HI = EI \cdot FI$

b) Xét tứ giác DHEC ta có:

$\widehat {HDC} = \widehat {BEC} = 90^\circ$

⇒ Tứ giác DHEC nội tiếp

Xét tứ giác BFEC ta có:

$\widehat {BFC} = \widehat {BEC} = 90^\circ$

⇒ Tứ giác BFEC nội tiếp

$\Rightarrow \widehat {AFE} = \widehat {ACB}$ mà $\widehat {ACB} = \widehat {AKB}$ (chứng minh trên)

$\Rightarrow \widehat {AFE} = \widehat {AKB}$

⇒ Tứ giác KBFI nội tiếp

c) Theo như trên ta đã có:

$\widehat {BKH} = \widehat {BHK}$ mà $\widehat {BHK} = \widehat {IHE}$ (2 góc đối đỉnh)

$\Rightarrow \widehat {BKH} = \widehat {IHE}$

Xét △HEI và △KAB ta có:

$\widehat {BKH} = \widehat {IHE}$ (chứng minh trên)

$\widehat {IHE} = \widehat {BAK}$ (tứ giác AFHE nội tiếp)

⇒ △HEI ∼ △KAB (g.g)

$\Rightarrow \frac{{KB}}{{AB}} = \frac{{HI}}{{EI}}$

Chứng minh tương tự ta có: $\frac{{KC}}{{AC}} = \frac{{HI}}{{FI}}$

Từ đó suy ra:

$\begin{gathered} \frac{{KB}}{{AB}} + \frac{{KC}}{{AC}} = IH\left( {\frac{1}{{EI}} + \frac{1}{{FI}}} \right) = IH \cdot \frac{{EI + EF}}{{EI \cdot FI}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \\ {} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{\begin{array}{*{20}{c}} {}&{} \end{array}} \end{array} = \frac{{IH \cdot EF}}{{AI \cdot HI}} = \frac{{EF}}{{AI}} \hfill \\ \end{gathered}$

(Theo chứng minh ở câu a ta có: IF⋅IE = IH⋅IA)

d) Ta có: $\widehat {BME} = \widehat {BKH}$ (2 góc ở vị trí đồng vị do HK // ME)

Mà $\widehat {BKH} = \widehat {BHK};{\text{ }}\widehat {BKH} = \widehat {BME}$ (2 góc ở vị trí đồng vị do HK // ME)

$\Rightarrow \widehat {BME} = \widehat {BEM}$

⇒ △BEM là tam giác cân

Ta có: AD ⊥ BC mà EM // BC ⇒ EM ⊥ BC

Trong tam giác cân BEM có BC là đường cao của tam giác (do BC ⊥ ME)

⇒ BC là trung trực của ME

Ta có: D nằm trên đường trung trực của ME ⇒ DM = DE

⇒ Tam giác DME là tam giác cân

$\Rightarrow \widehat {MDC} = \widehat {EDC}$

Xét tứ giác ABDE ta có: $\widehat {ADB} = \widehat {AEB} = 90^\circ$

⇒ Tứ giác ABDE nội tiếp

$\Rightarrow \widehat {EDC} = \widehat {BAC}$

Xét tứ giác AFDC ta có: $\widehat {AFC} = \widehat {ADC} = 90^\circ$

⇒ Tứ giác AFDC nội tiếp

$\Rightarrow \widehat {BAC} = \widehat {BDF}$

Từ đó suy ra: $\widehat {MDC} = \widehat {BDF}$ . Ta có:

$\begin{gathered} 180^\circ = \widehat {BDC} = \widehat {MDC} + \widehat {BDM}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ \hfill \\ \end{gathered} \end{array} = \widehat {BDF} + \widehat {BDM} = \widehat {FDM} \hfill \\ \end{gathered}$

⇒ Ba điểm F, D, M thẳng hàng

Câu 12. Cho tam giác ABC nhọn với AB < AC có AD là đường phân giác. Đường thẳng qua C song song với AD cắt đường trung trực của AC tại E. Đường thẳng qua B song song với AD cắt đường trung trực của AB tại F.

a) Chứng minh rằng tam giác ABF đồng dạng với tam giác ACE.

b) Chứng minh rằng các đường thẳng BE, CF, AD đồng quy tại một điểm, gọi điểm đó là G.

c) Đường thẳng qua G song song với AE cắt đường thẳng BF tại Q. Đường thẳng QE cắt đường tròn ngoại tiếp tam giác GEC và P khác E. Chứng minh rằng các điểm A, P, G, Q, F cùng thuộc một đường tròn.

Hướng dẫn giải

a) Ta có: △ABF, △ACE là tam giác cân tại F và E

Và $\widehat {FBA} = \widehat {BAD} = \widehat {DAC} = \widehat {ECA}$

⇒ △ABF ~ △ACE

b) Gọi G là giao điểm của BE và CF

Ta có: $\frac{{GF}}{{GC}} = \frac{{BF}}{{CE}} = \frac{{AB}}{{AC}} = \frac{{DB}}{{DC}}$

⇒ DG // BF

Mặt khác: DA // BF suy ra A, D, G thẳng hàng.

Suy ra điều phải chứng minh.

c) Ta có: $\widehat {BQG} = \widehat {QGA} = \widehat {GAE} = \widehat {GAC}$

$= \widehat {GAC} + \widehat {CAE} = \widehat {GAB} + \widehat {BAF} = \widehat {GAF}$

Suy ra AGQF là tứ giác nội tiếp

Mặt khác: $\widehat {QPG} = \widehat {GCE} = \widehat {GFQ}$ nên QGPF là tứ giác nội tiếp.

Suy ra điều phải chứng minh.

Câu 13. Cho 19 điểm nằm trong hay trên cạnh của một lục giác đều cạnh bằng 4 cm. Chứng minh rằng luôn tồn tại 2 trong số 19 điểm đã cho mà khoảng cách giữa chúng không vượt quá $\frac{{4\sqrt 3 }}{3}$ cm.

Hướng dẫn giải

Chia lục giác đều ABCDEF tâm O thành 6 tam giác đều cạnh 4cm (hình vẽ).

Theo nguyên lý Đi-rích-lê có ít nhất 4 điểm trong 19 điểm nằm trong hay trên cạnh một trong 6 tam giác đó. Không mất tính tổng quát giả sử tam giác đó là OAB.

Chia tam giác đều OAB trọng tâm G thành 3 tứ giác nội tiếp (hình vẽ) với GM ⊥ AB; GN ⊥ OB; GP ⊥ OA.

△OAB đều cạnh bằng 4 có đường cao

$\frac{{4\sqrt 3 }}{2} = 2\sqrt 3 \Rightarrow GA = \frac{{4\sqrt 3 }}{3}$

Các tứ giác GMBN, GMAP, GPON nội tiếp trong đường tròn đường kính GB, GA, GO đều bằng $\frac{{4\sqrt 3 }}{3}$

Theo nguyên lý Đi-rích-lê có ít nhất 2 điểm trong 4 điểm đang xét nằm trong hay trên cạnh một trong 4 tứ giác nói trên, giả sử tứ giác đó là GMBN.

⇒ Khoảng cách giữa hai điểm đó không vượt quá đường kính GB = $\frac{{4\sqrt 3 }}{3}$ của đường tròn ngoại tiếp tứ giác

⇒ Điều phải chứng minh.

Câu 14. Cho tam giác ABC (AB < AC) có các góc nhọn, nội tiếp trong đường tròn tâm O. Gọi M là trung điểm cạnh BC, E là điểm chính giữa của cung nhỏ BC, F là điểm đối xứng của E qua M.

a) Chứng minh rằng: EB² = EF⋅EO

b) Gọi D là giao điểm của AE và BC. Chứng minh các điểm A, D, O, F cùng thuộc một đường tròn.

c) Gọi I là tâm đường tròn nội tiếp tam giác ABC và P là điểm thay đổi trên đường tròn ngoại tiếp △IBC sao cho P, O, F không thẳng hàng. Chứng minh rằng tiếp tuyến tại P của đường tròn ngoại tiếp △POF đi qua một điểm cố định.

Hướng dẫn giải

a) Ta có: E, M, O, F thẳng hàng, ME = MF (E, F đối xứng qua M)

⇒ EF ⊥ BC

⇒ △BEF cân tại B

$\Rightarrow \widehat {BFE} = \widehat {FEB}$

Mặt khác: OB = OE suy ra △OBE cân tại O

$\Rightarrow \widehat {OBE} = \widehat {OEB}$

Ta có: $\widehat {BFE} = \widehat {FEB} = \widehat {OBE}$

⇒ △BEF ∼ △OEB (g.g)

$\Rightarrow \frac{{EB}}{{OE}} = \frac{{EF}}{{EB}} \Rightarrow E{B^2} = EF \cdot EO$

b) Không giảm tính tổng quát xét O nằm giữa M và F.

Dễ thấy △FBD ∼ △EAB (g.g)

$\Rightarrow \frac{{EB}}{{EA}} = \frac{{ED}}{{EB}} \Rightarrow E{B^2} = ED \cdot EA$

Ta có: $ED \cdot EA = EF \cdot EO\left( { = E{B^2}} \right)$

$\Rightarrow \frac{{EO}}{{EA}} = \frac{{ED}}{{EF}}$

Xét △EOD và △EAF có:

$\frac{{EO}}{{EA}} = \frac{{ED}}{{EF}}$ , $\widehat {OED}$ chung

⇒ △EOD ∼ △EAF (c.g.c)

$\Rightarrow \widehat {EOD} = \widehat {EAF}$ , dẫn đến tứ giác DAFO nội tiếp.

Vậy các điểm A, D, O, F cùng thuộc một đường tròn.

c) $\widehat {EIB} = \widehat {ABI} + \widehat {BAI};{\text{ }}\widehat {ABI} = \widehat {IBC};{\text{ }}\widehat {BAI} = \widehat {CBE}$

$\Rightarrow \widehat {EBI} = \widehat {IBC} + \widehat {CBE} = \widehat {ABI} + \widehat {BAI} = \widehat {EIB}$

⇒ △EBI cân tại E ⇒ EB = EI

Mà EB = EC nên EB = EI = EC

⇒ E là tâm đường tròn nội tiếp tam giác IBC.

Do đó EP = EB nên EP² = EF⋅EO

Xét △EPO và △EFP, có:

$\frac{{EP}}{{EF}} = \frac{{EO}}{{EP}}$ , $\widehat {PEO}$ chung

⇒ △EPO ∼ △EFP (c.g.c)

$\Rightarrow \widehat {EPO} = \widehat {EFP}$

⇒ EP là tiếp tuyến của đường tròn ngoại tiếp tam giác POF.

Vậy tiếp tuyến của đường tròn ngoại tiếp tam giác POF đi qua điểm E cố định.

Bài tập

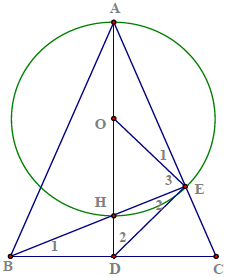
Câu 1. Cho tam giác ABC cân tại A, các đường cao AD, BE cắt nhau tại H. Gọi O là tâm đường tròn ngoại tiếp tam giác △AHE

a) Tứ giác CEHD nội tiếp

b) A, E, D, B cùng nằm trên một đường tròn

c) ED = $\frac{1}{2}$ BC

d) DE là tiếp tuyến của đường tròn (O)

e) Tính DE biết DH = 2 cm, AH = 6 cm

Hướng dẫn giải

a) Ta có: $\widehat {BEC} = \widehat {ADC} = 90^\circ$

⇒ Tứ giác CEHD nội tiếp

b) Ta có: $\widehat {AEB} = \widehat {ADB} = 90^\circ$

⇒ Tứ giác AEDB nội tiếp (hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc vuông)

⇒ Đpcm

c) △ABC cân tại △ABC, AD là đường cao

⇒ AD là đường trung trực

⇒ D là trung điểm của BC △BEC có ED là đường trung tuyến

⇒ ED = $\frac{1}{2}$ BC

d) Ta có: O là tâm đường tròn ngoại tiếp △AHE

⇒ O là trung điểm của AH

$\Rightarrow OA = OE \Rightarrow \widehat {{A_1}} = \widehat {{E_1}}\left( 1 \right)$

△BDE cân tại D $\Rightarrow \widehat {{B_1}} = \widehat {{E_3}}$

Mà $\widehat {{B_1}} = \widehat {{A_1}}$ (phụ $\widehat C$ ) $\Rightarrow \widehat {{E_1}} = \widehat {{E_3}}$

Lại có: $\widehat {{E_1}} + \widehat {{E_2}} = 90^\circ$

$\Rightarrow \widehat {{E_2}} + \widehat {{E_3}} = 90^\circ \Rightarrow \widehat {OED} = 90^\circ$

⇒ DE ⊥ OE tại E

e) Ta có: AH = 6 ⇒ OH = OE = 3;

HD = 2 ⇒ OD = 5

△OED vuông tại E ⇒ DE = 4 cm

Câu 2. Cho tam giác có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt (O) lần lượt tại M, N, P. Kẻ đường kính AK, I là trung điểm của BC. Chứng minh rằng:

a) Tứ giác CEHD, BCEF nội tiếp và ba điểm H, I, K thẳng hàng

b) Chứng minh tứ giác BMKC là hình thang cân

c) OH cắt AI tại G. Chứng minh G là trọng tâm của tam giác ABC

d) AE⋅AC = AH⋅AD; AD⋅BC = BE⋅AC

AE⋅AC = FA⋅BA (△AFE ∼ △ABC)

e) H và M đối xứng nhau qua BC

f) Xác định tâm đường tròn nội tiếp △DEF

g) Chứng minh MN // EF và OA ⊥ EF

h) Chứng minh bán kính đường tròn ngoại tiếp của tam giác AEF và diện tích hình tròn (AEF) không đổi khi A di động trên cung lớn BC

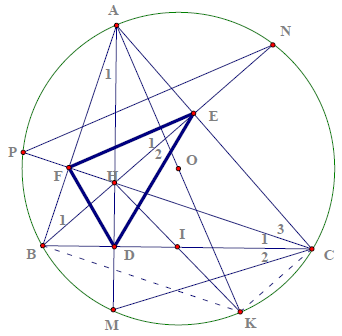
Hướng dẫn giải

a) Xét tứ giác CEHD, có: $\widehat E = \widehat D = 90^\circ \Rightarrow \widehat E + \widehat D = 180^\circ$

⇒ Đpcm

Tứ giác BHCK là hình bình hành ⇒ I là trung điểm của HK

b) Ta có: MK // BC ⇒ Tứ giác BMKC là hình thang

Lại có: BC là đường trung trực của HM

⇒ CH = CM mà CH = BK ⇒ CM = BK

Hình thang BMCK có hai đường chéo bằng nhau nên là hình thang cân

c) Ta có: G là trọng tâm tam giác AHK

⇒ GI = $\frac{1}{3}$ AI

Xét △ABC có AI là trung tuyến và GI = $\frac{1}{3}$ AI

⇒ G là trọng tâm △ABC

d) △AEH ∼ △ADC (g.g)

⇒ AE⋅AC = AH⋅AD

△BEC ∼ △ADC (g.g)

⇒ AD⋅BC = BE⋅AC

e) Ta đi chứng minh CB là đường trung trực của HM

Có: $\widehat {{C_1}} = \widehat {{A_1}}$ (phụ $\widehat {ABC}$ );

⇒ CB là phân giác của $\widehat C$

Mà CB ⊥ HM ⇒ △CHM cân tại C nên CB là đường trung trực của HM

f) Ta có tứ giác BCEF nội tiếp

Ta có tứ giác CEHD nội tiếp

$\Rightarrow \widehat {{E_1}} = \widehat {{E_2}}$ ⇒ EB là phân giác $\widehat {FED}$

Chứng minh tương tự, ta có FC là phân giác của $\widehat F$

Từ (1) và (2) ⇒ OA ⊥ EF

h) Chứng minh được tứ giác BHCK là hình bình hành (các cạnh đối song song)

Xét △AHK, có OI là đường trung bình của △AHK

O, I cố định nên OI không đổi ⇒ AH không đổi.

Vậy bán kính đường tròn ngoại tiếp △AEF không đổi.

Tứ giác AEHF nội tiếp đường tròn đường kính AH ⇒ △AEF nội tiếp đường tròn đường kính AH

S_AEF = π⋅OI² (không đổi).

Câu 3. Cho đường tròn (O; R) từ một điểm A trên (O) kẻ tiếp tuyến d với (O). Trên đường thẳng d lấy điểm M bất kỳ (M khác A) kẻ cát tuyến MNP và gọi K là trung điểm của NP, kẻ tiếp tuyến MB, B là tiếp điểm). Kẻ AC ⊥ MB, BD ⊥ MA gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB

a) Tứ giác AMBO nội tiếp

b) O, K, A, M, B cùng nằm trên một đường tròn

c) OI⋅OM = R²; OI⋅IM = IA²

d) Tứ giác OAHB là hình thoi

e) O, H, M thẳng hàng

f) Tìm quỹ tích điểm H khi M di chuyển trên đường thẳng d

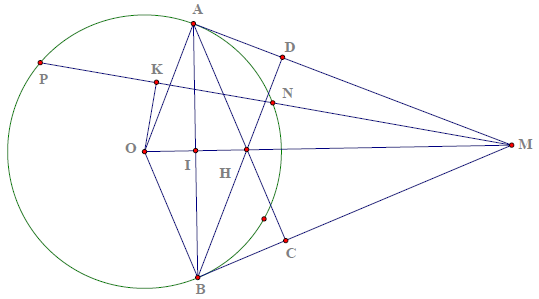
Hướng dẫn giải

a) Ta có: $\widehat {OAM} = \widehat {OBM} = 90^\circ$

⇒ Tứ giác AMBO nội tiếp

b) Ta có: K là trung điểm của NP ⇒ OK ⊥ NP

Lại có: A, B, K cùng nhìn OM dưới 1 góc 90°

⇒ K nằm trên đường tròn đường kính OM.

Vậy 5 điểm cùng nằm trên 1 đường tròn

c) Ta có: MA = MB (tính chất hai tiếp tuyến);

OA = OB = R ⇒ OM là đường trung trực của AB

⇒ OM ⊥ AB ≡ I

Xét △OAM vuông tại A

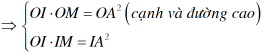
d) $\left\{ \begin{gathered} OB\parallel AH\left( { \bot BM} \right) \hfill \\ OA\parallel BH\left( { \bot AM} \right) \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} OA = OB \hfill \\ HA = HB \hfill \\ \end{gathered} \right.$

⇒ OAHB là hình thoi

e) Tứ giác OAHB là hình thoi

⇒ OH ⊥ AB, OM ⊥ AB

⇒ O, H, M thẳng hàng

Vì qua O chỉ có 1 đường thẳng vuông góc với AB

f) Theo chứng minh trên tứ giác OAHB là hình thoi

⇒ AH = AO = R

Vậy khi M di động trên d thì H di động nhưng luôn cách A cố định 1 khoảng bằng R.

Do đó quỹ tích của H khi M di chuyển trên đường thẳng d là nửa đường tròn tâm A bán kính AH = R.

Câu 4. Cho đường tròn (O; R) đường kính AB. Kẻ tiếp tuyến Ax và lấy trên tiếp tuyến đó một điểm P sao cho AP > R, từ P kẻ tiếp tuyến tiếp xúc với (O) tại M.

a) Tứ giác APMO nội tiếp

b) BM // OP

c) Đường thẳng vuông góc với AB tại O cắt tia BM tại N. Chứng minh rằng: tứ giác OBNP là hình bình hành.

d) Biết AN cắt OP tại K, PM cắt ON tại I, PN và OM kéo dài cắt nhau tại I. Chứng minh rằng: I, J, K thẳng hàng

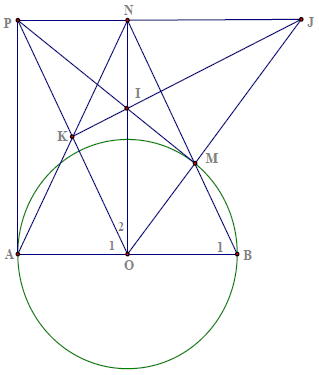
Hướng dẫn giải

a) (tính chất hai tiếp tuyến)

Mà hai góc ở vị trí đồng vị ⇒ BN // OP ⇒ đpcm

b) △AOP = △OBN (g.c.g) ⇒ OP = BN

Vậy tứ giác OBNP là hình bình hành

c) Ta có: PN // OB ⇒ PJ // AB

Mà ON ⊥ AB ⇒ ON ⊥ PJ

Lại có: PM ⊥ OJ

Mà ON ∩ PM ≡ I ⇒ I là trực tâm △PJO

Tứ giác PNOA là hình chữ nhật

$\Rightarrow \left\{ \begin{gathered} KO = KP \hfill \\ \widehat {APO} = \widehat {NOP}\left( {so{\text{ }}le{\text{ }}trong} \right) \hfill \\ \end{gathered} \right.$

Có: PO là phân giác $\widehat {APM}$ ⇒ △IOP cân tại I

IK là đường trung tuyến nên là đường cao ⇒ IK ⊥ OP

Xét △OPJ, I là trực tâm, mà IK ⊥ OP ⇒ I, J, K thẳng hàng.

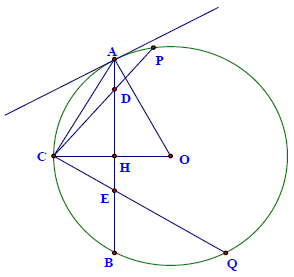
Câu 5. Cho đường tròn (O), dây AB. C là điểm chính giữa cung nhỏ AB. Lấy các điểm D, E thuộc dây AB (D nằm giữa A, E). Tia CD, CE cắt (O) lần lượt tại P, Q.

a) Chứng minh rằng tứ giác PQED nội tiếp được

b) Nếu AD = BE thì tứ giác PQED là hình gì?

c) Chứng minh rằng: CA² = CP⋅CD

d) Xác định vị trí tương đối của đường thẳng AC với đường tròn ngoại tiếp tam giác ADP.

Hướng dẫn giải

a) Xét (O) có C là điểm chính giữa cung nhỏ (gt)

Ta có: 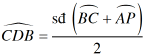(góc có đỉnh bên trong đường tròn)

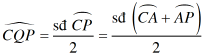(góc nội tiếp)

$\Rightarrow \widehat {CDB} = \widehat {CQP}$

Ta có: $\widehat {CDB} + \widehat {BDP} = 180^\circ$ (kề bù)

Mà $\widehat {CDB} = \widehat {CQP}$ (chứng minh trên)

$\Rightarrow \widehat {CQP} + \widehat {BQP} = 180^\circ$

Hay $\widehat {EQP} + \widehat {CDP} = 180^\circ$

Xét tứ giác PQED có:

$\widehat {EQP} + \widehat {EDP} = 180^\circ$

⇒ Tứ giác PQED nội tiếp đường tròn

b) Gọi H là giao điểm của OC và AB

– Xét (O) có: OC là đường kính, C là điểm chính giữa cung nhỏ AB (gt)

⇒ H là trung điểm của dây AB và OC ⊥ AB ⇒ AH = BH

Ta lại có: AD = EB ⇒ HD = HE

– Vì OC ⊥ AB; HD = HE (chứng minh trên)

⇒ CH là đường trung trực của AB

⇒ CD = CE ⇒ △CDE cân tại C

$\Rightarrow \widehat {CDE} = \widehat {CED} \Rightarrow \widehat {EDP} = \widehat {DEQ}{\text{ }}\left( 1 \right)$

– Vì $\widehat {CDE} = \widehat {CQP};{\text{ }}\widehat {CDE} = \widehat {CED}$ (chứng minh trên)

$\Rightarrow \widehat {CED} = \widehat {CQP} \Rightarrow DE\parallel PQ$

⇒ Tứ giác PQED là hình thang (2)

Từ (1), (2) ⇒ Tứ giác PQED là hình thang cân (dấu hiệu nhận biết)

– Xét (O), có:

(góc nội tiếp);

$\Rightarrow \widehat {CAB} = \widehat {APC}$

– Xét △CAD, △CPA có:

$\widehat C$ chung

$\widehat {CAD} = \widehat {CPA}$

⇒ △CAD ∼ △CPA (g.g)

$\Rightarrow \frac{{CA}}{{CP}} = \frac{{CD}}{{CA}} \Rightarrow C{A^2} = CP \cdot CD$

d) Chứng minh định lý đảo của định lý về góc tạo bởi tia tiếp tuyến và dây cung, cụ thể là: Nếu góc $\widehat {BAx}$ (với đỉnh A nằm trên một đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn. Hình minh họa.

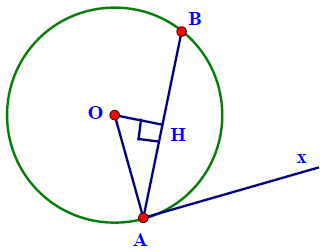
Chứng minh:

Kẻ OH là tia phân giác của $\widehat {AOB}$

Vì OA = OB ⇒ △AOB cân tại O nên OH đồng thời là đường cao của tam giác AOB

$\Rightarrow OH{\text{ }} \bot {\text{ }}AB;{\text{ }}\widehat {OHA} = 90^\circ$

Xét △AOH vuông tại H có: $\widehat {HOA} + \widehat {OAH} = 90^\circ$ (tính chất)

Ta lại có: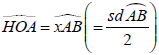

$\Rightarrow \widehat {OAH} + \widehat {xAB} = 90^\circ \Rightarrow OA{\text{ }} \bot {\text{ }}Ax$

⇒ Ax là tia tiếp tuyến (O)

Chứng minh: Xét đường tròn ngoại tiếp tam giác ADP, có: (góc nội tiếp)

Mà $\widehat {CAD} = \widehat {APD}$ (chứng minh trên) nên theo định lý đảo của định lý về góc tạo bởi tia tiếp tuyến và dây cung ta có AC là tiếp tuyến của đường tròn ngoại tiếp tam giác ADP.

Câu 6. Cho đường tròn (O) đường kính AB, các điểm C và D thuộc (O) sao cho CD không cùng thuộc một nửa mặt phẳng bờ AB, đồng thời AD > AC. Gọi M, N lần lượt là điểm chính giữa cung AC, AD, MN cắt AC, AD lần lượt tại H, I. MD cắt CN tại K

a) Chứng minh rằng tam giác NKD và tam giác MAK cân

b) KH // AD

c) So sánh $\widehat {CAK} = \widehat {DAK}$

d) Tìm một hệ thức giữa số đo cung AC, số đo AD là điều kiện cần và đủ để AK // ND.

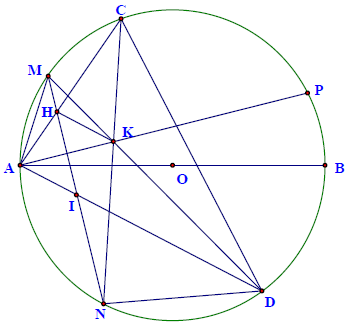
Hướng dẫn giải

a) Xét đường tròn (O), có:

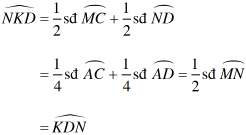
⇒ △NKD cân tại N

Xét △CAD có CN, DM là phân giác góc C và D

⇒ K là giao điểm của 3 đường phân giác

⇒ AK cắt (O) tại P

⇒ PC = PD

Xét (O), có:

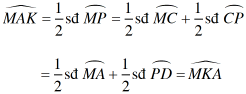
⇒ △MAK cân tại M

b) Xét △MAD có MI là phân giác

$\Rightarrow \widehat {HMK} = \widehat {HMA} = \widehat {HCK}$

⇒ Tứ giác MCKH nội tiếp

$\Rightarrow \widehat {MKH} = \widehat {MCH} = \widehat {MDA} \Rightarrow HK\parallel AD$

c) Vì AP là phân giác $\widehat {CAD}$

$\Rightarrow \widehat {CAK} = \widehat {DAK}$

d) △AMK cân tại M có AN là đường phân giác ⇒ MN ⊥ AK

Để AK // ND ⇒ MN ⊥ ND

⇒ MD là đường kính

Câu 7. Cho đường tròn (O; R) và (O’; R’) có R > R’ tiếp xúc ngoài nhau tại C. Gọi AC và BC là hai đường kính đi qua điểm C của (O) và (O’). DE là dây cung của (O) vuông góc với AB tại trung điểm M của AB. Gọi giao điểm thứ hai của DC với (O’) là F, BD cắt (O’) tại G. Chứng minh rằng:

a) Tứ giác MDGC nội tiếp

b) M, D, B, F cùng nằm trên một nửa đường tròn

c) Tứ giác ADBE là hình thoi

d) B, E, F thẳng hàng

e) DF, EG, AB đồng quy

f) MF = $\frac{1}{2}$ DE

g) MF là tiếp tuyến của đường tròn (O’)

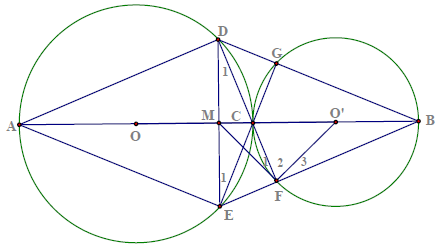
Hướng dẫn giải

a) Ta có: $\widehat {DMC} = \widehat {DGC} = 90^\circ$

⇒ Tứ giác MDGC nội tiếp

b) Ta có: $\widehat {DMB} = \widehat {DFB} = 90^\circ$

⇒ Tứ giác MDBF nội tiếp (hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc vuông)

⇒ M, D, B, F cùng nằm trên một nửa đường tròn

c) M là trung điểm của AB, mà DE ⊥ AB ≡ M

⇒ M là trung điểm của DE (đường kính và dây)

Nên ADBE là hình thoi (hai đường chéo vuông góc tại trung điểm của mỗi đường).

d) Ta có: AD // EB (tính chất hình thoi), AD ⊥ DF (góc nội tiếp)

⇒ BE ⊥ DF ≡ F

Lại có: BF ⊥ DF, mà qua B chỉ có 1 đường thẳng ⊥ DF

⇒ B, E, F thẳng hàng

e) Xét △BDE có C là trực tâm

⇒ EC ⊥ BD, CG ⊥ DB

⇒ E, C, G thẳng hàng.

Vậy DF, EG, AB đồng quy

f) △DEF vuông tại

⇒ MF = $\frac{1}{2}$ DE (đpcm)

g) MF = MD ⇒ △MDF cân tại M

$\Rightarrow \widehat {{D_1}} = \widehat {{F_1}}$

△O’BE cân tại O’

$\Rightarrow \widehat {{B_1}} = \widehat {{F_3}}$ mà $\widehat {{B_1}} = \widehat {{D_1}}$ (phụ $\widehat {DEB}$ )

Vậy $\widehat {{F_1}} = \widehat {{F_3}} \Rightarrow \widehat {{F_1}} + \widehat {{F_2}} = \widehat {{F_2}} + \widehat {{F_3}} = 90^\circ$

⇔ MF ⊥ O’F ⇒ MF là tiếp tuyến của (O’).

Câu 8. Cho nửa đường tròn đường kính AB. Từ A và B kẻ hai tiếp tuyến Ax, By. Qua M thuộc nửa đường tròn kẻ tiếp tuyến thứ 3 cắt các tiếp tuyến Ax, By tại C và D. Các đường thẳng AD, BC cắt nhau tại N. Nối MA cắt CO tại D, nối MB cắt OD tại F.

a) OEMF là hình chữ nhật

b) AC + BD = CD

c) Khi M chuyển động trên nửa đường tròn thì AC⋅BD không đổi (hoặc lớp B thì $AC \cdot BD = \frac{{A{B^2}}}{4}$ )

d) AB là tiếp tuyến của đường tròn đường kính CD

e*) MN ⊥ AB

f) Cho $BD = R\sqrt 3$ tính AM

g*) Gọi H là giao điểm của MN với AB, Chứng minh rằng khi M di động trên nửa đường tròn thì đường tròn ngoại tiếp △HEF luôn đi qua điểm cố định

h) Xác định vị trí của điểm M để chu vi tứ giác ACDB đạt GTNN

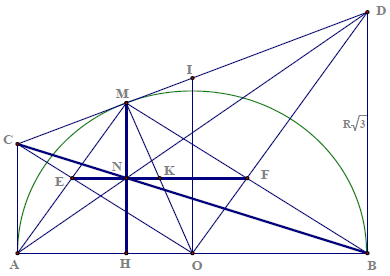
Hướng dẫn giải

a) OM = OA = R

CM = CA (tính chất hai tiếp tuyến)

⇒ OC là đường trung trực của AM $\Rightarrow \widehat E = 90^\circ$

Chứng minh tương tự: $\widehat F = 90^\circ$ ⇒ OEMF là hình chữ nhật

b) AC + BD = CM + MD = CD

c) Xét △COD vuông tại O

⇒ MC⋅MD = OM²

⇔ AC⋅BD = OM² = R² (không đổi)

d) Gọi I là trung điểm của CD

⇒ I là tâm đường tròn ngoại tiếp △COD đường kính CD, bán kính OI

Ta có: AC ⊥ AB, BD ⊥ AB ⇒ AC // BD

⇒ Tứ giác ACDB là hình thang, mà I là trung điểm CD

⇒ OI là đường trung bình của hình thang ACDB

⇒ OI // AC và AC ⊥ AB ⇒ OI ⊥ AB

⇒ AB là tiếp tuyến của đường tròn đường kính CD.

e) Ta có: AC // BD

$\Rightarrow \frac{{CN}}{{NB}} = \frac{{AC}}{{BD}} \Leftrightarrow \frac{{CN}}{{AB}} = \frac{{CM}}{{DM}}$

⇒ MN // BD, BD ⊥ AB

⇒ MN ⊥ AB

f) Xét △BOD vuông tại B

$\begin{gathered} \Rightarrow \tan \widehat {BOD} = \frac{{BD}}{{BO}} = \sqrt 3 \Rightarrow \widehat {BOD} = 60^\circ \begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ AM\parallel OD \Rightarrow \widehat {MAB} = \widehat {BOD} = 60^\circ \hfill \\ \end{gathered}$

Xét △MAB vuông tại M

$AM = AB \cdot \cos \widehat {MAB} = 2R \cdot \cos 60^\circ = R\left( {cm} \right)$

g) Gọi K là giao điểm của OM và EF

⇒ KO = KM = KE = KF

Xét △MHO vuông tại H

⇒ KH = KM = KO

⇒ KH = KO = KE = KF

⇒ Đường tròn ngoại tiếp △HEF luôn đi O cố định.

h) Ta có chu vi tứ giác ABDC là

C_ABCD = AB + BD + CD + AC

Mà AC + BD = CB = CD

⇒ C_ABCD = AB + 2CD

⇒ CD phải nhỏ nhất (AB cố định)

⇒ Khi CD là khoảng cách giữa Ax và By ta có CD là khoảng cách giữa Ax và By tức là CD ⊥ AC khi đó CD // AB.

⇒ M là trung điểm của cung .

Câu 9. Cho điểm B nằm giữa hai điểm A, C. Vẽ đường thẳng d vuông góc với AC tại A. Vẽ (O) đường kính BC và trên đó lấy một điểm M bất kỳ. Tia CM cắt d tại D, tia AM cắt (O) tại điểm thứ hai N. Tia DB cắt (O) tại điểm thứ hai P

a) Chứng minh rằng tứ giác ABMD, APCD nội tiếp được

b) Chứng minh CM CD. không phụ thuộc vào vị trí điểm M trên (O)

c) Tứ giác APND là hình gì? Vì sao?

d) Chứng minh trọng tâm G của tam giác MAC chạy trên một đường tròn cố định khi điểm M di chuyển trên đường tròn (O).

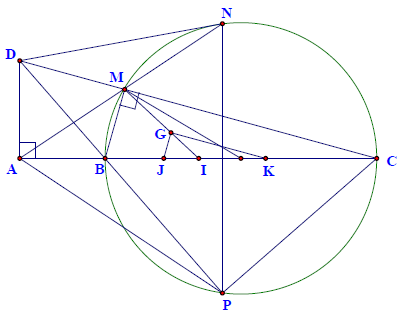
Hướng dẫn giải

a) Ta có: $\widehat {BMC} = 90^\circ \Rightarrow \widehat {BMD} = 90^\circ$

$\Rightarrow \widehat {BMD} + \widehat {DAB} = 180^\circ$

⇒ Tứ giác ABMD là tứ giác nội tiếp đường tròn.

Ta lại có: $\widehat {DPC} = 90^\circ$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow \widehat {DAC} + \widehat {DPC} = 90^\circ$

⇒ Tứ giác APCD là tứ giác nội tiếp đường tròn.

b) Vì △CMB ∼ △CAD (g.g)

$\Rightarrow \frac{{CM}}{{CA}} = \frac{{CB}}{{CD}} \Rightarrow CM \cdot CD = CA \cdot CB$

Mà các điểm C, A, B cố định nên CA⋅CB không đổi khi M di chuyển trên đường tròn (O)

Vậy CM⋅CD không phụ thuộc vào vị trí điểm M trên đường tròn (O).

c) Vì ABMD là tứ giác nội tiếp được đường tròn nên $\widehat {DAM} = \widehat {DBM}\left( 1 \right)$ (chắn )

Lại có: BMNP là tứ giác nội tiếp đường tròn (O) nên $\widehat {DBM} = \widehat {MNP}\left( 2 \right)$ (chắn )

Từ (1), (2) $\Rightarrow \widehat {DAM} = \widehat {MNP} \Rightarrow AD\parallel NP$

⇒ APND là hình thang.

d) Gọi I là trung điểm của AC, J là điểm nằm giữa B và I, K là điểm nằm giữa I và C sao cho:

BJ = $\frac{2}{3}$ BI; CK = $\frac{2}{3}$ CI

Vì A, B, C là các điểm cố định nên I, J, K là các điểm cố định.

Do G là trọng tâm △AMC

$\Rightarrow MG = \frac{2}{3}MI \Rightarrow \frac{{MG}}{{MI}} = \frac{{BJ}}{{BI}} = \frac{2}{3} \Rightarrow GJ\parallel BM$

Lại có: $\frac{{MG}}{{MI}} = \frac{{CK}}{{CI}} = \frac{2}{3} \Rightarrow GK\parallel CM$

Mà $\widehat {BMC} = 90^\circ \Rightarrow \widehat {JGK} = 90^\circ$

⇒ G thuộc đường tròn đường kính JK cố định

Vậy khi M di chuyển trên đường tròn (O) thì trọng tâm G của tam giác AMC di chuyển trên đường tròn đường kính JK cố định.

Câu 10. Cho (O; R) và dây AB < 2R. Lấy điểm C thuộc tia AB sao cho AC > AB. Từ C kẻ hai tiếp tuyến với (O) tại P và K. Gọi I là trung điểm của AB

a) Chứng minh rằng ngũ giác CPIOK nội tiếp đường tròn

b) Chứng minh: CP² = CA⋅CB

c) Gọi H là trực tâm của tam giác CPK. Tính KH theo R

d) Giả sử AP // CK. Chứng minh tia đối của tia BK là tia phân giác của góc CBP.

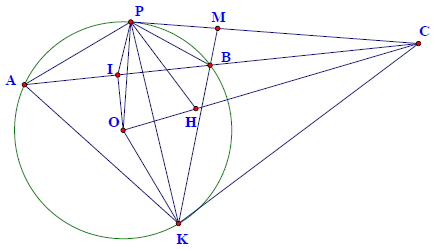
Hướng dẫn giải

a) Xét ◊CPOK: $\widehat {CPO} + \widehat {CKO} = 180^\circ$ ⇒ ◊CPOK nội tiếp

Xét ◊CIOK: $\widehat {CIO} + \widehat {CKO} = 180^\circ$ ⇒ ◊CIOK nội tiếp

Vậy 5 điểm thuộc 1 đường tròn.

b) Xét △CPB và △CAP, có:

$\widehat {CAP} = \widehat {CPB}$

$\widehat {PCB}$ chung

⇒ △CPB ∼ △CAP (g.g)

$\Rightarrow \frac{{CP}}{{CB}} = \frac{{CA}}{{CP}} \Rightarrow C{P^2} = CA \cdot CB$

c) Vì H là trực tâm △CPK

⇒ PH ⊥ CK; KH ⊥ CP

Mà OK ⊥ CK; OP ⊥ CP

⇒ PH // OK; KH // OP

⇒ ◊OPHK là hình bình hành

⇒ HK = OP = R

d) Gọi M = KB ∩

Vì tứ giác PBKA nội tiếp (O) nên $\widehat {PBM} = \widehat {PAK}$ (cùng bù với $\widehat {PBK}$ ).

Xét (O) có $\widehat {ABK} = \widehat {AKx}$ (hệ quả của góc tạo bởi tia tiếp tuyến và dây cung)

Lại có: $\widehat {MBC} = \widehat {ABK}$ (đối đỉnh); $\widehat {AKx} = \widehat {PAK}$ (so le trong, AP // CK)

Do đó: $\widehat {PBM} = \widehat {MBC}$ ⇒ Tia đối của tia BK là tia phân giác của $\widehat {CBP}$

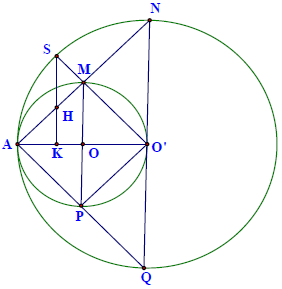
Câu 11. Cho (O; R) và (O’; 2R) tiếp xúc trong tại A. Qua A kẻ hai cát tuyến AMN và APQ với M, P thuộc (O) và N, Q thuộc (O’)

a) Chứng minh rằng: (O) ∈ (O’)

b) Chứng minh: MP // NQ

c) Tia O’M cắt (O’) tại S. Gọi H là trực tâm của tam giác SAO’. Chứng minh rằng tứ giác SHO’N nội tiếp được.

d) Khi $\widehat {MAP} = 90^\circ$ . Tính độ dài MP và NQ theo R.

Hướng dẫn giải

a) Ta có: A là tiếp điểm chung của (O) và (O’) nên:

$\left\{ \begin{gathered} OA = R \hfill \\ O'A = 2R \hfill \\ \end{gathered} \right. \Rightarrow O'A = 2OA$

Mà (O) và (O’) tiếp xúc trong tại A nên các điểm A, O’, O thẳng hàng (đường nối tâm của 2 đường tròn tiếp xúc nhau luôn đi qua tiếp điểm)

⇒ O là trung điểm của O’A

⇒ O’ và A đối xứng nhau qua O

Mà A ∈ (O) ⇒ O’ ∈ (O) ⇒ Đpcm

b) Xét △O’MA có $\widehat {O'MA}$ chắn nửa đường tròn $\left( {O;\frac{{O'A}}{2}} \right)$

⇒ △O’MA vuông tại M ⇒ O’M ⊥ AN

Ta có: O’M ⊥ AN ⇒ M là trung điểm của AN (1)

Tương tự ta có: P là trung điểm của AQ (2)

Từ (1) và (2) ⇒ MP là đường trung bình của △ANQ ⇒ MP // NQ

c) Gọi K là giao điểm của SH và O’A, do H là trực tâm của △SAO’

⇒ SK là đường cao △SAO’

⇒ △O’KS vuông tại K.

Xét △O’MA vuông tại M và △O’KS, có:

$\widehat {MO'A}$ chung

⇒ △O’MA ∼ △O’KS

$\Rightarrow \widehat {O'KS} = \widehat {O'MA} \Rightarrow \widehat {O'SH} = \widehat {O'AN}{\text{ }}\left( 3 \right)$

Lại có: △O’NA cân tại O’ (vì O’N, O’A đều là bán kính của (O’))

$\Rightarrow \widehat {O'AN} = \widehat {O'NA} \Rightarrow \widehat {O'AN} = \widehat {O'NH}{\text{ }}\left( 4 \right)$

Từ (3), (4) $\Rightarrow \widehat {O'SH} = \widehat {O'NH}$

⇒ ◊SHO’N nội tiếp đường tròn.

d) Nếu $\widehat {MAP} = 90^\circ$ ⇒ ◊MAP’O là hình chữ nhật

⇒ PM = AO’ = 2R; QN = 2PM = 4R

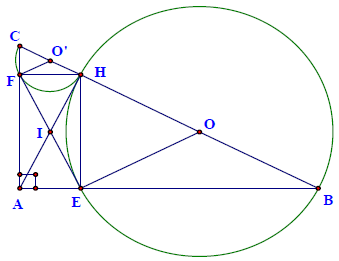
Câu 12. Cho tam giác ABC vuông tại A, AB > AC, đường cao AH. Trên nửa mặt phẳng bờ BC chứa điểm A vẽ nửa (O) đường kính BH cắt AB tại E, nửa đường tròn (O’) đường kính HC cắt AC tại F.

a) Chứng minh rằng tứ giác AFHE là hình chữ nhật

b) Chứng minh tứ giác BEFC nội tiếp được

c) Chứng minh: AE⋅AB = AC⋅AF

d) Chứng minh FE là tiếp tuyến chung của hai nửa đường tròn (O) và (O’)

e) Giả sử $\widehat {ABC} = 30^\circ$ . Chứng minh rằng bán kính của nửa đường tròn (O) gấp ba lần bán kính của nửa (O’).

Hướng dẫn giải

a) Ta có: $\widehat {HEB} = \widehat {HFC} = 90^\circ$ (góc nội tiếp)

$\Rightarrow \widehat {AFH} = \widehat {AEH} = 90^\circ$ (kề bù với góc vuông)

⇒ ◊AEHF là hình chữ nhật.

b) Gọi I là giao điểm của AH và FE, ta có tam giác AIE cân tại I (tính chất hình chữ nhật)

$\Rightarrow \widehat {IAE} = \widehat {IEA}$ . Mà $\widehat {IAE} = \widehat {ACB}$ (cùng phụ với $\widehat {IAF}$ )

$\Rightarrow \widehat {IEA} = \widehat {ACB}\left( { = \widehat {IAE}} \right)$

Tứ giác BEFC có góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện nên nội tiếp được.

c) Xét △AEF và △ACB, có:

$\left\{ \begin{gathered} \widehat {EAF}{\text{ }}chung \hfill \\ \widehat {AEF} = \widehat {ACB} \hfill \\ \end{gathered} \right.$

⇒ △AEF ∼ △ACB (g.g)

$\Rightarrow \frac{{AE}}{{AF}} = \frac{{AC}}{{AB}} \Rightarrow AE \cdot AB = AF \cdot AC$

d) Ta có: $\widehat {AEF} = \widehat {ACB}$ (theo câu b)

△OBE cân tại O

$\begin{gathered} \Rightarrow \widehat {OEB} = \widehat {OBE}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \Rightarrow \widehat {AEF} + \widehat {OEB} = \widehat {ACB} + \widehat {OBE} = 90^\circ \begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \Rightarrow \widehat {FEO} = 180^\circ - \left( {\widehat {AEF} + \widehat {OEB}} \right) = 90^\circ \begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \Rightarrow FE{\text{ }} \bot {\text{ }}OE\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered}$

Mà FE ∩ (O) ≡ E ⇒ FE là tiếp tuyến của (O).

Chứng minh tương tự ta có FE là tiếp tuyến của (O’)

Vậy FE là tiếp tuyến chung của (O) và (O’).

e) Gọi R = $\frac{1}{2}$ HB là bán kính của (O)

Gọi r = $\frac{1}{2}$ HC là bán kính của (O’)

$\widehat {ABC} = 30^\circ \Rightarrow \sin \widehat {ABC} = \sin 30^\circ = \frac{1}{2}$

Trong tam giác BHE vuông tại E ta có:

$\sin \widehat {ABC} = \frac{{HE}}{{HB}} \Rightarrow \frac{{HE}}{{HB}} = \frac{1}{2} \Rightarrow HE = \frac{1}{2}HB = R$

⇒ ◊AEHF là hình chữ nhật ⇒ AF = HE = R.

Vì $\widehat {FHC} = \widehat {ABC} = 30^\circ$ . Chứng minh tương tự như trên, ta có:

FC = $\frac{1}{2}$ HC = r

Vì $\widehat {FHA} = \widehat {ABC} = 30^\circ$ (cùng phụ với $\widehat {HAB}$ ). Chứng minh tương tự ta có:

HC = $\frac{1}{2}$ AC = 2r

⇒ AC = 4r ⇔ AF + FC = 4r ⇔ R + r = 4r ⇒ R = 3r

Vậy bán kính của nửa (O) gấp ba lần bán kính của nửa (O’).

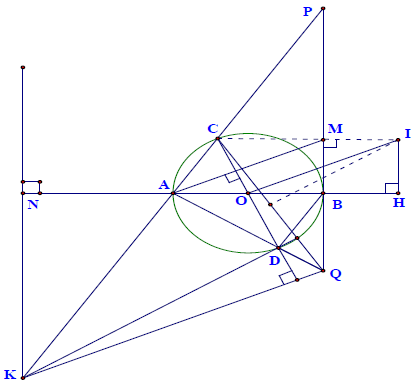
Câu 13. Cho (O) đường kính AB. Đường kính CD thay đổi. Các tia AC, AD cắt tiếp tuyến tại B lần lượt tại P và Q. Gọi M là trung điểm của PQ

a) Chứng minh rằng tứ giác PCDQ nội tiếp

b) Chứng minh: AM ⊥ CD

c) Chứng minh: AC⋅PC + AD⋅DQ không đổi khi CD di động

d) Tìm vị trí của CD để PQ nhỏ nhất

e) Tìm tập hợp I của đường tròn ngoại tiếp tam giác PCQ

f) Tìm tập hợp trực tâm tam giác CDQ.

Hướng dẫn giải

a) Ta có: $\widehat {ADB} = 90^\circ$ (chắn nửa đường tròn)

$\Rightarrow \widehat {DQB} = \widehat {ABD}$ (phụ $\widehat {DBQ}$ )

Mà: $\widehat {ABD} = \widehat {ACD}$ (chắn )

$\Rightarrow \widehat {ACD} = \widehat {DQB} \Rightarrow \widehat {DQB} + \widehat {DCQ} = 180^\circ$

⇒ ◊PCDQ nội tiếp.

b) $\widehat {CAD} = 90^\circ$ (chắn nửa đường tròn)

△APQ vuông tại A, AM là trung tuyến ứng với cạnh huyền nên:

$AM = MP = MQ \Rightarrow \widehat {APM} = \widehat {PAM}$

Mặt khác theo ý a thì tứ giác PCDQ nội tiếp

$\Rightarrow \widehat {APM} = \widehat {CDA}$ (bù $\widehat {CQD}$ ) $\Rightarrow \widehat {PAM} = \widehat {CDA}$

Ta lại có: $\widehat {CDA} + \widehat {ACD} = 90^\circ$

$\Rightarrow \widehat {PAM} + \widehat {ACD} = 90^\circ \Rightarrow AM{\text{ }} \bot {\text{ }}CD$

c) Ta có: $\widehat {ACB} = 90^\circ$ (chắn nửa đường tròn), BC ⊥ AP.

Theo trên ta cũng có BD ⊥ AQ.

Hai tam giác vuông ABP và ABQ có đường cao BC và BD tương ứng.

Do đó ta có hệ thức:

AC⋅CP = BC²; AD⋅DQ = BD²

⇒ AC⋅CP + AD⋅DQ = BC² + BD² = CD² = AB² không đổi khi CD thay đổi.

d) Tam giác APQ vuông tại A có AB là đường cao nên:

$A{B^2} = PB \cdot BQ \leqslant {\left( {\frac{{PB + BQ}}{2}} \right)^2} = \frac{{P{Q^2}}}{4}$

⇒ PQ_min = 2AB ⇔ PB = BQ

⇒ △APB vuông cân ⇔ DC ⊥ AB

e) Gọi I là tâm đường tròn ngoại tiếp tam giác PCQ.

Khi đó: IO ⊥ CD; MI ⊥ PQ

⇒ IO // AM; IM // AB

⇒ ◊AMIO là hình bình hành.

Hạ IH ⊥ AB ⇒ ◊MIHB là hình chữ nhật

⇒ BH = MI = AO không đổi nên H là điểm cố định

⇒ Đường thẳng HI cố định.

Vậy quỹ tich điểm I là đường thẳng đi qua H và vuông góc với đường thẳng AB

f) Gọi K là trực tâm của tam giác CDQ, khi đó KQ // AM (⊥ CD)

Ta có: A, K, P thẳng hàng (vì $\widehat {CAD} = 90^\circ$ )

△KPQ có M là trung điểm của PQ và KQ // AM

Nên AM là đường trung bình của △KPQ ⇒ AP = KA

Từ K hạ KN ⊥ AB ⇒ △KNA = △PBA

⇒ NA = AB không đổi hay N là điểm cố định

⇒ Đường thẳng NK cũng cố định

Do đó quỹ tích điểm K là đường thẳng đi qua N và vuông góc với đường thẳng AB.

Một số tiêu chuẩn nhận biết tứ giác nội tiếp

Tiêu chuẩn 1. Điều kiện cần và đủ để bốn đỉnh của một tứ giác lồi nằm trên cùng một đường tròn là tổng số đo của hai góc tứ giác tại hai đỉnh đối diện bằng 180°

[content_4]

Phương pháp giải

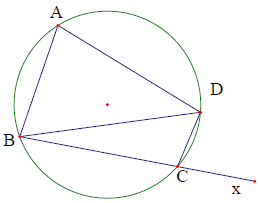
Điều kiện để tứ giác lồi ABCD nội tiếp là: $\widehat A + \widehat C = 180^\circ$ hoặc $\widehat B + \widehat D = 180^\circ$

Hệ quả: Tứ giác ABCD nội tiếp ⇒ $\widehat {BAD} = \widehat {DCx}$

Bài tập vận dụng

Câu 1. Cho tam giác ABC vuông tại A. Kẻ đường cao AH và phân giác trong AD của góc $\widehat {HAC}$ . Phân giác trong góc $\widehat {ABC}$ cắt AH, AD lần lượt tại M, N. Chứng minh rằng: $\widehat {BND} = 90^\circ$ .

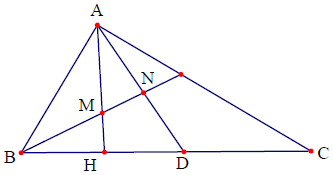
Phân tích và Hướng dẫn giải

Ta có: $\widehat {MHD} = 90^\circ$ . Nếu $\widehat {MND} = 90^\circ$ thì tứ giác MHDN nội tiếp.

Vì vậy thay vì trực tiếp chỉ ra góc $\widehat {BND} = 90^\circ$ ta sẽ đi chứng minh tứ giác MHDN nội tiếp.

Tức là ta chứng minh: $\widehat {AMN} = \widehat {ADH}$

Thật vậy ta có: $\widehat {AMN} = \widehat {BMH} = 90^\circ - \widehat {MBH}$ , $\widehat {NDH} = 90^\circ - \widehat {HAD}$

Mà $\widehat {MBH} = \frac{1}{2}\widehat {ABC},{\text{ }}\widehat {HAD} = \frac{1}{2}\widehat {HAC}$ và $\widehat {ABC} = \widehat {HAC}$ do cùng phụ với góc $\widehat {BCA}$

Từ đó suy ra: $\widehat {AMN} = \widehat {ADH}$ hay tứ giác MHDN nội tiếp

$\Rightarrow \widehat {MND} = \widehat {MHD} = 90^\circ$

Câu 2. Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O) có trực tâm là điểm H. Gọi M là điểm trên dây cung BC không chứa điểm A (M khác B, C). Gọi N, P theo thứ tự là các điểm đối xứng của M qua các đường thẳng AB, AC.

a) Chứng minh AHCP là tứ giác nội tiếp

b) N, H, P thẳng hàng.

c) Tìm vị trí của điểm M để độ dài đoạn NP lớn nhất.

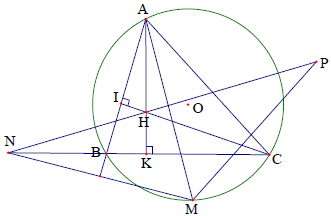
Phân tích và Hướng dẫn giải

a) Giả sử các đường cao của tam giác là AK, CI.

Để chứng minh AHCP là tứ giác nội tiếp ta sẽ chứng minh $\widehat {AHC} + \widehat {APC} = 180^\circ$

Mặt khác ta có: $\widehat {AHC} = \widehat {IHK}$ (đối đỉnh), $\widehat {APC} = \widehat {AMC} = \widehat {ABC}$ (do tính đối xứng và góc nội tiếp cùng chắn một cung).

Như vậy ta chỉ cần chứng minh $\widehat {ABC} + \widehat {IHK} = 180^\circ$ nhưng điều này là hiển nhiên do tứ giác BIHK là tứ giác nội tiếp.

b) Để chứng minh N, H, P thẳng hàng ta sẽ chứng minh $\widehat {NHA} + \widehat {AHP} = 180^\circ$

Do đó ta sẽ tìm cách quy hai góc này về 2 góc đối nhau trong một tứ giác nội tiếp.

Thật vậy ta có: $\widehat {AHP} = \widehat {ACP}$ (tính chất góc nội tiếp),

$\widehat {ACP} = \widehat {ACM}\left( 1 \right)$ (Tính chất đối xứng)

Ta thấy vai trò tứ giác AHCP giống với AHBN nên ta cũng dễ chứng minh được AHBN là tứ giác nội tiếp.

Từ đó suy ra: $\widehat {AHN} = \widehat {ABN}$

Mặt khác: $\widehat {ABN} = \widehat {ABM}\left( 2 \right)$ (Tính chất đối xứng).

Từ (1), (2) ta suy ra chỉ cần chứng minh $\widehat {ABM} + \widehat {ACM} = 180^\circ$ nhưng điều này là hiển nhiên do tứ giác ABMC nội tiếp.

Vậy $\widehat {NHA} + \widehat {AHP} = 180^\circ$ hay N, H, P thẳng hàng.

Chú ý: Đường thẳng qua N, H, P chính là đường thẳng Steiners của điểm M. Thông qua bài toán này các em học sinh cần nhớ tính chất. Đường thẳng Steiners của tam giác thì đi qua trực tâm của tam giác đó. (Xem thêm phần “Các định lý hình học nổi tiếng”).

c) Ta có: $\widehat {MAN} = 2\widehat {BAM},{\text{ }}\widehat {MAP} = 2\widehat {MAC}$

$\Rightarrow \widehat {NAP} = 2\widehat {BAC}$

Mặt khác ta có: AM = AN = AP nên các điểm M, N, P thuộc đường tròn tâm A bán kính AM.

Áp dụng định lý sin trong tam giác NAP ta có:

$NP = 2R \cdot \sin \widehat {NAP} = 2AM \cdot \sin 2\widehat {BAC}$

Như vậy NP lớn nhất khi và chỉ khi AM lớn nhất. Hay AM là đường kính của đường tròn (O)

Câu 3. Cho tam giác ABC và đường cao AH gọi M, N lần lượt là trung điểm của AB, AC. Đường tròn ngoại tiếp tam giác BHM cắt đường tròn ngoại tiếp tam giác CNH tại E. Chứng minh AMEN là tứ giác nội tiếp và HE đi qua trung điểm của MN.

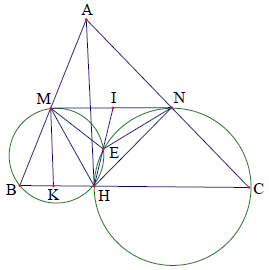
Phân tích, định hướng cách giải:

Để chứng minh AMEN là tứ giác nội tiếp ta sẽ chứng minh:

$\widehat {MAN} + \widehat {MEN} = 180^\circ$

Ta cần tìm sự liên hệ của các góc $\widehat {MAN};\widehat {MEN}$ với các góc có sẵn của những tứ giác nội tiếp khác. Ta có:

$\begin{gathered} \widehat {MEN} = 360^\circ - \left( {\widehat {MEH} + \widehat {NEH}} \right)\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ \hfill \\ \end{gathered} \end{array}}&{ = 360^\circ - \left( {180^\circ - \widehat {ABC} + 180^\circ - \widehat {ACB}} \right)} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ \hfill \\ \end{gathered} \end{array}}&{ = \widehat {ABC} + \widehat {ACB} = 180^\circ - \widehat {BAC}} \end{array} \hfill \\ \end{gathered}$

Suy ra: $\widehat {MAN} + \widehat {MEN} = 180^\circ$

Hay tứ giác AMEN là tứ giác nội tiếp.

Kẻ MK ⊥ BC, giả sử HE cắt MN tại I thì IH là cát tuyến của hai đường tròn (BMH), (CNH).

Lại có: MB = MH = MA (Tính chất trung tuyến tam giác vuông).

Suy ra tam giác MBH cân tại M ⇒ KB = KH

⇒ MK luôn đi qua tâm đường tròn ngoại tiếp tam giác MBH.

Hay MN là tiếp tuyến của (MBH) suy ra IM² = IE⋅IH

Tương tự ta cũng có MN là tiếp tuyến của (HNC) suy ra IN² = IE⋅IH do đó IM = IN.

Xem thêm phần: “Các tính chất của cát tuyến và tiếp tuyến”

Câu 4. Cho tam giác cân ABC (AB = AC) P là điểm trên cạnh đáy BC. Kẻ các đường thẳng PE, PD lần lượt song song với AB, AC (E ∈ AC, D ∈ AB) gọi Q là điểm đối xứng với P qua DE. Chứng minh bốn điểm Q, A, B, C cùng thuộc một đường tròn.

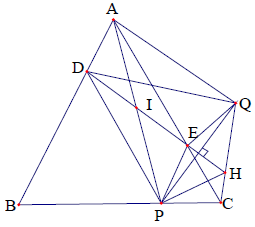
Phân tích định hướng giải

Bài toán có 2 giả thiết cần lưu ý.

Đó là các đường thẳng song song với 2 cạnh tam giác, và điểm Q đối xứng với P qua DE.

Do đó ta sẽ có: AD = EF = EC = EQ và DP = DQ (đây là chìa khóa để ta giải bài toán này)

Từ định hướng đó ta có lời giải như sau:

Do AD // PE, PD // AE

⇒ ADPE là hình bình hành

⇒ AE = DP = DQ. Mặt khác do P, Q đối xứng nhau qua DE ⇒ AD = PE = EQ.

Suy ra DAQE là hình thang cân $\Rightarrow \widehat {DAQ} = \widehat {AQE}$

Kéo dài DE cắt CQ tại H ta có: $\widehat {DAQ} = \widehat {AQE} = \widehat {PEH}$

Như vậy để chứng minh ABCQ nội tiếp ta cần chứng minh: $\widehat {PCH} + \widehat {PEH} = 180^\circ$

⇔ PEHC là tứ giác nội tiếp.

Mặt khác ta có: $\widehat {ECQ} = \widehat {EQC}$ (do tam giác EQC cân)

$\widehat {EPH} = \widehat {EQH}$ (do tính đối xứng)

Suy ra: $\widehat {ECH} = \widehat {EPH}$

⇒ EPCH là tứ giác nội tiếp.

Câu 5. Cho tam giác ABC nội tiếp đường tròn (O). Dựng đường tròn qua B và tiếp xúc với cạnh AC tại A dựng đường tròn qua C và tiếp xúc với AB tại A hai đường tròn này cắt nhau tại D. Chứng minh: $\widehat {ADO} = 90^\circ$

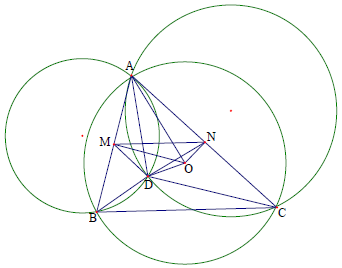
Phân tích định hướng giải

Ta thấy rằng $\widehat {ADO} = 90^\circ$ thì các điểm A, D, O cùng nằm trên đường tròn đường kính OA.

Ta mong muốn tìm ra được một góc bằng $\widehat {ADO} = 90^\circ$ . Điều này làm ta nghĩ đến tính chất quen thuộc “Đường kính đi qua trung điểm của một dây cung thì vuông góc với dây đó”.

Vì vậy nếu ta gọi M, N là trung điểm của AB, AC thì ta sẽ có:

$\widehat {OMA} = \widehat {ONA} = 90^\circ$

Do đó tứ giác OMAN nội tiếp. Công việc còn lại là ta chứng minh AMDO hoặc ANOD hoặc DMAN là tứ giác nội tiếp.

Mặt khác ta có: $\widehat {ABD} = \widehat {CAD}$ và $\widehat {ACD} = \widehat {BAD}$ (Tính chất góc tạo bởi tiếp tuyến và dây cung)

⇒ △BDA và △ADC đồng dạng nên ta suy ra $\widehat {DMA} = \widehat {DNC}$

⇒ $\widehat {DMA} + \widehat {DNA} = \widehat {DNC} + \widehat {DNA} = 180^\circ$

⇒ AMDN nội tiếp suy ra năm điểm A, M, D, O, N nằm trên đường tròn đường kính OA

⇒ $\widehat {ADO} = 90^\circ$

Ví dụ 6: Cho tam giác ABC vuông cân tại A một đường tròn (O)tiếp xúc với AB, AC tại B, C. Trên cung BC nằm trong tam giác ABC lấy một điểm M (M ≠ B, C). Gọi I, H, K lần lượt là hình chiếu của M trên BC; CA; AB và P là giao điểm của MB với IK, Q là giao điểm của MC với IH. Chứng minh PQ // BC.

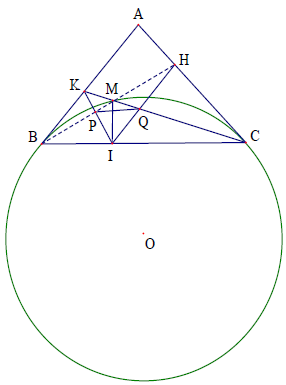
Phân tích định hướng giải

Để chứng minh PQ // BC ta chứng minh $\widehat {MPQ} = \widehat {MBC}$ nhưng tứ giác BIMK nội tiếp nên $\widehat {MBC} = \widehat {MKI}$

Mặt khác: AC là tiếp tuyến của (O) nên ta có: $\widehat {ACK} = \widehat {MBC}$ và CIMH nội tiếp nên $\widehat {ACK} = \widehat {MIH}$

Như vậy để chứng minh PQ // BC ta cần chứng minh $\widehat {MIH} = \widehat {MPQ}$

Tức là ta cần chứng minh tứ giác MPIQ nội tiếp.

Để ý rằng: $\widehat {BMC} = \widehat {KMH} = 135^\circ$

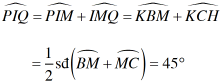
Suy ra đpcm.(Các em học sinh tự hoàn thiện lời giải)

Tiêu chuẩn 2: Tứ giác ABCD nội tiếp $\widehat {ADB} = \widehat {ACB}$

[content_5]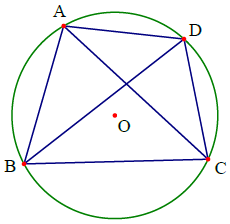

Câu 1. Trên các cạnh BC, CD của hình vuông ABCD ta lấy lần lượt các điểm M, N sao cho $\widehat {MAN} = 45^\circ$ . Đường thẳng BD cắt các đường thẳng AM, AN tương ứng tại các điểm P, Q.

a) Chứng minh rằng các tứ giác ABMQ và ADNP nội tiếp.

b) Chứng minh rằng các điểm M, N, Q, P, C nằm trên cùng một đường tròn.

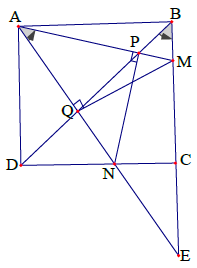
Hướng dẫn giải

a) Gọi E là giao điểm của AN và BC.

Các điểm M và Q nằm trên hai cạnh EB và EA của tam giác EBA, nên tứ giác ABMQ là lồi.

Các đỉnh A và B cùng nhìn đoạn thẳng MQ dưới một góc 45°.

Vì vậy tứ giác ABMQ nội tiếp.

Lập luận tương tự ta suy ra tứ giác ADNP nội tiếp.

b) Từ kết quả câu a, suy ra

$\begin{gathered} \widehat {ADP} = \widehat {ANP} = 45^\circ ,{\text{ }}\widehat {QAM} = \widehat {QBM} = 45^\circ \begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \Rightarrow NP{\text{ }} \bot {\text{ }}AM,{\text{ }}MQ{\text{ }} \bot {\text{ }}AN \hfill \\ \end{gathered}$

Tập hợp các điểm P, Q, C nhìn đoạn MN dưới một góc vuông, nên các điểm này nằm trên đường tròn đường kính MN.

Câu 2. Cho điểm M thuộc cung nhỏ BC của đường tròn (O). Một đường thẳng d ở ngoài (O) và vuông góc với OM; CM, BM cắt d lần lượt tại D, E. Chứng minh rằng B, C, D, E cùng thuộc một đường tròn.

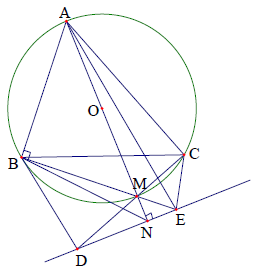
Hướng dẫn giải

Kẻ đường kính AM cắt d tại N.

Ta có: $\widehat {ANE} = \widehat {ABE} = 90^\circ$ nên tứ giác ABNE nội tiếp, suy ra $\widehat {BEN} = \widehat {BAN}$

Mặt khác: $\widehat {BAN} = \widehat {BCM}$

Do đó: $\widehat {BCM} = \widehat {BEN}$ hay $\widehat {BCD} = \widehat {BED}$

Vậy B, C, D, E cùng thuộc một đường tròn.

Câu 3. Cho tam giác ABC có các đường cao AD, BE, CF đồng quy tại H. Gọi K là giao điểm của EF và AH, M là trung điểm của AH. Chứng minh rằng K là trực tâm của tam giác MBC.

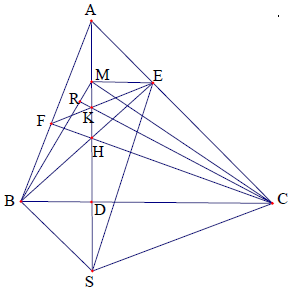
Hướng dẫn giải

Lấy điểm S đối xứng với H qua BC, R là giao điểm của KC với MB.

Vì ME = MA = MH (tính chất trung tuyến), kết hợp tính đối xứng của điểm S ta có:

$\widehat {MSB} = \widehat {BHD} = \widehat {MHE} = \widehat {MEB}$ nên tứ giác MESB nội tiếp.

Suy ra: $\widehat {RBE} = \widehat {MSE}\left( 1 \right)$

Lại có: $\widehat {KSC} = \widehat {CHD} = \widehat {AHF} = \widehat {AEK}$ nên tứ giác KSCE cũng nội tiếp, do đó $\widehat {MSE} = \widehat {RCE}\left( 2 \right)$

Từ (1) và (2) suy ra $\widehat {RBE} = \widehat {RCE}$ nên tứ giác RBCE nội tiếp.

Từ đó suy ra: $\widehat {BRC} = \widehat {BEC} = 90^\circ$

Trong tam giác MBC, ta có MK ⊥ BC và CK ⊥ MB nên K là trực tâm của tam giác MBC.

Câu 4. Cho tam giác ABC nội tiếp đường tròn tâm O. Đường tròn (O’) tiếp xúc với các cạnh AB, AC tại E, F tiếp xúc với (O) tại S. Gọi I là tâm đường tròn nội tiếp tam giác ABC. Chứng minh: BEIS, CFIS là các tứ giác nội tiếp.

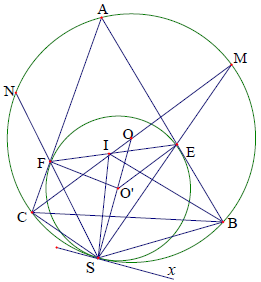
Hướng dẫn giải

Nhận xét: bài toán này thực chất là định lý Lyness được phát biểu theo cách khác (Xem thêm phần: “Các định lý hình học nổi tiếng”)

Kéo dài SE, SFcắt đường tròn (O) tại E, F. Ta có các tam giác OMS, O’EF cân tại O, O’ nên

$\widehat {O'ES} = \widehat {OMS} \Rightarrow OE\parallel OM \Rightarrow OM{\text{ }} \bot {\text{ }}AB$

Hay M là điểm chính giữa của cung AB.

Kẻ đường phân giác trong góc ACB cắt EF tại I, ta chứng minh I là tâm đường tròn nội tiếp tam giác ABC.

Thật vậy ta có: C, I, M thẳng hàng và $\widehat {ICS} = \widehat {MCS} = \widehat {MSx}$ và $\widehat {IFS} = \widehat {EFS} = \widehat {MSx}$ nên $\widehat {ICS} = \widehat {IFS}$

⇒ Tứ giác IFCS là tứ giác nội tiếp

$\Rightarrow \widehat {EIS} = \widehat {SCF}$

Mặt khác tứ giác ACSB nội tiếp nên $\widehat {ACS} + \widehat {ABS} = 180^\circ \Rightarrow \widehat {EIS} + \widehat {ABS} = 180^\circ$ hay tứ giác EISB nội tiếp.

Công việc còn lại là chứng minh: IB là phân giác trong của góc $\widehat {ABC}$

Vì $\widehat {EBI} = \widehat {ESI}$ mà

$\begin{gathered} \widehat {ESI} = \widehat {ISB} - \widehat {ESB} = \widehat {AEF} - \widehat {MSB}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ \hfill \\ \hfill \\ \end{gathered} \end{array} = \frac{{180^\circ - \widehat A}}{2} - \widehat {MCB} \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = \frac{{180^\circ - \widehat A}}{2} - \frac{{\widehat C}}{2} = \frac{{\widehat B}}{2} \hfill \\ \end{gathered}$

Điều này chứng tỏ IB là phân giác trong của góc $\widehat {ABC}$ . Hay I là tâm vòng tròn nội tiếp tam giác ABC.

Chú ý: Nếu thay giả thiết điểm I là tâm vòng tròn nội tiếp tam giác ABC thành các đường tròn ngoại tiếp tam giác FCS, SBE cắt nhau tại I thì hình thức bài toán khác đi nhưng bản chất vẫn là định lý Lyness. Để ý rằng: △AEF cân tại A nên ta dễ dàng suy ra được: I là trung điểm của EF.

Câu 5. Cho hai đường tròn (O₁), (O₂) tiếp xúc ngoài với nhau. Kẻ đường thẳng O₁O₂ cắt hai đường tròn (O₁), (O₂) lần lượt tại A, B, C (B là tiếp điểm). Đường thẳng ∆ là tiếp tuyến chung của hai đường tròn với các tiếp điểm tương ứng là D₁, D₂. Đường thẳng (∆’) là tiếp tuyến với (O₂) qua C. Đường thẳng BD₁ cắt (∆’) tại E. AD₁ cắt ED₂ tại M, AD₂ cắt BD₁ tại H. Chứng minh AE ⊥ MH.

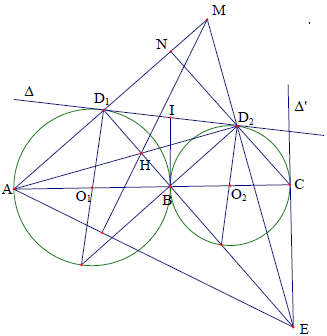
Phân tích định hướng giải

– Vì ED₁ ⊥ MA do góc $\widehat {A{D_1}B}$ là góc nội tiếp chắn nửa đường tròn.

Vì vậy để chứng minh AE ⊥ MH ta phải chứng minh AD₂ ⊥ ME, tức là ta chứng minh H là trực tâm của tam giác MAE. Khi đó ta sẽ có:

$\widehat {A{D_1}E} = \widehat {A{D_2}E}$

Hay tứ giác AD₁D₂E là tứ giác nội tiếp.

– Gọi N là giao điểm của CD₂ và AM.

Xét tiếp tuyến chung của (O₁) và (O₂) qua B cắt (∆) tại I. Khi đó ta có:

⇒ ID₁ = IB = ID₂ ⇒ △BD₁D₂ vuông tại B, D₁E // CN (cùng vuông góc với BD₂).

Do đó: $\widehat {BA{D_1}} = \widehat {B{D_1}{D_2}}$ (góc tạo bởi tia tiếp tuyến và dây cung)

Mặt khác: $\widehat {B{D_1}{D_2}} = \widehat {{D_1}{D_2}N}$ (so le trong).

Suy ra: $\widehat {CA{D_1}} = \widehat {N{D_2}{D_1}}$ ⇒ AD₁D₂C là tứ giác nội tiếp (1)

Xét tứ giác ED₁D₂C ta có:

$E{D_1}\parallel C{D_2},{\text{ }}\widehat {BEC} = \widehat {IB{D_1}}$ (góc đồng vị)

Suy ra: $\widehat {E{D_1}{D_2}} = \widehat {{D_1}EC}$ ⇒ Tứ giác ED₁D₂C là hình thang cân nên nội tiếp (2)

Từ (1), (2) suy ra 5 điểm A, D₁, D₂, C, E cùng thuộc một đường tròn.

Suy ra tứ giác AD₁D₂E nội tiếp.

Câu 6. Cho tam giác ABC có hai đường cao BD, CE cắt nhau tại H gọi I là trung điểm của BC. Hai đường tròn ngoại tiếp tam giác BEI và CDI cắt nhau ở K, DE cắt BC tại M. Chứng minh tứ giác BKDM nội tiếp.

Phân tích định hướng giải

Ta thấy ngay đường tròn ngoại tiếp các tam giác ADE, BEI, CDI sẽ cắt nhau.

Mặt khác từ giả thiết ta cũng có: AEHD là tứ giác nội tiếp.

Nên suy ra 5 điểm A, E, H, K, D thuộc một đường tròn đường kính AH. Đây chính là chìa khóa để giải quyết bài toán.

Hướng dẫn giải

Trước tiên ta chứng minh: tứ giác AEKD nội tiếp (Bạn đọc có thể tham khảo ở phần “Các định lý hình học nổi tiếng”) Ta có:

$\widehat A + \widehat B + \widehat C + \widehat {EKC} + \widehat {EKI} + \widehat {IKD} = 540^\circ$

Theo giả thiết:

$\widehat B + \widehat {EKI} = \widehat {IKD} + \widehat C = 180^\circ \Rightarrow \widehat A + \widehat {EKD} = 180^\circ$

⇒ Tứ giác AEKD nội tiếp

$\Rightarrow \widehat {ADE} = \widehat {AKE},{\text{ }}BD{\text{ }} \bot {\text{ }}AC,{\text{ }}CE{\text{ }} \bot {\text{ }}AB$

⇒ Tứ giác BEDC nội tiếp $\Rightarrow \widehat {ADE} = \widehat B$ .

Kết hợp với $\widehat {ADE} = \widehat {AKE}$ được:

$\widehat B = \widehat {AKE} \Rightarrow \widehat {EKI} + \widehat {AKE} = \widehat {EKI} + \widehat B = 180^\circ$

⇒ A, K, I thẳng hàng.

△BDC là tam giác vuông nên ID = IC, IKDC là tứ giác nội tiếp nên ta có:

$\widehat {IKC} = \widehat {IDC} = \widehat {ICD},{\text{ }}\widehat {IKC} = \widehat {KAC} = \widehat {ACK}$ (Tính chất góc ngoài)

$\widehat {ICD} = \widehat {ICK} + \widehat {KCD} \Rightarrow \widehat {KAC} = \widehat {ICK}$ mà $\widehat {KAD} = \widehat {DEK}$ (chắn cung )

$\Rightarrow \widehat {ICK} = \widehat {DEK}$

⇒ Tứ giác MEKC nội tiếp $\Rightarrow \widehat {MEC} = \widehat {MKC}$ . Theo kết quả trên suy ra:

$\begin{gathered} \widehat {IKC} = \widehat {AED} = \widehat {MEB},{\text{ }}\widehat {MEC} = \widehat {MEB} + 90^\circ \begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \widehat {MKC} = \widehat {MKI} + \widehat {IKC} \Rightarrow \widehat {MKI} = 90^\circ \begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered}$

⇒ MK ⊥ KI ⇒ A, E, H, D, K nằm trên đường tròn đường kính AH

⇒ HK ⊥ AI ⇒ M, H, K thẳng hàng.

Tứ giác DEHK nội tiếp

$\Rightarrow \widehat {HEK} = \widehat {HDK}$

Tứ giác MEKC nội tiếp $\Rightarrow \widehat {KEC} = \widehat {KMC}$

$\Rightarrow \widehat {KMC} = \widehat {HDK} \Rightarrow \widehat {KMB} = \widehat {BDK}$

⇒ Tứ giác BKDM nội tiếp.

Câu 7. Cho hai đường tròn (O₁), (O₂) cắt nhau tại A, B. Kéo dài AB về phía B lấy điểm M. Qua M kẻ hai tiếp tuyến ME, MF với đường tròn (O₁) (E, F là các tiếp điểm), điểm F nằm cùng phía so với AB. Đường thẳng BE, BF cắt đường tròn (O₂) tại P, Q. Gọi I là giao điểm của PQ và EF. Chứng minh I là trung điểm của PQ.

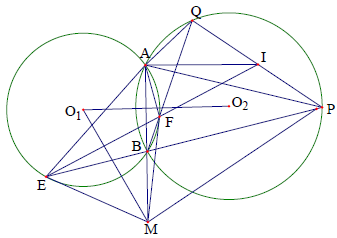
Phân tích định hướng giải

Để ý rằng: Đường thẳng EFI cắt ba cạnh của tam giác BPQ lần lượt tại I, E, F.

Theo định lý Menelauyt ta có: $\frac{{QI}}{{IP}} \cdot \frac{{EP}}{{EB}} \cdot \frac{{FB}}{{FQ}} = 1$ . Để chứng minh I là trung điểm của PQ ta sẽ chứng minh: $\frac{{EP}}{{EB}} \cdot \frac{{FB}}{{FQ}} = 1$ . Bây giờ ta sẽ tìm cách thay thế các đại lượng trong $\frac{{EP}}{{EB}} \cdot \frac{{FB}}{{FQ}} = 1{\text{ }}(*)$ thành các đại lượng tương đương để thông qua đó ta có thể quy về việc chứng minh tứ giác nội tiếp, hoặc tam giác đồng dạng.

Xét đường tròn (O₁) với cát tuyến M, B, A và hai tiếp tuyến ME, MF.

Ta có tính chất quen thuộc: $\frac{{FA}}{{FB}} = \frac{{EA}}{{EB}}$ (Xem phần chùm bài tập cát tuyến và tiếp tuyến). Từ đó suy ra $\frac{{FB}}{{EB}} = \frac{{FA}}{{EA}}$ thay vào (*) ta quy bài toán về chứng minh:

$\frac{{EP}}{{FQ}} \cdot \frac{{FA}}{{EA}} = 1 \Leftrightarrow \frac{{EP}}{{FQ}} = \frac{{EA}}{{FA}} \Leftrightarrow \Delta EPA \sim \Delta FQA$

Nhưng ta có: $\widehat {EPA} = \widehat {FQA}$ góc nội tiếp chắn cung

$\widehat {AEP} = \widehat {AFQ}$ (tứ giác AEBF nội tiếp). Qua đó ta có kết quả cần chứng minh:

Các em học sinh tự hoàn chỉnh Hướng dẫn giải dựa trên những phân tích định hướng mà tác giả vừa trình bày.

⊗ Nếu không dùng định lý Menelaus ta có thể giải theo các khác như sau:

Vì MF là tiếp tuyến của đường tròn (O₁) nên ta có: $\widehat {MFB} = \widehat {FAB}$ (Tính chất góc tạo bởi tiếp tuyến và dây cung). Suy ra: △MFB, △MAF đồng dạng

$\Rightarrow \frac{{MF}}{{MA}} = \frac{{FB}}{{FA}}$ . Tương tự ta cũng có: △MEB, △MAE đồng dạng

$\Rightarrow \frac{{ME}}{{MA}} = \frac{{EB}}{{EA}}$ mà $ME = MF \Rightarrow \frac{{FB}}{{FA}} = \frac{{EB}}{{EA}}{\text{ }}\left( 1 \right)$ , mặt khác $\widehat {AFE} = \widehat {ABE}$ (chắn cung ) và $\widehat {ABE} = \widehat {AQP}$ (do tứ giác ABPQ nội tiếp).

Suy ra: $\widehat {AFE} = \widehat {AQP}$ ⇒ AFIQ là tứ giác nội tiếp, suy ra $\widehat {AFQ} = \widehat {AIQ} \Rightarrow \widehat {AFB} = \widehat {AIP}$

Ta cũng có: $\widehat {ABF} = \widehat {APQ}$ suy ra △FBA, △IPA đồng dạng suy ra $\frac{{BF}}{{AF}} = \frac{{PI}}{{AI}}{\text{ }}\left( 2 \right)$

Tương tự ta chứng minh được: △ABE, △AQI đồng dạng suy ra $\frac{{QI}}{{IA}} = \frac{{BE}}{{AE}}$

Từ (1), (2), (3) suy ra: $\frac{{QI}}{{IA}} = \frac{{PI}}{{AI}} \Leftrightarrow IP = IQ$

Câu 8. Cho tam giác ABC. Đường tròn (O) đi qua A và C cắt AB, AC theo thứ tự tại K và N. Đường tròn tâm I ngoại tiếp tam giác ABC và đường tròn tâm J ngoại tiếp tam giác KBN cắt nhau tại B và M. Chứng minh BIOJ là hình bình hành từ đó suy ra $\widehat {OMB}$ vuông.

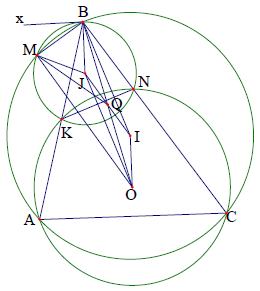
Phân tích định hướng giải

Để chứng minh BIOJ là hình bình hành ta chứng minh: BI / OJ, BJ // OI

Mặt khác dễ thấy OI là trung trực của AC nên OI ⊥ AC. Ta cần chứng minh BJ ⊥ AC, việc tìm liên hệ trực tiếp là tương đối khó vì vậy ta nghĩ đến hướng tạo một đường thẳng “đặc biệt” vuông góc với BJ sau đó chứng minh đường thẳng này song song với AC từ đó ta nghĩ đến dựng tiếp tuyến Bx của đường tròn ngoại tiếp tam giác BKN.

Khi đó ta có: $Bx{\text{ }} \bot {\text{ }}BJ,{\text{ }}\widehat {KBx} = \widehat {BNK}$ (tính chất góc tạo bởi tiếp tuyến và một dây).

Mặt khác AKNC nội tiếp

$\Rightarrow \widehat {BAC} = \widehat {BNK} \Rightarrow \widehat {MKx} = \widehat A \Rightarrow Bx\parallel AC$

Từ đó suy ra: BJ // OI

Tương tự, từ B kẻ tiếp tuyến By với đường tròn ngoại tiếp △ABC

Chứng minh như trên ta có: BI // OJ ⇒ Tứ giác BIOJ là hình bình hành.

Gọi Q là giao điểm BO và IJ ⇒ QO = QB, IJ là trung trực BM (Tính chất đường nối tâm của hai đường tròn cắt nhau).

⇒ QM = QB ⇒ QM = QB = QO ⇒ △BMO là tam giác vuông $\Rightarrow \widehat {OMB} = 90^\circ$

Câu 9. Cho hai đường tròn (O₁) và (O₂) tiếp xúc trong tại M (đường tròn (O₂) nằm trong). Hai điểm P và Q thuộc đường tròn (O₂) qua P kẻ tiếp tuyến với (O₂) cắt (O₁) tại B và D qua Q kẻ tiếp tuyến với (O2) cắt (O₁) tại A và C. Chứng minh rằng tâm đường tròn nội tiếp các tam giác ACD, BCD nằm trên PQ.

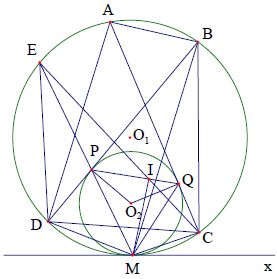
Phân tích định hướng giải

Vì giả thiết hai đường tròn tiếp xúc trong với nhau tại điểm M nên ta nghĩ đến việc tiếp tuyến chung Mx để tận dụng các yếu tố về góc:

Bài toán này làm ta nghĩ đến định lý Lyness nổi tiếng (Xem thêm phần các định lý hình học nổi tiếng – Định lý Lyness mở rộng) và các tính chất quen thuộc liên quan đến chứng minh định lý này là: MP là phân giác góc $\widehat {DMB}$ , kéo dài MP cắt (O₁) tại E thì E là trung điểm của BD,…

Từ những định hướng trên ta suy ra cách giải cho bài toán như sau:

– Dựng tiếp tuyến chung Mx của hai đường tròn (O₁), (O₂) khi đó ta có:

Mà $\widehat {DPM} = \widehat {PMB} + \widehat {PBM}$ (tính chất góc ngoài của tam giác)

$\widehat {PMx} = \widehat {PMD} + \widehat {DMx} \Rightarrow \widehat {PMD} = \widehat {PMB}$

⇒ MP là phân giác $\widehat {DMB}$ , gọi E là giao điểm MP với (O₁) thì E là trung điểm của BD

⇒ CE là phân giác $\widehat {BCD}$

– Gọi I là giao điểm của CE và PQ ta cần chứng minh DI là phân giác của $\widehat {BDC}$

Mặt khác nếu I là tâm vòng tròn nội tiếp tam giác BCD thì ta sẽ có: EI = ED = EB (Tính chất quen thuộc liên quan đến tâm vòng tròn nội tiếp, bạn đọc có thể xem thêm phần “góc” ở phần đầu).

– Ta có:

⇒ IQCM nội tiếp suy ra $\widehat {MIC} = \widehat {MQC}$

Mà (Tính chất góc tạo bởi tiếp tuyến và dây cung)

Suy ra: $\widehat {MIC} = \widehat {MPQ} \Rightarrow \widehat {EPI} = \widehat {EIM}$

⇒ △EIM ∼ △EPI ⇒ EI² = EP⋅EM

Tương tự ta cũng chứng minh được DPIM là tứ giác nội tiếp và △DEP ∼ △MDE

⇒ ED² = EP⋅EM ⇒ ED = EI = EB

⇒ $\widehat {EDI} = \widehat {EID}$ ⇒ I là tâm đường tròn nội tiếp △BCD.

– Tương tự, tâm của đường tròn nội tiếp △ACD nằm trên PQ.

Nhận xét: Đối với các bài toán có giả thiết hai đường tròn tiếp xúc trong với nhau thì việc kẻ tiếp tuyến chung để suy ra các góc bằng nhau và từ đó phát hiện ra các tứ giác nội tiếp là một hướng quan trọng để giải toán

Câu 10. Cho tam giác ABC vuông tại A và B < C. Tiếp tuyến với đường tròn ngoại tiếp tam giác ABC tại A cắt cạnh BC kéo dài tại D gọi E là điểm đối xứng của A qua BC, H là hình chiếu của A trên BE. Gọi I là trung điểm của AH đường thẳng BI cắt đường tròn ngoại tiếp tam giác ABC tại K. Chứng minh rằng BD là tiếp tuyến của đường tròn ngoại tiếp tam giác ADK.

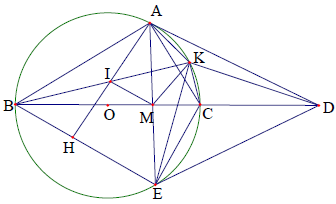
Phân tích định hướng giải

Để chứng minh một đường thẳng là tiếp tuyến của đường tròn thông thường ta chứng minh đường thẳng đó vuông góc với một bán kính tại tiếp điểm. Muốn làm được điều này điều kiện cần là phải xác định rõ tâm đường tròn. Nhưng việc làm này là không dễ nếu tâm đường tròn không phải là điểm đặc biệt. Để khắc phục khó khăn này ta thường chọn cách chứng minh theo tính chất của góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung.

Trở lại bài toán: Để chứng minh BD là tiếp tuyến của đường tròn (AKD) ta phải chứng minh: $\widehat {KDB} = \widehat {KAD}$

– Vì E là điểm đối xứng của A qua BC

⇒ DE là tiếp tuyến của đường tròn ngoại tiếp △ABC

⇒ AE ⊥ BC và MA = ME. Theo giả thiết IA = IH nên IM // BE

$\Rightarrow \widehat {KIM} = \widehat {KBE} = \widehat {KAE}$

⇒ A, I, M, K nằm trên một đường tròn $\Rightarrow \widehat {IAM} = \widehat {IKM}{\text{ }}$

$\widehat {BAH} = \widehat {BAE} - \widehat {HAE} = \widehat {BKE} - \widehat {IKM} = \widehat {MKE}{\text{ }}\left( 1 \right)$

Mặt khác: $\widehat {ABE} = \widehat {EAD}$ (chắn cung )

$\begin{gathered} \widehat {BAH} = 90^\circ - \widehat {ABH} = 90^\circ - \widehat {EAD}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {}&{ = \widehat {ADM} = \widehat {EDM}{\text{ }}\left( 2 \right)} \end{array}} \end{array} \hfill \\ \end{gathered}$

– Từ (1) và (2) suy ra: $\widehat {MKE} = \widehat {EDM}$ ⇒ Bốn điểm M, K, D, E nằm trên một đường tròn

$\Rightarrow \widehat {KDM} = \widehat {KEM} = \widehat {KEA} = \widehat {KAD}$

⇒ BD là tiếp tuyến của đường tròn ngoại tiếp tam giác ADK.

Tiêu chuẩn 3

[content_6]

Phương pháp giải

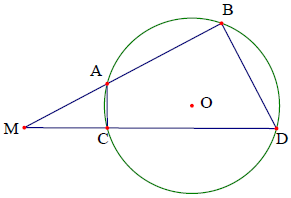
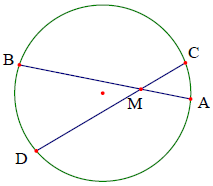
Cho hai đường thẳng ∆₁, ∆₂ cắt nhau tại điểm M. Trên hai đường thẳng ∆₁, ∆₂ lần lượt lấy các điểm A, B và C, D khi đó 4 điểm A, B, C, D cùng thuộc một đường tròn khi và chỉ khi MA⋅MB = MC⋅MD.

Bài tập vận dụng

Câu 1. Cho đường tròn tâm (O) đường kính AB và đường thẳng ∆ nằm ngoài đường tròn (O) vuông góc với AB tại C. Kẻ cát tuyến CMN với đường tròn (O), AM, AN cắt ∆ tại D, E. Chứng minh MNED nội tiếp được:

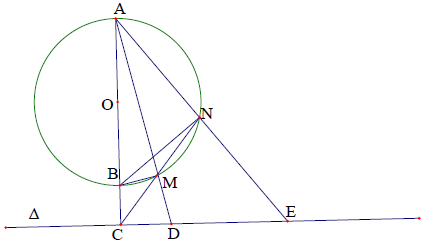
Phân tích định hướng giải

Vì $\widehat {AMB} = 90^\circ$ ⇒ BCDM là tứ giác nội tiếp, suy ra AB⋅AC = AM⋅AD (1).

Tương tự vì góc $\widehat {ANB} = 90^\circ \Rightarrow \widehat {BNE} = \widehat {BCE} = 90^\circ$ hay tứ giác BCNE nội tiếp, từ đó suy ra: AB⋅AC = AN⋅AE (2)

Kết hợp (1), (2) ta có: AM⋅AD = AN⋅AE

⇒ MNED là tứ giác nội tiếp.

Câu 2. Cho tam giác ABC cân (AB = AC, A < 90°) có đường cao BD. Gọi M, N, I theo thứ tự là trung điểm của các đoạn BC, BM, BD. Tia NI cắt cạnh AC tại K. Chứng minh các tứ giác ABMD, ABNK nội tiếp và 3BC² = 4CA⋅CK.

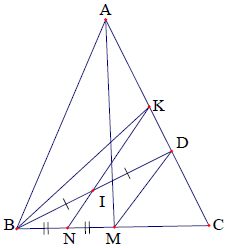
Giải:

Do tam giác ABC cân tại A nên AM ⊥ BC

Mặt khác: BD ⊥ AC ⇒ ABMD là tứ giác nội tiếp.

Vì $NI = \frac{1}{2}MD \Rightarrow \widehat {KNC} = \widehat {DMC}$

Ta cũng có: $\widehat {DMC} = \widehat {KAB}$ (tính chất tứ giác nội tiếp)

Suy ra $\widehat {KNC} = \widehat {KAB}$ hay ABNK là tứ giác nội tiếp.

Ta có: CA⋅CK = CN⋅CB

Mà: CN = $\frac{3}{4}$ CB

⇒ $\frac{3}{4}$ BC² = CA⋅CK

⇔ 3BC² = 4CA⋅CK

Câu 3. Cho tứ giác lồi ABCD có giao điểm 2 đường chéo là M. Đường phân giác trong góc ACD cắt BA tại K. Giả sử MA⋅MC + MA⋅CD = MB⋅MD. Chứng minh: $\widehat {BKC} = \widehat {CDB}$

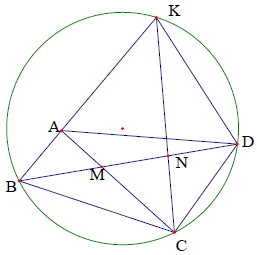
Phân tích định hướng giải

Ta gọi N là giao điểm của CK và BD. Theo tính chất đường phân giác trong tam giác MCD ta có:

$\frac{{ND}}{{NM}} = \frac{{CD}}{{CM}} \Rightarrow CD = \frac{{MC \cdot DN}}{{MN}}$ thay vào biểu thức

MA⋅MC + MA⋅CD = MB⋅MD ta có:

$\begin{gathered} MB \cdot MD = MA \cdot MC + MA \cdot \frac{{MC \cdot DN}}{{MN}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&\begin{gathered} = MA \cdot MC \cdot \frac{{MD}}{{MN}} \hfill \\ \hfill \\ \end{gathered} \end{array} \hfill \\ \Leftrightarrow MA \cdot MC = MB \cdot MN \hfill \\ \end{gathered}$

Do M nằm trong tứ giác ABCN.

Theo tiêu chuẩn 3 ta có: ABCN là tứ giác nội tiếp nên $\widehat {ABD} = \widehat {ACK} = \widehat {KCD}$

Theo tiêu chuẩn 2 ta có: BCDK là tứ giác nội tiếp.

Suy ra: $\widehat {BKC} = \widehat {CDB}$

Câu 4. Cho tam giác ABC. Đường tròn (O) đi qua A và C cắt AB, AC theo thứ tự tại K và N. Đường tròn tâm I ngoại tiếp tam giác ABC và đường tròn tâm J ngoại tiếp tam giác KBN cắt nhau tại B và M. Chứng minh $\widehat {OMB}$ vuông.

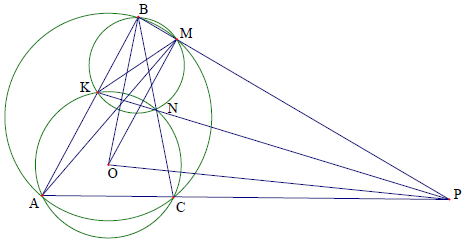
Phân tích định hướng giải

Gọi P là giao điểm của các đường thẳng AC và KN. Ta có:

$\widehat {KMA} = \widehat {BMA} - \widehat {BMK} = \widehat {BCA} - \widehat {BNK} = \widehat {KPA}$

Nên 4 điểm M, P, A, K nằm trên một đường tròn. Ngoài ra ta cũng có:

$\widehat {AMP} = \widehat {AKP} = 180^\circ - \widehat {ACB} = 180^\circ - \widehat {AMB}$ (do ACNK là tứ giác nội tiếp) nên ta suy ra điểm M nằm trên đoạn BP.

Gọi R là bán kính của đường tròn (O). Ta có:

BM⋅BP = BN⋅BC = BK⋅BA = BO² – R² và

PM⋅PB = PN⋅PK = PA⋅PC = PO² – R² cộng từng vế hai đẳng thức trên ta thu được:

BM⋅BP + PM⋅BP = BO² + PO² – 2R²

⇔ BP² = BO² + PO² – 2R²

Khi đó ta có:

$\begin{gathered} B{M^2} - P{M^2} \hfill \\ = {\left( {\frac{{B{O^2} - {R^2}}}{{BP}}} \right)^2} - {\left( {\frac{{O{P^2} - {R^2}}}{{BP}}} \right)^2}\begin{array}{*{20}{c}} {} \\ {} \\ {} \\ {} \end{array} \hfill \\ = \frac{{\left( {B{O^2} + P{O^2} - 2{R^2}} \right)\left( {B{O^2} - O{P^2}} \right)}}{{B{P^2}}} \hfill \\ = B{O^2} - O{P^2}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Từ đó suy ra OM ⊥ BP.

Chú ý: Để chứng minh OM ⊥ BP ta đã dùng kết quả: Cho tam giác ABC và điểm H nằm trên cạnh BC. Khi đó AH là đường cao khi và chỉ khi AB² – AC² = HB² – HC².

Thật vậy:

Nếu AH là đường cao thì ta luôn có: AB² – AC² = HB² – HC² (Theo định lý Pytago)

Ngược lại nếu ta có: AB² – AC² = HB² – HC² (*), gọi M là điểm trên BC sao cho:

AB² – AC² = MB² – MC² hay

(HB + HC)(HB – HC) = (MB + MC)(MB – MC)

⇔ BC(HB – HC) = BC(MB – MC)

⇔ HB – HC = MB – MC

⇔ M ≡ H

Suy ra điều phải chứng minh.

Thầy Tú dạy toán