Trong bài viết này, VerbaLearn sẽ giúp bạn đọc tìm hiểu chi tiết các điểm kiến thức thuộc chuyên đề hệ thức lượng trong tam giác vuông bao gồm: Cạnh và đường cao, tỷ số lượng giác góc nhọn và hệ thức cạnh – góc trong tam giác vuông. Từ đó áp dụng vào giải các dạng toán điển hình như giải tam giác, tính cạnh và góc tam giác, các bài toán thực tế, …

Cạnh và đường cao trong tam giác vuông
Tóm tắt lý thuyết
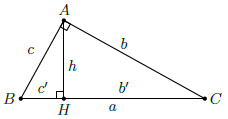
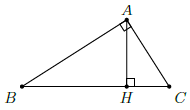
Cho tam giác ABC vuông tại A, đường cao AH. Đặt AB = c, BC = a, CA = b, AH = h, BH = c’, CH = b’. Khi đó ta có: các hệ thức sau:
– a2 = b2 + c2
– a ⋅ h = b ⋅ c
– a ⋅ b’ = b2
– a ⋅ c’ = c2
– b’ ⋅ c’ = h2
–
Bài tập vận dụng
Câu 1. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 3cm, AC = 4cm. Tính BC, AH, BH, CH.
Hướng dẫn giải
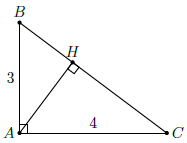
Ta có: BC2 = AB2 + AC2 = 32 + 42 = 25
⇒ BC = 5cm.
AH ⋅ BC = AB ⋅ AC ⇔ AH × 5 = 3 × 4
⇒ AH = 2,4cm
BH ⋅ BC = AB2 ⇔ BH × 5 = 32
⇒ BH = 1,8cm.
CH = BC − BH = 3,2cm
Câu 2. Cho tam giác ABC vuông tại A có đường cao AH (H thuộc cạnh BC) biết AB = a, BC = 2a. Tính theo a độ dài AC và AH.
Hướng dẫn giải
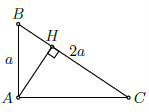
Theo định lí Pitago, Ta có: BC2 = AB2 + AC2, suy ra:
AC2 = BC2 − AB2 = (2a)2 − a2 = 3a2 ⇒ AC = a
Lại có: AH ⋅ BC = AB ⋅ AC
⇔ AH × 2a = a × a
⇒ AH =
Câu 3. Cho tam giác ABC vuông tại có AB = 3cm, AC = 4cm, đường cao AH. Gọi E, F là hình chiếu của H lên AB, AC. Tính diện tích tứ giác AEHF.
Hướng dẫn giải
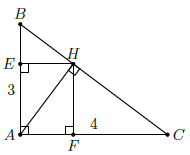
Tứ giác AEHF có ba góc A, E, F là góc vuông nên AEHF là hình chữ nhật.
Do đó: SAEHF = AE ⋅ AF
Ta có: BC = 5cm, AH = 2,4cm nên trong các tam giác vuông AHB và AHC ta có:
AE ⋅ AB = AH2 ⇒ AE × 3 = 2,42
⇒ AE = 2,76cm.
AF ⋅ AC = AH2 ⇒ AF × 4 = 2,42
⇒ AF = 1,44cm.
Suy ra: SAEHF = 2,76 × 1,44 = 3,9744 cm2
Câu 4. Cho tam giác ABC vuông tại A có đường cao AH. Biết BH = 25cm, CH = 144cm. Tính AB, AC, BC, AH.
Hướng dẫn giải
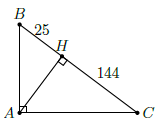
Ta có:
BC = BH + HC = 25 + 144 = 169cm.
AB2 = BH ⋅ BC = 25 × 169 ⇒ AB = 65cm.
AC2 = CH ⋅ CB = 144 × 169 ⇒ AC = 156cm.
AH = BH ⋅ CH = 25 × 144 ⇒ AH = 60cm.
Câu 5. Cho tam giác ABC vuông tại A có đường cao AH. Biết BH = cm, AH =
cm. Tính AB, AC, BC, CH.
Hướng dẫn giải
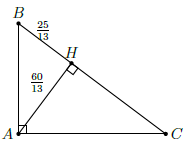
Ta có: BH ⋅ CH = AH2
⇔ × CH =
⇒ CH = cm.
BC = BH + CH = 13cm.
AB2 = BH2 + AH2 = 25 ⇒ AB = 5 cm.
AC2 = CH ⋅ CB = 144 ⇒ AC = 12cm.
Câu 6. Cho tam giác ABC vuông tại B, đường cao BH = cm và 4AB = 3BC. Tính AB, AC, BC, AH, CH.
Hướng dẫn giải
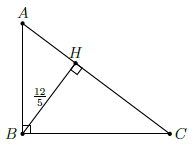
Từ giả thiết ta suy ra AB = BC.
Mặt khác, ta có: . Suy ra:
Suy ra BA = 3cm. Từ đây, ta tìm được: AC = 5cm, AH = 1,8cm, CH = 3,2cm.
Câu 7. Cho hình vuông ABCD có cạnh bằng cm. Gọi M, N lần lượt là trung điểm của AD, DC và I là giao điểm của AN và BM.
a) Chứng minh rằng AN vuông góc với MB.
b) Tính AI, MI.
c) Tính diện tích tứ giác BINC.
Hướng dẫn giải
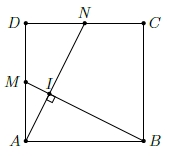
a) Xét hai tam giác ADN và BAM có , AD = AB, DN = AM.
Suy ra: ∆ADN = ∆BAM (c–g–c)
Do đó:
Suy ra:
Từ đây, ta có: AN ⊥ BM.
b) Ta có: BM2 = AM2 + AB2 = 5 + 20 = 25 ⇒ BM = 5cm.
Suy ra:
AI2 = AM2 − MI2 = 5 − 1 = 4 ⇒ AI = 2cm.
c) Ta có: SBCNI = SBCN + SBIN = (BI ⋅ IN + BC ⋅ CN) = 11cm2.
Câu 8. Cho tam giác ABC vuông tại A có BC = 5cm, đường cao AH = cm. Tính BH, CH.
Hướng dẫn giải
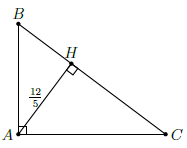
Giả sử BH ≥ CH. Ta có: BH + HC = BC = 5 (1)
Mặt khác: BH ⋅ CH = AH2 =
Từ (1) Ta có: (BH + CH)2 = 25.
Suy ra: BH2 + 2BH ⋅ CH + CH2 = 25
⇒ BH2 + CH2 = 25 – =
Do đó: (BH − CH)2 = BH2 − 2BH ⋅ CH + CH2
= –
=
Suy ra: BH − CH = (2)
Từ (1) và (2) ta có:
Câu 9. Cho tam giác ABC vuông tại A, đường cao AH, kẻ HM vuông góc với AB tại M. Chứng minh rằng:
Hướng dẫn giải
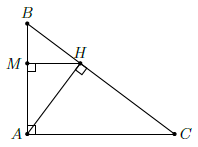
Trong tam giác vuông AHB ta có: BM ⋅ BA = BH2, suy ra:
Mặt khác, trong tam giác vuông ABC, ta có: BH ⋅ BC = AB2 hay
Do đó:
Vậy bài toán được chứng minh.
Câu 10. Cho hình vuông ABCD, I là điểm thay đổi trên cạnh AB (I khác A và B). Đường thẳng DI cắt BC tại K. Chứng minh rằng không đổi.
Hướng dẫn giải
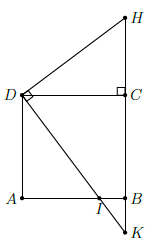
Qua D kẻ đường thẳng vuông góc với DI, cắt BC tại H.
Xét hai tam giác ADI và CDH có , AD = DC,
(cùng phụ với góc
).
Suy ra: ∆ADI = ∆CDH (g–c–g), do đó DI = DH.
Suy ra:
Từ đó ta có đpcm.
Câu 11. Cho tam giác ABC cân tại A, có góc A nhọn. Vẽ BM vuông góc với AC. Chứng minh rằng
Hướng dẫn giải
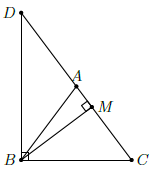
Gọi D là điểm đối xứng với C qua A, khi đó AB = AD = AC nên tam giác BCD vuông tại B và có đường cao BM.
Suy ra: CM ⋅ CD = BC2 ⇒ CM ⋅ 2AC = BC2, suy ra
Mà AB = AC, nên ta có:
Vậy bài toán được chứng minh.
Câu 12. Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 6cm và HC − HB = 9cm. Tính HB, HC.
Hướng dẫn giải
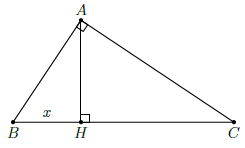
Đặt BH = x ⇒ CH = 9 + x với x > 0.
Ta có: AH2 = BH ⋅ HC
⇔ x(9 + x) = 36
⇔ x2 + 9x − 36 = 0
⇔ x = −9 ∨ x = 3.
Vậy HB = 3cm, HC = HB + 9 = 12cm.
Câu 13. Cho tam giác ABC vuông tại A, , đường cao AH = 18cm. Tính chu vi tam giác ABC.
Hướng dẫn giải
Đặt AB = 3x ⇒ AC = 4x với x > 0.
Suy ra:
Ta có:
Chu vi tam giác ABC bằng AB + BC + CA = 12x = 90cm.
Câu 14. Cho tam giác ABC vuông tại A với AB < AC và đường cao AH. Tính AB, AC biết AH = 6cm và diện tích tam giác ABC bằng 37,5cm2.
Hướng dẫn giải

Giả sử tam giác đó là ∆ABC có đường cao AH.
Ta có:
Đặt BH = x (x > 0). Ta có:
AH2 = BH ⋅ CH
⇔ 36 = x(12,5 − x)
⇔ x2 − 12,5x + 36 = 0
⇔ x = 4,5 ∨ x = 8.
Khi BH = 4,5 cm: AB2 = BH ⋅ BC = 4,5 × 12,5
⇒ AB = 7,5cm; AC = 10cm
Khi BH = 8cm: AB2 = BH ⋅ BC = 8 × 12,5
⇒ AB = 10cm; AC = 7,5cm.
Khi đó là ba cạnh của tam giác là AB = 7,5cm, AC = 10cm và BC = 12,5cm.
Câu 15. Cho hình thang ABCD vuông tại A và D. Hai đường chéo vuông góc với nhau tại O. Biết AB = , OA = 6. Tính diện tích hình thang.
Hướng dẫn giải
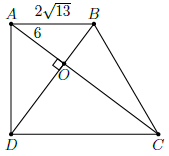
Xét ∆OAB vuông tại O, ta có:
Xét ∆ABD vuông tại A, đường cao AO ta có:
Ta có: OD = BD − OB = 13 − 4 = 9.
Xét ∆ADC vuông tại D ta có:
Mà
Vậy SABCD = AD (AB + DC) = 126,75 (đvdt)
Câu 16. Cho tam giác ABC vuông tại A. Đường cao AH, cạnh bên AC = 30, HB = 32. Tính độ dài AH, HC, AB.
Hướng dẫn giải
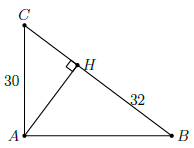
Đặt HC = x (x > 0). Xét ∆ABC vuông tại A, đường cao AH.
Ta có: AH2 = HC ⋅ HB
⇔ 302 = x(x + 32)
⇔ (x − 18)(x + 50) = 0
⇔ x = 18 (nhận) ∨ x = –50 (loại)
Xét ∆AHC vuông tại H ta có:
Xét ∆ABC vuông tại A ta có:
AB2 = HB ⋅ BC = 32(32 + 18) = 40
Câu 17. Cho hình chữ nhật ABCD có các cạnh AB = 60cm, AD = 32cm. Từ D kẻ đường thẳng vuông góc với đường chéo AC. Đường này cắt AC tại E và AB tại F. Tính độ dài các đoạn EA, EC, ED, FB, FD.
Hướng dẫn giải
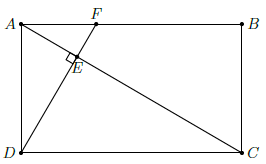
Xét tam giác vuông ADC ta có:
Xét tam giác vuông ADE có:
Câu 18. Tính diện tích hình thang ABCD, có đường cao bằng 12cm, hai đường chéo AC và BD vuông góc với nhau, DB = 15cm.
Hướng dẫn giải
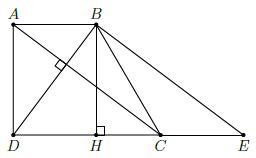
Qua B vẽ đường thẳng song song với AC, cắt DC ở E.
Gọi BH là đường cao của hình thang.
Ta có: BE // AC, AC ⊥ BD nên BE ⊥ BD.
Áp dụng định lí Pytago vào tam giác vuông BDH, ta có:
BH2 + HD2 = BD2
⇒ 122 + HD2 = 152
⇒ HD2 = 225 − 144 = 81
⇒ HD = 9cm.
Xét tam giác BDE vuông tại B, ta có:
BD2 = DE ⋅ DH ⇒ 152 = DE × 9
⇒ DE = 25cm.
Ta có: AB = CE nên AB + CD = CE + CD = DE = 25cm.
Do đó: SABCD = × 25 × 12 = 150cm2
Câu 19. Hình thang cân ABCD có đáy lớn CD = 10cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tìm đường cao của hình thang.
Hướng dẫn giải
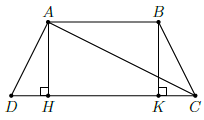
Gọi AH, BK là đường cao của hình thang.
Đặt AB = AH = BK = x.
Dễ dàng chứng minh được
Do đó:
Xét ∆ADC vuông tại A, ta có: AH2 = HD ⋅ HC. Do đó:
Từ đó suy ra x = cm.
Đường cao của hình thang bằng cm.
Câu 20. Tính diện tích một tam giác vuông có chu vi 72cm, hiệu giữa đường trung tuyến và đường cao ứng với cạnh huyền bằng 7cm.
Hướng dẫn giải
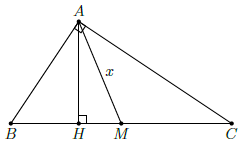
Đặt AM = x (x > 0), Ta có: BC = 2x, AH = x − 7.
Theo các hệ thức trong tam giác vuông
AB2 + AC2 = BC2 = 4x2 (1)
AB ⋅ AC = BC ⋅ AH = 2x(x − 7) (2)
Từ (1) và (2) suy ra
AB2 + AC2 + 2AB ⋅ AC = 4x2 + 4x(x − 7)
⇔ (AB + AC)2 = 8x2 − 28x
⇔ (72 − 2x)2 = 8x2 − 28x
⇔ x2 + 65x − 1296 = 0
⇔ (x − 16)(x + 81) = 0
⇔ x = 16 (nhận) ∨ x = −81 (loại).
Từ đó BC = 32cm, AH = 9cm.
Diện tích tam giác ABC là:
SABC = × 32 × 9 = 144cm2.
Câu 21. Cho tam giác ABC có độ dài các cạnh AB, BC, CA là ba số tự nhiên liên tiếp tăng dần. Kẻ đường cao AH, đường trung tuyến AM. Chứng minh rằng HM = 2.
Hướng dẫn giải
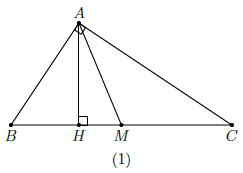
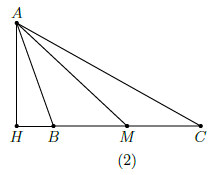
Đặt BC = a thì AB = a − 1, AC = a + 1.
Đặt HM = x. Ta thấy:
HB = MB − MH (nếu B ≤ 90°, xem hình (1))
HB = MH − MB (nếu B > 90°, xem hình (2))
Nên . Ta có: AC2 − HC2 = AB2 − HB2 (cùng bằng AH2) nên
Câu 22. Tam giác ABC cân tại A, gọi I là giao điểm của các đường phân giác. Biết IA = cm, IB = 3cm. Tính độ dài AB.
Hướng dẫn giải
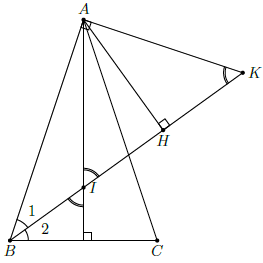
Đường vuông góc với AB tại A cắt BI ở K.
Ta có: phụ với
,
phụ với
Mà nên
Kẻ AH ⊥ BK. Đặt IH = HK = x.
Xét tam giác vuông ABK có
Suy ra:
Câu 23. Tam giác ABC có BC = 40cm, đường phân giác trong AD dài 45cm, đường cao AH dài 36cm. Tính các độ dài BD, DC.
Hướng dẫn giải
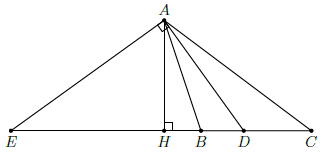
Đặt BD = x, DC = y. Giả sử x < y.
Ta tính được HD = 27cm. Vẽ tia phân giác của góc ngoài tại A, cắt BC ở E.
Ta có: AE ⊥ AD nên AD2 = DE ⋅ DH. Suy ra:
Theo tính chất đường phân giác trong và ngoài của tam giác ta có:
Mặt khác, thay y = 40 − x vào (1) và rút gọn được:
x2 − 115x + 1500 = 0
⇔ (x − 15)(x − 100) = 0
⇔ x = 15 (nhận) ∨ x = 100 (loại).
Từ đó suy ra y = 40 − x = 25cm
Vậy DB = 15cm, DC = 25cm.
Câu 24. Cho tam giác ABC vuông tại A, đường cao AH. Tính BH, CH biết AB = 12cm, BC = 20cm.
Hướng dẫn giải
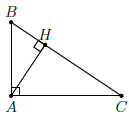
AB2 = BH ⋅ BC ⇔ 122 = BH × 20 ⇒ BH = 7,2cm
HC = 20 – 7,2 = 12,8cm
Câu 25. Cho tam giác ABC vuông tại A, đường cao AH. Tính AC, CH biết AH = 2cm, HB = 1cm.
Hướng dẫn giải

AH2 = BH ⋅ CH ⇔ 22 = 1 × CH ⇒ CH = 4cm
Nên BC = HB + HC = 1 + 4 = 5cm.
AC2 = CH ⋅ BC = 4 ⋅ 5 = 20 ⇒ AC = cm.
Câu 26. Cho tam giác ABC vuông tại A, đường cao AH. Tính AH, HB, HC biết AB = 3cm, AC = 4cm.
Hướng dẫn giải

Ta có:
Suy ra:
Câu 27. Cho tam giác ABC vuông tại A, đường cao AH. Tính AB, AC biết HB = 1cm, HC = 2cm.
Hướng dẫn giải

Ta có: BC = HB + HC = 2 + 1 = 3cm.
AB2 = BH ⋅ BC = 1 ⋅ 3 = 3 ⇒ AB = cm.
AC2 = CH ⋅ BC = 2 ⋅ 3 = 6 ⇒ AC = cm.
Câu 28. Cho tam giác ABC vuông tại A, đường cao AH. Tính BC, AC, AH biết AB = 15cm, HC = 16cm.
Hướng dẫn giải

Ta có:
AB2 = BH ⋅ BC
⇔ AB2 = BH(BH + 16)
⇔ 152 = BH2 + 16BH
⇔ BH2 + 16BH − 225 = 0
⇔ BH2 + 16BH − 225 = 0
⇔ (BH + 25)(BH − 9) = 0
⇔ BH = −25 (loại) ∨ BH = 9 (nhận).
Do đó: BH = 9cm, suy ra:
BC = HB + HC = 16 + 9 = 25cm.
AB2 = BH ⋅ BC = 9 ⋅ 25 = 225 ⇒ AB = 15cm.
AC2 = CH ⋅ BC = 16 ⋅ 25 = 400 ⇒ AC = 20cm.
Câu 29. Cho tam giác ABC vuông tại A, đường cao AH. Tính AB, AC biết AH = 12cm, BC = 25cm.
Hướng dẫn giải

Ta có: AH2 = HB ⋅ HC
⇔ 144 = HB ⋅ (25 − HB)
⇔ HB2 − 25HB + 144 = 0
⇔ (HB − 9)(HB – 16) = 0
⇔ HB = 9 ∨ HB = 16.
Vai trò của HB, HC như nhau, có thẻ giả sử HB = 9cm và HC = 16cm, nên
AB2 = BH ⋅ BC = 9 ⋅ 25 = 225 ⇒ AB = 15cm.
AC2 = CH ⋅ BC = 16 ⋅ 25 = 400 ⇒ AC = 20cm.
Câu 30. Cho tam giác ABC cân tại A có AH, BK là 2 đường cao. Chứng minh rằng
a)
b) BC2 = 2CK ⋅
Hướng dẫn giải
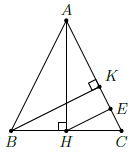
a) Kẻ HE vuông góc với AC, suy ta HE // BK, nên HE là đường trung bình trong tam giác BCK.
Trong tam giác AHC vuông tại H
Vậy
b) Ta có:
Vậy BC2 = 4CK ⋅ CA.
Câu 31. Cho tam giác ABC vuông cân tại A và một điểm M thuộc cạnh huyền BC. Chứng minh rằng MB2 + MC2 = 2MA2.
Hướng dẫn giải
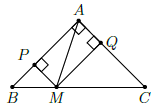
Từ M kẻ MP ⊥ AB; MQ ⊥ AC
Do , khi đó tam giác MPQ và MQC vuông cân
Nên MB2 = 2MP2 và MC2 = 2MQ2.
Suy ra: MB2 + MC2 = 2(MP2 + MQ2).
Mà APMQ là hình chữ nhật nên:
MP2 + MQ2 = PQ2 = MA2 (*)
Do đó từ (*), ta có: MB2 + MC2 = 2MA2.
Tỷ số lượng giác của góc nhọn
Tóm tắt lý thuyết
Khái niệm tỉ số lượng giác của một góc nhọn
Cho tam giác vuông và góc nhọn α như hình vẽ.
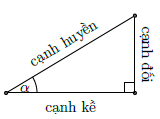
Khi đó:

Nhận xét:
– Tỉ số lượng giác của một góc nhọn luôn dương.
– sin α < 1, cos α < 1.
Tỉ số lượng giác của hai góc phụ nhau
Định lí 1. Nếu hai góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia.
Hệ quả 1.
Cho hai góc α và β với α + β = 90°, khi đó:
– sin α = cos β;
– cos α = sin β;
– tan α = cot β;
– cot α = tan β.
Bảng tỉ số lượng giác một số góc đặc biệt
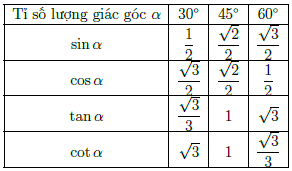
Bài tập vận dụng
Câu 1. Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Viết các tỉ số lượng giác của góc B.
Hướng dẫn giải
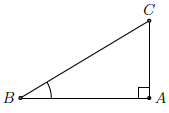
∆ABC vuông tại A nên
Ta có:
Câu 2. Dựng góc nhọn α biết tan α = .
Hướng dẫn giải
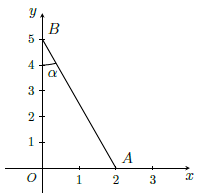
Dựng góc vuông xOy.
Trên tia Ox, lấy điểm A sao cho OA = 2; trên tia Oy, lấy điểm B sao cho OB = 5.
Góc OBA là góc α cần dựng.
Thật vậy,
Câu 3. Hãy viết tỉ số lượng giác của các góc sau thành tỉ số lượng giác của các góc nhỏ hơn 45°:
sin 75°, cos 60°, tan 80°, cot 50°.
Hướng dẫn giải
sin 75° = cos 15°;
cos 60° = sin 30°;
tan 80° = cot 10°;
cot 50° = tan 40°.
Câu 4. Cho tam giác ABC vuông tại A có và BC = 10. Tính độ dài cạnh AB và BC.
Hướng dẫn giải
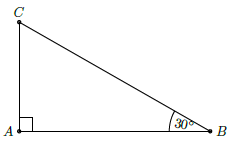
Tam giác ABC vuông tại A nên
Bài tập tự luyện
Câu 1.. Dựng góc nhọn α biết
a) sin α =
b) cos α = 0,6
c) tan α =
d) cot α =
Hướng dẫn giải
a) sin α =
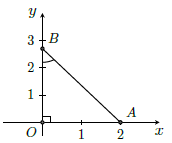
Vẽ góc vuông xOy.
Trên Ox lấy điểm A sao cho OA = 2cm.
Lấy A làm tâm, vẽ cung tròn bán kính 3cm sao cho cung tròn này cắt tia Oy tại B.
Khi đó: nên
b) cos α = 0,6
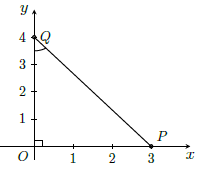
Vẽ góc vuông xOy.
Trên Ox lấy điểm P sao cho OP = 3cm.
Lấy P làm tâm, vẽ cung tròn bán kính 5cm sao cho cung tròn này cắt tia Oy tại Q.
Khi đó: nên
c) tan α =
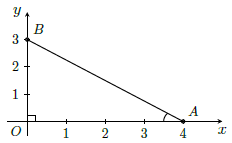
Vẽ góc vuông xOy.
Trên Ox lấy điểm A sao cho OA = 4cm.
Trên Oy lấy điểm B sao cho OB = 3cm.
Khi đó: nên
d) cot α =
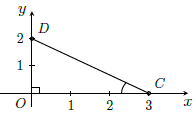
Vẽ góc vuông xOy.
Trên Ox lấy điểm C sao cho OC = 3cm.
Trên Oy lấy điểm D sao cho OD = 2cm.
Khi đó: nên
Câu 2. Cho tam giác ABC vuông tại A có AB = 6cm, . Biết tan α =
. Hãy tìm độ dài cạnh AC và BC.
Hướng dẫn giải
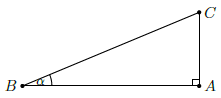
Xét ∆ABC vuông tại A có
Áp dụng định lý Py–ta–go vào ∆ABC vuông tại A ta có:
Câu 3. Tính giá trị của các biểu thức
a)
b) B = tan 76° − cot 14°
Hướng dẫn giải
a) Ta có: 32° + 58° = 90°
⇒ sin 32° = cos 58°
⇒ A = 1.
b) Ta có: 76° + 14° = 90°
⇒ tan 76° = cot 14°
⇒ B = 0.
Câu 4. Cho tam giác ABC có . Chứng minh rằng: BC2 = AB2 + AC2 − AB ⋅ AC.
Hướng dẫn giải
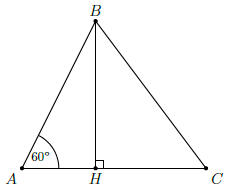
Kẻ đường cao BH của ∆ABC.
Khi đó ta có: HC2 = (AC − AH)2.
Áp dụng định lý Py–ta–go ta có:
BC2 = BH2 + HC2
= BH2 + (AC − AH)2
= BH2 + AH2 + AC2 − 2AC ⋅ AH
= AB2 + AC2 − 2AC ⋅ AH.
Lại có:
Vậy BC2 = AB2 + AC2 − AB ⋅ AC.
Câu 5. Cho tứ giác ABCD có α là góc nhọn tạo bởi hai đường chéo. Chứng minh rằng:
SABCD = AC ⋅ BC ⋅ sin α.
Hướng dẫn giải
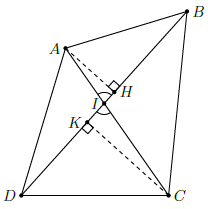
Giả sử hai đường chéo AC, BD cắt nhau tại I, là góc nhọn.
Kẻ đường cao AH của ∆ABD và đường cao CK của ∆CBD.
Ta có: AH = AI⋅sin α, CK = CI⋅sin α.
Diện tích ∆ABD là S∆ABD = BD ⋅ AH.
Diện tích ∆CBD là S∆CBD = BD ⋅ CK.
Khi đó: SABCD = S∆ABD + S∆CBD
= BD(AH + CK)
= BD(AI + CI) sin α
= BD ⋅ AC ⋅ sin α
Hệ thức về cạnh và góc trong tam giác vuông
Tóm tắt lý thuyết
Định lí 1. Trong tam giác vuông, mỗi cạnh góc vuông bằng:
– Cạnh huyền nhân với sin góc đối hoặc nhân với cos góc kề;
– Cạnh góc vuông kia nhân với tan góc đối hoặc nhân với cot góc kề.
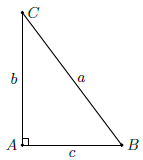
Vậy trong tam giác ABC vuông tại A, ta có các hệ thức:
– b = a ⋅ sin B = a ⋅ cos C.
– b = c ⋅ tan B = c ⋅ cot C.
– c = a ⋅ sin C = a ⋅ cos B.
– c = b ⋅ tan C = b ⋅ cot B.
Phân dạng bài tập
Dạng 1. Giải tam giác vuông
Phương pháp
Sử dụng mối quan hệ giữa cạnh và góc trong tam giác vuông để giải.
Bài tập vận dụng
Câu 1. Cho tam giác ABC với các cạnh góc vuông AB = 5, AC = 8. Hãy giải tam giác vuông ABC.
Hướng dẫn giải
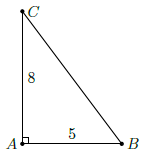
Theo định lí Py–ta–go, ta có:
Mặt khác:
Tra bảng hay dùng máy tính bỏ túi, ta tìm được .
Do đó:
Câu 2. Cho tam giác OPQ vuông tại O có , PQ = 7. Hãy giải tam giác vuông OPQ.
Hướng dẫn giải
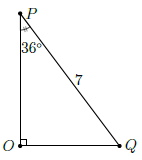
Ta có:
Theo các hệ thức giữa cạnh và góc trong tam giác vuông, ta có:
OP = PQ ⋅ sin Q = 7 ⋅ sin 54° ≈ 5,663
OQ = PQ ⋅ sin P = 7 ⋅ sin 36° ≈ 4,114.
Câu 3. Cho tam giác ABC vuông tại A có AB = 12cm, . Hãy tính độ dài:
a) AC.
b) BC.
c) Phân giác BD.
Hướng dẫn giải
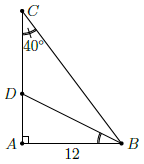
Ta có:
Ta có:
Vì BD là phân giác góc nên
. Do đó:
Dạng 2. Tính cạnh và góc của tam giác
Phương pháp
Kẻ thêm đường cao để xuất hiện tam giác vuông; áp dụng các hệ thức lượng trong tam giác vuông.
Bài tập vận dụng
Câu 1. Cho tam giác ABC, trong đó BC = 11cm, . Gọi điểm N là chân của đường vuông góc kẻ từ A đến cạnh BC. Hãy tính độ dài đoạn thẳng AN.
Hướng dẫn giải
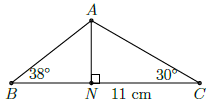
Ta có:
Tương tự: . Khi đó ta có:
Câu 2. Cho tam giác ABC có BC = 6cm, . Hãy tính:
a) Chiều cao CH và cạnh AC.
b) Diện tích tam giác ABC.
Hướng dẫn giải
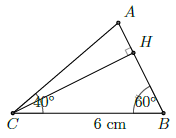
a) Tam giác BHC vuông tại H
Mà
Tam giác AHC vuông tại H
b) Ta có:
Do vậy:
Ta có:
Dạng 3. Toán thực tế
Phương pháp
Dùng hệ thức giữa cạnh và góc trong tam giác vuông để giải quyết các tình huống thực tế.
Bài tập vận dụng
Câu 1. Một cột đèn điện AB cao 6m có bóng in trên mặt đất là AC dài 3,5m. Hãy tính góc (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất.

Hướng dẫn giải
Tam giác ABC vuông tại A, ta có:
Suy ra:
Câu 2. Một cầu tuột trong công viên có độ dốc là 28°, và có độ cao là 2,1m. Tính độ dài của mặt cầu trượt (làm tròn đến chữ số thập phân thứ nhất).
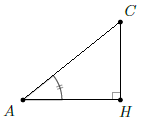
Hướng dẫn giải
Đặt độ dốc là góc ; độ cao là CH = 2,1m; chiều dài mặt cầu trượt là cạnh AC.
Ta cần tính độ dài cạnh AC.
Tam giác AHC vuông tại H, ta có:
Bài tập tự luyện
Câu 1.. Cho tam giác ABC vuông tại A, có BC = a, AC = b, AB = c. Giải tam giác ABC, biết rằng b = 10cm, .
Hướng dẫn giải
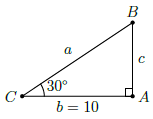
Vì ∆ABC vuông tại A, b = 10cm, nên ta có:
Câu 2. Một cột đèn có bóng trên mặt đất dài 7,5m. Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 42°. Tính chiều cao của cột đèn.
Hướng dẫn giải
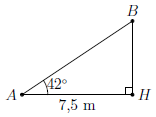
Giả sử chiều cao cột đèn là BH và chiều dài tia nắng trên mặt đất là AH.
Xét tam giác ABH vuông tại H có:
Câu 3. Một chiếc diều với đoạn dây thả diều AB dài 100m, dây thả diều tạo với phương thẳng đứng một góc 40° (hình bên). Tính chiều cao của diều.
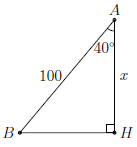
Hướng dẫn giải
Trong tam giác vuông AHB vuông tại H, ta có:
AH = AB ⋅ cos 40° = 100 × 0,766 = 76,6 (m).
Câu 4. Cho ∆ABC vuông tại A, đường cao AH. Biết HB = 25cm, HC = 64cm. Tính số đo các góc B và C.
Hướng dẫn giải
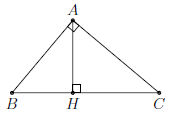
Áp dụng hệ thức lượng trong tam giác vuông ABC, ta có:
AH2 = HB ⋅ HC = 25 × 64 nên AH = 5 × 8 = 40 (cm).
Trong tam giác vuông AHB, ta có:
Câu 5. Cho tam giác ABC có BC = 15cm, và
. Gọi H là chân đường cao hạ từ đỉnh A xuống BC. Hãy tính
a) Độ dài đoạn thẳng AH.
b) Độ dài đoạn thẳng AC.
Hướng dẫn giải
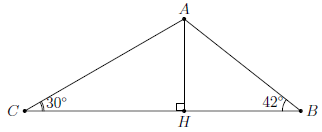
a) Đặt AH = x. Ta có:
Do đó: BC = CH + HB ≈ 2,8426x
b) Ta có:
Câu 6. Cho tam giác ABC vuông tại A. Biết AB = 3cm, BC = 5cm.
a) Giải tam giác vuông ABC.
b) Từ B kẻ đường thẳng vuông góc với BC, đường thẳng này cắt đường thẳng AC tại D. Tính độ dài các đoạn thẳng AD và BD.
Hướng dẫn giải
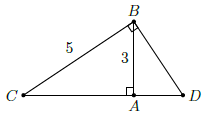
a) Do tam giác ABC vuông tại A nên
Ta có:
b) Vì BD ⊥ BC nên . Xét tam giác ABD vuông tại A có AB = 3cm, do vậy
AB2 = AD ⋅ AC ⇒ AD = = 2,25cm.
BD2 = DA ⋅ DC = 2,25(2,25 + 4) = 14,0625 ⇒ BD = 3,75cm.
Câu 7. Cho ∆ABC vuông tại A, AB = 21cm, . Tính độ dài đường phân giác BD.
Hướng dẫn giải
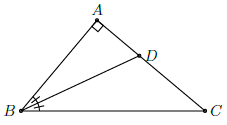
Ta có:
Vì BD là tia phân giác của góc nên
Trong tam giác vuông ABD, ta có:
Câu 8. Tính diện tích ∆ABC có BC = 40cm, .
Hướng dẫn giải
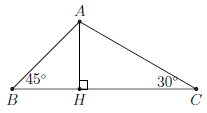
Ta có:
Kẻ đường cao AH. Ta có: HC = AH ⋅ cot 30° = AH.
Mặt khác:
Vậy
Câu 9. Khoảng cách giữa hai chân tháp AB và MN là x (như hình vẽ). Từ đỉnh A của tháp AB nhìn lên đỉnh M của tháp MN ta được góc α. Từ đỉnh A nhìn xuống chân N của tháp MN ta được góc β (so với phương nằm ngang AH). Hãy tìm chiều cao MN nếu x = 120 m, α = 30° và β = 20°.
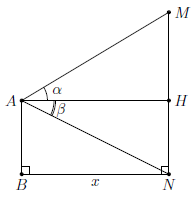
Hướng dẫn giải
Xét tam giác MAH vuông tại H có HM = AH ⋅ tan α.
Xét tam giác NAH vuông tại H có HN = AH ⋅ tan β.
Do đó MN = MH + HN = AH(tan α + tan β)
= 120 ⋅ (tan 30° + tan 20°) ≈ 113m.
Câu 1.0. Cho hình thang ABCD có AB // CD, , AB = 3,5 và AD = 3,1. Tính diện tích hình thang ABCD.
Hướng dẫn giải

Vẽ BH ⊥ CD tại H, khi đó ta có: BH = AD = 3,1 và DH = AB = 3,5.
Xét tam giác BHC vuông tại H, có
HC = BH ⋅ cot C = 3,1 ⋅ cot 38° ≈ 4.
Do vậy CD = CH + HD ≈ 4 + 3,5 ≈ 7,5.
Diện tích hình thang ABCD là
Câu 11. Cho hình thang cân ABCD (AB // CD), AB = 2cm, CD = 6cm, chiều cao bằng 4cm. Tính góc nhọn tạo bởi hai đường thẳng chứa cạnh bên hình thang.
Hướng dẫn giải
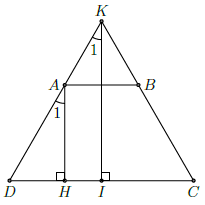
Gọi K là giao điểm của AD và BC. Kẻ AH và KI vuông góc với CD.
Ta có:
Nên . Suy ra
Câu 12. Cho ∆ABC có , đường trung tuyến AM. Tính số đo góc AMC.
Hướng dẫn giải
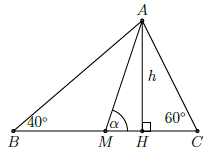
Kẻ đường cao AH.
Ta có: HB − HC = (HM + MB) − (MC − HM) = 2HM.
Đặt AH = h, . Ta có:
Câu 13. Tính diện tích tam giác ABC biết , BC = 2cm.
Hướng dẫn giải
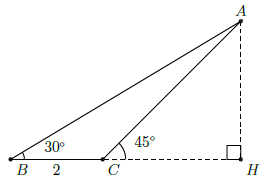
Kẻ đường cao AH. Ta có:
Suy ra:
Vậy
Bài tập trắc nghiệm
Câu 1.. Cho tam giác ABC vuông tại A, kẻ đường cao AH. Hệ thức nào sau đây là đúng?
A. AH2 = BH ⋅ BC
B. AC2 = CH ⋅ BC
C. AH2 = AB ⋅ AC
D. AH = BH ⋅ AB
Hướng dẫn giải
Chọn B
Theo hệ thức lượng trong tam giác vuông.
Câu 2. Cho tam giác ABC vuông tại A và có đường cao AH. Hệ thức nào sau đây là sai?
A. AB2 = BH ⋅ BC.
B. AH2 = BH ⋅ CH
C.
D.
Hướng dẫn giải
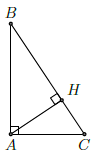
Chọn D
Ta có:
Câu 3. Cho tam giác ABC có AB = 3; AC = 4; BC = 5, kẻ đường cao AH. Hệ thức nào sau đây là sai?
A. AH2 = BH ⋅ CH
B. BH2 = AH ⋅ CH
C. AB2 = BH ⋅ BC
D.
Hướng dẫn giải
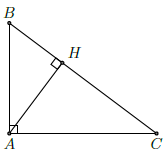
Chọn B
Có AB2 + AC2 = BC2 ⇒ ABC là tam giác vuông tại A.
Câu 4. Cho tam giác ABC vuông tại B và có đường cao BH. Hệ thức nào sau đây là đúng?
A. BH2 = AH ⋅ CH
B. AH2 = BH ⋅ CH
C. AB2 = BH ⋅ BC
D. AB2 + AC2 = BC2
Hướng dẫn giải
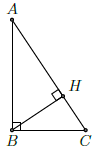
Chọn A
Chú ý là tam giác vuông tại B và đường cao là BH.
Câu 5. Tam giác ABC có đường cao AH thỏa mãn AH2 = BH ⋅ CH thì khẳng định nào sau đây là đúng?
A. Tam giác ABC vuông tại A
B. AB2 = BH ⋅ BC
C. ∆AHB ~ ∆CHA
D. AB2 + AC2 = BC2
Hướng dẫn giải
Chọn C
Ta chỉ có ∆AHB ~ ∆CHA chứ tam giác ABC có thể không vuông.
Câu 6. Cho tam giác ABC vuông tại A có AB = 3; AC = 4. Kẻ đường cao AH. Độ dài AH là:
A. AH = 5
B. AH = 2,4
C. AH = 2,25
D. AH = 4
Hướng dẫn giải

Chọn B
Ta có:
Câu 7. Cho tam giác vuông tại A có AB = 5. Kẻ đường cao AH. Biết BH = , độ dài AH là:
A. AH =
B. AH = 5
C. AH =
D. AH = 13
Hướng dẫn giải

Chọn A
Ta có: AB2 = BH ⋅ BC ⇒ BC = 13
⇒ CH = BC − BH =
Ta có: AH2 = BH ⋅ CH ⇒ AH =
Câu 8. Cho tam giác ABC vuông tại A và đường cao AH. Biết AH = 9, BH = 12. Giá trị là:
A.
B.
C.
D.
Hướng dẫn giải

Chọn D
Ta có:
Câu 9. Cho tam giác vuông ABC vuông tại A có AB = 6, BC = 10. AH là đường cao. Độ dài BH và AH lần lượt là
A. BH = 6,4; AH = 4,6
B. BH = 3,6; AH = 4,8
C. BH = 3,6; AH = 6,4
D. BH = 6,4; AH = 4,8
Hướng dẫn giải

Chọn B
Ta có: AB2 = BH ⋅ BC ⇒ BH = 3,6.
Ta có: CH = BC − BH = 6,4
Mà AH2 = BH ⋅ CH ⇒ AH = 4,8.
Câu 1.0. Cho tam giác vuông tại A có đường cao AH. Biết BH = 9, CH = 7. Độ dài AB và AC lần lượt là
A. AB = ; AC = 12
B. AB = 12; AC =
C. AB = 12; AC =
D. AB = ; AC =
Hướng dẫn giải

Chọn C
Ta có: AH2 = BH ⋅ CH ⇒ AH =
Ta có tam giác ABH vuông tại H nên ta có:
AB2 = AH2 + BH2 ⇒ AB = 12.
Ta có tam giác ACH vuông tại H nên ta có:
AC2 = AH2 + CH2 ⇒ AC =
Câu 11. Tam giác vuông ABC có AB : AC lần lượt tỉ lệ với 3 : 4. Biết AH = 6. Cạnh BC có độ dài là bao nhiêu
A. BC = 11,5
B. BC = 12
C. BC = 12,5
D. BC = 13
Hướng dẫn giải

Chọn C
Ta có:
Mà
Từ đó
Vậy
Câu 12. Cho tam giác ABC vuông tại A và đường cao AH. Biết AH = 6 và AB2 = 135 + AC2. Tính tỉ số
A. 5
B. 3
C. 4
D. 6
Hướng dẫn giải

Chọn C
Ta có: . Mà
Câu 13. Cho tam giác ABC vuông tại A và đường cao AH. Kẻ HE ⊥ AB (H ∈ AB). Cho AB = 4; AC = 2, hãy tính độ dài đoạn HE.
A. HE =
B. HE =
C. HE =
D. HE = 2
Hướng dẫn giải
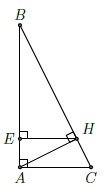
Chọn A
Ta có:
Ta có: AH2 = AE ⋅ AB ⇒ AE =
HE2 = AH2 − AE2 =
Câu 14. Cho tam giác ABC vuông tại A và đường cao AH. Kẻ HE ⊥ AB (H ∈ AB).Cho HE = 6; AC = 9, tính độ dài đoạn BC.
A. BC =
B. BC =
C. BC =
D. BC = 18
Hướng dẫn giải

Chọn C
Ta có:
Gọi BE = x ⇒ AE = x − x =
x.
Mà HE2 = BE ⋅ AE ⇒ x ⋅ x = 62 ⇔ x =
Ta có: BH2 = BE2 + EH2 ⇒ BH =
Mà
Câu 15. Cho hình thang vuông ABCD có , AB = AD = 2, DC =
. Tính độ dài đường chéo AC.
A. AC = 8
B. AC = 6
C. AC =
D. AC =
Hướng dẫn giải
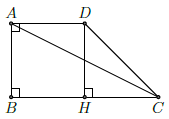
Chọn D
Kẻ DH ⊥ BC (H ∈ BC).
Ta có: DC2 = DH2 + HC2 ⇒ HC = 2.
Vậy BC = BH + HC = AD + HC = 4
Câu 16. Cho tam giác ABC vuông tại A có . Khẳng định nào sau đây sai?
A.
B.
C.
D.
Hướng dẫn giải
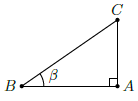
Chọn C
Theo định nghĩa về tỉ số lượng giác của góc nhọn trong tam giác vuông, ta có:
;
;
;
Câu 17. Cho , với 0° < α < 90°. Giá trị của sin α bằng:
A.
B.
C.
D.
Hướng dẫn giải
Chọn A
Ta có:
Suy ra: (do sin α > 0, với 0° < α < 90°)
Câu 18. Cho tam giác ABC vuông tại A, có AB = BC. Tính cot C.
A.
B.
C.
D.
Hướng dẫn giải
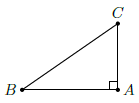
Chọn B
Ta có:
Mặt khác: sin2 C + cos2 C = 1
⇒ cos2 C = 1 − sin2 C =
Do 0 < cos C < 1 nên cos C =
Suy ra:
Câu 19. Khẳng định nào sau đây là đúng?
A. sin 55° = cos 45°
B. cos 12° = sin 78°
C. tan 60° = sin 30°
D. cot 75° = sin 15°
Hướng dẫn giải
Chọn B
Định lý: Nếu hai góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia.
Do đó, chỉ có khẳng định cos 12° = sin 78° là đúng.
Câu 20. Cho tam giác như hình bên. Hỏi khẳng định nào sau đây đúng?
A. sin α = sin β
B. cos α = cos β
C. cot α = sin β
D. tan α = cot β
Hướng dẫn giải
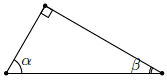
Chọn D
Vì α và β là hai góc phụ nhau nên sin góc này bằng cos góc kia, tan góc này bằng cot góc kia.
Câu 21. Trong hình bên, cạnh x được tính như thế nào?
A.
B. x = 15 ⋅ tan 60°
C. x = 15 ⋅ cos 30°
D.
Hướng dẫn giải
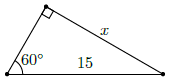
Chọn C
Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông, ta có:
Câu 22. Cho hình vẽ bên. Hỏi khẳng định nào sau đây đúng?
A.
B.
C.
D.
Hướng dẫn giải
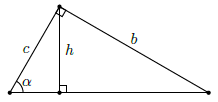
Chọn D
Chỉ có công thức là đúng.
Câu 23. Cho tam giác ABC vuông tại A và cos C = 0,6. Hãy tính tan B.
A.
B.
C.
D.
Hướng dẫn giải
Chọn A
Ta có: sin B = cos (90° − B) = cos C = 0,6.
Mặt khác, 0 < cos B < 1 và sin2 B + cos2 B = 1
⇒ cos2 B = 1 − 0,62 = 0,64
⇒ cos B = 0,8.
Suy ra:
Câu 24. Tìm x trong hình vẽ bên.
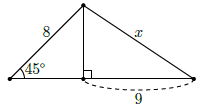
A.
B.
C.
D.
Hướng dẫn giải
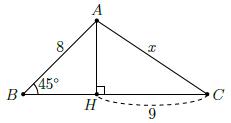
Chọn D
Gọi tên các đỉnh như hình vẽ.
Ta có:
Áp dụng định lý Py–ta–go trong tam giác vuông AHC
Suy ra:
Câu 25. Khẳng định nào sau đây là sai?
A. sin2 25° + cos2 25° = 1
B. cos2 12° + cos2 78° = 1
C. tan 35° ⋅ cot 55° = 1
D. cot 85° ⋅ tan 85° = 1.
Hướng dẫn giải
Chọn C
Vì sin2 α + cos2 α = 1 nên sin2 25° + cos2 25° = 1.
cos2 12° + cos2 78° = cos2 12° + sin2 12° = 1.
Vì tan α ⋅ cot α = 1 nên cot 85° ⋅ tan 85° = 1.
tan 35° ⋅ cot 55° = 1 là khẳng định sai.
Câu 26. Cho hình vẽ bên. Hãy tính sin C.
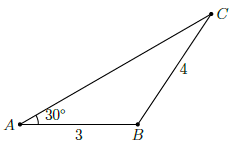
A.
B.
C.
D.
Hướng dẫn giải
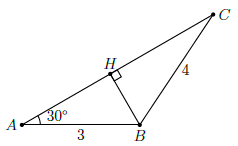
Chọn A
Kẻ BH ⊥ AC tại H. Tam giác AHB vuông tại B, ta có:
Ta lại có, tam giác BHC vuông tại H, suy ra:
Câu 27. Cho góc nhọn α với . Tính giá trị biểu thức
A.
B.
C.
D.
Hướng dẫn giải
Chọn B
Vì sin α > 0 nên chia tử và mẫu của P cho sin α ta được:
Câu 28. Cho tam giác ABC, biết BC = 11cm và . Tính độ dài đoạn AB (kết quả làm tròn đến hai chữ số thập phân).
A. 7,32cm
B. 7,66cm
C. 6,98cm
D. 8,16cm
Hướng dẫn giải
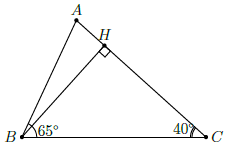
Chọn A
Ta có:
Kẻ BH ⊥ AC tại H. Ta có:
Lại có:
Suy ra: AB ≈ 7,32cm.
Câu 29. Cho hình thang cân ABCD với AB // CD. Biết AB = 5cm, CD = 9cm và . Diện tích hình thang ABCD gần bằng với số nào dưới đây?
A. 12,12cm2
B. 48,49cm2
C. 24,25cm2
D. 19,8cm2
Hướng dẫn giải
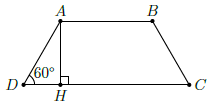
Chọn C
Kẻ AH ⊥ CD tại H.
Vì ABCD là hình thang cân với AB // CD nên
Tam giác ADH vuông tại H, suy ra
Khi đó, diện tích hình thang ABCD là:
Câu 30. Cho tứ giác ABCD có diện tích S và α là góc nhọn tạo bởi hai đường chéo AC và BD. Khẳng định nào sau đây là đúng?
A. S = AC ⋅ BD ⋅ sin α
B. S = AC ⋅ BD ⋅ cos α
C. S = AC ⋅ BD ⋅ sin α
D. S = AC ⋅ BD ⋅ cos α
Hướng dẫn giải
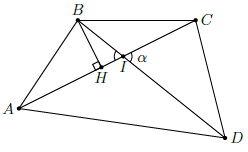
Chọn C
Kẻ BH ⊥ AC tại H.
Ta có: SABC = BH ⋅ AC =
BI ⋅ sin α ⋅ AC.
Tương tự: SACD = DI ⋅ sin α ⋅ AC.
Suy ra: SABCD = SABC + SACD
= BI ⋅ sin α ⋅ AC +
DI ⋅ sin α ⋅ AC
= AC ⋅ BD ⋅ sin α.
Câu 31. Cho tam giác ABC vuông tại B. Mệnh đề nào sau đây sai?
A. AC2 = AB2 + BC2
B. AB = BC ⋅ sin C
C. BC = AB ⋅ tan A
D. sin A = cos C
Hướng dẫn giải
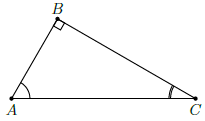
Chọn B
Trong tam giác ABC tại B ta có:
Theo định lí Pi–ta–go thì AC2 = AB2 + BC2
Câu 32. Trong tam giác vuông có góc nhọn α, mệnh đề nào sau đây đúng?
A. Mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hay nhân với cô–sin góc kề
B. Mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc kề hay nhân với cô–tang góc đối
C. Tỉ số giữa cạnh đối và cạnh huyền được gọi là cô–sin của góc α
D. Tỉ số giữa cạnh kề và cạnh đối được gọi là tang của góc α
Hướng dẫn giải
Chọn A
Ta có:
Mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hay nhân với cô–sin góc kề.
Mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối hay nhân với cô–tang góc kề.
Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α.
Tỉ số giữa cạnh kề và cạnh đối được gọi là cô–tang của góc α.
Câu 33. Cho tam giác MNP vuông tại M có NP = 15cm và sin P = . Độ dài của cạnh MN bằng
A. cm
B. cm
C. 8cm
D. cm
Hướng dẫn giải
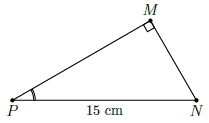
Chọn C
Trong tam giác MNP vuông tại M thì MN là cạnh đối của , còn NP là cạnh huyền nên
Câu 34. Cho tam giác IJK vuông tại J có IJ = 10cm và tan K = . Tính độ dài của KJ.
A. cm
B. cm
C. cm
D. cm
Hướng dẫn giải
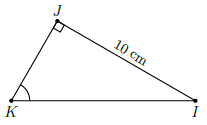
Chọn B
Trong tam giác IJK vuông tại J thì IJ, KJ lần lượt là cạnh đối, cạnh kề của nên
Câu 35. Cho tam giác ABC vuông tại A có và AB = 10cm. Độ dài của BC bằng bao nhiêu?
A. cm
B. cm
C. cm
D. cm
Hướng dẫn giải
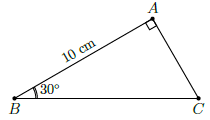
Chọn D
Trong tam giác vuông ABC ta có:
Câu 36. Cho tam giác ABC vuông tại A có AB = 3cm và . Độ dài cạnh AC bằng
A. 6cm
B. cm
C. cm
D. 1,5cm
Hướng dẫn giải
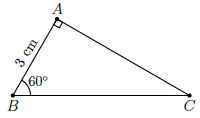
Chọn C
Trong tam giác ABC ta có:
Câu 37. Cho tam giác ABC vuông tại A có AB = 6 và cos C = . Độ dài của cạnh AC bằng
A.
B.
C.
D.
Hướng dẫn giải
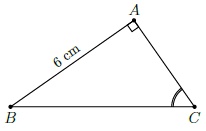
Chọn A
Trong tam giác ABC vuông tại A thì là góc nhọn. Suy ra:
Lại có:
Vậy
Câu 38. Cho tam giác ABC vuông tại A có AB = 12cm và tan B = . Tính độ dài cạnh BC.
A. BC = 16cm
B. BC = 18cm
C. BC = cm
D. BC = cm
Hướng dẫn giải
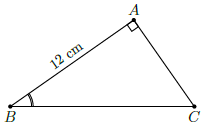
Chọn D
Trong tam giác ABC ta có:
Vậy
Câu 39. Cho tam giác ABC có đường cao AH và trung tuyến AM (với H, M thuộc BC). Biết HB = 9cm, HC = 16cm. Tính
A.
B.
C.
D.
Hướng dẫn giải
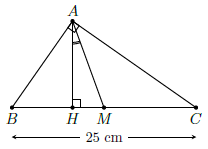
Chọn D
Ta có: AH2 = HB ⋅ HC = 144 nên AH = 12cm.
Lại có: BC = HB + HC = 25cm, nên BM = BC= 12,5cm.
Suy ra: HM = BM − HB = 3,5cm.
Vậy
Câu 40. Cho tam giác ABC vuông tại A, đường cao AH. Cho biết CH = 6cm và . Độ dài đường cao AH là
A. 2cm
B. cm
C. 4cm
D. cm.
Hướng dẫn giải
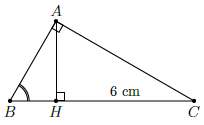
Chọn B
Tam giác ABC vuông tại A có , suy ra
Trong tam giác vuông AHC ta có:
Vậy
Câu 41. Cho tam giác ABC vuông tại A có AB = 3cm và BC = 5cm. Tính giá trị của biểu thức P = cot B + cot C.
A.
B.
C.
D.
Hướng dẫn giải
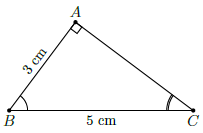
Chọn B
Ta có:
Khi đó:
Vậy
Câu 42. Cho tam giác ABC vuông tại A có BC = 25, AC = 15. Số đo của góc C (làm tròn đến phút) bằng
A. 53°8′
B. 36°52′
C. 53°13′
D. 36°53′
Hướng dẫn giải
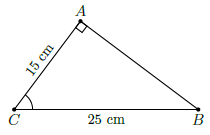
Chọn A
Trong tam giác vuông ABC ta có:
Câu 43. Cho tam giác MNP có và MN = 4cm. Tính độ dài đường cao kẻ từ đỉnh M.
A. 3,28cm
B. 3,76cm
C. 2,29cm
D. 4,26cm
Hướng dẫn giải
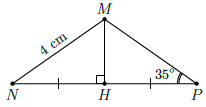
Chọn C
Trong tam giác MNP có nên nó là tam giác cân tại M, suy ra MP = MN = 4cm.
Kẻ đường cao MH ⊥ NP tại H. Xét tam giác vuông MHP có
Câu 44. Cho tam giác ABC có AB = 8cm, AC = 12cm và . Độ dài của cạnh BC bằng
A.
B.
C.
D.
Hướng dẫn giải
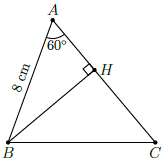
Chọn C
Kẻ BH ⊥ AC tại H. Xét tam giác vuông ABH ta có:
Như vậy CH = AC − AH = 12 − 4 = 8cm.
Xét tam giác BHC vuông tại C ta có:
Câu 45. Cho tam giác ABC có AB = 8cm, AC = 12cm và . Tính diện tích S của tam giác ABC.
A. S = 48cm2
B. S = 24cm2
C. S = 96cm2
D. S = 72cm2.
Hướng dẫn giải
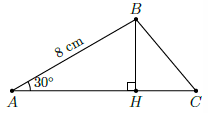
Chọn B
Kẻ BH ⊥ AC tại H nên BH là đường cao của tam giác ABC.
Xét tam giác vuông ABH ta có:
Diện tích tam giác ABC là:
S = AC ⋅ BH =
⋅ 12 ⋅ 4 = 24cm2.
Câu 46. Cho tam giác ABC có và BC = 4. Độ dài của AB bằng bao nhiêu?
A.
B.
C.
D.
Hướng dẫn giải
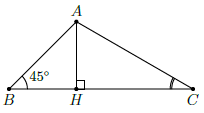
Chọn D
Trong tam giác ABC ta có:
Kẻ AH ⊥ BC tại H.
Xét tam giác ABH vuông tại H có BH = AH ⋅ cot B = AH.
Xét tam giác ACH vuông tại H có CH = AH ⋅ cot C = AH
Lại có:
Trong tam giác ABH vuông tại H ta có:
Câu 47. Cho ∆ABC vuông tại A, đường cao AH. Biết AB = cm, HC = 2cm. Tính HB?
A. HB = 1cm
B. HB = 2cm
C. HB = 3cm
D. HB = 4cm
Hướng dẫn giải
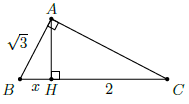
Gọi BH = x (x > 0). Ta có ∆ABC vuông tại A, AH ⊥ BC
Nên AB2 = BH ⋅ BC
⇔ 3 = x(x + 2)
⇔ x2 + 2x − 3 = 0
⇔ (x − 1)(x + 3) = 0
⇔ x = 1.
Vậy BH = 1cm.
Câu 48. Cho ∆ABC vuông tại A, đường cao AH, biết 9HB = 4HC, AH = 6cm. Tính BC.
A. BC = 13cm
B. BC = 12cm
C. BC = 11cm
D. BC = 9cm
Hướng dẫn giải
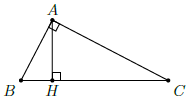
Chọn A
Ta có: ∆ABC vuông tại A, AH ⊥ BC nên AH2 = HB ⋅ CH. Do đó:
9HB = 4HC
⇔ 9HB2 = 4HC ⋅ HB
⇔ 9HB2 = 4AH2 = 144
⇔ HB = 4
⇒ HC = 9, BC = 13.
Câu 49. Cho ∆ABC vuông tại A, có AB = 4, tia phân giác trong và phân giác ngoài tại đỉnh B của ∆ABC cắt AC tại D và E. Biết AD = 2cm. Tính độ dài DE.
A. DE = 6cm
B. DE = 8cm
C. DE = 9cm
D. DE = 10cm
Hướng dẫn giải
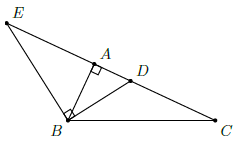
Chọn B
Ta có: BD, BE là phân giác trong và ngoài đỉnh B của ∆ABC nên BD ⊥ BE.
Xét ∆DBE vuông tại B, BA ⊥ DE nên
AB2 = AD ⋅ AE
⇔ 16 = 2 ⋅ AE
⇔ AE = 8 ⇒ DE = 10cm.
Câu 50. Cho ∆ABC vuông tại B, phân giác trong AD, biết CD = 2BD. Tính .
A. = 20°
B. = 30°
C. = 45°
D. = 60°
Hướng dẫn giải
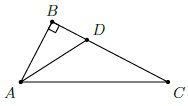
Chọn B
Ta có: AD là phân giác trong đỉnh A của ∆ABC nên
Mà ∆ABC vuông tại B nên
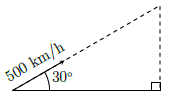
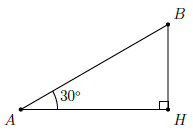
Câu 51. Một chiếc máy bay, bay lên với vận tốc 500km/h. Đường bay lên tạo với phương nằm ngang một góc 30°. Hỏi sau 1,2 phút máy bay lên cao được bao nhiêu km theo phương thẳng đứng?
A. 50km
B. 10km
C. 25km
D. 5km.
Hướng dẫn giải
Chọn D
Sau 1,2 phút = 0,02 giờ quãng đường máy bay bay được là:
AB = 500 × 0,02 = 10 km.
Xét ∆ABC vuông tại H, . Ta có:
Câu 52. Lúc 2 giờ chiều, ánh nắng mặt trời chiếu nghiêng tạo với mặt đất một góc 68°, lúc đó bóng một cây cau dài 1,2 m. Chiều cao của cây cau đó gần bằng:
A. 2,5m
B. 3m
C. 3,3m
D. 3,5m.
Hướng dẫn giải
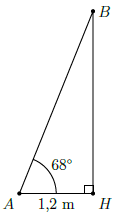
Chọn B
Xét ∆ABH vuông tại H có , AH = 1,2 m. Ta có:
Vậy độ cao cây cau gần bằng 3 m.
Câu 53. Cho ∆ABC vuông tại A, AH⊥BC. Biết . Tính
.
A.
B.
C.
D.
Hướng dẫn giải
Chọn B
Ta có: nên tan B = cot C. Mà ∆AHC vuông tại H
Nên suy ra
. Khi đó:
Câu 54. Cho góc nhọn α thỏa mãn sin α ⋅ cos α = . Tính B = sin α + cos α.
A.
B.
C.
D.
Hướng dẫn giải
Chọn A
Ta có: sin α > 0, cos α > 0
Và sin2 α + cos2 α = 1.
Do đó: B2 = (sin α + cos α)2
= sin2 α + cos2 α + 2 sin α ⋅ cos α
= 1 + =
⇒ B =