Định nghĩa hình vuông
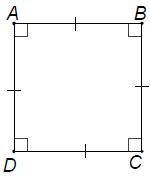
Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau
Tứ giác ABCD là hình vuông ![\[ \Leftrightarrow \left\{ \begin{gathered} \widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \hfill \\ AB = BC = CD = DA \hfill \\ \end{gathered} \right.\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-1.svg)
Từ định nghĩa hình vuông suy ra hình vuông vừa là hình chữ nhật, vừa là hình thoi.
Tính chất hình vuông
Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.
Dấu hiệu nhận biết
Ba dấu hiệu từ hình chữ nhật:
+) Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
+) Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
+) Hình chữ nhật có một đường chéo là đường phân giác thì nó là hình vuông.
Hai dấu hiệu từ hình thoi:
+) Hình thoi có một góc vuông là hình vuông.
+) Hình thoi có hai đường chéo bằng nhau là hình vuông.
Nhận xét: Một tứ giác vừa là hình chữ nhật, vừa là hình thoi thì tứ giác đó là hình vuông.
Cách vẽ hình vuông
Có năm cách vẽ hình vuông, nhưng hay dùng hai cách sau:
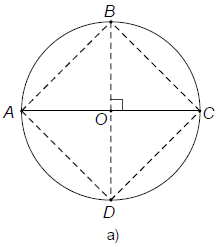
Cách 1 (hình a): Vẽ một đường chéo, dựng đường trung trực của đường chéo đó. Lấy trung điểm vừa dựng làm tâm vẽ đường tròn có đường kính bằng đường chéo vừa vẽ, nó cắt đường trung trực tại hai điểm ta được đường chéo thứ hai.
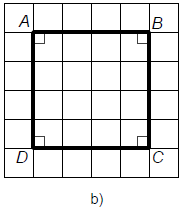
Cách 2 (hình b): Sử dụng lưới ô vuông để vẽ tứ giác có bốn góc vuông và bốn cạnh bằng nhau. Lưu ý:
+) Cách 1 chứng minh được là hình vuông.
+) Cách 2 không chứng minh được là nhận được hình vuông, chỉ là ảnh hình vuông.
Phân dạng bài tập
Dạng 1. Nhận dạng hình vuông
Phương pháp giải
Sử dụng một trong hai cách sau:
Cách 1: Chứng minh tứ giác là hình chữ nhật có thêm dấu hiệu hai cạnh kề bằng nhau hoặc hai đường chéo vuông góc hoặc một đường chéo là đường phân giác của một góc.
Cách 2: Chứng minh tứ giác là hình thoi có thêm dấu hiệu có một góc vuông hoặc hai đường chéo bằng nhau.
Bài 1. Cho hình sau, tứ giác AEDF là hình gì? Vì sao?
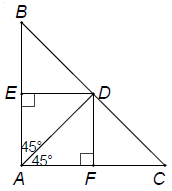
Hướng dẫn giải
Tứ giác AEDF là hình vuông.
Giải thích:
Theo hình vẽ thì ![\[\widehat A = \widehat E = \widehat F = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-2.svg)
. Tứ giác AEDF có ba góc vuông nên nó là hình chữ nhật. Hình chữ nhật AEDF có AD là đường phân giác của góc ![\[\widehat A\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-3.svg)
nên nó là hình vuông.
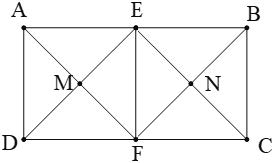
Bài 2. Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F lần lượt là trung điểm của AB và CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.
a) Tứ giác ADFE là hình gì? Vì sao?
b) Tứ giác MENF là hình gì? Vì sao?
Hướng dẫn giải
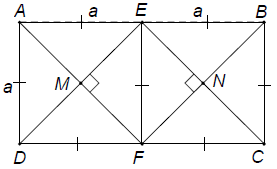
Đặt AD = a thì AB = 2a.
Áp dụng tính chất về cạnh và giả thiết vào hình chữ nhật ABCD, ta được:
AE = EB = BC = CF = FA = a
a) Tứ giác ADFE là hình vuông.
Giải thích: Vì tứ giác ADFE có bốn cạnh bằng nhau nên nó là hình thoi.
Hình thoi ADFE có ![\[\widehat A = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-4.svg)
nên nó là hình vuông.
b) Tứ giác MENF là hình vuông.
Giải thích:
Chứng minh tương tự như câu a) ta cũng có tứ giác EBCF là hình vuông.
Áp dụng tính chất về đường chéo vào hai hình vuông ADFE và MENF, ta được:
![\[\left\{ \begin{gathered} AF{\text{ }} \bot {\text{ }}DE;{\text{ }}EC{\text{ }} \bot {\text{ }}FB \hfill \\ \widehat {{E_1}} = \widehat {{E_2}} = 45^\circ \hfill \\ \end{gathered} \right. \Rightarrow \widehat M = \widehat N = \widehat E = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-5.svg)
Tứ giác MENF có ba góc vuông nên nó là hình chữ nhật.
Hình chữ nhật MENF lại có EF là đường phân giác của góc MEN nên nó là hình vuông.
Bài 3. Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho AM = BN = CP = DQ. Chứng minh rằng tứ giác MNPQ là hình vuông.
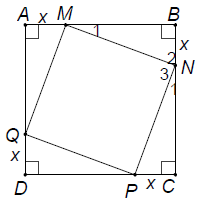
Hướng dẫn giải
Gọi độ dài cạnh hình vuông là a và AM = BN = CP = DQ = x
Áp dụng định nghĩa và giả thiết vào hình vuông ABCD, ta được:
![\[\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-6.svg)
và MB = NC = PD = QA = a – x
Nên bốn tam giác vuông MBN, NCP, PDQ, QAM bằng nhau trường hợp (c.g.c)
Suy ra bốn cạnh tương ứng của các tam giác đó bằng nhau là MN = NP = PQ = QA.
Tứ giác MNPQ có bốn cạnh bằng nhau nên nó là hình thoi.
Áp dụng tính chất về góc và kết quả hai tam giác bằng nhau vào hai tam giác MBN, NCP ta được:
![\[\left\{ \begin{gathered} \widehat {{M_1}} + \widehat {{N_2}} = 90^\circ \hfill \\ \widehat {{M_1}} = \widehat {{N_1}} \hfill \\ \end{gathered} \right. \Rightarrow \widehat {{N_1}} + \widehat {{N_2}} = 90^\circ {\text{ }}\left( 1 \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-7.svg)
Lại có góc ![\[\widehat {BNC}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-8.svg)
là góc bẹt hay
![\[\widehat {BNC} = \widehat {{N_1}} + \widehat {{N_2}} + \widehat {{N_3}} = 180^\circ {\text{ }}\left( 2 \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-9.svg)
Từ (1) và (2) suy ra ![\[\widehat {{N_3}} = 180^\circ - 90^\circ = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-10.svg)
Điều này chứng tỏ hình thoi MNPQ có một góc vuông nên nó là hình vuông.
Bài tập tự luyện
Bài 1. Nêu các tính chất về đường chéo của hình vuông. Chỉ rõ tính chất nào có ở hình bình hành, ở hình chữ nhật, ở hình thoi.
Hướng dẫn giải
Hình vuông có các tính chất sau về đường chéo.
+) Hai đường chéo cắt nhau tại trung điểm của mỗi đường (có ở hình bình hành).
+) Hai đường chéo bằng nhau (có ở hình chữ nhật).
+) Hai đường chéo vuông góc với nhau (có ở hình thoi).
+) Hai đường chéo là các đường phân giác của các góc của hình vuông (có ở hình thoi).
Bài 2. Tứ giác có bốn cạnh bằng nhau và hai đường chéo vuông góc có phải là hình vuông không? Nếu không hãy sửa lại một dấu hiệu để tứ giác là hình vuông.
Hướng dẫn giải
Câu trả lời là không. Phải sửa lại dấu hiệu về đường chéo là: Hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau.
Bài 3. Các câu sau đúng hay sai?
a) Hình chữ nhật có hai đường chéo bằng nhau là hình vuông.
b) Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
c) Hình thoi có hai đường chéo vuông góc với nhau là hình vuông.
d) Hình thoi có hai đường chéo bằng nhau là hình vuông.
Hướng dẫn giải
Các câu đúng là: a, b, d. Câu sai là c.
Bài 4. Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy hai điểm D, E sao cho BD = DE = EC. Qua D và E kẻ các đường vuông góc với BC, chúng cắt AB AC, lần lượt ở K và H. Tứ giác KHED là hình gì? Vì sao?
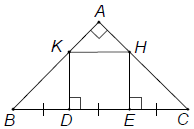
Hướng dẫn giải
Tứ giác KHED là hình vuông.
Giải thích: Tam giác vuông BDK có ![\[\widehat B = 45^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-11.svg)
nên là tam giác cân, do đó BD = DK. Chứng minh tương tự, HE = EC.
Vì BD = DE = EC theo giả thiết, nên: KD = DE = EH
Tứ giác KHED có KD // HE, KD = HE nên là hình bình hành.
Hình bình hành này lại có ![\[\widehat D = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-12.svg)
nên nó là hình chữ nhật.
Hình chữ nhật này lại có KD = DE nên nó là hình vuông.
Bài 5. Cho một hình chữ nhật có hai cạnh kề không bằng nhau. Chứng minh rằng các tia phân giác của các góc của hình chữ nhật đó cắt nhau tạo thành một hình vuông.
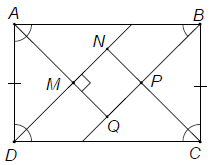
Hướng dẫn giải
Vì △NCD có ![\[\widehat {{C_1}} = \widehat {{D_1}} = 45^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-13.svg)
nên NCD vuông cân tại N.
Suy ra: ![\[\widehat N = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-14.svg)
và ND = NC (1)
Chứng minh tương tự, ![\[\widehat P = \widehat Q = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-15.svg)
. Tứ giác MNPQ có ba góc vuông nên là hình chữ nhật.
△AMD = △BPC (g.c.g) ⇒ MD = PC (2)
Trừ theo vế đẳng thức (1) cho đẳng thức (2) ta được NM = NP.
Như vậy hình chữ nhật MNPQ có hai cạnh kề bằng nhau nên là hình vuông.
Bài 6. Cho hình vuông ABCD. Trên AD lấy điểm E, trên tia đối của tia AD lấy điểm F, trên tia đối của tia BA lấy điểm I sao cho DE = AF = BI. Vẽ hình vuông AFGH, H thuộc cạnh AB. Chứng minh rằng tứ giác EGIC là hình vuông.
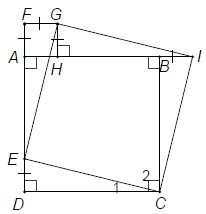
Hướng dẫn giải
Chứng minh bốn tam giác vuông EFG, IHG, CBI, CDE bằng nhau để suy ra EG = GI = IC = CE và ![\[\widehat {{C_1}} = \widehat {{C_3}}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-16.svg)
. Sau đó chứng minh ![\[\widehat {ECI} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-17.svg)
Dạng 2. Sử dụng định nghĩa, tính chất của hình vuông để chứng minh các quan hệ bằng nhau, song song, vuông góc, thẳng hàng
Phương pháp giải
Sử dụng định nghĩa, tính chất và bổ đề về hình vuông.
Bài 1. Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, trên cạnh CD lấy điểm N sao cho BM = CN và AM ⊥ BN.
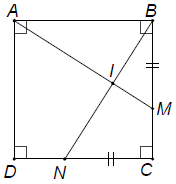
Hướng dẫn giải
Áp dụng định nghĩa và giả thiết vào hình vuông ABCD, ta được:
![\[\left\{ \begin{gathered} AB = BC \hfill \\ \widehat A = \widehat B = 90^\circ \hfill \\ BM = CN \hfill \\ \end{gathered} \right.\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-18.svg)
⇒ △ABM = △BCN (c.g.c) nên AM = BN
Gọi I là giao diểm của AM và BN.
Áp dụng tính chất về góc vào tam giác vuông ABM và BCN kết quả của hai tam giác bằng nhau, ta được:
![\[\left\{ \begin{gathered} \widehat {{A_1}} + \widehat {{M_1}} = 90^\circ \hfill \\ \widehat {{B_1}} = \widehat {{A_1}} \hfill \\ \end{gathered} \right. \Rightarrow \widehat {{B_1}} + \widehat {{M_1}} = 90^\circ {\text{ }}\left( 1 \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-19.svg)
Áp dụng tính chất về góc vào tam giác BIM ta có: ![\[\widehat {{B_1}} + \widehat {{M_1}} + \widehat {{I_1}} = 180^\circ {\text{ }}\left( 2 \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-20.svg)
Từ (1) và (2) suy ra: ![\[\widehat I = 180^\circ - 90^\circ = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-21.svg)
hay AM ⊥ BN
Bài 2. Bổ đề về hình vuông
Cho hình vuông ABCD. Nếu các điểm M, N, P, Q lần lượt nằm trên các đường thẳng AB, BC, CD và DA thì MP = NQ ⇔ MP ⊥ NQ
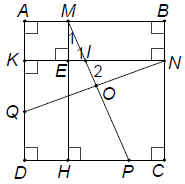
Hướng dẫn giải
Ta cần chứng minh bài toán đúng với các điểm M, N, P, Q nằm trên các cạnh AB, BC, CD, DA (các trường hợp còn lại chứng minh tương tự).
Gọi H, K lần lượt là chân các đường vuông góc kẻ từ M, N đến hai cạnh CD, DA và E, I, O thứ tự là giao điểm của MH với NK, MP với NQ.
Áp dụng định nghĩa vào hình vuông ABCD và tính chất góc đồng vị của KN // DC, ta được:
![\[\widehat A = \widehat B = \widehat C = \widehat E = \widehat K = \widehat N = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-22.svg)
Các tứ giác MBHC, KNCD và MBNE là các tứ giác có ba góc vuông nên chúng là các hình chữ nhật.
+) MP = NQ ⇒ MP ⊥ NQ
Áp dụng tính chất về cạnh và giả thiết vào hai hình chữ nhật MBHC, KNCD và hình vuông ABCD ta được:
![\[\left\{ \begin{gathered} MH = BC,{\text{ }}NK = CD \hfill \\ BC = CD,{\text{ }}MP = NQ \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} MH = MK \hfill \\ MP = NQ \hfill \\ \end{gathered} \right.\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-23.svg)
⇒ △MHP = △NKQ (trường hợp cạnh huyền, cạnh góc vuông).
Áp dụng tính chất về góc vào hai tam giác bằng nhau ở trên và tính chất của hai góc đối đỉnh ta có:
![\[\left\{ \begin{gathered} \widehat {{M_1}} = \widehat {{N_1}} \hfill \\ \widehat {{I_1}} = \widehat {{I_2}} \hfill \\ \end{gathered} \right. \Rightarrow \widehat O = \widehat E = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-24.svg)
(vì hai tam giác, có hai cặp góc bằng nhau thì cặp góc thứ ba cũng bằng nhau).
Vậy MP vuông góc với NQ tại O.
b) MP ⊥ NQ ⇒ MP = NQ
Xét hai tam giác MEI và NOI có ![\[\widehat {{I_1}} = \widehat {{I_2}}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-25.svg)
vì đối đỉnh, ![\[\widehat O = \widehat E = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-26.svg)
suy ra ![\[\widehat {{M_1}} = \widehat {{N_1}}\left( 1 \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-27.svg)
vì hai tam giác, có hai cặp góc bằng nhau thì cặp góc còn lại cũng bằng nhau.
Lại có: ![\[\widehat H = \widehat K = 90^\circ ,MH = NK\left( 2 \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-28.svg)
theo câu a).
Từ (1) và (2) suy ra △MHB = △NKQ (c.g.c) nên MP = NQ.
Bài 3. Cho hình vuông ABCD cạnh a. Trên hai cạnh BC, CD lấy hai điểm M, N sao cho ![\[\widehat {MAN} = 45^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-29.svg)
, trên tia đối của tia DC lấy điểm K sao cho DK = BM. Hãy tính:
a) Số đo góc ![\[\widehat {KAN}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-30.svg)
.
b) Chu vi tam giác MCN theo a.
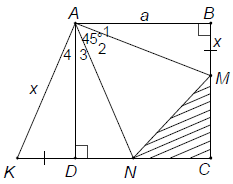
Hướng dẫn giải
a) Áp dụng định nghĩa và giả thiết vào hình vuông ABCD, ta được:
![\[\left\{ \begin{gathered} \widehat A = \widehat D = 90^\circ \hfill \\ AB = AD,BM = DK \hfill \\ \end{gathered} \right.\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-31.svg)
⇒ △ABM = △ADK (c.g.c).
Áp dụng kết quả của hai tam giác bằng nhau ở trên và giả thiết, ta có:
![\[\begin{gathered} \left\{ \begin{gathered} \widehat {{A_1}} + \widehat {{A_2}} + \widehat {{A_3}} = 90^\circ \hfill \\ \widehat {{A_1}} = \widehat {{A_4}},{\text{ }}\widehat {{A_2}} = 45^\circ \hfill \\ \end{gathered} \right.\begin{array}{*{20}{c}} {} \\ {} \\ {} \\ {} \end{array} \hfill \\ \Rightarrow \widehat {KAN} = \widehat {{A_3}} + \widehat {{A_4}} = \widehat {{A_1}} + \widehat {{A_3}} = 90^\circ - 45^\circ = 45^\circ \hfill \\ \end{gathered} \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-32.svg)
b) Đặt BM = DK = x thì KN = x + DN, MC = a – x, CN = a – DN.
Từ kết quả của hai tam giác bằng nhau ở câu a) và giả thiết, ta được:
![\[\left\{ \begin{gathered} AM = AK,{\text{ }}AM = AN \hfill \\ \widehat {MAN} = \widehat {KAN} = 45^\circ \hfill \\ \end{gathered} \right.\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-33.svg)
⇒ △AMN = △AKN (c.g.c) ⇒ MN = KN
Vậy chu vi tam giác MCN bằng
MC + CN + NM = a – x + a – DN + x + DN = 2a
Bài 4. Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, qua A kẻ AN ⊥ AM (điểm N thuộc tia đối của tia DC). Gọi I là trung điểm của MN. Chứng minh rằng:
a) AM = AN
b) Ba điểm B, I, D thẳng hàng.
Hướng dẫn giải
a) Áp dụng định nghĩa và giả thiết vào hình vuông ABCD, ta được:
![\[\left\{ \begin{gathered} \widehat A = \widehat B = \widehat D \hfill \\ \widehat {{A_1}} + \widehat {{A_2}} = \widehat {{A_2}} + \widehat {{A_3}} = \widehat A = 90^\circ \hfill \\ AB = AD \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} \widehat B = \widehat D = 90^\circ \hfill \\ AB = AD \hfill \\ \widehat {{A_3}} = \widehat {{A_1}} \hfill \\ \end{gathered} \right.\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-34.svg)
⇒ △ABM = △ADN (c.g.c).
Do đó: AM = AN
b)
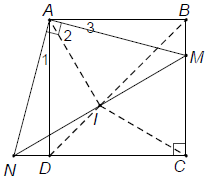
Cách 1: Nối IA, IC thì IA và IC lần lượt là các đường trung tuyến ứng với cạnh huyền của hai tam giác vuông AMN, CMN.
Áp dụng tính chất đường trung tuyến ứng với cạnh huyền vào hai tam giác vuông trên và định nghĩa hình vuông ta được: ![\[\left\{ \begin{gathered} IA = IC = \frac{1}{2}MN\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ BA = BC \hfill \\ \end{gathered} \right.\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-35.svg)
Điều này chứng tỏ hai điểm B và I cách đều hai điểm A và C nên BI là đường trung trực của đoạn AC. Mặt khác theo tính chất về đường chéo của hình vuông thì BD là trung trực của AC mà đoạn AC thì chỉ có một đường trung trực nên BI trùng với BD hay B, I, D thẳng hàng.
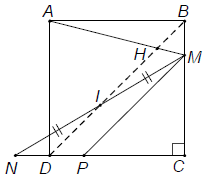
Cách 2: Qua M kẻ MP // BD (1) (điểm P ∈ DC) suy ra DI // MP (2).
Lại có NI = MI (3) theo giả thiết. Từ (2) và (3) suy ra ND = DP (4) theo định lí đường trung bình.
Từ (3) và (4) ta có DI là đường trung bình của tam giác NMP.
Áp dụng định lí đường trung bình vào tam giác NMP ta được DI // MP (5).
Từ (1) và (5) suy ra B, I, D thẳng hàng, vì từ điểm I ở ngoài đường thẳng MP chỉ kẻ được một đường thẳng song song với MP.
Cách 3: Qua M kẻ MH // ND (1) (điểm H ∈ BD) thì ![\[\widehat {{D_1}} = \widehat {{H_1}}\left( 2 \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-36.svg)
do đồng vị.
Mà BD là đường chéo của hình vuông ABCD nên BD là đường phân giác của hai góc vuông B và D do đó ![\[\widehat {{D_1}} = \widehat {{H_1}} = 45^\circ \left( 3 \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-37.svg)
.
Từ (2) và (3) ta có BM = MH (4) vì trong một tam giác, đối diện với hai góc bằng nhau là hai cạnh bằng nhau.
Kết hợp (1) với (4) ta được tứ giác NHMD có hai cạnh đối song song và bằng nhau nên nó là hình bình hành.
Áp dụng tính chất về đường chéo vào hình bình hành NHMD, ta được đường chéo DH đi qua trung điểm I của đường chéo NM nên BD đi qua I.
Điều đó chứng tỏ B, I, D thẳng hàng.
Bài tập tự luyện
Bài 1. Cho hình vuông ABCD cạnh a. Gọi E là một điểm nằm giữa C và D. Tia phân giác của góc ![\[\widehat {DAE}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-38.svg)
cắt CD ở F. Kẻ FH ⊥ AE (H ∈ AE), FH cắt BC ở K.
a) Tính độ dài AH.
b) Tính số đo góc ![\[\widehat {FAK}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-39.svg)
.
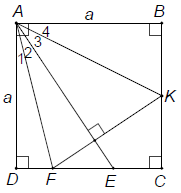
Hướng dẫn giải
a) △ADF = △AHF (cạnh huyền – góc nhọn)
⇒ AH = AD = a
b) AHK = ABK (cạnh huyền – cạnh góc vuông)
![\[ \Rightarrow \widehat {{A_3}} = \widehat {{A_4}}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-40.svg)
Kết hợp với giả thiết, ta có:
![\[\widehat {FAK} = \widehat {{A_2}} + \widehat {{A_3}} = \frac{1}{2} \cdot 90^\circ = 45^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-41.svg)
Bài 2. Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của BC, CD và I là giao điểm của AN, DM.
Chứng minh rằng:
a) AN ⊥ DM
b) BA = BI
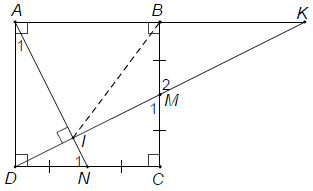
Hướng dẫn giải
a) Áp dụng định nghĩa và giả thiết vào hình vuông ABCD ta được:
![\[\left\{ \begin{gathered} AD = DC,{\text{ }}\widehat D = \widehat C \hfill \\ DN = CM \hfill \\ \end{gathered} \right.\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-42.svg)
⇒ △ADN = △DCM (c.g.c).
![\[ \Rightarrow \widehat {{A_1}} = \widehat {{D_1}}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-43.svg)
Vì AND vuông ở D, nên ![\[\widehat {{A_1}} + \widehat {{N_1}} = 90^\circ {\text{ }}\left( 1 \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-44.svg)
Thay ![\[\widehat {{A_1}} = \widehat {{D_1}}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-45.svg)
vào đẳng thức (1) ta được ![\[\widehat {{D_1}} + \widehat {{N_1}} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-46.svg)
Điều này chứng tỏ tam giác DIN vuông ở I hay AN ⊥ DM
b) Gọi giao điểm của DM với AB là K, khi đó
⇒ △DMC = △KMB (g.c.g) ⇒ BK = DC
Lại có AB = DC nên AB = BK suy ra IB là trung tuyến ứng với cạnh huyền của tam giác vuông AIK. Do đó: IB = BA
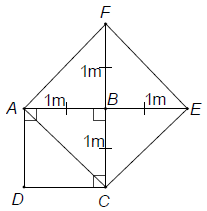
Bài 3. Cho một hình vuông cạnh dài 1m. Vẽ hình vuông thứ hai nhận đường chéo của hình vuông đã cho làm cạnh. Tính độ dài đường chéo của hình vuông này.
Hướng dẫn giải
Xét hình vuông ABCD có AB = BC = 1m
Ta đi dựng hình vuông nhận đường chéo AC làm cạnh để tính đường chéo của hình vuông mới này.
Trên tia đối của tia BA lấy điểm E, tia đối của tia BC lấy điểm F sao cho BE = BF = 1m.
Ta được tứ giác AFEC có hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường nên nó là hình vuông cạnh AC.
Hình vuông này có đường chéo AE = 2m
Bài 4. Cho hình vuông ABCD. Trên tia đối của tia CB lấy điểm M, trên tia đối của tia DC lấy điểm N sao cho BM = DN. Vẽ hình bình hành MANF, gọi O là trung điểm của AF. Chứng minh rằng:
a) Tứ giác MANF là hình vuông.
b) F thuộc tia phân giác của góc ![\[\widehat {MCN}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-47.svg)
.
c) AC ⊥
d) Tứ giác BOFC là hình thang.
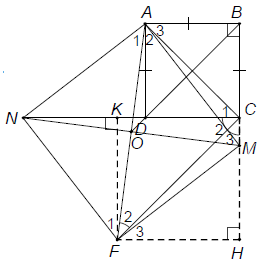
Hướng dẫn giải
a) △ABM = △AND (c.g.c)
![\[ \Rightarrow AM = AN,\widehat {{A_1}} = \widehat {{A_3}}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-48.svg)
Hình bình hành MANF có hai cạnh kề bằng nhau nên là hình thoi.
Do góc ![\[\widehat {{A_2}}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-49.svg)
phụ với góc ![\[\widehat {{A_3}}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-50.svg)
nên góc ![\[\widehat {{A_1}}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-51.svg)
phụ với ![\[\widehat {{A_2}}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-52.svg)
hay ![\[\widehat {MAN} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-53.svg)
Điều này chứng tỏ hình thoi MANF là hình vuông vì có một góc vuông.
b) Kẻ FH, FK theo thứ tự vuông góc với hai đường thẳng BC, NC thu được tứ giác KCHF có ba góc vuông nên là hình chữ nhật, suy ra: ![\[\widehat {KFH} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-54.svg)
Lại có: ![\[\widehat {NFM} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-55.svg)
vì là góc của hình vuông nên ![\[\widehat {{F_1}} = \widehat {{F_3}}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-56.svg)
do cùng phụ với ![\[\widehat {{F_2}}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-57.svg)
Từ đó: △FKN = △FHM (cạnh huyền – góc nhọn)
Điều nay chứng tỏ điểm F cách đều hai cạnh CM, CN của góc nên F thuộc tia phân giác của góc
c) Theo tính chất về đường chéo của hình vuông và từ câu b) ta có:
![\[\widehat {{C_1}} = \widehat {{C_2}} = 45^\circ \Rightarrow \widehat {ACF} = 90^\circ \Rightarrow AC{\text{ }} \bot {\text{ }}CF\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-58.svg)
d) Tương tự như trên ta có:
![\[\widehat {{B_1}} = \widehat {{C_3}} = 45^\circ \Rightarrow OB\parallel CF\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-59.svg)
Tứ giác BOFC có hai cạnh đối song song nên là hình thang.
Dạng 3. Tìm điều kiện để một hình trở thành hình vuông
Phương pháp giải
+) Sử dụng các dấu hiệu nhận biết hình vuông.
+) Nếu bài toán chỉ yêu cầu tìm vị trí của một điểm nào đó để một hình trở thành hình vuông ta làm như sau: Giả sử hình đó là hình vuông rồi dựa vào các tính chất của hình vuông để chỉ ra vị trí cần tìm.
Bài 1. Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB thứ tự ở E và F.
a) Tứ giác AEDF là hình gì? Vì sao?
b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi?
c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông?
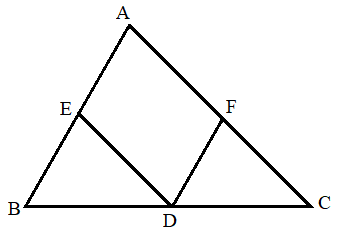
Hướng dẫn giải
a) Tứ giác AEDF là hình bình hành.
Giải thích: Từ giả thiết ![\[\left\{ \begin{gathered} DE\parallel AC \hfill \\ DF\parallel AB \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} DE\parallel AF \hfill \\ DF\parallel AE \hfill \\ \end{gathered} \right.\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-60.svg)
Tứ giác AEDF có các cạnh đối song song nên nó là hình bình hành.
b) Giả sử AEDF là hình thoi khi đó theo tính chất vẽ đường chéo của hình thoi thì AD là đường phân giác của góc
Vậy nếu D là giao điểm của tia phân giác góc với cạnh BC thì tứ giác AEDF là hình thoi.
c) Nếu tam giác ABC vuông tại A thì hình bình hành AEDF là hình chữ nhật.
Nếu tam giác ABC vuông tại A và D là giao điểm của tia phân giác góc với cạnh BC thì AEDF vừa là hình chữ nhật vừa là hình thoi nên nó là hình vuông.
Bài 2. Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD và DA. Hai đường chéo AC và BD phải thoả mãn những điều kiện nào để M, N, P, Q là bốn đỉnh của:
a) Hình chữ nhật?
b) Hình thoi?
c) Hình vuông?
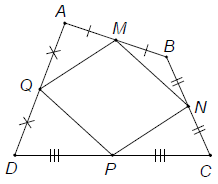
Hướng dẫn giải
Trước hết ta chứng minh tứ giác MNPQ là hình bình hành
a) MNPQ là hình chữ nhật ⇔ MN ⊥ NP
⇔ AC ⊥ BD (vì MN // AC, NP //BD).
Điều kiện cần tìm là hai đường chéo AC, BD vuông góc với nhau.
b) MNPQ là hình thoi ⇔ MN = NP
⇔ AC = BD (vì MN = ![\[\frac{1}{2}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-62.svg)
AC, NP = BD)
Điều kiện cần tìm là các đường chéo AC và BD bằng nhau.
c) MNPQ là hình vuông
![\[ \Leftrightarrow \left\{ \begin{gathered} MN{\text{ }} \bot {\text{ }}PQ \hfill \\ MN = PQ \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} AC{\text{ }} \bot {\text{ }}BD \hfill \\ AC = BD \hfill \\ \end{gathered} \right.\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-63.svg)
Điều kiện cần tìm là các đường chéo AC, BD bằng nhau và vuông góc với nhau.
Bài tập tự luyện
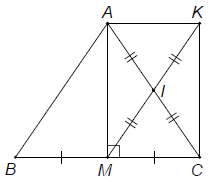
Bài 1. Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng với M qua điểm I.
a) Tứ giác AMCK là hình gì? Vì sao?
b) Tứ giác AKMB là hình gì? Vì sao?
c) Tìm điều kiện của tam giác ABC để tứ giác AMCK là hình vuông.
Hướng dẫn giải
Tứ giác AMCK là hình chữ nhật.
Giải thích:
Tứ giác AMCK có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
Hình bình hành này lại có ![\[\widehat {AMC} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-64.svg)
theo tính chất của tam giác cân nên nó là hình chữ nhật.
b) Tứ giác AKMB là hình bình hành vì có hai cạnh đối là AK, BM song song và bằng nhau.
c) Hình chữ nhật AMCK là hình vuông
⇔ AM = MC ⇔ AM = BC
⇔ △ABC vuông tại A
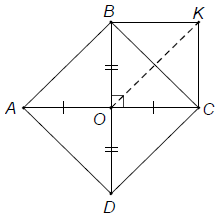
Bài 2. Cho hình thoi ABCD, gọi O là giao điểm của hai đường chéo. Qua B vẽ đường thẳng song song với AC, qua C vẽ đường thẳng song song với BD, hai đường thẳng này cắt nhau ở K.
a) Tứ giác OBKC là hình gì? Vì sao?
b) Chứng minh AB =
c) Tìm điều kiện của hình thoi ABCD để tứ giác OBKC là hình vuông.
Hướng dẫn giải
a) Tứ giác BOCK là hình chữ nhật.
Giải thích:
Tứ giác BOCK có các cạnh đối song song nên là hình bình hành. Hình bình hành lại có ![\[\widehat {BOC} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-65.svg)
do hai đường chéo của hình thoi vuông góc với nhau tại O. Vậy nó là hình chữ nhật.
b) Tứ giác ABKO có hai cạnh đối AO và BK song song và bằng nhau do BK song song và bằng OC. Suy ra AB = OK
c) Hình chữ nhật BOCK là hình vuông
⇔ BO = OC ⇔ BD = AC ⇔ ABCD là hình vuông.
Điều kiện cần tìm là ABCD là hình vuông.
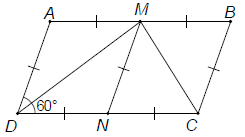
Bài 3. Cho hình bình hành ABCD có BC = 2AB và ![\[\widehat A = 60^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-66.svg)
. Gọi E, F thứ tự là trung điểm của BC, AD.
a) Tứ giác ECDF là hình gì? Vì sao?
b) Tứ giác ABED là hình gì? Vì sao?
c) Tính số đo của góc AED.
Hướng dẫn giải
a) Tứ giác ECDF là hình thoi vì có bốn cạnh bằng nhau.
b) Hình thang ABED có ![\[\widehat A = \widehat {{D_1}} = 60^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-67.svg)
nên là hình thang cân.
c) △AED có EF = AF = FD nên ![\[\widehat {AED} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-68.svg)
Bài tập
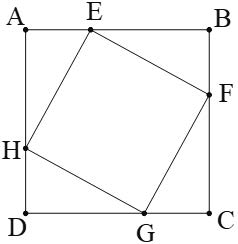
Bài 1. Cho hình vuông ABCD. Trên cạnh AB, BC, CD, DA, lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Chứng minh EFGH là hình vuông.
Hướng dẫn giải
Chỉ ra AH = BE = CF = DG. Từ đó suy ra:
△AEH = △BFE = △CGF = △DHG (c.g.c)
Do đó: HE = EF = FG = GH (1)
Mặt khác, vì △AEH = △BFE
![\[ \Rightarrow \widehat {BEF} = \widehat {AHE}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-69.svg)
Suy ra: ![\[\widehat {AEH} + \widehat {BEF} = 90^\circ \Rightarrow \widehat {FEH} = 90^\circ \left( 2 \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-70.svg)
Từ (1), (2) suy ra EFGH là hình vuông
Bài 2. Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tụ là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.
a) Tứ giác ADFE là hình gì? Vì sao?
b) Tứ giác EMFN là hình gì? Vì sao?
Hướng dẫn giải
a) E, F lần lượt là trung điểm của AB, CD nên ta có EF // AD // BC, do đó dễ thấy ADFE là hình chữ nhật.
Mặt khác AD = AE = AB. Vậy ADFE là hình vuông.
b) Chứng minh tương tự câu a, ta có BCFE cũng là hình vuông.
Do đó hai tam giác MEF và NEF là hai tam giác vuông cân tại M, N.
Từ đó suy ra EMFN là hình vuông.
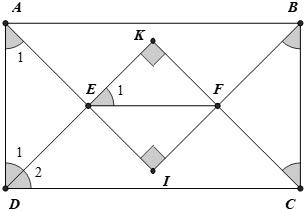
Bài 3. Cho hình chữ nhật ABCD (AD < AB < 2AD). Vẽ các tam giác vuông cân ABI, CDK ![\[\left( {\widehat I = \widehat K = 90^\circ } \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-71.svg)
, I và K nằm trong hình chữ nhật. Gọi E là giao điểm của AI và DK, F là giao điểm của BI và CK. Chứng minh rằng:
a) EF song song với CD.
b) EKFI là hình vuông.
Hướng dẫn giải
a) Tam giác KCD cân tại K nên KD = KC (1).
△EAD = △FBC (g.c.g) nên DE = CF (2).
Từ (1) và (2) suy ra:
KD – DE = KC – CF ⇔ KE = KF
Tam giác vuông KEF có KE = KF nên ![\[\widehat {{E_1}} = 45^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-72.svg)
Ta lại có: ![\[\widehat {{D_2}} = 45^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-73.svg)
⇒ EF // CD (2 góc đồng vị bằng nhau).
b) Tam giác EAD có ![\[\widehat {{A_1}} = \widehat {{D_1}} = 45^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-74.svg)
nên ![\[\widehat {AED} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-75.svg)
Tứ giác EKFI có ![\[\widehat E = \widehat K = \widehat I = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-76.svg)
nên EKFI là hình chữ nhật.
Lại có KE = KF ⇒ EKFI là hình vuông.
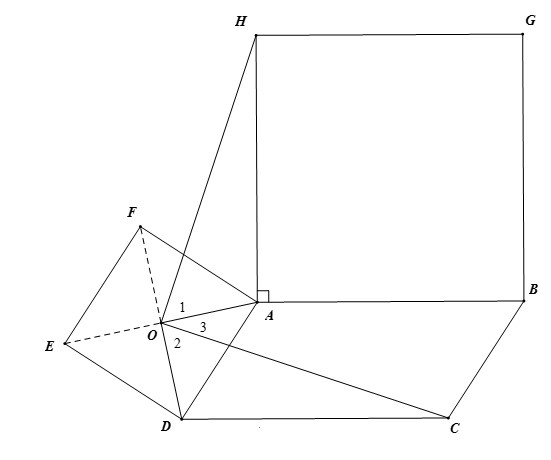
Bài 4. Cho hình bình hành ABCD. Ở phía ngoài hình bình hành vẽ các hình vuông ADEF và ABGH. Gọi O là giao điểm các đường chéo của hình vuông ADEF. Chứng minh rằng:
a) ![\[\widehat {OAH} = \widehat {ODC}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-77.svg)
b) OH = OC
c) OH ⊥ OC
Hướng dẫn giải
a) Ta có: OA ⊥ OD (tính chất đường chéo hình vuông); AH ⊥ DC (vì AH ⊥ AB, AB // CD).
Vậy (góc có cạnh tương ứng vuông góc).
b) Xét △OAH và △ODC, có:
OA = OD (tính chất đường chéo hình vuông)
(câu a)
AH = DC (cùng bằng AB)
Vậy △OAH = △ODC (c.g.c) suy ra OH = OC.
c) △OAH = △ODC
![\[ \Rightarrow \widehat {{O_1}} = \widehat {{O_2}}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-79.svg)
mà ![\[\widehat {{O_2}} + \widehat {{O_3}} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-80.svg)
(tính chất đường chéo hình vuông), nên ![\[\widehat {{O_1}} + \widehat {{O_3}} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-81.svg)
Vậy OH ⊥ OC.
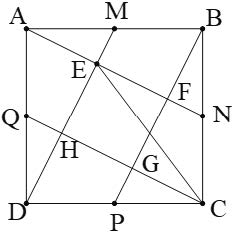
Bài 5. Cho hình vuông ABCD. Gọi M, N, P, Q theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA.
a) Chứng minh: AN = DM và AN ⊥ DM
b) Chứng minh rằng các đoạn thẳng DM, AN, BP, CQ giao nhau tạo thành một hình vuông.
c) Gọi E là giao điểm của DM và AN. Chứng minh: CE = CD.
Hướng dẫn giải
a) Xét hai tam giác ABN và DAM vuông tại B và A, có:
AB = AD và BN = AM
Do đó: △ABN = △DAM (c.g.c)
Suy ra: AN = DM và ![\[\widehat {BAN} = \widehat {ADM}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-82.svg)
Mà ![\[\widehat {BAN} + \widehat {DAN} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-83.svg)
, do đó: ![\[\widehat {ADM} + \widehat {DAN} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-84.svg)
hay ![\[\widehat {AED} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-85.svg)
Vậy ta có: AN = DM và AN ⊥ DM
b) Giả sử các đoạn thẳng DM, AN, BP, CQ giao nhau tạo thành tứ giác EFGH
MB // DP và MB = DP ⇒ MBPD là hình bình hành
Suy ra: BP // DM ⇒ AN ⊥ BP
Tương tự ta cũng có: CQ ⊥ DM
Như vậy tứ giác EFGH có: ![\[\widehat E = \widehat F = \widehat H = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-86.svg)
⊛ Ta chứng minh EF = EH
Dễ thấy EM là đường trung bình trong tam giác ABF, E là trung điểm của AF
Tương tự H là trung điểm của DE
Xét hai tam giác ABF và DAE vuông tại F là E, có:
AB = DA
![\[\widehat {BAF} = \widehat {ADE}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-87.svg)
(Vì △ABN = △DAM)
Suy ra: △ABF = △DAE ⇒ AF = DE
Từ đó ta có: EF = EH. Vậy EFGH là hình vuông.
c) H là trung điểm của DE và CH ⊥ DE, do đó ta suy ra △CDE cân tại C, hay là CE = CD.
Bài 6. Cho tứ giác ABCD có ![\[\widehat {ADC} + \widehat {BCD} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-88.svg)
và AD = BC. Gọi M, N, P, Q lần lượt là trung điểm của AB, AC, CD, BD. Chứng minh rằng tứ giác MNPQ là hình vuông.
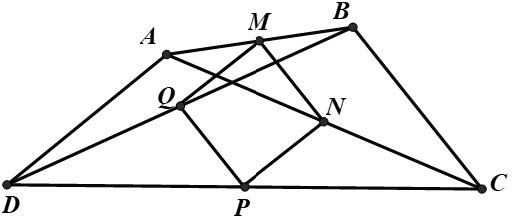
Hướng dẫn giải
Trong tam giác ABC, MN là đường trung bình nên MN = BC
Lập luận tương tự, ta có:
PQ = BC; MQ = AD; NP = AD
Theo giả thiết, AD = BC suy ra: MN = QP = MQ = NP
Vậy MNPQ là hình thoi (1). Mặt khác ta có:
![\[\widehat {DPQ} = \widehat {DCB},{\text{ }}\widehat {NPC} = \widehat {ADC}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-89.svg)
(góc đồng vị)
Theo giả thiết ![\[\widehat {DCB} + \widehat {ADC} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-90.svg)
, suy ra ![\[\widehat {DPQ} + \widehat {NPC} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-91.svg)
Do vậy ta được góc ![\[\widehat {QPN} = 90^\circ \left( 2 \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-92.svg)
Từ (1) và (2) cho ta MNPQ là hình vuông
Bài 7. Cho hình vuông ABCD. Gọi E, F lần lượt trên cạnh AB, AD sao cho AE = DF. Chứng minh rằng DE = CF và DE ⊥ CF
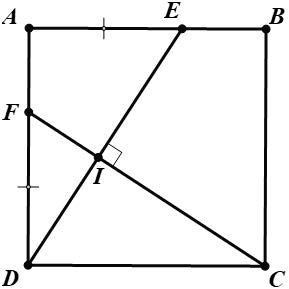
Hướng dẫn giải
Gọi I là giao điểm của DE và CF.
Xét hai tam giác ADE và DCF, có:
AD = DC (vì ABCD là hình vuông)
![\[\widehat {EAD} = \widehat {FDC} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-93.svg)
AE = DF (theo giả thiết)
Vậy △ADE = △DCF, khi đó ta có:
DE = CF và ![\[\widehat {ADE} = \widehat {DCF}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-94.svg)
Mặt khác: ![\[\widehat {DCF} + \widehat {DFC} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-95.svg)
, suy ra:
![\[\widehat {ADE} + \widehat {DFC} = 90^\circ \Rightarrow \widehat {DIF} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-96.svg)
Vậy DE ⊥ CF.
Bài 8. Cho tam giác ABC cân tại A ![\[\left( {\widehat A < 90^\circ } \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-97.svg)
, các đường cao BD và CE cắt nhau tại H. Tia phân giác của góc ABD cắt EC và AC theo thứ tự tại M và P. Tia phân giác của góc ACE cắt DB và AB theo thứ tự tại Q và N. Chứng minh rằng:
a) ![\[\widehat {ABD} = \widehat {ACE}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-98.svg)
b) BH = CH
c) Tam giác BOC vuông cân
d) MNPQ là hình vuông
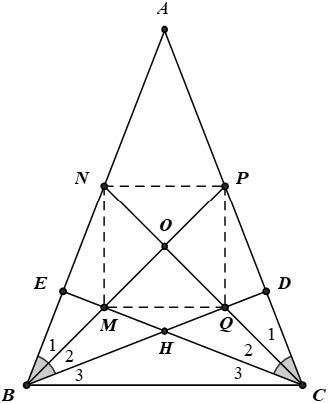
Hướng dẫn giải
a) (cùng phụ với )
b) Ta có: ![\[\widehat {ABC} = \widehat {ACB}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-100.svg)
mà ![\[\widehat {ABD} = \widehat {ACE}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-101.svg)
(chứng minh trên)
![\[\begin{gathered} \Rightarrow \widehat {ABC} - \widehat {ABD} = \widehat {ACB} - \widehat {ACE}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \Leftrightarrow \widehat {{B_3}} = \widehat {{C_3}} \hfill \\ \Rightarrow BH = CH\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-102.svg)
c) Tam giác OBC có: ![\[\widehat {{B_3}} = \widehat {{C_3}},\widehat {{B_2}} = \widehat {{C_2}}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-103.svg)
Nên ![\[\widehat {{B_3}} + \widehat {{B_2}} = \widehat {{C_3}} + \widehat {{C_2}} \Leftrightarrow \widehat {OBC} = \widehat {OCB}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-104.svg)
⇒ △OBC cân tại O (1)
Mặt khác, vì ![\[\widehat {{C_2}} = \widehat {{B_1}}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-105.svg)
nên ta có:
![\[\begin{gathered} \widehat {{B_3}} + \widehat {{B_2}} + \widehat {{C_3}} + \widehat {{C_2}} = \widehat {{B_3}} + \widehat {{B_2}} + \widehat {{B_1}} + \widehat {{C_3}} = 90^\circ \begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \Rightarrow \widehat {BOC} = 90^\circ \left( 2 \right) \hfill \\ \end{gathered} \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-106.svg)
Từ (1) và (2) suy ra △OBC vuông cân
d) Tam giác OBC cân tại O nên OB = OC (3)
△BMH = △CQH (g.c.g) ⇒ BM = CQ (4)
Từ (3) và (4) suy ra:
OB – BM = OC – CQ ⇔ OM = OQ
Mà △BNQ cân tại B có đường cao BO cũng là đường trung tuyến nên O là trung điểm của QN hay ON = OQ.
Tương tự ta có: OP = OM
⇒ OM = ON = OQ = OP ⇒ MNPQ là hình thoi
Ta lại có MP ⊥ NQ nên MNPQ là hình vuông
Bài 9. Cho hình vuông ABCD. Lấy điểm M tùy ý trên cạnh BC. Từ M, vẽ một đường thẳng cắt cạnh CD tại K sao cho: ![\[\widehat {AMB} = \widehat {AMK}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-107.svg)
. Chứng minh: ![\[\widehat {KAM} = 45^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-108.svg)
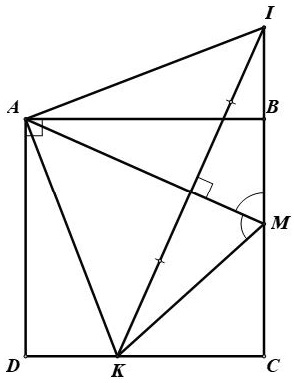
Hướng dẫn giải
MA là phân giác góc ![\[\widehat {BMK}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-109.svg)
nên MA là trục đối xứng của hai đường thẳng MK và MB.
Gọi I là điểm đối xứng của K qua MA, suy ra I thuộc đường thẳng BC.
Ta có: AI = AK, AB = AD.
Hai tam giác vuông ABI và ADK có hai cạnh bằng nhau nên △ABI = △ADK.
Từ đó ta có: ![\[\widehat {IAB} = \widehat {KAD}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-110.svg)
![\[\widehat {IAK} = \widehat {IAB} + \widehat {BAK} = \widehat {KAD} + \widehat {BAK} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-111.svg)
Vậy ta có: ![\[\widehat {MAK} = \frac{1}{2}\widehat {IAK} = 45^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/hinh-vuong-112.svg)
