Hình thang cân

Lý thuyết hình thang cân

Khái niệm

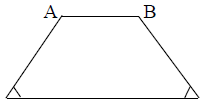
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

Tính chất

+) Trong hình thang cân, hai cạnh bên bằng nhau.

+) Trong hình thang cân, hai đường chéo bằng nhau.

Dấu hiệu nhận biết

+) Hình thang có hai góc kề một cạnh đáy bằng nhau là hình thang cân.

+) Hình thang có hai đường chéo bằng nhau là hình thang cân.

Chú ý: Hình thang có hai cạnh bên bằng nhau không phải luôn là hình thang cân.

Phân dạng bài tập

Dạng 1. Tính số đo góc, độ dài cạnh và diện tích hình thang cân

Phương pháp giải: Sử dụng tính chất hình thang cân về cạnh góc, đường chéo và công thức tính diện tích hình thang để tính toán.

Bài 1. Cho hình thang cân ABCD (AB // CD) có $\widehat A = 2\widehat C$ . Tính các góc của hình thang cân.

Hướng dẫn giải

Ta có: $\widehat A + \widehat D = 180^\circ$ và $\widehat A = 2\widehat C = 2\widehat D$

Suy ra: $\widehat C = \widehat D = 60^\circ ,{\text{ }}\widehat A = \widehat B = 120^\circ$

Bài 2. Cho hình thang cân ABCD (AB // CD) có $\widehat A = 3\widehat D$ . Tính các góc của hình thang cân.

Hướng dẫn giải

Tương tự bài 1. Ta có:

$\widehat C = \widehat D = 45^\circ ,{\text{ }}\widehat A = \widehat B = 135^\circ$

Bài 3. Cho hình thang cân ABCD (AB // CD) có AH và BK là hai đường cao của hình thang.

a) Chứng minh: $DH = \frac{{CD - AB}}{2}$

b) Biết AB = 6 cm, CD = 14 cm, AD = 5 cm. Tính DH, AH và diện tích hình thang cân ABCD.

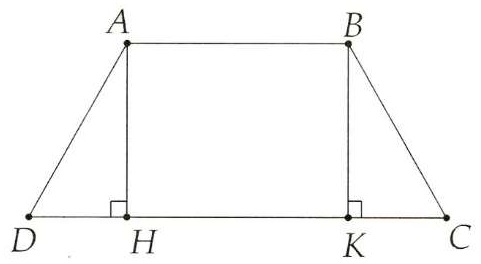
Hướng dẫn giải

a) Chứng minh △ADH = △BCK (cạnh huyền – góc nhọn)

⇒ DH = CK

Vận dụng nhận xét hình thang ABKH (AB // KH) có:

AH // BK ⇒ AB = HK

b) Vậy $DH = \frac{{CD - AB}}{2}$

c) DH = 4 cm, AH = 3 cm, S_ABCD = 30 cm²

Bài 4. Cho hình thang cân ABCD (AB // CD) có $\widehat A = \widehat B = 60^\circ$ , AB = 4,5cm; AD = BC = 2 cm. Tính độ dài đáy CD và diện tích hình thang cân ABCD.

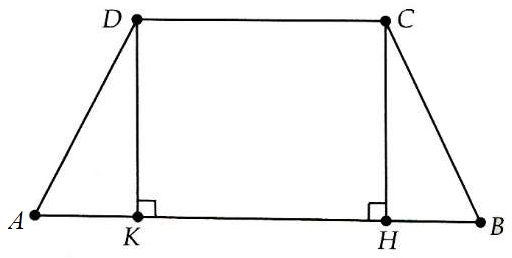
Hướng dẫn giải

Hạ CH và DK vuông góc với AB. Ta có:

$AK = BH = \frac{1}{2}AD = 1cm$

Từ đó: $CD = 2,5cm,{\text{ }}CH = \sqrt 3 cm$

${S_{ABCD}} = \frac{{\left( {AB + CD} \right) \cdot CD}}{2} = \frac{{7\sqrt 3 }}{2}c{m^2}$

Dạng 2. Chứng minh hình thang cân

Phương pháp giải: Sử dụng dấu hiệu nhận biết hình thang cân.

Bài 1. Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến của tam giác. Chứng minh BCDE là hình thang cân.

Hướng dẫn giải

Sử dụng tính chất đường trung bình, ta chứng minh được DE // BC.

Bài 2. Cho tam giác ABC cân tại A có BH và CK là hai đường cao của tam giác. Chứng minh BCHK là hình thang cân.

Hướng dẫn giải

Chứng minh △BKC = △CHB (cạnh huyền – góc nhọn)

Suy ra CK = BH và AK = AH.

Từ đó $\widehat {AKH} = \frac{{180^\circ - \widehat {KAH}}}{2} = \widehat {ABC}$ hay KH // BC

Dạng 3. Chứng minh các cạnh bằng nhau, các góc bằng nhau trong hình thang cân

Bài 1. Cho hình thang cân ABCD (AB // CD, AB < CD). Gọi O là giao điểm của AD và BC, gọi E là giao điểm của AC và BD. Chứng minh:

a) Tam giác AOB cân tại O;

b) Các tam giác ABD và BAC bằng nhau;

c) EC = ED;

d) OE là trung trực chung của AB và CD.

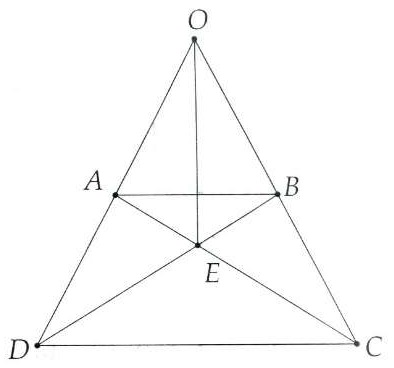
Hướng dẫn giải

a) $\widehat {OAB} = \widehat {OBA}$

Suy ra △OAB cân tại O

b) Xét △ABD và △BAC, có:

DA = BC (ABCD là hình thang cân)

AB chung

AC = BD (ABCD là hình thang cân)

⇒ △ABD = △BAC (c.c.c)

c) $\widehat {ADB} = \widehat {BCA}$ , suy ra $\widehat {EDC} = \widehat {ECD}$ hay △ECD cân tại E

d) Ta có: OA = OB, EA = EB, suy ra OE là đường trung trực của đoạn AB.

Tương tự có OE cũng là đường trung trực của đoạn CD.

Vậy OE là đường trung trực chung của AB và CD

Bài 2. Cho tam giác ABC cân tại A và điểm M tùy ý nằm trong tam giác. Kẻ tia Mx song song với BC cắt AB ở D, tia My song song với AC cắt BC ở E. Chứng minh: $\widehat {DME} = 90^\circ + \frac{{\widehat A}}{2}$

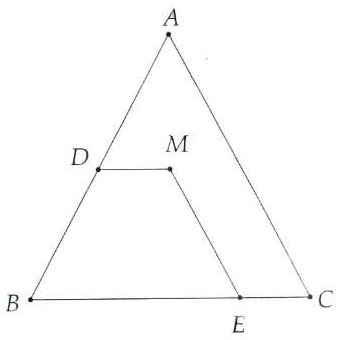
Hướng dẫn giải

Do $MD\parallel BC \Rightarrow \widehat {DME} + \widehat {MEB} = 180^\circ$ . Suy ra:

$\widehat {DME} = 180^\circ - \widehat {MEB} = 180^\circ - \widehat {ACB} = 90^\circ + \frac{{\widehat A}}{2}$

Bài tập tự luyện số 1

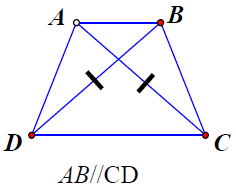
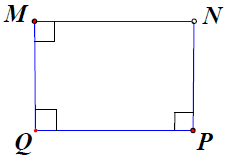
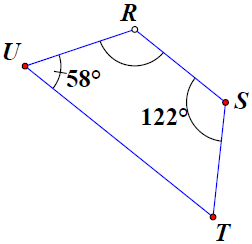
Bài 1. Trong các hình vẽ sau, hình nào là hình thang cân. Giải thích.

Hướng dẫn giải

a) Xét tứ giác ABCD có AB // CD và AC = BD nên là hình thang cân (hình thang có hai đường chéo bằng nhau).

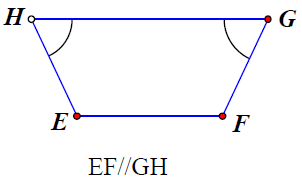
b) Tứ giác EFGH có EF // GH và $\widehat H = \widehat G$ nên là hình thang cân (hình thang có hai góc kề đáy bằng nhau là hình thang cân)

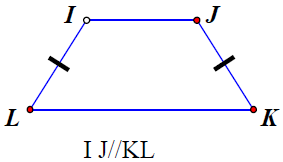
c) Tứ giác IJKL là hình thang có hai cạnh bên bằng nhau nên chưa thể khẳng định là hình thang cân.

d) Tứ giác MNPQ có MN // PQ (cùng vuông góc với MQ) và $\widehat Q = \widehat P = 90^\circ$ nên là hình thang cân.

e) Tứ giác RSTU có RS // UT (hai góc trong cùng phía bù nhau) và $\widehat R = \widehat S$ nên là hình thang cân.

Bài 2. Cho hình thang cân ABCD (AB // CD) có $\widehat A = 110^\circ$ . Tính các góc còn lại của hình thang ABCD.

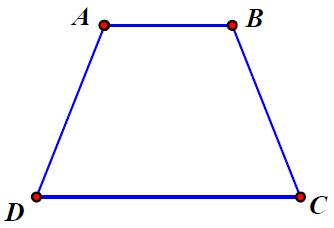
Hướng dẫn giải

Ta có: ABCD là hình thang cân nên $\widehat B = \widehat A = 110^\circ$ (hai góc kề đáy)

Mà AB // CD nên $\widehat A + \widehat D = 180^\circ$ (hai góc trong cùng phía)

Nên $\widehat D = 70^\circ \Rightarrow \widehat C = \widehat D = 70^\circ$

Bài 3. Cho tam giác ABC cân tại A. Đường thẳng song song với BC cắt hai cạnh AB, AC lần lượt tại M, N. Chứng minh BCNM là hình thang cân.

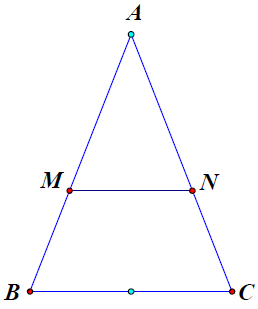
Hướng dẫn giải

Ta có: MN // BC (giả thiết) nên BCNM là hình thang.

Mà $\widehat B = \widehat C$ (tam giác ABC cân tại A) nên BCNM là hình thang cân.

Bài 4. Cho hình thang cân ABCD (AB // CD) có các đường cao AE, BF. Chứng minh DE = CF.

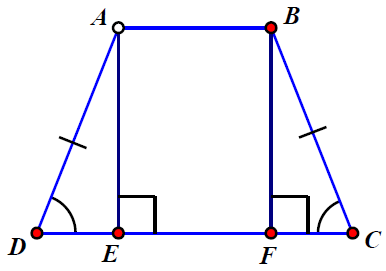
Hướng dẫn giải

Xét hai tam giác vuông AED và BFC có:

AD = BC và $\widehat D = \widehat C$ (ABCD là hình thang cân)

Nên △AED = △BFC (cạnh huyền – góc nhọn)

⇒ DE = FC

Bài 5. Cho hình thang cân ABCD (AB // CD) có hai đường chéo cắt nhau tại O. Chứng minh OA = OB; OC = OD.

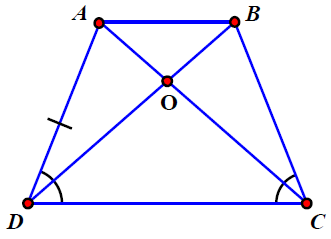
Hướng dẫn giải

Xét hai tam giác BDC và ACD có: cạnh DC chung; $\widehat {BCD} = \widehat {ADC}$ và AD = BC (tính chất hình thang cân)

⇒ △BDC = △ACD (c.g.c)

$\Rightarrow \widehat {BDC} = \widehat {ACD}$

⇒ △ODC cân tại O ⇒ OD = OC

Chứng minh tương tự ta có OB = OC

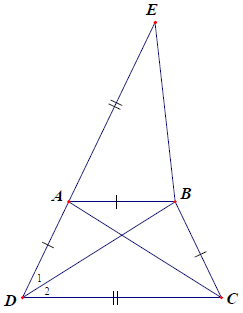
Bài 6. Cho tam giác ABC cân tại A. Trên tia đối của tia AB lấy điểm D; trên tia đối của tia AC lấy điểm E sao cho AD = AE. Tứ giác BCDE là hình gì? Vì sao?

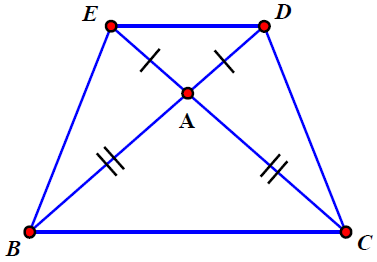
Hướng dẫn giải

Theo giả thiết ta có các tam giác ABC và ADE là các tam giác cân nên

$\widehat {AED} = \frac{{180^\circ - \widehat {EAD}}}{2}$ và $\widehat {ACB} = \frac{{180^\circ - \widehat {BAC}}}{2}$

Mặt khác: $\widehat {EAD} = \widehat {BAC}$ (đối đỉnh) nên $\widehat {AED} = \widehat {ACB}$

Mà hai góc này ở vị trí so le trong nên DE // BC

⇒ BCDE là hình thang

Lại có: EC = EA + AC = DA + AB = DB nên BCDE là hình thang cân.

Bài 7. Tứ giác ABCD có AB = BC = AD; $\widehat A = 110^\circ ;\widehat C = 70^\circ$ . Chứng minh rằng:

a) DB là tia phân giác $\widehat D$ .

b) ABCD là hình thang cân.

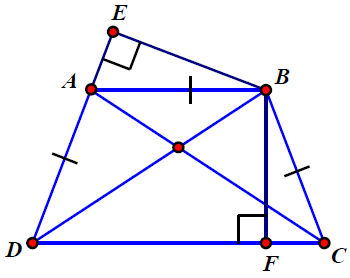
Hướng dẫn giải

a) Kẻ BE vuông góc với tia DA; BF vuông góc với tia DC

Khi đó do hai tam giác vuông BEA và BFC có: $\widehat {BAE} = \widehat {BCF} = 70^\circ$ và AB = BC nên chúng bằng nhau.

Do đó: BE = BF

⇒ B thuộc tia phân giác $\widehat {ADC}$ hay DB là tia phân giác của $\widehat {ADC}$

b) Tam giác ADB cân tại A có $\widehat {DAB} = 110^\circ$ nên $\widehat {ADB} = 35^\circ$

$\Rightarrow \widehat {ADC} = 70^\circ$ (DB là tia phân giác $\widehat {ADC}$ )

$\Rightarrow \widehat {ADC} + \widehat {DAB} = 70^\circ + 110^\circ = 180^\circ$

⇒ AB // DC

Mà $\widehat D = \widehat C = 70^\circ$ nên ABCD là hình thang cân.

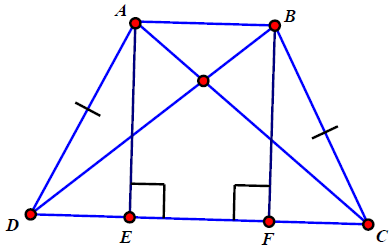
Bài 8. Tính chiều cao của hình thang cân ABCD biết rằng cạnh bên BC = 25 cm, các cạnh đáy AB = 10 cm và CD = 24 cm.

Hướng dẫn giải

Kẻ các đường cao AE, BF của hình thang. Khi đó hình thang ABFE có hai cạnh bên song song nên hai cạnh đáy EF = AB = 10 cm.

Mặt khác theo câu 4 thì DE = CF nên

$DE = CF = \frac{{24 - 10}}{2} = 2{\text{ }}cm$

Áp dụng định lí Py-ta-go trong tam giác tính được $BF = 3\sqrt {69} cm$

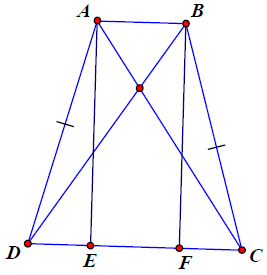
Bài 9. Cho tam giác đều ABC, điểm M nằm trong tam giác đó. Qua M, kẻ các đường thẳng song song với AC cắt BC ở D, kẻ đường thẳng song song với AB cắt AC ở E, kẻ đường thẳng song song với BC cắt AB ở F. Chứng minh rằng:

a) $\widehat {DME} = \widehat {EMF} = \widehat {DMF}$

b) Trong ba đoạn MA, MB, MC đoạn lớn nhất nhỏ hơn tổng hai đoạn kia.

Hướng dẫn giải

a) Các tứ giác AEMF, BDMF, CDME có một cặp cạnh đối song song và có các góc ở đáy đều bằng 60° nên chúng là các hình thang cân.

Do đó: $\widehat {EMF} = \widehat {EMD} = \widehat {DMF} = \widehat A = 60^\circ$

b) Vì các tứ giác AEMF, BDMF, CDME là các hình thang cân nên MA = EF, MB = FD, MC = ED

MA, MB, MC bằng độ dài ba cạnh của một tam giác nên suy ra đpcm

Bài 10. Chứng minh rằng trong một hình thang cân, đường chéo luôn lớn hơn đường trung bình.

Hướng dẫn giải

Xét hình thang cân ABCD có hai cạnh đáy AB và CD (AB ≤ CD), kẻ các đường cao AE và BF.

Ta có hình thang ABFE có hai cạnh bên song song (cùng vuông góc với DC) nên suy ra hai cạnh đáy bằng nhau.

Do đó: EF = AB và $DE = CF = \frac{{CD - AB}}{2}$

Ta có:

$EC = EF + FC = AB + \frac{{CD - AB}}{2} = \frac{{AB + CD}}{2}$

⇒ EC bằng độ dài đường trung bình của hình thang ABCD

Lại xét trong tam giác vuông AEC vuông tại E ta có: EC < AC

Vậy trong hình thang cân, độ dài đường trung bình luôn bé hơn đường chéo.

Bài tập tự luyện số 2

Bài 1. Hai đoạn thẳng AB và CD cắt nhau tại O, biết OA = OC, OB = OD. Tứ giác ACBD là hình gì?

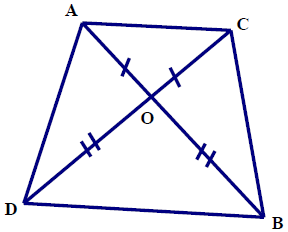
Hướng dẫn giải

Vì OA = OC, OB = OD nên AB = CD (1); OA = OC; OB = OD

Nên △OAC và △OBD cân tại O

$\Rightarrow \widehat {OBA} = \frac{{180^\circ - \widehat {AOC}}}{2};{\text{ }}\widehat {ODC} = \frac{{180^\circ - \widehat {DOC}}}{2}$

Mà $\widehat {AOC} = \widehat {DOC}$ (hai góc đối đỉnh)

$\Rightarrow \widehat {OBA} = \widehat {ODC}$ mà hai góc này so le trong nên AC // BD (2)

Từ (1) và (2) suy ra tứ giác ACBD là hình thang cân.

Bài 2. Cho hình thang cân ABCD (AB // CD)

a) Chứng minh: $\widehat {ACD} = \widehat {BDC}$

b) Gọi E là giao điểm của AC và BD. Chứng minh: EA = EB

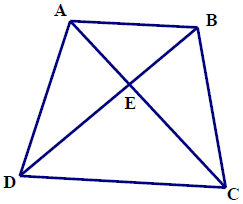
Hướng dẫn giải

a) ABCD là hình thang cân nên AD = BC; $\widehat {ADC} = \widehat {BCD}$

Dễ chứng minh: △ADC = △BCD (c.g.c)

⇒ $\widehat {ACD} = \widehat {BDC}$

b) Theo câu a) ta có $\widehat {ACD} = \widehat {BDC}$ suy ra △CED cân tại E

⇒ ED = EC mà AC = BD (do ABCD là hình thang cân)

⇒ EA = EB

Bài 3. Hình thang cân ABCD (AB// CD), có góc $\widehat C = 60^\circ$ , DB là tia phân giác của góc $\widehat D$ ; chu vi hình thang bằng 20 cm.

a) Tính các cạnh của hình thang.

b) Tính diện tích tam giác BDC.

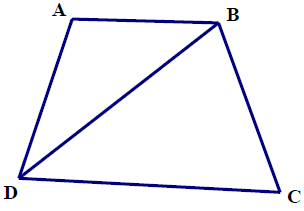
Hướng dẫn giải

a) Ta có: ABCD là hình thang cân nên $\widehat D = \widehat C = 60^\circ$

$\Rightarrow \widehat {ADB} = \widehat {CDB} = \frac{{60^\circ }}{2} = 30^\circ$

Tam giác CBD vuông tại B có $\widehat {CDB} = 30^\circ$

BC = $\frac{1}{2}$ DC hay 2AD = DC

AB // CD nên $\widehat {ABD} = \widehat {BDC} = 30^\circ$

$\Rightarrow \widehat {ABD} = \widehat {ADB} = 30^\circ$

⇒ △ADB cân tại A nên AD = AB

Từ đó suy ra chu vi hình thang bằng 5AD

⇒ 5⋅AD = 20 cm ⇒ AD = 4 cm.

Vậy AD = AB = BC = 4cm, CD = 8cm

b) Vì △BCD vuông tại B. Áp dụng định lý Py-ta-go vào △BDC:

BD² = DC² – BC² hay DB² = 8² – 4² = 48 ⇒ BD = $4\sqrt 3$ cm

Diện tích tam giác BDC là:

$\frac{1}{2} \cdot 4 \cdot 4\sqrt 3 = 8\sqrt 3 {\text{ }}c{m^2}$

Bài 4. Cho hình thang MNPQ (MN là đáy nhỏ) có 2 đường chéo MP và NQ cắt nhau tại O và $\widehat {NMP} = \widehat {MNQ}$ . Qua O vẽ đường thẳng EF // QP (E ∈ MQ, F ∈ NP). Chứng minh rằng các tứ giác MNPQ, MNFE, FEQP là những hình thang cân.

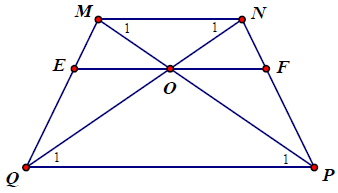
Hướng dẫn giải

Vì MN // QP nên $\left\{ \begin{gathered} \widehat {{M_1}} = \widehat {{P_1}} \hfill \\ \widehat {{N_1}} = \widehat {{Q_1}} \hfill \\ \widehat {{M_1}} = \widehat {{N_1}} \hfill \\ \end{gathered} \right. \Rightarrow \left\{ {\widehat {{Q_1}} = \widehat {{P_1}}} \right.$

⇒ Các △OMN và △OPQ cân tại O

⇒ OM = ON, OP = OQ, MP = NQ mà MNPQ là hình thang

⇒ MNPQ là hình thang cân

Do EF // QP (gt), mà QP // MN nên EF // QP // MN

⇒ Tứ giác MNEF và FEQP là hình thang.

Do MNPQ là hình thang cân nên:

$\widehat {MQP} = \widehat {NPQ}$ và $\widehat {QMN} = \widehat {PNM}$

⇒ MNEF và FEQP là hình thang cân.

Bài 5. Cho hình thang cân ABCD có $\widehat C = 60^\circ$ , đáy nhỏ AD bằng cạnh bên của hình thang. Biết chu vi của hình thang bằng 20 cm.

a) Tính các cạnh của hình thang.

b) Tính chiều cao của hình thang.

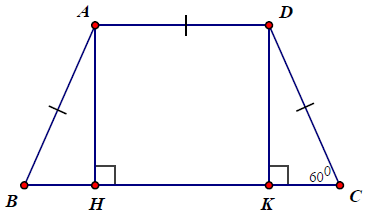
Hướng dẫn giải

a) Đặt AD = AB = DC = x.

Kẻ AH ⊥ BC, DK ⊥ BC (H, K ∈ BC) ⇒ AH // DK

⇒ Hình thang ADKH có hai cạnh bên song song nên AD = HK = x; AH = DK.

Có △AHB = △DKC (cạnh huyền – góc nhọn) ⇒ BH = KC.

Xét △ABH có:

$\widehat B = 60^\circ \Rightarrow BH = \frac{{AB}}{2} = \frac{x}{2} \Rightarrow x = 2BH$

⇒ Chu vi hình thang là 5x = 20 ⇒ x = 4

⇒ AD = DC = AB = 4 cm; BC = 8 cm

b) Từ câu a) ta có BH = 2 cm

Áp dụng định lý Py-ta-go vào tam giác ABH vuông tại H ta có đường cao AH = $2\sqrt 3$

Bài 6. Chứng minh rằng tứ giác ABCD có $\widehat C = \widehat D \ne 90^\circ$ và AD = BC thì tứ giác đó là hình thang cân.

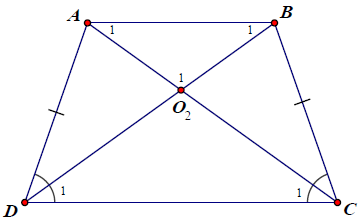
Hướng dẫn giải

Ta chứng minh được △ADC = △BCD (c.g.c)

⇒ AC = BD và $\widehat {{C_1}} = \widehat {{D_1}}$

⇒ △OCD cân tạị O

$\Rightarrow \widehat {{C_1}} = \frac{{180^\circ - \widehat {{O_2}}}}{2}{\text{ }}\left( 1 \right)$

Từ đây ta chứng minh được △ABD = △BAC (c.c.c)

$\Rightarrow \widehat {{A_1}} = \widehat {{B_1}}$

⇒ △OBA cân tạị O

$\Rightarrow \widehat {{A_1}} = \frac{{180^\circ - \widehat {{O_1}}}}{2}{\text{ }}\left( 2 \right)$

Từ (1), (2) và $\widehat {{O_1}} = \widehat {{O_2}}$ suy ra $\widehat {{A_1}} = \widehat {{C_1}}$

Mà 2 góc này ở vị trí so le trong nên AB //CD

Suy ra ABCD là hình thang mà $\widehat C = \widehat D$

⇒ ABCD là hình thang cân.

Bài 7. Cho △ABC đều. Lấy điểm O nằm trong tam giác. Kẻ OI // AB (I thuộc AC), OM // BC (M thuộc AB), OK // AC (K thuộc BC). Chứng minh rằng: Chu vi △IMK bằng tổng khoảng cách từ O đến các đỉnh của △ABC.

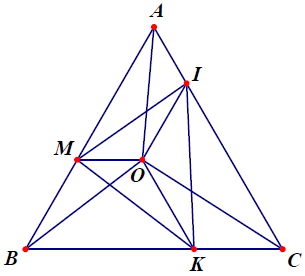
Hướng dẫn giải

Có △ABC đều $\Rightarrow \widehat A = \widehat B = \widehat C = 60^\circ$ . Do OI // AB; OM // BC; OK // AB (gt)

⇒ Các tứ giác OIAM, OMBK, OKCI là hình thang.

Ta có: $\widehat {OKB} = \widehat {ACB} = 60^\circ$ (đồng vị, OK // AC)

Mà $\widehat {ABC} = \widehat {ACB} = 60^\circ \Rightarrow \widehat {OKB} = \widehat {MBK}$

⇒ Hình thang OMBK là hình thang cân.

Chứng minh tương tự ta có OKCI, OIAM là các hình thang cân

Do đó: OC = IK, OA = IM, OB = MK

⇒ C_IMK = IK + IM + MK = OA+ OB + OC.

Bài 8. Cho tam giác ABC cân tại A, M là điểm bất kì nằm giữa hai điểm A và B. Trên tia đối của tia CA lấy điểm N sao cho CN = BM. Vẽ ME và NF lần lượt vuông góc với đường thẳng BC. Gọi I là giao điểm của MN và BC.

a) Chứng minh: IE = IF.

b) Trên cạnh AC lấy điểm D sao cho CD = CN. Chứng minh tứ giác BMDC là hình thang cân.

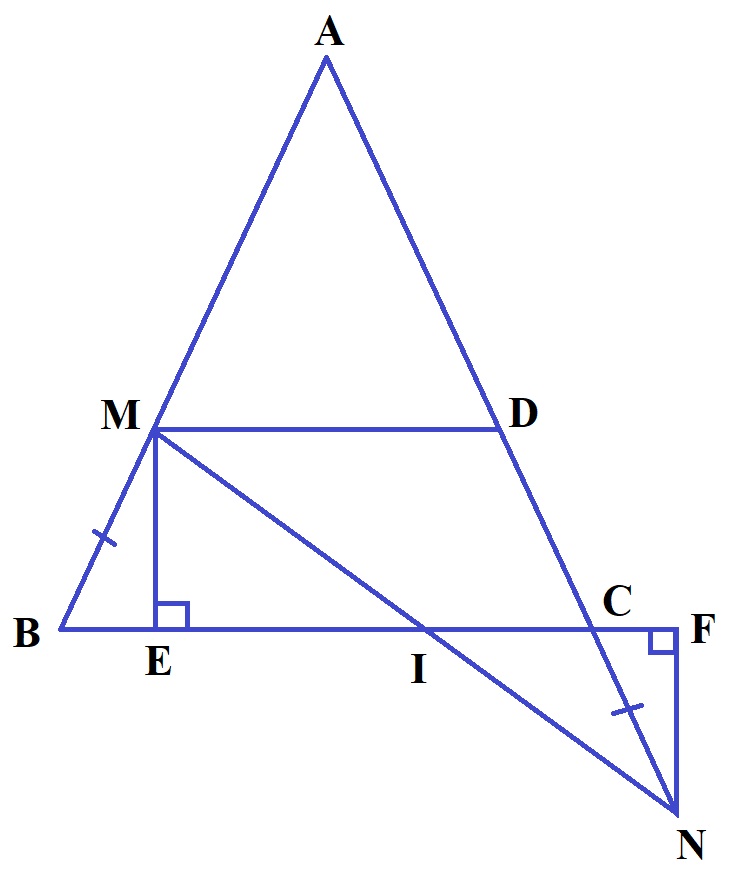
Hướng dẫn giải

a) △MBE = △NCF (cạnh huyền – góc nhọn)

⇒ ME = NF

Từ đó chứng minh được: △MIE = △NIF (cạnh góc vuông – góc nhọn kề)

⇒ IE = IF.

b) Do △ABC là tam giác cân nên AB = AC, mà MB = DC (= CN) nên AM = AD

⇒ △AMD cân tại A

$\Rightarrow \widehat {AMD} = \frac{{180^\circ - \widehat A}}{2}$

Xét △ABC có:

$\widehat {ABC} = \frac{{180^\circ - \widehat A}}{2} \Rightarrow \widehat {AMD} = \widehat {ABC}$

⇒ MD // BC ⇒ MDCB là hình thang.

Do $\widehat {MBC} = \widehat {DCB}$ (△ABC cân tại A)

⇒ BMDC là hình thang cân (đpcm)

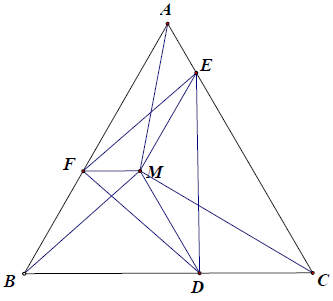
Bài 9. Cho △ABC đều, điểm M nằm trong tam giác đó. Qua M kẻ đường thẳng song song với AC và cắt BC ở E, kẻ đường thẳng song song với AB và cắt AC ở F, kẻ đường thẳng song song với BC và cắt AB ở D. Chứng minh rằng:

a) AFMD, BDME, CEMF là các hình thang cân.

b) $\widehat {DME} = \widehat {FME} = \widehat {DMF}$

c) Điểm M phải ở vị trí nào để △DEF là tam giác đều? Trong trường hợp này, tính chu vi của △DEF theo chiều cao AH của △

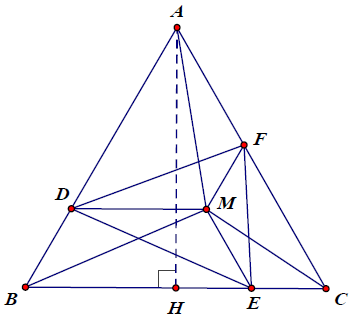
Hướng dẫn giải

a) Có △ABC đều $\Rightarrow \widehat {BAC} = \widehat {ABC}$ . Mà FM // AD

$\Rightarrow \widehat {ADM} = \widehat {ABC}$ (đồng vị)

$\Rightarrow \widehat {BAC} = \widehat {ADM}$

Xét tứ giác AFMD có:

$\left\{ \begin{gathered} AD\parallel FM{\text{ }}\left( {gt} \right) \hfill \\ \widehat {ADM} = \widehat {BAC}{\text{ }}\left( {cmt} \right)\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right.$