Hằng đẳng thức đáng nhớ

Các hằng đẳng thức đáng nhớ và ứng dụng

Một số kiến thức cần nhớ

Nhắc lại những hằng đẳng thức đáng nhớ

Bình phương của một tổng:

(A + B)² = A² + 2AB + B² = (A – B)² + 4AB

Bình phương của một hiệu:

(A – B)² = (B – A)² = A² – 2AB + B² = (A + B)² – 4AB

Hiệu của hai bình phương:

A² – B² = (A – B)(A + B)

Lập phương của tổng:

(A + B)³ = A³ + 3A²B + 3AB² + B³ = A³ + B³ + 3AB(A + B)

Lập phương của hiệu:

(A – B)³ = A³ – 3A²B + 3AB² – B³ = A³ – B³ – 3AB(A – B)

Tổng hai lập phương:

A³ + B³ = (A + B)(A² – AB + B²) = (A + B)³ – 3AB(A – B)

Hiệu hai lập phương:

A³ – B³ = (A – B)(A² + AB + B²) = (A – B)³ + 3AB(A – B)

Một số hằng đẳng thức tổng quát

aⁿ – bⁿ = (a – b)(a^n–1 + a^n–2b + … + ab^n–2 + b^n–1)

a^2k – b^2k = (a – b)(a^2k–1 + a^2k–1b + … + a^2k–3b² + b^2k–1)

a^2k–1 + b^2k–1 = (a + b)(a^2k – a^2k–1b + a^2k–2 – … + b^2k)

(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca

Nhị thức Newton

${\left( {a + b} \right)^n} = {a^n} + C_n^1{a^{n - 1}}b + \cdots + C_n^{n - 1}a{b^{n - 1}} + {b^n}$

Trong đó: $C_n^k = \frac{{n\left( {n - 1} \right)\left( {n - 2} \right) \ldots \left[ {n - \left( {k - 1} \right)} \right]}}{{1.2.3 \ldots k}}$

Cách xác định hệ số của khai triển Newton.

+) Cách 1. Dùng công thức $C_n^k = \frac{{n\left( {n - 1} \right)\left( {n - 2} \right) \ldots \left[ {n - \left( {k - 1} \right)} \right]}}{{1.2.3 \ldots k}}$

Chẳng hạn hệ số của hạng tử a⁴b³ trong khai triển của (a + b)⁷ là:

$C_7^4 = \frac{{7.6.5.4}}{{4!}} = \frac{{7.6.5.4}}{{4.3.2.1}} = 35$

⨂ Chú ý:

$C_n^k = \frac{{n!}}{{n!\left( {n - k} \right)!}}$ với quy ước 0! = 1

Ta có: $C_n^k = C_n^{n - k}$ nên $C_7^4 = C_7^3 = \frac{{7.6.5}}{{3!}} = 35$

+) Cách 2. Dùng tam giác Pascal

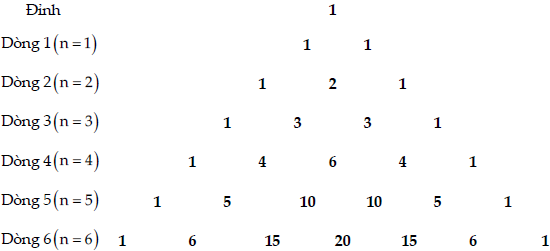
Trong tam giác hai cạnh bên gồm các số 1 và dòng k + 1 được thành lập từ dòng k (k ≥ 1)

Với n = 4 thì ta có:

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

Với n = 5 thì ta có:

(a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

Với n = 6 thì ta có:

(a + b)⁶ = a⁶ + 6a⁵b + 15a⁴b² + 20a³b³ + 15a²b⁴ + 6ab⁵ + b⁶

Phân dạng bài tập

Dạng 1. Biến đổi biểu thức

Phương pháp: Áp dụng 7 hằng đẳng thức đáng nhớ để thực hiện biến đổi biểu thức.

Bài 1. Thực hiện phép tính:

a) (–3x + 2y)²

b) (–x – xy)²

c) x² – 4y²

d) (x + y)² – (2 – y)²

Hướng dẫn giải

Áp dụng hằng đẳng thức ta có:

a) (–3x + 2y)²

= (–3x)² + 2(–3x)(2y) + (2y)²

= 9x² – 12xy + 4y²

b) (–x – xy)²

= (–x)² – 2(–x)(xy) + (xy)²

= x² + 2x²y + x²y²

c) x² – 4y²

= x² – (2y)²

= (x – 2y)(x + 2y)

d) (x + y)² – (2 – y)²

= [(x + y) – (2 – y)][(x + y) + (2 – y)]

= (x + 2y – 2)(x + 2)

Bài 2. Thực hiện phép tính:

a) (x + y)(x² – xy + y²) – (–x + y)(x² + xy + y²)

b) 2x³ – 6x² + 6x – 2

c) x³ + 6x² + 12x + 8

d) (x + y)³ – (x – 2y)³

Hướng dẫn giải

Áp dụng bất đẳng thức ta được:

a) (x + y)(x² – xy + y²) – (–x + y)(x² + xy + y²)

= x³ + y³ + (x – y)(x² + xy + y²)

= x³ + y³ + x³ – y³ = 2x³

b) 2x³ – 6x² + 6x – 2

= 2(x³ – 3x² + 3x – 1)

= 2(x – 1)³

c) x³ + 6x² + 12x + 8

= x³ + 3⋅2⋅x² + 3⋅2²⋅x + 2³

= (x + 2)³

d) (x + y)³ – (x – 2y)³

= (x³ + 3x²y + 3xy² + y³) – [x³ – 3⋅x²⋅2y + 3⋅x⋅(2y)² – (2y)³]

= x³ + 3x²y + 3xy² + y³ – x³ + 6x²y – 12xy² + 8y³

= 9x²y – 9xy² + 9y³

Bài 3. Rút gọn biểu thức:

a) (a – b + c + d)(a – b – c – d)

b) (x + 2y + 3z)(x – 2y + 3z)

c) (x – 1)(x² + x + 1)(x + 1)(x² + x +1)

d) (x + y)³ – (x – y)³

e) (x² + 3x + 1)² + (3x + 1)² – 2(x² + 3x + 1)(3x – 1)

Hướng dẫn giải

a) (a – b + c + d)(a – b – c – d)

= [(a – b) + (c + d)][(a – b) – (c + d)]

= (a – b)² – (c + d)²

= a² – 2ab + b² – c² – 2cd – d²

= a² + b² – c² – d² – 2ab – 2cd

b) (x + 2y + 3z)(x – 2y + 3z)

= [(x + 3z) + 2y][(x + 3z) – 2y]

= (x + 3z)² – (2y)²

= x² + 6xz + 9z² – 4y²

c) (x – 1)(x² + x + 1)(x + 1)(x² + x +1)

= (x³ – 1)(x³ + 1)

= x⁶ – 1

d) (x + y)³ – (x – y)³

= (x³ + 3x²y +3xy² + y³) – (x³ – 3x²y + 3xy² – y³)

= x³ + 3x²y +3xy² + y³ – x³ + 3x²y – 3xy² + y³

= 6x²y + 2y³

=2y(3x² + y²)

e) (x² + 3x + 1)² + (3x + 1)² – 2(x² + 3x + 1)(3x – 1)

= [(x² + 3x + 1)– (3x – 1)]²

= (x² + 3x + 1 – 3x + 1)²

= (x² + 2)²

Dạng 2. Tính giá trị biểu thức

Phương pháp: Dạng bài toán này rất đa dạng ta có thể giải theo phương pháp cơ bản như sau:

+) Biến đổi biểu thức cho trước thành những biểu thức cần thiết sao cho phù hợp với biểu thức cần tính giá trị.

+) Áp dụng 7 hằng đẳng thức đáng nhớ để thực hiện biến đổi biểu thức cần tính giá trị về biểu thức có liên quan đến giá trị đề bài đã cho.

+) Thay vào biểu thức cần tính tìm được giá trị.

Bài 1. Cho x + y = 1. Tính giá trị biểu thức sau: A = x³ + 3xy + y³

Hướng dẫn giải

Áp dụng hằng đẳng thức bậc 3, ta được:

A = x³ + 3xy + y³

= (x + y)(x² – xy + y²) + 3xy

= (x + y)[(x + y)² – 3xy] + 3xy

Theo bài ra x + y = 1, thay vào A ta được:

A = (x + y)[(x + y)² – 3xy] + 3xy

= 1⋅(1² – 3xy) + 3xy

= 1 – 3xy + 3xy = 1

Vậy A = 1

Bài 2. Cho x – y = 4 và xy = 5. Tính B = x³ – y³ + (x – y)²

Hướng dẫn giải

Áp dụng hằng đẳng thức, ta được:

B = x³ – y³ + (x – y)²

= (x – y)(x² + xy + y²) + (x – y)²

= (x – y)[(x – y)² + 3xy] + (x – y)²

Theo bài ra x – y = 4 và xy = 5, thay vào B ta được:

B = (x – y)[(x – y)² + 3xy] + (x – y)²

= 4⋅(4² + 3⋅5) +16 = 140

Vậy B = 140

Bài 3. Tính giá trị biểu thức:

a) 9x² – 48x + 64 – 5x³ tại x = 2

b) x³ – 9x² + 27x – 27 tại x = –4

c) $\frac{{{x^3} - 1}}{{{x^2} - 1}}$ tại x = 6

d) $\frac{{{x^2} - 2x + 1}}{{{x^3} - 1}} + \frac{{{x^2} - 1}}{{{{\left( {x - 1} \right)}^2}}}$ tại x = 3

Hướng dẫn giải

a) 9x² – 48x + 64 – 5x³ = (3x – 8)² – 5x³

Thay x = 2 vào ta được:

(3⋅2 – 8)² – 5⋅2³ = –36

Áp dụng hằng đẳng thức, ta được:

b) x³ – 9x² + 27x – 27 = (x – 3)³

Thay x = –4 vào ta được:

(x – 3)³ = (–4 – 3)³ = –7³ = –343

c) $\frac{{{x^3} - 1}}{{{x^2} - 1}} = \frac{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \frac{{{x^2} + x + 1}}{{x + 1}}$

Thay x = 6 vào ta được:

$\frac{{{x^2} + x + 1}}{{x + 1}} = \frac{{{6^2} + 6 + 1}}{{6 + 1}} = \frac{{43}}{7}$

d) Ta có: $\frac{{{x^2} - 2x + 1}}{{{x^3} - 1}} + \frac{{{x^2} - 1}}{{{{\left( {x - 1} \right)}^2}}}$

$\begin{gathered} = \frac{{{{\left( {x - 1} \right)}^2}}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} + \frac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{{{\left( {x - 1} \right)}^2}}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \\ {} \end{array} \hfill \\ = \frac{{x - 1}}{{{x^2} + x + 1}} + \frac{{x + 1}}{{x - 1}} \hfill \\ \end{gathered}$

Thay x = 3 vào ta được:

$\frac{{3 - 1}}{{{3^2} + 3 + 1}} + \frac{{3 + 1}}{{3 - 1}} = \frac{2}{{13}} + 2 = \frac{{28}}{{13}}$

Dạng 3. Tìm giá trị lớn nhất, giá trị nhỏ nhất

Phương pháp:

+) Giá trị lớn nhất của biểu thức A(x). Áp dụng bất đẳng thức ta biến đổi được về dạng:

m – Q²(x) ≤ m (với m là hằng số) ⇒ GTLN của A(x) = m.

+) Giá trị lớn nhất của biểu thức A(x). Áp dụng bất đẳng thức ta biến đổi được về dạng:

Q²(x) + n ≥ n (với n là hằng số) ⇒ GTNN của A(x) = n.

Bài 1. Tìm giá trị lớn nhất của biểu thức:

a) A = –x² – 2x + 5

b) B = 9x – 3x² + 4

Hướng dẫn giải

a) Ta có:

A = –x² – 2x + 5

= –x² – 2x – 1 + 6

= 6 – (x + 1)² ≤ 6

Vậy giá trị lớn nhất của biểu thức A là 6 khi x + 1 = 0 ⇔ x = –1

b) Ta có:

$\begin{gathered} B = 9x - 3{x^2} + 4 \hfill \\ = 3\left( { - \frac{9}{4} + 2 \cdot \frac{3}{2} \cdot x - {x^2}} \right) + \frac{{27}}{4} + 4\begin{array}{*{20}{c}} {} \\ {} \\ {} \\ {} \end{array} \hfill \\ = \frac{{43}}{4} - 3{\left( {\frac{3}{2} - x} \right)^2} \leqslant \frac{{43}}{4} \hfill \\ \end{gathered}$

Vậy giá trị lớn nhất của biểu thức B là $\frac{{43}}{4}$ khi $\frac{3}{2} - x = 0 \Leftrightarrow x = \frac{3}{2}$

Bài 2. Tìm giá trị nhỏ nhất của biểu thức

a) A = 8x² – 8x + 14

b) B = x² + x + 2

Hướng dẫn giải

a) Ta có:

A = 8x² – 8x + 14

= 2(4x² – 4x + 1) + 12

= 2(2x – 1)² + 12 ≥ 12

Vậy giá trị nhỏ nhất của biểu thức A là 12 khi 2x – 1 = 0 ⇔ x = $\frac{1}{2}$

b) Ta có:

$\begin{gathered} B{\text{ }} = {x^2} + x + 2 = {x^2} + 2 \cdot \frac{1}{2} \cdot x + \frac{1}{4} - \frac{1}{4} + 2\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} = {\left( {x + \frac{1}{2}} \right)^2} + \frac{7}{4} \geqslant \frac{7}{4} \hfill \\ \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

Vậy giá trị nhỏ nhất của biểu thức B là $\frac{7}{4}$ khi $x + \frac{1}{2} = 0 \Leftrightarrow x = - \frac{1}{2}$

Bài 3. Tìm giá trị nhỏ nhất của biểu thức

a) A = (x² – x + 1)²

b) B = x⁴ – 2x³ + 2x² – 2x + 1

Hướng dẫn giải

a) Ta có:

$\begin{gathered} {x^2} - x + 1 = {x^2} - 2 \cdot \frac{1}{2} \cdot x + \frac{1}{4} + \frac{3}{4} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{\begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ = {\left( {x - \frac{1}{2}} \right)^2} + \frac{3}{4} \geqslant \frac{3}{4} \hfill \\ \end{gathered} \end{array}} \end{array} \hfill \\ \end{gathered}$

Ta thấy A đạt giá trị nhỏ nhất bằng $\frac{3}{4}$

Giá trị nhỏ nhất của $A = {\left( {\frac{3}{4}} \right)^2}$ khi và chỉ khi $x - \frac{1}{2} = 0 \Leftrightarrow x = \frac{1}{2}$

b) Ta có:

B = x⁴ – 2x³ + 2x² – 2x + 1

= x⁴ – 2x³ + 2x² – 2x + 1

= x⁴ – 2x³ + x² + x² – 2x + 1

= x²(x² – 2x + 1) + (x² – 2x + 1)

= x²(x – 1)² + (x – 1) ≥ 0

Mặt khác:

$B = 0 \Leftrightarrow \left\{ \begin{gathered} \left[ \begin{gathered} {x^2} = 0 \hfill \\ x - 1 = 0 \hfill \\ \end{gathered} \right. \hfill \\ x - 1 = 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} \left[ \begin{gathered} x = 0 \hfill \\ x = 1 \hfill \\ \end{gathered} \right. \hfill \\ x = 1 \hfill \\ \end{gathered} \right. \Leftrightarrow x = 1$

Vậy giá trị nhỏ nhất của biểu thức B = 0 khi và chỉ khi x = 1

Bài 4. Chứng minh rằng x² – 4x + 10 luôn dương với mọi x

Hướng dẫn giải

Ta có: x² – 4x + 10 = x² – 2⋅2x + 4 + 6 = (x – 2)² + 6

Ta thấy (x – 2)² ≥ 0 ⇒ (x – 2)² + 6 luôn dương với mọi x.

Các dạng bài tập minh họa n ng cao tổng hợp

Bài 1. Tìm hệ số x² của đa thức sau khi khai triển:

a) A = (x – 2)³ + (x + 2)² + (x + 3)³ + (3x + 1)³

b) B = (2x – 1)² + (x – 2)² + (x – 3)² + (3x – 1)³

Hướng dẫn giải

a) A = (x – 2)³ + (x + 2)² + (x + 3)³ + (3x + 1)³

= x² – 4x + 4 + x² + 4x + 4 + x³ + 9x² + 27x + 27 + 27x³ + 27x² + 9x + 1

= 28x³ + 38x² + 36x + 36

Vậy hệ số của x² là 38

b) B = (2x – 1)² + (x – 2)² + (x – 3)² + (3x – 1)³

= 4x²– 4x + 1 + x² – 4x + 4 + x³ – 9x² + 27x + 27x³ – 27x² + 9x – 1

= 28x³ – 31x² + 28x – 23

Vậy hệ số của x² là –31

Bài 2. Tính giá trị biểu thức

a) A = x² + 0,2x + 0,01 tại x = 0,9

b) B = x³ + 3x² + 3x + 2 tại x = 19

c) C = x⁴ – 2x³ + 3x² – 2x + 2 tại x² – x = 8

Hướng dẫn giải

a) Ta có:

A = x² + 0,2x + 0,01

= x² + 0,2x + (0,1)² = (x + 0,1)²

Với x = 0,9 ⇒ A = (0,9 + 0,1)² = 1

b) Ta có:

B = x³ + 3x² + 3x + 2

= x³ + 3x² + 3x + 1 + 1

= (x + 1)³ + 1

Với x = 19 ⇒ B = (19 + 1)³ + 1 = 8000 + 1 = 8001

c) Ta có:

C = x⁴ – 2x³ + 3x² – 2x + 2

= x⁴ – 2x³ + x² + 2x² – 2x + 2

= (x² – x)² + 2(x² – x) + 1 +1

= (x² – x + 1)² + 1

Với x² – x = 8 ⇒ C = (8 + 1)² + 1 = 81 + 1 = 82

Bài 3. Tính hợp lý

a) $A = \frac{{{{356}^2} - {{144}^2}}}{{{{256}^2} - {{244}^2}}}$

b) B = 253² + 94⋅253 +47²

c) C = 136²– 92⋅136 + 46²

d) D = (100² + 98² + … + 2²) – (99² + 97² + … +1²)

Hướng dẫn giải

a) $A = \frac{{{{356}^2} - {{144}^2}}}{{{{256}^2} - {{244}^2}}}$

$\begin{gathered} = \frac{{\left( {356 + 144} \right)\left( {356 - 144} \right)}}{{\left( {256 + 244} \right)\left( {256 - 244} \right)}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \\ {} \end{array} \hfill \\ = \frac{{500 \cdot 212}}{{500 \cdot 12}} = \frac{{53}}{3} \hfill \\ \end{gathered}$

b) B = 253² + 94⋅253 +47²

= 253² + 2⋅47⋅253 + 47²

= (253 + 47)² = 300² = 90000

c) C = 136²– 92⋅136 + 46²

= 136² – 2⋅46⋅136 + 46²

= (136 – 46)² = 90² = 8100

d) D = (100² + 98² + … + 2²) – (99² + 97² + … +1²)

= (100² – 99²) + (98² – 97²) + … + (2² – 1²)

= (100 – 99)(100 + 99) + (98 – 97)(98 + 97) + … + (2 – 1)(2 +1)

= 1⋅(100 +99) + 1⋅(98 + 97) + … + 1⋅(2 + 1)

= 100 + 99 + … + 1

= (100 + 1) + (99 + 2) + … + (51 + 50)

= 101 + 101 + … + 101 = 101⋅50 = 5050

Bài 4. Tính giá trị biểu thức:

$A = \frac{{{{2021}^2}\left( {2020 - 2019} \right)}}{{\left( {2020 - 1} \right)\left( {{{2020}^3} + 1} \right)}} \cdot \frac{{{{2019}^2}\left( {{{2020}^2} + 2021} \right)}}{{{{2020}^3} - 1}}$

Hướng dẫn giải

$\begin{gathered} A = \frac{{{{2021}^2}\left( {{{2020}^2} - 2019} \right)}}{{\left( {{{2020}^2} - 1} \right)\left( {{{2020}^3} + 1} \right)}} \cdot \frac{{{{2019}^2}\left( {{{2020}^2} + 2021} \right)}}{{{{2020}^3} - 1}} \hfill \\ = \frac{{{{2021}^2}\left( {{{2020}^2} - 2020 + 1} \right)}}{{\left( {2020 + 1} \right)\left( {2020 - 1} \right)\left( {2020 + 1} \right)\left( {{{2020}^2} - 2020 + 1} \right)}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \\ {} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} \times \frac{{{{2019}^2}\left( {{{2020}^2} + 2020 + 1} \right)}}{{\left( {2020 - 1} \right)\left( {{{2020}^2} + 2020 + 1} \right)}} \hfill \\ = \frac{1}{{2019}} \cdot 2019 = 1\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Bài 5. Tìm giá trị nhỏ nhất của biểu thức:

a) A = 5x² + 5y² + 8xy + 2y – 2x + 2020

b) M = 5x² + y² + z² – 4x – 2xy – z – 1

Hướng dẫn giải

a) Ta có:

A = 5x² + 5y² + 8xy + 2y – 2x + 2020

= 4x² + 8xy + 4y² + x² – 2x + 1 + y² + 2y + 1 +2018

= 4(x + y)² + (x – 1)² + (y + 1)² + 2018 ≥ 2018

Vậy giá trị nhỏ nhất của A = 2018 tại x = 1; y = –1

b) Ta có:

$\begin{gathered} M = 5{x^2} + {y^2} + {z^2} - 4x - 2xy - z - 1 \hfill \\ = {x^2} - 2xy + {y^2} + 4{x^2} - 4x + 1 + {z^2} - z + \frac{1}{4} - 2\frac{1}{4}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ = {\left( {x + y} \right)^2} + {\left( {2x - 1} \right)^2} + {\left( {z - \frac{1}{2}} \right)^2} - 2\frac{1}{4} \geqslant - 2\frac{1}{4} \hfill \\ \end{gathered}$

Dấu bằng xảy ra khi

$\left\{ \begin{gathered} x - y = 0 \hfill \\ 2x - 1 = 0 \hfill \\ z - \frac{1}{2} = 0 \hfill \\ \end{gathered} \right. \Rightarrow x = y = z = \frac{1}{2}$

Vậy giá trị nhỏ nhất của M là $- 2\frac{1}{4}$ khi $x = y = z = \frac{1}{2}$

Bài 6. Tìm x, biết:

a) (x + 2)² + (x + 3)² – (x – 2)(x – 3) = 19

b) (x + 2)(x² – 2x + 4) – x(x² – 5) = 15

c) (x – 1)³ + (2 – x)(4 + 2x + x²) + 3x(x + 2) = 17

Hướng dẫn giải

a) (x + 2)² + (x + 3)² – (x – 2)(x – 3) = 19

⇔ (x – 2)² + 8x + (x – 3)² + 12x – 2(x – 2)(x – 3) = 19

⇔ 20x + [(x – 2) – (x – 3)]² = 19

⇔ 20x + 1 = 19

⇔ 20x = 18 ⇔ x = $\frac{9}{{10}}$

b) (x + 2)(x² – 2x + 4) – x(x² – 5) = 15

⇔ x³ + 8 – x³ + 5x = 15

⇔ 5x + 8 = 15

⇔ 5x = 7 ⇔ x = $\frac{7}{5}$

c) (x – 1)³ + (2 – x)(4 + 2x + x²) + 3x(x + 2) = 17

⇔ (x – 1)³ + 8 – x³ + 3x² + 6x = 17

⇔ x³ – 3x² + 3x – 1 + 8 – x³ + 6x = 17

⇔ 9x + 7 =17

⇔ 9x = 10 ⇔ x = $\frac{{10}}{9}$

Bài 7. Biết xy = 11 và x²y + xy² + x + y = 2016. Hãy tính giá trị: x² + y²

Hướng dẫn giải

Ta có: x²y + xy² + x + y = 2016

⇔ xy(x + y) + x + y = 2016

⇔ 11(x + y) + (x + y) = 2016

⇔ 12(x + y) = 2016

⇔ x + y = 168

Mà x² + y² = (x + y)² – 2xy = 168² – 2⋅11 = 28202

Bài 8. Cho a – b = 7. Tính giá trị biểu thức:

A = a²(a + 1) – b²(b – 1) – 3ab(a – b + 1) + ab

Hướng dẫn giải

A = a²(a + 1) – b²(b – 1) – 3ab(a – b + 1) + ab

= a³ + a² – b³ + b² – 3ab(a – b) – 3ab + ab

= a³ – 3ab(a – b) – b³ + a² + b² – 2ab

= (a – b)³ + (a – b)²

=7³ + 7² = 392

Bài 9. Chứng minh rằng với mọi x ta có:

a) x(x – 6) + 10 > 0

b) (x – 3)(x – 5) + 3 > 0

c) x² + x + 1 > 0

Hướng dẫn giải

a) x(x – 6) + 10 > 0

⇔ x² – 6x + 9 + 1 > 0

⇔ (x – 3)² + 1 > 0 (luôn đúng)

b) (x – 3)(x – 5) + 3 > 0

⇔ x² – 8x + 18 > 0

⇔ x² – 8x + 16 + 2 > 0

⇔ (x – 4)² + 2 > 0 (luôn đúng)

c) ${x^2} + x + 1 > 0$

$\begin{gathered} \Leftrightarrow {x^2} + x + \frac{1}{4} + \frac{3}{4} > 0 \hfill \\ \Leftrightarrow {\left( {x + \frac{1}{2}} \right)^2} + \frac{3}{4} > 0\begin{array}{*{20}{c}} {} \\ {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Bài 10. Tìm x, y biết:

a) x² – 2x + 5 + y² – 4y = 0

b) 4x² + y² – 20x – 2y + 26 = 0

c) 9x² + 4y² + 4y – 12x + 5 = 0

Hướng dẫn giải

a) x² – 2x + 5 + y² – 4y = 0

⇔ (x² – 2x + 1) + (y² – 4y + 4) = 0

⇔ (x – 1)² + (y – 2)² = 0

⇔ (x – 1)² = 0 và (y – 2) = 0

⇔ x = 1 và y = 2

b) 4x² + y² – 20x – 2y + 26 = 0

⇔ (4x² – 20x + 25) + (y² – 2y + 1) = 0

⇔ (2x – 5)² + (y – 1)² = 0

⇔ (2x – 5)² = 0 và (y – 1)² = 0

⇔ x = $\frac{5}{2}$ và y = 1

c) 9x² + 4y² + 4y – 12x + 5 = 0

⇔ (9x² – 12x + 4) + (4y² + 4y + 1) = 0

⇔ (3x – 2)² + (2y + 1)² = 0

⇔ (3x – 2)² = 0 và (2y + 1)² = 0

⇔ x = $\frac{2}{3}$ và y = $- \frac{1}{2}$

Bài 11. Chứng minh không tồn tại x; y thỏa mãn:

a) x² + 4y² + 4x – 4y + 10 = 0

b) 3x² + y² + 10x – 2xy + 29 = 0

c) 4x² + 2y² + 2y – 4xy + 5 = 0

Hướng dẫn giải

a) x² + 4y² + 4x – 4y + 10 = 0

⇔ x² + 4x + 4 + 4y² – 4y + 1 + 5 = 0

⇔ (x + 2)² + (2y – 1)² + 5 = 0

Mà (x + 2)² + (2y – 1)² + 5 ≥ 5 > 0

Suy ra không có x, y thỏa mãn đề bài.

b) 3x² + y² + 10x – 2xy + 29 = 0

⇔ x² – 2xy + y² + 2x² + 10x + 29 = 0

⇔ (x – y)² + 2(x + 2,5)² + 16,5 = 0

Mà (x – y)² + 2(x + 2,5)² + 16,5 ≥ 16,5 > 0

Suy ra không có x, y thỏa mãn đề bài.

c) 4x² + 2y² + 2y – 4xy + 5 = 0

⇔ (4x² – 4xy + y²) + (y² + 2y + 1) + 4 = 0

⇔ (2x – y)² + (y + 1)² + 4 = 0

Mà (2x – y)² + (y + 1)² + 4 ≥ 4 > 0

Suy ra không có x, y thỏa mãn đề bài.

Bài 12. Tìm giá trị lớn nhất của biểu thức:

a) A = 15 – 8x – x²

b) B = 4x – x² + 2

c) C = x² – y² + 4x – 4y + 2

Hướng dẫn giải

a) A = 15 – 8x – x²

= 31 – (16 + 8x + x²)

= 31 – (4 + x)² ≤ 31

Vậy giá trị lớn nhất của A là 31 khi x = –4

b) B = 4x – x² + 2

= 6 – (4 – 4x + x²)

= 6 – (2 – x)² ≤ 6

Vậy giá trị lớn nhất của B là 6 khi x = 2

c) C = x² – y² + 4x – 4y + 2

= 10 – (x² – 4x + 4) – (y² + 4y + 4)

= 10 – (x – 2)² – (y + 2)² ≤ 10

Vậy giá trị lớn nhất của C là 10 khi x = 1, y = –2

Bài 13. Cho các số thực x; y thỏa mãn điều kiện x + y = 3; x² + y² = 17. Tính giá trị biểu thức x³ + y³.

Hướng dẫn giải

$\begin{gathered} {\left( {x + y} \right)^2} = {x^2} + {y^2} + 2xy = 17 + 2xy = 9\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \Leftrightarrow xy = \frac{{9 - 17}}{2} = - 4\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ {x^3} + {y^3} = {\left( {x + y} \right)^3} - 3xy\left( {x + y} \right)\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ \hfill \\ \end{gathered} \end{array}}&{ = 27 - 3 \cdot \left( { - 4} \right) \cdot 3 = 63} \end{array} \hfill \\ \end{gathered}$

Bài 14. Cho x + y = a + b (1) và x³ + y³ = a³ + b³ (2). Chứng minh rằng: x² + y² = a² + b².

Hướng dẫn giải

Ta có hằng đẳng thức:

(x + y)³ = x³ + y³ + 3xy(x + y) (1)

(a + b)³ = a³ + b³ + 3ab(a + b) (2)

Kết hợp với (1) và (2) suy ra xy = ab (3)

Mặt khác, từ (1) suy ra:

(x + y)³ = (a + b)³

⇔ x² + y² + 2xy = a² + b² + 2ab

Kết hợp với (3) suy ra: x² + y² = a² + b²

Bài 15. Cho a + b + c = 2p. Chứng minh rằng:

a) 2bc + b² + c² – a² = 4p(p – a)

b) (p – a)² + (p – b)² + (p – c)² = a² + b² + c² – p²

Hướng dẫn giải

a) 2bc + b² + c² – a²

= (b + c)² – a²

= (b + c + a)(b + c – a)

= 2p(2p – 2a) = 4p(p – a)

Vế trái bằng vế phải. Điều phải chứng minh

b) (p – a)² + (p – b)² + (p – c)²

= p² – 2ap + a² + p² – 2pb + b² + p² – 2pc + c2

= 3p² – 2p(a + b + c) + a² + b² + c²

= 3p² – 2p⋅2p + a² + b² + c²

= a² + b² + c² – p²

Vế trái bằng vế phải. Điều phải chứng minh

Bài 16. Cho . Hãy so sánh tổng các chữ số của A² với tổng các chữ số của A.

Hướng dẫn giải

Ta có:

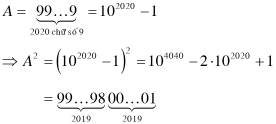
Tổng các chữ số của A² là: 9⋅2019 + 8 + 1 = 18180

Tổng các chữ số của A là: 9⋅2020 = 18180

Vậy tổng các chữ số của A² và tổng các chữ số của A bằng nhau.

Bài 17. Chứng minh rằng:

Nếu (a – b)² + (b – c)² + (c – a)²

= (a + b – 2c)² + (b + c – 2a)² + (c + a – 2b)² thì a = b = c

Hướng dẫn giải

(a + b – 2c)² – (a – b)² + (b + c – 2a)² – (b – c)² + (c + a – 2b)² – (c – a)² = 0 (*)

Áp dụng hằng đẳng thức: x² – y² = (x + y)(x – y) ta có:

(a + b – 2c)² – (a – b)²

= (2a – 2c)(2b – 2c)

= 4(a – c)(b – c)

(b + c – 2a)² – (b – c)²

= (2b – 2a)(2c – 2a)

= 4(b – a)(c – a)

(c + a – 2b)² – (c – a)²

= (2c – 2b)(2a – 2b)

= 4(c – b)(a – b)

Kết hợp với (*) ta có:

4(a – c)(b – c) + 4(b – a)(c – a) + 4(c – b)(a – b) = 0

⇔ (a – c)(b – c) + (b – a)(c – a) + (c – b)(a – b) = 0

⇔ ab – ac + bc + c² + bc – ba – ac + a² + ac – bc – ab + b² = 0

⇔ a² + b² + c² – ab – bc – ac = 0

⇔ 2a² + 2b² + 2c² – 2ab – 2bc – 2ac = 0

⇔ a² – 2ab + b² + b² – 2bc + c² + c² – 2ca + a² = 0

⇔ (a – b)² + (b – c)² + (c – a)² = 0

⇔ a – b = 0 và b – c = 0 và c – a = 0

⇔ a = b = c

Bài 18. Cho n là số tự nhiên lớn hơn 1. Chứng minh rằng: n⁴ + 4ⁿ là hợp số.

Hướng dẫn giải

+) Với n là số chẵn n = 2k (k ∈ ℕ^*) thì n⁴ + 4ⁿ = 16k⁴ + 4^2k ⋮ 4 nên n⁴ + 4ⁿ là hợp số

+) Với n là số lẻ. Đặt n = 2k – 1 (k ∈ ℕ^*, k > 1) thì ta có:

n⁴ + 4ⁿ = n⁴ + 2⋅n²⋅2ⁿ + 4ⁿ – n²⋅2ⁿ⁺¹

= (n² + 2ⁿ)² – n²⋅2^2k

= (n² + 2ⁿ – 2^k⋅n)(n² + 2ⁿ + 2^k⋅n)

Ta có: n² + 2ⁿ – 2^k⋅n

= n² – 2^k⋅n + 2^2k–2 + 2ⁿ – 2^2k–2

= (n – 2^k–1)² + 2^2k–1 – 2^2k–2

= (n – 2^k–1)² + 2^2k–2 > 1

Mà n² + 2ⁿ + 2^k⋅n > n² + 2ⁿ – 2^k⋅n suy ra n⁴ + 4ⁿ là hợp số

Vậy n⁴ + 4ⁿ là hợp số với n là số tự nhiên lớn hơn 1.

Bài 19.

a) Cho a + b = 2. Tìm giá trị nhỏ nhất của A = a² + b²

b) Cho x + 2y = 8. Tìm giá trị lớn nhất của B = xy

Hướng dẫn giải

a) Ta có: (a + b)² + (a – b)² =2(a² + b²)

⇒ 4 + (a – b)² = 2A

⇒ 4 ≤ 2A ⇒ A ≥ 2

Vậy giá trị nhỏ nhất của A là 2 khi a = b = 1.

b) Từ x + 2y = 8 ⇒ x = 8 – 2y suy ra:

B = (8 – 2y)y = 8y – 2y² = 8 – 8 + 8y – 2y²

B = 8 – 2(2 – y)² ≤ 8

Vậy giá trị lớn nhất của B là 8 khi y = 2; x = 4.

Bài 20. Tìm giá trị nhỏ nhất của A = 3(x² + y²) biết x² + y² = xy + 12

Hướng dẫn giải

Từ giả thiết ta có:

(x + y)² = 3xy + 12

⇔ 6xy = 2(x + y)² – 24

Ta có: A = 3(x² + y²) = 3(x + y)² – 6xy

= 3(x + y)² – 2(x + y)² + 24

= (x + y)² + 24

Vậy giá trị nhỏ nhất của A là 24 khi

$x + y = 0 \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} x = 2 \hfill \\ y = - 2 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} x = - 2 \hfill \\ y = 2 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right.$

Bài 21. Cho các số nguyên a, b, c thỏa mãn: (a – b)³ + (b – c)³ + (c – a)³ = 2010. Tính giá trị của biểu thức A = |a – b| + |b – c| + |c – a|.

Hướng dẫn giải

Đặt a – b = x; b – c = y; c – a = z

⇒ x + y + z = 0 ⇒ z = –(x + y)

Ta có: x³ + y³ + z³ = 210

⇔ x³ + y³ – (x + y)³ = 210

⇔ –3xy (x + y) = 210

⇔ xyz = 70

Do x, y, z là số nguyên có tổng bằng 0 và xyz = 70 = (–2)⋅(–5)⋅7 nên x, y, z ∈ {–2; –5; –7}

⇒ A = |a – b| + |b – c| + |c – a| = 14

Bài 22. Chứng minh không tồn tại hai số nguyên x, y thỏa mãn x² – y² = 2020.

Hướng dẫn giải

Từ x² – y² = 2020 suy ra x, y cùng chẵn hoặc cùng lẻ

TH1: Nếu x; y cùng chẵn. Đặt x = 2m; y = 2n

Ta có: 4m² – 4n² = 2018 ⇒ 2m² – 2n² = 1009

Vế trái chẵn, còn vế phải lẻ. Vô lí

TH2: Xét x; y cùng lẻ. Đặt x = 2k + 1; y = 2q + 1

Ta có: (2m + 1)² – (2n + 1)² = 2018

⇔ 4m² + 4m – 4n² – 4n = 2018

Vế trái chia hết cho 4, vế phải không chia hết cho 4, vô lí.

Vậy không tồn tại số nguyên x; y thỏa mãn x² – y² = 2020.

Thầy Tú dạy toán