Đường trung bình của tam giác
Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Định lí 1. Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Định lí 2. Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy
Đường trung bình của hình thang
Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
Định lí 3. Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
Định lí 4. Đường trung bình của hình thang song song với hai đáy và bằng nửa tổng hai đáy.
Phân dạng bài tập
Dạng 1. Sử dụng định nghĩa và định lí về đường trung bình của tam giác để chứng minh
Phương pháp giải: Sử dụng Định nghĩa đường trung bình của tam giác, Định lí 1, Định lí 2 để suy ra điều cần chứng minh.
Bài 1. Cho tam giác ABC cân tại A, có M là trung điểm của BC. Kẻ tia Mx song song với AC cắt AB tại E và tia My song song với AB cắt AC tại F. Chứng minh:
a) EF là đường trung bình của tam giác ABC
b) AM là đường trung trực của EF
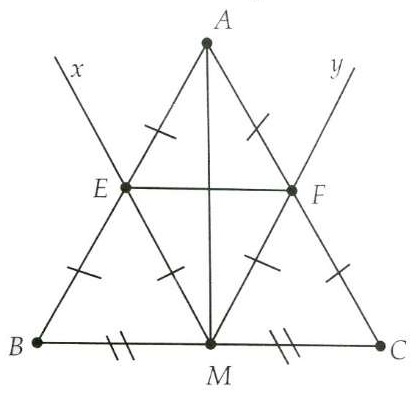
Hướng dẫn giải
a) Mx đi qua trung điểm M của BC và song song với AC.
Suy ra: Mx đi qua trung điểm E của AB (theo Định lí 1).
Tương tự, ta được F cũng là trung điểm của AC.
Khi đó: EF trở thành đường trung bình của tam giác ABC
b) Do ME và MF cũng là đường trung bình nên có ME = MF = AE = AF.
Suy ra: AM là đường trung trực của EF.
Bài 2. Cho tam giác ABC, có AM là trung tuyến ứng với BC. Trên cạnh AB lấy điểm D và E sao cho AD = DE = EB. Đoạn CD cắt AM tại I. Chứng minh:
a) EM song song với DC
b) I là trung điểm của AM
c) DC = 4DI
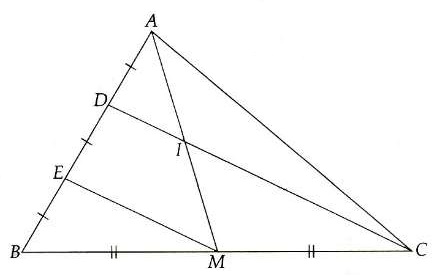
Hướng dẫn giải
a) Ta có EM là đường trung bình của tam giác BCD ⇒ Đpcm
b) DC đi qua trung điểm D của AE và song song với EM
⇒ DC đi qua trung điểm I của AM.
c) Vì DI là đường trung bình của tam giác AEM nên DI = ![\[\frac{1}{2}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-1.svg)
EM (1)
Tương tự, ta được: EM = DC (2)
Từ (1) và (2) ⇒ DC = 4DI
Dạng 2. Sử dụng định nghĩa và định lí về đường trung bình của hình thang để chứng minh
Phương pháp giải: Sử dụng Định nghĩa đường trung bình của hình thang, Định lí 3, Định lí 4 để suy ra điều cần chứng minh.
Bài 1. Cho hình thang vuông ABCD tại A và D. Gọi E, F lần lượt là trung điểm của AD, BC. Chứng minh:
a) △AFD cân tại F;
b) ![\[\widehat {BAF} = \widehat {CDF}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-2.svg)
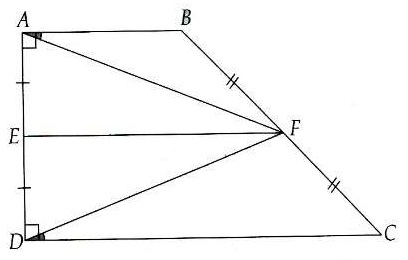
Hướng dẫn giải
a) Ta có: EF là đường trung bình của hình thang ABCD ⇒ EF // AB.
Suy ra: EF ⊥ AD
Khi đó EF vừa trung tuyến, vừa là đường cao của tam giác AFD ⇒ Đpcm
b) Tam giác AFD cân tại F nên ![\[\widehat {EAF} = \widehat {EDF}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-3.svg)
Suy ra:
Bài 2. Cho hình thang ABCD (AB // CD). Các đường phân giác ngoài của ![\[\widehat A\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-4.svg)
và ![\[\widehat D\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-5.svg)
cắt nhau tại E, các đường phân giác ngoài của ![\[\widehat B\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-6.svg)
và ![\[\widehat C\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-7.svg)
cắt nhau tại F. Chứng minh:
a) EF song song với AB và CD;
b) EF có độ dài bằng nửa chu vi hình thang ABCD.
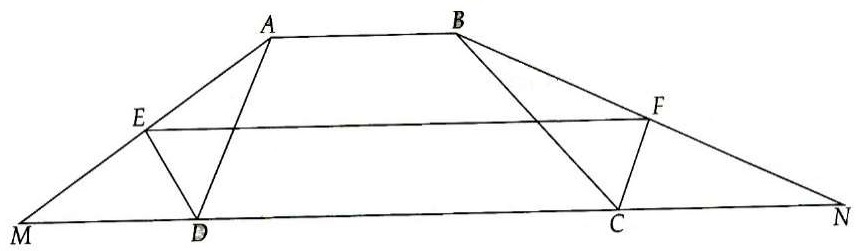
Hướng dẫn giải
a) Gọi M và N lần lượt là giao điểm của AE, BF với CD.
Ta có: ![\[\widehat {ADE} = \frac{1}{2}\widehat D\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-8.svg)
ngoài, ![\[\widehat {DAE} = \frac{1}{2}\widehat A\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-9.svg)
ngoài.
Mà ngoài + ngoài = 180° (do AB // CD)
![\[ \Rightarrow \widehat {ADE} + \widehat {DAE} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-10.svg)
, tức là tam giác ADE vuông tại E.
Khi đó, tam giác ADM cân tại D (do có DE vừa là đường phân giác, vừa là đường cao) và E là trung điểm của AM.
Chứng minh tương tự, ta được F là trung điểm của BN.
Từ khó, suy ra EF là đường trung bình của hình thang ABNM và ta được ĐPCM
b) Từ ý a), ta có:
EF = (AB + BC + CD + DA)
Lưu ý: Có thể sử dụng tính chất đường phân giác để chứng minh.
Dạng 3. Sử dụng phối hợp đường trung bình của tam giác và đường trung bình của hình thang để chứng minh
Phương pháp giải: Sử dụng Định nghĩa đường trung bình của tam giác, Định nghĩa đường trung bình của hình thang và các Định lí: 1, 2, 3, 4 để suy ra điều cần chứng minh.
Bài 1. Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q lần lượt là trung điểm của AD, BD, AC, BC. Chứng minh:
a) M, N, P, Q cùng nằm trên một đường thẳng;
b) NP = |DC – AB|
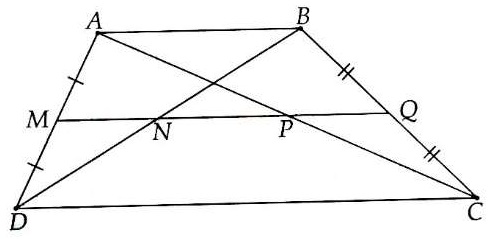
Hướng dẫn giải
a) Ta có: MN là đường trung bình của tam giác ABD
⇒ MN // AB
Tương tự, ta được MP // CD và MQ // AB, MQ // CD
Như vậy, MN, MP, MQ cùng song song AB ⇒ Đpcm
b) Ta có: |DC – AB|
= |2MP – 2MN|
= |MP – MN| = NP
Bài 2. Cho hình thang ABCD (AB // CD) với AB = a, BC = b, CD = c và DA = d. Các tia phân giác của góc và góc cắt nhau tại E, các tia phân giác của và cắt nhau tại F. Gọi M, N theo thứ tự là trung điểm của AD và BC.
a) Chứng minh M, E, N, F cùng nằm trên một đường thẳng.
b) Tính độ dài MN, MF, FN theo a, b, c, d.
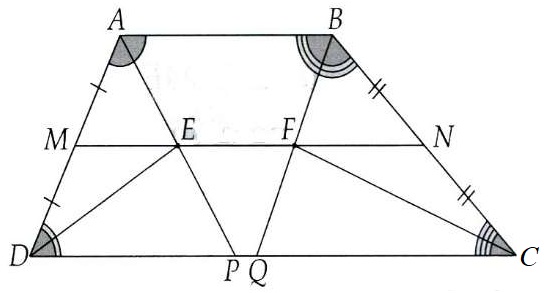
Hướng dẫn giải
a) Gọi P và Q lần lượt là giao điểm của AE, AF với CD.
Chứng minh tương tự 4.
b) Ta có:
MN = (AB + CD) = (a + c)
Lại có: c = CD = CQ + QD = BC + QD = b + QD (do tam giác BCQ cân)
⇒ QD = c – b
Trong hình thang ABQD có M là trung điểm của AD và MF // DQ nên chứng minh được F là trung điểm của BQ, từ đó chứng minh MF là đường trung bình của hình thang ABQD.
Vì MF là đường trung bình của hình thang ABQD.
⇒ MF = (AB + DQ) = (a + c – b)
Mặt khác, FN là đường trung bình của tam giác BCQ, tức là:
FN = CQ = b
Dạng 4. Tổng hợp
Bài 1. Cho tam giác ABC vuông tại A, kẻ đường cao AH. Từ H kẻ tia Hx vuông góc với AB tại P và tia Hy vuông góc với AC tại Q. Trên các tia Hx, Hy lần lượt lấy các điếm D và E sao cho PH = PD, QH = QE. Chứng minh:
a) A là trung điểm của DE
b) PQ = DE
c) PQ = AH
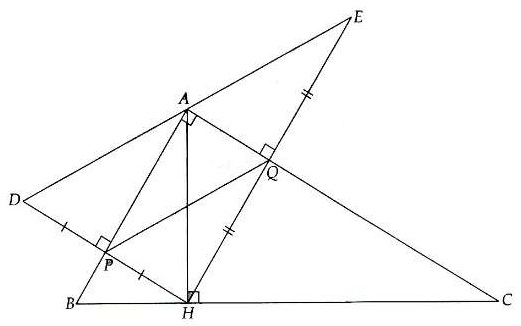
Hướng dẫn giải
a) Chứng minh được tam giác ADH và AEH cân tại A
Khi đó: ![\[\widehat {DAP} = \widehat {HAP},{\text{ }}\widehat {EAQ} = \widehat {HAQ}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-11.svg)
và AD = AH = AE
Từ đó, suy ra được A, D, E thẳng hàng và A là trung điểm DE
b) PQ là đường trung bình của tam giác DHE ⇒ Đpcm
c) Có AH = AD = AE = DE
Mà PQ = DE ⇒ AH = PQ
Bài 2. Cho tam giác ABC có AM là trung tuyến ứng với BC. Trên cạnh AC lấy điểm D sao cho AD = DC. Kẻ Mx song song với BD và cắt AC tại E. Đoạn BD cắt AM tại I. Chứng minh:
a) AD = DE = EC
b) SAIB = SIBM
C)SABC = 2SIBC
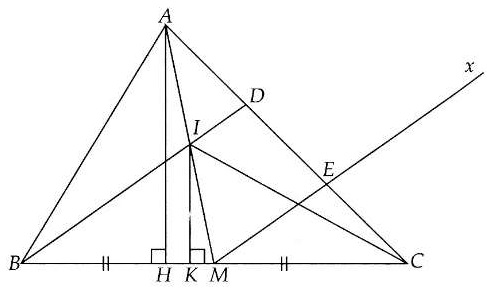
Hướng dẫn giải
a) Theo định lý 1, trong tam giác BDC có: M là trung điểm của BC và ME // BD
⇒ E là trung điểm của DC ⇒ DE = EC = DC.
Suy ra: AD = DE = EC.
b) Từ ý a) D là trung điểm của AE.
Suy ra: ID là đường trung bình của tam giác AME hay IA = IM.
Vậy SAIB = SIBM.
c) Hạ hai đường cao AH và IK của tam giác ABC và IBC
Chứng minh được IK là đường trung bình của tam giác AHM
⇒ IK = AH.
Xét hai tam giác ABC và IBC có chung đáy BC và hai đường cao AH = 2IK
⇒ Đpcm
Bài 3. Cho tứ giác ABCD. Gọi E, F, K lần lượt là trung điểm của AD, BC, AC.
a) Chứng minh EK song song với CD, FK song song với AB.
b) So sánh EF và (AB + CD).
c) Tìm điều kiện của tứ giác ABCD để ba điểm E, F, K thẳng hàng. Từ đó chứng minh EF = (AB + CD).
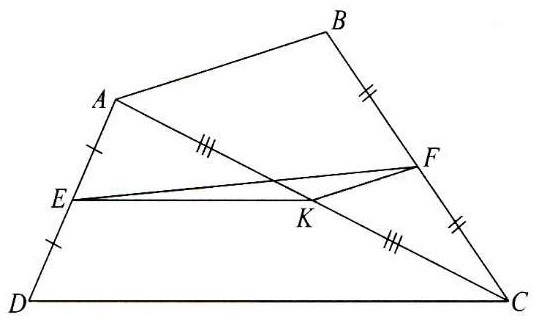
Hướng dẫn giải
a) HS tự chứng minh.
b) Xét tam giác EFK, có:
EF ≤ EK + KF = CD + AB = (AB + CD)
c) Để E, F, K thẳng hàng, khi đó EF đồng thời song song với AB và CD.
Tức là tứ giác ABCD là hình thang (AB // CD)
Theo định lý 4, EF = (AB + CD)
Bài 4. Cho tứ giác ABCD. Có G là trung điểm của đoạn nối các trung điểm của hai đường chéo AC và BD. Gọi m là một đường thẳng không cắt cạnh nào của hình thang ABCD; Gọi A’, B’, C’, D’, G’ lần lượt là hình chiếu của A, B, C, D, G lên đường thẳng m. Chứng minh:
GG’ = (AA’ + BB’ + CC’ + DD’).
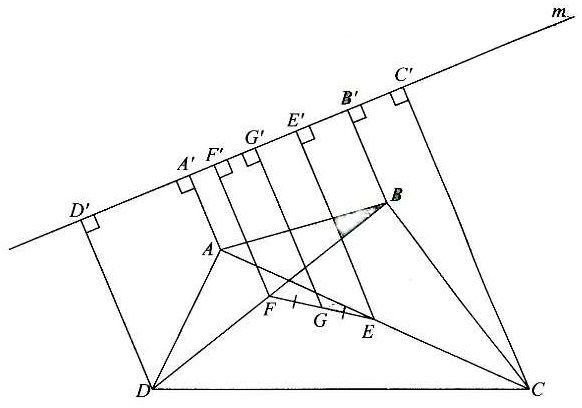
Hướng dẫn giải
Gọi E và F lần lượt là trung điểm của AC và BD, E’ và F’ lần lượt là hình chiếu của E, F trên đường thẳng m.
Khi đó: GG’ là đường trung bình của hình thang EE’F’F
⇒ GG’ = (EE’ + FF’)
Mà EE’ và FF’ lần lượt là đường trung bình của hình thang AA’C’C và BB’D’D
⇒ EE’ = (AA’ + CC’) và FF’ = (BB’ + DD’)
Thay vào (1) ta được đpcm.
Các dạng bài nâng cao phát triển tư duy
⋆ Đường trung bình của tam giác
Bài 1. Cho tứ giác ABCD, đường chéo BD là đường trung trực của AC. Gọi M, N lần lượt là trung điểm của AD và AB. Vẽ ME ⊥ BC và NF ⊥ CD (E ∈ BC, F ∈ CD). Chứng minh rằng ba đường thẳng ME, NF và AC đồng quy.
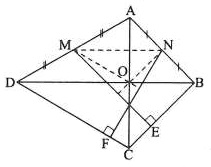
Hướng dẫn giải
Gọi O là giao điểm của AC và BD.
Ta có: AC ⊥ BD và OA = OC.
Xét △ABD có MN là đường trung bình
⇒ MN // BD và OA ⊥ MN (vì OA ⊥ BD).
Xét △ABC có ON là đường trung bình
⇒ ON // BC và ON ⊥ ME (vì ME ⊥ BC).
Xét △ACD có OM là đường trung bình
⇒ OM // CD và OM ⊥ NF (vì NF ⊥ CD).
Xét △OMN có OA, ME, NF là ba đường cao nên chúng đồng quy.
Bài 2. Cho tam giác ABC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E. Gọi M, N lần lượt là trung điểm của BE và CD. Đường thẳng MN cắt tia AB và AC lần lượt là tại P và Q. Hỏi hai điểm D và E phải có điều kiện gì để tam giác APQ cân tại A?
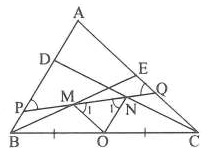
Hướng dẫn giải
Gọi O là trung điểm của BC.
Xét △EBC có OM là đường trung bình
⇒ OM CE // và OM = CE
Xét △DBC có ON là đường trung bình
⇒ ON BD // và ON = BD
Ta có: ![\[\widehat {{M_1}} = \widehat {AQP},{\text{ }}\widehat {{N_1}} = \widehat {APQ}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-12.svg)
(so le trong).
△APQ cân tại A
![\[\begin{gathered} \Leftrightarrow \widehat Q = \widehat P \Leftrightarrow \widehat {{M_1}} = \widehat {{N_1}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \Leftrightarrow OM = ON \Leftrightarrow CE = BD \hfill \\ \end{gathered} \]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-13.svg)
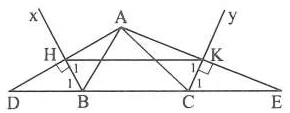
Bài 3. Cho tam giác ABC. Gọi Bx và Cy lần lượt là các đường chứa tia phân giác của các góc ngoài tại đỉnh B và C. Gọi H và K lần lượt là hình chiếu của A trên Bx và Cy.
a) Chứng minh rằng tứ giác BCKH là hình thang;
b) Tam giác ABC phải có điều kiện gì để hình thang BCKH là hình thang cân?
Hướng dẫn giải
a) Gọi D và E thứ tự là giao điểm của AH và AK với đường thẳng BC.
△ABD có BH vừa là đường phân giác, vừa là đường cao nên là tam giác cân
⇒ HA = HD. Tương tự, ta có: KA = KE
Xét △ADE có HK là đường trung bình nên HK // DE
⇒ HK // BC
Do đó tứ giác BCKH là hình thang.
b) Ta có: ![\[\widehat {{H_1}} = \widehat {{B_1}},{\text{ }}\widehat {{K_1}} = \widehat {{C_1}}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-14.svg)
(so le trong).
Hình thang BCKH là hình thang cân
![\[\begin{gathered} \Leftrightarrow \widehat {{H_1}} = \widehat {{K_1}} \Leftrightarrow \widehat {{B_1}} = \widehat {{C_1}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \Leftrightarrow \widehat {ABD} = \widehat {ACE} \Leftrightarrow \widehat {ABC} = \widehat {ACB} \hfill \\ \end{gathered} \]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-15.svg)
⇒ △ABC cân tại A.
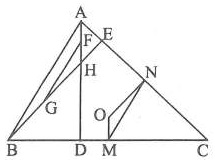
Bài 4. Cho tam giác ABC, trực tâm H. Gọi O là giao điểm của ba đường trung trực. Chứng minh rằng khoảng cách từ O đến BC bằng nửa độ dài AH.
Hướng dẫn giải
Gọi M và N lần lượt là trung điểm của BC và CA.
Gọi F và G lần lượt là trung điểm của AH và BH.
Ta có: MN là đường trung bình của △ABC, FG là đường trung bình của △ABH.
Suy ra: MN // AB và MN = AB
FG // AB và FG = AB
Do đó: MN // FG và MN = FG.
Dễ thấy OM // AD, ON // BE.
△OMN và △HFG có:
![\[MN = FG;{\text{ }}\widehat {OMN} = \widehat {HFG};{\text{ }}\widehat {ONM} = \widehat {HGF}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-16.svg)
(hai góc có cạnh tương ứng song song).
Vậy △OMN và △HFG (g.c.g)
⇒ OM = HF = AH
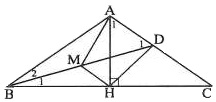
Bài 5. Cho tam giác ABC cân tại A, đường cao AH và đường phân giác BD. Biết rằng AH = BD, tính số đo các góc của tam giác ABC.
Hướng dẫn giải
Gọi M là trung điểm của BD thì:
MD = BD = AH
Trong △ABC cân tại A, có AH là đường cao nên HB = HC.
Ta có: HM là đường trung bình của △BCD ⇒ HM // AC
Hình thang HMAD có hai đường chéo bằng nhau nên là hình thang cân.
△ADH = △DAM (c.c.c)
![\[ \Rightarrow \widehat {{A_1}} = \widehat {{D_1}} \Leftrightarrow 90^\circ - \widehat C = \widehat {{B_1}} + \widehat C{\text{ }}\left( 1 \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-17.svg)
Ta đặt ![\[\widehat B = \widehat C = x\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-18.svg)
thì
![\[\left( 1 \right) \Leftrightarrow 90^\circ - x = \frac{x}{2} + x \Leftrightarrow x = 36^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-19.svg)
Vậy △ABC có ![\[\widehat B = \widehat C = 36^\circ ;{\text{ }}\widehat A = 108^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-20.svg)
Bài 6. Cho đoạn thẳng AB và n điểm O1, O2, …, On không nằm giữa A và B sao cho:
O1A + O2A + … + OnA = O1B + O2B + … + OnB = a
Chứng minh rằng tồn tại một điểm M sao cho: O1M + O2M + … + OnM ≤ a
Hướng dẫn giải
Gọi M là trung điểm của AB và O là một điểm tùy ý không nằm giữa A và B.
⋄ Trường hợp O nằm trên tia đối của tia AB hay tia đối của tia BA
Ta chứng minh được: OM = (OA + OB) (1)
⋄ Trường hợp O không thẳng hàng với A và B
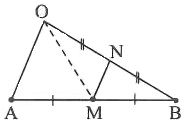
Gọi N là trung điểm của OB, khi đó MN là đường trung bình của △OAB
⇒ MN = OA
Xét △OMN, ta có:
OM < MN + ON
⇒ OM < (OA + OB) (2)
Từ (1) và (2) suy ra: OM ≤ (OA + OB) (*)
Áp dụng hệ thức (*) đối với n điểm O1, O2, …, On ta có:
O1M ≤ (O1A + O1B); O2M ≤ (O2A + O2B); …; OnM ≤ (OnA + OnB).
Cộng từng vế các bất đẳng thức trên ta được:
O1M + O2M + … + OnM
≤ (O1A + O1B) + (O2A + O2B) + … + (OnA + OnB)
= (O1A + O2A + … + OnA) + (O1B + O2B + … + OnB)
= a + a = a
Như vậy điểm cần tìm chính là trung điểm M của AB.
⋆ Đường trung bình của hình thang
Bài 1. Cho hình thang cân ABCD (AB < CD). Vẽ AH ⊥ CD. Chứng minh rằng:
a) HD bằng đoạn thẳng nối trung điểm hai đường chéo
b) HC bằng đường trung bình của hình thang
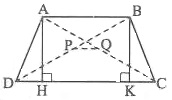
Hướng dẫn giải
a) Vẽ BK ⊥ CD ta được AH // BK và AB // HK
⇒ AB = HK.
△ADH = △BCK ⇒ HD = KC.
Ta có: HD + KC = CD – HK
⇔ 2HD = CD – AB
⇔ HD = (CD – AB)
Theo ví dụ 4 thì đoạn thẳng PQ nối trung điểm của hai đường chéo bằng nửa hiệu hai đáy.
Vậy HD = PQ.
b) Ta có: HC = CD – HD
= CD – (CD – AB)
= (CD + AB)
Đường trung bình của hình thang bằng nửa tổng hai đáy.
Do đó HC bằng độ dài đường trung bình của hình thang.
Bài 2. Cho tam giác ABC. Gọi M là trung điểm của AB. Trên tia đối của tia BC lấy điểm O sao cho BO = BC. Đường thẳng OM cắt OC tại N. Chứng minh rằng: AN = AC.
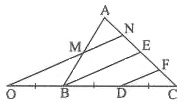
Hướng dẫn giải
Gọi D là trung điểm của BC.
Vẽ BE // ON, DF // ON (E, F ∈ AC)
Ta có: OB = BD = DC = BC
⋄ Xét △ABE có:
MN // BE và MA = MB nên NA = NE (1)
⋄ Xét hình thang ONFD có:
BE // ON và OB = BD nên NE = EF (2)
⋄ Xét △CBE có:
DF // BE và BD = DC nên EF = FC (3)
Từ (1), (2) và (3) suy ra: AN = NE = EF = FC
Do đó: AN = ![\[\frac{1}{4}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-21.svg)
AC
Bài 3. Cho tam giác ABC, cạnh BC cố định. Vẽ ra ngoài tam giác này các tam giác ABM vuông cân tại B, tam giác CAN vuông cân tại C. Chứng minh rằng khi A di động trên một nửa mặt phẳng bờ BC thì đường thẳng MN luôn đi qua một điểm cố định.
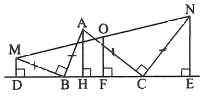
Hướng dẫn giải
Gọi O là trung điểm của MN.
Vẽ OF ⊥ BC; AH ⊥ BC; MD ⊥ BC và NE ⊥ BC
Ta có: OF // AH // MD // NE
△BMD = △ABH (cạnh huyền – góc nhọn)
⇒ MD = BH và BD = AH (1)
Tương tự, △CNE = △ACH
⇒ NE = CH và CE = AH (2)
Từ (1) và (2) suy ra BD = CE (= AH)
Dễ thấy OF là đường trung bình của hình thang MDEN
![\[ \Rightarrow OF = \frac{{MD + NE}}{2} = \frac{{BH + CH}}{2} = \frac{{BC}}{2}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-22.svg)
(không đổi).
Ta có: FD = FE; BD = CE ⇒ FB = FC
Vậy O nằm trên đường trung trực của BC và cách BC một khoảng không đổi là ![\[\frac{{BC}}{2}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-23.svg)
.
Do đó O là một điểm cố định.
Suy ra MN đi qua một điểm cố định là điểm O.
Bài 4. Cho điểm M nằm giữa hai điểm A và B nhưng không là trung điểm của đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tam giác CAM và DBM cân tại C và D sao cho ![\[\widehat C = \widehat D\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-24.svg)
. Gọi H và F lần lượt là trung điểm của AD và BC. Chứng minh rằng: HF = CD.
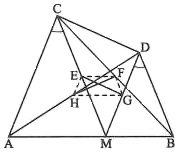
Hướng dẫn giải
⋆ Tìm hướng giải
Điều phải chứng minh là HF = CD gợi ý cho ta nghĩ đến định lí đường trung bình của tam giác.
Ta vẽ đường trung bình EG của △MCD thì EG = CD. Chỉ còn phải chứng minh HF = EG.
⋆ Trình bày lời giải
Gọi E là trung điểm của CM, G là trung điểm của DM.
Khi đó EG là đường trung bình của △MCD
⇒ EG = CD (1)
△CAM và △DBM cân tại C và D mà nên các góc ở đáy của chúng bằng nhau:
![\[\widehat {CAM} = \widehat {CMA} = \widehat {DMB} = \widehat {DBM}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-25.svg)
⇒ CA // DM và CM // DB (vì có các cặp góc đồng vị bằng nhau).
Xét △CMB có EF là đường trung bình
⇒ EF // MB
Xét △DAM có HG là đường trung bình
⇒ HG // AM
Suy ra: EF // HG (vì cùng song song với AB). Vậy tứ giác EFGH là hình thang.
Trong hình thang ACDM có EH là đoạn thẳng nối trung điểm của hai đường chéo nên EH // AC.
Tương tự, xét hình thang CDBM ⇒ FG // DB.
Do đó: ![\[\widehat {EHG} = \widehat {CAM},{\text{ }}\widehat {FGH} = \widehat {DBM}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-26.svg)
Mặt khác: ![\[\widehat {CAM} = \widehat {DBM}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-27.svg)
(chứng minh trên) nên ![\[\widehat {EHG} = \widehat {FGH}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-28.svg)
Vậy hình thang EFGH là hình thang cân
⇒ HF = EG (2)
Từ (1) và (2) suy ra: HF = CD
Phiếu bài tự luyện cơ bản và nâng cao
⋆ Đường trung bình của tam giác
Bài 1. Cho tam giác ABC. Trên tia đối của tia BC lấy điểm D sao cho BD = AB. Trên tia đối của tia CD lấy điểm E sao cho CE = AC. Gọi H là chân đường vuông góc kẻ từ D đến AD, K là chân đường vuông góc kẻ từ C đến AE.
a) Chứng minh rằng HK song song với DE.
b) Tính HK, biết chu vi tam giác ABC bằng 10.
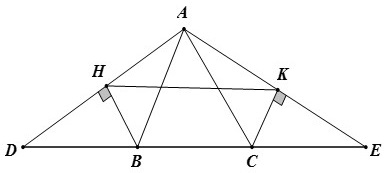
Hướng dẫn giải
a) △ABD cân tại B có BH là đường cao nên BH đồng thời là đường trung tuyến
⇒ AH = HD
Tương tự AK = KE nên HK là đường trung bình của △ADE nên HK // DE; HK = DE
b) HK = DE = ⋅ 10 = 5 cm
(Vì DE = DB + BC + CF = AB + BC + CA = 10)
Bài 2. Cho △ABC có AB < AC, AH là đường cao. Gọi M, N, K lần lượt là trung điểm của AB, AC, BC.
a) Chứng minh MNKH là hình thang cân.
b) Trên tia AH và AK lần lượt lấy điểm E và D sao cho H là trung điểm của AE và K là trung điểm của AD. Chứng minh tứ giác BCDE là hình thang cân.
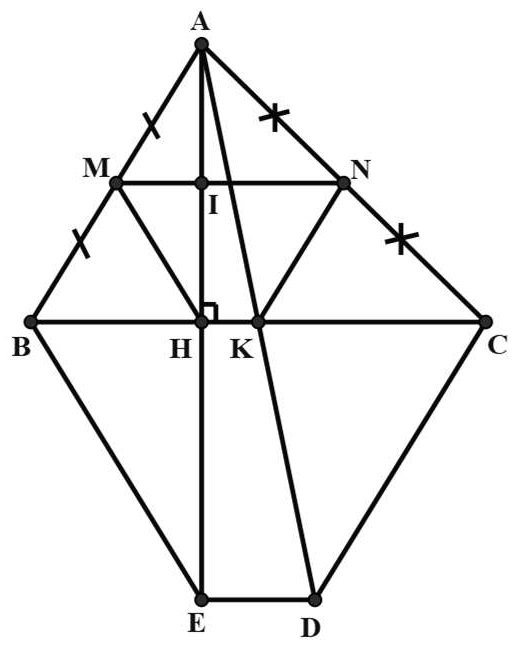
Hướng dẫn giải
a) MN là đường trung bình của △ABC
⇒ MN // BC ⇒ MN // HK hay MI // BH
Ta có: MI // BH và MA = MB ⇒ IA = IH
△MAH cân tại A nên ![\[\widehat {HMI} = \widehat {IMA}{\text{ }}\left( 1 \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-29.svg)
NK là đường trung bình của △ABC
⇒ NK // AB ⇒ ![\[\widehat {MNK} = \widehat {IMA}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-30.svg)
(hai góc ở vị tri so le trong) (2)
Từ (1) và (2) suy ra ![\[\widehat {HMI} = \widehat {MNK}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-31.svg)
(so le trong) hay ![\[\widehat {HMN} = \widehat {MNK}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-32.svg)
Tứ giác MNHK có MN // HK nên tứ giác là hình thang, lại có là hình thang cân.
b) HK là đường trung bình của △AED
⇒ HK // ED hay BC // ED nên tứ giác BCDE là hình thang.
⇒ NK là đường trung bình của △ACD
⇒ NK // CD mà NK // AB nên AB // CD
⇒ ![\[\widehat {ABH} = \widehat {BCD}{\text{ }}\left( 3 \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-33.svg)
(so le trong)
Dễ thấy △ABE cân tại B vì BH vừa là đường cao vừa là trung tuyến
⇒ BH là phân giác của ![\[\widehat {ABE}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-33a.svg)
![\[ \Rightarrow \widehat {ABH} = \widehat {HBE}{\text{ }}\left( 4 \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-34.svg)
Từ (3), (4) ![\[ \Rightarrow \widehat {HBE} = \widehat {BCD}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-35.svg)
![\[ \Rightarrow \widehat {CBE} = \widehat {BCD}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-36.svg)
Hình thang BCDE có ![\[\widehat {CBE} = \widehat {BCD}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-37.svg)
⇒ Tứ giác BCDE là hình thang cân.
Bài 3. Cho △ABC có trung tuyến AM, I là một điểm thuộc đoạn thẳng AM, BI cắt AC ở D.
a) Nếu AD = DC. Khi đó hãy chứng minh I là trung điểm của AM.
b) Nếu I là trung điểm của AM. Khi đó hãy chứng minh: AD = DC, ID = BD
c) Nếu AD = DC. Khi đó trên cạnh AB lấy điểm E sao cho AB = 3AE. Chứng minh BD, CE, AM đồng quy.
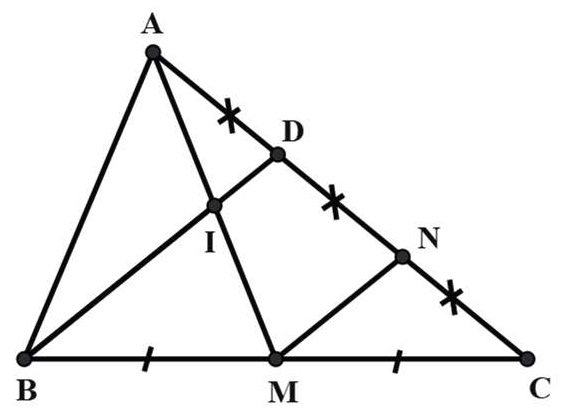
Hướng dẫn giải
a) Khi AD = DC
Gọi N là trung điểm của DC, khi đó MN là đường trung bình của △BCD
⇒ MN // BD ⇒ MN // ID
△AMN có MN // ID và AD = DN ⇒ AI = IM
b) Khi AI = Kẻ MN // BD. Xét △AMN ta có:
ID // MN và AI = IM nên AD = DN
Xét △BCD có:
MN // BD và MB // MC
Nên ND = NC.
Vậy AD = DC và dễ dàng chỉ ra ID = BD
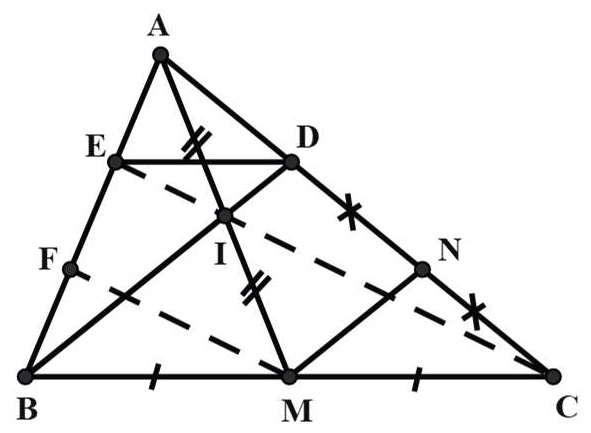
c) Khi AD = DC, AB = 3 AE
Ta có: I là giao điểm của BD và AM
Gọi F là trung điểm của BE.
Ta có: MF là đường trung bình của △BEC
⇒ FM // CE
AD = DC thì IA = IM (theo câu a)
Nên EI là đường trung bình của △AFM
⇒ EI // FM
Ta có: FM // CE và EI // FM nên E, I, C thẳng hàng hay EC đi qua điểm I.
Bài 4. Dùng tính chất đường trung bình của tam giác chứng minh trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
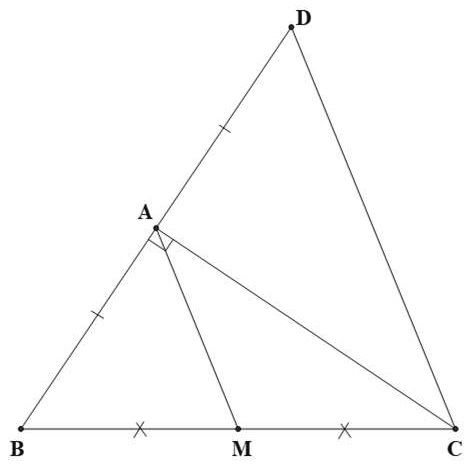
Hướng dẫn giải
Trên tia đối của tia AB lấy điểm D sao cho AD = AB.
Khi đó: △BCD cân tại C nên BC = CD
Ta có: AM là đường trung bình của △BCD
⇒ AM = DC = BC
Bài 5. Cho tứ giác ABCD có AB = CD. Gọi E, F lần lượt là trung điểm của AC, DB. Đường thẳng EF lần lượt cắt AB, CD tại H, K. Chứng minh rằng: ![\[\widehat {KHB} = \widehat {HKC}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-38.svg)
Hướng dẫn giải
E là trung điểm của AC, F là trung điểm của BD.
Gọi M là trung điểm của BC
Nên EM là đường trung bình của △ABC
⇒ EM = AB và EM // AB
![\[ \Rightarrow \widehat {MEF} = \widehat {AHK}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-39.svg)
Và FM là đường trung bình của △BCD
⇒ FM = CD và FM // CD
![\[ \Rightarrow \widehat {EFM} = \widehat {HKD}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-40.svg)
Mà AB = CD nên AB = CD ⇒ △FME cân
![\[\begin{gathered} \Rightarrow \widehat {MEF} = \widehat {AHK} = \widehat {EFM} = \widehat {HKD}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \Rightarrow \widehat {AHK} = \widehat {HKD} \Rightarrow \widehat {KHB} = \widehat {HKC} \hfill \\ \end{gathered} \]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-41.svg)
Bài 6. Hình thang cân ABCD (AB // CD) có AB = 4 cm, CD = 10 cm, BD = 5 cm. Tính khoảng cách từ trung điểm I của BD đến cạnh CD.
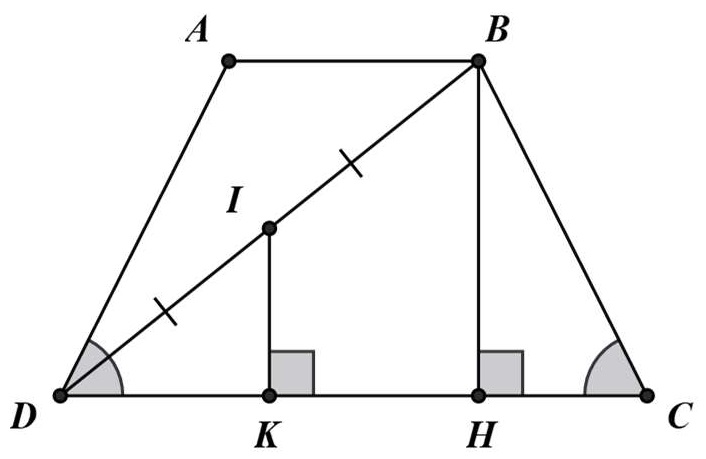
Hướng dẫn giải
Kẻ BH ⊥ CD, IK ⊥ CD
Ta có: ![\[CH = \frac{{CD - AB}}{2} = \frac{{10 - 4}}{2} = 3{\text{ }}cm\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-42.svg)
Áp dụng định lí Py-ta-go vào ΔBHC, ta có:
BH2 = BC2 – CH2 = 52 – 32 = 16 = 42
⇒ BH = 4 cm.
Tam giác BDH có BI = ID và IK // BH nên IK là đường trung bình.
![\[ \Rightarrow IK = \frac{{BH}}{2} = \frac{4}{2} = 2{\text{ }}cm\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-43.svg)
Bài 7. Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AH, E là giao điểm của BI và AC. Tính các độ dài AE và EC, biết AH = 12 cm, BC = 18 cm.
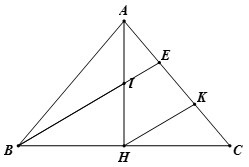
Hướng dẫn giải
Kẻ HK // BE chứng minh được AE = EK = KC
Kết quả: AE = 5cm, EC = 10cm
Bài 8. Cho tam giác ABC vuông tại A, đường cao AH. Gọi M là trung điểm của HC, K là trung điểm của AH. Chứng minh rằng BK vuông góc với AM.
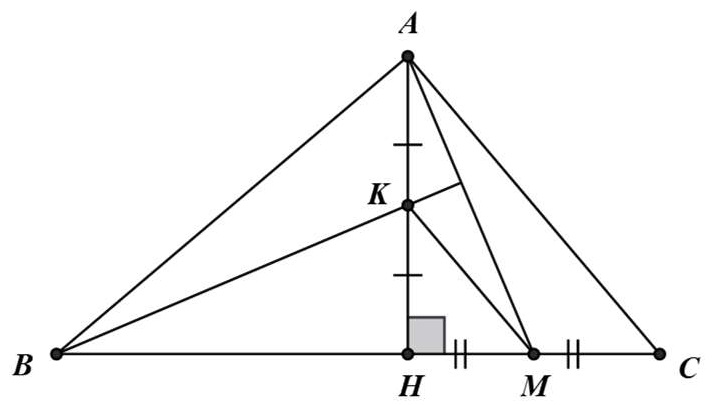
Hướng dẫn giải
Tam giác AHC có AK = KH và HM = MC
⇒ MK là đường trung bình của ΔAHC
⇒ MK // AC. Ta lại có: AC ⊥ AB nên MK ⊥ AB
Tam giác ABM có: AH ⊥ BM và MK ⊥ AB
⇒ K là trực tâm, suy ra BK ⊥ AM
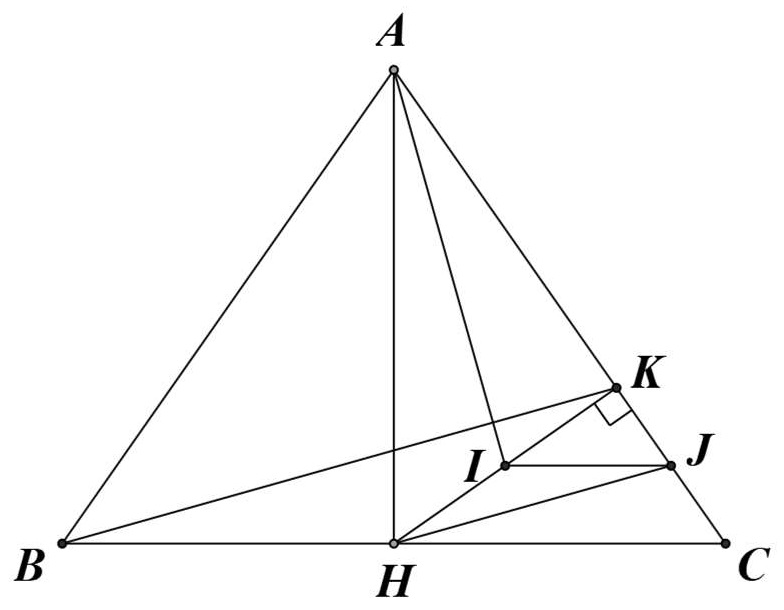
Bài 9. Cho tam giác ABC cân tại A, đường cao AH. Gọi K là hình chiếu vuông góc của H lên AC. Gọi I là trung điểm HK. Chứng minh rằng: AI ⊥ BK.
Hướng dẫn giải
Gọi J là trung điểm của KC, ta có IJ là đường trung bình trong tam giác KHC.
Do đó: IJ // HC ⇒ IJ ⊥ AH
Trong tam giác AHJ có IJ ⊥ AH, HI ⊥ AJ. Từ đó, I là trực tâm tam giác AHJ.
⇒ AI ⊥ HJ (1).
Trong tam giác BKC, HJ là đường trung bình, suy ra: HJ // BK (2).
Từ (1) và (2) suy ra: AI ⊥ BK
⋆ Đường trung bình của hình thang
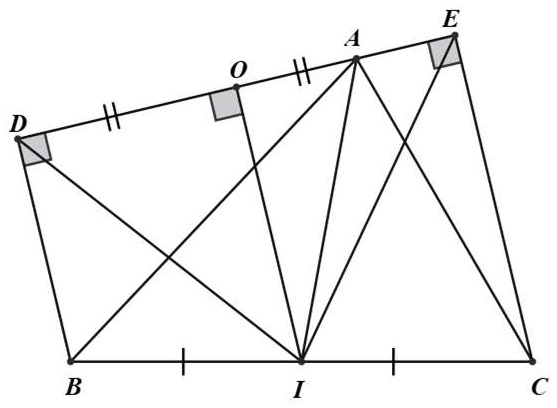
Bài 1. Cho △ABC và đường thẳng d qua A không cắt đoạn thẳng BC. Vẽ BD ⊥ d, CE ⊥ d (D, E ∈ d). Gọi I là trung điểm của BC. Chứng minh: ID = IE.
Hướng dẫn giải
BD // AE (cùng vuông góc với d)
Tứ giác BDEC là hình thang,
Từ I kẻ IO ⊥ DE ⇒ IO // BD // CE
Hình thang BDEC có IO // BD // CE và IB = IC nên OD = OE
Ta có: OD = OE, IO ⊥ DE
Nên IO là đường trung trực của đoạn thẳng DE ⇒ ID = IE
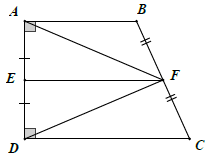
Bài 2. Cho hình thang vuông ABCD tại A và D. Gọi E F, lần lượt là trung điểm của AD, BC. Chứng minh:
a) △AFD cân tại F
b) ![\[\widehat {BAF} = \widehat {CDF}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-44.svg)
Hướng dẫn giải
Chỉ ra EF là đường trung bình của hình thang ABCD nên EF // AB // CD
AD ⊥ AB ⇒ AD ⊥ EF
AE = ED ⇒ EF là đường trung trực của AB
Nên FA = FD hay △AFD cân tại F
△AFD ![\[ \Rightarrow \widehat {DAF} = \widehat {ADF}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-45.svg)
b) (cùng phụ với 2 góc bằng nhau ![\[\widehat {DAF} = \widehat {ADF}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-46.svg)
)
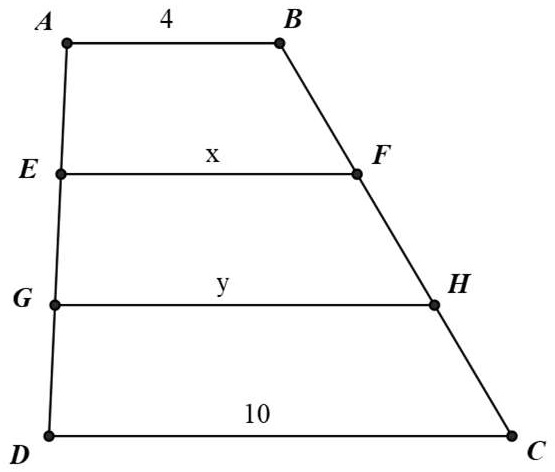
Bài 3. Tính các độ dài x và y trên hình. Biết: AB // EF // GH // CD, AE = EG = GD, AB = 4 cm, CD = 10 cm.
Hướng dẫn giải
Theo tính chất đường trung bình của hình thang, ta có: 2x = y + 4 hay y = 2x – 4 (1)
Và ![\[y = \frac{{x + 10}}{2}{\text{ }}\left( 2 \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-48.svg)
Từ (1) và (2) suy ra ![\[2x - 4 = \frac{{x + 10}}{2}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-49.svg)
Ta tính được x = 6 và y = 8
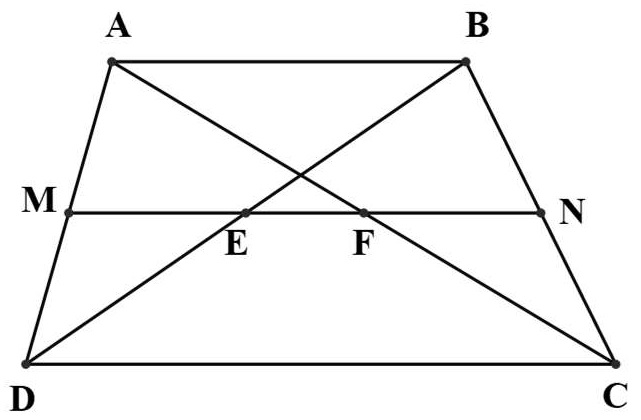
Bài 4. Cho hình thang ABCD có AB // CD (AB < CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với hai đáy của hình thang cắt hai đường chéo BD và AC tại E và F, cắt BC tại N.
a) Chứng minh rằng N, E, F lần lượt là trung điểm của BC, BD, AC.
b) Gọi I là trung điểm của AB, đường thẳng vuông góc với IE tại E và đường thẳng vuông góc với IF tại F cắt nhau ở K. Chứng minh: KC = KD
Hướng dẫn giải
a) Xét hình thang ABCD có MA = MD
N ∈ BC, MN // AB // CD (gt) ⇒ N là trung điểm của BC
Xét △ADC có:
MA = MD, MF // DC ⇒ FA = FC
Xét △ADB có:
MA = MD, MF // DC ⇒ ED = EB
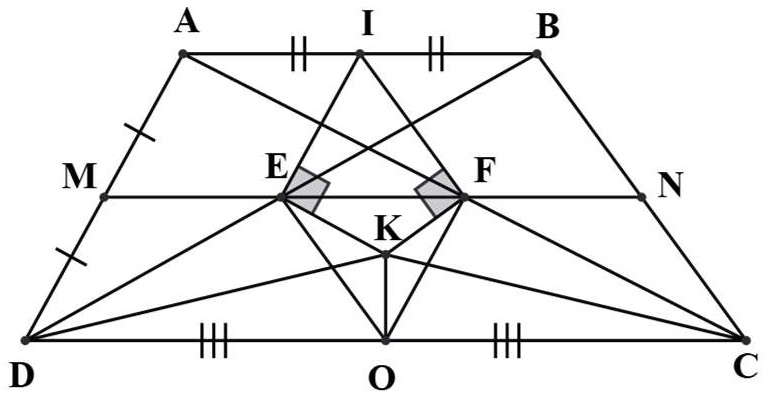
b) IE là đường trung bình của △ABD
⇒ IE // AD
OF là đường trung bình của △ACD
⇒ OF // AD
Vậy IE // FO
Có IE // FO, IE ⊥ EK ⇒ EK ⊥ OF
Chứng minh tương tự ta có IF // EO // BC
IF ⊥ KF ⇒ EO ⊥ KF
△EFO có EK ⊥ OF, EO ⊥ KF nên K là trực tâm
⇒ OK ⊥ EF mà EF // CD
⇒ OK ⊥ DC, OD = OC
Vậy KO là đường trung trực của DC hay KC = KD
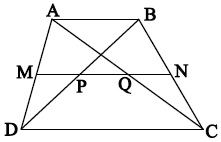
Bài 5. Cho hình thang ABCD, AB là đáy nhỏ. Gọi M, N, P, Q lần lượt là trung điểm của AD, BC, BD và AC.
a) Chứng minh bốn điểm M, N, P, Q thẳng hàng;
b) Chứng minh PQ // CD và ![\[PQ = \frac{{CD - AB}}{2}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-49a.svg)
c) Hình thang ABCD phải có điều kiện gì để MP = PQ = QN.
Hướng dẫn giải
a) Xét △ABD có MP là đường trung bình
⇒ MP // AB ⇒ MP // CD
Xét △ADC có MQ là đường trung bình
⇒ MQ // CD.
Xét hình thang ABCD có MN là đường trung bình
⇒ MN // CD
Qua điểm M có các đường thẳng MP, MQ, MN cùng song song với CD nên các đường thẳng này trùng nhau, suy ra bốn điểm M, N, P, Q thẳng hàng.
b) Ta có: MN // CD nên PQ // CD
![\[PQ = MQ - MP = \frac{{CD}}{2} - \frac{{AB}}{2} = \frac{{CD - AB}}{2}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-50.svg)
c) Ta có: ![\[MP = NQ = \frac{{AB}}{2}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-51.svg)
![\[MP = PQ \Leftrightarrow \frac{{AB}}{2} = \frac{{CD - AB}}{2}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-52.svg)
![\[ \Leftrightarrow AB = CD - AB \Leftrightarrow 2AB = CD\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-53.svg)
(đáy lớn gấp đôi đáy nhỏ)
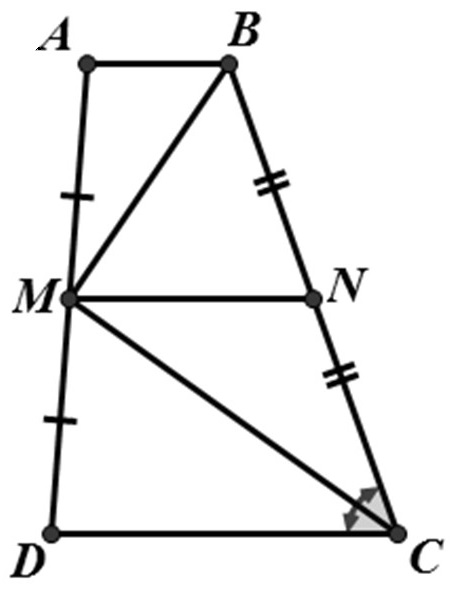
Bài 6. Cho hình thang ABCD (AB // CD), tia phân giác của góc C đi qua trung điểm M của cạnh bên AD. Chứng minh rằng:
a) ![\[\widehat {BMC} = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-54.svg)
b) BC = AB + CD
Hướng dẫn giải
a) Gọi N là trung điểm BC.
Ta có: ![\[MN\parallel CD \Rightarrow \widehat {MCD} = \widehat {CMN}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-55.svg)
Mà ![\[\widehat {MCD} = \widehat {MCN}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-56.svg)
(vì CM là phân giác )
Suy ra: ![\[\widehat {CMN} = \widehat {MCN} = \frac{1}{2}\widehat {DCB}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-57.svg)
Tam giác MCN cân tại N
⇒ MN = NC = NB, do đó △MNB cân tại N
![\[ \Rightarrow \widehat {NMB} = \widehat {NBM}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-58.svg)
Mặt khác: ![\[\widehat {NMB} = \widehat {MBA}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-59.svg)
Suy ra: ![\[\widehat {NMB} = \frac{1}{2}\widehat {ABC}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-60.svg)
![\[\widehat {BMC} = \widehat {CMN} + \widehat {NMB} = \frac{1}{2}\left( {\widehat {BCD} + \widehat {ABC}} \right) = 90^\circ \]](https://danchuyentoan.com/wp-content/uploads/2023/10/duong-trung-binh-cua-tam-giac-61.svg)
b) Vì MN là đường trung bình của hình thang ABCD nên
MN = (AB + CD)
Ta lại có: MN = BC. Do đó: BC = AB + CD
Bài 7. Cho tam giác ABC, AM là trung tuyến. Vẽ đường thẳng d qua trung điểm I của AM cắt các cạnh AB, AC. Gọi A’, B’, C’ thứ tự là hình chiếu của A, B, C lên đường thẳng d. Chứng minh rằng: BB’ + CC’ = 2AA’.
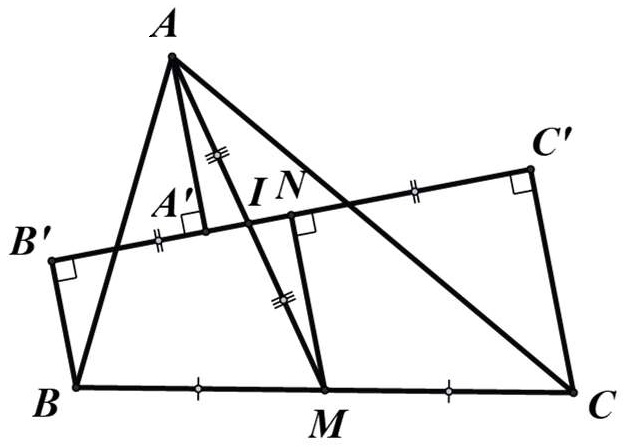
Hướng dẫn giải
Gọi N là hình chiếu của M trên d.
Xét tứ giác BB’C’C có BB’ // CC’ (cùng vuông góc d)
⇒ BB’C’C là hình thang.
M là trung điểm BC và MN // BB’ // CC’ (cùng vuông góc d)
⇒ MN là đường trung bình của hình thang BB’C’C
⇒ BB’ + CC’ = 2MN (1)
Chứng minh được △AA’I = △MNI (g.c.g)
⇒ AA’ = MN (2)
Từ (1), (2) suy ra BB’ + CC’ = 2AA’.
