Định lí Talet

Tỉ số của hai đoạn thẳng

Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng đơn vị đo (tỉ số này không phụ thuộc vào cách chọn đơn vị đo).

Đoạn thẳng tỉ lệ

Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức $\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}}$ hay $\frac{{AB}}{{A'B'}} = \frac{{CD}}{{C'D'}}$

Định lí Ta-lét trong tam giác

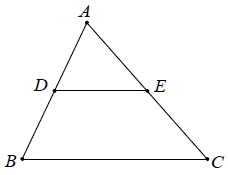
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

$\left\{ \begin{gathered} \Delta ABC \hfill \\ DE\parallel BC \hfill \\ \end{gathered} \right. \Rightarrow \frac{{AD}}{{AB}} = \frac{{AE}}{{AC}},\frac{{DB}}{{BA}} = \frac{{EC}}{{CA}},\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}$

Nhớ lại tỉ lệ thức và tính chất của dãy tỉ số bằng nhau

+) Tỉ lệ thức là đẳng thức của hai tỉ số $\frac{a}{b} = \frac{c}{d}$

+) Tính chất

Tính chất 1 (Tính chất cơ bản của tỉ lệ thức): Nếu $\frac{a}{b} = \frac{c}{d}$ thì ad = bc

Tính chất 2: Nếu ad = bc và abcd ≠ 0 thì ta có bốn tỉ lệ thức sau:

$\frac{a}{b} = \frac{c}{d};\frac{a}{c} = \frac{b}{d};\frac{d}{b} = \frac{c}{a};\frac{d}{c} = \frac{b}{a}$

+) Tính chất của dãy tỉ số bằng nhau

Từ dãy tỉ số bằng nhau $\frac{a}{b} = \frac{c}{d} = \frac{e}{f}$ suy ra:

$\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = \frac{{a + c + e}}{{b + d + f}} = \frac{{a - c + e}}{{b - d + f}}$

Từ định lí Ta-lét ta thu được kinh nghiệm thứ năm

Cứ nói đến tỉ số của hai đoạn thẳng phải nghĩ đến định lí Ta-lét, ta cứ nói đến định lí Ta-lét phải nghĩ đến đường thẳng song song.

Ý nghĩa của kinh nghiệm này là: Với các bài toán đề cập đến tỉ số của hai đoạn thẳng mà phải vẽ thêm đường phụ, ta vẽ thêm đường thẳng song song để sử dụng định lí Ta-lét.

Phân dạng bài tập

Dạng 1. Tính tỉ số hai đoạn thẳng. Chia đoạn thẳng theo tỉ số cho trước

Phương pháp giải

+) Sử dụng định nghĩa tỉ số của hai đoạn thẳng.

+) Một điểm C thuộc đoạn thẳng AB (hoặc đường thẳng AB), được gọi là chia đoạn thẳng AB theo tỉ số $\frac{m}{n} \ne 1$ (m, n là các số dương), nếu ta có: $\frac{{CA}}{{CB}} = \frac{m}{n}$

+) Sử dụng kĩ thuật đại số hóa hình học:

Nếu ta có: $\frac{{CA}}{{CB}} = \frac{m}{n}$ thì $\left\{ \begin{gathered} CA = mt \hfill \\ CB = nr \hfill \\ \end{gathered} \right.$ (với t > 0)

+) Lập tỉ lệ thức giữa các đoạn thẳng tỉ lệ rồi áp dụng tính chất của dãy tỉ số bằng nhau.

Ví dụ

Ví dụ 1. Điểm C thuộc đoạn thẳng AB và chia AB theo tỉ số $\frac{3}{5}$ . Hãy tính các tỉ số: $\frac{{AB}}{{AC}};\frac{{AB}}{{CB}}$

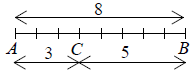
Hướng dẫn giải

Vì C chia đoạn AB theo tỉ số $\frac{3}{5}$ nên:

$\frac{{CA}}{{CB}} = \frac{3}{5} \Rightarrow \left\{ \begin{gathered} CA = 3t \hfill \\ CB = 5t \hfill \\ \end{gathered} \right.{\text{ }}\left( {t > 0} \right)$

Do đó AB = AC + CB = 8t

Vậy $\frac{{AB}}{{AC}} = \frac{{8t}}{{3t}} = \frac{8}{3};{\text{ }}\frac{{AB}}{{CB}} = \frac{{8t}}{{5t}} = \frac{8}{5}$

Ví dụ 2. Cho đoạn thẳng AB = 10 cm.

a) Trên đoạn thẳng AB lấy điểm C sao cho $\frac{{CA}}{{CB}} = \frac{3}{2}$ . Tính độ dài CB.

b) Trên tia đối của tia BA lấy điểm D sao cho $\frac{{DA}}{{DB}} = \frac{3}{2}$ . Tính độ dài CD.

Hướng dẫn giải

a) Cách 1: Từ giả thiết:

$\frac{{CA}}{{CB}} = \frac{3}{2} \Rightarrow \left\{ \begin{gathered} CA = 3t \hfill \\ CB = 2t \hfill \\ \end{gathered} \right.{\text{ }}\left( {t > 0} \right)$

Nên AB = 10 cm = CA + CB = 5t ⇔ t = 2 cm

Vậy CB = 4 cm.

Cách 2: Từ giả thiết $\frac{{CA}}{{CB}} = \frac{3}{2}$

$\Rightarrow \frac{{CA}}{3} = \frac{{CB}}{2} = \frac{{CA + CB}}{{3 + 2}} = \frac{{AB}}{5} = \frac{{10}}{5} = 2$

Vậy CB = 4 cm

Cách 3: Đặt CB = x thì CA = 10 – x

Từ giả thiết và tính chất cơ bản của tỉ lệ thức ta có 3CB = 2CA hay

3x – 2(10 – x) ⇔ 5x = 20 ⇔ x = 4 cm

b) Từ giả thiết

$\frac{{DA}}{{DB}} = \frac{3}{2} \Rightarrow \left\{ \begin{gathered} DA = 3t \hfill \\ DB = 2t \hfill \\ \end{gathered} \right.{\text{ }}\left( {t > 0} \right)$

Mặt khác D thuộc tia đối của tia BA nên DA > DB

Do đó: AB = 10 = DA – DB = 3t – 2t ⇔ t = 10 cm

Suy ra: DB = 20 cm

Vậy CD = 20 + 4 = 24 cm

Ví dụ 3. Đoạn thẳng AB = 44 dm được chia thành các đoạn thẳng liên tiếp AM, MN, NP và PB lần lượt tỉ lệ với 10, 2, 3 và 5.

a) Tính độ dài mỗi đoạn thẳng đó.

b) Chứng minh rằng hai điểm M và P chia đoạn AN theo cùng một tỉ số k và tính k.

c) Còn hai điểm nào chia đoạn thẳng nào theo cùng một tỉ số nữa không?

Hướng dẫn giải

a) Từ giả thiết và tính chất của dãy tỉ số bằng nhau ta có:

$\begin{gathered} \frac{{AM}}{{10}} = \frac{{MN}}{2} = \frac{{NP}}{3} = \frac{{PB}}{5}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ = \frac{{AM + MN + NP + PB}}{{10 + 2 + 3 + 5}} = \frac{{44}}{{20}} = 2,2 \hfill \\ \end{gathered}$

Vậy AM = 22 dm, MN = 4,4 dm, NP = 6,6 dm, PB = 11 dm

b) Từ câu a) ta có:

$\frac{{MA}}{{MN}} = \frac{{22}}{{4,4}} = 5;{\text{ }}\frac{{PA}}{{PN}} = \frac{{33}}{{6,6}} = 5$

Điều này chứng tỏ M và P chia đoạn AN theo cùng một tỉ số k = 5.

c) Vì $\frac{{AM}}{{AP}} = \frac{{22}}{{33}} = \frac{2}{3};{\text{ }}\frac{{NM}}{{NP}} = \frac{{4,4}}{{6,6}} = \frac{2}{3}$

Nên còn hai điểm A và N chia đoạn MP theo cùng một tỉ số $\frac{2}{3}$

Dạng 2. Tính độ dài đoạn thẳng, dựng đoạn thẳng tỉ lệ thứ tư

Phương pháp giải

Tính độ dài đoạn thẳng:

+) Áp dụng định lí Ta-lét để lập hệ thức của các đoạn thẳng tỉ lệ.

+) Xác định đường thẳng song song với một cạnh của tam giác.

+) Thay số vào hệ thức rồi giải phương trình.

Trong bốn đoạn thẳng tỉ lệ, dựng đoạn thẳng thứ tự khi biết độ dài của ba đoạn kia:

+) Đặt ba đoạn thẳng trên hai cạnh của một góc.

+) Dựng đường thẳng song song để xác định đoạn thẳng thứ tư.

Ví dụ

Ví dụ 1. Tính x trong các trường hợp sau, biết rằng các số trên hình có cùng đơn vị đo là cm.

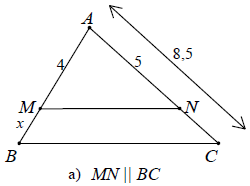
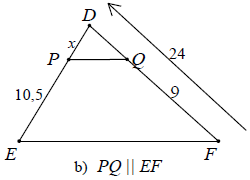
Hướng dẫn giải

a) Áp dụng định lí Ta-lét vào △ABC có MN // BC, ta được:

$\frac{{BM}}{{MA}} = \frac{{CN}}{{NA}}{\text{ hay }}\frac{x}{4} = \frac{{8,5 - 5}}{5} \Leftrightarrow x = 2,8$

b) Áp dụng định lí Ta-lét vào △DFE có PQ // EF, ta được:

$\frac{{DP}}{{PE}} = \frac{{DQ}}{{QF}}{\text{ hay }}\frac{x}{{10,5}} = \frac{{24 - 9}}{9} \Leftrightarrow x = 17,5$

Ví dụ 2. Tính x trên hình sau

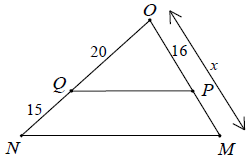
Hướng dẫn giải

Áp dụng định lí Ta-lét vào △OMN có PQ // MN, ta được:

$\frac{{MP}}{{PO}} = \frac{{NQ}}{{QO}}{\text{ hay }}\frac{{x - 16}}{{16}} = \frac{{15}}{{20}} \Leftrightarrow x = 28$

Ví dụ 3. Cho ba đoạn thẳng có độ dài là m, n, p (cùng đơn vị đo). Hãy dựng đoạn thẳng có độ dài x sao cho $\frac{m}{x} = \frac{n}{p}$

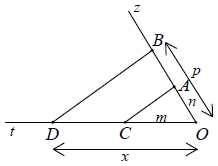
Hướng dẫn giải

+) Vẽ góc zOt bất kì

+) Trên tia Oz đặt các đoạn OA = n, OB = p

+) Trên tia Ot đặt OC = m

+) Vẽ BD // AC thì OD = x là đoạn thẳng cần dựng

Thật vậy, áp dụng định lí Ta-lét vào △OBD có AC // BD, ta được:

$\frac{{OA}}{{OB}} = \frac{{OC}}{{OD}}$ hay $\frac{m}{x} = \frac{n}{p}$

Dạng 3. Chứng minh các hệ thức hình học

Phương pháp giải

+) Xác định đường thẳng song song với một cạnh của tam giác.

+) Áp dụng định lí Ta-lét để lập hệ thức của các đoạn thẳng tỉ lệ.

+) Sử dụng các tính chất của tỉ lệ thức hoặc cộng theo vế các đẳng thức hình học.

Ví dụ

Ví dụ 1. Cho hình thang ABCD (AB // CD). Một đường thẳng song song với hai đáy, cắt các cạnh bên AD và BC theo thứ tự ở M và N. Chứng minh rằng:

a) $\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}$

b) $\frac{{AM}}{{AD}} + \frac{{CN}}{{CB}} = 1$

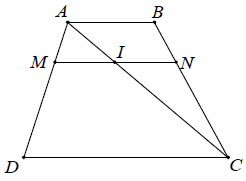
Hướng dẫn giải

a) Gọi I là giao điểm của đường chéo AC với MN.

Áp dụng định lí Ta-lét vào hai tam giác ACD và ACB có MI // CD, IN // AB ta được:

$\frac{{AM}}{{MD}} = \frac{{AI}}{{IC}}\left( 1 \right);{\text{ }}\frac{{BN}}{{NC}} = \frac{{AI}}{{IC}}\left( 2 \right)$

Từ (1) và (2) suy ra: $\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}$

b) Áp dụng định lí Ta-lét vào hai tam giác ACD và ACB ta có MI // CD, IN // AB ta được:

$\frac{{AM}}{{AD}} = \frac{{AI}}{{AC}}\left( 3 \right);{\text{ }}\frac{{CN}}{{CB}} = \frac{{CI}}{{CA}}\left( 4 \right)$

Cộng theo vế các đẳng thức (3) và (4), thu được:

$\frac{{AM}}{{AD}} + \frac{{CN}}{{CB}} = \frac{{CI + AI}}{{CA}} = \frac{{CA}}{{CA}} = 1$

Ví dụ 2. Cho hình bình hành ABCD có M, N lần lượt là trung điểm của AB và CD. Gọi P, Q thứ tự là giao điểm của AN và CM với đường chéo BD. Chứng minh rằng: DP = PQ = QB.

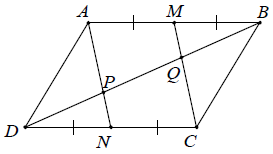
Hướng dẫn giải

Áp dụng định nghĩa và giả thiết vào hình bình hành ABCD, ta được:

AM = NC, AM // NC

Tứ giác AMCN có hai cạnh đối song song và bằng nhau nên nó là hình bình hành

Do đó: MC // AN.

Suy ra: MQ // AP, PN // QC.

Áp dụng định lí Ta-lét vào hai tam giác APB và DQC có MQ // AP, PN // QC, ta được:

$\begin{gathered} \frac{{BQ}}{{QP}} = \frac{{BM}}{{MA}} = 1 \Rightarrow BQ = QP{\text{ }}\left( 1 \right) \hfill \\ \frac{{DP}}{{PQ}} = \frac{{DN}}{{NC}} = 1 \Rightarrow DP = PQ{\text{ }}\left( 2 \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Từ (1) và (2) ta có: DP = PQ = QB

Dạng 4. Vẽ thêm đường thẳng song song để tính tỉ số hai đoạn thẳng

Phương pháp giải

+) Vẽ thêm đường thẳng song song.

+) Sử dụng kĩ thuật đại số hóa hình học.

+) Áp dụng định lí Ta-lét.

Ví dụ

Ví dụ 1. Cho tam giác ABC. Trên cạnh BC lấy điểm D sao cho $\frac{{BC}}{{BD}} = \frac{4}{1}$ . Điểm I thuộc đoạn AD sao cho $\frac{{AI}}{{ID}} = \frac{1}{2}$ . Gọi K là giao điểm của BI và AC. Tính tỉ số $\frac{{AK}}{{KC}}$ .

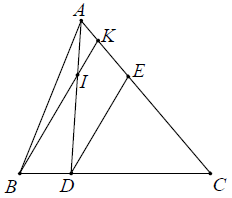
Hướng dẫn giải

Kẻ thêm DE // BK thì DE // IK

Áp dụng định lí Ta-lét vào tam giác ADE có IK // DE, ta được:

$\frac{{AK}}{{KE}} = \frac{{AI}}{{ID}} = \frac{1}{2} \Rightarrow \left\{ \begin{gathered} AK = 1t \hfill \\ KE = 2t \hfill \\ \end{gathered} \right.{\text{ }}\left( {t > 0} \right)$

Áp dụng định lí Ta-lét vào tam giác BCK có DE // BK, ta được:

$\frac{{KC}}{{KE}} = \frac{{BC}}{{BD}} = \frac{4}{1} \Rightarrow KC = 4KE = 8t$

Vậy $\frac{{AK}}{{KC}} = \frac{{1t}}{{8t}} = \frac{1}{8}$

Ví dụ 2. Cho tam giác ABC. Trên cạnh BC lấy điểm D sao cho BC = 2BD. Trên đoạn AD lấy điểm O sao cho $\frac{{AO}}{{OD}} = \frac{3}{2}$ . Gọi I là giao điểm của CO và AB. Tính tỉ số $\frac{{AI}}{{IB}}$ .

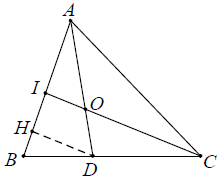
Hướng dẫn giải

Kẻ thêm DH // CI thì DH // IO.

Áp dụng định lí Ta-lét vào tam giác ADH có DH // IO, ta được:

$\frac{{AI}}{{IH}} = \frac{{AO}}{{OD}} = \frac{3}{2} \Rightarrow \left\{ \begin{gathered} AI = 3t \hfill \\ IH = 2t \hfill \\ \end{gathered} \right.{\text{ }}\left( {t > 0} \right)$

Áp dụng định lí Ta-lét vào tam giác BIC có DH // IC, ta được:

$\frac{{BI}}{{IH}} = \frac{{BC}}{{CD}} = \frac{2}{1} \Rightarrow BI = 2IH = 2 \cdot 2t = 4t$

Vậy $\frac{{AI}}{{IB}} = \frac{{3t}}{{4t}} = \frac{3}{4}$

Phiếu bài tự luyện dạng bài cơ bản

Bài 1: Cho tam giác ABC, các trung tuyến AD, BE, CF cắt nhau tại G.

a) Tính $\frac{{AE}}{{AC}}$

b) Tính $\frac{{AG}}{{GD}}$

b) Kể hai cặp đoạn thẳng tỉ lệ với AG và GD.

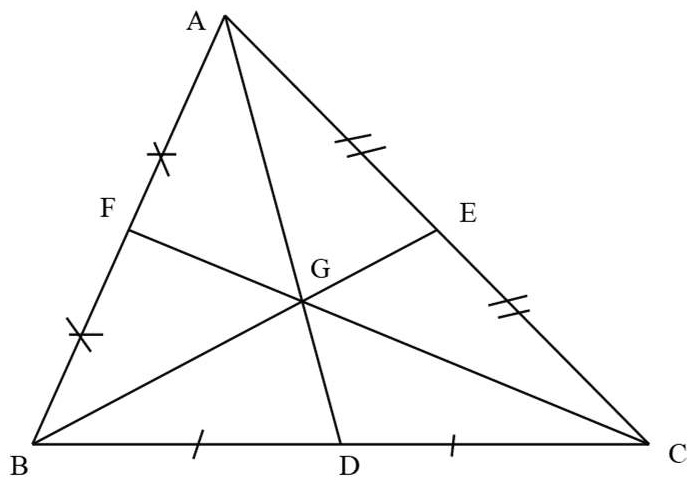
Hướng dẫn giải

a) Có E là trung điểm của AC (vì BE là trung tuyến)

$\Rightarrow \frac{{AE}}{{AC}} = \frac{1}{2}$ (tính chất trung điểm của đoạn thẳng)

b) △ABC có các trung tuyến AD, BE, CF cắt nhau tại G

⇒ G là trọng tâm △ABC

$\Rightarrow \frac{{AG}}{{GD}} = \frac{2}{1} = 2$

c) G là trọng tâm △ABC

$\Rightarrow \frac{{AG}}{{GD}} = \frac{{BG}}{{GE}} = \frac{{CG}}{{GF}}$

⇒ BG và GE là cặp đoạn thẳng tỉ lệ với AG và GD.

⇒ CG và GF là cặp đoạn thẳng tỉ lệ với AG và GD.

Bài 2: Cho đoạn thẳng AM, M là một điểm trên đoạn AB. Tính các tỉ số $\frac{{AM}}{{AB}}$ và $\frac{{MB}}{{AB}}$ nếu:

a) $\frac{{MA}}{{MB}} = \frac{1}{2}$

b) $\frac{{MA}}{{MB}} = \frac{7}{4}$

c) $\frac{{MA}}{{MB}} = \frac{m}{n}$

Hướng dẫn giải

a) $\frac{{MA}}{{MB}} = \frac{1}{2}$

$\begin{gathered} \Rightarrow \frac{{MA}}{1} = \frac{{MB}}{2} = \frac{{MA + MB}}{{1 + 2}} = \frac{{AB}}{3} \hfill \\ \Rightarrow \frac{{MA}}{{MB}} = \frac{1}{3};\frac{{MA}}{{MB}} = \frac{2}{3}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

b) $\frac{{MA}}{{MB}} = \frac{7}{4}$

$\begin{gathered} \Rightarrow \frac{{MA}}{7} = \frac{{MB}}{4} = \frac{{MA + MB}}{{7 + 4}} = \frac{{AB}}{{11}} \hfill \\ \Rightarrow \frac{{MA}}{{MB}} = \frac{7}{{11}};\frac{{MA}}{{MB}} = \frac{4}{{11}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

c) $\frac{{MA}}{{MB}} = \frac{m}{n}$

$\begin{gathered} \Rightarrow \frac{{MA}}{m} = \frac{{MB}}{n} = \frac{{MA + MB}}{{m + n}} = \frac{{AB}}{{m + n}} \hfill \\ \Rightarrow \frac{{MA}}{{MB}} = \frac{m}{{m + n}};\frac{{MA}}{{MB}} = \frac{n}{{m + n}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Bài 3: Cho góc xOy. Trên tia Ox, lấy theo thứ tự 2 điểm A, B sao cho OA = 2 cm, AB = 3 cm. Trên tia Oy, lấy điểm C với OC = 3cm. Từ B, kẻ đường thẳng song song với AC cắt Oy tại D. Tính độ dài CD.

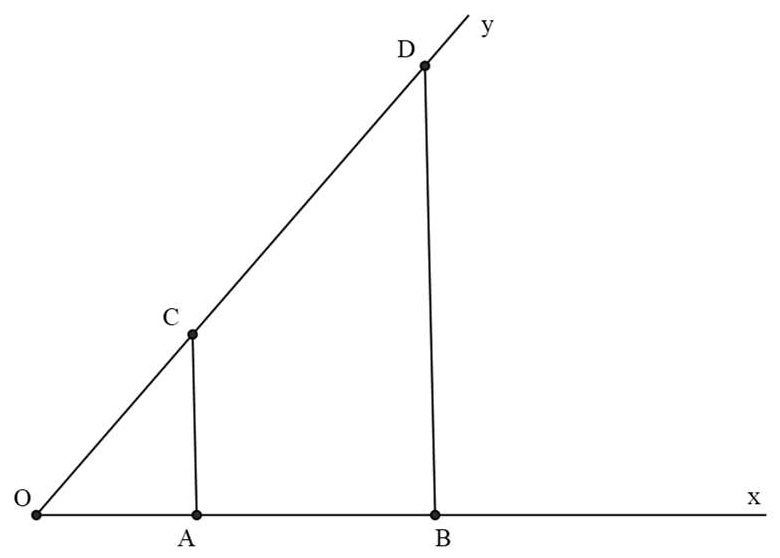
Hướng dẫn giải

Xét △OBD có: AC // BD (gt)

$\Rightarrow \frac{{AO}}{{AB}} = \frac{{OC}}{{CD}}$ (định lí Ta-lét trong tam giác)

$\Rightarrow CD = \frac{{AB \cdot OC}}{{OA}} = \frac{{3 \cdot 3}}{2} = 4,5{\text{ }}cm$

Bài 4: Cho tam giác ACE có AC = 11 cm. Lấy điểm B trên cạnh AC sao cho BC = 6 cm. Lấy điểm D trên cạnh AE sao cho DB // EC. Giả sử AE + ED = 25,5 cm. Hãy tính:

a) Tỉ số $\frac{{DE}}{{AE}}$

b) Độ dài các đoạn thẳng AE, DE và AD.

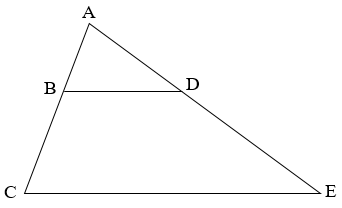
Hướng dẫn giải

a) Theo định lý Ta-lét trong △ACE, ta có:

$\frac{{DE}}{{AE}} = \frac{{BC}}{{AC}} \Rightarrow \frac{{DE}}{{AE}} = \frac{6}{{11}}$

b) Cách 1. Theo tính chất của tỉ lệ thức ta có: $\frac{{DE + AE}}{{AE}} = \frac{{17}}{{11}}$

Từ đó tính được Ae = 16,5 cm; DE = 9 cm và AD = 7,5 cm.

Cách 2. Áp dụng tính chất của dãy tỉ số bằng nhau

Cách 3. Thay DE = 25,5 – AE vào $\frac{{DE}}{{AE}} = \frac{6}{{11}}$

Bài 5: Cho tam giác ABC và điểm D trên cạnh BC sao cho $\frac{{BD}}{{BC}} = \frac{3}{4}$ , điểm E trên đoạn AD sao cho $\frac{{AE}}{{AD}} = \frac{1}{3}$ . Gọi K là giao điểm của BE và AC. Tính tỉ số $\frac{{AK}}{{KC}}$ .

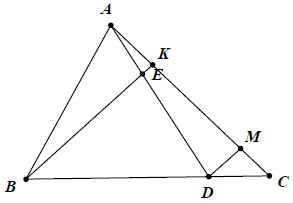
Hướng dẫn giải

Kẻ DM // BK (M ∈ AC)

Áp dụng định lý Ta-lét trong △CBK, ta có:

$\frac{{KM}}{{KC}} = \frac{{BD}}{{BC}} \Rightarrow \frac{{KM}}{{KC}} = \frac{3}{4}{\text{ }}\left( 1 \right)$

Tương tự với △ADM, ta có: $\frac{{AK}}{{KM}} = \frac{1}{2}{\text{ }}\left( 2 \right)$

Từ (1) và (2), tìm được: $\frac{{AK}}{{KC}} = \frac{3}{8}$

Bài 6: Cho tam giác ABC có AM là trung tuyến và điểm E thuộc đoạn thẳng MC. Qua E kẻ đường thẳng song song với AC, cắt AB ở D và cắt AM ở K. Qua E kẻ đường thẳng song song với AB, cắt AC ở F. Chứng minh: CF = DK.

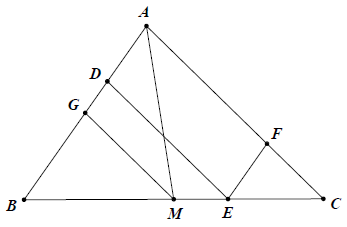
Hướng dẫn giải

Chứng minh được ADEF là hình bình hành, từ đó: EF = AD (1)

Kẻ MG // AC (G ∈ AB), ta được G là trung điểm của AB

Áp dụng định lý Ta-lét trong △ABC, ta có: $\frac{{CF}}{{EF}} = \frac{{AC}}{{AB}}{\text{ }}\left( 2 \right)$

Tương tự với △AGM và △ABC, ta có:

$\frac{{DK}}{{AD}} = \frac{{MG}}{{AG}} = \frac{{MG}}{{BG}} = \frac{{AC}}{{AB}}{\text{ }}\left( 3 \right)$

Từ (1), (2), (3) ta suy ra CF = DK.

Bài 7: Cho △ABC. Từ D trên cạnh AB, kẻ đường thẳng song song với BC cắt AC tại E. Trên tia đối của tia CA, lấy điểm F sao cho CF = DB. Gọi M là giao điểm của DF và BC. Chứng minh: $\frac{{DM}}{{MF}} = \frac{{AC}}{{AB}}$ .

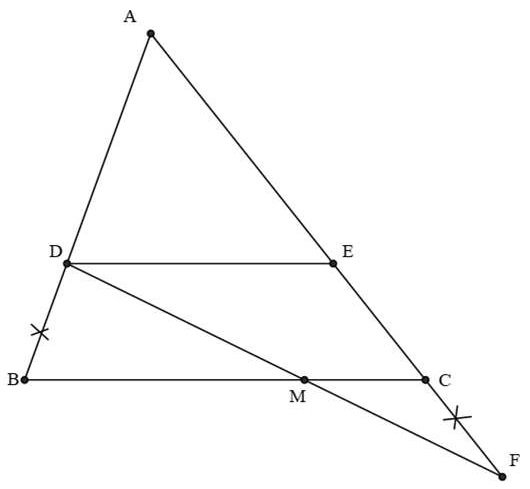
Hướng dẫn giải

Xét △ABC có: DE // BC

$\Rightarrow \frac{{AC}}{{EC}} = \frac{{AB}}{{BD}}{\text{ hay }}\frac{{AC}}{{AB}} = \frac{{EC}}{{BD}}{\text{ }}\left( 1 \right)$ (định lí Ta-lét trong tam giác)

Xét △DEF có: DE // MC (vì DE // BC)

$\Rightarrow \frac{{DM}}{{MF}} = \frac{{EC}}{{CF}}{\text{ }}\left( 2 \right)$ (định lí Ta-lét trong tam giác)

Mà CF = DB (gt) (3)

Từ (1), (2), (3) suy ra: $\frac{{DM}}{{MF}} = \frac{{AC}}{{AB}}$

Bài 8: Cho tam giác ABC có đường cao AH. Trên AH, lấy các điểm K, I sao cho AK = KI = IH. Qua I, K lần lượt vẽ các đường thẳng EF // BC, MN // BC (E, M ∈ AB, F, N ∈ AC).

a) Tính $\frac{{MN}}{{BC}}$ và $\frac{{EF}}{{BC}}$

b) Cho biết diện tích của tam giác ABC là 90 cm². Tính diện tích tứ giác MNFE.

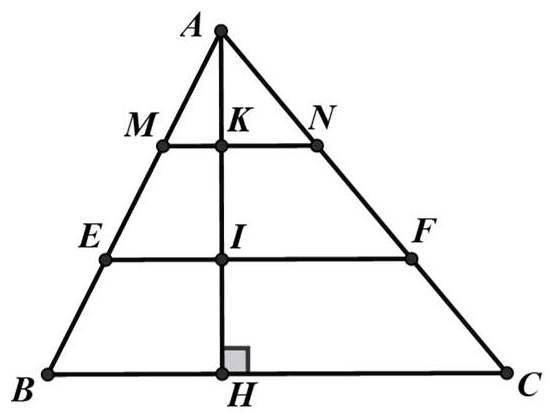
Hướng dẫn giải

$\begin{gathered} \bullet {\text{ }}NK\parallel CH \Rightarrow \frac{{AK}}{{AH}} = \frac{{AN}}{{AC}} \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{3} \hfill \\ MN\parallel BC \Rightarrow \frac{{MN}}{{BC}} = \frac{{AN}}{{AC}} \Rightarrow \frac{{MN}}{{BC}} = \frac{1}{3}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \bullet {\text{ }}IF\parallel CH \Rightarrow \frac{{AI}}{{AH}} = \frac{{AF}}{{AC}} \Rightarrow \frac{{AF}}{{AC}} = \frac{2}{3} \hfill \\ EF\parallel BC \Rightarrow \frac{{EF}}{{BC}} = \frac{{AF}}{{AC}} \Rightarrow \frac{{EF}}{{BC}} = \frac{2}{3}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

b) MNFE có MN // FE và KI ⊥ MN

Do đó MNEF là hình thang có 2 đáy MN, FE và chiều cao KI. Suy ra:

$\begin{gathered} {S_{MNEF}} = \frac{{\left( {MN + FE} \right)KI}}{2} = \frac{\begin{gathered} \hfill \\ \left( {\frac{1}{3}BC + \frac{2}{3}BC} \right) \cdot \frac{1}{3}AH \hfill \\ \end{gathered} }{2}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array} = \frac{1}{3} \cdot {S_{ABC}} = 30{\text{ }}c{m^2} \hfill \\ \end{gathered}$

Định lí đảo và hệ quả của định lí Ta-lét

Kiến thức cần nhớ

Định lí Ta-lét đảo

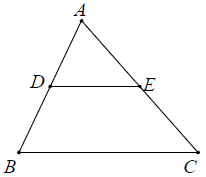
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

$\left\{ \begin{gathered} \Delta ABC \hfill \\ \frac{{AD}}{{DB}} = \frac{{AE}}{{EC}} \hfill \\ \end{gathered} \right. \Rightarrow DE\parallel BC$

Hệ quả của định lí Ta-lét

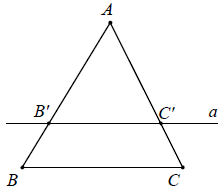
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tỉ lệ với ba cạnh của tam giác đã cho.

$\left\{ \begin{gathered} \Delta ABC \hfill \\ BC\parallel B'C' \hfill \\ \end{gathered} \right. \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}}$

Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng a song song với một cạnh của tam giác và cắt phần kéo dài của hai cạnh còn lại.

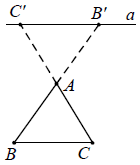
Bài tập minh họa

Các dạng toán cơ bản

Dạng 1. Tính độ dài đoạn thẳng. Chia đoạn thẳng cho trước thành các phần bằng nhau

Phương pháp giải

Tính độ dài đoạn thẳng:

+) Xác định đường thẳng song song với một cạnh của tam giác.

+) Áp dụng hệ quả của định lí Ta-lét để lập tỉ lệ thức của các đoạn thẳng.

+) Thay số vào hệ thức rồi giải phương trình.

Chia đoạn thẳng cho trước thành các phần bằng nhau cách sử dụng hệ quả của định lí Ta-lét hoặc tính chất của đường thẳng song song cách đều.

Ví dụ

Ví dụ 1. Tính các độ dài x, y trong hình sau

Hướng dẫn giải

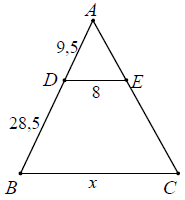
a) Áp dụng hệ quả định lí Ta-lét cho DE // BC, ta được: $\frac{{BC}}{{DE}} = \frac{{AB}}{{AD}}$

Hay $\frac{x}{8} = \frac{{28,5}}{{9,5}} \Leftrightarrow x = \frac{{8 \cdot 28,5}}{{9,5}} = \frac{{456}}{{19}} \approx 31,58$

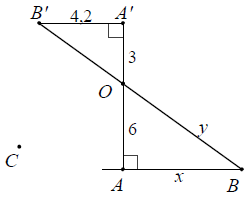
b) Từ hình trên ta thấy A’B’ // AB vì cùng vuông góc với AA’.

Áp dụng hệ quả định lí Ta-lét cho A’B’ // AB, ta được: $\frac{{AB}}{{A'B'}} = \frac{{AO}}{{A'O'}}$

Hay $\frac{x}{{4,2}} = \frac{6}{3} \Leftrightarrow x = 4,2 \cdot 2 = 8,4$

Áp dụng định lí Py-ta-go vào tam giác OAB vuông ở A, ta được:

OB² = BA² + AO² hay y² = 8,4² + 6² = 106,06 ⇒ y ≈ 10,32

Ví dụ 2. Cho tam giác ABC. Trên cạnh AB lấy điểm D sao cho AD = 8 cm và DB = 4 cm. Tính tỉ số khoảng cách từ các điểm D và B đến cạnh AC.

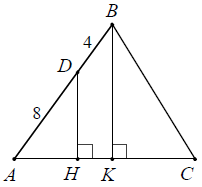
Hướng dẫn giải

Kẻ DH và BK cùng vuông góc với AC thì DH // BK và DH, BK lần lượt là khoảng cách từ các điểm D và B đến cạnh AC.

Áp dụng hệ quả định lí Ta-lét cho DH // BK thu được

$\frac{{DH}}{{BK}} = \frac{{AD}}{{AB}}{\text{ hay }}\frac{{DH}}{{BK}} = \frac{8}{{12}} = \frac{2}{3}$

Ví dụ 3. Hãy chia đoạn AB cho trước thành 5 đoạn bằng nhau. Hỏi có bao nhiêu cách chia như vậy? Hãy nêu rõ cách làm.

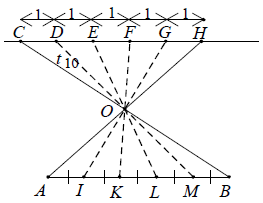
Hướng dẫn giải

Có hai cách chia một đoạn AB cho trước thành 5 phần bằng nhau.

Cách 1: Sử dụng hệ quả của định lí Ta-lét.

Kẻ đường thẳng a // AB.

Từ điểm C bất kì trên a, đặt liên tiếp các đoạn thẳng bằng nhau:

CD = DE = EF = FG = GH

Gọi O là giao điểm của AH và BC.

Vẽ các đường thẳng DO, EO, FO, GO cắt AB theo thứ tự ở I, K, L, M thì các điểm này chia đoạn AB thành 5 phần bằng nhau.

Thật vậy: Áp dụng hệ quả định lí Ta-lét cho CD ⊥ MB, GH // AI ta được:

$\frac{{CO}}{{OB}} = \frac{{CD}}{{MB}} = \frac{{HO}}{{OA}} = \frac{{HG}}{{AI}}$

⇒ MB = AI do CD = GH

Chứng minh tương tự, ta được: AI = IK = KL = LM = MB.

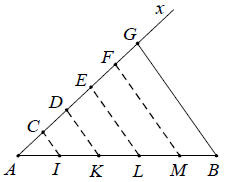
Cách 2: Sử dụng tính chất của đường thẳng song song cách đều.

Kẻ tia Ax, trên đó đặt liên tiếp các đoạn thẳng bằng nhau:

CD = DE = EF = FG = GH

Nối GB. Từ C, D, E, F kẻ các đường thẳng song song với GB, chúng cắt AB lần lượt ở I, K, L, M thì CI, DK, EL, EM, GB là năm đường thẳng song song cách đều nên chúng chắn trên đường thẳng AB những đoạn thẳng liên tiếp bằng nhau là AI = IK = KL = LM = MB.

Dạng 2. Chứng minh hệ thức hình học

Phương pháp giải

+) Xác định đường thẳng song song với một cạnh của tam giác.

+) Áp dụng hệ quả của định lí Ta-lét để lập tỉ lệ thức của các đoạn thẳng.

+) Sử dụng các tính chất của tỉ lệ thức hoặc cộng hay nhân theo vế các đẳng thức hình học.

Ví dụ

Ví dụ 1. Cho hình thang ABCD (AB // CD) có O là giao điểm của hai đường chéo. Đường thẳng qua O song song với hai đáy cắt AD, BC lần lượt ở E và F. Chứng minh rằng OE = OF.

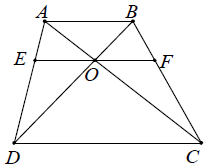
Hướng dẫn giải

Áp dụng hệ quả định lí Ta-lét cho EO // DC, OF // DC và AB // DC ta được:

$\left\{ \begin{gathered} \frac{{EO}}{{DC}} = \frac{{AO}}{{AC}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \frac{{OF}}{{DC}} = \frac{{BO}}{{BD}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \frac{{AO}}{{AC}} = \frac{{BO}}{{BD}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right. \Rightarrow \frac{{EO}}{{DC}} = \frac{{OF}}{{DC}} \Rightarrow EO = OF$

Ví dụ 2. Cho hình thang ABCD (AB // CD). Một đường thẳng qua giao điểm O của hai đường chéo và song song với hai đáy, cắt BC ở I. Chứng minh rằng: $\frac{1}{{AB}} + \frac{1}{{CD}} = \frac{1}{{OI}}$

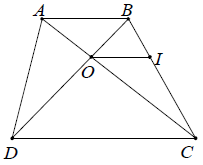
Hướng dẫn giải

Áp dụng hệ quả định lí Ta-lét cho OI // AB, OI // DC ta được:

$\frac{{OI}}{{AB}} = \frac{{CI}}{{CB}}\left( 1 \right);\frac{{OI}}{{DC}} = \frac{{BI}}{{BC}}\left( 2 \right)$

Cộng theo vế các đẳng thức (1) và (2), ta được:

$\begin{gathered} \frac{{OI}}{{AB}} + \frac{{OI}}{{DC}} = \frac{{BI + IC}}{{BC}} = \frac{{BC}}{{BC}} = 1 \hfill \\ \Rightarrow \frac{1}{{AB}} + \frac{1}{{CD}} = \frac{1}{{OI}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Ví dụ 3. Cho hình thang ABCD (AB // CD, AB ≠ CD) có O là giao điểm của AC và BD, I là giao điểm của AD và BC. Đường thẳng IO cắt AB và CD theo thứ tự ở M và N. Chứng minh rằng: M là trung điểm của AB, N là trung điểm của CD. Có nhận xét gì về kết quả của bài toán.

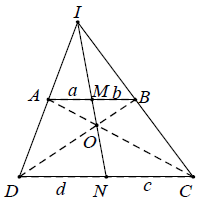
Hướng dẫn giải

Đặt AM = a, MB = b, DN = c, NC = d

Ta phải chứng minh a = b, c = d

Áp dụng hệ quả định lí Ta-lét cho AM // CN, MB // ND và AM // DN, MB // NC ta được:

$\left\{ \begin{gathered} \frac{{AM}}{{CN}} = \frac{{MO}}{{ON}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \frac{{MB}}{{ND}} = \frac{{MO}}{{ON}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right. \Rightarrow \frac{{AM}}{{CN}} = \frac{{MB}}{{ND}}$ hay $\frac{a}{c} = \frac{b}{d} \Rightarrow \frac{a}{b} = \frac{c}{d}{\text{ }}\left( 1 \right)$

$\left\{ \begin{gathered} \frac{{AM}}{{DN}} = \frac{{IM}}{{IN}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \frac{{MB}}{{NC}} = \frac{{IM}}{{IN}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right. \Rightarrow \frac{{AM}}{{DN}} = \frac{{MB}}{{NC}}$ hay $\frac{a}{d} = \frac{b}{c} \Rightarrow \frac{a}{b} = \frac{d}{c}{\text{ }}\left( 2 \right)$

Nhân theo vế các đẳng thức (1) và (2) ta được:

${\left( {\frac{a}{b}} \right)^2} = \frac{{cd}}{{cd}} = 1 \Rightarrow \frac{a}{b} = 1 \Rightarrow a = b$

Thay a = b vào (1) ta được: c = d

Nhận xét: Trong một hình thang có hai đáy không bằng nhau thì giao điểm của hai cạnh bên, giao điểm của hai đường chéo và trung điểm của hai đáy là bốn điểm thẳng hàng. Đây chính là nội dung của: Bổ đề về hình thang.

Dạng 3. Chứng minh hai đường thẳng song song

Phương pháp giải

+) Sử dụng định lí Ta-lét, lập tỉ lệ thức giữa các đoạn thẳng.

+) Áp dụng định lí Ta-lét đảo, kết luận hai đường thẳng song song.

Ví dụ

Ví dụ 1. Trên đường chéo AC của hình bình hành ABCD lấy một điểm I. Qua I kẻ hai đường thẳng bất kì sao cho đường thứ nhất cắt AB, CD lần lượt ở E và F, đường thẳng thứ hai cắt AD, BC theo thứ tự ở G và H. Chứng minh rằng: GE // FH.

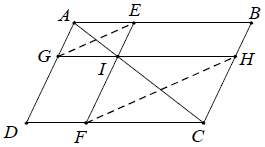
Hướng dẫn giải

ABCD là hình bình hành nên AB // CD và AD // BC, suy ra AE // FC, AG // HC

Áp dụng hệ quả định lí Ta-lét cho AE // FC và AG // HC, ta được:

$\left\{ \begin{gathered} \frac{{EI}}{{IF}} = \frac{{AI}}{{IC}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \frac{{GI}}{{IH}} = \frac{{AI}}{{IC}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right. \Rightarrow \frac{{EI}}{{IF}} = \frac{{GI}}{{IH}}$

Điều này chứng tỏ đường thẳng EG cắt hai cạnh IF, IH của tam giác IHF và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ, nên EG // HF (theo định lí Ta-lét đảo).

Ví dụ 2. Cho tứ giác ABCD. Đường thẳng qua A và song song với BC cắt BD ở E. Đường thẳng qua B và song song với AD cắt AC ở G. Chứng minh rằng: EG // CD.

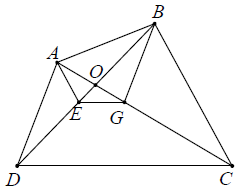
Hướng dẫn giải

Áp dụng hệ quả định lí Ta-lét cho AE // BC và BG // AD, ta được:

$\frac{{OE}}{{OB}} = \frac{{OA}}{{OC}}\left( 1 \right);{\text{ }}\frac{{OB}}{{OD}} = \frac{{OG}}{{OA}}\left( 2 \right)$

Nhân theo vế các đẳng thức (1) và (2), ta được:

$\frac{{OE}}{{OB}} \cdot \frac{{OB}}{{OD}} = \frac{{OA}}{{OC}} \cdot \frac{{OG}}{{OA}} \Rightarrow \frac{{OE}}{{OD}} = \frac{{OG}}{{OC}}$

Điều này chứng tỏ đường thẳng EG cắt hai cạnh OD, OC của tam giác OCD và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ nên EG // DC (theo định lí Ta-lét đảo).

Ví dụ 3. Cho hình thang ABCD và điểm E trên cạnh bên BC. Qua C vẽ đường thẳng song song với AE cắt AD ở K. Chứng minh rằng: BK // DE.

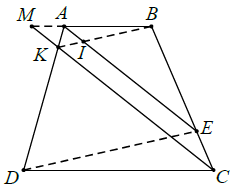
Hướng dẫn giải

Gọi I, M lần lượt là giao điểm của AE với BK và CK với AB.

Áp dụng hệ quả định lí Ta-lét cho AI // MK và IE // KC, thu được:

$\left\{ \begin{gathered} \frac{{AI}}{{MK}} = \frac{{BI}}{{BK}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \frac{{BI}}{{BK}} = \frac{{IE}}{{KC}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right. \Rightarrow \frac{{AI}}{{MK}} = \frac{{IE}}{{KC}} \Rightarrow \frac{{AI}}{{KE}} = \frac{{MK}}{{KC}}\left( 1 \right)$

Áp dụng hệ quả định lí Ta-lét cho MA // DC, ta được:

$\frac{{MK}}{{KC}} = \frac{{AK}}{{KD}}\left( 2 \right)$

Từ (1) và (2) suy ra $\frac{{AI}}{{IE}} = \frac{{AK}}{{KD}}$ . Điều này chứng tỏ đường thẳng KI cắt hai cạnh AD, AE của tam giác ADE và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ nên KI // DE, hay KB // DE (theo định lí Ta-lét đảo).

Dạng 4. Vẽ thêm đường thẳng song song để chứng minh hệ thức hình học, tính tỉ số hai đoạn thẳng

Phương pháp giải

+) Vẽ thêm đường thẳng song song.

+) Áp dụng hệ quả của định lí Ta-lét để lập tỉ lệ thức giữa các đoạn thẳng.

+) Biến đổi tỉ lệ thức.

Ví dụ

Ví dụ 1. Cho tam giác ABC, I là một điểm trong tam giác, IA, IB, IC theo thứ tự cắt BC, CA, AB ở M, N, P. Chứng minh rằng: $\frac{{NA}}{{NC}} + \frac{{PA}}{{PB}} = \frac{{IA}}{{IM}}$

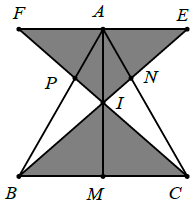
Hướng dẫn giải

Qua A kẻ đường thẳng song song với BC. Đường thẳng này cắt BN, CP lần lượt ở E và F.

Áp dụng hệ quả định lí Ta-lét cho AE // BC và FA // BC, ta được:

$\frac{{NA}}{{NC}} = \frac{{EA}}{{BC}}\left( 1 \right);{\text{ }}\frac{{PA}}{{PB}} = \frac{{AF}}{{BC}}\left( 2 \right)$

Cộng theo vế các đẳng thức (1) và (2), ta được:

$\frac{{NA}}{{NC}} + \frac{{PA}}{{PB}} = \frac{{IA}}{{IM}}$

Ví dụ 2. Cho tam giác ABC, lấy D ∈ AB, E ∈ AC sao cho BD = CE. Gọi K là giao điểm của DE và BC. Chứng minh rằng tỉ số $\frac{{KE}}{{KD}} = \frac{{AB}}{{AC}}$

Hướng dẫn giải

Đặt BD = CE = a.

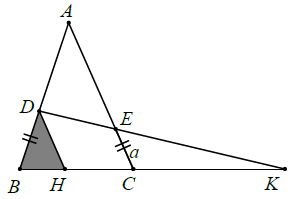
Cách 1: Kẻ DH // AC thì DH // EC.

Áp dụng hệ quả định lí Ta-lét cho DH // EC và DH // AC, ta được:

$\begin{gathered} \frac{{KE}}{{KD}} = \frac{{EC}}{{DH}} = \frac{a}{{DH}}{\text{ }}\left( 1 \right) \hfill \\ \frac{{DH}}{{AC}} = \frac{{BD}}{{BA}} = \frac{a}{{BA}} \Rightarrow \frac{a}{{DH}} = \frac{{AB}}{{AC}}{\text{ }}\left( 2 \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Từ (1) và (2) suy ra: $\frac{{KE}}{{KD}} = \frac{{AB}}{{AC}}$

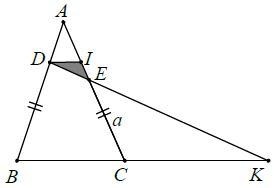
Cách 2: Kẻ DI // BC thì DI // CK.

Áp dụng hệ quả định lí Ta-lét cho DI // CK và DI // BC, ta được:

$\begin{gathered} \frac{{KE}}{{KD}} = \frac{{CE}}{{CI}} = \frac{a}{{CI}}{\text{ }}\left( 3 \right) \hfill \\ \frac{{CI}}{{CA}} = \frac{{BD}}{{BA}} = \frac{a}{{BA}} \Rightarrow \frac{{BA}}{{CA}} = \frac{a}{{CI}}{\text{ }}\left( 4 \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Từ (3) và (4) suy ra: $\frac{{KE}}{{KD}} = \frac{{AB}}{{AC}}$

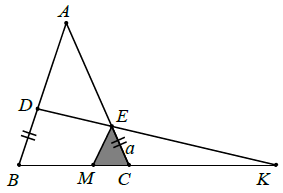
Cách 3: Kẻ EM // AB thì EM // BD.

Áp dụng hệ quả định lí Ta-lét cho EM // BD và EM // AB, ta được:

$\begin{gathered} \frac{{KE}}{{KD}} = \frac{{EM}}{{BD}} = \frac{{EM}}{a}{\text{ }}\left( 5 \right) \hfill \\ \frac{{CE}}{{CA}} = \frac{{EM}}{{AB}} = \frac{a}{{CA}} \Rightarrow \frac{{EM}}{a} = \frac{{AB}}{{CA}}{\text{ }}\left( 6 \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Từ (5) và (6) suy ra: $\frac{{KE}}{{KD}} = \frac{{AB}}{{AC}}$

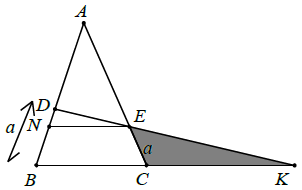
Cách 4: Kẻ EN // BC thì EN // BK.

Áp dụng hệ quả định lí Ta-lét cho EN // BK và EN // BC, ta được:

$\begin{gathered} \frac{{KE}}{{KD}} = \frac{{BN}}{{BD}} = \frac{{BN}}{a}{\text{ }}\left( 7 \right) \hfill \\ \frac{{BN}}{{BA}} = \frac{{CE}}{{CA}} = \frac{a}{{CA}} \Rightarrow \frac{{BN}}{a} = \frac{{BA}}{{CA}}{\text{ }}\left( 8 \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Từ (7) và (8) suy ra: $\frac{{KE}}{{KD}} = \frac{{AB}}{{AC}}$

Phiếu bài tự luyện dạng cơ bản

Bài 1: Tìm x trong hình

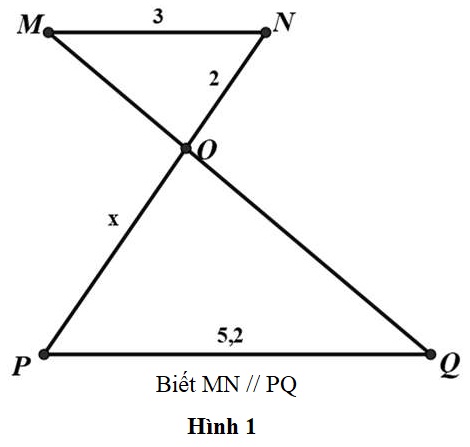
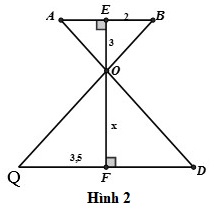
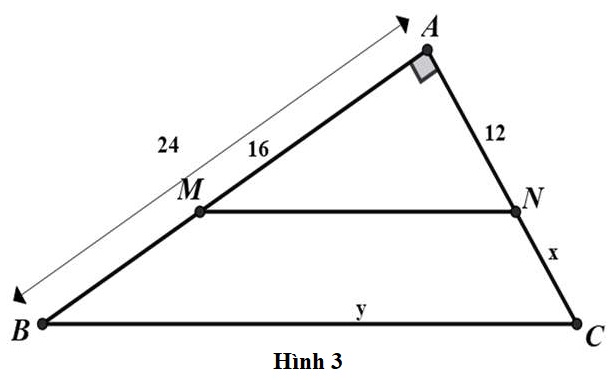
Hướng dẫn giải

Hình 1. Trong △OMN và △OPQ, có: MN // PQ

Suy ra: $\frac{{OP}}{{ON}} = \frac{{PQ}}{{MN}}$ (hệ quả của định lí Ta-lét)

$\Leftrightarrow \frac{x}{2} = \frac{{5,2}}{3} \Leftrightarrow x = \frac{{5,2 \cdot 2}}{3} = \frac{{52}}{{15}}\left( {cm} \right)$

Hình 2. Ta có: EF ⊥ AB, EF ⊥ QD

Suy ra: AB // QD

Trong △OQF và △OBE có: QF // EB

Suy ra: $\frac{{OF}}{{OE}} = \frac{{FQ}}{{EB}}$ (hệ quả của định lí Ta-lét)

$\Leftrightarrow \frac{x}{3} = \frac{{3,5}}{2} \Leftrightarrow x = \frac{{3 \cdot 3,5}}{2} = 5,25\left( {cm} \right)$

Hình 3. Áp dụng định lí Pytago trong △AMN vuông tại A, ta có:

MN² = AM² + AN² = 16² + 12² =400

MN = 20 cm

Trong △ABC có: MN // BC

Suy ra: $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}$ (hệ quả của định lí Ta-lét)

$\begin{gathered} \Leftrightarrow \frac{{16}}{{24}} = \frac{{12}}{{AC}} \Leftrightarrow AC = \frac{{24 \cdot 12}}{{16}} = 18\left( {cm} \right);\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \Rightarrow NC = 18 - 12 = 6\left( {cm} \right) \hfill \\ \end{gathered}$

Trong △ABC có: MN // BC

Suy ra: $\frac{{AM}}{{AB}} = \frac{{MN}}{{BC}}$ (hệ quả của định lí Ta-lét)

$\Leftrightarrow \frac{{16}}{{24}} = \frac{{20}}{{BC}} \Leftrightarrow BC = \frac{{24 \cdot 20}}{{16}} = 30\left( {cm} \right)$

Bài 2: Cho tam giác ABC, điểm I nằm trong tam giác, các tia AI, BI, CI cắt các cạnh BC, AC, AB theo thứ tự ở D, E, F. Qua A kẻ đường thẳng song song với BC cắt tia CI tại H và cắt tia BI tại K. Chứng minh:

a) $\frac{{AK}}{{BD}} = \frac{{HA}}{{DC}}$

b) $\frac{{AF}}{{BF}} + \frac{{AE}}{{CE}} = \frac{{AI}}{{ID}}$

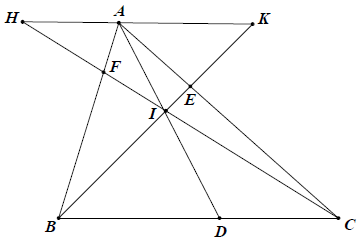
Hướng dẫn giải

a) $AK\parallel BD \Rightarrow \frac{{AI}}{{ID}} = \frac{{AK}}{{BD}}$

Từ $AH\parallel DC \Rightarrow \frac{{AI}}{{ID}} = \frac{{AH}}{{DC}}$

Do đó: $\frac{{AK}}{{BD}} = \frac{{HA}}{{DC}}$

b) Ta có:

$\frac{{AK}}{{BD}} = \frac{{AH}}{{DC}} = \frac{{AK + AH}}{{BD + DC}} = \frac{{HK}}{{BC}} = \frac{{AI}}{{ID}}$

Ta chứng minh

$\frac{{AF}}{{BF}} = \frac{{AH}}{{BC}}\left( 2 \right);{\text{ }}\frac{{AE}}{{CE}} = \frac{{AK}}{{BC}}\left( 3 \right)$

Từ (1), (2), (3) ta có: $\frac{{AF}}{{BF}} + \frac{{AE}}{{CE}} = \frac{{AI}}{{ID}}$ (đpcm)

Bài 3: Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH lần lượt tại B’, C’ và H’.

a) Chứng minh rằng: $\frac{{AH'}}{{AH}} = \frac{{B'C'}}{{BC}}$

b) Áp dụng: Cho biết $AH' = \frac{{AH}}{3}$ và diện tích tam giác ABC là 67,5 cm². Hãy tính diện tích tam giác AB’C’

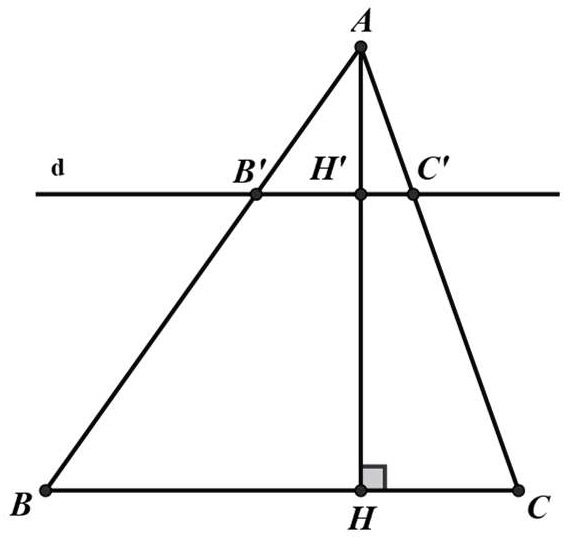
Hướng dẫn giải

a) Trong △ABH có B’H’ // BH suy ra

$\frac{{AH'}}{{AH}} = \frac{{AB'}}{{AB}}\left( 1 \right)$ (hệ quả của định lí Ta-lét)

Trong △ACH có C’H’ // CH suy ra

$\frac{{AH'}}{{AH}} = \frac{{AC'}}{{AC}}\left( 2 \right)$ (hệ quả của định lí Ta-lét)

Trong △ABC có B’C’ // BC suy ra

$\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}}\left( 3 \right)$ (hệ quả của định lí Ta-lét)

Từ (1), (2) và (3) suy ra: $\frac{{AH'}}{{AH}} = \frac{{B'C'}}{{BC}}$

b) Ta có: $\frac{{AH'}}{{AH}} = \frac{{B'C'}}{{BC}}$ (theo câu a)

$\frac{{B'C'}}{{BC}} = \frac{1}{3} \Rightarrow B'C' = \frac{1}{3}BC$

Từ đó suy ra:

$\frac{{{S_{AB'C'}}}}{{{S_{ABC}}}} = \frac{\begin{gathered} \hfill \\ \frac{1}{2}AH' \cdot B'C' \hfill \\ \end{gathered} }{\begin{gathered} \frac{1}{2}AH \cdot BC \hfill \\ \hfill \\ \end{gathered} } = \frac{{AH'}}{{AH}} \cdot \frac{{B'C'}}{{BC}} = \frac{1}{9}$

$\Rightarrow {S_{AB'C'}} = \frac{1}{9}{S_{ABC}} = \frac{{67,5}}{9} = 9,5\left( {c{m^2}} \right)$

Bài 4: Cho tam giác ABC, điểm I thuộc cạnh AB, điểm K thuộc cạnh AC. Kẻ IM // BK (M ∈ AC), kẻ KN // CI (N ∈ AB). Chứng minh: MN // BC.

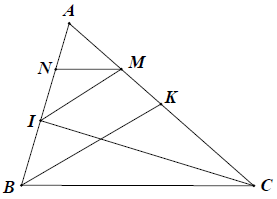
Hướng dẫn giải

Từ IM // BK và KN // IC ta suy ra:

$\frac{{AI}}{{AB}} = \frac{{AM}}{{AK}}$ và $\frac{{AN}}{{AI}} = \frac{{AK}}{{AC}}$

Do đó: $\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}$

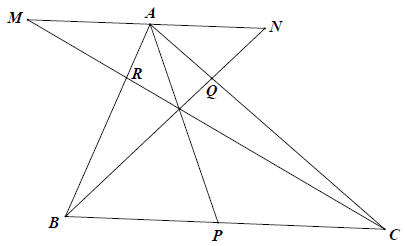
Bài 5: (Định lý Ceva) Trên ba cạnh BC, CA, AB của tam giác ABC lấy tương ứng ba điểm P, Q, R. Chứng minh nếu AP, BQ, CR đồng quy thì $\frac{{PB}}{{PC}} \cdot \frac{{QC}}{{QA}} \cdot \frac{{RA}}{{RB}} = 1$

Hướng dẫn giải

Qua A kẻ đường thẳng song song với BC cắt BQ và CR lần lượt tại N và M

Ta chứng minh được:

$\frac{{QC}}{{AQ}} = \frac{{BC}}{{AN}}\left( 1 \right);{\text{ }}\frac{{RA}}{{BR}} = \frac{{AM}}{{BC}}\left( 2 \right);{\text{ }}\frac{{BP}}{{CP}} = \frac{{AN}}{{AM}}\left( 3 \right)$

Từ (1), (2) và (3) suy ra: $\frac{{PB}}{{PC}} \cdot \frac{{QC}}{{QA}} \cdot \frac{{RA}}{{RB}} = 1$ (đpcm)

Bài 6: Cho tứ giác ABCD. Qua E ∈ AD kẻ đường thẳng song song với DC cắt AC ở G. Qua G kẻ đường thẳng song song với CB cắt AB tại H. Chứng minh rằng:

a) HE // BD

b) Qua B kẻ đường thẳng song song với CD, cắt đường thẳng Ac tại I. Qua C kẻ đường thẳng song song với BA, cắt BD tại F. Chứng minh IF // AD.

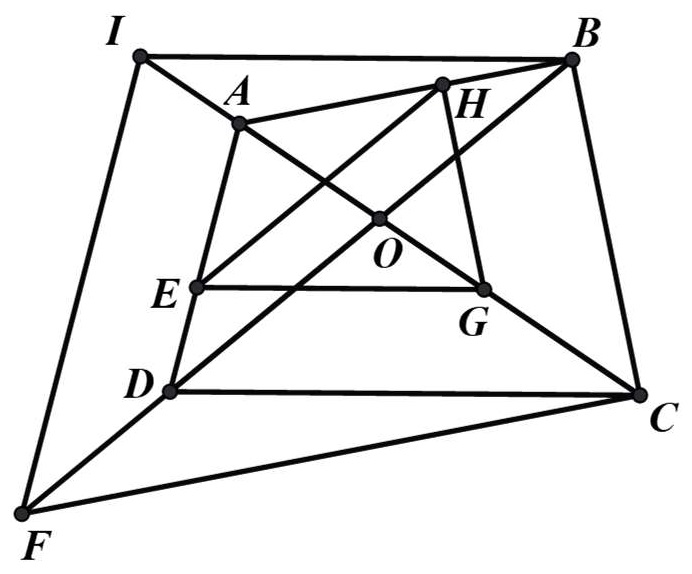
Hướng dẫn giải

a) $\left\{ \begin{gathered} EG\parallel DC \Rightarrow \frac{{AE}}{{AD}} = \frac{{AG}}{{AC}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ GH\parallel BC \Rightarrow \frac{{AG}}{{AC}} = \frac{{AH}}{{AB}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right.$

$\Rightarrow \frac{{AE}}{{AD}} = \frac{{AH}}{{AB}} \Rightarrow EH\parallel BD$

b) Gọi O là giao điểm của AC và BD

$\begin{gathered} \left\{ \begin{gathered} BI\parallel DC \Rightarrow \frac{{OI}}{{OC}} = \frac{{OB}}{{OD}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ AB\parallel CF \Rightarrow \frac{{OC}}{{OA}} = \frac{{OF}}{{OB}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right. \hfill \\ \Rightarrow \frac{{OI}}{{OA}} = \frac{{OF}}{{OD}} \Rightarrow AD\parallel IF\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Bài 7: Cho hình thang ABCD (AB // CD). M là trung điểm của CD. Gọi I là giao điểm của AM và BD, K là giao điểm của BM và AC.

a) Chứng minh: IK // AB

b) Đường thẳng IK cắt AD, BC theo thứ tự ở E và F. Chứng minh rằng: EI = IK =

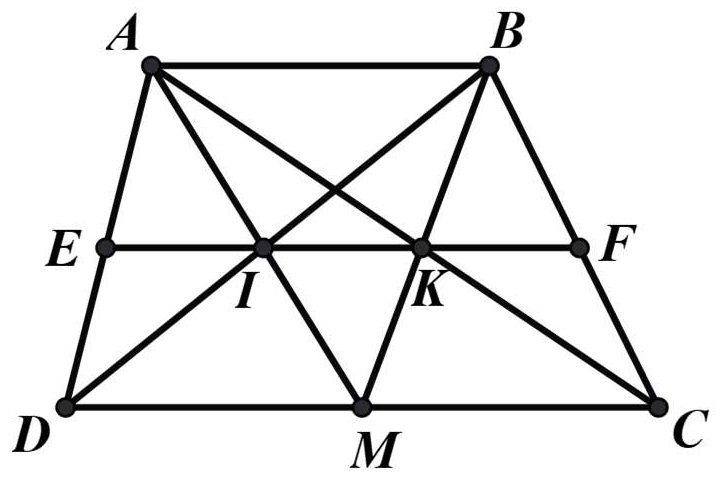
Hướng dẫn giải

a) $\left\{ \begin{gathered} AB\parallel DM \Rightarrow \frac{{IM}}{{IA}} = \frac{{MD}}{{AB}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ AB\parallel MC \Rightarrow \frac{{MK}}{{KB}} = \frac{{MC}}{{AB}}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right.$

$\Rightarrow \frac{{IM}}{{IA}} = \frac{{MK}}{{KB}} \Rightarrow IK\parallel AB$

b) Ta có:

$\begin{gathered} \left\{ \begin{gathered} AB\parallel EI \Rightarrow \frac{{IE}}{{AB}} = \frac{{ID}}{{DB}} \hfill \\ AB\parallel IK \Rightarrow \frac{{IK}}{{AB}} = \frac{{IM}}{{MA}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ AB\parallel DM \Rightarrow \frac{{DI}}{{BI}} = \frac{{IM}}{{IA}} \Rightarrow \frac{{DI}}{{BD}} = \frac{{IM}}{{AM}} \hfill \\ \end{gathered} \right. \hfill \\ \Rightarrow \frac{{IE}}{{AB}} = \frac{{IK}}{{AB}} \Rightarrow EI = IK\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Tương tự: IK = KF. Do đó: EI = IK = KF.

Bài 8: Cho △ABC có AD là trung tuyến. Từ một điểm M bất kỳ trên cạnh BC, vẽ đường thẳng song song với AD, cắt AB và AC lần lượt tại E và F. Gọi I là trung điểm của EF. Chứng minh:

a) ME + MF = 2AD

b) ADMI là hình hình hành

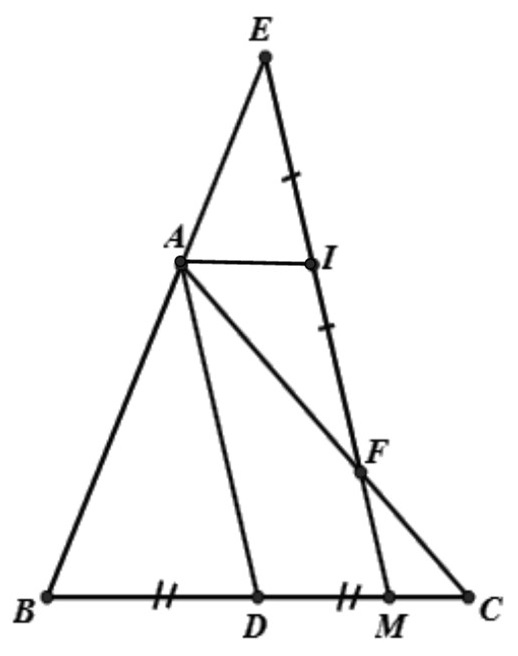
Hướng dẫn giải

a) $MF\parallel AD \Rightarrow \frac{{MF}}{{AD}} = \frac{{CM}}{{CD}}$

$\begin{gathered} AD\parallel ME \Rightarrow \frac{{ME}}{{AD}} = \frac{{BM}}{{BD}} \hfill \\ \Rightarrow \frac{{MF}}{{AD}} + \frac{{ME}}{{AD}} = \frac{{CM}}{{CD}} + \frac{{BM}}{{BD}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Mà CD = BD (gt)

$\begin{gathered} \Rightarrow \frac{{MF + ME}}{{AD}} = \frac{{CM + BM}}{{CD}} = \frac{{BC}}{{CD}} = 2\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \Rightarrow ME + MF = 2AD \hfill \\ \end{gathered}$

b) ME + MF = 2AD (chứng minh trên)

Mà: ME + MF = FE + MF + MF = FE + 2MF = 2IF + 2MF = 2IM

⇒ AD = IM và AD // IM

⇒ ADIN là hình bình hành

Dạng bài nâng cao tổng hợp Ta-lét và liên quan

Ví dụ 1. Cho tam giác ABC có $\widehat A = 120^\circ$ , AD là đường phân giác. Chứng minh rằng:

$\frac{1}{{AB}} + \frac{1}{{AC}} = \frac{1}{{AD}}$

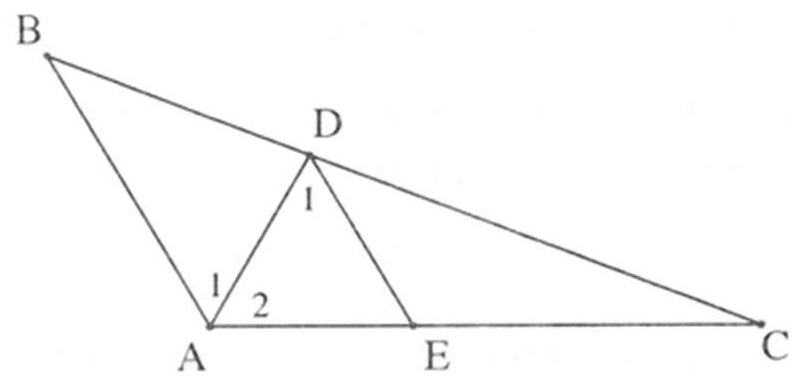
Hướng dẫn giải

Kẻ DE // AB, ta có: $\widehat {{D_1}} = \widehat {{A_1}} = 60^\circ ;{\text{ }}\widehat {{A_2}} = 60^\circ$ nên tam giác ADE đều. Suy ra: AD = AE = DE.

Áp dụng hệ quả định lý Ta-lét:

$\frac{{DE}}{{AB}} = \frac{{CE}}{{AC}}$ hay $\frac{{AD}}{{AB}} = \frac{{CE}}{{AC}}$

Mặt khác $\frac{{AD}}{{AC}} = \frac{{AE}}{{AC}}$ nên

$\frac{{AD}}{{AB}} + \frac{{AD}}{{AC}} = \frac{{CE}}{{AC}} + \frac{{AE}}{{AC}} = \frac{{AC}}{{AC}} = 1$

Suy ra: $\frac{1}{{AB}} + \frac{1}{{AC}} = \frac{1}{{AD}}$

Nhận xét. Những bài toán chứng minh đẳng thức có nghịch đảo độ dài đoạn thẳng, bạn nên biến đổi và chứng minh hệ thức tương đương có tỉ số của hai đoạn thẳng.

Ví dụ 2. Một đường thẳng đi qua trọng tâm G của tam giác ABC cắt cạnh AB, AC lần lượt tại M và N. Chứng minh rằng:

a) $\frac{{AB}}{{AM}} + \frac{{AC}}{{AN}} = 3$

b) $\frac{{BM}}{{AM}} + \frac{{CN}}{{AN}} = 1$

Hướng dẫn giải

⋆ Tìm cách giải. Để tạo ra tỉ số $\frac{{AB}}{{AM}};\frac{{AC}}{{AN}}$ chúng ta cần vận dụng định lý Ta-lét, mà hình vẽ chưa có yếu tố song song do vậy chúng ta cần kẻ thêm yếu tố song song. Kẻ đường thẳng song song với MN từ B và C vừa khai thác được yếu tố trọng tâm, vừa tạo ra được tỉ số yêu cầu.

⋆ Trình bày lời giải

Trường hợp 1. Nếu MN // BC, thì lời giải đơn giản (dành cho bạn đọc tự giải).

Trường hợp 2. Xét MN không song song với BC.

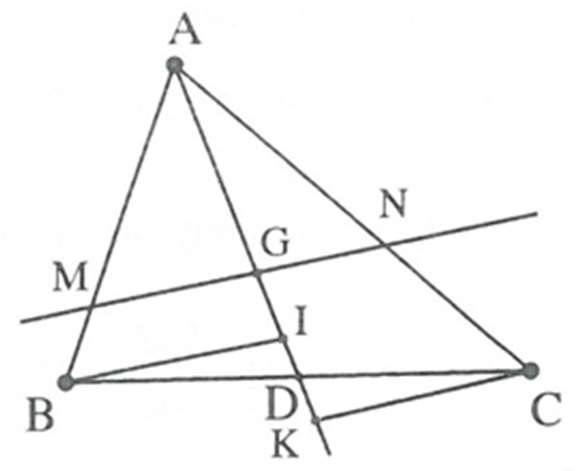
a) Gọi giao điểm của AG và BC là D ⇒ BD = CD

Kẻ BI // CK // MN (I, K ∈ AD)

Xét △BDI và △CDK, có:

BD = CD

$\widehat {IBD} = \widehat {KCD};{\text{ }}\widehat {IDB} = \widehat {KDC}$

Nên △BDI = △CDK (g.c.g) ⇒ DI = DK

Áp dụng định lý Ta-lét, ta có $\frac{{AB}}{{AM}} = \frac{{AI}}{{AG}}$ (vì MG // BI)

$\frac{{AC}}{{AN}} = \frac{{AK}}{{AG}}$ (vì GN // CK).

Suy ra:

$\frac{{AB}}{{AM}} + \frac{{AC}}{{AN}} = \frac{{2AD}}{{AG}} = 3{\text{ }}\left( 1 \right){\text{ }}\left( {{\text{Do }}AD = \frac{3}{2}AG} \right)$

b) Xét $\frac{{BM}}{{AM}} = \frac{{GI}}{{AG}};{\text{ }}\frac{{CN}}{{AN}} = \frac{{KG}}{{AG}}$

Hay $\frac{{BM}}{{AM}} + \frac{{CN}}{{AN}} = \frac{{GI + GK}}{{AG}} = \frac{{2GD}}{{AG}} = 1$

Suy ra: $\frac{{BM}}{{AM}} + \frac{{CN}}{{AN}} = 1$

Nhận xét. Từ kết quả (1), chúng ta thấy rằng bởi G là trọng tâm nên $\frac{{2AD}}{{AG}} = 3$ . Vậy nếu G không phải là trọng tâm thì ta có bài toán sau:

+) Một đường bất kỳ cắt cạnh AB, AC và đường trung tuyến AD của tam giác ABC lần lượt tại M, N và G. Chứng minh rằng: $\frac{{AB}}{{AM}} + \frac{{AC}}{{AN}} = \frac{{2AD}}{{AG}}$

+) Nếu thay yếu tố trung tuyến bằng hình bình hành, ta có bài toán sau: Cho hình bình hành ABCD. Một đường thẳng bất kỳ cắt AB, AD và AC lần lượt tại M, N và G. Chứng minh rằng:

$\frac{{AB}}{{AM}} + \frac{{AD}}{{AN}} = \frac{{AC}}{{AG}}$

Ví dụ 3. Cho ABCD là hình bình hành có tâm O. Gọi M, N là trung điểm BO, AO. Lấy F trên cạnh AB sao cho FM cắt cạnh BC tại E và tia FN cắt cạnh AD tại K. Chứng minh rằng:

a) $\frac{{BA}}{{BF}} + \frac{{BC}}{{BE}} = 4$

b) BE + AK ≥ BC

Hướng dẫn giải

⋆ Tìm cách giải.

Với phân tích và suy luận như câu a – ví dụ 2 thì câu a – ví dụ này không quá khó.

Tương tự câu a, chúng ta có kết quả: $\frac{{AD}}{{AK}} + \frac{{AB}}{{AF}} = 4$ và suy ra $\frac{{AD}}{{AK}} + \frac{{AB}}{{AF}} + \frac{{BA}}{{BF}} + \frac{{BC}}{{BE}} = 8$ để liên kết được BE + AK với nhau, mà với suy luận trên thì BE, AK cùng nằm ở mẫu số, do đó chúng ta liên tưởng tới bất đẳng thức đại số $\frac{1}{x} + \frac{1}{y} \geqslant \frac{4}{{x + y}}$ sẽ cho chúng ta yêu cầu. Với suy luận đó, chúng ta có lời giải sau:

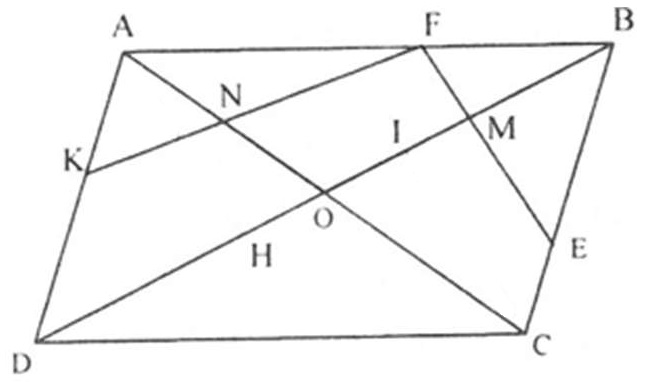
⋆ Trình bày lời giải

a) Kẻ CI // AH // EF (với I, H ∈ BD)

Xét △AOH và △COI, có:

$\widehat {AOH} = \widehat {COI}$ (đối đỉnh);

OA = OB;

$\widehat {HAO} = \widehat {ICO}$ (so le trong)

⇒ △AOH = △COI (c.g.c)⇒ IO = OH.

Áp dụng định lý Ta-lét, ta có:

$\begin{gathered} \frac{{BA}}{{BF}} + \frac{{BC}}{{BE}} \hfill \\ = \frac{{BH}}{{BM}} + \frac{{BI}}{{BM}} = \frac{{BH + BI}}{{BM}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ = \frac{{BO + OH + BO - OI}}{{BM}} = \frac{{2BO}}{{BM}} = 4 \hfill \\ \end{gathered}$

b) Tương tự ta có:

$\begin{gathered} \frac{{AD}}{{AK}} + \frac{{AB}}{{AF}} = 4 \Rightarrow \frac{{AD}}{{AK}} + \frac{{AB}}{{AF}} + \frac{{BA}}{{BF}} + \frac{{BC}}{{BE}} = 8\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \Rightarrow BC\left( {\frac{1}{{AK}} + \frac{1}{{BE}}} \right) + AB\left( {\frac{1}{{AF}} + \frac{1}{{BF}}} \right) = 8{\text{ }}\left( 1 \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Áp dụng bất đẳng thức $\frac{1}{x} + \frac{1}{y} \geqslant \frac{4}{{x + y}}$ (với x, y > 0)

Ta có: $\frac{1}{{AF}} + \frac{1}{{BF}} \geqslant \frac{4}{{AF + BF}} = \frac{4}{{AB}}$

$\Rightarrow AB\left( {\frac{1}{{AF}} + \frac{1}{{BF}}} \right) \geqslant 4{\text{ }}\left( 2 \right)$

Từ (1) và (2) suy ra: $BC\left( {\frac{1}{{AK}} + \frac{1}{{BE}}} \right) \leqslant 4$

Mà $\frac{1}{{AK}} + \frac{1}{{BE}} \geqslant \frac{4}{{AK + BE}}$

$\begin{gathered} \Rightarrow BC\left( {\frac{1}{{AK}} + \frac{1}{{BE}}} \right) \geqslant \frac{{4BC}}{{AK + BE}} \hfill \\ \Rightarrow \frac{{4BC}}{{AK + BE}} \leqslant 4 \Rightarrow AK + BE \geqslant BC\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Ví dụ 4. Cho tam giác ABC nhọn có AH là đường cao. Trên AH, AB, AC lần lượt lấy điểm D, E, F sao cho $\widehat {EDC} = \widehat {FDB} = 90^\circ$ . Chứng minh rằng: EF // BC.

Hướng dẫn giải

* Tìm cách giải. Để chứng minh EF // BC, suy luận một cách tự nhiên chúng ta cần vận dụng định lý Ta-lét đảo. Do vậy cần chứng minh tỉ lệ $\frac{{AB}}{{AE}} = \frac{{AC}}{{AF}}$ . Nhận thấy để định hướng tỉ lệ thức ấy cũng như khai thác được $\widehat {EDC} = \widehat {FDB} = 90^\circ$ chúng ta cần kẻ BO ⊥ CD, CM ⊥ DB, để có các đường thẳng song song rồi vận dụng định lý Ta-lét. Từ đó chúng ta có lời giải sau:

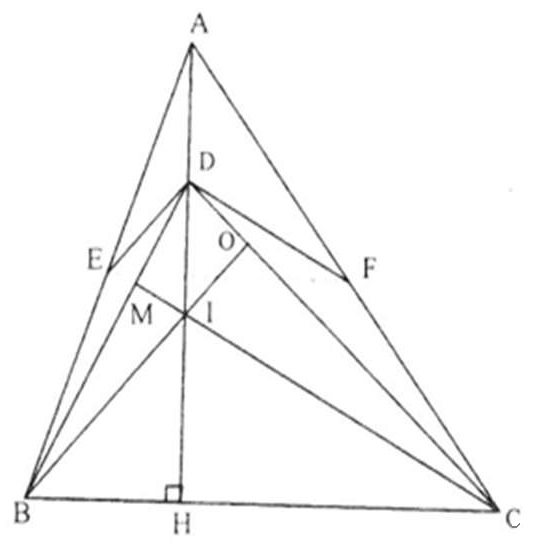
⋆ Trình bày lời giải.

Kẻ BO ⊥ CD, CM ⊥ DB, BO và CM cắt nhau tại I

⇒ D là trực tâm của △BIC

⇒ DI ⊥ BC ⇒ I, D, A thẳng hàng.

$\begin{gathered} DE\parallel BI \Rightarrow \frac{{AI}}{{AD}} = \frac{{AB}}{{AE}} \hfill \\ IC\parallel FD \Rightarrow \frac{{AI}}{{AD}} = \frac{{AC}}{{AF}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Suy ra: $\frac{{AB}}{{AE}} = \frac{{AC}}{{AF}} \Rightarrow EF\parallel BC$ (Định lý Ta-lét đảo)

Ví dụ 5. Cho tam giác ABC có AD là đường trung tuyến. Gọi M là điểm tùy ý thuộc khoảng BD. Lấy E thuộc AB và F thuộc AC sao cho ME // AC, MF // AB. Gọi H là giao điểm MF và AD. Đường thẳng qua B song song với EH cắt MF tại K. Đường thẳng AK cắt BC tại I. Tính tỉ số $\frac{{IB}}{{ID}}$ ?

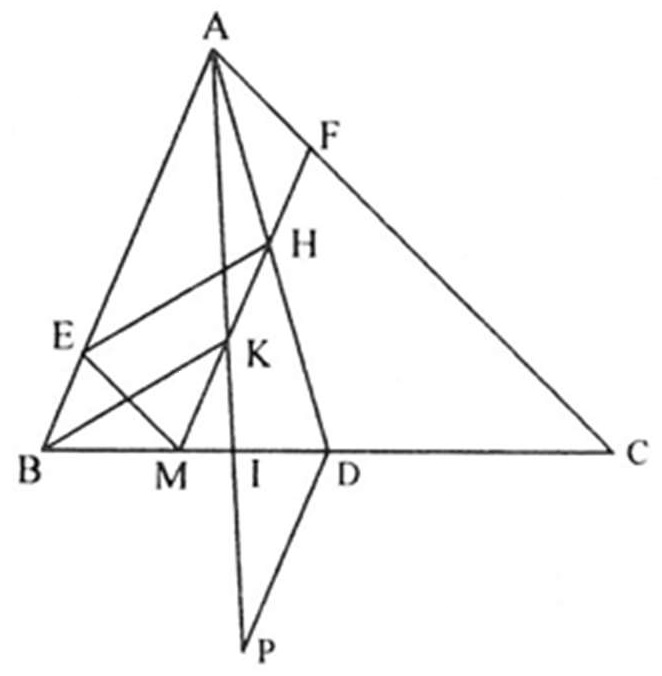
Hướng dẫn giải

Qua D kẻ đường thẳng song song với AB, cắt tia AI tại P.

Áp dụng định lý Ta-lét, cho các đoạn thẳng song song ta có:

$\begin{gathered} DP\parallel AB \Rightarrow \frac{{IB}}{{ID}} = \frac{{AB}}{{DP}} = \frac{{AB}}{{HK}} \cdot \frac{{HK}}{{DP}}{\text{ }}\left( 1 \right)\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ ME\parallel AC \Rightarrow \frac{{AB}}{{HK}} = \frac{{AB}}{{BE}} = \frac{{BC}}{{BM}}{\text{ }}\left( 2 \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \left\{ \begin{gathered} HK\parallel DP \hfill \\ MH\parallel AB \hfill \\ \end{gathered} \right. \Rightarrow \frac{{HK}}{{DP}} = \frac{{AH}}{{AD}} = \frac{{BM}}{{BD}}{\text{ }}\left( 3 \right) \hfill \\ \end{gathered}$

Từ (1), (2) và (3) suy ra:

$\frac{{IB}}{{ID}} = \frac{{BC}}{{BM}} \cdot \frac{{BM}}{{BD}} = \frac{{BC}}{{BD}} = 2$

Vậy $\frac{{IB}}{{ID}} = 2$

Thầy Tú dạy toán