Tổng ba góc của một tam giác
Tổng ba góc của một tam giác bằng 180°.
Áp dụng vào tam giác vuông
Trong tam giác vuông, hai góc nhọn phụ nhau.
Góc ngoài của tam giác
Góc ngoài của một tam giác là góc kề bù với một góc của tam giác đó.
Góc là góc ngoài tại đỉnh C của tam giác ABC.
Các góc của tam giác ABC gọi là các góc trong.

Tính chất: Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.
Nhận xét: Góc ngoài của tam giác lớn hơn mỗi góc trong không kề với nó.
Phân dạng bài tập
Dạng 1. Tính số đo góc của một tam giác
Phương pháp giải:
Lập các đẳng thức thể hiện:
+) Tổng ba góc của tam giác bằng 180°.
+) Trong tam giác vuông, hai góc nhọn phụ nhau.
+) Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó.
Sau đó tính số đo góc phải tìm.
Bài toán.
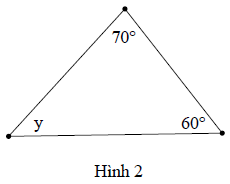
Bài 1. Tính số đo x, y trong hình vẽ dưới đây

Hướng dẫn giải
Hình 1:
Ta có: x + 120° + 35° = 180° (định lý tổng ba góc trong một tam giác)
⇒ x = 180° – 120° – 35° = 25°
Vậy x = 25°
Hình 2:
Ta có: y + 70° + 60° = 180° (định lý tổng ba góc trong một tam giác)
⇒ y = 180° – 70° – 60° = 50°
Vậy y = 50°
Bài 2. Cho tam giác △PQR có . Tính góc còn lại của tam giác?
Hướng dẫn giải
Xét △PQR
Ta có: (định lý tổng ba góc trong một tam giác)
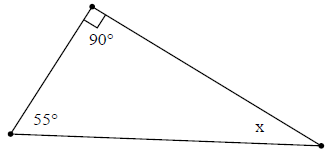
Bài 3. Tính số đo x trong hình vẽ dưới đây
Hướng dẫn giải
Cách 1:
Ta có: x + 90° + 55° = 180° (định lý tổng ba góc trong một tam giác)
⇒ x = 180° – 90° – 55° = 35°
Vậy x = 35°
Cách 2:
Ta có: x + 55° = 90° (trong tam giác vuông hai góc nhọn phụ nhau)
⇒ x = 90° – 55° = 35°
Vậy x = 35°
Bài 4. Tính số đo x trong hình vẽ dưới đây
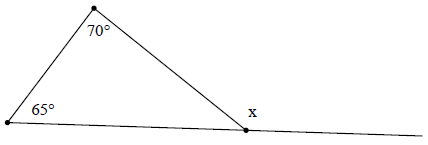
Hướng dẫn giải
Ta có: x = 70° + 65° (góc ngoài của tam giác bằng tổng hai góc trong không kề với nó)
⇒ x = 135°.
Vậy x = 135°
Bài 5. Tính số đo x, y trong hình vẽ dưới đây
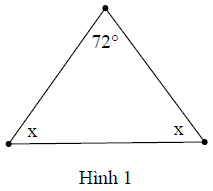
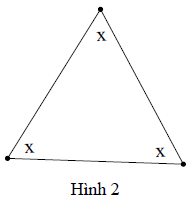

Hướng dẫn giải
Hình 1:
Ta có: x + x + 72° = 180° (định lý tổng ba góc trong một tam giác)
⇒ 2x = 180° – 72° = 108°
⇒ x = 54°
Hình 2:
Ta có: x + x + x = 180° (định lý tổng ba góc trong một tam giác)
⇒ 3x = 180° ⇒ x = 60°
Vậy x = 60°
Hình 3:
Ta có: x = 180° – 105° (hai góc kề bù)
⇒ x = 75°
Ta có: y + 40° + 72° = 180° (định lý tổng ba góc trong một tam giác)
⇒ y = 180° – 70° – 40° = 65°
Vậy y = 65°
Bài 6. Tính số đo x, y trong hình vẽ sau: Biết và
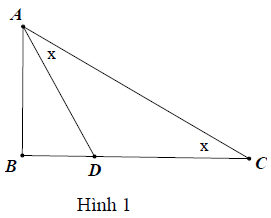
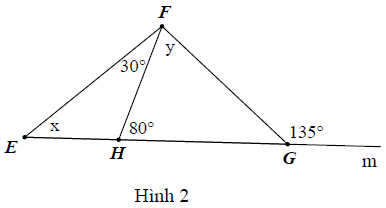
Hướng dẫn giải
Hình 1:
Xét △ABD, có:
(tính chất tam giác vuông)
Lại có:
Trong △ADC ta có:
Mà
Hình 2:
Ta có: (hai góc kề bù).
Xét △EHF, có:
(định lý tổng ba góc trong một tam giác)
Ta lại có: (góc ngoài của tam giác).
Bài 7. Cho hình vẽ. Chứng minh rằng: BC ⊥ CD
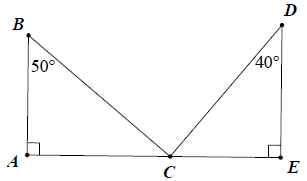
Hướng dẫn giải
Xét △ABC, có:
(tính chất tam giác vuông)
Xét △DEC, có:
(tính chất tam giác vuông)
Lại có:
Mặt khác:
Hay BC ⊥ CD
Bài 8. Tính các góc của △ABC, biết: và
Hướng dẫn giải
Xét △ABC, có:
Mà
Lại có:
Bài 9. Tính các góc của tam giác ABC biết:
a)
b)
Hướng dẫn giải
a) Ta có:
Mà
b) Ta có:
Mà
Bài 10. Cho tam giác ABC, tia phân giác AD của góc cắt BC tại D. Tính góc
biết
.
Hướng dẫn giải

Ta có: (định lý tổng 3 góc của một tam giác)
Vì AD là tia phân giác của góc nên
Ta lại có: (định lý tổng 3 góc của một tam giác)
Bài 11. Cho △MNP. Tính các góc của tam giác biết
a)
b)
Hướng dẫn giải
a) Áp dụng định lí tổng 3 góc trong một tam giác ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau ta được:
b) Ta có:
Áp dụng định lí tổng 3 góc trong một tam giác ta có:
Bài 12. Cho △DEG biết D ∶ E ∶ G = 1 ∶ 3 ∶ 5
a) Tính các góc của tam giác △DEG.
b) Tia phân giác ngoài tại E cắt DG tại A. Tính .
Hướng dẫn giải
a) Từ D ∶ E ∶ G = 1 ∶ 3 ∶ 5 suy ra:
mà
(tổng 3 góc trong một tam giác)
Áp dụng tính chất của dãy tỉ số bằng nhau ta được:
b)
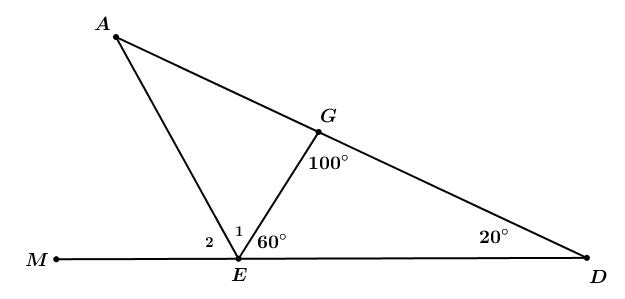
Ta có:
(mà EA là phân giác ngoài tại E nên )
Ta có:
Dạng 2. Các dạng bài toán chứng minh
Phương pháp giải:
Sử dụng các tính chất trong phần kiến thức cần nhớ.
Lưu ý thêm về các tính chất đã học về quan hệ song song, vuông góc, tia phân giác góc…
Bài toán.
Bài 1. Cho △ABC có . Kẻ BD vuông góc với AC (D ∈ AC). Kẻ CE vuông góc với AB (E ∈ AB). Gọi H là giao điểm của BD và CE. Chứng minh:
Hướng dẫn giải
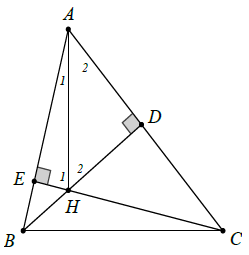
Trong △AEH vuông tại E, ta có:
(hai góc phụ nhau) (1)
Trong △ADH vuông tại D, ta có:
(hai góc phụ nhau) (2)
Cộng (1) với (2) vế theo vế, ta có:
Suy ra:
Bài 2. Cho góc , điểm A thuộc tia Ox. Kẻ AB vuông góc với Ox (B ∈ Oy), kẻ BC vuông góc với Oy (C ∈ Ox), kẻ CD vuông góc với Ox (D ∈ Oy). Chứng minh:
và
Hướng dẫn giải
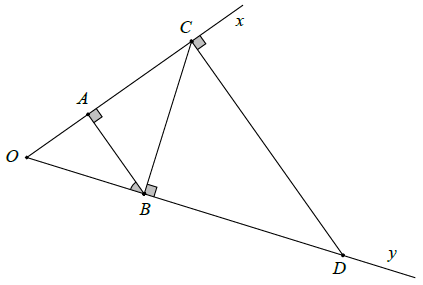
Ta có: (cùng phụ với
)
Ta có: BA ⊥ Ox, DC ⊥ Ox (gt)
Suy ra: AB // CD
Suy ra: (đồng vị)
Bài 3. Cho △ABC vuông tại A. Vẽ AH vuông góc với BC tại H. Vẽ Ax là tia đối của tia AC. Chứng minh:
a)
b) và
bù nhau
Hướng dẫn giải

a) Xét △ABH, ta có:
Xét △ABC, ta có:
Mà nên
b) Tương tự câu a, ta có:
Mà kề bù với
nên
bù với
Bài 4. Cho tam giác △MNP, E là một điểm trên MN. Chứng minh:
Hướng dẫn giải
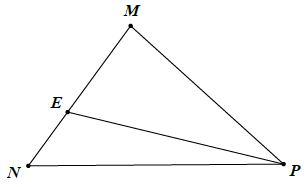
Ta có: là góc ngoài tam giác △PEM.
Từ đó suy ra:
Bài 5. Cho tam giác△ABC có tù. Chứng minh rằng các góc
và
nhọn.
Hướng dẫn giải
Cách 1. Do B tù nên ta có góc ngoài của đỉnh là góc nhọn, suy ra các góc
và
nhọn.
Cách 2. Do mà
nên
và
đều là các góc nhọn.
Bài 6. Cho △ABC vuông tại A, điểm E nằm trong tam giác đó. Chứng minh là góc tù.
Hướng dẫn giải

Gọi K là giao điểm của BE và AC
Xét △ABK, ta có:
Xét △KEC, ta có:
Từ (1) và (2) suy ra:
⇒ là góc tù.
Bài 7. Cho tam giác MNP có .Vẽ phân giác MK.
a) Chứng minh:
b) Đường thẳng chứa tia phân giác góc ngoài đỉnh M của tam giác MNP, cắt đường thẳng NP tại E. Chứng minh rằng:
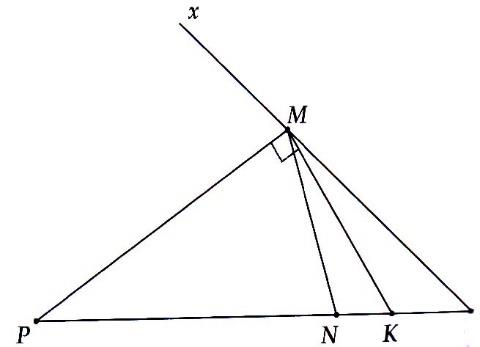
Hướng dẫn giải
a) Sử dụng tính chất góc ngoài.
Ta được:
b) Ta có:
Mà . Từ đó suy ra:
Bài 8. Cho tam giác ABC vuông tại A. Gọi d là đường thẳng vuông góc với BC tại C. Tia phân giác của góc cắt AC ở D và cắt d ở E. Chứng minh rằng:
Hướng dẫn giải
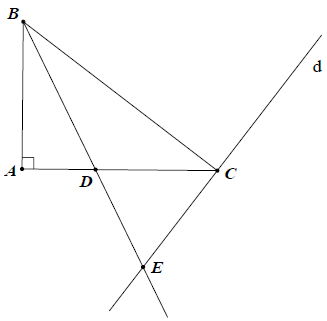
Ta có:
Suy ra:
Bài 9. Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC tại H. Các tia phân giác của và
cắt nhau tại I. Chứng minh rằng:
Hướng dẫn giải
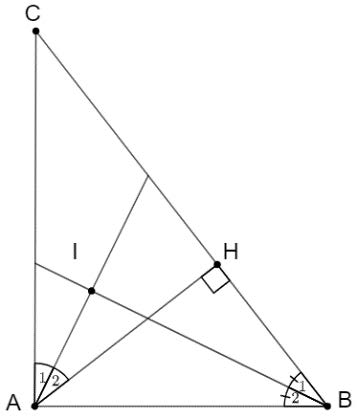
Ta có: BI, AI lần lượt là tia phân giác của và
Nên và
Mà (cùng phụ với
) nên
Xét △AIB, có:
(định lý tổng 3 góc của một tam giác)
Bài 10. Chứng minh rằng: Tổng ba góc ngoài ở ba đỉnh của một tam giác bằng 360°.
Hướng dẫn giải
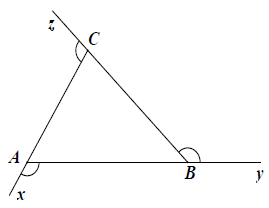
Giả sử : Xét △ABC, cần chứng minh
Ta có:
Cộng vế theo vế ta có:
Mà
Cách khác: Dựa vào tính chất góc ngoài tam giác, tính số đo từng góc ngoài △ABC và thực hiện tương tự.
Bài 11. Tam giác ABC có . Tia phân giác
cắt BC tại D.
a) Chứng minh:
b) Đường thẳng chứa tia phân giác góc ngoài ở đỉnh A của tam giác ABC cắt đường thẳng BC tại E. Chứng minh rằng:
Hướng dẫn giải

a) △ABD, có:
△ACD, có:
Mà nên
⇒
b) △ABC, có: (góc ngoài tam giác)
△ACE, có: (góc ngoài)
Bài 12. Cho tam giác ABC, O là điểm nằm trong tam giác.
a) Chứng minh rằng:
b) Biết và tia BO là tia phân giác của góc
. Chứng minh rằng tia CO là tia phân giác của góc
.
Hướng dẫn giải
a) △ABO, có: (góc ngoài tam giác).
△ACO, có: (góc ngoài tam giác).
Hay
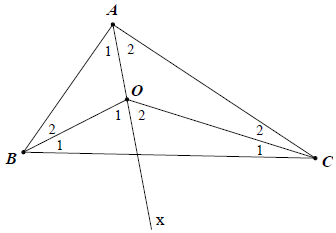
b) Từ
Mà BO là tia phân giác của
Nên
Hay CO là tia phân giác của góc .