Tính chất đồng quy của ba đường trung tuyến
+) Ba đường trung tuyến của một tam giác cùng đi qua một điểm.
+) Điểm gặp nhau của ba đường trung tuyến gọi là
trọng tâm của tam giác.
Vị trí của trọng tâm trên đường trung tuyến
+) Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng độ dài đường trung tuyến đi qua đỉnh ấy.
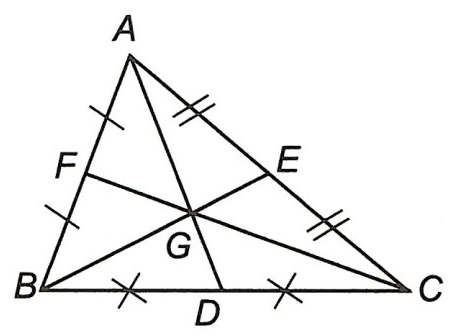
Ta có G là trọng tâm tam giác ABC thì
Hay
Phân dạng bài tập
Dạng 1. Sử dụng tính chất trọng tâm tam giác
Phương pháp giải
+) Ba đường trung tuyến của tam giác đồng quy tại một điểm. Điểm này gọi là trọng tâm của tam giác.
+) Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng độ dài đường trung tuyến đi qua đỉnh ấy.
Bước 1. Xác định trọng tâm nằm trên đường trung tuyến nào.
Bước 2. Sử dụng linh hoạt tỉ lệ khoảng cách từ trọng tâm đến hai đầu đoạn thẳng trung tuyến.
Ví dụ: Cho tam giác ABC có hai đường trung tuyến BM, CN cắt nhau tại G. Chứng minh rằng:
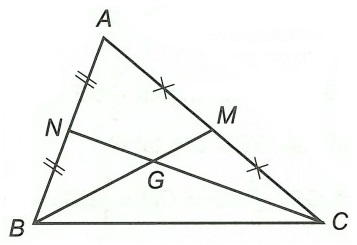
Hướng dẫn giải
Xét tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G.
Suy ra G là trọng tâm tam giác ABC
Do đó ta phải chứng minh
hay
Bất đẳng thức (1) luôn đúng vì trong một tam giác tổng độ dài hai cạnh lớn hơn độ dài cạnh còn lại.
Vậy (đpcm).
Ví dụ mẫu
Ví dụ 1. Cho tam giác ABC cân tại A có hai đường trung tuyến BD và CE cắt nhau tại G.
a) Chứng minh BD = CE.
b) Chứng minh tam giác GBC là tam giác cân.
c) Chứng minh GD + GE > BC
Hướng dẫn giải
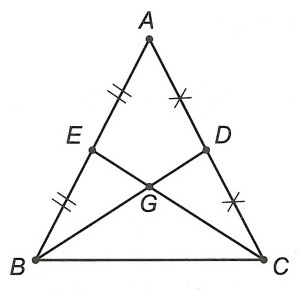
a) Ta có: △ABC cân tại A ⇒ AB = AC
Mà AB = 2BE; AC = 2CD (vì E, D theo thứ tự là trung điểm của AB, AC).
Do đó ta có: 2BE = 2CD hay BE = CD.
Xét △BCE và △CBD, có:
BE = CD (cmt);
BC là cạnh chung.
Do đó: △BCE = △CBD (c.g.c)
⇒ CE = BD (hai cạnh tương ứng)
b) Ta có: G là trọng tâm tam giác ABC nên
BG = BD và CG =
CE (tính chất trọng tâm).
Mà CE = BD (theo câu a)
Nên CE =
BD hay CG = BG.
Vậy tam giác GBC cân tại G.
c) Ta có: GB = BD
⇒ GD = BD
⇒ GB = 2GD
⇒ GD = GB
Chứng minh tương tự, ta có: GE = GC
Do đó: GD + GE = GB +
GC =
(GB + GC)
Mà: GB + GC > BC (trong một tam giác tổng độ dài hai cạnh lớn hơn cạnh còn lại).
Do đó: GD + GE > BC (đpcm).
Ví dụ 2. Cho tam giác ABC. Trên cạnh BC lấy điểm G sao cho BG = 2GC. Vẽ điểm D sao cho C là trung điểm của AD. Gọi E là trung điểm của BD. Chứng minh:
a) Ba điểm A, G, E thẳng hàng.
b) Đường thẳng DG đi qua trung điểm của AB.
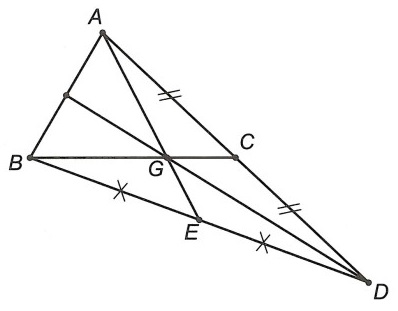
Hướng dẫn giải
a) Xét △ABD có C là trung điểm của cạnh AD
⇒ BC là trung tuyến của △ABD.
Hơn nữa G ∈ BC và GB = 2GC
⇒ GB = BC
⇒ G là trọng tâm △ABD.
Lại có: AE là đường trung tuyến của △ABD nên A, G, E thẳng hàng.
b) Ta có: G là trọng tâm △ABD
⇒ DG là đường trung tuyến của tam giác này.
Suy ra DG đi qua trung điểm của cạnh AB (đpcm).
Bài tập tự luyện dạng 1
Câu 1. Cho tam giác ABC cân ở A, đường trung tuyến AM.
a) Chứng minh: AM ⊥ BC
b) Tính AM biết rằng AB = 10 cm, BC = 12 cm
Hướng dẫn giải
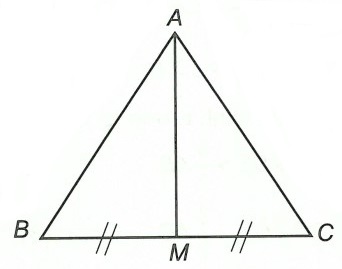
a) AM là đường trung tuyến của tam giác ABC ⇒ MB = MC.
Xét △AMB và △AMC, có:
AB = AC (△ABC cân ở A)
AM là cạnh chung
MB = MC
Do đó: △AMB = △AMC (c.c.c)
(hai góc tương ứng).
Mà (hai góc kề bù) nên
Hay AM ⊥ BC (đpcm).
b) Ta có:
Áp dụng định lí Pi-ta-go vào tam giác vuông AMB , ta có:
AB2 = AM2 + MB2 ⇒ AM2 = AB2 – MB2
Thay AB = 10 cm, MB = 6 cm. Ta được: AM2 = 64.
Suy ra: AM = 8 cm
Câu 2. Cho tam giác ABC có ba đường trung tuyến AX, BY, CZ cắt nhau tại G. Biết GA = GB = GC. Chứng minh: GX = GY = GZ.
Hướng dẫn giải
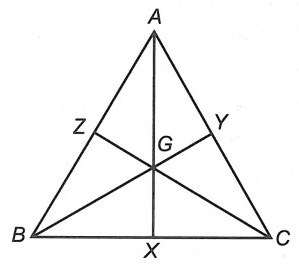
Ta có: GA = AX; GB =
BY; GC =
CZ (tính chất trọng tâm).
Suy ra: GX = AX; GY =
BY; GZ =
CZ
Do đó: GA = 2GX; GB = 2GY; GC = 2GZ
Lại có: GA = GB = GC (giả thiết)
Nên 2GX = 2GY = 2GZ hay GX = GY = GZ (đpcm).
Câu 3. Cho tam giác ABC có hai đường trung tuyến AD và BE vuông góc với nhau tại G. Biết AD = 4,5 cm, BE = 6 cm. Tính độ dài AB.
Hướng dẫn giải
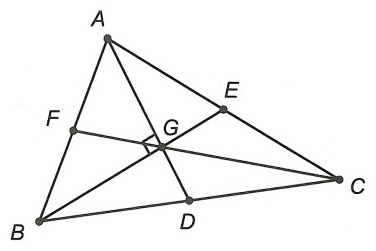
Xét △ABC có AD và BE là hai đường trung tuyến cắt nhau tại G
⇒ G là trọng tâm của △ABC
Ta có: AG = AD; BG =
BE (tính chất trọng tâm tam giác)
Thay AD = 4,5 cm, BE = 6 cm vào.
Ta được: AG = 3 cm, BG = 4 cm
Áp dụng định lí Pi-ta-go vào tam giác vuông AGB, ta có:
AB2 = AG2 + BG2 ⇒ AB2 = 32 + 42 = 25
⇒ AB = 5 cm
Chú ý:
Gọi F là giao điểm của CG và AB ⇒ FA = FB
Ta có thể mở rộng bài toán và tính được CF
Tam giác AGB vuông tại G có trung tuyến ứng với cạnh huyền AB là GF
⇒ GF = FA = FB = AB =
cm
Mà: GF = CF (do G là trọng tâm △ABC)
⇒ CF = 3GF = 7,5 cm
Câu 4. Chứng minh rằng trong tam giác tổng độ dài ba đường trung tuyến nhỏ hơn chu vi nhưng lớn hơn chu vi tam giác đó.
Hướng dẫn giải
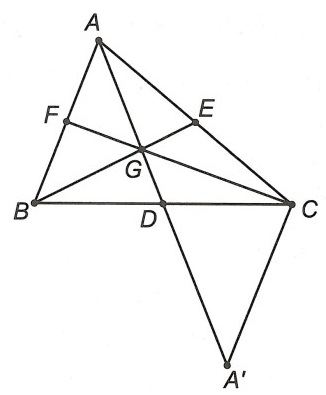
Xét tam giác ABC có trung tuyến AD, BE, CF và trọng tâm G.
Xét △GBC, có:
GB + GC > BC (bất đẳng thức trong tam giác)
⇒ BE +
CF > BC (tính chất trọng tâm)
⇒ BE + CF > BC (1)
Chứng minh tương tự ta được:
AD + BE > AB (2)
AD + CF > AC (3)
Cộng (1), (2), (3) vế theo vế ta được:
2 (AD + BE + CF) > (AB + BC + CA)
⇒ AD + BE + CF > (AB + BC + CA) (*)
Bây giờ ta cần chứng minh:
AD + BE + CF < AB + BC + CA.
Trên tia AD lấy điểm A’ sao cho DA’ = DA.
Xét △ADB và △A’DC, có:
BD = CD
AD = A’D.
Do đó: △ADB = △A’DC (c.g.c)
⇒ AB = A’C (hai cạnh tương ứng)
Lại có: AA’ < AC + A’C (bất đẳng thức trong tam giác △AA’C).
Suy ra: AA’ < AC + AB hay 2AD < AB + AC hay AD < (AB + AC)
Chứng minh tương tự ta được:
BE < (AB + BC) và CF <
(CA + BC)
Cộng vế theo vế ba bất đẳng thức trên lại, ta có:
AD + BE + CF < AB + BC + CA (**)
Từ (*) và (**) suy ra đpcm.
Dạng 2. Chứng minh một điểm là trọng tâm tam giác
Phương pháp giải
Sử dụng tính chất trọng tâm. Chẳng hạn để chứng minh G là trọng tâm tam giác ABC, có ba đường trung tuyến AD, BE, CF thì ta chứng minh
Cách 1: G ∈ AD và GA = AD
hoặc G ∈ BE và GB = BE
hoặc G ∈ CF và GC = CF
Cách 2: Chứng minh G là giao điểm của hai trong ba đường trung tuyến của tam giác ABC.
Ví dụ: Cho tam giác ABC có đường trung tuyến AD, trên đoạn thẳng AD lấy hai điểm E, G sao cho AE = EG = GD. Chứng minh G là trọng tâm tam giác ABC.
Hướng dẫn giải
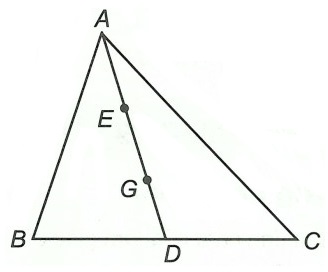
Ta có: AD = AE + EG + GD
Mà AE = EG = GD nên AD = 3AE
⇒ AE = EG = GD = AD
⇒ AG = AD
Vì AD là đường trung tuyến và AG = AD nên G là trọng tâm tam giác ABC.
Ví dụ mẫu
Ví dụ. Cho tam giác ABC, D là trung điểm của AC. Trên đoạn BD lấy điểm E sao cho BE = 2ED. Điểm F thuộc tia đối của tia DE sao cho BF = 2BE. Gọi K là trung điểm của CF và G là giao điểm của EK với AC.
a) Chứng minh G là trọng tâm tam giác EFC.
b) Tính các tỉ số
Hướng dẫn giải
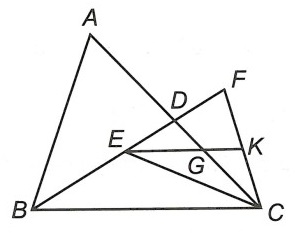
a) Ta có: BF = 2BE ⇒ BE = EF
Mà BE = 2ED nên EF = 2ED
⇒ D là trung điểm của EF
⇒ CD là đường trung tuyến của tam giác EFC.
Vì K là trung điểm của CF nên EK là đường trung tuyến của △EFC.
△EFC có hai đường trung tuyến CD và EK cắt nhau tại G nên G là trọng tâm của △EFC.
b) Ta có: G là trọng tâm tam giác EFC
Nên và
Bài tập tự luyện dạng 2
Câu 1. Cho △ABC, điểm M thuộc đoạn thẳng BC sao cho BM = 2MC. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Gọi E là giao điểm của AM và BD.
a) Chứng minh M là trọng tâm tam giác ABD.
b) Chứng minh AM đi qua trung điểm của BD.
Hướng dẫn giải
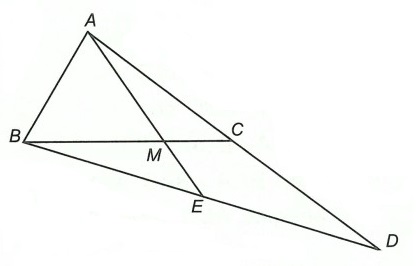
a) Xét △ABD, có: AC = CD
⇒ BC là trung tuyến của △ABD.
Mà BM = 2MC nên BM = BC
⇒ M là trọng tâm của △ABD
b) Vì M là trọng tâm của △ABD nên AM đi qua trung điểm của BD.
Câu 2. Cho △ABC có hai đường trung tuyến BD, CE cắt nhau tại G. Trên tia đối của tia DB lấy điểm M sao cho DM = DG. Trên tia đối của tia EG lấy điểm N sao cho EN = EG. Chứng minh rằng:
a) BG = GM; CG = GN
b) MN = BC và MN // BC
Hướng dẫn giải
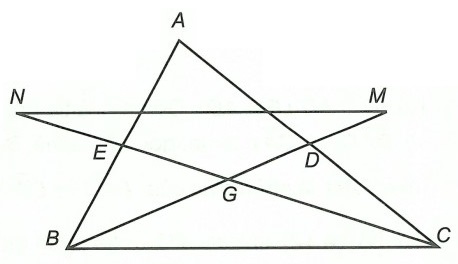
a) Ta có: DM = DG ⇒ GM = 2GD
Ta lại có: G = BD ∩ CE
⇒ G là trọng tâm của △ABC
⇒ BG = 2GD
Suy ra: BG = GM.
Chứng minh tương tự ta được: CG = GN.
b) Xét △GMN và △GBC, có:
GM = GB (cmt);
(2 góc đối đỉnh);
GN = GC (cmt).
Do đó: △GMN = △GBC (c.g.c)
⇒ MN = BC (hai cạnh tương ứng).
Theo chứng minh trên: △GMN = △GBC
(hai góc tương ứng).
Mà và
ở vị trí so le trong nên MN // BC.
Dạng 3. Đường trung tuyến của tam giác cân, tam giác đều, tam giác vuông
Phương pháp giải
Chú ý đến tính chất của tam giác cân, tam giác đều và tam giác vuông.
Ví dụ mẫu
Ví dụ. Cho tam giác đều ABC có ba đường trung tuyến AD, BE, CF cắt nhau tại G. Chứng minh:
a) AD = BE = CF.
b) GA = GB = GC.
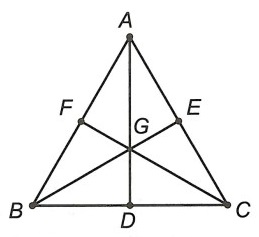
Hướng dẫn giải
a) Ta có BE, CF là các đường trung tuyến của △ABC
⇒ CE = AC; BF =
AB
Vì AC = AB nên AC =
AB hay CE = BF.
Xét △BCE và △CBF, có:
BC chung;
(do △ABC cân ở A)
CE = BF (cmt).
Do đó: △BCE = △CBF (c.g.c)
⇒ BE = CF (2 cạnh tương ứng)
Chứng minh tương tự ta có: AD = BE.
Từ đó suy ra: AD = BE = CF (đpcm).
b) Vì G là trọng tâm tam giác ABC nên
AG = AD; BG =
BE; CG =
CF
Vì AD = BE = CF (theo câu a) nên
AD =
BE =
CF hay AG = BG = CG (đpcm)
Bài tập tự luyện dạng 3
Câu 1. Cho △ABC có hai đường trung tuyến BE và CF cắt nhau tại G. Biết BE = CF. Chứng minh: AG ⊥ BC.
Hướng dẫn giải
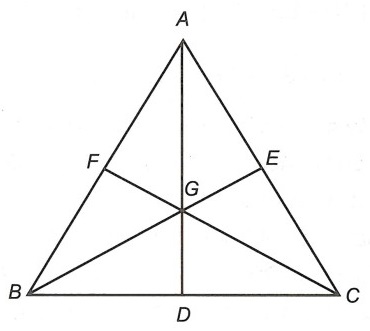
Gọi D là giao điểm của AG và BC ⇒ DB = DC.
Ta có: BG = BE; CG =
CF (tính chất trọng tâm).
Vì BE = CF nên BG = CG ⇒ △BCG cân tại G
Xét △BFC và △CEB, có:
CF = BE (giả thiết)
(cmt);
BC là cạnh chung.
Do đó: △BFC = △CEB (c.g.c)
⇒ (hai góc tương ứng)
⇒ △ABC cân tại A
⇒ AB = AC.
Từ đó suy ra: △ABD = △ACD (c.c.c)
⇒ (hai góc tương ứng)
Mà
⇒ AD ⊥ BC hay AG ⊥ BC.
Câu 2. Chứng minh rằng trong một tam giác, đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
Hướng dẫn giải
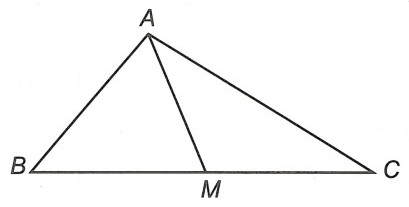
Xét △ABC có trung tuyến
AM = BC ⇒ AM = MB = MC
Khi đó tam giác AMB cân tại M và tam giác AMC cân tại M.
Suy ra: và
Do đó:
Hay
Xét △ABC, có:
Mà nên
Vậy tam giác ABC vuông ở A.