Định nghĩa đường cao của tam giác
Đoạn thẳng vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện của tam giác gọi là đường cao của tam giác đó. Mỗi tam giác có 3 đường cao.

Tính chất ba đường cao của tam giác
+) Ba đường cao của một tam giác cùng đi qua một điểm. Điểm đó được gọi là trực tâm của tam giác.
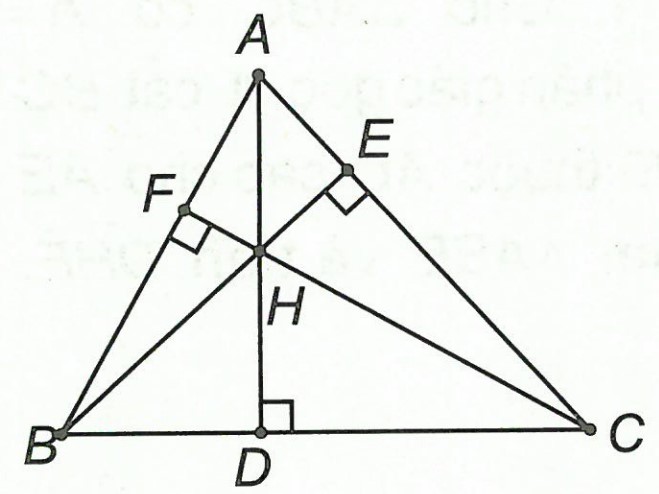
+) Trong hình bên AD, BE, CF lần lượt là các đường cao hạ từ A, B, C của △ABC. H là giao điểm của 3 đường cao và được gọi là trực tâm của tam giác.
Các định lí về đường cao trong tam giác
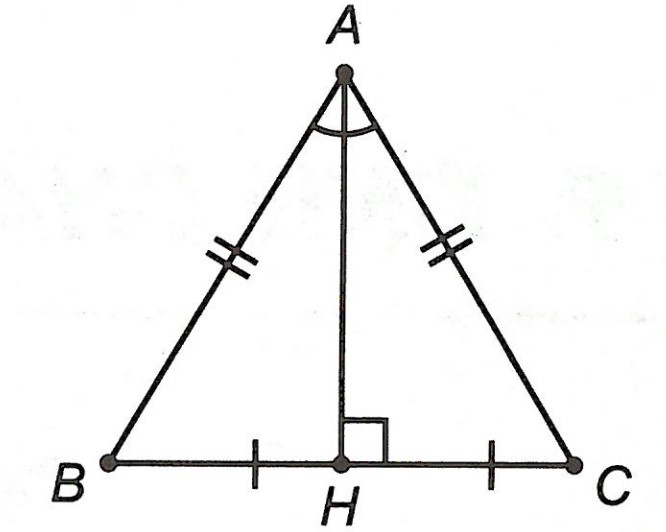
Định lí 1: Trong một tam giác cân, đường trung trực ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến và đường cao cùng xuất phát từ đỉnh đối diện với cạnh đó.
Định lí 2: Trong một tam giác, nếu hai trong bốn loại đường (đường trung tuyến, đường phân giác, đường cao cùng xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện) trùng nhau thì tam giác đó là tam giác cân.
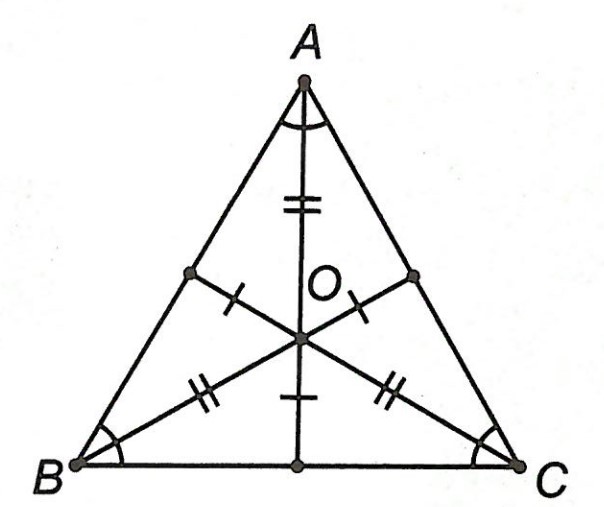
Lưu ý: Trong tam giác đều, trọng tâm, trực tâm, điểm cách đều ba đỉnh của tam giác, điểm nằm trong tam giác và cách đều ba cạnh của tam giác là bốn điểm trùng nhau.
Phân dạng bài tập
Dạng 1. Xác định trực tâm của tam giác
Phương pháp giải
Để xác định trực tâm của tam giác, ta đi tìm giao điểm của hai đường cao trong tam giác đó.
Ví dụ: Cho △ABC nhọn, có H là trực tâm. Xác định trực tâm của △HAB, △HAC, △HBC.

Hướng dẫn giải
Vì H là trực tân của △ABC, nên
AH ⊥ BC, BH ⊥ AC, CH ⊥ AB.
Xét △HAB, có: BC ⊥ AH và AC ⊥ BH
⇒ {C} = BC ∩ AC ⇒ C là trực tâm △HAB.
Tương tự ta có B là trực tâm △HAC và A là trực tâm △HBC.
Ví dụ mẫu
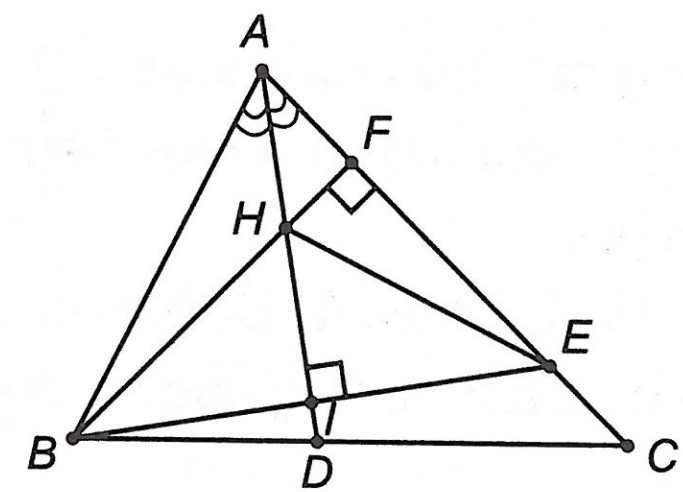
Ví dụ 1. Cho △ABC có , AB < AC, đường phân giác góc
cắt BC tại D, BF ⊥ AC tại F, E thuộc AC sao cho AE = AB. Xác định trực tâm △ABE và tính
.
Hướng dẫn giải
Gọi {I} = AD ∩ BE
Vì AB = AE nên △ABE cân tại A.
Mặt khác AD là phân giác góc của △ABC
⇒ AI là đường cao của △ABE.
BF ⊥ AE ⇒ BF là đường cao của △ABE.
Mà {H} = BF ∩ AI nên H là trực tâm △ABE.
Xét △HEF, có:
Xét △HIE, có:
Từ (1) và (2) ta có:
Vì △ABE cân tại A nên
Ví dụ 2. Cho △ABC đều, G là trọng tâm của tam giác. Xác định trực tâm các tam giác GAB, GAC, GBC.
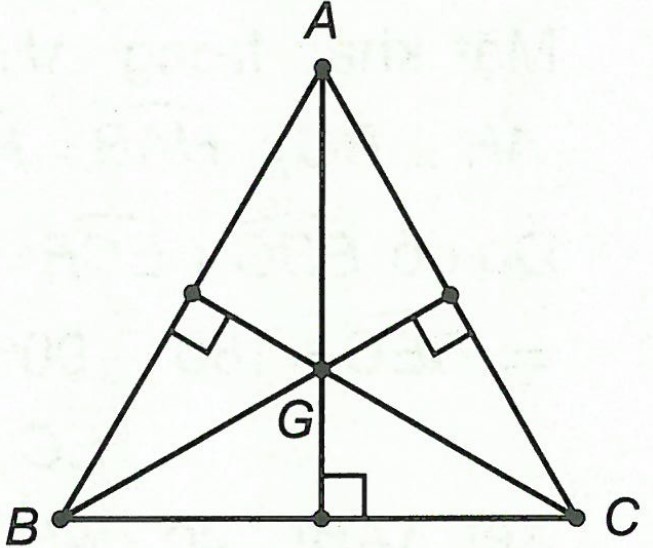
Hướng dẫn giải
Vì △ABC đều, G là trọng tâm nên G cũng là trực tâm của △ABC
⇒ AG ⊥ BC; BG ⊥ AC; CG ⊥ AB
Xét △GAB, có: BC ⊥ AG; AC ⊥ BG
Mà {C} = AC ∩ BC nên C là giao của 2 đường cao trong △ABG
⇒ C là trực tâm △GAB.
Tương tự B là trực tâm △GAC; A là trực tâm △GBC.
Bài tập tự luyện dạng 1
Câu 1: Cho △ABC vuông tại A, đường cao AH. Gọi trung điểm của BH là D, trung điểm của AH là E. Xác định trực tâm △ADE.
Hướng dẫn giải
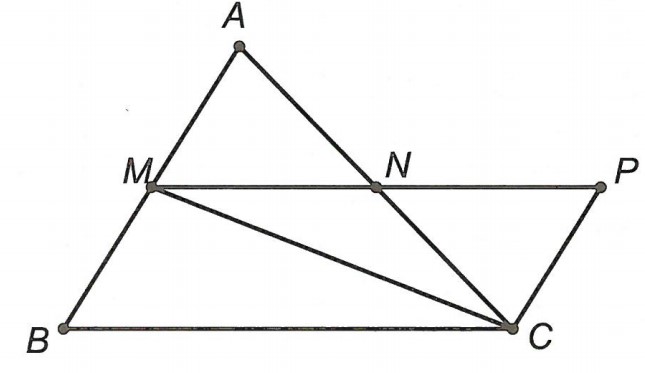
Xét bài toán phụ nếu △ABC có M, N lần lượt là trung điểm AB và AC thì MN // BC và MN = BC
Thật vậy, trên tia đối của tia NM lấy điểm P sao cho NP = MN.
Xét △NAM và △NCP, có:
AN = NC
(đối đỉnh)
MN = NP
Do đó: △NAM = △NCP (c.g.c)
⇒ MA = CP và (hai cạnh và hai góc tương ứng)
Hai góc ở vị trí so le trong nên MA // CP
⇒ (hai góc so le trong).
Xét △BMC và △PCM, có:
MB = CP (cùng bằng MA)
(chứng minh trên);
MC là cạnh chung.
Do đó: △BMC = △PCM (c.g.c)
⇒ BC = MP và (hai cạnh và hai góc tương ứng).
Hai góc ở vị trí so le trong nên MN // BC
Lại có: MP = MN + NP = 2MN (do cách vẽ)
Suy ra BC = 2MN hay MN = BC
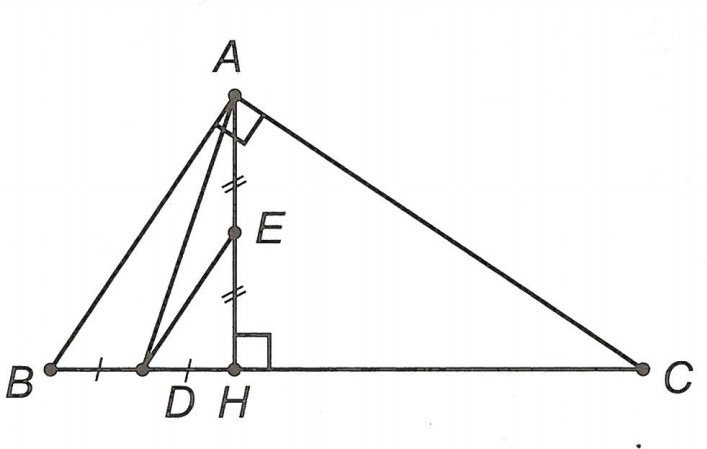
Xét △HAB, có: D là trung điểm BH, E là trung điểm AH, theo kết quả bài toán trên DE // AB
Xét △ADE, có: DC ⊥ AE
Mặt khác: AB ⊥ AC và DE // AB nên AC ⊥ DE
⇒ AC và DC là đường cao của △ADE.
Mà {C} = AC ∩ DC
⇒ C là trực tâm của △ADE.
Câu 2: Cho △ABC có M là trung điểm của BC và MA = MB = MC. Tìm trực tâm △ABC.
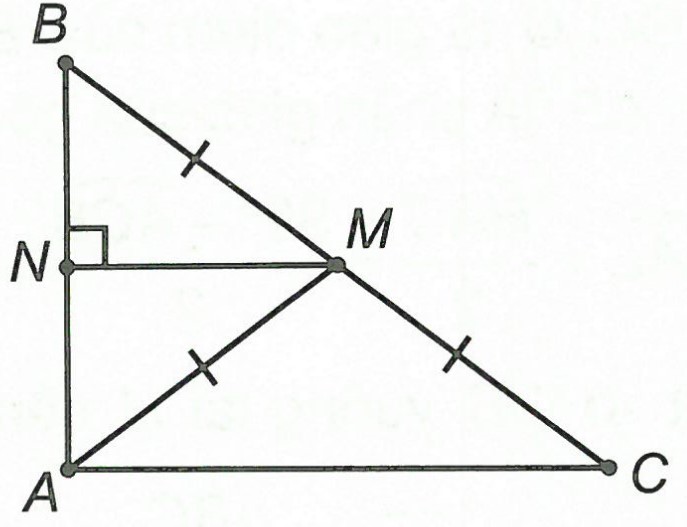
Hướng dẫn giải
Kẻ MN ⊥ AB (N ∈ AB)
Xét △MAB, có: MA = MB ⇒ △MAB cân tại M.
Mặt khác MN ⊥ AB tại N
⇒ N là trung điểm của AB (tính chất tam giác cân).
Xét △ABC, có: N là trung điểm AB, M là trung điểm của BC
Theo kết quả của câu 1 nên MN // AC
Mà MN ⊥ AB ⇒ AB ⊥ AC nên A là trực tâm △ABC.
Dạng 2. Chứng minh hai đường thẳng vuông góc
Phương pháp giải
Cách 1. Sử dụng tính chất ba đường cao trong tam giác đồng quy tại một điểm.
Ví dụ 1: Cho △ABC nhọn, có AH ⊥ BC (H ∈ BC). Trên AH lấy điểm D sao cho . Chứng minh rằng: BD ⊥ AC.
Hướng dẫn giải
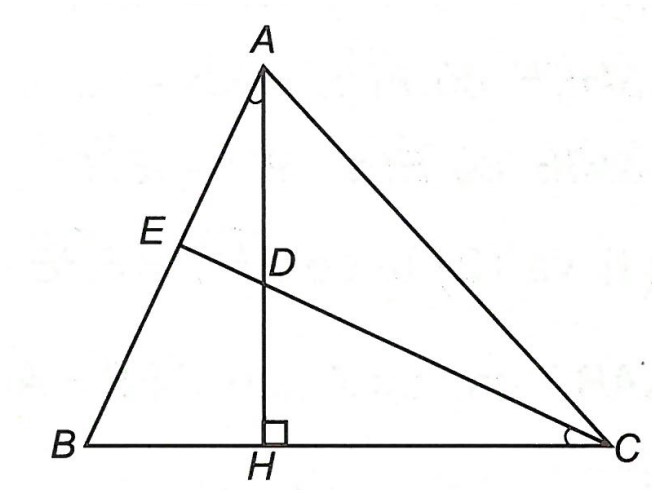
Gọi E là giao điểm của AB và CD kéo dài.
Xét △EBC, có:
Mặt khác trong △HAB có:
(do AH ⊥ BC);
(giả thiết).
Do đó:
Xét △ABC, có:
Suy ra D là trực tâm của △ABC
⇒ D thuộc đường cao hạ từ B của △ABC
⇒ BD ⊥ AC.
Cách 2. Sử dụng định lí trong tam giác cân thì đường trung tuyến, đường phân giác ứng với cạnh đáy đồng thời là đường cao.
Ví dụ 2: Cho △ABC cân tại A, M là trung điểm của BC, đường cao CN cắt AM tại H. Chứng minh rằng: BH ⊥ AC.
Hướng dẫn giải
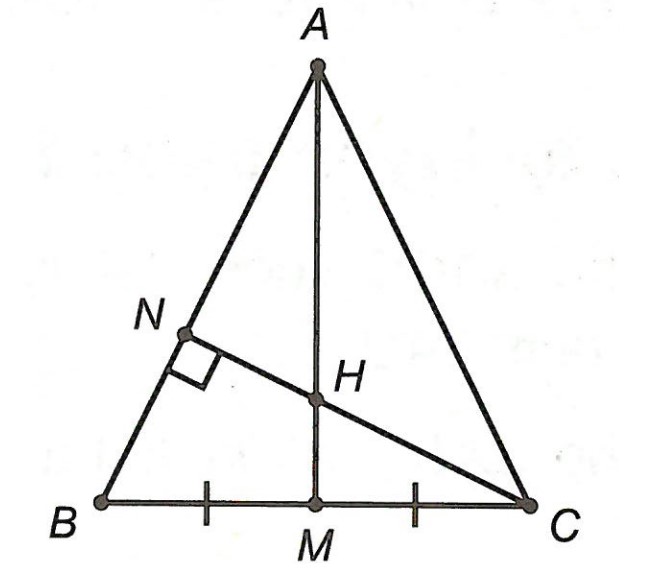
Vì △ABC cân tại A và M là trung điểm của BC nên AM vừa là trung tuyến, vừa là đường cao ứng với BC ⇒ AM ⊥ BC.
Mặt khác: CN ⊥ AB; {H} = AM ∩ CN
Suy ra H là trực tâm của △ABC
⇒ BH thuộc đường cao hạ từ B của △ABC
⇒ BH ⊥ AC.
Cách 3. Hai đường thẳng song song với nhau thì cùng vuông góc với đường thẳng thứ ba.
Ví dụ 3: Cho △ABC vuông ở A, đường cao AH. Gọi M và N lần lượt là trung điểm của AH và CH. Chứng minh: BM ⊥ AN.
Hướng dẫn giải
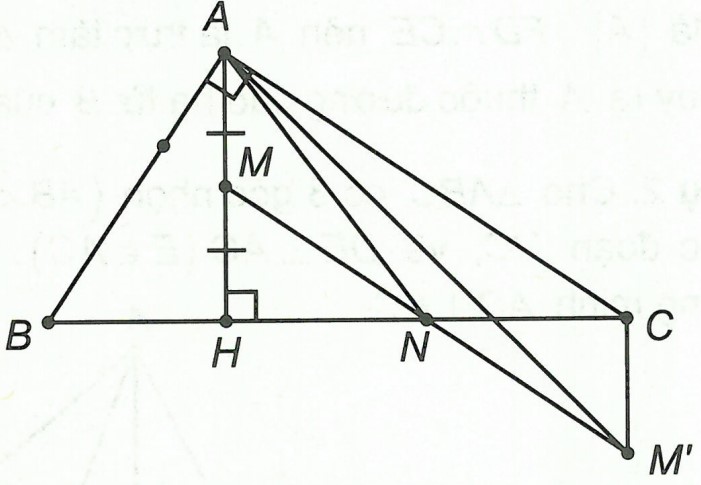
Trên tia đối của tia NM ta lấy M’ sao cho NM = NM’
Xét △NMH và △NM’C, có:
MN = NM’ (theo cách vẽ hình)
(hai góc đối đỉnh)
HN = NC (do N là trung điểm HC)
Do đó: △NMH = △NM’C (c.g.c)
⇒ CM’ = HM và (hai cạnh, hai góc tương ứng)
Mà hai góc này ở vị trí so le trong nên HM // CM’
Xét △AMM’ và △M’CA, có:
AM = CM’ (cùng bằng HM)
(so le trong do AM // CM)
AM là cạnh chung.
Do đó: △AMM’ = △M’CA (c.g.c)
⇒
Mà 2 góc này ở vị trí so le trong nên AC // MM’.
Mặt khác: AC ⊥ AB nên MN ⊥ AB.
Xét △ABN, có: AH ⊥ BN và MN ⊥ AB
⇒ M là giao điểm của hai đường cao
⇒ M là trực tâm △ABN
⇒ M thuộc đường cao hạ từ B xuống AN
⇒ BM ⊥ AN
Ví dụ mẫu
Ví dụ 1. Cho △ABC có , AD vuông góc với BC tại D, BE vuông góc với AC tại E. Gọi F là giao điểm của đường thẳng AD và BE. Chứng minh: AB ⊥ FC.
Hướng dẫn giải
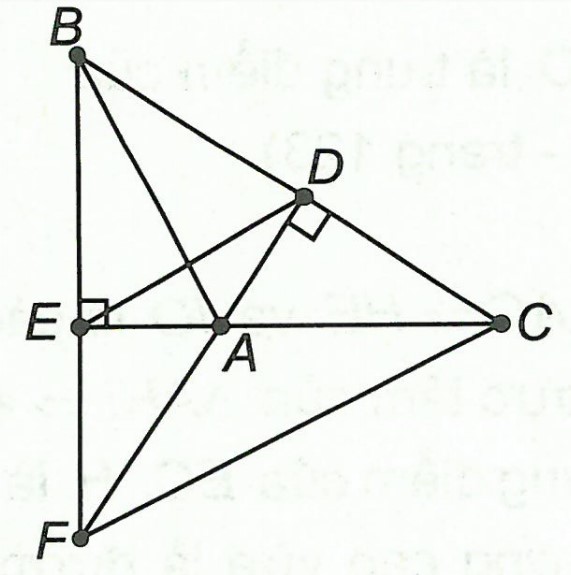
Xét △FBC, có:
AD ⊥ BC ⇒ FD ⊥ BC (1)
BE ⊥ AC ⇒ CE ⊥ BF (2)
Từ (1) và (2) suy ra: CE và FD là các đường cao của △FBC.
Mà {A} = FD ∩ CE ⇒ A là trực tâm △FBC.
Suy ra: A thuộc đường cao hạ từ B của △FBC
⇒ AB ⊥ FC.
Ví dụ 2. Cho △ABC có 3 góc nhọn (AB < AC), đường cao AH. Lấy D là điểm thuộc đoạn HC, vẽ DE ⊥ AC (E ∈ AC). Gọi K là giao điểm của AH và DE. Chứng minh: AD ⊥ KC.

Hướng dẫn giải
Xét △AKC, có:
AH ⊥ BC ⇒ CH ⊥ AK (1)
DE ⊥ AC ⇒ KE ⊥ AC (2)
Từ (1) và (2) suy ra KE và CH là hai đường cao của △AKC.
Mà {D} = KE ∩ CH nên D là trực tâm của △AKC
⇒ D thuộc đường cao hạ từ A của △AKC
⇒ AD ⊥ KC.
Ví dụ 3. Cho △ABC cân tại A, đường cao AH, vẽ HE ⊥ AC (E ∈ AC). Gọi O và I lần lượt là trung điểm của EH và EC. Chứng minh rằng: AO ⊥ BE.
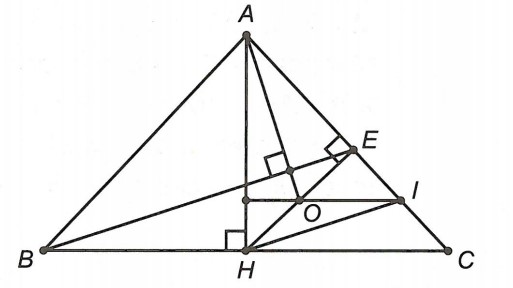
Hướng dẫn giải
Với I là trung điểm của EC, O là trung điểm của EH
⇒ IO // HC
Mà AH ⊥ BC nên OI ⊥ AH
Xét △AHI, có: IO ⊥ AH, HE ⊥ AC
⇒ HE và IO là các đường cao của △AHI
Mà {O} = HE ∩ IO nên O là trực tâm của △AHI ⇒ AO ⊥ HI
Mặt khác △CBE có: I là trung điểm của EC và H là trung điểm BC (do △ABC cân tại A nên AH vừa là đường cao vừa là đường trung tuyến)
⇒ AO ⊥ HI.
Mặt khác xét △CBE có I là trung điểm của EC, H là trung điểm của BC (do △ABC cân tại A nên AH vừa là đường cao vừa là đường trung tuyến)
⇒ HI // BE
Mà AO ⊥ HI (chứng minh trên) nên AO ⊥ BE.
Bài tập tự luyện dạng 2
Câu 1: Cho △ABC cân tại A, có , đường cao BH cắt đường trung tuyến AM (M ∈ BC) ở K. Chứng minh: CK ⊥ AB và tính
.
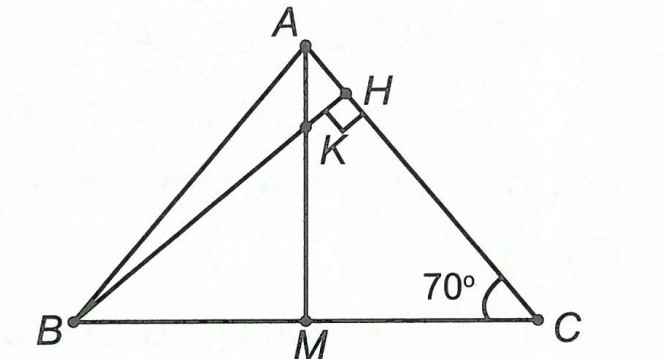
Hướng dẫn giải
Do △ABC cân tại A và AM là trung tuyến
⇒ AM cũng là đường cao ứng với BC
⇒ AM ⊥ BC tại M.
Mặt khác: BH ⊥ AC và {K} = BH ∩ AM
⇒ K là trực tâm △ABC
⇒ K thuộc đường cao hạ từ C của △ABC
⇒ CK ⊥ AB
Ta có:
Câu 2: Cho △ABC vuông cân tại A. Trên cạnh AB lấy điểm D bất kì (D ≠ A, B), trên tia đối của tia AC lấy điểm E sao cho AD = AE. Chứng minh: ED ⊥ BC.
Hướng dẫn giải
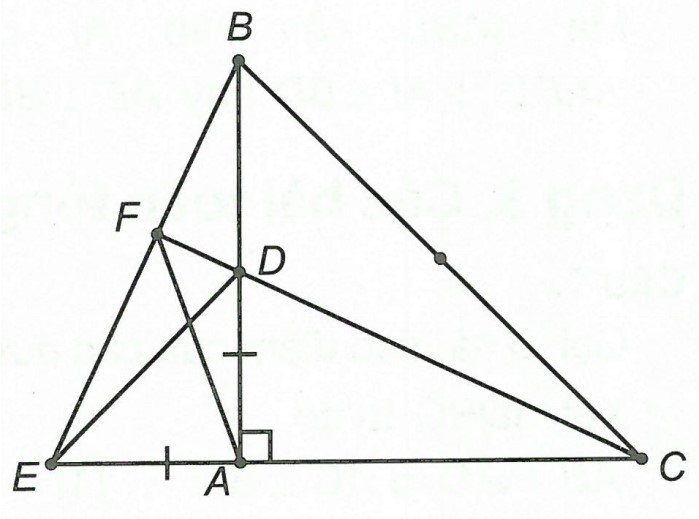
Xét △ABE và △ACD, có:
AE = AD (giả thiết),
(giả thiết),
AB = AC (do △ABC vuông cân tại A).
Do đó: △ABE = △ACD (c,g,c)
⇒ (hai góc tương ứng) (1)
Gọi F là giao điểm của CD và BE.
Ta có: (hai góc đối đỉnh) (2)
(3)
Từ (1), (2) và (3) ta có:
Trong △FDB có:
⇒ CD ⊥ BE
Xét △BEC, có: AB ⊥ EC; CD ⊥ BE
Mà {D} = CD ∩ AB nên D là trực tâm △BEC
⇒ ED là đường cao của △BEC
⇒ ED ⊥ BC.
Câu 3: Cho △ABC có ba góc nhọn (AB < AC), đường cao AH. Lấy D là một điểm thuộc đoạn thẳng HC, vẽ DE ⊥ AC (E ∈ AC). Gọi F là giao điểm của AD và DE. Chứng minh rằng: AD ⊥ FC.
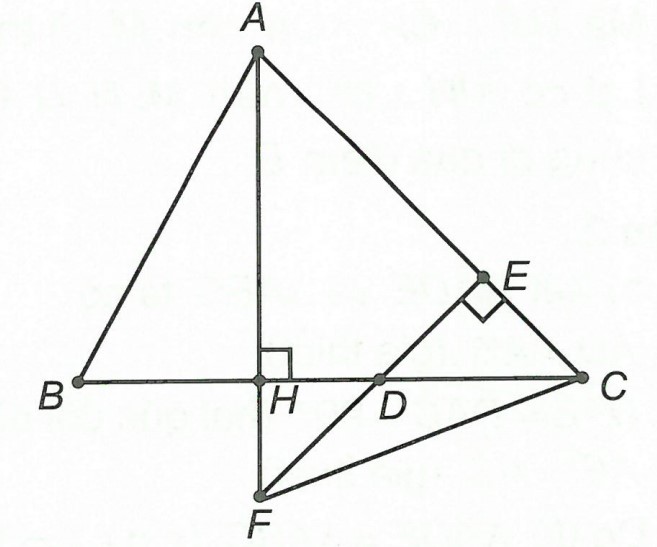
Hướng dẫn giải
Vì DE ⊥ AC ⇒ FE ⊥ AC
AH ⊥ BC ⇒ CH ⊥ AF
Xét △AFC có FE ⊥ AC và CH ⊥ AF.
Mà {D} = FE ∩ CH nên D là trực tâm của △AFC
⇒ AD ⊥ FC.
Câu 4: Cho △ABC vuông ở A, đường cao AH, phân giác AD. Gọi I, J lần lượt là giao điểm các đường phân giác trong của △ABH, △ACH. E là giao điểm của đường thẳng BI với AJ. Chứng minh rằng:
a) △ABE là tam giác vuông.
b) IJ ⊥ AD.
Hướng dẫn giải
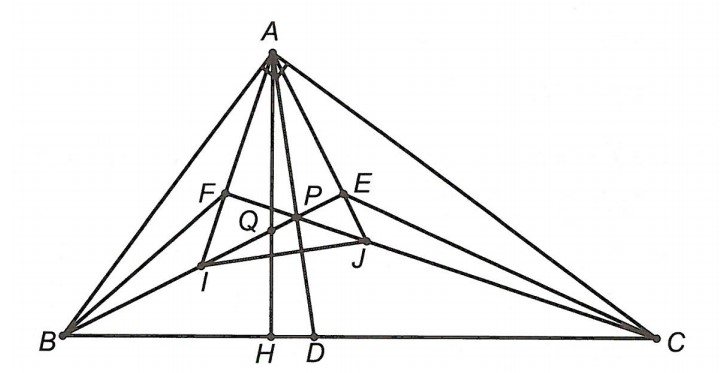
a) Gọi Q là giao điểm của BE và AH.
Vì AE là phân giác của góc nên
Xét △HQB vuông tại H nên
Mặt khác: và
(hai góc đối đỉnh)
⇒
⇒ BE ⊥ AE ⇒ △ABE vuông tại E.
b) Hoàn toàn tương tự nếu gọi F là giao của CJ và AI thì CJ ⊥ AI.
Xét △AIJ, có:
⇒ P là giao điểm ba đường cao của △ABC.
Do đó: P là trực tâm của △AIJ
⇒ P thuộc đường cao của △AIJ
⇒ AP ⊥ IJ hay AD ⊥ IJ
Câu 5: Cho △ABC, có , đường cao AH. Trên cạnh AC lấy điểm D sao cho
. Vẽ đường phân giác của góc
cắt BC ở E. Chứng minh rằng: AE ⊥ BD.
Hướng dẫn giải

Vì là góc ngoài △DBC nên
Trong △ABC, có:
Xét △ABD, có:
⇒ △ABD cân tại A.
Gọi I là giao của AE và BD thì AI là phân giác của .
Mà △ABD cân nên AI cũng là đường cao của △ABD
⇒ AI ⊥ BD hay AE ⊥ BD.
Dạng 3. Các bài toán tổng hợp
Phương pháp giải
Sử dụng tính chất ba đường cao trong tam giác đồng quy tại một điểm.
Ví dụ mẫu
Ví dụ. Cho △ABC nhọn, đường cao AH. Vẽ ra phía ngoài của tam giác hai tam giác vuông cân ABD và ACE . Chứng minh ba đường thẳng AH, BE và CD cùng đi qua một điểm.
Hướng dẫn giải
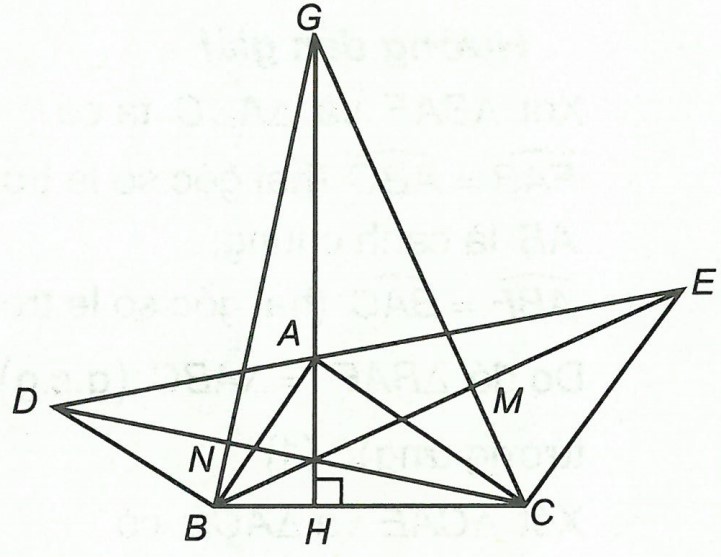
Trên tia đối của tia AH lấy G sao cho GA = BC.
Ta có:
Xét △AGC và △CBE, có:
AG = CB (theo cách vẽ hình)
(chứng minh trên)
AC = CE (do △ACE vuông cân tại C)
Do đó: △AGC = △CBE (c.g.c)
⇒ (hai góc tương ứng).
Gọi M là giao điểm của GC và BE.
Xét △MEC có:
⇒ BM ⊥ GC
Chứng minh tương tự nếu gọi N là giao điểm của BG và CD, ta có CN ⊥ GB.
Xét △GBC, có:
GH ⊥ BC, CN ⊥ BG, BM ⊥ GC
⇒ CN, BM, GH là ba đường cao của △GBC
⇒ CN, BM và GH cùng đi qua trực tâm △GBC hay AH, BE và CD cùng đi qua một điểm chính là trực tâm △GBC.
Bài toán 2. Một số dạng toán khác
Phương pháp giải
Vận dụng linh hoạt tính chất ba đường cao trong tam giác kết hợp với kiến thức hình học đã biết để giải bài tập.
Ví dụ: Cho △ABC, qua các đỉnh A, B, C kẻ đường thẳng song song với cạnh đối diện, chúng cắt nhau tạo thành △DEF. Chứng minh rằng đường cao của △ABC là đường trung trực của △DEF.
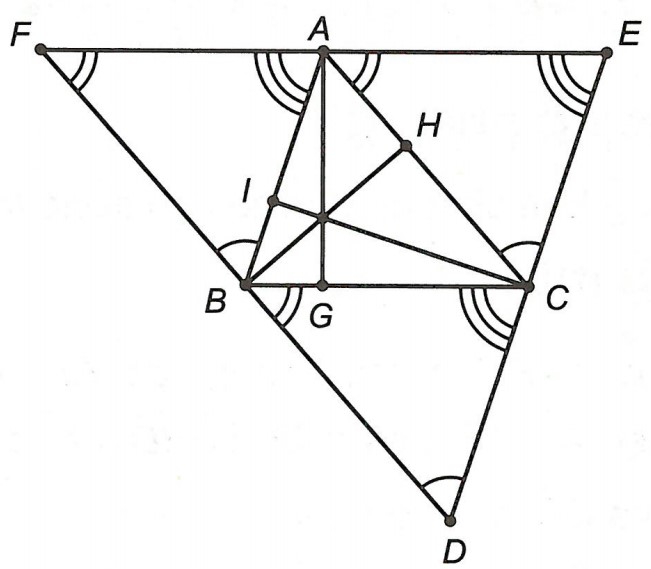
Hướng dẫn giải
Xét △BAF và △ABC, có:
(hai góc so le trong do BC // EF)
AB là cạnh chung
(hai góc so le trong do AC // DF)
Do đó: △BAF = △ABC (g.c.g)
⇒ FA = BC (hai cạnh tương ứng) (1)
Xét △CAE và △ACB, có:
(hai góc so le trong do BC // EF)
AC là cạnh chung
(hai góc so le trong do AB // ED)
Do đó: △CAE = △ACB (g.c.g)
⇒ AE = BC (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: AF = AE.
Tương tự ta chứng minh được BF = BD và CD = CE.
Xét AG là đường cao của △ABC
⇒ AG ⊥ BC (G ∈BC)
Mà BC // FE nên AG ⊥ FE.
A là trung điểm FE ⇒ AG là trung trực của FE.
Chứng minh tương tự:
BH là đường cao của △ABC ⇒ BH là trung trực của DF
CI là đường cao △ABC ⇒ CI là trung trực của DE.
Vậy các đường cao của △ABC là các đường trung trực của △DEF.
Ví dụ mẫu
Ví dụ 1. Cho △ABC nhọn, hai đường cao BM và CN. Trên tia đối của các tia BM lấy điểm P sao cho BP = AC, trên tia đối của tia CN lấy Q sao cho CQ = AB. Chứng minh rằng △APQ vuông cân tại A.
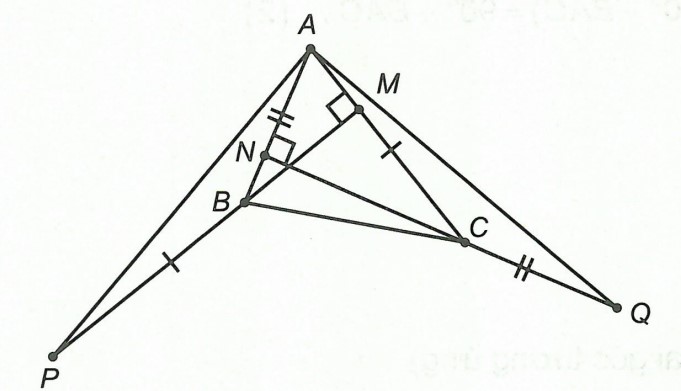
Hướng dẫn giải
Ta có: và
Mà ;
Nên
Xét △BAP và △CQA, có:
BA = CQ (giả thiết)
(chứng minh trên)
BP = AC (giả thiết)
Do đó: △BAP = △CQA (c.g.c)
⇒ AP = AQ và (hai cạnh và góc tương ứng)
Xét △APQ, có:
Và AP = AQ ⇒ △APQ vuông cân tại A.
Ví dụ 2. Cho △ABC, I là trung điểm của BC. Vẽ ra phía ngoài của tam giác ABC, hai tam giác đều ABE và ACF. Gọi H là trực tâm của △ABE. Trên tia đối của tia IH, lấy điểm K sao cho HI IK. Chứng minh:
a) △AHF = △CKF.
b) △KHF là tam giác đều.
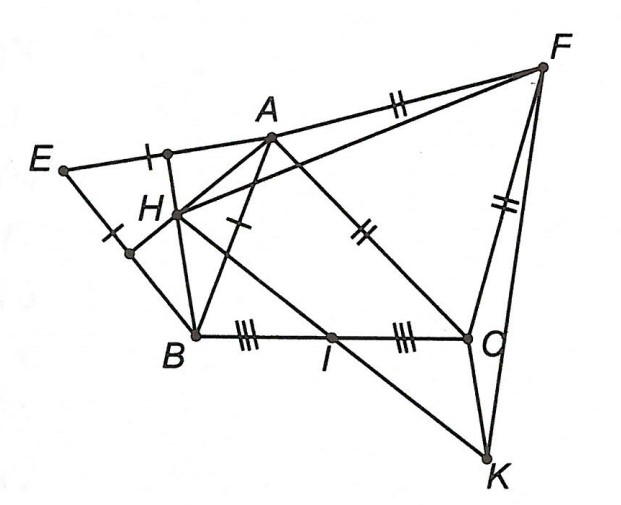
Hướng dẫn giải
a) Xét △IBH và △ICK, có:
IB = IC (giả thiết)
(hai góc đối đỉnh)
IH = IK (giả thiết)
Do đó: △IBH = △ICK (c.g.c)
⇒ BH = CK (hai cạnh tương ứng)
và (do AH là phân giác
).
Mà H là trực tâm của △ABE đều nên BH = AH ⇒ CK = AH.
Ta có:
Từ (1) và (2) suy ra:
Xét △AHF và △CKF, có:
AF = CF (vì △ACF đều)
(chứng minh trên)
AH = CK (chứng minh trên)
Do đó: △AHF = △CKF (c.g.c)
⇒ và HF = KF (hai cạnh và hai góc tương ứng)
b) Xét △KHF, có: HF = KF
⇒ △KHF cân tại F.
Mặt khác:
⇒ △KHF đều.
Bài tập tự luyện dạng 3
Câu 1: Cho △ABC vuông tại A. Trên cạnh AC lấy điểm M bất kì (M ∈ A, C). Qua M kẻ đường thẳng vuông góc với BC tại N; từ C kẻ đường thẳng vuông góc với BM tại P. Chứng minh ba đường thẳng AB, CP, MN cùng đi qua một điểm.
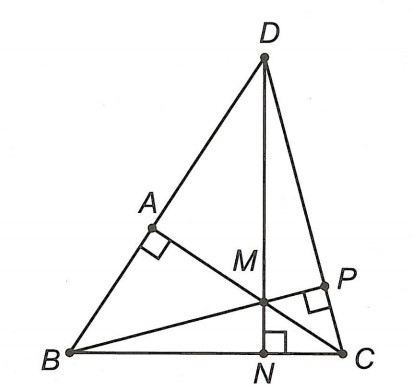
Hướng dẫn giải
Gọi D là giao điểm của các đường thẳng AB và CP.
Xét △DBC, có:
AB ⊥ AC ⇒ AC ⊥ BD (1)
CP ⊥ BP ⇒ BP ⊥ DC (2)
Từ (1) và (2) suy ra CA và BP là các đường cao của △DBC.
Mà {M} = BP ∩ CA nên M là trực tâm △DBC
⇒ DM ⊥ BC.
Lại có: MN ⊥ BC nên M, N, D thẳng hàng
⇒ AB, MN và CP cùng đi qua điểm D.
Câu 2: Cho △ABC vuông tại A (AB < AC). Trên tia đối của tia AC lấy điểm D sao cho AD = AB. Trên tia đối của tia AB lấy điểm E sao cho AE = AC.
a) Chứng minh: BC = DE
b) Chứng minh △ABD vuông cân và BD // CE
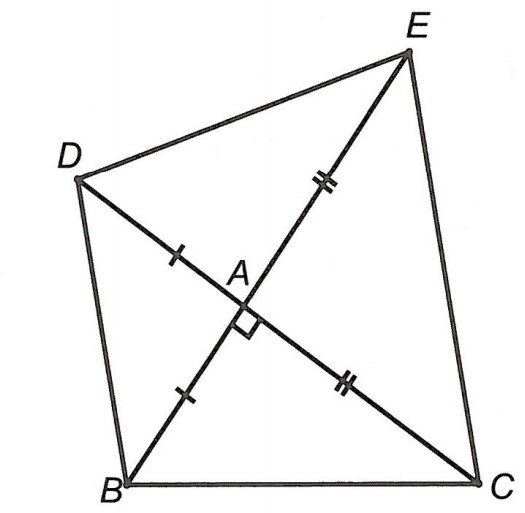
Hướng dẫn giải
a) Xét △ADE và △ABC, có:
AD = AB (giả thiết);
(hai góc đối đỉnh);
AE = AC (giả thiết)
Do đó: △ADE = △ABC (c.g.c)
⇒ DE = BC (hai cạnh tương ứng).
b) Xét △ABD, có: DA ⊥ AB (do △ABC vuông tại A)
⇒
Mà AD = AB nên △ABD vuông cân tại A.
Chứng minh tương tự ta có △ACE vuông cân tại A
⇒
Mặt khác hai góc và
ở vị trí so le trong.
Suy ra: BD // CE
Câu 3: Cho △ABC có ba góc nhọn biết , trực tâm H. Gọi K là điểm đối xứng với H qua BC.
a) Chứng minh:
b) Tính
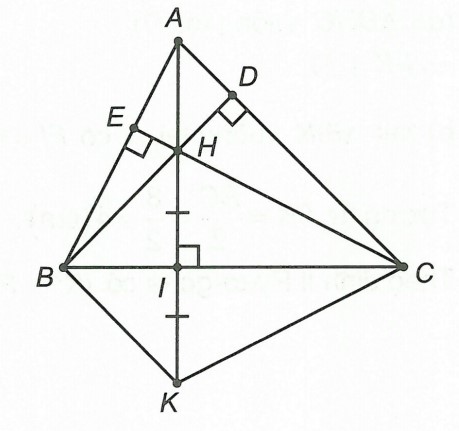
Hướng dẫn giải
a) Vì K là đối xứng của H qua BC nên
Lại có: (hai góc đối đỉnh)
và
Từ (1) và (2) ta có:
b) Vì K là đối xứng của H qua BC nên
Ta có: và
Hơn nữa (hai góc đối đỉnh) nên
Trong △IAC, có:
Vậy
Câu 4: Cho △ABC có BD và CE lần lượt là các đường cao hạ từ B, C và BD CE. H là giao điểm của BD và CE. Chứng minh rằng △ABC cân và AH là phân giác góc .
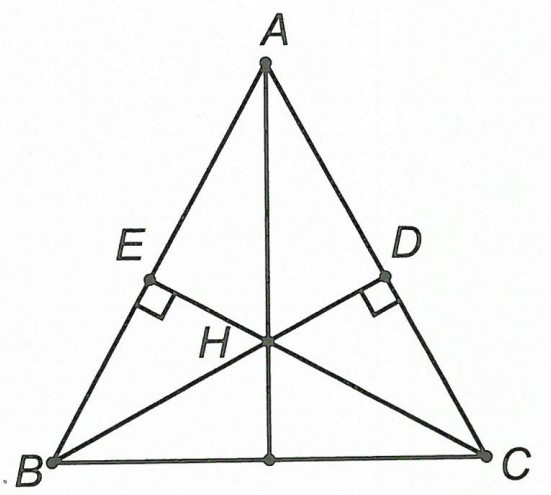
Hướng dẫn giải
Xét △DBA và △ECA, có:
CE = BD (giả thiết);
là góc chung.
Do đó: △DBA = △ECA (g.c.g)
⇒ AB = AC (hai cạnh tương ứng)
⇒ △ABC cân tại A
Xét △ABC, có: BD ⊥ AC; CE ⊥ AB
Mà {H} = CE ∩ BD nên H là trực tâm của △ABC.
Suy ra AH là đường cao của △ABC.
Hơn nữa △ABC cân tại A
⇒ AH là phân giác của góc .
Câu 5: Cho △ABC có các đường cao BE, CF cắt nhau tại H (E ∈ AC, F ∈ AB). Gọi I, K lần lượt là trung điểm các cạnh AH, BC.
a) Chứng minh: FK ⊥ FI.
b) Cho AH = 6 cm; BC = 8 cm. Tính IK.
Hướng dẫn giải
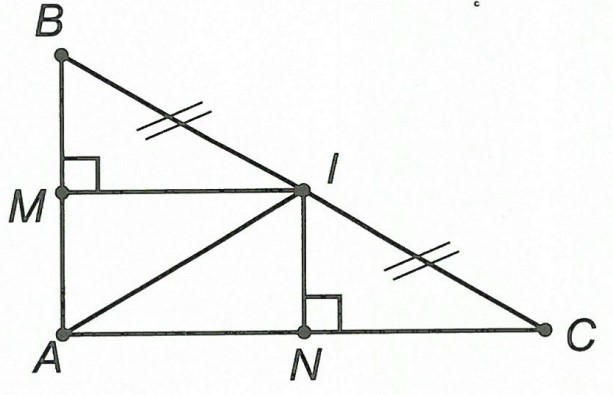
a) Xét bài toán phụ: Nếu △ABC vuông tại A, I là trung điểm của BC thì IA = IB = IC. Thật vậy, gọi M, N lần lượt là chân đường vuông góc hạ từ I xuống AB và AC.
Ta có: IM ⊥ AB, AC ⊥ AB ⇒ IM // AC
⇒ (hai góc đồng vị).
Xét △MBI và △NIC, có:
BI = IC
Do đó: △MBI = △NIC (cạnh huyền – góc nhọn)
⇒ BM = IN và MI = NC (hai cạnh tương ứng)
Mặt khác: IM ⊥ AB; NA ⊥ AB
⇒ IM // AN
⇒ (so le trong)
Xét △AMI vuông tại M và △ANI vuông tại N, có:
AI chung và
Do đó: △AMI = △ANI (cạnh huyền – góc nhọn)
⇒ MI = AN
⇒ NC = AN (cùng bằng MI)
⇒ N là trung điểm AC.
Trong △IAC có IN vừa là đường cao, vừa là đường trung tuyến ứng với AC
⇒ △IAC cân tại I
⇒ IA = IC ⇒ IA = IB = IC
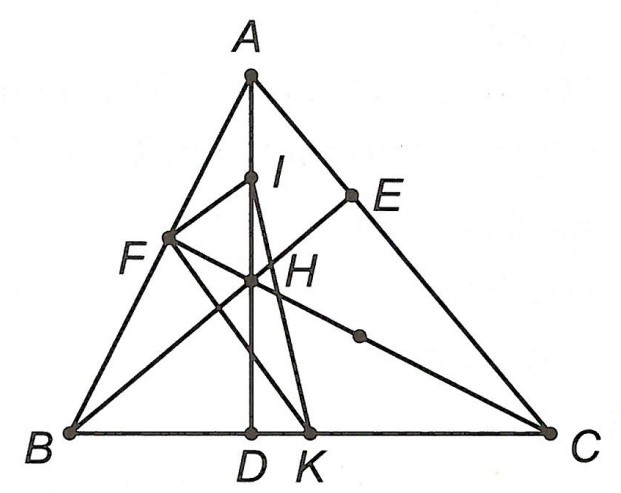
Xét △FAH, có: và I là trung điểm của AH
⇒ IA = IF = IH.
⇒ △IFH cân tại I
⇒
Xét △FBC có: và K là trung điểm của BC
⇒ KC = KB = KF.
⇒ △KFC cân tại K
⇒
Ta có:
Lại có: (hai góc đối đỉnh) nên
(do △DHC vuông tại D)
⇒ FK ⊥ FI.
b) Xét △FIK vuông tại F có
Tương tự:
Theo định lý Pi-ta-go ta có:
IK2 = FI2 + FK2 = 32 + 42 = 25
⇒ IK = 5 cm