Số hữu tỉ

Lý thuyết Tập hợp ℚ các số hữu tỉ

Số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b}\left( {a,b \in \mathbb{Z},b \ne 0} \right)$

Ta có thể biểu diễn mọi số hữu tỉ trên trục số. Trên chục số, điểm biểu diễn số hữu tỉ được gọi là điểm x

Với hai số hữu tỉ bất kỳ x, y ta luôn có hoặc x = y hoặc x < y hoặc x > y. Ta có thể so sánh hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi so sánh hai phân số đó.

+) Nếu x < y thì trên trục số, điểm x ở bên trái điểm y;

+) Số hữu tỉ lớn hơn 0 được gọi là số hữu tỉ dương;

+) Số hữu tỉ nhỏ hơn 0 được gọi là số hữu tỉ âm;

+) Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.

Phân dạng bài tập

Dạng 1. Sử dụng các kí hiệu ∈, ∉, ⊂, ℕ, ℤ, ℚ

Phương pháp giải

Cần nắm vững ý nghĩa của từng ký hiệu:

+) Kí hiệu ∈ đọc là “phần tử của” hoặc “thuộc”.

+) Kí hiệu ∉ đọc là “không phải là phần tử của” hoặc “không thuộc”.

+) Kí hiệu ⊂ đọc là “là tập hợp con của”.

+) Kí hiệu ℕ chỉ tập hợp các số tự nhiên.

+) Kí hiệu ℤ chỉ tập hợp các số nguyên.

+) Kí hiệu ℚ chỉ tập hợp các số hữu tỉ.

Ví dụ 1. Điền ký hiệu (∈, ∉, ⊂) thích hợp vào ô trống:

–3 ℕ

–3 ℤ

–3 ℚ

$- \frac{2}{3}$ ℤ

$- \frac{2}{3}$ ℚ

ℕ ℤ ℚ

Hướng dẫn Hướng dẫn giải

–3 ∉ ℕ

–3 ∈ ℤ

–3 ∈ ℚ

$- \frac{2}{3}$ ∉ ℤ

$- \frac{2}{3}$ ∈ ℚ

ℕ ⊂ ℤ ⊂ ℚ

Dạng 2. Biểu diễn số hữu tỉ

Phương pháp giải

+) Số hữu tỉ thường được biểu diễn dưới dạng phân số tối giản.

+) Khi biểu diến số hữu tỉ trên trục số, ta thường viết số đó dưới dạng phân số tối giản có mẫu dương. Khi đó mẫu cửa phân số cho biết đoạn thẳng đơn vị cần được chia thành bao nhiêu phần bằng nhau.

Ví dụ 2.

a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ $\frac{3}{{ - 4}}$

$\frac{{ - 12}}{{15}};\frac{{ - 15}}{{20}};\frac{{24}}{{ - 32}};\frac{{ - 20}}{{28}};\frac{{ - 27}}{{36}}?$

b) Biểu diễn số hữu tỉ $\frac{3}{{ - 4}}$ trên trục số.

Hướng dẫn giải

a) Ta có: $\frac{3}{{ - 4}} = \frac{{ - 3}}{4}$ . Rút gọn các phân số đã cho ta được:

$\frac{{ - 12}}{{15}} = \frac{{ - 4}}{5};\frac{{ - 15}}{{20}} = \frac{{ - 3}}{4};\frac{{ - 15}}{{20}} = \frac{{ - 3}}{4};\frac{{ - 20}}{{28}} = \frac{{ - 5}}{7};\frac{{ - 15}}{{20}} = \frac{{ - 3}}{4}$

Vậy các phân số biểu diễn số hữu tỉ $\frac{3}{{ - 4}}$ là: $\frac{{ - 15}}{{20}};\frac{{ - 15}}{{20}};\frac{{ - 15}}{{20}}$

b) Biểu diễn số hữu tỉ $\frac{3}{{ - 4}}$ trên trục số.

Ta viết: $\frac{3}{{ - 4}} = \frac{{ - 3}}{4}$ và biểu diễn trên trục số như sau:

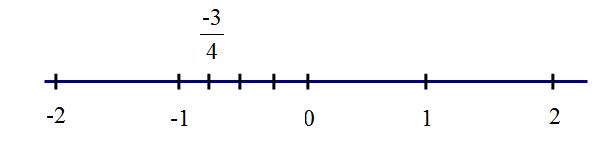
Dạng 3. So sánh các số hữu tỉ

Phương pháp giải

+) Viết các số hữu tỉ dưới dạng phân số có cùng một mẫu dương;

+) So sánh các tử, phân số nào tử nhỏ hơn thì phân số đó nhỏ hơn.

+) Có thể sử dụng tính chất sau để so sánh: Nếu a, b, c ∈ ℤ và a < b thì a + c < b + c

Ví dụ 3. So sánh các số hữu tỉ:

a) $x = \frac{2}{{ - 7}}$ và $y = \frac{{ - 3}}{{11}}$

b) $x = \frac{{ - 213}}{{300}}$ và $y = \frac{{18}}{{ - 25}}$

Hướng dẫn giải

a) $x = \frac{2}{{ - 7}} = \frac{{ - 2}}{7} = \frac{{ - 22}}{{77}};y = \frac{{ - 3}}{{11}} = \frac{{ - 21}}{{77}}$

–22 < –21 và 77 > 0 nên $\frac{{ - 22}}{{77}} < \frac{{ - 21}}{{77}}$ hay $\frac{2}{{ - 7}} < \frac{{ - 3}}{{11}}{\text{ }}\left( {x < y} \right)$

b) $x = \frac{{ - 213}}{{300}};y\frac{{ - 216}}{{300}} = \frac{{18}}{{ - 25}} = \frac{{ - 18}}{{25}} = \frac{{ - 216}}{{300}}$

Ta có: $\frac{{ - 213}}{{300}} > \frac{{ - 216}}{{300}}$ hay $\frac{{ - 213}}{{300}} > \frac{{18}}{{ - 25}}{\text{ }}\left( {x > y} \right)$

Ví dụ 4. So sánh số hữu tỉ $\frac{a}{b}\left( {a,b \in \mathbb{Z},b \ne 0} \right)$ với số 0 khi a, b cùng dấu và khi a, b khác dấu.

Hướng dẫn giải

Nhờ tính chất cơ bản của phân số, ta luôn có thể viết một phân số có mẫu âm thành một phân số bằng nó và có mẫu dương. Vì vậy, ta chỉ cần nhận xét số hữu tỉ $\frac{a}{b}\left( {a,b \in \mathbb{Z},b \ne 0} \right)$

Nếu cùng dấu thì ta có a > 0. Do đó: $\frac{a}{b} > \frac{0}{b}$ hay $\frac{a}{b} > 0$

Nếu a, b khác dấu thì ta có a < 0. Do đó: $\frac{a}{b} < \frac{0}{b}$ hay $\frac{a}{b} < 0$

Nhận xét: Số hữu tỉ $\frac{a}{b}\left( {a,b \in \mathbb{Z},b \ne 0} \right)$ là số dương nếu a, b cùng dấu, là số âm nếu a, b khác dấu, bằng 0 nếu a ≠ 0.

Ví dụ 5. Giả sử:

$x = \frac{a}{m};y = \frac{b}{m}\left( {a,b,m \in \mathbb{Z},m > 0} \right)$ và x < y.

Hãy chứng tỏ rằng nếu chọn $z = \frac{{a + b}}{{2m}}$ thì ta có x < z < y.

Hướng dẫn: Sử dụng tính chất: Nếu a, b, c ∈ ℤ thì a < b thì a + c < b + c.

Hướng dẫn giải

Theo đề bài $x = \frac{a}{m};y = \frac{b}{m}\left( {a,b,m \in \mathbb{Z},m > 0} \right)$ . Vì x < y nên a < b.

Ta có: $x = \frac{a}{m};y = \frac{b}{m};z = \frac{{a + b}}{{2m}}$

a < b nên a + a < a + b hay 2a < a + b (1)

a < b nên a + b < b + b hay a + b < 2b (2)

Từ (1) và (2) ta có: 2a < a + b < 2b. Suy ra:

$\frac{{2a}}{{2m}} < \frac{{a + b}}{{2m}} < \frac{{2b}}{{2m}}{\text{ }}\left( {x < y < z} \right)$

Nhận xét: Bài toán này cho thấy hai số hữu tỉ khác nhau bất kỳ bao giờ cũng có ít nhất một số hữu tỉ nữa. Do đó có vô số số hữu tỉ.

Cộng trừ số hữu tỉ

Tóm tắt lý thuyết

Cộng, trừ hai số hữu tỉ.

+) Ta có thể cộng, trừ hai số hữu tỉ x, y bằng cách viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi áp dụng quy tắc cộng, trừ phân số.

+) Phép cộng số hữu tỉ có các tính chất của phép cộng phân số: Giao hoán, kết hợp, cộng với số 0. Mỗi số hữu tỉ đều có một số đối.

Quy tắc “chuyển vế”.

Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đối dấu số hạng đó.

Với mọi x, y, z ∈ ℚ: x + y = z ⇒ x = z – y

Chú ý.

Trong ℚ, ta cũng có những tổng đại số, trong đó có thể đổi chỗ các số hạng, đặt dấu ngoặc để nhóm các số hạng một cách tùy ý như các tổng đại số trong ℤ.

Các dạng toán

Dạng 1. Cộng trừ hai số hữu tỉ

Phương pháp giải

+) Viết hai số hữu tỉ dưới dạng hai phân số có cùng một mẫu dương (bằng cách quy đồng mẫu của chúng)

+) Cộng, trừ hai tử số, mẫu chung giữ nguyên

+) Rút gọn kết quả (nếu có thể)

Ví dụ. Tính:

a) $\frac{{ - 1}}{{21}} + \frac{{ - 1}}{{28}}$

b) $\frac{{ - 8}}{{18}} - \frac{{15}}{{27}}$

c) $\frac{{ - 5}}{{12}} + 0,75$

d) $3,5 - \left( { - \frac{2}{7}} \right)$

Hướng dẫn

a) $\frac{{ - 1}}{{21}} + \frac{{ - 1}}{{28}} = \frac{{ - 4}}{{84}} + \frac{{ - 3}}{{84}} = \frac{{ - 4 - 3}}{{84}} = \frac{{ - 7}}{{84}} = \frac{{ - 1}}{{12}}$

b) Nên rút gọn các phân số trước khi trừ:

$\frac{{ - 8}}{{18}} - \frac{{15}}{{27}} = \frac{{ - 4}}{9} - \frac{5}{9} = \frac{{ - 4 - 5}}{9} = \frac{{ - 9}}{9} = - 1$

c) Đáp số: $\frac{1}{3}$

d) Đáp số: $\frac{{53}}{{14}} = 3\frac{{11}}{{14}}$

Dạng 2. Viết một số hữu tỉ dưới dạng tổng hoặc hiệu của hai số hữu tỉ.

Phương pháp giải

Một trong các Phương pháp giải có thể là:

+) Viết số hữu tỉ dưới dạng phân số có mẫu dương.

+) Viết tử của phân số thành tổng hoặc hiệu của hai số nguyên.

+) “Tách” ra hai phân số có tử là các số nguyên vừa tìm được.

+) Rút gọn phân số (nếu có thể).

Ví dụ. Ta có thể viết số hữu tỉ $\frac{{ - 5}}{{16}}$ dưới các dạng sau đây:

a) $\frac{{ - 5}}{{16}}$ là tổng của hai số hữu tỉ âm. Ví dụ: $\frac{{ - 5}}{{16}} = \frac{{ - 1}}{8} + \frac{{ - 3}}{{16}}$

b) $\frac{{ - 5}}{{16}}$ là hiệu của hai số hữu tỉ dương. Ví dụ: $\frac{{ - 5}}{{16}} = 1 - \frac{{21}}{{16}}$

Với mỗi câu, em hãy lấy thêm ví dụ.

Hướng dẫn giải

a) Ta có thể viết:

$\begin{gathered} \frac{{ - 5}}{{16}} = \frac{{\left( { - 1} \right) + \left( { - 4} \right)}}{{16}} = \frac{{ - 1}}{{16}} + \frac{{ - 4}}{{16}} = \frac{{ - 1}}{{16}} + \frac{1}{4} \hfill \\ \frac{{ - 5}}{{16}} = \frac{{ - 10}}{{32}} = \frac{{\left( { - 1} \right) + \left( { - 9} \right)}}{{32}} = \frac{{ - 1}}{{32}} + \frac{{ - 9}}{{32}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \frac{{ - 5}}{{16}} = \frac{{ - 10}}{{32}} = \frac{{\left( { - 3} \right) + \left( { - 7} \right)}}{{32}} = \frac{{ - 3}}{{32}} + \frac{{ - 7}}{{32}}; \cdots \hfill \\ \end{gathered}$

b) $\frac{{ - 5}}{{16}} = \frac{{6 - 11}}{{16}} = \frac{6}{{16}} - \frac{{11}}{{16}} = \frac{3}{8} - \frac{{11}}{{16}}$

$\frac{{ - 5}}{{16}} = \frac{{7 - 12}}{{16}} = \frac{7}{{16}} - \frac{{12}}{{16}} = \frac{7}{{16}} - \frac{3}{4}$

Dạng 3. Tính tổng hoặc hiệu của nhiều số hữu tỉ

Phương pháp giải

+) Áp dụng quy tắc “dấu ngoặc” đối với các số hữu tỉ:

Với mọi x, y ∈ ℚ: –(x + y) = –x – y

+) Nếu có các dấu ngoặc tròn, ngoặc vuông, ngoặc nhọn thì làm theo thứ tự trước hết tính trong ngoặc tròn rồi đến ngoặc vuông, cuối cùng là ngoặc nhọn.

+) Có thể bỏ dấu ngoặc rồi nhóm các số hạng một cách thích hợp.

Ví dụ. Tính:

a) $\frac{3}{7} + \left( { - \frac{5}{2}} \right) + \left( { - \frac{3}{5}} \right)$

b) $\left( { - \frac{4}{3}} \right) + \left( { - \frac{2}{5}} \right) + \left( { - \frac{3}{2}} \right)$

c) $\frac{4}{5} - \left( { - \frac{2}{7}} \right) - \frac{7}{{10}}$

d) $\frac{2}{3} - \left[ {\left( { - \frac{7}{4}} \right) - \left( {\frac{1}{2} + \frac{3}{8}} \right)} \right]$

Hướng dẫn giải

a) $\frac{3}{7} + \left( { - \frac{5}{2}} \right) + \left( { - \frac{3}{5}} \right)$

$\begin{gathered} = \frac{3}{7} + \frac{{ - 5}}{2} + \frac{{ - 3}}{5} \hfill \\ = \frac{{30}}{{70}} + \frac{{ - 175}}{{70}} + \frac{{ - 42}}{{70}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ = \frac{{ - 187}}{{70}} = - 2\frac{{47}}{{70}} \hfill \\ \end{gathered}$

b) Đáp số: $\frac{{ - 97}}{{30}} = - 3\frac{7}{{30}}$

c) Đáp số: $\frac{{27}}{{70}}$

d) $\frac{2}{3} - \left[ {\left( { - \frac{7}{4}} \right) - \left( {\frac{1}{2} + \frac{3}{8}} \right)} \right]$

$\begin{gathered} = \frac{2}{3} - \left[ {\frac{{ - 7}}{4} - \left( {\frac{4}{8} + \frac{3}{8}} \right)} \right] \hfill \\ = \frac{2}{3} - \left( {\frac{{ - 7}}{4} - \frac{7}{8}} \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ = \frac{2}{3} - \left( {\frac{{ - 14}}{8} - \frac{7}{8}} \right) = \frac{2}{3} - \frac{{ - 21}}{8} \hfill \\ = \frac{{16}}{{24}} - \frac{{ - 63}}{{24}} = \frac{{79}}{{24}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ = 3\frac{7}{{24}} \hfill \\ \end{gathered}$

Dạng 4. Tìm số hạng chưa biết trong một tổng hoặc một hiệu

Phương pháp giải

Áp dụng quy tắc “chuyển vế”.

Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó.

Ví dụ. Tìm x, biết:

a) $x + \frac{1}{3} = \frac{3}{4}$

b) $x - \frac{2}{5} = \frac{5}{7}$

c) $- x - \frac{2}{3} = - \frac{6}{7}$

d) $\frac{4}{7} - x = \frac{1}{3}$

Hướng dẫn giải

a) $x + \frac{1}{3} = \frac{3}{4}$

$\begin{gathered} \Leftrightarrow x = \frac{3}{4} - \frac{1}{3} \hfill \\ \Leftrightarrow x = \frac{5}{{12}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

b) $x - \frac{2}{5} = \frac{5}{7}$

$\begin{gathered} \Leftrightarrow x = \frac{5}{7} + \frac{2}{5} \hfill \\ \Leftrightarrow x = \frac{{39}}{{35}} = 1\frac{4}{{35}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

c) $- x - \frac{2}{3} = - \frac{6}{7}$

$\begin{gathered} \Leftrightarrow x = \frac{6}{7} - \frac{2}{3} \hfill \\ \Leftrightarrow x = \frac{4}{{21}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

d) $\frac{4}{7} - x = \frac{1}{3}$

$\begin{gathered} \Leftrightarrow x = \frac{4}{7} - \frac{1}{3} \hfill \\ \Leftrightarrow x = \frac{5}{{21}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Dạng 5. Tính giá trị của biểu thức có nhiều dấu ngoặc

Phương pháp giải

+) Có thể tính giá trị của biểu thức trong ngoặc rồi tính tổng hoặc hiệu của các kết quả.

+) Có thể bỏ dấu ngoặc rồi nhóm các số hạng thích hợp bằng cách áp dụng tính chất giao hoán và kết hợp.

Ví dụ 1. Cho biểu thức:

$A = \left( {6 - \frac{2}{3} + \frac{1}{2}} \right) - \left( {5 + \frac{5}{3} - \frac{3}{2}} \right) - \left( {3 - \frac{7}{3} + \frac{5}{2}} \right)$

Hãy tính giá trị của A theo hai cách:

Cách 1: Trước hết tính giá trị của từng biểu thức trong ngoặc.

Cách 2: Bỏ dấu ngoặc rồi nhóm các số hạng thích hợp.

Hướng dẫn giải

Cách 1:

$\begin{gathered} A = \left( {6 - \frac{2}{3} + \frac{1}{2}} \right) - \left( {5 + \frac{5}{3} - \frac{3}{2}} \right) - \left( {3 - \frac{7}{3} + \frac{5}{2}} \right) \hfill \\ = \frac{{36 - 4 + 3}}{6} - \frac{{30 + 10 - 9}}{6} - \frac{{18 - 14 + 15}}{6}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ = \frac{{35}}{6} - \frac{{31}}{6} - \frac{{19}}{6} \hfill \\ = \frac{{ - 15}}{6} = \frac{{ - 5}}{2} = - 2\frac{1}{2}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Cách 2:

$\begin{gathered} A = \left( {6 - \frac{2}{3} + \frac{1}{2}} \right) - \left( {5 + \frac{5}{3} - \frac{3}{2}} \right) - \left( {3 - \frac{7}{3} + \frac{5}{2}} \right) \hfill \\ = 6 - \frac{2}{3} + \frac{1}{2} - 5 - \frac{5}{3} + \frac{3}{2} - 3 + \frac{7}{3} - \frac{5}{2}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ = \left( {6 - 5 - 3} \right) - \left( {\frac{2}{3} + \frac{5}{3} - \frac{7}{3}} \right) + \left( {\frac{1}{2} + \frac{3}{2} - \frac{5}{2}} \right) \hfill \\ = - 2 - 0 - \frac{1}{2} = - \frac{5}{2} = - 2\frac{1}{2}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Ví dụ 2. Tính nhanh giá trị của biểu thức sau:

$B = \left( { - \frac{1}{2}} \right) + \left( { - \frac{3}{5}} \right) + \left( { - \frac{1}{9}} \right) + \frac{1}{{131}} - \left( { - \frac{2}{7}} \right) + \frac{4}{{35}} - \frac{7}{{18}}$

Hướng dẫn giải

$\begin{gathered} B = \left( { - \frac{1}{2}} \right) + \left( { - \frac{3}{5}} \right) + \left( { - \frac{1}{9}} \right) + \frac{1}{{131}} - \left( { - \frac{2}{7}} \right) + \frac{4}{{35}} - \frac{7}{{18}} \hfill \\ = \left[ {\left( { - \frac{1}{2}} \right) + \left( { - \frac{1}{9}} \right) + \left( { - \frac{7}{{18}}} \right)} \right] + \left( {\frac{3}{5} + \frac{4}{{35}} + \frac{2}{7}} \right) + \frac{1}{{131}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ = \frac{{ - 9 - 2 - 7}}{{18}} + \frac{{21 + 4 + 10}}{{35}} + \frac{1}{{131}} \hfill \\ = - 1 + 1 + \frac{1}{{131}} = \frac{1}{{131}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Dạng 6. Tìm phần nguyên, phần lẻ của số hữu tỉ

Phương pháp giải

Cần nắm vững các định nghĩa sau:

Phần nguyên của một số hữu tỉ x, kí hiệu [x] là số nguyên lớn nhất không vượt quá x.

Ví dụ: $\left[ {\frac{5}{2}} \right] = 2;\left[ { - \frac{3}{2}} \right] = - 2;\left[ {0,2} \right] = 0$

Như vậy, [x] là số nguyên sao cho: [x] ≤ x < [x] + 1

Phần lẻ của một số hữu tỉ x, kí hiệu {x} là hiệu của x – {x}

{x} = x – [x]

Vì ta có: [x] ≤ x < [x] + 1 nên suy ra 0 ≤ x – [x] < 1, tức là với mọi x ∈ ℚ ta luôn có 0 ≤ {x} < 1

Rõ ràng {x} = 0 khi và chỉ x = [x] tức là khi và chỉ khi x ∈ ℤ

Ví dụ 1. Tìm: $\left[ {\frac{1}{2}} \right];\left[ {3\frac{1}{3}} \right];\left[ { - 5} \right];\left[ { - 1,2} \right]$

Hướng dẫn giải

$\left[ {\frac{1}{2}} \right] = 0;\left[ {3\frac{1}{3}} \right] = 3;\left[ { - 5} \right] = - 5;\left[ { - 1,2} \right] = - 2$

Ví dụ 2. Tìm [x], biết:

a) 2 < x < $\frac{5}{2}$

b) $- \frac{{10}}{3}$ < x < –3

c) –1 < x < 0

Hướng dẫn giải

a) Ta có: 2 < x < $\frac{5}{2}$ nên [x] = 2

b) $- \frac{{10}}{3}$ < x < –3 suy ra –4 < x < –3. Do đó: [x] = –4

c) –1 < x < 0 nên [x] = –1

Ví dụ 3. Cho n là số tự nhiên, chứng minh rằng: $\left[ {\frac{n}{2}} \right] + \left[ {\frac{{n + 1}}{2}} \right] = n$

Hướng dẫn giải

Xét hai trường hợp: n là số chẵn, n là số lẻ.

a) n = 2k (n ∈ ℕ). Ta có:

$\begin{gathered} \left[ {\frac{n}{2}} \right] + \left[ {\frac{{n + 1}}{2}} \right] \hfill \\ = \left[ {\frac{{2k}}{2}} \right] + \left[ {\frac{{2k + 1}}{2}} \right]\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ = \left[ k \right] + \left[ {k + \frac{1}{2}} \right] \hfill \\ = k + k = 2k = n\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered}$

b) n = 2k + 1 (n ∈ ℕ). Ta có:

$\begin{gathered} \left[ {\frac{n}{2}} \right] + \left[ {\frac{{n + 1}}{2}} \right] \hfill \\ = \left[ {\frac{{2k + 1}}{2}} \right] + \left[ {\frac{{2k + 2}}{2}} \right]\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ = \left[ {k + \frac{1}{2}} \right] + \left[ {k + 1} \right] \hfill \\ = k + k + 1 = 2k + 1 = n\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered}$

Ví dụ 4. Tìm {x}, biết:

a) x = $- \frac{3}{2}$

b) x = $- 3\frac{2}{7}$

Hướng dẫn giải

a) x = $- \frac{3}{2}$ ⇒ [x] = –2. Do đó:

{x} = x – [x] = $- \frac{3}{2}$ + 2 = $\frac{1}{2}$

b) x = $- 3\frac{2}{7}$ ⇒ [x] = –4. Do đó:

{x} = x – [x] = $- 3\frac{2}{7}$ + 4 = $\frac{5}{7}$

Nhân chia số hữu tỉ

Tóm tắt lí thuyết

Nhân, chia hai số hữu tỉ.

+) Ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.

+) Phép nhân số hữu tỉ có các tính chất của phép nhân phân số: giao hoán, kết hợp, nhân với số 1, tính chất phân phối của phép nhân đối với phép cộng. Mỗi số hữu tỉ khác 0 đều có một số nghịch đảo.

Tỉ số.

Thương của phép chia số hữu tỉ x cho số hữu tỉ y (y ≠ 0) gọi là tỉ số của hai số x và y, kí hiệu là $\frac{x}{y}{\text{ hay }}x:y$

Các dạng toán

Dạng 1. Nhân, chia hai số hữu tỉ.

Phương pháp giải

+) Viết hai số hữu tỉ dưới dạng phân số.

+) Áp dụng quy tắc nhân, chia phân số;

+) Rút gọn kết quả (nếu có thể).

Ví dụ 1. Tính:

a) $3,5 \cdot \left( { - 1\frac{2}{5}} \right)$

b) $\frac{{ - 5}}{{23}}:\left( { - 2} \right)$

Hướng dẫn giải

a) $3,5 \cdot \left( { - 1\frac{2}{5}} \right)$

$= \frac{7}{2} \cdot \frac{{ - 7}}{5} = \frac{{ - 49}}{{10}} = - 4,9$

b) $\frac{{ - 5}}{{23}}:\left( { - 2} \right)$

$= \frac{{ - 5}}{{23}}:\frac{{ - 2}}{1} = \frac{{ - 5}}{{23}} \cdot \frac{{ - 1}}{2} = \frac{5}{{46}}$

Ví dụ 2. Tính

a) $\frac{{ - 2}}{7} \cdot \frac{{21}}{8}$

b) $0,24 \cdot \left( {\frac{{ - 15}}{4}} \right)$

c) $\left( { - 2} \right) \cdot \left( { - \frac{7}{{12}}} \right)$

d) $\left( { - \frac{3}{{25}}} \right):6$

Hướng dẫn giải

a) $\frac{{ - 3}}{4}$

b) $\frac{{ - 9}}{{10}}$

c) $\frac{7}{6} = 1\frac{1}{6}$

d) $\frac{{ - 1}}{{50}}$

Ví dụ 3. Điền các số hữu tỉ thích hợp vào ô trống:

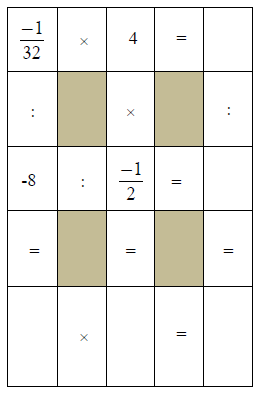
Hướng dẫn giải

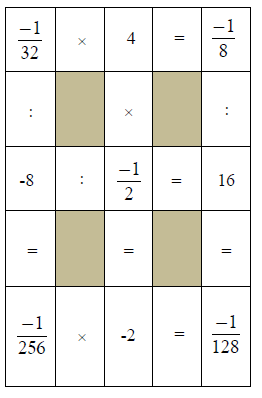
Dạng 2. Viết một số hữu tỉ dưới dạng tích hoặc thương của hai số hữu tỉ

Phương pháp giải

+) Viết số hữu tỉ dưới dạng phân số;

+) Viết tử và mẫu của phân số dưới dạng tích của hai số nguyên;

+) “Tách” ra hai phân số có tử và mẫu là các số nguyên tìm được;

+) Lập tích hoặc thương của các phân số đó

Ví dụ 1. Ta có thể viết số hữu tỉ $\frac{{ - 5}}{{16}}$ dưới các dạng sau đây:

a) $\frac{{ - 5}}{{16}}$ là tích của hai số hữu tỉ. Ví dụ: $\frac{{ - 5}}{{16}} = \frac{{ - 5}}{2} \cdot \frac{1}{8}$

b) $\frac{{ - 5}}{{16}}$ là thương của hai số hữu tỉ. Ví dụ: $\frac{{ - 5}}{{16}} = \frac{{ - 5}}{2}:8$

Với mỗi căn, em hãy tìm thêm một ví dụ.

Hướng dẫn giải

a) $\frac{{ - 5}}{{16}} = \frac{{\left( { - 1} \right) \cdot 5}}{{4 \cdot 4}} = \frac{{ - 1}}{4} \cdot \frac{5}{4}$

b) $\frac{{ - 5}}{{16}} = \frac{{ - 1}}{4}:\frac{4}{5}$

Ví dụ 2. Tìm nhiều cách khác nhau để viết số hữu tỉ $\frac{{ - 7}}{{30}}$ dưới dạng tích của hai số hữu tỉ.

Hướng dẫn giải

Ta có: $\frac{{ - 7}}{{30}} = - 7 \cdot \frac{1}{{30}} = 7 \cdot \frac{{ - 1}}{{30}}$

Nhận xét: $\frac{{ - 7}}{{30}} = \frac{{1 \cdot \left( { - 7} \right)}}{{2 \cdot 15}} = \frac{{\left( { - 1} \right) \cdot 7}}{{2 \cdot 15}}$ . Do đó ta có thể viết:

$\frac{{ - 7}}{{30}} = \frac{1}{2} \cdot \frac{{ - 7}}{{15}} = \frac{{ - 1}}{2} \cdot \frac{7}{{15}} = \frac{1}{{15}} \cdot \frac{{ - 7}}{2} = \frac{{ - 1}}{{15}} \cdot \frac{7}{2}$

Ta lại có: $\frac{{ - 7}}{{30}} = \frac{{1 \cdot \left( { - 7} \right)}}{{6 \cdot 5}} = \frac{{\left( { - 1} \right) \cdot 7}}{{6 \cdot 5}}$ . Do đó ta có thể viết:

$\frac{{ - 7}}{{30}} = \frac{1}{6} \cdot \frac{{ - 7}}{5} = \frac{{ - 1}}{6} \cdot \frac{7}{5} = \frac{1}{5} \cdot \frac{{ - 7}}{6} = \frac{{ - 1}}{5} \cdot \frac{7}{6}$

Ta cũng có: $\frac{{ - 7}}{{30}} = \frac{{1 \cdot \left( { - 7} \right)}}{{3 \cdot 10}} = \frac{{\left( { - 1} \right) \cdot 7}}{{3 \cdot 10}}$ . Do đó ta có:

$\frac{{ - 7}}{{30}} = \frac{1}{3} \cdot \frac{{ - 7}}{{10}} = \frac{{ - 1}}{3} \cdot \frac{7}{{10}} = \frac{1}{{10}} \cdot \frac{{ - 7}}{3} = \frac{{ - 1}}{{10}} \cdot \frac{7}{3}$

Dạng 3. Thực hiện các phép tính với nhiều số hữu tỉ phương pháp giải

+) Nắm vững quy tắc thực hiện các phép tính, chú ý đến dấu của kết quả;

+) Đảm bảo thứ tự thực hiện các phép tính;

+) Chú ý vận dụng tính chất các phép tính trong các trường hợp có thể.

Ví dụ 1. Tính:

a) $\frac{{ - 3}}{4} \cdot \frac{{12}}{{ - 5}} \cdot \left( { - \frac{{25}}{6}} \right)$

b) $\left( { - 2} \right) \cdot \frac{{ - 38}}{{21}} \cdot \frac{{ - 7}}{4} \cdot \left( { - \frac{3}{8}} \right)$

c) $\left( {\frac{{11}}{{12}}:\frac{{33}}{{16}}} \right) \cdot \frac{3}{5}$

d) $\frac{7}{{23}} \cdot \left[ {\left( { - \frac{8}{6}} \right) - \frac{{45}}{{18}}} \right]$

Hướng dẫn giải

a) $\frac{{ - 3}}{4} \cdot \frac{{12}}{{ - 5}} \cdot \left( { - \frac{{25}}{6}} \right)$

$\begin{gathered} = \frac{{ - 3}}{4} \cdot \frac{{12}}{5} \cdot \frac{{25}}{6} = - \frac{{3 \cdot 12 \cdot 25}}{{4 \cdot 5 \cdot 6}} \hfill \\ = - \frac{{1 \cdot 3 \cdot 5}}{{1 \cdot 1 \cdot 2}} = - \frac{{15}}{2} = - 7\frac{1}{2}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

b) $\left( { - 2} \right) \cdot \frac{{ - 38}}{{21}} \cdot \frac{{ - 7}}{4} \cdot \left( { - \frac{3}{8}} \right)$

$\begin{gathered} = 2 \cdot \frac{{38}}{{21}} \cdot \frac{7}{4} \cdot \frac{3}{8} = \frac{{2 \cdot 38 \cdot 7 \cdot 3}}{{21 \cdot 4 \cdot 8}} \hfill \\ = \frac{{1 \cdot 19 \cdot 1 \cdot 1}}{{1 \cdot 1 \cdot 8}} = \frac{{19}}{8} = 2\frac{3}{8}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

c) $\left( {\frac{{11}}{{12}}:\frac{{33}}{{16}}} \right) \cdot \frac{3}{5}$

$\begin{gathered} = \frac{{11}}{{12}} \cdot \frac{{16}}{{33}} \cdot \frac{3}{5} = \frac{{11 \cdot 16 \cdot 3}}{{12 \cdot 33 \cdot 5}} \hfill \\ = \frac{{1 \cdot 4 \cdot 3}}{{3 \cdot 3 \cdot 5}} = \frac{4}{{15}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

d) $\frac{7}{{23}} \cdot \left[ {\left( { - \frac{8}{6}} \right) - \frac{{45}}{{18}}} \right]$

$\begin{gathered} = \frac{7}{{23}} \cdot \left[ { - \frac{8}{6} - \frac{{15}}{6}} \right] \hfill \\ = \frac{7}{{23}} \cdot \frac{{ - 23}}{6} = \frac{{ - 7}}{6}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ = - 1\frac{1}{6} \hfill \\ \end{gathered}$

Ví dụ 2. Tính:

a) $\left( {\frac{{ - 2}}{3} + \frac{3}{7}} \right):\frac{4}{5} + \left( {\frac{{ - 1}}{3} + \frac{4}{7}} \right):\frac{4}{5}$

b) $\frac{5}{9}:\left( {\frac{1}{{11}} - \frac{5}{{22}}} \right) + \frac{5}{9}:\left( {\frac{1}{{15}} - \frac{2}{3}} \right)$

Hướng dẫn giải

a) $\left( {\frac{{ - 2}}{3} + \frac{3}{7}} \right):\frac{4}{5} + \left( {\frac{{ - 1}}{3} + \frac{4}{7}} \right):\frac{4}{5}$

$\begin{gathered} = \left( {\frac{{ - 2}}{3} + \frac{3}{7} + \frac{{ - 1}}{3} + \frac{4}{7}} \right):\frac{4}{5} \hfill \\ = \left( {\frac{{ - 3}}{3} + \frac{7}{7}} \right):\frac{4}{5}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ = 0:\frac{4}{5} = 0 \hfill \\ \end{gathered}$

(Áp dụng tính chất a ∶ c = b ∶ c = (a + b) ∶ c

b) $\frac{5}{9}:\left( {\frac{1}{{11}} - \frac{5}{{22}}} \right) + \frac{5}{9}:\left( {\frac{1}{{15}} - \frac{2}{3}} \right)$

$\begin{gathered} = \frac{5}{9}:\frac{{2 - 5}}{{22}} + \frac{5}{9}:\frac{{1 - 10}}{{15}} \hfill \\ = \frac{5}{9} \cdot \frac{{22}}{{ - 3}} + \frac{5}{9} \cdot \frac{{ - 15}}{9}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ = \frac{5}{9} \cdot \left( {\frac{{ - 22}}{3} + \frac{{ - 5}}{3}} \right) \hfill \\ = \frac{5}{9} \cdot \frac{{ - 27}}{3} = - 5\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Dạng 4. Lập biểu thức từ các số cho trước

Phương pháp giải

Khi giải loại toán này, cần quan sát để phát hiện ra đặc điểm và quan hệ của các số đã cho, từ đó lập được biểu thức thích hợp. Sau khi có biểu thức, cần kiểm tra lại theo yêu cầu đề bài.

Ví dụ 1. Đố: Em hãy tìm cách “nối” các số ở những chiếc lá bằng dấu các phép tính cộng, trừ, nhân, chia và dấu ngoặc để được một biểu thức có giá trị đúng bằng số ở bông hoa ở hình vẽ bên.

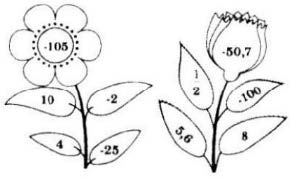
Hướng dẫn giải

Với bông hoa bên trái ta có thể lập được hai biểu thức:

4⋅(–25) + 10 ∶ (–2 ) = –100 + (–5) = –105

4⋅10⋅(–2) + (–25) = –80 + (–25) = –105

Với bông hoa bên phải ta có thể lập được biểu thức:

$\frac{1}{2}$ ⋅(–100) – 5⋅6 ∶ 8 = –50⋅6 ∶ 8 = –50 – 0.7 = –50,7

Giá trị tuyệt đối của một số hữu tỉ.

Cộng, trừ, nhân, chia số thập phân.

Tóm tắt lí thuyết

Giá trị tuyệt đối của một số hữu tỉ.

Giá trị tuyệt đối của một số hữu tỉ x, kí hiệu |x| là khoảng cách từ điểm x đến điểm 0 trên trục số.

$\left| x \right| = \left\{ \begin{gathered} x{\text{ khi }}x \geqslant 0 \hfill \\ - x{\text{ khi }}x < 0 \hfill \\ \end{gathered} \right.$

Cộng, trừ, nhân, chia số thập phân.

+) Để cộng, trừ, nhân, chia số thập phân, ta có thể viết chúng dưới dạng phân số thập phân rồi làm theo quy tắc các phép tính đã biết về phân số.

Trong thực hành ta thường cộng, trừ nhân hai số thập phân theo các quy tắc về giá trị tuyệt đối và về dấu tương tự đối với số nguyên.

+) Khi chia số thập phân x cho số thập phân y (y ≠ 0), ta thường áp dụng quy tắc: Thương của hai số thập phân x, y là thương của |x| và |y| với dấu “+” đằng trước nếu x, y cùng dấu và dấu “–” đằng trước nếu x, y khác dấu.

Các dạng toán

Dạng 1. Các bài tập về dấu giá trị tuyệt đối của một số hữu tỉ.

Phương pháp giải

+) Cần nắm vững định nghĩa giá trị tuyệt đối của một số hữu tỉ:

|x| = x nếu x ≥ 0;

|x| = –x nếu x < 0.

+) Các tính chất hay sử dụng của giá trị tuyệt đối:

Với mọi x ∈ ℚ: |x| ≥ 0; |x| = |–x|; |x| ≥ x

Ví dụ 1. Tìm |x|, biết:

a) x = $- \frac{1}{7}$

b) x = $\frac{1}{7}$

c) x = $- 3\frac{1}{5}$

d) x = 0

Hướng dẫn giải

a) $\left| { - \frac{1}{7}} \right| = \frac{1}{7}$

b) $\left| {\frac{1}{7}} \right| = \frac{1}{7}$

c) $\left| { - 3\frac{1}{5}} \right| = 3\frac{1}{5}$

d) |0| = 0

Ví dụ 2.

1) Trong các khẳng định sau đây, khẳng định nào đúng?

A |–2,5| = 2,5

B |–2,5| = –2,5

C |–2,5| = –(–2,5)

2) Tìm x, biết:

a) |x| = $\frac{1}{5}$

b) |x| = 0,37

c) |x| = 0

d) |x| = $1\frac{2}{3}$

Hướng dẫn giải

1) Các khẳng định đúng là: a) và c).

a) x = $\pm \frac{1}{5}$

b) x = ±0,37

c) x = 0

d) x = $\pm 1\frac{2}{3}$

Ví dụ 3. Tìm x, biết:

a) |x – 1,7| = 2,3

b) $\left| {x + \frac{3}{4}} \right| - \frac{1}{3} = 0$

Hướng dẫn giải

a) Bài này có thể Hướng dẫn giải theo hai cách:

Cách 1: (Căn cứ vào định nghĩa của giá trị tuyệt đối)

+) Nếu x – 1,7 ≥ 0, tức là x ≥ 1,7 thì |x – 1,7| = x – 1,7

Trong trường hợp này ta có:

x – 1,7 = 2,3 ⇔ x = 2,3 + 1,7 ⇔ x = 4 (TMĐK x ≥ 1,7)

+) Nếu x – 1,7 < 0, tức là x < 1,7 thì |x – 1,7| = –(x – 1,7) = 1,7 – x

Trong trường hợp này ta có:

1,7 – x = 2,3 ⇔ x = 1,7 – 2,3 ⇔ x = –0,6 (TMĐK x < 1,7)

Vậy x = 4 và x = –0,6

Cách 2. (Căn cứ vào tính chất |x| = |–x|).

|x – 1,7| = 2,3

⇒ x – 1,7 = 2,3 (1) ∨ x – 1,7 = –2,3 (2)

Từ (1) ta có: x = 2,3 + 1,7 = 4

Từ (2) ta có: x = 1,7 – 2,3 = –0,6

Vậy x = 4 và x = –0,6

b) Hướng dẫn: viết $\left| {x + \frac{3}{4}} \right| - \frac{1}{3} = 0$ thành $\left| {x + \frac{3}{4}} \right| = \frac{1}{3}$ rồi giải bằng một trong hai cách như câu a)

Đáp số: $x = \frac{{ - 5}}{{12}};x = \frac{{ - 13}}{{12}}$

Ví dụ 4. Tìm giá trị nhỏ nhất của các biểu thức sau:

$\begin{array}{*{20}{c}} \begin{gathered} A = \left| {x - \frac{1}{2}} \right|; \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} B = \left| {x + \frac{3}{4}} \right| + 2 \hfill \\ \hfill \\ \end{gathered} \end{array}$

Hướng dẫn giải

+) Với mọi x ∈ ℚ ta luôn có |x| ≥ 0. Vì vậy: $A = \left| {x - \frac{1}{2}} \right| \geqslant 0$ .

Biểu thức A có giá trị nhỏ nhất bằng 0 khi:

$x - \frac{1}{2} = 0 \Leftrightarrow x = \frac{1}{2}$

+) Ta có: $\left| {x + \frac{3}{4}} \right| \geqslant 0 \Rightarrow \left| {x + \frac{3}{4}} \right| + 2 \geqslant 2$

Vậy $B = \left| {x + \frac{3}{4}} \right| + 2$ có giá trị nhỏ nhất bằng 2 khi:

$x + \frac{3}{4} = 0 \Leftrightarrow x = - \frac{3}{4}$

Ví dụ 5. Tìm giá trị lớn nhất của các biểu thức sau:

$\begin{array}{*{20}{c}} \begin{gathered} C = - \left| {x + \frac{2}{5}} \right|; \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} D = \frac{5}{7} - \left| {3x - 2} \right| \hfill \\ \hfill \\ \end{gathered} \end{array}$

Hướng dẫn giải

+) Với mọi x ∈ ℚ ta luôn có |x| ≥ 0 nên –|x| ≤ 0.

Do đó: $C = - \left| {x + \frac{2}{5}} \right| \leqslant 0$ . Biểu thức C có giá trị lớn nhất bằng 0 khi:

$x + \frac{2}{5} = 0 \Leftrightarrow x = - \frac{2}{5}$

+) Ta có: –|3x – 2| ≤ 0 nên $\frac{5}{7} - \left| {3x - 2} \right| \leqslant \frac{5}{7}$

Vậy biểu thức D có giá trị lớn nhất là $\frac{5}{7}$ khi:

3x – 2 = 0 ⇒ x = $\frac{2}{3}$

Ví dụ 6. Chứng minh rằng với mọi x, y ∈ ℚ ta luôn có: |x + y| ≤ |x| + |y|. Dấu “=” xảy ra khi nào?

Hướng dẫn giải

Với mọi x ∈ ℚ ta luôn có x ≤ |x| (dấu bằng xảy ra khi x ≥ 0).

a) Nếu x + y ≥ 0 thì |x + y| = x + y

Vì x ≤ |x|, y ≤ |y|, với mọi x, y ∈ ℚ nên |x + y| = x + y ≤ |x| + |y|

b) Nếu x + y < 0 thì |x + y| = –(x + y) = –x – y

Vì –x ≤ |x|, –y ≤ |y|, với mọi x, y ∈ ℚ nên |x + y| = –x – y ≤ |x| + |y|

Vậy với mọi x, y ∈ ℚ ta có: |x + y| ≤ |x| + |y|

Dấu “=” xảy ra khi x, y cùng dấu hoặc khi ít nhất một số bằng 0.

Dạng 2. Biểu diễn số hữu tỉ bằng các phân số khác nhau.

Phương pháp giải

Sử dụng tính chất cơ bản của phân số:

$\begin{gathered} \frac{a}{b} = \frac{{a \cdot m}}{{b \cdot m}},{\text{ }}m \in \mathbb{Z},{\text{ }}m \ne 0 \hfill \\ \frac{a}{b} = \frac{{a:n}}{{b:n}},{\text{ }}n \in {\text{UC}}\left( {a;b} \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Ví dụ 1.

a) Trong các phân số sau, những phân số nào biểu diễn cùng một số hữu tỉ:

$\frac{{ - 14}}{{35}};\frac{{ - 27}}{{63}};\frac{{ - 26}}{{65}};\frac{{ - 36}}{{84}};\frac{{34}}{{ - 85}}$

b) Viết ba phân số cùng biểu diễn số hữu tỉ $\frac{{ - 3}}{7}$

Hướng dẫn giải

a) Rút gọn các phân số đã cho.

Các phân số $\frac{{ - 27}}{{63}};\frac{{ - 36}}{{84}}$ biểu diễn cùng một số hữu tỉ

Các phân số $\frac{{ - 14}}{{35}};\frac{{ - 26}}{{65}};\frac{{34}}{{ - 85}}$ biểu diễn cùng một số hữu tỉ.

b) Chú ý rằng $\frac{{ - 3}}{7}$ là phân số tối giản nên chỉ cần nhân cả tử và mẫu của nó cùng một số nguyên khác 0.

Dạng 3. Cộng, trừ, nhân, chia các số thập phân

Phương pháp giải

+) Áp dụng các quy tắc cộng, trừ, nhân, chia các số thập phân.

+) Chú ý vận dụng các tính chất: giao hoán, kết hợp, phân phối,… trong các trường hợp có thể để việc tính toán được nhanh chóng và chính xác.

Ví dụ 1. Tính:

a) –5,7 – 0,469

b) –2,05 + 1,73

c) (–5,17)⋅(–3,1)

d) (–9,18) ∶ 4,25

Hướng dẫn giải

a) –6,169

b) –0,32

c) 16,027

d) –2,16

Ví dụ 2. Với bài tập: Tính tổng S = (–2,3) + (+41,5) + (–0,7) + (–1,5), hai bạn Hùng và Liên đã làm như sau:

Bài làm của Hùng

S = (–2,3) + (+41,5) + (–0,7) + (–1,5)

= [(–2,3) + (–0,7) + (–1,5)] + 41,5

= (–4,5) + 41,5 = 37

Bài làm của Liên

S = (–2,3) + (+41,5) + (–0,7) + (–1,5)

= [(–2,3) + (–0,7)] + [(–1,5) + 41,5]

= –3 + 40 = 37

a) Hãy giải thích cách làm của mỗi bạn.

b) Theo em nên làm cách nào?

Hướng dẫn giải

a) Bạn Hùng cộng các số âm với nhau được –4 5, rồi cộng tiếp với 41,5 để được kết quả là 37.

Bạn Liên đã nhóm từng cặp số hạng có tổng là số nguyên được –3 và 40 rồi cộng hai số này được 37.

b) Hai cách làm của hai bạn đều áp dụng các tính chất giao hoán và kết hợp của phép cộng để tính được hợp lí nhưng cách của bạn Liên có thể tính nhẩm nhanh hơn. Do đó nên làm theo cách của bạn Liên.

Ví dụ 3. Tính nhanh:

a) 6,3 + (–3,7) + 2,4 + (–0,3)

b) (–4,9) + 5,5 + 4,9 + (–5,5)

c) 2,9 + 3,7 + (–4,2) + (–2,9) + 4,2

d) (–6,5)⋅2,8 + 2,8⋅(–3,5)

Hướng dẫn giải

a) (6,3 + 2,4) + [(–3,7) + (–0,3)]

= 8,7 – 4 = 4,7

b) [(–4,9) + 4,9] + [5,5 + (–5,5)]

= 0 + 0 = 0

c) [2,9 + (–2,9)] + [(–4,2) + 4,2] + 3,7

= 0 + 0 + 3,7 = 3,7

d) 2,8⋅[(–6,5) + (–3,5)]

= 2,8⋅10 = 28

Ví dụ 4. Áp dụng tính chất các phép tính để tính nhanh:

a) (–2,5⋅0,38⋅0,4) – [0,125⋅3,15⋅(–8)]

b) [(–20,83)⋅0,2 + (–9,17)⋅0,2] ∶ [2,47⋅0,5 – (–3,53)⋅0,5]

Hướng dẫn giải

a) (–2,5⋅0,38⋅0,4) – [0,125⋅3,15⋅(–8)]

= [(–2.5)⋅0,4⋅0,38] – [(–8⋅0,125)⋅3,15]

= 2,77

b) [(–20,83)⋅0,2 + (–9,17)⋅0,2] ∶ [2,47⋅0,5 – (–3,53)⋅0,5]

= [(–20,83 – 9,17)⋅0,2] ∶ [(2,47 + 3,53)⋅0,5]

= –2

Dạng 4. So sánh các số hữu tỉ.

Phương pháp giải

Khi so sánh hai số hữu tỉ cần chú ý:

+) Số hữu tỉ dương lớn hơn số.

+) Số hữu tỉ âm nhỏ hơn số 0.

+) Trong hai số hữu tỉ âm, số nào có giá trị tuyệt đối nhỏ hơn thì số đó lớn hơn.

+) Có thể sử dụng tính chất “bắc cầu” để so sánh.

Ví dụ 1. Sắp xếp các số hữu tỉ sau theo thứ tự lớn dần:

$0,3;\frac{{ - 5}}{6}; - 1\frac{2}{3};\frac{4}{{13}};0; - 0,875$

Hướng dẫn giải

$- 1\frac{2}{3} < - 0,875 < \frac{{ - 5}}{6} < 0 < 0,3 < \frac{4}{{13}}$

Ví dụ 2. Dựa vào tính chất “Nếu x < y và y < z thì x < z”, hãy so sánh:

a) $\frac{4}{5}$ và 1,1

b) –500 và 0,001

c) $\frac{{13}}{{38}}$ và $\frac{{ - 12}}{{ - 37}}$

Hướng dẫn giải

a) $\frac{4}{5}$ < 1 và 1 < 1,1 nên $\frac{4}{5}$ < 1,1

b) –500 < 0 và 0 < 0,001 nên –500 < 0,001

c) $\frac{{ - 12}}{{ - 37}} < \frac{{ - 12}}{{ - 36}} = \frac{1}{3} \Rightarrow \frac{{ - 12}}{{ - 37}} < \frac{1}{3}{\text{ }}\left( 1 \right)$

$\frac{1}{3} = \frac{{13}}{{39}} < \frac{{13}}{{38}} \Rightarrow \frac{1}{3} < \frac{{13}}{{38}}{\text{ }}\left( 2 \right)$

Từ (1) và (2) ta có: $\frac{{ - 12}}{{ - 37}} < \frac{{13}}{{38}}$

Dạng 5. Sử dụng máy tình bỏ túi để làm các phép tính cộng, trừ, nhân, chia số thập phân.

Phương pháp giải

Nắm vững cách sử dụng các nút:

Ví dụ 1. Dùng máy tính bỏ túi để tính:

a) (–3,1597) + (–2,39)

b) (–0,793) – (–2,1068)

c) (–0,5)⋅(–3,2) + (–10,2)⋅0,2

d) 1,2⋅(–2,6) + (–1,4) ∶ 0,7

Hướng dẫn giải

a) –5,5497

b) 1,3138

c) –0,42

d) –5,12

Lũy thừa của một số hữu tỉ

Tóm tắt lí thuyết

Lũy thừa với số mũ tự nhiên

Lũy thừa bậc N của một số hữu tỉ x, kí hiệu xⁿ, là tích của n thừa số x (n là một số tự nhiên lớn hơn 1): xⁿ = x.x…x (x ∈ ℚ, n ∈ ℕ, n > 1)

Quy ước: x¹ = x; x⁰ = 1 (x ≠ 0)

Khi viết số hữu tỉ x dưới dạng $\frac{a}{b}\left( {a,b \in \mathbb{Z},b \ne 0} \right)$ , ta có: ${\left( {\frac{a}{b}} \right)^n} = \frac{{{a^n}}}{{{b^n}}}$

Tích và thương của hai lũy thừa cùng cơ số

+) x^m⋅xⁿ = x^m+n (Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ)

+) x^m ∶ xⁿ = x^m–n (x ≠ 0, m ≥ n) (Khi chia hai lũy thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia).

Lũy thừa của lũy thừa

+) (x^m)ⁿ = x^m^⋅ⁿ (Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ).

Lũy thừa của một tích

(x⋅y)ⁿ = xⁿyⁿ (Lũy thừa của một tích bằng tích các lũy thừa)

Lũy thừa của một thương

${\left( {\frac{x}{y}} \right)^n} = \frac{{{x^n}}}{{{y^n}}}{\text{ }}\left( {y \ne 0} \right)$ (Lũy thừa của một thương bằng thương các lũy thừa)

Các dạng bài toán

Dạng 1. Sử dụng định nghĩa của lũy thừa với số mũ tự nhiên

Phương pháp giải

Cần nắm vững định nghĩa: xⁿ = x.x…x (x ∈ ℚ, n ∈ ℕ, n > 1)

Quy ước:

Ví dụ 1. Tính: ${\left( {\frac{{ - 1}}{3}} \right)^4};{\left( { - 2\frac{1}{4}} \right)^3};{\left( { - 0,2} \right)^2};{\left( { - 5,3} \right)^0}$

Hướng dẫn giải

$\begin{gathered} {\left( {\frac{{ - 1}}{3}} \right)^4} = \frac{1}{{81}} \hfill \\ {\left( { - 2\frac{1}{4}} \right)^3} = \left( { - \frac{9}{4}} \right) = - \frac{{729}}{{64}} = - 11\frac{{25}}{{64}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ {\left( { - 0,2} \right)^2} = 0,04 \hfill \\ {\left( { - 5,3} \right)^0} = 1\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered}$

Ví dụ 2. Tính:

${\left( { - \frac{1}{2}} \right)^2};{\left( { - \frac{1}{2}} \right)^3};{\left( { - \frac{1}{2}} \right)^4};{\left( { - \frac{1}{2}} \right)^5}$

Hãy rút ra nhận xét về dấu của lũy thừa với số mũ chẵn và lũy thừa với số mũ lẻ của một số hữu tỉ âm.

Hướng dẫn giải

$\begin{gathered} {\left( { - \frac{1}{2}} \right)^2} = \frac{1}{4};{\text{ }}{\left( { - \frac{1}{2}} \right)^3} = - \frac{1}{8}; \hfill \\ {\left( { - \frac{1}{2}} \right)^4} = \frac{1}{{16}};{\text{ }}{\left( { - \frac{1}{2}} \right)^5} = \frac{1}{{32}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Lũy thừa với sỗ mũ chẵn của một số âm là một số dương, lũy thừa với số mũ lẻ của một số âm là một số âm.

Ví dụ 3. Viết số $\frac{{16}}{{81}}$ dưới dạng một lũy thừa, ví dụ $\frac{{16}}{{81}} = {\left( {\frac{4}{9}} \right)^2}$ . Hãy tìm các cách viết khác.

Hướng dẫn giải

Các cách viết khác:

$\frac{{16}}{{81}} = {\left( {\frac{{16}}{{81}}} \right)^1} = {\left( { - \frac{4}{9}} \right)^2} = {\left( {\frac{2}{3}} \right)^4} = {\left( { - \frac{2}{3}} \right)^4}$

Ví dụ 4. Đố: Hãy chọn hai chữ số sao cho có thể viết hai chữ số đó thành một lũy thừa để được kết quả là số nguyên dương nhỏ nhất. (Chọn được càng nhiều càng tốt)

Hướng dẫn giải

Số nguyên dương nhỏ nhất là 1. Ta có:

1¹ = 1² = 1³ = 1⁴ = … = 1⁹ = 1

1⁰ = 2⁰ = 3⁰ = 4⁰ = … = 9⁰ = 1

Ví dụ 5. Dùng máy tính bỏ túi để tính:

(3,5)²; (–0,12)³; (1,5)⁴; (–0,1)⁵; (1,2)⁶

Hướng dẫn giải

(3,5)² = 12,25

(–0,12)³ = 0,001728

(1,5)⁴ = 5,0625

(–0,1)⁵ = –0,00001

(1,2)⁶ = 2,985984

Dạng 2. Tính tích và thương của hai lũy thừa cùng cơ số

Phương pháp giải

Áp dụng các công thức tính tích và thương của hai lũy thừa cùng cơ số.

x^m⋅xⁿ = x^m+n

x^m ∶ xⁿ = x^m–n (x ≠ 0, m ≥ n)

Ví dụ 1. Tìm x, biết:

a) $x:{\left( { - \frac{1}{2}} \right)^3} = - \frac{1}{2}$

b) ${\left( {\frac{3}{4}} \right)^5} \cdot x = {\left( {\frac{3}{4}} \right)^7}$

Hướng dẫn giải

a) $x:{\left( { - \frac{1}{2}} \right)^3} = - \frac{1}{2}$

$\begin{gathered} \Leftrightarrow x = - \frac{1}{2} \cdot {\left( { - \frac{1}{2}} \right)^3} \hfill \\ \Leftrightarrow x = {\left( { - \frac{1}{2}} \right)^4} = \frac{1}{{16}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

b) ${\left( {\frac{3}{4}} \right)^5} \cdot x = {\left( {\frac{3}{4}} \right)^7}$

$\begin{gathered} \Leftrightarrow x = {\left( {\frac{3}{4}} \right)^7}:{\left( {\frac{3}{4}} \right)^5} \hfill \\ \Leftrightarrow x = {\left( {\frac{3}{4}} \right)^2} = \frac{9}{{16}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Dạng 3. Tính lũy thừa của một lũy thừa

Phương pháp giải

Áp dụng các công thức tính lũy thừa của một lũy thừa: (x^m)ⁿ = x^m^⋅ⁿ

Chú ý:

+) Trong nhiều trường hợp ta phải sử dụng công thức này theo chiều từ hải sang trái: x^m^⋅ⁿ = (x^m)ⁿ = (xⁿ)^m

+) Cần tránh sai lầm do lẫn lộn hai công thức:

x^m⋅xⁿ = x^m+n và (x^m)ⁿ = x^m^⋅ⁿ

Ví dụ 1. Viết các số (0,25)⁸ và (0,125)⁴ dưới dạng các lũy thừa của cơ số 0,5.

Hướng dẫn giải

Ta có: (0,25)⁸ = [(0,5)²]⁸ = (0,5)¹⁶

(0,125)⁴ = [(0,5)³]⁴ = (0,5)¹²

Ví dụ 2.

a) Viết các số 2²⁷ và 3¹⁸ dưới dạng các lũy thừa có số mũ là 9.

b) Trong hai số 2²⁷ và 3¹⁸, số nào lớn hơn?

Hướng dẫn giải

a) Nhận xét: 27 = 3⋅9; 18 = 2⋅9. Ta có:

2²⁷ = 2³^⋅⁹ = (2³)⁹ = 8⁹

3¹⁸ = 3²^⋅⁹ = (3²)⁹ = 9⁹

b) Vì 9⁹ > 8⁹ nên 3¹⁸ > 2²⁷

Ví dụ 3. Trong vở bài tập của Dũng có bài làm sau:

a) (–5)²⋅(–5)³ = (–5)⁶

b) (0,75)³ ∶ 0,75 = (0,75)²

c) (0,2)¹⁰ ∶ (0,2)⁵ = (0,2)²

d) ${\left[ {{{\left( { - \frac{1}{7}} \right)}^2}} \right]^4} = {\left( { - \frac{1}{7}} \right)^6}$

e) $\frac{{{{50}^3}}}{{125}} = \frac{{{{50}^3}}}{{{5^3}}} = {\left( {\frac{{50}}{5}} \right)^3} = {10^3} = 1000$

f) $\frac{{{8^{10}}}}{{{4^8}}} = {\left( {\frac{8}{4}} \right)^{10 - 8}} = {2^2}$

Hãy kiểm tra lại các đáp số và sửa lại chỗ sai (nếu có).

Hướng dẫn giải

Các câu a, c, d, f: sai.

Các câu b, e: đúng.

Sửa lại chỗ sai:

a) (–5)²⋅(–5)³ = (–5)²⁺³ = (–5)⁵

c) (0,2)¹⁰ ∶ (0,2)⁵ = (0,2)^10–5 = (0,2)⁵

d) ${\left[ {{{\left( { - \frac{1}{7}} \right)}^2}} \right]^4} = {\left( { - \frac{1}{7}} \right)^{2 \times 4}} = {\left( { - \frac{1}{7}} \right)^8}$

f) $\frac{{{8^{10}}}}{{{4^8}}} = \frac{{{{\left( {{2^3}} \right)}^{10}}}}{{{{\left( {{2^2}} \right)}^8}}} = \frac{{{2^{30}}}}{{{2^{16}}}} = {2^{14}}$

Ví dụ 4. Cho x ∈ ℚ và x ≠ 0. Viết x¹⁰ dưới dạng:

a) Tích của hai lũy thừa trong đó có một số thừa số là x⁷.

b) Lũy thưà của x².

c) Thường của hai lũy thừa trong đó số bị chia là x¹².

Hướng dẫn giải

a) x¹⁰ = x⁷⋅x³

b) x¹⁰ = (x²)⁵

c) x¹⁰ = x¹² ∶ x²

Dạng 4. Tính lũy thừa của một tích, lũy thừa của một thương

Phương pháp giải

Áp dụng các công thức

+) (x⋅y)ⁿ = xⁿyⁿ (Lũy thừa của một tích bằng tích các lũy thừa)

+) ${\left( {\frac{x}{y}} \right)^n} = \frac{{{x^n}}}{{{y^n}}}{\text{ }}\left( {y \ne 0} \right)$ (Lũy thừa của một thương bằng thương các lũy thừa)

Các công thức trên còn được sử dụng theo chiều từ trái sang phải:

+) xⁿyⁿ = (x⋅y)ⁿ (Quy tắc nhân hai lũy thừa cùng số mũ)

+) $\frac{{{x^n}}}{{{y^n}}} = {\left( {\frac{x}{y}} \right)^n}{\text{ }}\left( {y \ne 0} \right)$ (Quy tắc chia hai lũy thừa cùng cơ số)

Ví dụ 1. Tính:

a) (0,125)³⋅8³

b) (–39)⁴ ∶ 13⁴

Hướng dẫn giải

a) Nhận xét: 0,125⋅8 = 1, ta có cách giải 1:

(0,125)³⋅8³ = (0,125⋅8)³ = 1³ = 1

Nhận xét: 0,125 = $\frac{1}{8}$ , ta có cách giải 2:

${\left( {0,125} \right)^3} \cdot {8^3} = {\left( {\frac{1}{8}} \right)^3} \cdot {8^3} = \frac{{{1^3}}}{{{8^3}}} \cdot {8^3} = 1$

b) Nhận xét: –39 = –3⋅13, ta có:

Cách 1: (–39)⁴ ∶ 13⁴ = (–3⋅13)⁴ ∶ 13⁴ = (–3)⁴⋅13⁴ ∶ 13⁴ = (–3)⁴ = 81

Cách 2: ${\left( { - 39} \right)^4}:{13^4} = {\left( {\frac{{ - 39}}{{13}}} \right)^4} = {\left( { - 3} \right)^4} = 81$

Ví dụ 2. Viết các biểu thức sau dưới dạng lũy thừa của một số hữu tỉ

a) 10⁸⋅2⁸

b) 10⁸ ∶ 2⁸

c) 25⁴⋅2⁸

d) 15⁸⋅9⁴

e) 27² ∶ 25³

Hướng dẫn giải

a) 10⁸⋅2⁸ = (10⋅2)⁸ = 20⁸

b) 10⁸ ∶ 2⁸ = (10 ∶ 2)⁸ = 5⁸

c) 25⁴⋅2⁸ = (5²)⁴⋅2⁸ = 5⁸⋅2⁸ = (5⋅2)⁸ = 10⁸

d) 15⁸⋅9⁴ = 15⁸⋅(3²)⁴ = 15⁸⋅3⁸ = (15⋅3)⁸ = 45⁸

e) 27² ∶ 25³ = (3³)² ∶ (5²)³ = 3⁶ ∶ 5⁶ = (0,6)⁶

Ví dụ 3. Đố: Biết rằng 1² + 2² + 3² + … + 10² = 385, đố em tính nhanh được tổng:

S = 2² + 4² + 6² + … + 20²

Hướng dẫn giải

S = 2² + 4² + 6² + … + 20²

= (2⋅1)² + (2⋅2)² + (2⋅3)² + … + (2⋅10)²

= 2²⋅1² + 2²⋅2² + 2²⋅3² + … + 2²⋅10²

= 2²⋅(1² + 2² + 3² + … + 100²)

= 4⋅385 = 1540

Dạng 5. Tìm số mũ của một lũy thừa

Phương pháp giải

Khi giải bài toán này, ta có thể sử dụng tính chất được thừa nhận sau đây

Với a ≠ 0, a ≠ ±1 nếu a^m = aⁿ thì m = n

Ví dụ 1. Ta thừa nhận tính chất sau đây:

Với a ≠ 0, a ≠ ±1 nếu a^m = aⁿ thì m = n

Dựa vào tính chất này, hãy tìm các số tự nhiên m, n biết:

a) ${\left( {\frac{1}{2}} \right)^m} = \frac{1}{{32}}$

b) $\frac{{343}}{{125}} = {\left( {\frac{7}{5}} \right)^n}$

Hướng dẫn giải

a) $\frac{1}{{32}} = \frac{1}{{{2^5}}} = {\left( {\frac{1}{2}} \right)^5}$

b) $\frac{{343}}{{125}} = \frac{{{7^3}}}{{{5^3}}} = {\left( {\frac{7}{5}} \right)^3}$

Ví dụ 2. Tìm số tự nhiên n, biết:

a) $\frac{{16}}{{{2^n}}} = 2$

b) $\frac{{{{\left( { - 3} \right)}^n}}}{{81}} = - 27$

c) 8ⁿ ∶ 2ⁿ = 4

Hướng dẫn giải

a) Cách 1:

$\frac{{16}}{{{2^n}}} = 2 \Rightarrow \frac{{{2^4}}}{{{2^n}}} = 2 \Rightarrow {2^{4 - n}} = {2^1} \Rightarrow n = 3$

Cách 2:

$\frac{{16}}{{{2^n}}} = 2 \Rightarrow {2^n} \cdot 2 = 16 \Rightarrow {2^{n + 1}} = {2^4} \Rightarrow n = 3$

b) Cách 1:

$\begin{gathered} \frac{{{{\left( { - 3} \right)}^n}}}{{81}} = - 27 \Rightarrow \frac{{{{\left( { - 3} \right)}^n}}}{{{{\left( { - 3} \right)}^4}}} = {\left( { - 3} \right)^3} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{\begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \hfill \\ \end{gathered} &{ \Rightarrow {{\left( { - 3} \right)}^{n - 4}} = {{\left( { - 3} \right)}^3} \Rightarrow n = 7} \end{array}} \end{array} \hfill \\ \end{gathered}$

Cách 2:

$\begin{gathered} \frac{{{{\left( { - 3} \right)}^n}}}{{81}} = - 27 \Rightarrow {\left( { - 3} \right)^n} = {\left( { - 3} \right)^4} \cdot {\left( { - 3} \right)^3} = {\left( { - 3} \right)^7} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{\begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \hfill \\ \end{gathered} &{ \Rightarrow n = 7} \end{array}} \end{array} \hfill \\ \end{gathered}$

c) 8ⁿ ∶ 2ⁿ = 4 ⇒ (8 ∶ 2)ⁿ = 4 ⇒ 4ⁿ = 4¹ ⇒ n = 1

Dạng 6. Tìm cơ số của một lũy thừa

Phương pháp giải

+) Sử dụng định nghĩa của lũy thừa với số mũ nguyên dương:

xⁿ = x.x…x (x ∈ ℚ, n ∈ ℕ, n > 1)

+) Sử dụng tính chất:

Nếu aⁿ = bⁿ thì a = b nếu n lẻ, a = ±b nếu n chẵn (n ∈ ℕ, n ≥ 1)

Ví dụ 1. Tìm x, biết:

a) x³ = 343

b) (x – 2,5)⁴ = (x – 2,5)²

Hướng dẫn giải

a) Ta có: 343 = 7³. Do đó x³ = 7³ nên x = 7.

b) Nếu x = 2,5 ta có 0⁴ = 0² (đúng)

Nếu x ≠ 2,5 chia hai vế cho (x – 2,5)² ≠ 0, ta được: (x – 2,5)² = 1

Suy ra: x – 2,5 = 1 hoặc x – 2,5 = –1

Nếu x – 2,5 = 1 ⇒ x = 3,5

Nếu x – 2,5 = –1 ⇒ x = 1,5

Vậy x ∈ {1,5; 2,5; 3,5}

Ví dụ 2. Tìm x, biết: $\frac{{{x^8}}}{{243}} = 27$

Hướng dẫn giải

Ta có: 243 = 3⁵; 27 = 3³

Do đó: $\frac{{{x^8}}}{{{3^5}}} = {3^3} \Rightarrow {x^8} = {3^5} \cdot {3^3} = {3^8}$

Vậy x ∈ {–3; 3}

Dạng 7. Tìm giá trị của biểu thức

Phương pháp giải

+) Cần thực hiện đúng thứ tự của các phép tính: lũy thừa, nhân, chia, cộng, trừ. Nếu có dấu ngoặc cần làm theo thứ tự: ngoặc tròn, ngoặc vuông, ngoặc nhọn.

+) Áp dụng các quy tắc của các phép tính và các tính chất của các phép tính đó.

Ví dụ 1.

a) $\frac{{{4^2} \cdot {4^3}}}{{{2^{10}}}}$

b) $\frac{{{{\left( {0,6} \right)}^5}}}{{{{\left( {0,2} \right)}^6}}}$

c) $\frac{{{2^7} \cdot {9^3}}}{{{6^5} \cdot {8^2}}}$

d) $\frac{{{6^3} + 3 \cdot {6^2} + {3^3}}}{{ - 13}}$

Hướng dẫn giải

a) $\frac{{{4^2} \cdot {4^3}}}{{{2^{10}}}} = \frac{{{4^5}}}{{{{\left( {{2^2}} \right)}^5}}} = \frac{{{4^5}}}{{{4^5}}} = 1$

b) $\frac{{{{\left( {0,6} \right)}^5}}}{{{{\left( {0,2} \right)}^6}}} = \frac{{{{\left( {0,2 \cdot 3} \right)}^5}}}{{{{\left( {0,2} \right)}^6}}} = \frac{{{{\left( {0,2} \right)}^5} \cdot {3^5}}}{{{{\left( {0,2} \right)}^6}}} = \frac{{243}}{{0,2}} = 1215$

c) $\frac{{{2^7} \cdot {9^3}}}{{{6^5} \cdot {8^2}}} = \frac{{{2^7} \cdot {{\left( {{3^2}} \right)}^3}}}{{{{\left( {2 \cdot 3} \right)}^5} \cdot {{\left( {{2^3}} \right)}^2}}}$

$\begin{gathered} = \frac{{{2^7} \cdot {3^6}}}{{{2^5} \cdot {3^5} \cdot {2^6}}} = \frac{{{2^7} \cdot {3^6}}}{{{2^7} \cdot {3^5} \cdot {2^4}}} \hfill \\ = \frac{3}{{{2^4}}} = \frac{3}{{16}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

d) $\frac{{{6^3} + 3 \cdot {6^2} + {3^3}}}{{ - 13}}$

$\begin{gathered} = \frac{{{{\left( {2 \cdot 3} \right)}^3} + 3 \cdot {{\left( {2 \cdot 3} \right)}^2} + {3^3}}}{{ - 13}} \hfill \\ = \frac{{{2^3} \cdot {3^3} + {2^2} \cdot {3^3} + {3^3}}}{{ - 13}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ = \frac{{{3^3}\left( {{2^3} + {2^2} + 1} \right)}}{{ - 13}} \hfill \\ = - {3^3} = - 27\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered}$

Ví dụ 2.

a) ${\left( {\frac{3}{7} + \frac{1}{2}} \right)^2}$

b) ${\left( {\frac{3}{4} - \frac{5}{6}} \right)^2}$

c) $\frac{{{5^4} \cdot {{20}^4}}}{{{{25}^5} \cdot {4^5}}}$

d) ${\left( { - \frac{{10}}{3}} \right)^5} \cdot {\left( {\frac{{ - 6}}{5}} \right)^4}$

Hướng dẫn giải

a) $\frac{{169}}{{196}}$

b) $\frac{1}{{144}}$

c) $\frac{1}{{100}}$

d) $\frac{{ - 2560}}{3} = - 853\frac{1}{3}$

Ví dụ 3. Tính:

a) $\left( {1 + \frac{2}{3} - \frac{1}{4}} \right){\left( {\frac{4}{5} - \frac{3}{4}} \right)^2}$

b) $2:{\left( {\frac{1}{2} - \frac{2}{3}} \right)^3}$

Hướng dẫn giải

a) $\frac{{17}}{{4800}}$

b) –432

Tỉ lệ thức

Tóm tắt lí thuyết

Định nghĩa.

Tỉ lệ thức là đẳng thức của hai tỉ số $\frac{a}{b} = \frac{c}{d}$

Ta còn viết: a ∶ b = c ∶ d

a và d là các ngoại tỉ; b và c là các trung tỉ.

Tính chất.

Tính chất 1. Nếu $\frac{a}{b} = \frac{c}{d}$ thì ad = bc

Tính chất 2. Nếu ad = bc và a, b, c, d khác 0 thì ta có các tỉ lệ thức:

$\frac{a}{b} = \frac{c}{d},{\text{ }}\frac{a}{c} = \frac{b}{d},{\text{ }}\frac{d}{b} = \frac{c}{a},{\text{ }}\frac{d}{c} = \frac{b}{a}$

Các dạng bài toán

Dạng 1. Thay tỉ số giữa các số hữu tỉ bằng tỉ số giữa các số nguyên

Phương pháp giải

+) Viết các số hữu tỉ dưới dạng phân số.

+) Thực hiện phép chia phân số

Ví dụ 1. Thay tỉ số giữa các số hữu tỉ bằng tỉ số giữa các số nguyên.

a) 1,2 ∶ 3,24

b) $2\frac{1}{5}:\frac{3}{4}$

c) $\frac{2}{7}:0,42$

Hướng dẫn giải

a) $1,2:3,24 = \frac{{12}}{{10}}:\frac{{324}}{{100}} = \frac{{12}}{{10}} \cdot \frac{{100}}{{324}} = \frac{{10}}{{27}}$

b) $2\frac{1}{5}:\frac{3}{4} = 44:15$

c) $\frac{2}{7}:0,42 = 100:147$

Dạng 2. Lập tỉ lệ thức từ các tỉ số cho trước

Phương pháp giải

+) Xét xem hai tỉ số đã cho co bằng nhau không?

+) Nếu hai tỉ số bằng nhau thì chúng lập thành một tỉ lệ thức.

Ví dụ 1. Từ các tỉ số sau đây có lập được tỉ lệ thức không?

a) $\frac{2}{5}:4$ và $\frac{4}{5}:8$

b) $- 3\frac{1}{2}:7$ và $- 2\frac{2}{5}:7\frac{1}{5}$

Hướng dẫn giải

a) $\frac{2}{5}:4 = 0,4 \cdot 4 = 1:10$

$\frac{4}{5}:8 = 0,8:8 = 1:10$

Hai tỉ số này bằng nhau nên ta có tỉ lệ thức: $\frac{2}{5}:4 = \frac{4}{5}:8$

Cách khác: ta có nhận xét $\frac{2}{5} \cdot 8 = 4\frac{4}{5}\left( { = \frac{{16}}{5}} \right)$ nên theo tính chất 2, ta có tỉ lệ thức:

$\frac{2}{5}:4 = \frac{4}{5}:8$

b) $- 3\frac{1}{2}:7 = - 3,5:7 = - 1:2$

$- 2\frac{2}{5}:7\frac{1}{5} = - 2,4:7,2 = - 1:3$

Hai tỉ số này không bằng nhau nên chúng không lập thành tỉ lệ thức.

Cách khác: $- 3\frac{1}{2} \cdot 7\frac{1}{5} \ne 7 \cdot \left( { - 2\frac{2}{5}} \right)$ nên hai tỉ số này không lập thành tỉ lệ thức.

Ví dụ 2. Tìm các tỉ số bằng nhau trong các tỉ số sau đây rồi lập các tỉ lệ thức:

$\begin{gathered} \begin{array}{*{20}{c}} \begin{gathered} \hfill \\ 28:14 \hfill \\ \end{gathered} &\begin{gathered} \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \hfill \\ 2\frac{1}{2}:2 \hfill \\ \end{gathered} \end{array}\begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \hfill \\ 8:4 \hfill \\ \end{gathered} &\begin{gathered} \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \hfill \\ \frac{1}{2}:\frac{2}{3} \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} {3:10}&{}&{_{}^{}{\text{ }}_{}^{}{\text{ }}2,1:7} \end{array}\begin{array}{*{20}{c}} {}&{3:0,3} \end{array}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered}$

Hướng dẫn giải

Có hai tỉ lệ thức: 28 ∶ 14 = 8 ∶ 4 và x

Ví dụ 3. Từ các tỉ số sau đây có lập được tỉ lệ thức không?

a) 3,5 ∶ 5,25 và 14 ∶ 21

b) $39\frac{3}{{10}}:52\frac{2}{5}$ và 2,1 ∶ 3,5

c) 6,51 ∶ 15,19 và 3 ∶ 7

d) $- 7:4\frac{2}{3}$ và 0,9 ∶ (–0,5)

Hướng dẫn giải

Có hai tỉ lệ thức:

a) 3,5 ∶ 5,25 = 14 ∶ 21

c) 6,51 ∶ 15,19 = 3 ∶ 7

Dạng 3. Lập tỉ lệ thức từ đẳng thức cho trước, từ một tỉ lệ thức cho trước, từ các số cho trước.

Phương pháp giải

+) Lập tỉ lệ thức từ đẳng thức cho trước: Áp dụng tính chất 2.

Nếu ad = bc và a, b, c, d khác 0 thì ta có các tỉ lệ thức:

$\frac{a}{b} = \frac{c}{d},{\text{ }}\frac{a}{c} = \frac{b}{d},{\text{ }}\frac{d}{b} = \frac{c}{a},{\text{ }}\frac{d}{c} = \frac{b}{a}$

+) Lập tất cả các tỉ lệ thức từ một tỉ lệ thức cho trước:

Từ tỉ lệ thức $\frac{a}{b} = \frac{c}{d}$ ta có thể lập được ba tỉ lệ thức nữa bằng cách.

⋄ Giữ nguyên ngoại tỉ, đổi chỗ các trung tỉ: $\frac{a}{c} = \frac{b}{d}$

⋄ Giữ nguyên trung tỉ, đổi chỗ các ngoại tỉ: $\frac{d}{b} = \frac{c}{a}$

⋄ Đổi chỗ các ngoại tỉ với nhau, các trung tỉ với nhau: $\frac{d}{c} = \frac{b}{a}$

+) Lập tỉ lệ thức từ các số cho trước: Từ các số đã cho, trước hết phải lập được đẳng thức dạng ad = bc. Sau khi có đẳng thức này, áp dụng tính chất 2 để lập các tỉ lệ thức.

Ví dụ 1. Lập tất cả các tỉ lệ thức có thể được từ các đẳng thức sau:

a) 6⋅63 = 9⋅42

b) 0,24⋅1,61 = 0,84⋅0,46

Hướng dẫn giải

a) $\frac{6}{9} = \frac{{42}}{{63}},{\text{ }}\frac{6}{{42}} = \frac{9}{{63}},{\text{ }}\frac{{63}}{9} = \frac{{42}}{6},{\text{ }}\frac{{63}}{{42}} = \frac{9}{6}$

b) $\frac{{0,24}}{{0,84}} = \frac{{0,46}}{{1,61}},{\text{ }}\frac{{0,24}}{{0,46}} = \frac{{0.84}}{{1,61}},$

$\frac{{1,61}}{{0,84}} = \frac{{0,46}}{{0,24}},{\text{ }}\frac{{1,61}}{{0,46}} = \frac{{0,84}}{{0,24}}$

Ví dụ 2. Lập tất cả các tỉ lệ thức có thể được từ tỉ lệ thức sau: $\frac{{ - 1.5}}{{5.1}} = \frac{{ - 3,5}}{{11,9}}$

Hướng dẫn giải

$\frac{{ - 15}}{{ - 35}} = \frac{{5,1}}{{11,9}},{\text{ }}\frac{{11,9}}{{5,1}} = \frac{{ - 35}}{{ - 15}},{\text{ }}\frac{{11,9}}{{ - 35}} = \frac{{5,1}}{{ - 15}}$

Ví dụ 3. Lập tất cả các tỉ lệ thức có thể được từ bốn số sau:

1,5; 2; 3,6; 4,8

Hướng dẫn giải

Ta có: 1,5⋅4,8 = 2⋅3,6 (= 7,2). Do đó có các tỉ lệ thức sau:

$\frac{{1,5}}{2} = \frac{{3,6}}{{4,8}},{\text{ }}\frac{{1,5}}{{3,6}} = \frac{2}{{4,8}},{\text{ }}\frac{{4,8}}{2} = \frac{{3,6}}{{1,5}},{\text{ }}\frac{{4,8}}{{3,6}} = \frac{2}{{1,5}}$

Ví dụ 4. Từ tỉ lệ thức $\frac{a}{b} = \frac{c}{d}$ với a, b, c, d khác 0 ta có thể suy ra:

A. $\frac{a}{c} = \frac{b}{d}$

B. $\frac{a}{b} = \frac{d}{c}$

C. $\frac{d}{b} = \frac{c}{a}$

D. $\frac{a}{d} = \frac{b}{c}$

Hãy chọn câu trả lời đúng.

Hướng dẫn giải

Câu trả lời đúng là câu C.

Dạng 4. Tìm số hạng chưa biết của một tỉ lệ thức.

Phương pháp giải

Trong một tỉ lệ thức, ta có thể tìm một số hạng chưa biết khi biết ba số hạng kia.

$\frac{a}{b} = \frac{c}{d} \Rightarrow a = \frac{{bc}}{d},{\text{ }}b = \frac{{ad}}{c},{\text{ }}c = \frac{{ad}}{b},{\text{ }}d = \frac{{bc}}{a}$

Ví dụ 1. Tìm x trong các tỉ lệ thức sau:

a) $\frac{x}{{27}} = \frac{{ - 2}}{{3,6}}$

b) –0,52 ∶ x = –9,36 ∶ 16,38

c) $\frac{\begin{gathered} \hfill \\ 4\frac{1}{4} \hfill \\ \end{gathered} }{\begin{gathered} 2\frac{7}{8} \hfill \\ \hfill \\ \end{gathered} } = \frac{x}{{1,61}}$

Hướng dẫn giải

a) x = –15

b) x = 0,91

c) Ta biến đổi

$\frac{\begin{gathered} \hfill \\ 4\frac{1}{4} \hfill \\ \end{gathered} }{\begin{gathered} 2\frac{7}{8} \hfill \\ \hfill \\ \end{gathered} } = \frac{\begin{gathered} \hfill \\ \frac{{17}}{4} \hfill \\ \end{gathered} }{\begin{gathered} \frac{{23}}{8} \hfill \\ \hfill \\ \end{gathered} } = \frac{{17}}{4} \cdot \frac{8}{{23}} = \frac{{34}}{{23}}$

Ta có tỉ lệ thức:

$\frac{{34}}{{23}} = \frac{x}{{1,61}} \Rightarrow x = \frac{{34 \cdot 1,61}}{{23}} = 2,38$

Ví dụ 2. Tên một tác phẩm nổi tiếng của Hưng Đạo Vương Trần Quốc Tuấn.

Điền số thích hợp vào ô vuông dưới đây để có tỉ lệ thức. Sau đó, viết các chữ số tương ứng với các số tìm được vào các ô ở hàng dưới cùng của bài em sẽ biết được tên của tác phẩm nổi tiếng của Hưng Đạo Vương Trần Quốc Tuấn (1228 – 1300), vị anh hùng của dân tộc ta đồng thời là danh nhân quân sự của thế giới.

N) ∶ 6 = 7 ∶ 3

H) 20 ∶ = (–12) ∶ 15

C) 6 ∶ 27 = ∶ 72

I) (–15) ∶ 35 = 27 ∶

Ư) $\frac{{ - 4,4}}{{9,9}} = \frac{{\boxed{_{}^{}{\text{ }}_{}^{}{\text{ }}}}}{{1,89}}$

Ế) $\frac{{ - 0,65}}{{0,91}} = \frac{{ - 6,55}}{{\boxed{_{}^{}{\text{ }}_{}^{}{\text{ }}}}}$

Y) $\frac{4}{5}:1\frac{2}{5} = 2\frac{2}{5}:\boxed{_{}^{}{\text{ }}_{}^{}{\text{ }}}$

Ợ) $\frac{1}{2}:1\frac{1}{4} = \boxed{_{}^{}{\text{ }}_{}^{}{\text{ }}}:3\frac{1}{3}$

B) $\frac{1}{2}:\boxed{_{}^{}{\text{ }}_{}^{}{\text{ }}} = \frac{3}{4}:5\frac{1}{4}$

U) $\boxed{_{}^{}{\text{ }}_{}^{}{\text{ }}}:1\frac{1}{4} = 1\frac{1}{5}:2$

L) $\frac{{\boxed{_{}^{}{\text{ }}_{}^{}{\text{ }}}}}{{2,7}} = \frac{{0,7}}{{6,3}}$

T) $\frac{{2.4}}{{\boxed{_{}^{}{\text{ }}_{}^{}{\text{ }}}}} = \frac{{5,4}}{{13,5}}$

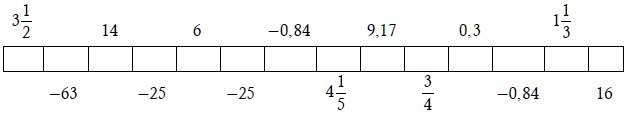
Hướng dẫn giải

N) 14

H) –25

C) 16

I) –63

Ư) –0,84

Ế) 9,17

Y) $4\frac{1}{5}$

Ợ) $1\frac{1}{3}$

B) $3\frac{1}{2}$

U) $\frac{3}{4}$

L) 0,3

T) 6

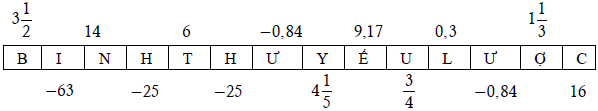
Ví dụ 3. Đố: Tỉ số $\frac{\begin{gathered} \hfill \\ 6\frac{1}{5} \hfill \\ \end{gathered} }{\begin{gathered} 5\frac{1}{6} \hfill \\ \hfill \\ \end{gathered} }$ có thể rút gọn như sau: $\frac{\begin{gathered} \hfill \\ 6\frac{1}{5} \hfill \\ \end{gathered} }{\begin{gathered} 5\frac{1}{6} \hfill \\ \hfill \\ \end{gathered} } = \frac{6}{5}$ (“Rút gọn” bằng cách xóa bỏ phần phân số ở hai hỗn số, giữ lại phần nguyên là được kết quả). Ta được kết quả đúng. (Hãy kiểm tra!) Đố em viết được một tỉ số khác cũng có thể “rút gọn” như vậy!

Hướng dẫn giải

$\frac{\begin{gathered} \hfill \\ 6\frac{1}{5} \hfill \\ \end{gathered} }{\begin{gathered} 5\frac{1}{6} \hfill \\ \hfill \\ \end{gathered} } = \frac{\begin{gathered} \hfill \\ \frac{{6 \cdot 5 + 1}}{5} \hfill \\ \end{gathered} }{\begin{gathered} \frac{{5 \cdot 6 + 1}}{6} \hfill \\ \hfill \\ \end{gathered} } = \frac{{31}}{5}:\frac{{31}}{6} = \frac{6}{5}$

Một tỉ số khác có thể “rút gọn”, chẳng hạn: $\frac{\begin{gathered} \hfill \\ 8\frac{1}{7} \hfill \\ \end{gathered} }{\begin{gathered} 7\frac{1}{8} \hfill \\ \hfill \\ \end{gathered} } = \frac{8}{7}$

Tổng quát: $\frac{\begin{gathered} \hfill \\ a\frac{1}{b} \hfill \\ \end{gathered} }{\begin{gathered} b\frac{1}{a} \hfill \\ \hfill \\ \end{gathered} } = \frac{\begin{gathered} \hfill \\ \frac{{ab + 1}}{b} \hfill \\ \end{gathered} }{\begin{gathered} \frac{{ab + 1}}{a} \hfill \\ \hfill \\ \end{gathered} } = \frac{a}{b}{\text{ }}\left( {a \ne 0,b \ne 0} \right)$

Tính chất của dãy tỉ số bằng nhau

Tóm tắt lí thuyết

Tính chất của dãy tỉ số bằng nhau

$\frac{a}{b} = \frac{c}{d} = \frac{{a + c}}{{b + d}} = \frac{{a - c}}{{b - d}}{\text{ }}\left( {b \ne d,b \ne - d} \right)$

Từ dãy tỉ số bằng nhau $\frac{a}{b} = \frac{c}{d} = \frac{e}{f}$ ta suy ra:

$\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = \frac{{a + b + c}}{{b + d + f}} = \frac{{a - c + e}}{{b - d + f}}$

(Giả thiết các tỉ số đều có nghĩa)

Khi nói các số x, y, z tỉ lệ với các số a, b, c tức là ta có: $\frac{x}{a} = \frac{y}{b} = \frac{z}{c}$

Ta cũng viết x ∶ y ∶ z = a ∶ b ∶ c

Các dạng toán

Dạng 1. Tìm hai số biết tổng (hoặc hiệu) và tỉ số của chúng

Phương pháp giải

Để tìm hai số x và y biết tổng x + y = s hoặc hiệu x – y = d và tỉ số $\frac{x}{y} = \frac{a}{b}$ ta làm như sau:

+) $\frac{x}{y} = \frac{a}{b} \Rightarrow \frac{x}{a} = \frac{y}{b}$

Áp dụng tính chất của dãy tỉ số bằng nhau:

$\begin{gathered} \frac{x}{a} = \frac{y}{b} = \frac{{x + y}}{{a + b}} = \frac{s}{{a + b}} \hfill \\ \Rightarrow x = \frac{s}{{a + b}} \cdot a;{\text{ }}y = \frac{s}{{a + b}} \cdot b\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

+) $\frac{x}{y} = \frac{a}{b} \Rightarrow \frac{x}{a} = \frac{y}{b}$

Áp dụng tính chất của dãy tỉ số bằng nhau:

$\begin{gathered} \frac{x}{a} = \frac{y}{b} = \frac{{x - y}}{{a - b}} = \frac{d}{{a - b}} \hfill \\ \Rightarrow x = \frac{d}{{a - b}} \cdot a;{\text{ }}y = \frac{d}{{a - b}} \cdot b\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Ví dụ 1. Tìm hai số x và y, biết: $\frac{x}{3} = \frac{y}{5}$ và x + y =16.

Hướng dẫn giải

Ta có: $\frac{x}{3} = \frac{y}{5} = \frac{{x + y}}{{3 + 5}} = \frac{{16}}{{18}} = 2$

Vậy x = 2⋅3 = 6; y = 2⋅5 = 10

Ví dụ 2. Tìm hai số x và y, biết: x ∶ 2 = y ∶ (–5) và x – y = –7

Hướng dẫn giải

x = –2; y = 5

Ví dụ 3. Tìm diện tích của một hình chữ nhật biết rằng tỉ số giữa hai cạnh của nó bằng $\frac{2}{5}$ và chu vi rằng 28 m.

Hướng dẫn giải

Gọi chiều rộng và chiều dài của hình chữ nhật lần lượt là x và y thì ta có:

$\left\{ \begin{gathered} \frac{x}{y} = \frac{2}{5}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ 2\left( {x + y} \right) = 28 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x = \frac{2}{5}y\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ x + y = 14 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x = 4 \hfill \\ y = 10 \hfill \\ \end{gathered} \right.$

Vậy diện tích hình chữ nhật là 4 × 10 = 40 m²

Ví dụ 4. Hai lớp 7A và 7B đi lao động trồng cây. Biết rằng tỉ số giữa số cây trồng được của lớp 7A và lớp 7B là 0 8, và lớp 7B trồng nhiều hơn lớp 7A là 20 cây. Tính số cây mỗi lớp đã trồng.

Hướng dẫn giải

Gọi số cây trồng được của lớp 7A và lớp 7B theo thứ tự là x và y thì ta có:

$\left\{ \begin{gathered} \frac{x}{y} = 0,8\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ y - x = 20 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x = 0,8y \hfill \\ y - x = 20 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x = 80 \hfill \\ y = 100 \hfill \\ \end{gathered} \right.$

Vậy lớp 7A trồng được 80 cây, lớp 7B trồng được 100 cây.

Ví dụ 5. Số học sinh khối bốn 6, 7, 8, 9 tỉ lệ với các số 9; 8; 7; 6. Biết rằng số học sinh khối 9 ít hơn số học sinh khối 7 là 70 học sinh. Tính học sinh mỗi khối.

Hướng dẫn giải

Gọi số học sinh khối 6, 7, 8, 9 theo thứ tự x, y, z, t thì ta có:

$\begin{gathered} \left\{ \begin{gathered} \frac{x}{9} = \frac{y}{8} = \frac{z}{7} = \frac{t}{6}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ y - t = 70 \hfill \\ \end{gathered} \right. \hfill \\ \Rightarrow \left\{ \begin{gathered} \frac{y}{8} = \frac{t}{6}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ y - t = 70 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} t = \frac{3}{4}y \hfill \\ y - t = 70 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} t = 210 \hfill \\ y = 280 \hfill \\ \end{gathered} \right.\begin{array}{*{20}{c}} {} \\ {} \\ {} \\ {} \end{array} \hfill \\ \Rightarrow \left\{ \begin{gathered} x = 315 \hfill \\ z = 245 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Đáp số: số học sinh các khối 6, 7, 8, 9 theo thứ tự là 315; 280; 245; 210.

Dạng 2. Chia một số thành các phần tỉ lệ với các số cho trước.

Phương pháp giải

Giả sử phải chia số S thành ba phần x, y, z tỉ lệ với các số a, b, c. Ta làm như sau:

$\begin{gathered} \frac{x}{a} = \frac{y}{b} = \frac{z}{c} = \frac{{x + y + z}}{{a + b + c}} = \frac{S}{{a + b + c}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \Rightarrow \left\{ \begin{gathered} x = \frac{S}{{a + b + c}} \cdot a\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ y = \frac{S}{{a + b + c}} \cdot b\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ z = \frac{S}{{a + b + c}} \cdot c\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Ví dụ 1. Số viên bi của ba bạn Minh, Hùng, Dũng tỉ lệ với các số 2; 4; 5. Tính số viên bi của mỗi bạn, biết rằng ba bạn có tất cả 44 viên bi.

Hướng dẫn giải

Ta phải chia số 44 thành ba phần tỉ lệ với 2; 4 và 5.

Đáp số: Số viên bi của Minh, Hùng, Dũng theo thứ tự là 8; 16; 20.

Ví dụ 2. Ba người thỏa thuận góp vốn để lập cơ sở sản xuất theo tỉ lệ 3; 5; 7. Hỏi mỗi người góp bao nhiêu, biết rằng số vốn cần huy động là 120 triệu đồng.

Hướng dẫn giải

Chia số 120 000 000 thành ba phần tỉ lệ với 3; 5; 7

Đáp án: 24 triệu đồng; 40 triệu đồng và 56 triệu đồng.

Ví dụ 3. Tìm ba số x, y, z, biết rằng: $\frac{x}{2} = \frac{y}{3},{\text{ }}\frac{y}{4} = \frac{z}{5}$ và x + y – x = 10

Hướng dẫn giải

BCNN(3; 4) = 12 nên ta biến đổi như sau:

$\begin{gathered} \frac{x}{2} = \frac{y}{3} \Rightarrow \frac{x}{{2 \cdot 4}} = \frac{y}{{3 \cdot 4}} \Rightarrow \frac{x}{8} = \frac{y}{{12}}{\text{ }}\left( 1 \right) \hfill \\ \frac{y}{4} = \frac{z}{5} \Rightarrow \frac{y}{{4 \cdot 3}} = \frac{z}{{5 \cdot 3}} \Rightarrow \frac{y}{{12}} = \frac{z}{{15}}{\text{ }}\left( 2 \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Từ (1) và (2) và từ giả thiết x + y – x = 10 ta có:

$\frac{x}{8} = \frac{y}{{12}} = \frac{z}{{15}} = \frac{{x + y - z}}{{8 + 12 - 15}} = \frac{{10}}{5} = 2$

Đáp số: x = 16; y = 24; z = 30.

Dạng 3. Tìm hai số biết tích và tỉ số của chúng

Phương pháp giải

Giả sử phải tìm hai số x, y biết xy = P và $\frac{x}{y} = \frac{a}{b}$

+) Đặt $\frac{x}{a} = \frac{y}{b} = k \Rightarrow x = ka,{\text{ }}y = kb$ . Do đó:

$xy = \left( {ka} \right) \cdot \left( {kb} \right) = {k^2}ab = P \Rightarrow {k^2} = \frac{P}{{ab}}$

+) Từ đó tìm được k rồi suy ra x và y.

Ví dụ 1. Tìm hai số x và y, biết rằng $\frac{x}{2} = \frac{y}{5}$ và xy =10.

Hướng dẫn giải

Đặt $k = \frac{x}{2} = \frac{y}{5}$ , ta có x = 2k, y = 5k

Vì xy =10 nên 2k⋅5k = 10 ⇒ 10k² = 10 ⇒ k² = 1 ⇒ k = ±1

+) Với k = 1 thì x = 2⋅1 = 2; y = 5⋅1 = 5

+) Với k = –1 thì x = 2⋅(–1) = –2; y = 5⋅(–1) = –5

Vậy: x = 2; y = 5; x = –2; y = –5

Ví dụ 2. Một miếng đất hình chữ nhật diện tích 76,95 m² có chiều rộng bằng $\frac{5}{{19}}$ chiều dài. Tính chiều rộng và chiều dài của miếng đất đó.

Hướng dẫn.

Gọi chiều rộng là x, chiều dài là y thì ta có: xy = 76,95 và $\frac{x}{y} = \frac{5}{{19}}$

Vậy chiều rộng là 4,5 m; chiều dài là 17,1 m.

Dạng 4. Chứng minh đẳng thức từ một tỉ lệ thức cho trước.

Phương pháp giải

Áp dụng các tính chất của tỉ lệ thức và của dãy tỉ số bằng nhau.

Ví dụ 1. Chứng minh rằng từ tỉ lệ thức $\frac{a}{b} = \frac{c}{d}{\text{ }}\left( {a - b \ne 0,{\text{ }}c - d \ne 0} \right)$ ta có thể suy ra tỉ lệ thức

$\frac{{a + b}}{{a - b}} = \frac{{c + d}}{{c - d}}$

Hướng dẫn giải

Đặt $k = \frac{a}{b} = \frac{c}{d}$ . Vì a – b ≠ 0, c – d ≠ 0 nên a ≠ b, c ≠ d, do đó k ≠ 1. Ta có: a = bk, c = dk

$\begin{gathered} \frac{{a + b}}{{a - b}} = \frac{{bk + b}}{{bk - b}} = \frac{{b\left( {k + 1} \right)}}{{b\left( {k - 1} \right)}} = \frac{{k + 1}}{{k - 1}}{\text{ }}\left( 1 \right) \hfill \\ \frac{{c + d}}{{c - d}} = \frac{{dk + d}}{{dk - d}} = \frac{{d\left( {k + 1} \right)}}{{d\left( {k - 1} \right)}} = \frac{{k + 1}}{{k - 1}}{\text{ }}\left( 2 \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Từ (1) và (2) suy ra: $\frac{{a + b}}{{a - b}} = \frac{{c + d}}{{c - d}}$

Ví dụ 2. Cho a, b, c, d là các số hữu tỉ dương và $\frac{a}{b} = \frac{c}{d}$ . Chứng minh rằng:

a) $\frac{{ac}}{{bd}} = \frac{{{a^2} + {c^2}}}{{{b^2} + {d^2}}}$

b) (a + 2c)(b + d) = (a + c)(b + 2d)

Hướng dẫn giải

a) Từ $\frac{a}{b} = \frac{c}{d}$ suy ra $\frac{{{a^2}}}{{{b^2}}} = \frac{{{c^2}}}{{{d^2}}} = \frac{{ac}}{{bd}}{\text{ }}\left( 1 \right)$

Áp dụng tính chất của dãy tỉ số bằng nhau:

$\frac{{{a^2}}}{{{b^2}}} = \frac{{{c^2}}}{{{d^2}}} = \frac{{{a^2} + {c^2}}}{{{b^2} + {d^2}}}{\text{ }}\left( 2 \right)$

So sánh (1) và (2) ta được: $\frac{{ac}}{{bd}} = \frac{{{a^2} + {c^2}}}{{{b^2} + {d^2}}}$

b) Từ $\frac{a}{b} = \frac{c}{d}$ suy ra $\frac{a}{b} = \frac{c}{d} = \frac{{a + c}}{{b + d}}{\text{ }}\left( 3 \right)$

Ta có: $\frac{a}{b} = \frac{{2c}}{{2d}} = \frac{{a + 2c}}{{b + 2d}}{\text{ }}\left( 4 \right)$

So sánh (3) và (4) ta được: $\frac{{a + c}}{{b + d}} = \frac{{a + 2c}}{{b + 2d}}$

Suy ra: (a + 2c)(b + d) = (a + c)(b + 2d)

Dạng 5. Thay tỉ số giữa các số hữu tỉ bằng tỉ số giữa các số nguyên.

Phương pháp giải

+) Viết các số hữu tỉ dưới dạng phân số.

+) Thực hiện phép chia phân số.

Ví dụ 1. Thay tỉ số giữa các số hữu tỉ bằng tỉ số giữa các số nguyên

a) 2,04 ∶ (–3,12)

b) $\left( { - 1\frac{1}{2}} \right):1,25$

c) $4:5\frac{3}{4}$

d) $10\frac{3}{7}:5\frac{3}{{14}}$

Hướng dẫn giải

a) 17 ∶ (–26)

b) –6 ∶ 5

c) 16 ∶ 23

d) 2 ∶ 1

Dạng 6. Tìm số hạng chưa biết trong một tỉ lệ thức.

Phương pháp giải

Trong một tỉ lệ thức, ta có thể tìm một số hạng chưa biết khi biết ba số hạng kia

$\frac{a}{b} = \frac{c}{d} \Rightarrow a = \frac{{bc}}{d},{\text{ }}b = \frac{{ad}}{c},{\text{ }}c = \frac{{ad}}{b},{\text{ }}d = \frac{{bc}}{a}$

Ví dụ 1. Tìm x trong các tỉ lệ thức sau:

a) $\left( {\frac{1}{3} \cdot x} \right):\frac{2}{3} = 1\frac{3}{4}:\frac{2}{5}$

b) 4,5 ∶ 0,3 = 2,25 ∶ (0,1x)

c) $8:\left( {\frac{1}{4} \cdot x} \right) = 2:0,02$

d) $3:2\frac{1}{4} = \frac{3}{4}:\left( {6 \cdot x} \right)$

Hướng dẫn giải

a) x = $8\frac{3}{4}$

b) x = 15

c) x = 0,32

d) x = $\frac{3}{{32}}$

Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn.

Tóm tắt lý thuyết

+) Nếu một phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn.

+) Nếu một phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân vô hạn tuần hoàn.

+) Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn. Ngược lại, mỗi số thập phân hữu hạn hoặc vô hạn tuần hoàn biểu diễn một số hữu tỉ.

Các dạng toán

Dạng 1. Nhận biết một phân số viết được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.

Phương pháp giải

+) Viết phân số dưới dạng phân số tối giản với mẫu dương.

+) Phân tích mẫu dương đó ra thừa số nguyên tố.

+) Nhận xét: nếu mẫu này không có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn; nếu mẫu này có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân vô hạn tuần hoàn.

Ví dụ 1. Trong hai phân số sau, phân số nào viết được dưới dạng số thập phân hữu hạn, phân số nào viết được dưới dạng số thập phân vô hạn tuần hoàn?

$\frac{{55}}{{ - 300}}$ và $\frac{{63}}{{ - 360}}$

Hướng dẫn giải

+) Xét phân số $\frac{{55}}{{ - 300}}$ , ta có: $\frac{{55}}{{ - 300}} = \frac{{ - 11}}{{60}};{\text{ }}60 = {2^2} \cdot 3 \cdot 5$

Mẫu này có ước nguyên tố 3 khác 2 và 5 nên phân số $\frac{{ - 11}}{{60}}$ viết được dưới dạng số thập phân vô hạn tuần hoàn. Ta có:

$\frac{{55}}{{ - 300}} = \frac{{ - 11}}{{60}} = - 0,18\left( 3 \right)$

+) Xét phân số $\frac{{63}}{{ - 360}}$ , ta có: $\frac{{63}}{{ - 360}} = \frac{{ - 7}}{{40}};{\text{ }}40 = {2^3} \cdot 5$

Mẫu này không có ước nguyên tố 3 khác 2 và 5 nên phân số $\frac{{ - 7}}{{40}}$ viết được dưới dạng số thập phân hữu hạn. Ta có:

$\frac{{63}}{{ - 360}} = \frac{{ - 7}}{{40}} = - 0,175$

Ví dụ 2. Trong các phân số sau đây phân số nào viết được dưới dạng số thập phân hữu hạn, phân số nào viết được dưới dạng số thập phân vô hạn tuần hoàn? Viết dạng thập phân của các phân số đó.

$\frac{1}{4};\frac{{ - 5}}{6};\frac{{13}}{{50}};\frac{{ - 17}}{{125}};\frac{{11}}{{45}};\frac{7}{{14}}$

Hướng dẫn giải

$\begin{gathered} \begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \frac{1}{4} = 0,25;{\text{ }} \hfill \\ \end{gathered} &{}&{\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {}&{} \end{array}} \end{array}}&\begin{gathered} \hfill \\ \frac{{ - 5}}{6} = - 0,8\left( 3 \right){\text{;}} \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \frac{{ - 17}}{{125}} = - 0,136; \hfill \\ \end{gathered} &{}&{\begin{array}{*{20}{c}} {}&{} \end{array}}&\begin{gathered} \hfill \\ \frac{{13}}{{50}} = 0,26; \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \frac{{11}}{{45}} = 0,2\left( 4 \right); \hfill \\ \end{gathered} &{\begin{array}{*{20}{c}} {}&{}&{} \end{array}}&{}&\begin{gathered} \hfill \\ \frac{7}{{14}} = \frac{1}{2} = 0,5 \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

Ví dụ 3. Giải thích vì sao các phân số sau viết được dưới dạng số thập phân hữu hạn rồi viết chúng dưới dạng đó:

$\frac{3}{8};\frac{{ - 7}}{5};\frac{{13}}{{20}};\frac{{ - 13}}{{125}}$

Hướng dẫn giải

Các phân số đã cho viết được dưới dạng số thập phân hữu hạn vì các mẫu của chúng không có ước nguyên tố khác 2 và 5:

8 = 2³; 5; 20 = 2²⋅5; 125 = 5³

Ta có: $\frac{3}{8} = 0,375;{\text{ }}\frac{{ - 7}}{5} = - 1,4;{\text{ }}$

$\frac{{13}}{{20}} = 0,65;{\text{ }}\frac{{ - 13}}{{125}} = - 0,104$

Ví dụ 4. Giải thích vì sao các phân số sau viết được dưới dạng số thập phân vô hạn tuần hoàn rồi viết chúng dưới dạng đó:

$\frac{1}{6};\frac{{ - 5}}{{11}};\frac{4}{9};\frac{{ - 7}}{{18}}$

Hướng dẫn giải

Các phân số đã cho viết được dưới dạng số thập phân vô hạn tuần hoàn vì chúng tối giản và các mẫu của chúng có ước nguyên tố khác 2 và 5:

6 = 2⋅3; 11; 9 = 3²; 18 = 2⋅3²

Ta có: $\frac{1}{6} = 0,1\left( 6 \right);{\text{ }}\frac{{ - 5}}{{11}} = - 0,\left( {45} \right);$

$\frac{4}{9} = 0,\left( 4 \right);{\text{ }}\frac{{ - 7}}{{18}} = - 0,3\left( 8 \right)$

Ví dụ 5. Cho $A = \frac{3}{{2 \cdot \boxed{_{}^{}{\text{ }}_{}^{}{\text{ }}}}}$ . Hãy điền vào ô vuông một số nguyên tố có một chữ số để A viết được dưới dạng số thập phân hữu hạn. Có thể điền mấy số như vậy?

Hướng dẫn giải

Có thể điền được ba số:

$A = \frac{3}{{2 \cdot \boxed{\text{2}}}};{\text{ }}A = \frac{3}{{2 \cdot \boxed{\text{3}}}} = \frac{1}{2};{\text{ }}A = \frac{3}{{2 \cdot \boxed{\text{5}}}}$

Ví dụ 6.

a) Trong các phân số sau đây, phân số nào viết được dưới dạng số thập phân hữu hạn, phân số nào viết được dưới dạng số thập phân vô hạn tuần hoàn? Giải thích.

$\frac{5}{8};\frac{{ - 3}}{{20}};\frac{4}{{11}};\frac{{15}}{{22}};\frac{{ - 7}}{{12}};\frac{{14}}{{35}}$

b) Viết các phân số trên dưới dạng số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn (viết gọn với chu kì trong dấu ngoặc).

Hướng dẫn giải

$\begin{gathered} \begin{array}{*{20}{c}} \begin{gathered} \frac{5}{8} = 0,625; \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \begin{array}{*{20}{c}} {}&{}&{} \end{array} \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \frac{{ - 3}}{{20}} = - 0,15; \hfill \\ \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} \begin{gathered} \frac{4}{{11}} = 0,\left( {36} \right); \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \begin{array}{*{20}{c}} {}&{} \end{array} \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \frac{{15}}{{22}} = 0,6\left( {81} \right); \hfill \\ \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} \begin{gathered} \frac{{ - 7}}{{12}} = - 0,58\left( {3;} \right) \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \frac{{14}}{{35}} = 0,4 \hfill \\ \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

Dạng 2. Viết một tỉ số hoặc một phân số dưới dạng số thập phân.

Phương pháp giải

Để viết một tỉ số hoặc một phân số $\frac{a}{b}$ dưới dạng số thập phân ta làm phép chia a ∶ b.

Ví dụ 1. Dùng dấu ngoặc để chỉ rõ chu kì trong thương (viết dưới dạng số thập phân vô hạn tuần hoàn) của các phép chia sau:

a) 8,5 ∶ 3

b) 18,7 ∶ 6

c) 58 ∶ 11

d) 14,2 ∶ 3,33

Hướng dẫn giải

a) 8,5 ∶ 3 = 2,8333… = 2,8(3)

b) 18,7 ∶ 6 = 3,11666… = 3,11(6)

c) 58 ∶ 11 = 5,272727… = 5,(27)

d) 14,2 ∶ 3,33 = 4,264264264… = 4,(264)

Ví dụ 2. Viết các phân số $\frac{1}{{99}},\frac{1}{{999}}$ dưới dạng số thập phân.

Hướng dẫn giải

$\begin{array}{*{20}{c}} \begin{gathered} \frac{1}{{99}} = 0,\left( {01} \right); \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \frac{1}{{999}} = 0,\left( {001} \right) \hfill \\ \hfill \\ \end{gathered} \end{array}$

Dạng 3. Viết số thập phân hữu hạn dưới dạng phân số tối giản

Phương pháp giải

+) Viết số thập phân hữu hạn dưới dạng một phân số có tử là số nguyên tạo bởi phần nguyên và phần thập phân của số đó, mẫu là một lũy thừa của 10 với số mũ bằng số chữ số ở phần thập phân của số đã cho;

+) Rút gọn phân số nói trên.

Ví dụ 1. Viết các số thập phân hữu hạn sau đây dưới dạng phân số tối giản:

a) 0,32

b) –0,124

c) 1,28

d) –3,12

Hướng dẫn giải

a) $0,32 = \frac{{32}}{{{{10}^2}}} = \frac{{32}}{{100}} = \frac{8}{{25}}$

b) $1,28 = \frac{{128}}{{100}} = \frac{{32}}{{25}}$

c) $- 0,124 = \frac{{ - 124}}{{{{10}^3}}} = \frac{{ - 124}}{{1000}} = \frac{{31}}{{250}}$

d) $- 3,12 = \frac{{ - 312}}{{100}} = - \frac{{78}}{{25}}$

Dạng 4. Viết số thập phân vô hạn tuần hoàn dưới dạng phân số tối giản

Phương pháp giải

+) Để giải dạng toán này cần có kiến thức bổ sung sau đây:

+) Số thập phân vô hạn tuần hoàn gọi là đơn nếu chu kì bắt đầu ngay sau dấu phẩy, ví dụ 0,(31); gọi là tạp nếu chu kì không bắt đầu ngay sau dấu phẩy, ví dụ 0,3(13).

+) Phần thập phân đứng trước chu kỳ gọi là phần bất thường.

+) Người ta đã chứng minh được các quy tắc sau:

⋄ Muốn viết phần thập phân của số thập phân vô hạn tuần hoàn đơn dưới dạng phân số, ta lấy chu kì làm tử, còn mẫu là một số gồm các chữ số 9, số chữ số 9 bằng số chữ số của chu kì.

Ví dụ: $\begin{array}{*{20}{c}} \begin{gathered} 0,\left( {31} \right) = \frac{{31}}{{99}}; \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} 1,\left( 3 \right) = 1\frac{3}{9} = 1\frac{1}{3} \hfill \\ \hfill \\ \end{gathered} \end{array}$

⋄ Muốn viết phần thập phân của số thập vô hạn tuần hoàn tạp dưới dạng phân số, ta lấy số gồm phần bất thường và chu kì trừ đi phần bất thường làm tử, còn mẫu là một số gồm các chữ số 0 bằng số chữ số của phần bất thường.

Ví dụ: $0,12\left( {53} \right) = \frac{{1253 - 12}}{{9900}} = \frac{{1241}}{{9900}}$

$2,3\left( {41} \right) = 2 + 0,3\left( {41} \right) = 2 + \frac{{341 - 3}}{{990}} = 2\frac{{169}}{{495}}$

Ví dụ 1. Đố: Các số sau đây có bằng nhau không? 0,(31); 0,3(13)

Hướng dẫn giải

Áp dụng hai quy tắc viết số thập phân vô hạn tuần hoàn (đơn và tạp) dưới dạng phân số, ta có:

$\begin{gathered} 0,\left( {31} \right) = \frac{{31}}{{99}} \hfill \\ 0,3\left( {13} \right) = \frac{{313 - 3}}{{990}} = \frac{{310}}{{990}} = \frac{{31}}{{99}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \Rightarrow 0,\left( {31} \right) = 0,3\left( {13} \right) \hfill \\ \end{gathered}$

Cách khác:

$\begin{gathered} 0,\left( {31} \right) = 0,\left( {01} \right) \cdot 31 = \frac{1}{{99}} \cdot 31 = \frac{{31}}{{99}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ 0,3\left( {13} \right) = 0,3 + 0,0\left( {13} \right) = 0,3 + \frac{1}{{10}} \cdot 0,\left( {01} \right) \cdot 13 \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array} = 0,3 + \frac{{13}}{{990}} = \frac{{31}}{{99}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \Rightarrow 0,\left( {31} \right) = 0,3\left( {13} \right) \hfill \\ \end{gathered}$

Để viết 0,(31) dưới dạng phân số còn có thể làm như sau:

Đặt a = 0,(31) = 0,313131… – 0,313131…

Suy ra: 100a – a = 31,313131… – 0,313131…

⇔ 99a = 31 ⇔ a = $\frac{{31}}{{99}}$

Để viết 0,3(13) dưới dạng phân số có thể làm như sau:

Đặt b = 0,3(13) thì 1000b = 313,131313…; 10b = 3,131313…

Suy ra: 990b = 310 ⇒ b = $\frac{{31}}{{99}}$

Làm tròn số

Tóm tắt lí thuyết

Quy ước làm tròn số

+) Trường hợp 1. Nếu chữ số đầu tiên trong các chữ số bị bỏ đi nhỏ hơn 5 thì ta giữ nguyên bộ phận còn lại. Trong trường hợp số nguyên thì ta thay các chữ số bị bỏ đi bằng các chữ số 0.

+) Trường hợp 2. Nếu chữ số đầu tiên trong các chữ số bị bỏ đi lớn hơn hoặc bằng 5 thì ta cộng thêm 1 vào chữ số cuối cùng của bộ phận còn lại. Trong trường hợp số nguyên thì ta thay các chữ số bị bỏ đi bằng các chữ số 0.

Các dạng toán

Dạng 1. Làm tròn các số theo một yêu cầu cho trước

Phương pháp giải

+) Áp dụng quy ước làm tròn số trong hai trường hợp.

+) Chú ý hiểu đúng các cụm từ “làm tròn số đến chữ số thập phân thứ…”, “làm tròn số đến hàng…”.

Ví dụ 1.

a) Làm tròn số 79,3826 đến chữ số thập phân thứ ba;

b) Làm tròn số 79,3826 đến chữ số thập phân thứ hai;

c) Làm tròn số 79,3826 đến chữ số thập phân thứ nhất.

Hướng dẫn giải

a) 79,383

b) 79,38

c) 79,4

Ví dụ 2. Làm tròn các số sau đến chữ số thập phân thứ hai:

7,923; 17,418; 79,1364; 50,401; 0,155; 60,996

Hướng dẫn giải

7,923 ≈ 7,92

17,418 ≈ 17,42

79,1364 ≈ 79,14

50,401 ≈ 50,40

0,155 ≈ 0,16

60,996 ≈ 61,00

Ví dụ 3. Kết quả cuộc tổng điều tra dân số nước ta tính đến 0 giờ ngày 01/04/1999 cho biết: Dân số nước ta là 76 324 753 người trong đó có 3695 cụ từ 100 tuổi trở lên.

Hướng dẫn giải

+) Làm tròn số 76 324 753:

76 324 750 (tròn chục)

76 324 800 (tròn trăm)

76 325 000 (tròn nghìn)

+) Làm tròn số 3695:

3700 (tròn chục)

3700 (tròn trăm)

4000 (tròn nghìn).

Dạng 2. Giải bài toán rồi làm tròn kết quả.

Phương pháp giải

Căn cứ vào đề bài, giải bài toán rồi làm tròn kết quả theo yêu cầu của đề bài.

Ví dụ 1. Hết học kì I, điểm toán của bạn Cường như sau:

Hệ số 1: 7; 8; 6; 10.

Hệ số 2: 7; 6; 5; 9.

Hệ số 3: 8.

Em hãy tính điểm trung bình môn Toán học kì I của bạn Cường

(Làm tròn đến chữ số thập phân thứ nhất)

Hướng dẫn giải

Điểm trung bình môn Toán học kì I của bạn Cường là:

$\frac{{7 + 8 + 6 + 10 + 2 \cdot \left( {7 + 6 + 5 + 9} \right) + 3 \cdot 8}}{{15}} = 7,2\left( 6 \right)$

7,2(6) ≈ 7,3 (làm tròn đến chữ số thập phân thứ nhất).

Ví dụ 2. Khi nói đến tivi loại 21 in – sơ ta hiểu rằng đường chéo màn hình của ti vi loại này dài 21 in – sơ (in – sơ (inch) kí hiệu “in” là đơn vị đo chiều dài theo hệ thống Anh, Mỹ (1 in ≈ 2,54 cm). Vì vậy đường chéo của màn hình loại này dài khoảng bao nhiêu centimet?

Hướng dẫn giải

Đáp số: 21 in ≈ 53,34 cm.

Ví dụ 3. Tính chu vi và diện tích của một mảnh vườn hình chữ nhật có chiều dài là 10,234 m và chiều rộng là 4,7 m (làm tròn đến hàng đơn vị).

Hướng dẫn giải

Đáp số: Chu vi ≈ 30 m, diện tích ≈ 48 m²

Ví dụ 4. Pao (pound) kí hiệu “lb” còn gọi là cân Anh, là đơn vị đo khối lượng của Anh, 1lb ≈ 0,45 kg. Hỏi 1 kg gần bằng bao nhiêu pao (làm tròn đến chữ số thập phân thứ hai)?

Đáp số:

1 kg ≈ 2,22 lb.

Ví dụ 5. Tính giá trị (làm tròn đến hàng đơn vị) của các biểu thức sau bằng hai cách:

Cách 1: Làm tròn các số trước rồi mới thức hiện phép tính:

Cách 2: Thực hiện phép tính rồi làm tròn kết quả:

a) 14,61 – 7,15 + 3,2

b) 7,56⋅5,173

Hướng dẫn giải

a) Hai cách đều cho kết quả: ≈ 11.

b) Cách 1: ≈ 40; cách 2: ≈ 39.

c) Hai cách đều cho ra kết quả: ≈ 5.

d) Cách 1: ≈ 3; cách 2: ≈ 2.

Dạng 3. Áp dụng quy ước làm tròn số để ước lượng kết quả các phép tính

Phương pháp giải

Để ước lượng kết quả các phép tính, ta thường áp dụng quy ước làm tròn số để làm tròn chữ số ở hàng cao nhất của mỗi số tham gia vào phép tính.

Ví dụ: Số 7329 được làm tròn số đến chữ số ở hàng cao nhất là ≈ 7000.

Ví dụ 1. Hãy ước lượng kết quả các phép tính sau:

a) 495⋅52

b) 82,36⋅5,1

c) 6730 ∶ 48

Hướng dẫn giải

a) 495⋅52 ≈ 500⋅50 = 25000

Tích phải tìm có 5 chữ số và xấp xỉ 25000.

b) 82,36⋅5,1 ≈ 80⋅5 = 400

Tích phải tìm khoảng trên 400.

c) 6730 ∶ 48 ≈ 7000 ∶ 50 = 140

Thương phải tìm xấp xỉ 140.

Số vô tỉ. Khái niệm về căn bậc hai

Tóm tắt lý thuyết

Số vô tỉ:

Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.

Tập hợp các số vô tỉ được kí hiệu là I

Khái niệm về căn bậc hai.

Căn bậc hai của một số a không âm là số x sao cho x² = a.

Số dương a có đúng hai căn bậc hai là $\sqrt a$ và $- \sqrt a$

Số 0 chỉ co một căn bậc hai là số 0: $\sqrt 0 = 0$

Các dạng toán

Dạng 1. Liên hệ giữa lũy thừa bậc hai và căn bậc hai

Phương pháp giải

Nếu x² = a (x ≥ 0, a ≥ 0) thì $\sqrt a = x$ và ngược lại.

(Lũy thừa bậc hai và căn bậc hai của một số không âm là hai phép toán ngược nhau).

Ví dụ 1. Theo mẫu: vì 2² = 4 nên $\sqrt 4 = 2$ , hãy hoàn thành bài tập sau:

a) Vì 5² = … nên $\sqrt {...} = 5$

b) Vì 7^… = 49 nên … = 7

c) Vì 1^… = 1 nên $\sqrt 1 = ...$

d) Vì ${\left( {\frac{2}{3}} \right)^2} = ...$ nên … = …

Hướng dẫn giải

a) Vì 5² = 25 nên $\sqrt {{\text{25}}} = 5$

b) Vì 7² = 49 nên $\sqrt {49} = 7$

c) Vì 1² = 1 nên $\sqrt 1 = 1$

d) Vì ${\left( {\frac{2}{3}} \right)^2} = \frac{4}{9}$ nên $\sqrt {\frac{4}{9}} = \frac{2}{3}$

Dạng 2. Tìm căn bậc hai của một số cho trước

Phương pháp giải

+) Sử dụng định nghĩa của căn bậc hai.

+) Lưu ý: Số dương có hai căn bậc hai là hai số đối nhau; số âm không có căn bậc hai.

+) Khi viết $\sqrt a$ ta phải có a ≥ 0 và $\sqrt a \geqslant 0$

+) Có thể sử dụng máy tính bỏ túi (nút dấu căn bậc hai).

Ví dụ 1. Tìm các căn bậc hai của 16.

Hướng dẫn giải

Các căn bậc hai của 16 là 4 và –4, vì ta có: 4² = 16 và (–4)² = 16

Ví dụ 2. Viết các căn bậc hai của 3; 10; 25.

Hướng dẫn giải

a) Các căn bậc hai của 3 là $\sqrt 3 ;{\text{ }} - \sqrt 3$

b) Các căn bậc hai của 10 là $\sqrt {10} ;{\text{ }} - \sqrt {10}$

c) Các căn bậc hai của 25 là $\sqrt {25} = 5;{\text{ }} - \sqrt {25} = - 5$

Ví dụ 3. Ta có:

$\sqrt {25} = 5;{\text{ }} - \sqrt {25} = - 5;{\text{ }}\sqrt {{{\left( { - 5} \right)}^2}} = \sqrt {25} = 5{\text{ }}$

Theo mẫu trên hãy tính:

a) $\sqrt {36}$

b) $- \sqrt {16}$

c) $\sqrt {\frac{9}{{25}}}$

d) $\sqrt {{3^2}}$

e) $\sqrt {{{\left( { - 3} \right)}^2}}$

Hướng dẫn giải

a) $\sqrt {36} = 6$

b) $- \sqrt {16} = - 4$

c) $\sqrt {\frac{9}{{25}}} = \frac{3}{5}$

d) $\sqrt {{3^2}} = 3$

e) $\sqrt {{{\left( { - 3} \right)}^2}} = \sqrt 9 = 3$

Dạng 3. Tìm một số biết căn bậc hai của nó

Phương pháp giải

Nếu $\sqrt x = a{\text{ }}\left( {\sqrt a \geqslant 0} \right) \Rightarrow x = {a^2}$

Ví dụ 1. Nếu $\sqrt x = 2$ thì x² bằng:

A. 2

B. 4

C. 8

D. 16

Hãy chọn câu trả lời đúng.

Hướng dẫn giải

Chọn D

Giải thích:

$\sqrt x = 2 \Rightarrow x = {2^2} = 4 \Rightarrow {x^2} = {4^2} = 16$

Ví dụ 2. Điền số thích hợp vào ô trống:

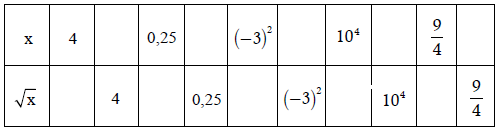
Hướng dẫn giải

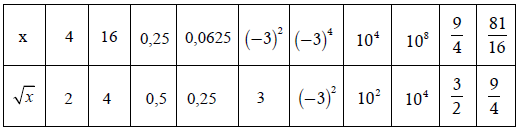
Dạng 4. Sử dụng máy tính bỏ túi để tính căn bậc hai của một số cho trước

Phương pháp giải

Nắm vững cách sử dụng nút dấu căn bậc hai của máy tính bỏ túi.

Ví dụ 1. Dùng máy tính bỏ túi để tính:

$\sqrt {3783025} ;{\text{ }}\sqrt {1125 \cdot 45} ;{\text{ }}\sqrt {\frac{{0,3 + 1,2}}{{0,7}}} ;{\text{ }}\sqrt {\frac{{6,4}}{{1,2}}}$

Hướng dẫn giải

Số thực

Tóm tắt lý thuyết

Số thực

+) Số hữu tỉ và số vô tỉ được gọi chung là số thực

Tập hợp các số thực được ký hiệu là ℝ

+) Nếu a là số thực thì a biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn. Khi đó, ta có thể so sánh hai số thực tương tự như so sánh hai số hữu tỉ viết dưới dạng thập phân.

Với a, b là hai số thực dương, nếu $a > b \Rightarrow \sqrt a > \sqrt b$

Trục số thực

Mỗi số thực được biểu diễn bởi một điểm trên trục số

Mỗi điểm trên trục số biểu diễn một số thực

Các phép toán

Trong tập hợp số thực ℝ, ta cũng định nghĩa các phép toán cộng, trừ, nhân, chia, nâng lên lũy thừa và khai căn. Các phép toán trong tập hợp số thực cũng có các tính chất như các phép toán trong tập hợp các số hữu tỉ.

Các dạng toán

Dạng 1. Câu hỏi và bài tập về định nghĩa các tập hợp số

Phương pháp giải

+) Nắm vững các ký hiệu tập hợp số

ℕ: tập hợp các số tự nhiên

ℤ: tập hợp các số nguyên

ℚ: tập hợp các số hữu tỉ

ℝ: tập hợp các số thực

I: tập hợp các số vô tỉ

+) Nắm vững quan hệ giữa các tập hợp số nói trên

ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ; I ⊂ ℝ

Ví dụ 1. Điền dấu ∈, ∉, ⊂ thích hợp vào ô trống:

3 ℚ

3 ℝ

3 I

–2,53 ℚ

0,2(35) I

ℕ ℤ

I ℝ

Hướng dẫn giải

3 ℚ

3 ℝ

3 I

–2,53 ℚ

0,2(35) I

ℕ ℤ

I ℝ

Ví dụ 2. Điền vào chỗ trống (…) trong các phát biểu sau:

a) Nếu a là số thực thì a là số … hoặc số …

b) Nếu b là số vô tỉ thì b viết dưới dạng …

Hướng dẫn giải

a) Nếu a là số thực thì a là số hữu tỉ hoặc số vô tỉ

b) Nếu b là số vô tỉ thì b viết dưới dạng số thập phân vô hạn không tuần hoàn

Ví dụ 3. Trong các câu sau đây, câu nào đúng câu nào sai:

a) Nếu a là số nguyên thì a cũng là số thực

b) Chỉ có số 0 không là số hữu tỉ dương và cũng không là số hữu tỉ âm

c) Nếu a là số tự nhiên thì a không phải là số vô tỉ

Hướng dẫn giải

Các câu a), c) đúng

Câu b) sai vì ngoài số 0 ra, số vô tỉ cũng không là số hữu tỉ dương và cũng không là số hữu tỉ âm

Ví dụ 4. Hãy tìm các tập hợp

a) ℚ ∩ I

b) ℝ ∩ I

Hướng dẫn giải

a) ℚ ∩ I = ∅

b) ℝ ∩ I = I

Dạng 2. So sánh các số thực

Phương pháp giải

Cần nắm vững:

+) Với hai số thực x, y bất kỳ, ta luôn có x = y hoặc x < y hoặc x > y.

+) Các số thực lớn hơn 0 gọi là số thực dương, các số thực nhỏ hơn 0 gọi là các số thực âm. Số 0 không là số thực dương cũng không là số thực âm.

+) Việc so sánh các số thực dương làm tương tự như so sánh các số hữu tỉ.

+) Với a, b là hai số thực dương, nếu $a > b \Rightarrow \sqrt a > \sqrt b$

Ví dụ 1. Điền chữ số thích hợp vào ô vuông:

a) –3,02 < –3,1

b) –7,58 > –7,513

c) –0,4854 < –0,49826

d) –1,0765 < –1,892

Hướng dẫn giải

a) –3,02 < –3,01

b) –7,508 > –7,513

c) –0,49854 < –0,49826

d) –1,90765 < –1,892

Ví dụ 2. Sắp xếp các số thực: –3,2; 1; $- \frac{1}{2}$ ; 7,4; 0; –1,5

a) Theo thứ tự từ nhỏ đến lớn

b) Theo thứ tự từ nhỏ đến lớn các giá trị tuyệt đối của chúng.

Hướng dẫn giải

a) –3,2 < –1,5 < $- \frac{1}{2}$ < 0 < 1 < 7,4

b) 0 < $\frac{1}{2}$ < 1 < 1,5 < 3,2 < 7,4. Do đó:

$\left| 0 \right| < \left| { - \frac{1}{2}} \right| < \left| 1 \right| < \left| { - 1,5} \right| < \left| { - 3,2} \right| < \left| {7,4} \right|$

Ví dụ 3.

1) Chứng minh rằng với a, b là hai số thực dương, ta có:

a) Nếu a > b thì a² > b²

b) Nếu a² > b² thì a > b

2) Chứng minh rằng với a, b là hai số thực dương, ta có:

a) Nếu a > b thì $\sqrt a > \sqrt b$

b) Nếu $\sqrt a > \sqrt b$ thì a > b

3) Áp dụng: So sánh (không dùng máy tính)

a) 5 và $\sqrt {29}$

b) $3\sqrt 2$ và $2\sqrt 3$

Hướng dẫn giải

a) a, b là hai số thực dương nên a + b > 0. Nếu a > b thì a – b > 0

Xét tích (a + b)(a – b)

= a(a – b) + b(a – b)

= a² – ab + ab – b²

= a² – b²

Vì a + b > 0, a – b > 0 nên (a + b)(a – b) > 0 hay a² – b² > 0. Suy ra: a² > b²

b) Nếu a² > b² thì a² – b² > 0 hay (a + b)(a – b) > 0

a + b > 0 (vì a > 0, b > 0) suy ra a – b > 0 hay a > b

2) a, b là hai số thực dương nên $a = {\left( {\sqrt a } \right)^2},b = {\left( {\sqrt b } \right)^2}$ . Theo câu 1, ta có:

a) Nếu a > b thì ${\left( {\sqrt a } \right)^2} > {\left( {\sqrt b } \right)^2} \Rightarrow \sqrt a > \sqrt b$

b) Nếu $\sqrt a > \sqrt b$ thì ${\left( {\sqrt a } \right)^2} > {\left( {\sqrt b } \right)^2} \Rightarrow a > b$

a) Theo kết quả ở câu 1, ta có: 29 > 25 hay ${\left( {\sqrt {29} } \right)^2} > {5^2}$ nên $\sqrt {29} > 5$

b) Xét ${\left( {3\sqrt 2 } \right)^2}$ và ${\left( {2\sqrt 3 } \right)^2}$ . Ta có:

$\begin{gathered} {\left( {3\sqrt 2 } \right)^2} = 3\sqrt 2 \cdot 3\sqrt 2 = 9 \cdot {\left( {\sqrt 2 } \right)^2} = 18\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ {\left( {2\sqrt 3 } \right)^2} = 2\sqrt 3 \cdot 2\sqrt 3 = 4 \cdot {\left( {\sqrt 3 } \right)^2} = 12\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered}$

Vì 18 > 12 hay ${\left( {3\sqrt 2 } \right)^2} > {\left( {2\sqrt 3 } \right)^2}$ nên suy ra $3\sqrt 2 > 2\sqrt 3$

Dạng 3. Tìm số chưa biết trong một đẳng thức

Phương pháp giải

+) Sử dụng tính chất của các phép toán

+) Sử dụng quan hệ giữa các số hạng trong một tổng, một hiệu; quan hệ giữa các thừa số trong một tích, quan hệ giữa số bị chia, số chia và thương trong một phép chia

+) Sử dụng quy tắc dấu ngoặc, chuyển vế

Ví dụ 1. Tìm x, biết:

a) 3,2x + (–1,2)x + 2,7 = –4,9

b) (–5,6)x + 2,9x – 3,86 = –9,8

Hướng dẫn giải

a) 3,2x + (–1,2)x + 2,7 = –4,9

⇔ (3,2 – 1,2)x = –4,9 – 2,7

⇔ 2x = –7,6

⇔ x = 3,8

b) (–5,6)x + 2,9x – 3,86 = –9,8

⇔ (–5,6 + 2,9)x = –9,8 + 3,86

⇔ –2,7x = –5,94

⇔ x = 2,2

Ví dụ 2. Tìm x, biết:

$\left( {1\frac{3}{7} - x} \right) \cdot 3\frac{1}{3} = - 2\frac{{31}}{{42}}$

Hướng dẫn giải

$\begin{gathered} \left( {1\frac{3}{7} - x} \right) \cdot 3\frac{1}{3} = - 2\frac{{31}}{{42}} \hfill \\ \Leftrightarrow 1\frac{3}{7} - x = - 2\frac{{31}}{{42}}:3\frac{1}{3}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \Leftrightarrow x = 1\frac{3}{7} + \frac{{23}}{{28}} \hfill \\ \Leftrightarrow x = 2\frac{1}{4}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Dạng 4. Tìm giá trị của biểu thức

Phương pháp giải

+) Thực hiện phối hợp các phép tính cộng, trừ, nhân, chia, lũy thừa, chú ý thực hiện đúng theo thứ tự đã quy định

+) Rút gọn các phân số khi có thể

+) Chú ý vận dụng tính chất các phép toán để tính toán được thuận tiện

Ví dụ 1. Thực hiện các phép tính

a) $\left( {\frac{9}{{25}} - 2 \cdot 18} \right):\left( {3\frac{4}{5} + 0,2} \right)$

b) $\frac{5}{{18}} - 1,456:\frac{7}{{25}} + 4,5 \cdot \frac{4}{5}$

Hướng dẫn giải

a) $\left( {\frac{9}{{25}} - 2 \cdot 18} \right):\left( {3\frac{4}{5} + 0,2} \right)$

$\begin{gathered} = \left( {0,36 - 36} \right):\left( {3,8 + 0,2} \right) \hfill \\ = - 35,64:4\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ = - 8,91 \hfill \\ \end{gathered}$

b) $\frac{5}{{18}} - 1,456:\frac{7}{{25}} + 4,5 \cdot \frac{4}{5}$

$\begin{gathered} = \frac{5}{{18}} - 1,456:0,28 + 4,5 \cdot 0,8 \hfill \\ = \frac{5}{{18}} - 5,2 + 3,6\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ = \frac{5}{{18}} - 1,6 = \frac{5}{{18}} - \frac{8}{5} \hfill \\ = \frac{{ - 119}}{{90}} = - 1\frac{{29}}{{90}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Ví dụ 2. Tính giá trị của các biểu thức

$\begin{gathered} A = - 5,13:\left( {5\frac{5}{{28}} - 1\frac{8}{9} \cdot 1,25 + 1\frac{{16}}{{63}}} \right) \hfill \\ B = \left( {3\frac{1}{3} \cdot 1,9 + 19,5:4\frac{1}{3}} \right)\left( {\frac{{62}}{{75}} - \frac{4}{{25}}} \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Hướng dẫn giải

$\begin{gathered} A = - 5,13:\left( {5\frac{5}{{28}} - 1\frac{8}{9} \cdot 1,25 + 1\frac{{16}}{{63}}} \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ _{}^{}{\text{ }}_{}^{}{\text{ }} = - 5,13:\left( {5\frac{5}{{28}} - \frac{{19}}{9} \cdot \frac{5}{4} + 1\frac{{16}}{{63}}} \right) \hfill \\ _{}^{}{\text{ }}_{}^{}{\text{ }} = - 5,13:\left( {5\frac{5}{{28}} - 2\frac{{13}}{{26}} + 1\frac{{16}}{{63}}} \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ _{}^{}{\text{ }}_{}^{}{\text{ }} = - 5,13:\left[ {\left( {5 - 2 + 1} \right) + \left( {\frac{5}{{28}} - \frac{{13}}{{26}} + \frac{{16}}{{63}}} \right)} \right] \hfill \\ _{}^{}{\text{ }}_{}^{}{\text{ }} = - 5,13:\left( {4 + \frac{1}{{14}}} \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ _{}^{}{\text{ }}_{}^{}{\text{ }} = - 5,13:\frac{{57}}{{14}} \hfill \\ _{}^{}{\text{ }}_{}^{}{\text{ }} = \frac{{ - 5,13 \cdot 14}}{{57}} = - 1,26\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ B = \left( {3\frac{1}{3} \cdot 1,9 + 19,5:4\frac{1}{3}} \right)\left( {\frac{{62}}{{75}} - \frac{4}{{25}}} \right) \hfill \\ _{}^{}{\text{ }}_{}^{}{\text{ }} = \left( {\frac{{10}}{3} \cdot \frac{{19}}{{10}} + \frac{{39}}{2} \cdot \frac{{13}}{3}} \right)\left( {\frac{{62}}{{75}} - \frac{4}{{25}}} \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ _{}^{}{\text{ }}_{}^{}{\text{ }} = \left( {\frac{{19}}{3} + \frac{{39 \cdot 3}}{{2 \cdot 13}}} \right) \cdot \frac{2}{3} \hfill \\ _{}^{}{\text{ }}_{}^{}{\text{ }} = \frac{{38}}{9} + \frac{{39}}{{13}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ _{}^{}{\text{ }}_{}^{}{\text{ }} = 4\frac{2}{9} + 3 = 7\frac{2}{9} \hfill \\ \end{gathered}$

Thầy Tú dạy toán