Trường hợp bằng nhau thứ nhất của tam giác
Tóm tắt lí thuyết
Hai tam giác bằng nhau
+) Hai tam giác ABC và A′B′C′ bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.
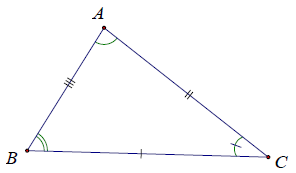

+) Tức là: △ABC = △A′B′C′
Ở đây hai đỉnh A và A′ (B và B′, C và C′) là hai đỉnh tương ứng. Hai góc và
(
và
,
và
) là hai góc tương ứng. Hai cạnh AB và A′B′ (BC và B′C′, AC và A′C′) là hai cạnh tương ứng.
Trường hợp bằng nhau thứ nhất của hai tam giác
Trường hợp bằng nhau cạnh – cạnh – cạnh (c.c.c): Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Tức là: △ABC và △A′B′C′ có AB = A′B′, BC = B′C′, AC = A′C′ thì △ABC = △A′B′C′
Phân dạng bài tập
Dạng 1. Bài tập lí thuyết: Viết kí hiệu về sự bằng nhau của hai tam giác, từ kí hiệu bằng nhau của hai tam giác suy ra các cạnh – góc bằng nhau.
Phương pháp giải
+) Từ kí hiệu tam giác bằng nhau suy ra các cạnh và các góc bằng nhau đúng thứ tự tương ứng.
Ví dụ: △ABC = △A′B′C′
+) Ngược lại, khi viết kí hiệu tam giác bằng nhau lưu ý kiểm tra lại xem các góc hay cạnh tương ứng đã bằng nhau thỏa mãn yêu cầu đề bài chưa.
Bài tập
Bài 1. Cho biết △ABC = △HIK. Hãy viết đẳng thức trên dưới một vài dạng khác.
Hướng dẫn giải
Viết đẳng thức △ABC = △HIK dưới một vài dạng khác: △ACB = △KHI, △CAB = △KHI,…
Bài 2. Cho △ABC = △DEF. Hãy chỉ ra các góc, các cạnh tương ứng bằng nhau.
Hướng dẫn giải
△ABC = △DEF
Bài 3. Cho △MNP = △IHG. Hãy chỉ ra các góc, các cạnh tương ứng bằng nhau.
Hướng dẫn giải
△MNP = △IHG
Bài 4. Cho hai tam giác bằng nhau: △ABC và △HIK. Viết kí hiệu về sự bằng nhau của 2 tam giác theo thứ tự đỉnh tương ứng, biết rằng:
Hướng dẫn giải
Hai tam giác △ABC và △HIK bằng nhau và thì kí hiệu bằng nhau của hai tam giác là: △ABC = △HIK.
Bài 5. Cho hai tam giác bằng nhau: △ABC và △HIK. Viết kí hiệu về sự bằng nhau của 2 tam giác theo thứ tự đỉnh tương ứng, biết rằng: AB = KI; BC = KH.
Hướng dẫn giải
Hai tam giác △ABC và △HIK bằng nhau và AB = KI; BC = KH thì kí hiệu bằng nhau của hai tam giác là: △ABC = △IKH.
Bài 6. Cho hai tam giác bằng nhau: △ABC và △HIK. Viết kí hiệu về sự bằng nhau của 2 tam giác theo thứ tự đỉnh tương ứng, biết rằng:
Hướng dẫn giải
Hai tam giác △ABC và △HIK bằng nhau và ; thì kí hiệu bằng nhau của hai tam giác là: △ABC = △KIH.
Dạng 2. Biết hai tam giác bằng nhau và một số điều kiện, tính số đo góc, độ dài cạnh của tam giác
Phương pháp giải
+) Từ kí hiệu tam giác bằng nhau suy ra các cạnh và các góc tương ứng bằng nhau.
+) Lưu ý các bài toán: tổng – hiệu, tổng – tỉ, hiệu – tỉ.
+) Sử dụng định lí tổng ba góc trong một tam giác.
Bài tập
Bài 1. Cho △ABC = △DEF với AB = 7 cm, BC = 5 cm, DF = 6 cm. Tính các cạnh còn lại của mỗi tam giác.
Hướng dẫn giải
Vì △ABC = △DEF nên AB = DE; BC = EF; AC = DF (các cạnh tương ứng).
Mà AB = 7 cm, BC = 5 cm, DF = 6 cm suy ra DE = 7 cm, EF = 5 cm, AC = 6 cm
Bài 2. Cho △ABC = △DEF với BC = 6 cm, AB = 8 cm, DF = 10 cm.
a) Tính các cạnh còn lại của mỗi tam giác.
b) Tính chu vi của mỗi tam giác.
Hướng dẫn giải
a) Vì △ABC = △DEF nên AB = DE, BC = EF, AC = DF (các cạnh tương ứng).
Mà BC = 6 cm, AB = 8 cm, DF = 10 cm suy ra EF = 6 cm, DE = 8 cm, AC = 10 cm
b) Chu vi △ABC là: AB + BC + AC = 8 + 6 + 10 = 24 cm.
Chu vi △DEF là: DE + EF + DF = 8 + 6 + 10 = 24 cm.
Bài 3. Cho △ABC = △IHK. Tính chu vi của mỗi tam giác, biết rằng AB = 6 cm, AC = 8 cm, HK =12 cm.
Hướng dẫn giải
Vì △ABC = △IHK nên AB = IH, BC = HK, AC = IK (các cạnh tương ứng).
Mà AB = 6 cm, AC = 8 cm, HK =12 cm suy ra IH = 6 cm, IK = 8 cm, BC =12 cm.
Chu vi △ABC là: AB + BC + AC = 6 + 12 + 8 = 26 cm.
Chu vi △IHK là: IH + IK + HK = 6 + 8 + 12 = 26 cm.
Bài 4. Cho △ABC = △MNP, biết
a) Tìm các góc tương ứng bằng nhau.
b) Tính các góc còn lại của hai tam giác.
Hướng dẫn giải
a) Vì △ABC = △MNP (các góc tương ứng).
b) Vì mà
Vì mà
Xét △ABC có: (định lí tổng ba góc trong một tam giác)
Mà
Vậy
Bài 5. Cho △ABC = △DEF, biết . Tính số đo góc
.
Hướng dẫn giải
Vì △ABC = △DEF ⇒ (các góc tương ứng) mà
nên
.
Vậy
Bài 6. Cho △ABC = △MNP. Biết AB + BC = 7 cm, MN – NP = 3 cm, MP = 4 cm. Tính độ dài các cạnh mỗi tam giác.
Hướng dẫn giải
Vì △ABC = △MNP nên AB = MN, BC = NP, AC = MP (các cạnh tương ứng).
Mà MP = 4 cm ⇒ AC = 4cm
MN – NP = 3 cm ⇒ AB – BC = 3 cm.
Lại có: AB + BC = 7 cm suy ra:
AB = (7 + 3) ∶ 2 = 5 cm, BC = (7 – 3) ∶ 2 = 2 cm
⇒ NP = BC = 2 cm, MN = AB = 5cm.
Vậy △ABC có: AB = 5 cm, BC = 2 cm, AC = 4 cm;
△MNP có: MN = 5 cm, NP = 2 cm, MP = 4 cm.
Bài 7. Cho △ABC = △IJK. Biết AB + BC = 9 cm, IJ = 2JK, AC = 5 cm. Tính chu vi mỗi tam giác.
Hướng dẫn giải
Vì △ABC = △IJK nên AB = IJ, BC = JK, AC = IK (các cạnh tương ứng).
Mà AC = 5 cm ⇒ IK = 5 cm
IJ = 2JK ⇒ AB = 2BC
Lại có: Biết AB + BC = 9 cm
⇒ BC = 9 ∶ (1 + 2) = 3 cm, AB = 2BC = 6 cm
⇒ IJ = AB = 6 cm, IK = BC = 3 cm
Chu vi △ABC là: AB + BC + AC = 6 + 3 + 5 = 14 cm
Chu vi △IJK là: IJ + JK + IK = 6 + 3 + 5 = 14 cm
Bài 8. Cho △ABC = △IJK. Biết AB – BC = 10 cm, 3IJ = 5JK, AC = 20 cm. Tính chu vi mỗi tam giác.
Hướng dẫn giải
Vì △ABC = △IJK nên AB = IJ, BC = JK, AC = IK (các cạnh tương ứng).
Mà AC = 20 cm ⇒ IK = 20 cm
Lại có: AB – BC = 10 cm
⇒ AB = 10 ∶ (5 – 3) ⋅ 5 = 25 cm
⇒ BC = 10 ∶ (5 – 3) ⋅ 3 = 15 cm
Chu vi △ABC là: AB + BC + AC = 25 + 15 + 20 = 60 cm
Chu vi △IJK là: IJ + JK + IK = 25 + 15 + 20 = 60 cm
Bài 9. Cho Cho △ABC = △MNP, biết . Tính số đo các góc còn lại của mỗi tam giác.
Hướng dẫn giải
Vì △ABC = △MNP nên (các góc tương ứng).
Vì mà
Xét △MNP có: (định lí tổng ba góc trong một tam giác)
Mà nên
Suy ra:
Vậy
Bài 10. Cho △ABC = △DEF với . Tính số đo các góc của △ABC.
Hướng dẫn giải
Vì △ABC = △DEF nên (các góc tương ứng).
Mà
Xét △ABC có: (định lí tổng ba góc trong một tam giác)
Mà
Vậy
Bài 11. Cho △ABC = △MNP, biết . Tính số đo các góc còn lại của △MNP.
Hướng dẫn giải
Vì △ABC = △MNP nên (hai góc tương ứng)
Mà
Xét △MNP có: (định lí tổng ba góc trong một tam giác)
Mặt khác:
Vậy
Bài 12. Cho △ABC = △MNP biết A ∶ B ∶ C = 3 ∶ 4 ∶ 5. Tính các góc của △MNP.
Hướng dẫn giải
Vì
Xét △ABC có: (định lí tổng ba góc trong một tam giác)
⇒ 3k + 4k + 5k = 180°
⇒ 12k = 180°
⇒ k = 15°
Vậy
Bài 13. Cho △ABC = △DEF. Biết 2 tia phân giác trong của góc và
cắt nhau tại O, tạo
. Tính các góc của △DEF.
Hướng dẫn giải
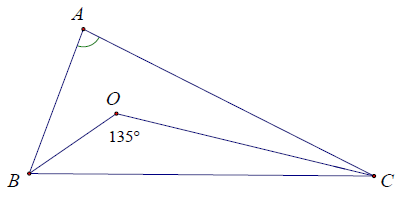
Ta có: (tổng ba góc trong △BOC bằng 180°)
(tính chất phân giác)
(tổng ba góc trong △ABC bằng 180°)
Do △ABC = △DEF nên (hai góc tương ứng) ⇒
Xét △DEF, có:
(tổng ba góc trong △DEF bằng 180°).
Mà nên
Vậy
Bài 14. Cho △ABC = △MNP biết AB ∶ BC ∶ AC = 5 ∶ 6 ∶ 8. Tính các cạnh của △MNP biết tam giác này có chu vi là 57 cm.
Hướng dẫn giải
Vì △ABC = △MNP nên AB = MN, BC = NP, AC = MP (các cạnh tương ứng).
Suy chu vi hai tam giác bằng nhau:
AB + BC + AC = MN + NP + MP = 57 (cm)
Vì
Ta có: AB + BC + AC = 57
⇒ 5k + 6k + 8k = 57
⇒ 19k = 57
⇒ k = 3
⇒ AB = 5k = 5 ⋅ 3 = 15 cm, BC = 6k = 6 ⋅ 3 = 18 cm, AC = 8k = 8 ⋅ 3 = 24 cm
⇒ MN = AB = 15 cm, NP = BC = 18 cm, MP = AC = 24 cm
Vậy MN = 15 cm, NP = 18 cm, MP = 24 cm.
Dạng 3. Chứng minh hai tam giác bằng nhau theo trường hợp bằng nhau thứ nhất. Từ đó chứng minh các bài toán liên quan: hai đoạn thẳng bằng nhau, hai góc bằng nhau, hai đường thẳng song song – vuông góc, đường phân giác, ba điểm thẳng hàng,…
Phương pháp giải
+) Chỉ ra các tam giác có ba cạnh bằng nhau để suy ra tam giác bằng nhau.
+) Từ tam giác bằng nhau suy ra các cặp cạnh tương ứng bằng nhau, cặp góc tương ứng bằng nhau.
+) Nắm vững các khái niệm: tia phân giác của góc, đường cao của tam giác, đường trung trực của đoạn thẳng, hai đường thẳng song song, hai đường thẳng vuông góc; nắm vững định lí tổng ba góc trong một tam giác, tiên đề Ơ-clit để giải các bài toán chứng minh.
Bài toán.
Bài 1. Tìm các tam giác bằng nhau trên hình vẽ, giải thích vì sao?
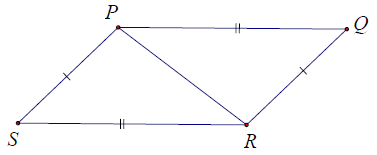
Hướng dẫn giải
Xét △PSR và △RQP, có:
PR là cạnh chung,
PS = QR
SR = PQ (theo giả thiết)
⇒ △PSR = △RQP (c.c.c).
Bài 2. Tìm các tam giác bằng nhau trên hình vẽ, giải thích vì sao?
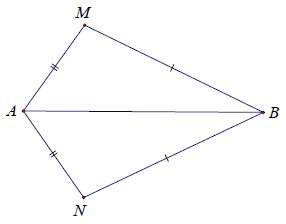
Hướng dẫn giải
Xét △AMB và △ANB, có:
AB là cạnh chung,
AM = AN
BM = BN (theo giả thiết)
⇒ △AMB = △ANB (c.c.c).
Bài 3. Tìm các tam giác bằng nhau trên hình vẽ, giải thích vì sao?
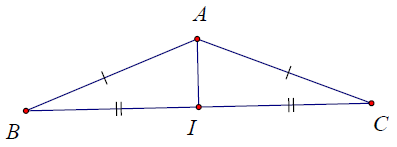
Hướng dẫn giải
Xét △ABI và △ACI, có:
AI là cạnh chung
AB = AC
BI = CI (theo giả thiết)
⇒ △ABI = △ACI (c.c.c).
Bài 4. Cho đoạn thẳng AB = 6 cm. Trên nửa mặt phẳng bờ AB, vẽ △ABD sao cho AD = 4 cm, BD = 5 cm. Trên nửa mặt phẳng còn lại vẽ △ABE sao cho BE = 4 cm, AE = 5 cm. Chứng minh:
a) △ABD = △BAE
b) △ADE = △BED
Hướng dẫn giải

a) Xét △ABD và △BAE có:
AB là cạnh chung
AD = BE (4cm)
BD = AE (5cm)
⇒ △ABD = △BAE (c.c.c).
b) Xét △ADE và △BED có:
DE là cạnh chung
AD = BE (4cm)
BD = AE (5cm)
⇒ △ADE = △BED (c.c.c).
Bài 5. Cho △ABC có AB = AC. Lấy M là trung điểm của BC. Chứng minh rằng:
a) △AMB = △AMC
b)
c) AM ⊥ BC
Hướng dẫn giải
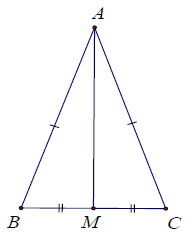
a) Xét △AMB và △AMC, có:
AM là cạnh chung
AB = AC (theo giả thiết)
BM = CM (vì M là trung điểm BC)
⇒ △AMB = △AMC (c.c.c)
b) Vì △AMB = △AMC (chứng minh trên)
⇒ (hai góc tương ứng)
c) Vì △AMB = △AMC (chứng minh trên)
⇒ (hai góc tương ứng)
Mà (kề bù)
⇒
⇒ AM ⊥ BC
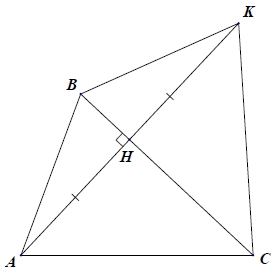
Bài 6. Cho hình vẽ dưới đây. Chứng minh rằng:
a) △ABK = △KHA
b) AB // HK
c) AH // BK.
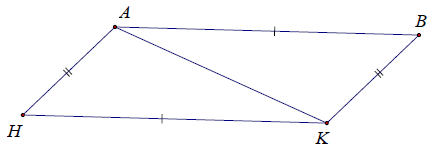
Hướng dẫn giải
a) Xét △ABK và △KHA, có:
AK là cạnh chung
AB = HK
BK = AH (theo giả thiết)
⇒ △ABK = △KHA (c.c.c)
b) Vì △ABK = △KHA (chứng minh trên)
⇒ (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong so với AB và HK nên AB // HK.
c) Vì △ABK = △KHA (chứng minh trên)
⇒ (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong so với AH và BK nên AH // BK.
Bài 7. Cho △ABC có AB = AC. Gọi M là trung điểm của BC. Chứng minh rằng:
a) AM là phân giác của góc .
b) AM là trung trực của BC.
Hướng dẫn giải

a) Xét △AMB và △AMC, có:
AM là cạnh chung
AB = AC (theo giả thiết)
BM = CM (vì M là trung điểm BC)
⇒ △AMB = △AMC (c.c.c)
⇒ (hai góc tương ứng)
⇒ AM là phân giác của góc
b) Vì △AMB = △AMC (chứng minh trên)
⇒ (hai góc tương ứng)
Mà (kề bù)
⇒
⇒ AM ⊥ BC
Mặt khác: M là trung điểm của BC
⇒ AM là trung trực của BC.
Bài 8. Cho △ABC, đường cao AH. Trên nửa mặt phẳng bờ AC không chứa B vẽ △ACD sao cho AD = BC, CD = AB. Chứng minh rằng: AB // CD và AH ⊥ AD.
Hướng dẫn giải
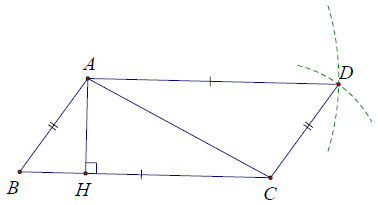
Xét △ADC và △CBA, có:
AC là cạnh chung
AD = BC (giả thiết)
CD = AB (giả thiết)
⇒ △ADC = △CBA (c.c.c)
⇒ (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong so với AD và BC nên AD // BC.
Lại có: AH ⊥ BC (AH là đường cao trong △ABC)
⇒ AH ⊥ AD (từ vuông góc tới song song)
Bài 9. Cho △ABC có AB = AC = BC. Giả sử O là một điểm nằm trong tam giác sao cho OA = OB = OC. Chứng minh rằng: O là giao điểm của 3 tia phân giác của .
Hướng dẫn giải
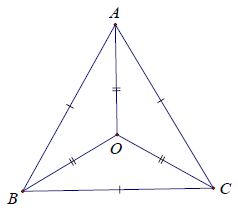
Xét △AOB và △AOC, có:
AO chung
OB = OC (giả thiết)
AB = AC (giả thiết)
⇒ △AOB = △AOC (c.c.c)
⇒ (hai góc tương ứng)
⇒ AO là tia phân giác
Chứng minh tương tự ta cũng có: BO là tia phân giác , CO là tia phân giác
.
Suy ra O là giao điểm của 3 tia phân giác của
Bài 10. Cho △ABC có AB = AC. Gọi D là trung điểm của BC. Chứng minh rằng:
a) △ADB = △ADC
b) AD là phân giác của , AD ⊥ BC
c) Trên nửa mặt phẳng bờ BC không chứa A lấy điểm E sao cho EB = EC. Chứng minh rằng: A, E, D thẳng hàng.
Hướng dẫn giải
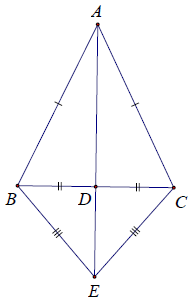
a) Xét △ADB và △ADC, có:
AD là cạnh chung
AB = AC (theo giả thiết)
BD = CD (vì D là trung điểm BC)
⇒ △ADB = △ADC (c.c.c)
b) Vì △ADB = △ADC (chứng minh trên)
⇒ (hai góc tương ứng)
⇒ AD là phân giác của
Vì △ADB = △ADC (chứng minh trên)
⇒ (hai góc tương ứng)
Mà (kề bù)
⇒
⇒ AD ⊥ BC
c) Xét △EDB và △EDC, có:
ED là cạnh chung
EB = EC (theo giả thiết)
BD = CD (vì D là trung điểm BC)
⇒ △EDB = △EDC (c.c.c)
⇒ (hai góc tương ứng)
Mà (kề bù)
⇒
⇒ ED ⊥ BC
Vì qua điểm D chỉ có duy nhất một đường thẳng vuông góc với BC mà ED ⊥ BC, AD ⊥ BC nên hai đường thẳng ED, AD trùng nhau hay A, E, D thẳng hàng.
Bài 11. Cho △ABC có AB = AC và . Tính số đo các góc còn lại của △ABC.
Hướng dẫn giải
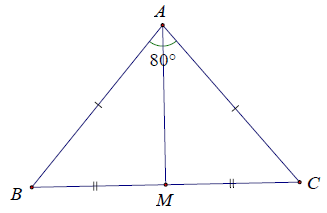
Lấy M là trung điểm của BC.
Xét △AMB và △AMC, có:
AM là cạnh chung
AB = AC (theo giả thiết)
BM = CM (vì M là trung điểm BC)
⇒ △AMB = △AMC (c.c.c)
⇒ (hai góc tương ứng)
⇒
Xét △ABC, có:
(tính chất tổng ba góc trong một tam giác)
⇒
Mà nên
Bài 12. Cho △ABC có AB = AC = BC. Tính số đo các góc của △ABC.
Hướng dẫn giải
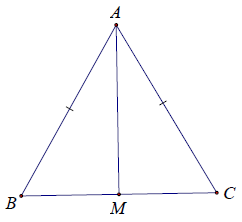
Lấy M là trung điểm của BC.
Xét △AMB và △AMC, có:
AM là cạnh chung,
AB = AC (theo giả thiết),
BM = CM (vì M là trung điểm BC)
⇒ △AMB = △AMC (c.c.c)
⇒ (hai góc tương ứng)
⇒
Tương tự lấy N là trung điểm AC ta cũng chứng minh được △ABN = △CBN (c.c.c)
⇒ (hai góc tương ứng)
⇒
Như vậy △ABC có ba góc bằng nhau.
Mà tổng ba góc trong tam giác bằng 180° nên các góc của △ABC có số đo 60°.
Trường hợp bằng nhau thứ hai và thứ ba của tam giác
Trường hợp bằng nhau: cạnh – góc – cạnh
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
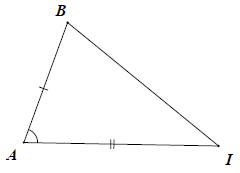
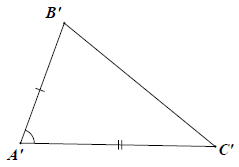
Xét △ABC và △A′B′C′, có:
⇒ △ABC = △A′B′C′ (c.g.c)
Trường hợp bằng nhau: góc – cạnh – góc
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
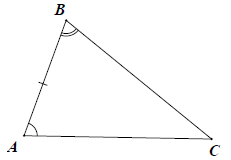
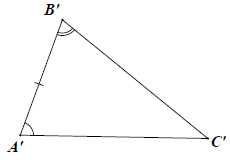
Xét △ABC và △A′B′C′, có:
⇒ △ABC = △A′B′C′ (g.c.g)
Phân dạng bài tập
Dạng 1. Tìm hoặc chứng minh hai tam giác bằng nhau
Phương pháp giải
+) Xét hai tam giác.
+) Kiểm tra ba điều kiện bằng nhau cạnh – góc – cạnh, góc – cạnh – góc.
+) Kết luận hai tam giác bằng nhau.
Bài toán.
Bài 1. Trong các hình vẽ sau, có các tam giác nào bằng nhau? Vì sao?
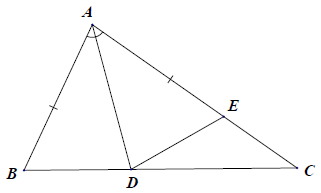
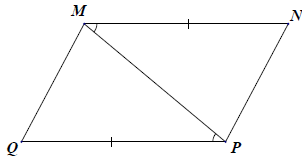
Hướng dẫn giải
Các tam giác bằng nhau: △ABD = △AED; △QMP = △NPM. Vì:
+) Xét △ABD và △AED, có:
AB = AE (giả thiết)
(giả thiết)
AD là cạnh chung
⇒ △ABD = △AED (c.g.c).
+) Xét △QMP và △NPM, có:
MN = PQ (giả thiết)
(giả thiết)
MP là cạnh chung
⇒ △QMP = △NPM (c.g.c).
Bài 2. Trong các hình vẽ sau, có hai tam giác nào bằng nhau? Vì sao?

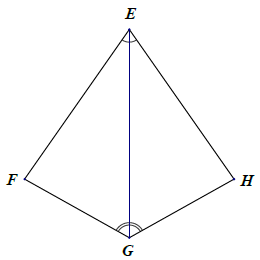
Hướng dẫn giải
Các tam giác bằng nhau: △ADB = △ADC; △EFG = △EHG. Thật vậy:
+) Xét △ADB và △ADC, có:
(giả thiết)
AD là cạnh chung
(giả thiết)
⇒ △ADB = △ADC (g.c.g).
+) Xét △EFG và △EHG, có:
(giả thiết)
EG là cạnh chung
(giả thiết)
⇒ △EFG = △EHG (g.c.g)
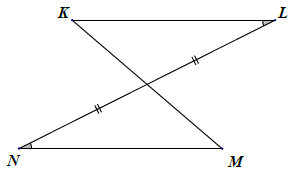
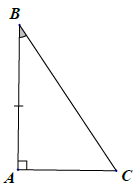
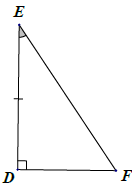
Bài 3. Trong các hình vẽ sau, có hai tam giác nào bằng nhau? Vì sao?
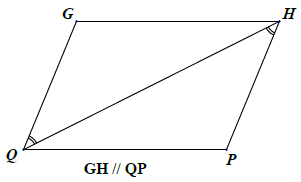
Hướng dẫn giải
Các tam giác bằng nhau: △GQH = △PHQ; △IKL = △IMN; △ABC = △DEF. Thật vậy:
+ Xét △GQH và △PHQ, có:
(theo giả thiết)
(hai góc so le trong, GH // QP)
QH là cạnh chung
⇒ △GQH = △PHQ (g.c.g).
+ Xét △IKL và △IMN, có:
IL = IK (theo giả thiết);
(hai góc đối đỉnh);
(theo giả thiết)
⇒ △IKL = △IMN (g.c.g)
Xét △ABC và △DEF, có:
(theo giả thiết);
(theo giả thiết);
AB = DE (theo giả thiết)
⇒ △ABC = △DEF (g.c.g)
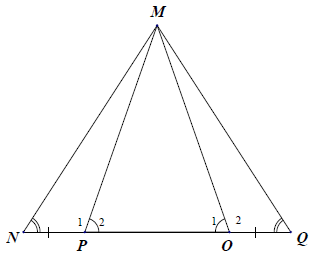
Bài 4. Trong các hình vẽ sau, có các tam giác nào bằng nhau? Vì sao?
Hướng dẫn giải
Các tam giác bằng nhau: △MNP = △MQO; △MNO = △MQP.
Thật vậy:
+) Ta có: (hai góc kề bù);
(hai góc kề bù)
Lại có:
Xét △MNP và △MQO, có:
(chứng minh trên);
NP = QO (theo giả thiết);
(theo giả thiết)
⇒ △MNP = △MQO (g.c.g)
+) Ta có: NO = NP + PO; QP = QO + OP. Mà NP = QO ⇒ NO = QP.
+ Xét △MNO và △MQP, có:
MN = MQ (vì △MNP = △MQO – theo chứng minh trên),
(theo giả thiết),
NO = QP (chứng minh trên)
⇒ △MNO = △MQP (c.g.c).
Bài 5. Nêu thêm một điều kiện để mỗi hình dưới đây là hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh.
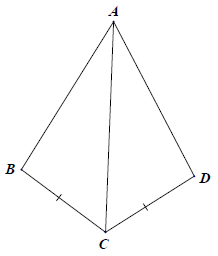


Hướng dẫn giải
Để △ABC = △ADC theo trường hợp cạnh – góc – cạnh thì thêm điều kiện:
Để △EFI = △GHI theo trường hợp cạnh – góc – cạnh thì thêm điều kiện: IF = IH
Để △MNP = △NMQ theo trường hợp cạnh – góc – cạnh thì thêm điều kiện: NP = MQ
Bài 6. Nêu thêm một điều kiện để mỗi hình dưới đây là hai tam giác bằng nhau theo trường hợp góc – cạnh – góc.
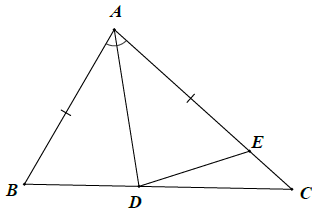
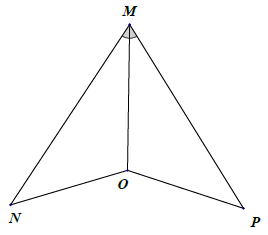
Hướng dẫn giải
Để △ABD = △AED theo trường hợp góc – cạnh – góc thì thêm điều kiện:
Để △MNO = △MPO theo trường hợp góc – cạnh – góc thì thêm điều kiện:
Bài 7. Qua trung điểm I của đoạn thẳng AB, kẻ đường thẳng vuông góc với AB, trên đường thẳng vuông góc đó lấy hai điểm C và D. Nối CA, CB, DA, DB. Tìm các cặp tam giác bằng nhau.
Hướng dẫn giải
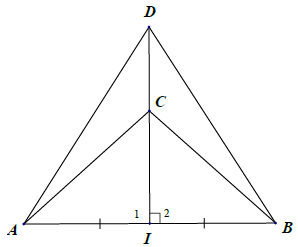
Xét △ACI và △BCI, có:
AI = BI (I là trung điểm của AB),
CI là cạnh chung,
⇒ △ACI = △BCI (c.g.c).
Xét △ADI và △BDI, có:
AI = BI (I là trung điểm của AB),
DI là cạnh chung,
⇒ △ADI = △BDI (c.g.c).
Vậy các cặp tam giác bằng nhau là: △ACI = △BCI; △ADI = △BDI.
Bài 8. Cho tam giác ABC, kẻ AH vuông góc với BC (H ∈ BC). Trên tia đối của tia HA lấy điểm K sao cho HK = HA nối KB, KC. Tìm các cặp tam giác bằng nhau.
Hướng dẫn giải
+) Xét △ABH và △KBH, có:
BH là cạnh chung;
AH = KH (giả thiết);
⇒ △ABH = △KBH (c.g.c).
+) Xét △CAH và △CKH, có:
CH là cạnh chung;
AH = KH (giả thiết);
⇒ △CAH = CKH (c.g.c)
+) Xét △ABC và △KBC, có:
BC là cạnh chung,
AC = KC (vì △CAH = CKH)
AB = KB (vì △ABH = △KBH)
⇒ △ABC = △KBC (c.c.c)
Vậy các cặp tam giác bằng nhau: △ABH = △KBH, △CAH = CKH, △ABC = △KBC.
Bài 9. Cho tam giác ABC có AB = AC. Gọi AM là tia phân giác góc . Chứng minh △ABM = △ACM.
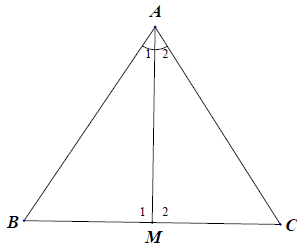
Hướng dẫn giải
Xét △ABM và △ACM, có:
AB = AC (giả thiết)
(AM là tia phân giác góc
)
AM là cạnh chung
⇒ △ABM = △ACM (c.g.c).
Bài 10. Cho tam giác ABC có . Gọi AM là tia phân giác góc
. Chứng minh: △ABM = △ACM.
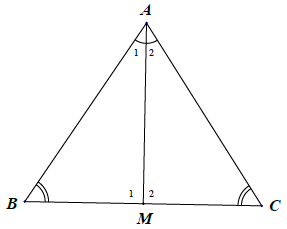
Hướng dẫn giải
Xét △ABM, có:
(tổng ba góc trong một tam giác bằng 180°).
Xét △ACM, có:
(tổng ba góc trong một tam giác bằng 180°).
Mà
Xét △ABM và △ACM, có:
(chứng minh trên)
AM là cạnh chung
(AM là tia phân giác góc
)
⇒ △ABM = △ACM (c.g.c)
Bài 11. Cho Oz là tia phân giác góc . Trên các tia Ox, Oy, Oz lần lượt lấy các điểm A, B, C (khác O) sao cho OA = OB. Chứng minh: △OAC = △OBC.
Hướng dẫn giải
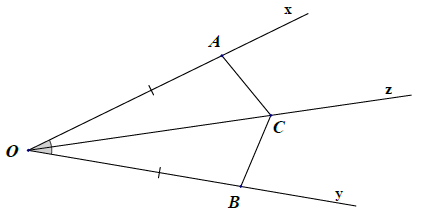
Xét △OAC và △OBC, có:
OA = OB (giả thiết)
(giả thiết)
OC là cạnh chung
⇒ △OAC = △OBC (c.g.c).
Bài 12. Cho góc khác góc bẹt. Trên cạnh Ox lấy hai điểm A và B, trên cạnh Oy lấy hai điểm C và D, sao cho OA = OC, OB = OD.
a) Chứng minh: △OAD = △OCB.
b) Chứng minh: △ACD = △CAB.
Hướng dẫn giải
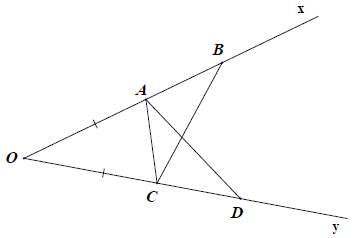
a) Xét △OAD và △OCB, có:
OA = OC (giả thiết)
chung
OD = OB (giả thiết)
⇒ △OAD = △OCB (c.g.c).
b) Ta có: OB = OA + AB , OD = OC + CD
Mà OA = OC; OB = OD nên AB = CD
Lại có: △OAD = △OCB (chứng minh trên)
Suy ra: AD = CB; (tương ứng).
Xét △ACD và △CAB, có:
AB = CD
AD = CB (chứng minh trên)
⇒ △ACD = △CAB (c.g.c).
Bài 13. Cho △ABC vuông ở A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.
a) Chứng minh: △ABC = △ABD.
b) Trên tia đối của tia AB lấy điểm M. Chứng minh: △MBD = △MBC.
Hướng dẫn giải
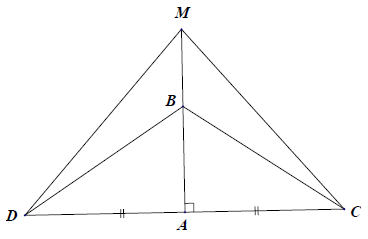
a) Xét △ABC và △ABD, có:
AD = AC (giả thiết)
AB là cạnh chung
⇒ △ABC = △ABD (c.g.c).
b) Xét △MBD và △MBC, có:
AD = AC (giả thiết)
AM là cạnh chung
⇒ △MBD = △MBC (c.g.c).
Bài 14. Cho hình vẽ sau, trong đó AB // CD, AB = CD. Chứng minh rằng:
a) △OAB = △ODC.
b) △OAC = △ODB.
Hướng dẫn giải
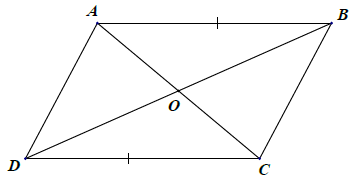
a) Xét △OAB và △ODC, có:
(hai góc so le trong),
AB = CD (giả thiết),
(hai góc so le trong)
⇒ △OAB = △ODC (g.c.g).
b) Vì △OAB = △ODC (chứng minh trên)
⇒ OA = OD; OB = OC (các cạnh tương ứng).
Xét △OAC và △ODB, có:
OA = OD; OB = OC (chứng minh trên)
(hai góc đối đỉnh)
⇒ △OAC = △ODB (c.g.c),
Bài 15. Cho góc nhọn có tia Oz là tia phân giác. Qua điểm A thuộc tia Ox, vẽ đường thẳng song song với Oy cắt Oz tại M. Qua M kẻ đường thẳng song song với Ox cắt Oy tại B.
a) Chứng minh: △OAM = △MBO.
b) Từ M vẽ MH ⊥ Ox; MK ⊥ Oy. Chứng minh: △MHO = △MKO.
Hướng dẫn giải
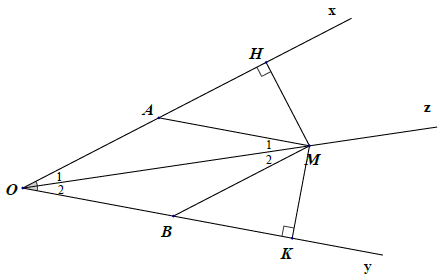
a) Xét △OAM và △MBO, có:
(hai góc so le trong),
OM là cạnh chung,
(hai góc so le trong)
⇒ △OAM = △MBO (g.c.g).
b) Ta có:
(hai góc nhọn phụ nhau)
(hai góc nhọn phụ nhau).
Lại có: (Oz là tia phân giác
)
⇒
Xét △OMH và △OMK, có:
(chứng minh trên),
OM chung,
(chứng minh trên)
⇒ △OMH = △OMK (g.c.g).
Bài 16. Cho tam giác ABC có và AB = AC. Trên các cạnh AB và AC lần lượt lấy điểm D và E sao cho AD = AE. Qua A và D kẻ đường vuông góc với BE cắt BC lần lượt tại M và N. Tia ND cắt tia CA tại I. Chứng minh rằng:
a) △AID = △ABE.
b) Chứng minh: CM = MN.
Hướng dẫn giải
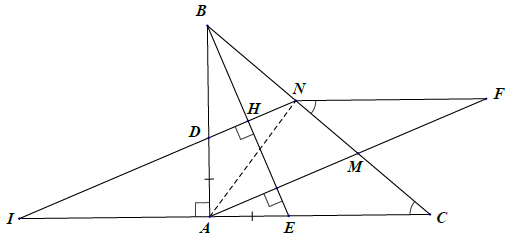
a) Gọi H là giao điểm của BE và IN.
Ta có: △AEB vuông tại A nên
△DHB vuông tại H nên
Suy ra:
Mà (hai góc đối đỉnh) suy ra
Xét △ADI và △ABE, có:
AE = AD (giả thiết)
(chứng minh trên)
⇒ △ADI = △ABE (g.c.g).
b) Ta có: AM ⊥ BE, IN ⊥ BE suy ra AM // IN
Qua N kẻ đường thẳng song song với AC cắt AM tại F
⇒ AC // NF ⇒ AI // NF
Xét △AIN và △NFA, có:
(so le trong, AI // NF),
(so le trong, AM // IN),
AN là cạnh chung
⇒ △AIN = △NFA (g.c.g)
⇒ NF = AI (hai cạnh tương ứng).
Mà △AID = △ABE (chứng minh trên)
⇒ AI = AB (hai cạnh tương ứng).
Lại có: AB = AC (giả thiết) ⇒ NF = AC.
Lại có: AC // NF
⇒ (hai góc so le trong).
Xét △MAC và △MFN, có:
(chứng minh trên),
(chứng minh trên),
NF = AC (chứng minh trên)
⇒ △MAC = △MFN (g.c.g).
Bài 17. Cho △ABC, kẻ BD vuông góc với AC, CE vuông góc với AB. Trên tia đối của tia BD, lấy điểm H sao cho BH = AC. Trên tia đối của tia CE lấy điểm K sao cho CK = AB. Chứng minh AH = AK.
Hướng dẫn giải
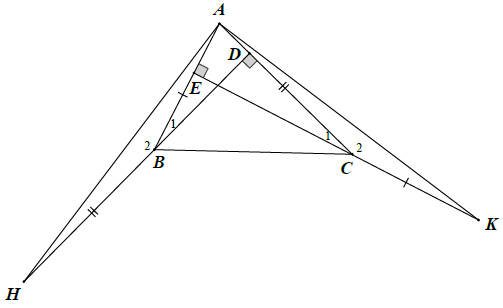
Xét △ABD vuông tại B (vì BD ⊥ AC)
⇒ (1)
Xét △ACE vuông tại E (vì CE ⊥ AB)
⇒ (2)
Từ (1) và (2) suy ra:
Mà
⇒
Xét △ABH và △KCA, có:
AB = CK (giả thiết)
(chứng minh trên)
BH = AC (giả thiết)
⇒ △ABH = △KCA (c.g.c)
⇒ AH = AK (hai cạnh tương ứng).
Dạng 2. Sử dụng trường hợp bằng nhau của tam giác để chứng minh một tính chất khác
Phương pháp giải
+) Chọn hai tam giác có cạnh (góc) là hai đoạn thẳng (góc) cần chứng minh bằng nhau.
+) Chứng minh hai tam giác ấy bằng nhau theo một trong hai trường hợp cạnh – góc – cạnh, góc – cạnh – góc rồi suy ra hai cạnh (góc) tương ứng bằng nhau. Kiểm tra ba điều kiện bằng nhau cạnh – góc – cạnh, góc – cạnh – góc.
+) Kết hợp với các tính chất đã học về tia phân giác, đường thẳng song song, đường trung trực, tổng ba góc trong một tam giác,… để chứng minh một tính chất khác.
Bài toán.
Bài 1. Cho tam giác ABC có AB = AC tia phân giác của góc cắt BC tạiM. Chứng minh: BM = CM.
Hướng dẫn giải
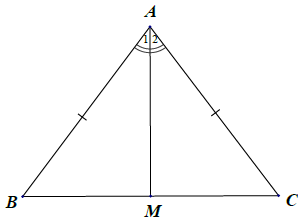
Xét △ABM và △ACM, có:
AB = AC (giả thiết)
(AM là tia phân giác góc
)
AM là cạnh chung
⇒ △ABM = △ACM (c.g.c)
⇒ BM = CM (hai cạnh tương ứng).
Bài 2. Cho góc nhọn có Om là tia phân giác, C ∈ Om (C ≠ O). Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Chứng minh: CA = CB.
Hướng dẫn giải
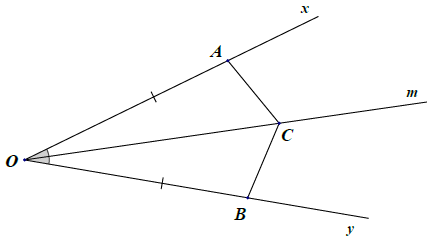
Xét △OAC và △OBC, có:
OA = OB (giả thiết)
(giả thiết)
OC là cạnh chung
⇒ △OAC = △OBC (c.g.c)
⇒ CA = CB (hai cạnh tương ứng).
Bài 3. Cho △ABC = △MNP. Gọi O và G lần lượt là trung điểm của các cạnh BC và NP. Chứng minh: AO = MG.
Hướng dẫn giải
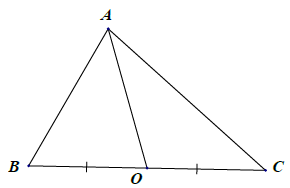

Ta có: △ABC = △MNP
⇒ AB = MN, , BC = NP (tương ứng)
Mà O là trung điểm BC nên BO = BC
G là trung điểm NP nên NG = NP
Từ đó suy ra: BO = NG.
Xét △ABO và △MNG, có:
AB = MN, , BO = NG (chứng minh trên)
⇒ △ABO = △MNG (c.g.c)
⇒ AO = MG (hai cạnh tương ứng).
Bài 4. Cho tam giác ABC có . Tia phân giác của góc
cắt BC tại D.
a) Chứng minh: AB = AC
b) Chứng minh: AD ⊥ BC
Hướng dẫn giải
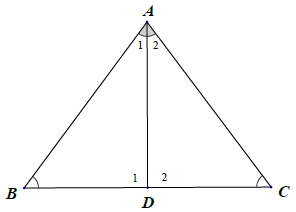
a) Xét △ADB, có: (tổng ba góc trong tam giác).
Xét △ADC, có: (tổng ba góc trong tam giác).
Mà: (vì AD là phân giác của
),
(giả thiết)
⇒
Xét △ADB và △ADC, có:
(AD là tia phân giác của góc
),
AD là cạnh chung,
(chứng minh trên)
⇒ △ADB = △ADC (g.c.g)
⇒ AB = AC (hai cạnh tương ứng).
b) Ta có: (chứng minh trên)
Mà (hai góc kề bù)
⇒
⇒ AD ⊥ BC
Bài 5. Cho △ABC có AB < AC. Phân giác của góc cắt cạnh BC tại điểm D. Trên cạnh AC lấy điểm E sao cho AE = AB. Chứng minh:
a) BD = ED.
b) DA là tia phân giác của góc .
Hướng dẫn giải
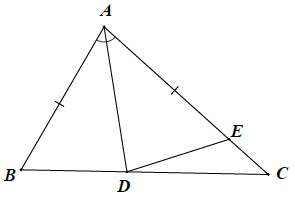
a) Xét △ADB và △ADE, có:
AE = AB (giả thiết),
(AD là tia phân giác góc
),
AD là cạnh chung
⇒ △ADB = △ADE (c.g.c)
⇒ BD = CE (hai cạnh tương ứng).
b) Ta có: △ADB = △ADE (chứng minh trên)
⇒ (hai góc tương ứng)
⇒ DA là tia phân giác của góc .
Bài 6. Cho góc khác góc bẹt và có Ot là tia phân giác. Lấy điểm C thuộc Ot (C ≠ O). Qua C kẻ đường vuông góc với Ot, cắt Ox, Oy theo thứ tự ở A, B.
a) Chứng minh: OA = OB.
b) Lấy điểm D thuộc Ct (D ≠ C). Chứng minh: DA = DB và .
Hướng dẫn giải
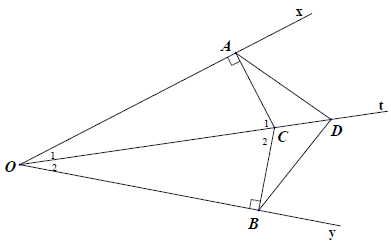
a) Xét △OAC, có:
(tổng ba góc trong một tam giác)
Xét △OBC, có:
(tổng ba góc trong một tam giác)
Mà (vì Ot là phân giác
),
nên
Xét △OAC và △OBC, có:
(Ot là tia phân giác
),
OC là cạnh chung,
(chứng minh trên)
⇒ △OAC = △OBC (g.c.g)
⇒ OA = OB (hai cạnh tương ứng)
b) Xét △OAD và △OBD, có:
(Ot là tia phân giác
),
OD là cạnh chung,
OA = OB (chứng minh trên)
⇒ △OAD = △OBD (c.g.c)
⇒ AD = BD (hai cạnh tương ứng), (hai góc tương ứng).
Bài 7. Cho △ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh:
a) △ABM = △ECM.
b) AB = CE và AC // BE.
Hướng dẫn giải
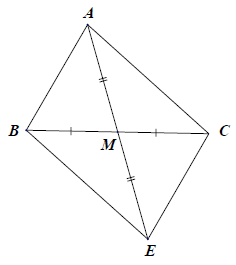
a) Xét △ABM và △ECM, có:
AM = EM (giả thiết),
BM = CM (M là trung điểm của BC),
(hai góc đối đỉnh)
⇒ △ABM = △ECM (c.g.c).
b) Ta có: △ABM = △ECM (chứng minh trên)
⇒ AB = CE (hai cạnh tương ứng)
Xét △AMC và △EMB, có:
AM = EM (giả thiết),
BM = CM (M là trung điểm của BC),
(hai góc đối đỉnh)
⇒ △AMC = △EMB (c.g.c)
⇒ (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong
⇒ AC // BE
Bài 8. Cho tam giác ABC có . Dựng AH ⊥ BC (H ∈ BC). Trên tia đối tia HA lấy điểm D sao cho HD = HA.
a) Chứng minh: AC DC.
b) Chứng minh: △ABC = △DBC.
c) Xác định số đo góc .
Hướng dẫn giải
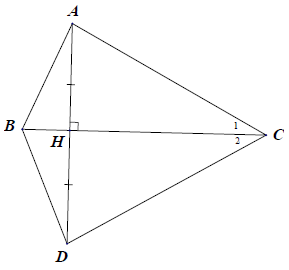
a) Xét △AHC và △DHC, có:
AH = AD (giả thiết),
HC là cạnh chung,
⇒ △AHC = △DHC (c.g.c)
⇒ AC = DC (hai cạnh tương ứng).
b) Vì △AHC = △DHC (chứng minh trên)
⇒ (hai góc tương ứng)
Xét △ABC và △DBC, có:
AC = DC (chứng minh trên),
BC là cạnh chung,
(chứng minh trên)
⇒ △ABC = △DBC (c.g.c)
c) Vì △ABC = △DBC (chứng minh trên)
⇒ (hai góc tương ứng)
⇒
Bài 9. Cho △ABC trên nửa mặt phẳng bờ AC không chứa điểm B, lấy điểm D sao cho AD // BC và AD = BC. Chứng minh:
a) AB = CD.
b) AB // CD và △ABD = △CDB.
Hướng dẫn giải
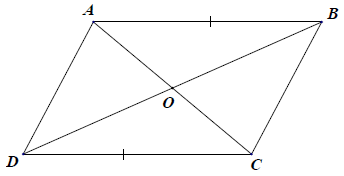
a) Xét △ABC và △CDA, có:
AD = BC (giả thiết),
AC là cạnh chung,
(hai góc so le trong)
⇒ △ABC = △CDA (c.g.c)
⇒ AB = CD (hai cạnh tương ứng).
b) Vì △ABC = △CDA (chứng minh trên)
⇒ (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong
⇒ AB // DC
Xét △ABD và △CBD, có:
AD = BC (giả thiết),
BD là cạnh chung,
(hai góc so le trong)
⇒ △ABD = △CBD (c.g.c).
Bài 10. Cho △ABC có , trên cạnh BC lấy điểm E sao cho BA = BE. Tia phân giác góc
cắt AC ở D.
a) Chứng minh: △ABD = △EBD
b) Chứng minh: DA = DE
c) Tính số đo
d) Xác định độ lớn góc để
Hướng dẫn giải
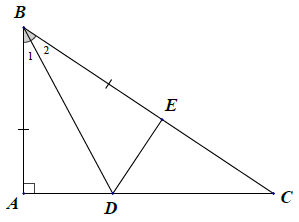
a) Xét △ABD và △EBD, có:
BA = BE (giả thiết),
(BD là tia phân giác góc
),
BD là cạnh chung
⇒ △ABD = △EBD (c.g.c).
b) Vì △ABD = △EBD (chứng minh trên)
⇒ DA = DE (hai cạnh tương ứng).
c) Vì △ABD = △EBD (chứng minh trên)
⇒ (hai góc tương ứng)
⇒
d) Để thì △EDB = △EDC
⇒ ⇒
Mà
Vậy thì
Bài 11. Cho △ABC có AB < AC. Kẻ tia phân giác AD của (D ∈ BC). Trên cạnh AC lấy điểm E sao cho AE = AB trên tia AB lấy điểm F sao cho AF = AC. Chứng minh:
a) BD = ED
b) BF = EC
c) △BDF = △EDC
d) AD ⊥ FC
Hướng dẫn giải
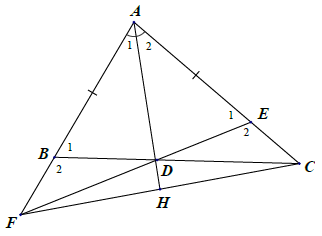
a) Xét △ABD và △AED, có:
AD là cạnh chung,
(AD là tia phân giác của
),
AB = AE (giả thiết)
⇒ △ABD = △AED (c.g.c)
⇒ BD = ED (hai cạnh tương ứng).
b) Ta có: AF AB + BF , AC = AE + EC
Mà AC = AF, AB = AE (giả thiết)
⇒ BF = EC
c) Vì △ABD = △AED (chứng minh trên)
⇒ (hai góc tương ứng).
Ta có: (kề bù)
Mà (chứng minh trên)
⇒
Xét △BDF và △EDC, có:
BD = ED (chứng minh trên)
(chứng minh trên)
BF = EC (chứng minh trên)
⇒ △BDF = △EDC (c.g.c)
d) Gọi H là giao điểm của AD và FC.
Xét △AFH và △ACH, có:
AH là cạnh chung,
(AD là tia phân giác của
),
AF = AC (giả thiết)
⇒ △AFH = △ACH (c.g.c)
⇒ (hai góc tương ứng).
Lại có: (kề bù)
⇒
⇒ AD ⊥ FC
Bài 12. Cho tam giác ABC (AB < AC), tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax (E, F ∈ Ax).
a) Chứng minh: BE // CF
b) So sánh BE và FC; CE và BF
c) Tìm điều kiện về △ABC để có BE = CE
Hướng dẫn giải

a) Ta có: BE ⊥ Ax, CF ⊥ Ax (giả thiết)
⇒ BE // CF (từ vuông góc đến song song)
b) Xét △MBE và △MCF, có:
(hai góc so le trong),
BM = CM (M là trung điểm của BC),
(hai góc đối đỉnh)
⇒ △MBE = △MCF (g.c.g)
⇒ BE = CF (hai cạnh tương ứng)
Xét △MBF và △MCE, có:
(hai góc so le trong),
BM = CM (M là trung điểm của BC),
(hai góc đối đỉnh)
⇒ △MBF = △MCE (g.c.g)
⇒ BF = CE (hai cạnh tương ứng).
d) Giả sử BE = CE
Xét △BEM và △CEM, có:
BE = CE (cmt)
BM = CM (cmt)
EM là cạnh chung
⇒ △BEM = △CEM (c.c.c)
⇒ (hai góc tương ứng)
Mặt khác, (hai góc kề bù) nên
Suy ra EM ⊥ BC hay AM ⊥ BC
Xét △BAM và △CAM, có:
;
BM = CM (cmt);
AM là cạnh chung
⇒ △BAM = △CAM (c.g.c)
⇒ BA = CA (hai cạnh tương ứng)
⇒ △ABC cân tại A.
Vậy △ABC cân tại A thì BE = CE.
Bài 13. Cho tam giác ABC. Đường thẳng qua A song song với BC cắt đường thẳng qua C song song với AB ở D. Gọi M là giao điểm của BD và AC.
a) Chứng minh: △ABC = △CDA.
b) Chứng minh M là trung điểm của AC.
c) Đường thẳng d qua M cắt các đoạn thẳng AD, BC lần lượt ở I, K. Chứng minh M là trung điểm của IK.
Hướng dẫn giải
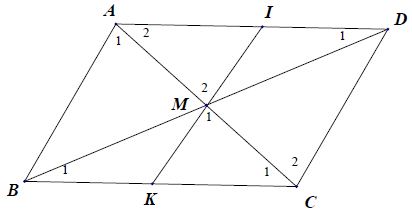
a) Xét △ABC và △CDA, có:
(AD // BC; hai góc so le trong),
AC là cạnh chung,
(AB // DC; hai góc so le trong),
⇒ △ABC = △CDA (g.c.g).
b) Vì △ABC = △CDA (chứng minh trên)
⇒ AD = BC(hai cạnh tương ứng)
Xét △AMD và △CMB, có:
(AD // BC, hai góc so le trong),
AC là cạnh chung,
(AD // CB, hai góc so le trong)
⇒ △AMD = △CMB (g.c.g)
⇒ AM = CM (hai cạnh tương ứng)
⇒ M là trung điểm của AC
c) Xét △AMI và △CMK, có:
(AD // BC, hai góc so le trong),
AM = CM (chứng minh trên),
(hai góc đối đỉnh)
⇒ △AMI = △CMK (g.c.g)
⇒ MI = MK (hai cạnh tương ứng)
⇒ M là trung điểm của IK
Bài 14. Cho tam giác ABC nhọn. Vẽ đoạn thẳng AD vuông góc với AB và AD = AB (D, C khác phía so với AB). Vẽ đoạn thẳng AE ⊥ AC và AE = AC (E, B khác phía so với AC). Chứng minh:
a) BE = DC
b) BE ⊥ DC
Hướng dẫn giải
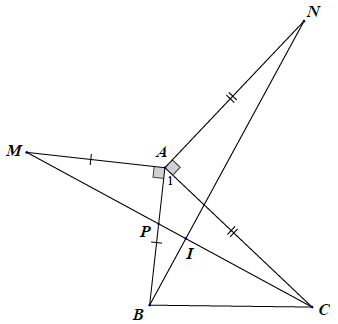
a) Vì AD ⊥ AB (giả thiết) nên
AE ⊥ AC (giả thiết) nên
Ta có: và
⇒
Xét △DAC và △BAE, có:
AD = AB, AC = AE (giả thiết)
(chứng minh trên)
⇒ △DAC = △BAE (c.g.c).
Vì △DAC = △BAE (chứng minh trên) nên DC = BE, (tương ứng).
b) Gọi P là giao điểm AB và CD; I là giao điểm BE và CD.
Ta có: (vì △ADP vuông).
Lại có: △DAC = △BAE (chứng minh trên)
⇒ hay
⇒
⇒ BE ⊥ CD.
Bài 15. Cho tam giác ABC nhọn. Gọi M, N lần lượt là trung điểm của AB, AC. Lấy điểm E, D sao cho M, N là trung điểm của CE, BD.
a) Chứng minh: AD // BC
b) Chứng minh: A, E, D thẳng hàng
Hướng dẫn giải
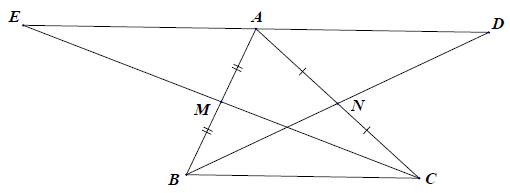
a) Xét △AND và △CNB, có:
NA = NC (vì N là trung điểm của AC),
ND = NB (vì N là trung điểm của BD),
(hai góc đối đỉnh)
⇒ △AND = △CNB (c.g.c)
⇒ (2 góc tương ứng).
Mà và
là 2 góc so le trong nên DA //BC
b) Hoàn toàn tương tự ta chứng minh được: AE // BC
Như vậy: AE // BC, DA // BC nên A, D, E thẳng hàng (tiên đề Ơ-clít về đường thẳng song song).