Đường vuông góc và đường xiên

Quan hệ giữa đường vuông góc và đường xiên

Định lí 1

Trong các đường vuông góc và đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó, đường vuông góc ngắn hơn mọi đường xiên.

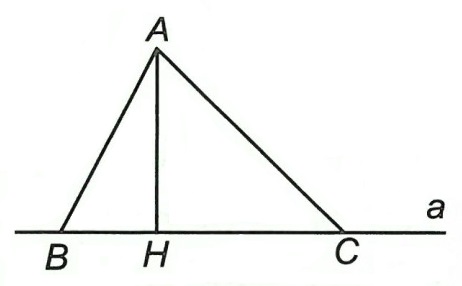
Trong hình vẽ:

AH ⊥ a ⇒ AH < AB, AH < AC

Quan hệ giữa các đường xiên và hình chiếu của chúng

Định lí 2

Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó

+) Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.

+) Đường xiên nào lớn hơn thì có hình chiếu lớn hơn.

+) Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau và ngược lại, nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.

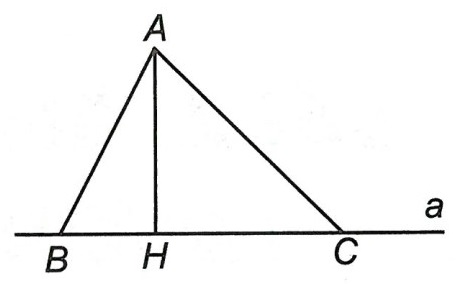
Trong hình vẽ:

AH ⊥ a, HC > HB ⇒ AC > AB

AH ⊥ a, AC > AB ⇒ HC > HB

AB = AC ⇒ HB = HC

Phân dạng bài tập

Dạng 1. So sánh hai đường xiên hoặc hai hình chiếu Phương pháp giải

Định lí: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì

+) Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.

+) Đường xiên nào lớn hơn thì có hình chiếu lớn hơn.

Thực hiện theo hai bước:

Bước 1: Xác định xem hai đoạn thẳng cần so sánh là đường xiên hay hình chiếu của đường xiên lên đường thẳng.

+) Nếu là đường xiên thì cần so sánh hai hình chiếu của chúng (dựa vào giả thiết bài toán).

+) Nếu là hình chiếu của hai đường xiên thì cần so sánh hai đường xiên (dựa vào giả thiết bài toán).

Bước 2: So sánh hai đoạn thẳng dựa vào định lí đường xiên – hình chiếu.

Ví dụ: Cho tam giác ABC (AB < AC), đường cao AH. So sánh HB và HC.

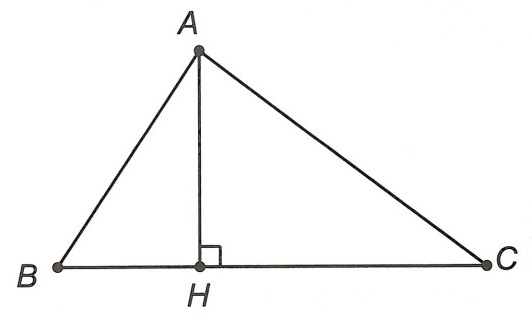
Hướng dẫn giải

Ta có: AH ⊥ BC nên AH là đường vuông góc còn AB và AC là các đường xiên và BH, CH tương ứng là hình chiếu của AB, AC lên đường thẳng BC.

Vì AB < AC nên HB < HC.

Ví dụ mẫu

Ví dụ 1. Cho tam giác ABC (AB < AC), đường cao AH. Gọi M là điểm tùy ý trên đoạn thẳng AH. Chứng minh: MB < MC.

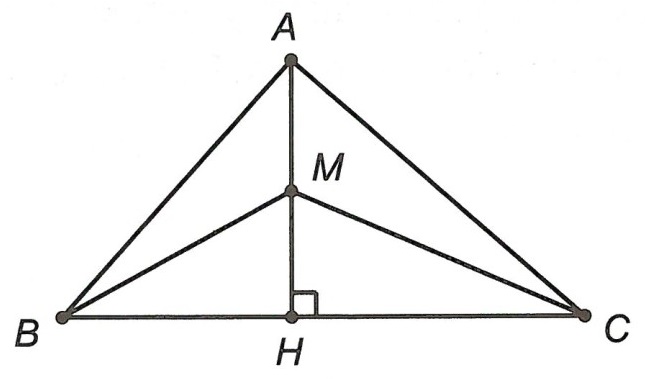
Hướng dẫn giải

Ta có: BH, CH tương ứng là hình chiếu của hai đường xiên AB, AC trên đường thẳng BC.

Vì AB < AC nên BH < CH.

Mặt khác: BH, CH tương ứng là hình chiếu của hai đường xiên BM, CM lên đường thẳng BC.

Do BH < CH nên BM < CM.

Ví dụ 2. Cho tam giác ABC vuông tại A. Trên cạnh AB lấy hai điểm D, E sao cho AD = DE = EB. Chứng minh rằng: CA < CD < CE < CB.

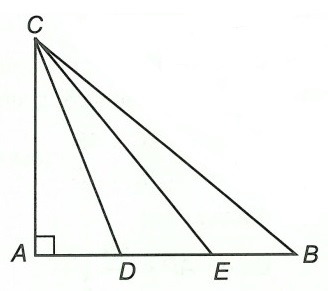
Hướng dẫn giải

Xét trên cạnh AB, ta có AD = DE = EB ⇒ AD < AE < AB.

Vì CA ⊥ AB nên AD, AE, AB tương ứng là hình chiếu của các đường xiên CD, CE, CB lên đường thẳng AB.

Do AD < AE < AB nên CD < CE < CB (1)

Mặt khác: CA < CD (đường vuông góc ngắn hơn đường xiên) (2)

Từ (1) và (2) suy ra: CA < CD < CE < CB.

Bài tập tự luyện dạng 1

Câu 1. Cho tam giác ABC có AB > AC, kẻ AH vuông góc với BC (H ∈ BC). So sánh BH và CH.

Hướng dẫn giải

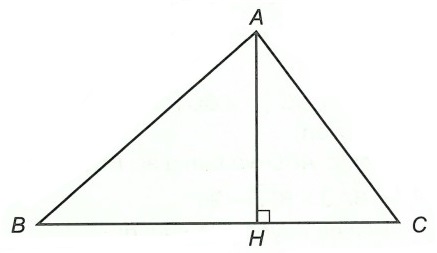
Ta có: BH là hình chiếu của đường xiên AB lên đường thẳng BC và CH là hình chiếu của đường

xiên AC lên đường thẳng BC.

Do AB > AC nên BH > CH.

Câu 2. Cho tam giác ABC (AB < AC), đường cao AH, H ∈ BC. Lấy điểm K bất kì thuộc AH (K ≠ H).

a) Chứng minh rằng: HB < HC.

b) BK < CK.

Hướng dẫn giải

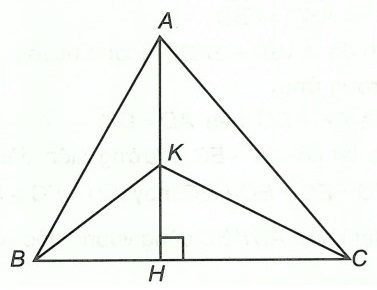
a) Ta có: AB, AC là các đường xiên và BH, CH tương ứng là hình chiếu của AB, AC lên đường

thẳng BC.

Vì AB < AC nên BH < CH (đường xiên bé hơn thì hình chiếu bé hơn).

b) Ta có: BH, CH lần lượt là hình chiếu của BK, CK lên BC.

Vì BH < CH nên BK < CK

Dạng 2. Quan hệ giữa đường vuông góc và đường xiên

Phương pháp giải

Sử dụng định lí: “Đường vuông góc ngắn hơn mọi đường xiên kẻ từ một điểm đến cùng một đường thẳng”.

Ví dụ: Cho tam giác nhọn ABC. Vẽ đường cao AD vuông góc với BC (D ∈ BC). Chứng minh rằng: $AD < \frac{{AB + AC}}{2}$

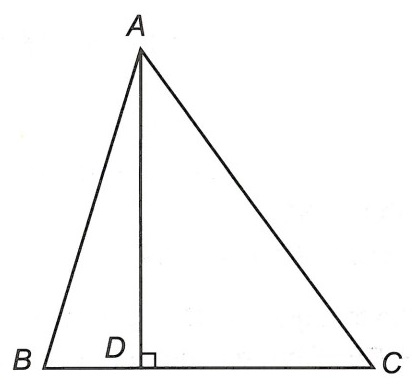
Hướng dẫn giải

Ta có: AD ⊥ BC nên AD là đường vuông góc; AB, AC là các đường xiên.

Suy ra: AD < AB và AD < AC (đường vuông góc nhỏ hơn đường xiên).

Do đó: $AD < \frac{{AB + AC}}{2}$

Ví dụ mẫu

Ví dụ 1. Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh rằng:

$AH + \frac{{BC}}{2} < AB + AC < AH + BC$

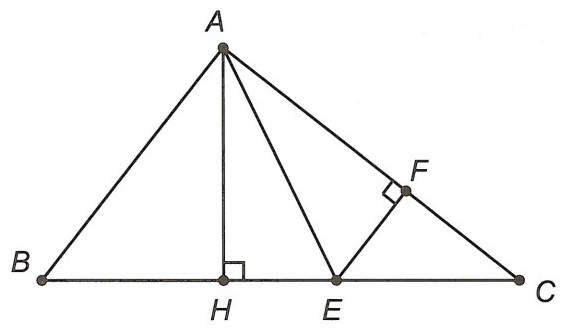
Hướng dẫn giải

Ta có: AB > AH, AC > AH (đường xiên lớn hơn đường vuông góc)

⇒ AB + AC > AH + AH hay AB + AC > 2AH (1)

Ta cũng có: AB > BH, AC > CH (đường xiên lớn hơn đường vuông góc)

⇒ AB + AC > BH + CH hay AB + AC > BC (2)

Từ (1) và (2) ta có:

$\begin{gathered} 2\left( {AB + AC} \right) > 2AH + BC \hfill \\ \Rightarrow AB + AC > AH + \frac{{BC}}{2}\left( * \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Kẻ EF vuông góc với AC tại F.

Trên cạnh BC lấy điểm E sao cho BA = BE ⇒ △ABE cân ở B

$\Rightarrow \widehat {BAE} = \widehat {BEA}$

Mặt khác: $\widehat {BAE} = \widehat {AEF}$ (cùng phụ với $\widehat {EAF}$ ) nên $\widehat {BEA} = \widehat {AEF}$

⇒ △AHE = △AFE (cạnh huyền – góc nhọn)

⇒ AH = AF (hai cạnh tương ứng).

Do đó: BC + AH = BE + EC + AH = BA + EC + AF

Vì EC > CF (đường xiên lớn hơn đường vuông góc) nên

BC + AH > BA + CF + AF hay BC + AH > BA + AC (**)

Từ (*) và (**) suy ra điều phải chứng minh.

Bài tập tự luyện dạng 2

Câu 1. Cho tam giác nhọn ABC có AB < AC. Kẻ AH vuông góc với BC. Trên đoạn thẳng AH lấy điểm M. Chứng minh rằng:

a) $AH < \frac{{AB + AC}}{2}$

b) BM < CM

Hướng dẫn giải

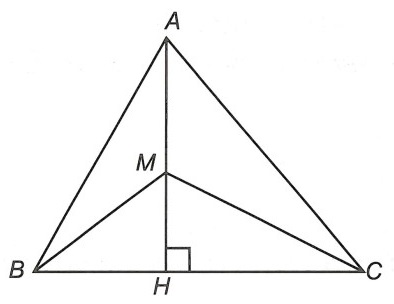
a) Ta có: AH ⊥ BC

⇒ AH là đường vuông góc còn AB là đường xiên

⇒ < AH < AB (1)

Lập luận tương tự AC là đường xiên còn AH là đường vuông góc

⇒ AH < AC (2)

Từ (1) và (2) suy ra:

$AH + AH < AB + AC \Rightarrow AH < \frac{{AB + AC}}{2}$

b) Ta có: BH và CH tương ứng là hình chiếu của đường xiên AB và AC lên đường thẳng BC.

Vì AB < AC nên BH < CH

Mặt khác: BH và CH là hình chiếu của đường xiên MB và MC trên BC và BH < CH

Nên MB < MC.

Câu 2. Cho tam giác ABC, điểm D nằm giữa B và C. Gọi H, K lần lượt là chân các đường vuông góc kẻ từ D xuống các đường thẳng AB, AC. So sánh BC và tổng DH + DK.

Hướng dẫn giải

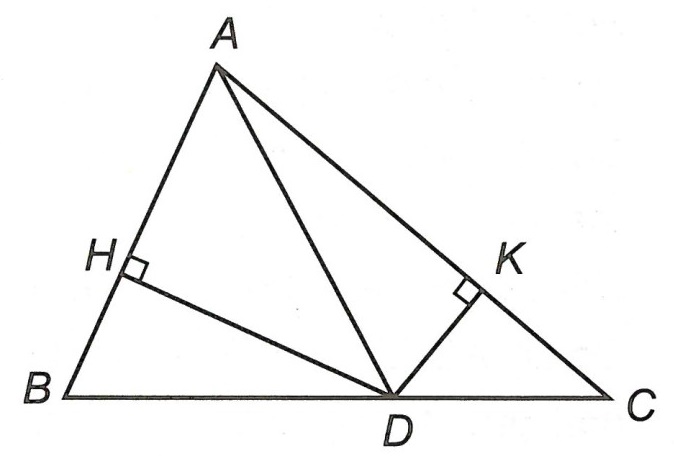
Ta có: DH < BD (đường vuông góc ngắn hơn đường xiên)

DK < DC (đường vuông góc ngắn hơn đường xiên)

Suy ra DH + DK < BD + DC hay DH + DK < BC

Câu 3. Cho tam giác ABC, D là điểm nằm giữa B và C (AD không vuông góc với BC). Gọi H, K lần lượt là chân các đường vuông góc kẻ từ B, C xuống đoạn thẳng AD. Chứng minh rằng:

a) AB + AC > BH + CK

b) BH + CK > BC

Hướng dẫn giải

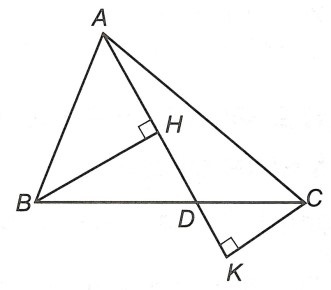
a) Xét tam giác ABH có AB là đường xiên, BH là đường vuông góc

⇒ AB > BH.

Xét tam giác AKC có AC là đường xiên, CK là đường vuông góc

⇒ AC > CK.

Do đó: AB + AC > BH + CK

b) Xét tam giác BHD có BH là đường vuông góc và BD là đường xiên nên BH < BD (đường vuông góc ngắn hơn đường xiên).

Tương tự ta chứng minh được: CK < CD

Do đó: BH + CK < BD + CD hay BH + CK < BC

Câu 4. Cho tam giác ABC vuông tại A, Bm là tia phân giác của góc B cắt AC tại D. Tại C kẻ Cn ⊥ AC (AB và Cn thuộc hai nửa mặt phẳng đối nhau có bờ là AC), Cn cắt Bm tại E. So sánh chu vi tam giác ABD và chu vi tam giác CDE.

Hướng dẫn giải

Kẻ DF ⊥ BC (F ∈ BC)

⇒ DF < DC (đường vuông góc ngắn hơn đường xiên).

Xét △ABD và △FBD, có:

$\widehat {BAD} = \widehat {BFD} = 90^\circ$

Cạnh huyền BD chung

$\widehat {ABD} = \widehat {FBD}$

Do đó: △ABD = △FBD (cạnh huyền – góc nhọn)

⇒ AD = FD (hai cạnh tương ứng)

Mà DF < DC nên AD < DC

Ta lại có: ED > EC (đường xiên dài hơn đường vuông góc).

Do đó: ED + EC > EC + EC hay ED + EC > 2EC

$\begin{gathered} ED + EC > EC + EC \hfill \\ \Leftrightarrow ED + EC > 2EC\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \Rightarrow \widehat {ABD} = \widehat {CED}\left( 1 \right) \hfill \\ \end{gathered}$