Tính chất chia hết của một tổng

Quan hệ chia hết

Số tự nhiên a chia hết cho số tự nhiên b (khác 0) nếu có số tự nhiên k sao cho a = b⋅k

+) Nếu a chia hết cho b, ta kí hiệu a ⋮ b

+) Nếu a không chia hết cho b, ta kí hiệu a b

Tính chất chia hết của một tổng

Tính chất 1

Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó

a ⋮ m, b ⋮ m, c ⋮ m ⇒ (a + b + c) ⋮ m

Ví dụ.

12 ⋮ 6 và 24 ⋮ 6 suy ra (12 + 4) ⋮ 6 và (24 – 12) ⋮ 6

10 5, 30 5 nhưng 7 5 nên (10 + 30 + 7) 5

Tính chất 2

Nếu chỉ có một số hạng của tổng không chia hết cho một số, các số hạng còn lại đều chia hết cho số đó thì tổng không chia hết cho số đó.

Dấu hiệu chia hết cho 2, cho 3, cho 5 và cho 9

+) Các số có chữ số tận cùng là chữ số chẵn thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.

+) Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.

+) Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.

+) Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.

Ví dụ.

32; 240; 144; 12346 chia hết cho 2.

35; 1030 chia hết cho 5.

2514 ⋮ 3 vì 2 + 5+ 1 + 4 = 12 ⋮ 3

126 ⋮ 9 vì 1 + 2 + 6 = 9 ⋮ 9

Sơ đồ hệ thống hóa

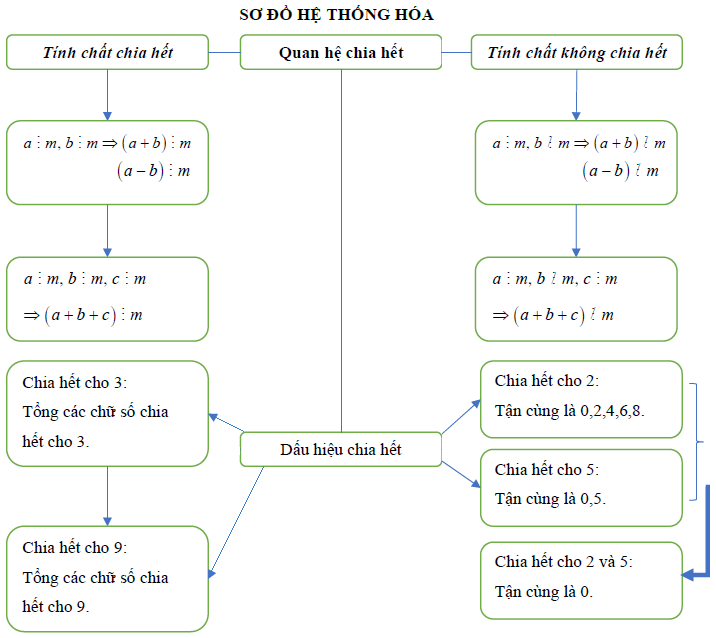
Phân dạng bài tập

Dạng 1. Xét tính chia hết hay không chia hết

Phương pháp giải

+) Sử dụng dấu hiệu chia hết cho 2, cho 5, cho 3 và cho 9.

+) Sử dụng tính chất chia hết của tổng, của hiệu.

a ⋮ m, b ⋮ m và c ⋮ m (a + b + c) ⋮ m

a m, b m và c m (a + b + c) m

Ví dụ.

6 ⋮ 3, 9 ⋮ 3 và 12 ⋮ 3 ⇒ (6 + 9 + 12) ⋮ 3

7 3, 9 ⋮ 3 và 12 ⋮ 3 ⇒ (7 + 9 +12) 3 .

Ví dụ mẫu

Ví dụ 1. Không tính tổng, hãy xét xem:

a) 27 + 81 + 63 có chia hết cho 3 không?

b) 21 + 49 + 32 có chia hết cho 7 không?

c) 45 + 99 + 180 có chia hết cho 9 không?

d) 125 + 350 – 234 có chia hết cho 5 không?

Hướng dẫn giải

a) Vì 27 ⋮ 3, 81 ⋮ 3 và 63 ⋮ 3 nên tổng (27 + 81 + 63) ⋮ 3.

b) Vì 21 ⋮ 7, 49 ⋮ 7 nhưng 32 7, do đó tổng (21 + 49 + 32) 7

c) Vì 45 ⋮ 9, 99 ⋮ 9 và 180 ⋮ 9 nên tổng (45 + 99 + 180) ⋮ 9

d) Vì 125 ⋮ 5, 350 ⋮ 5, nhưng 234 5 nên tổng (125 + 350 + 234) 5

Ví dụ 2. Không thực hiện phép tính, hãy chứng tỏ:

a) 39⋅2020 chia hết cho 13;

b) 2010⋅2011 chia hết cho 3;

c) 1411⋅2002 chia hết cho 17.

Hướng dẫn giải

a) Ta có: 39⋅2020 = 13⋅3⋅2020 chia hết cho 13 (theo định nghĩa).

b) Ta có: 2010 ⋮ 3 (theo dấu hiệu chia hết cho 3) nên tích 2010⋅2011 chia hết cho 3.

c) Ta có: 1411⋅2002 = 17⋅83⋅2002 chia hết cho 17 (theo định nghĩa).

Ví dụ 3. Cho các số: 115; 234; 560; 228; 117; 630; 738.

a) Những số nào chia hết cho 2?

b) Những số nào chia hết cho 3?

c) Những số nào chia hết cho 5?

d) Những số nào chia hết cho 9?

Hướng dẫn giải

a) Những số chia hết cho 2 là: 234; 560; 228; 630; 738 (vì có tận cùng là chữ số chẵn).

b) Những số chia hết cho 3 là: 234; 228; 117; 630; 738 (vì tổng các chữ số của chúng chia hết cho 3).

c) Những số chia hết cho 5 là: 115; 560; 630 (vì có tận cùng là 0 hoặc 5).

d) Những số chia hết cho 9 là: 234; 117; 630; 738 (vì tổng các chữ số của chúng chia hết cho 9).

Ví dụ 4. Một số tự nhiên a chia cho 15, được số dư là 5. Hỏi số a có chia hết cho 3 và cho 5 không?

Hướng dẫn giải

Số tự nhiên a chia cho 15, dư 5 nên a có dạng là a = 15k + 5 (với k ∈ ℕ).

Ta thấy 15k chia hết cho 3 và cho 5. Mà 5 chia hết cho 5, nhưng không chia hết cho 3.

Do đó: (15k + 5) ⋮ 5 và (15k + 5) 3.

Vậy a chia hết cho 5 và không chia hết cho 3.

Nhận xét:

+) Viết dạng tổng quát của số tự nhiên a chia cho 15, dư 5.

+) Dùng tính chất chia hết của một tổng để xét xem a có chia hết cho 3 và cho 5 hay không.

Ví dụ 5. Tìm số dư khi chia mỗi số sau cho 9 và cho 3:

145; 1378; 2456; 2789; 3568.

Hướng dẫn giải

Ta có: 1 + 4 + 5 = 10.

Số 10 chia cho 3 và cho 9 đều dư 1, nên 145 chia cho 3 và cho 9 có cùng số dư là 1.

1 + 3 + 7 + 8 = 19.

Số 19 chia cho 3 và cho 9 đều dư 1, nên 1378 chia cho 3 và cho 9 có cùng số dư là 1.

2 + 4 + 5 + 6 = 17.

Số 17 chia cho 3 dư 2, chia cho 9 dư 8.

Vậy 2456 chia cho 3 dư 2 và chia cho 9 dư 8.

Tương tự, 2789 chia cho 3 dư 2 và chia cho 9 dư 8.

3568 chia cho 3 dư 1 và chia cho 9 dư 4.

Nhận xét:

Một số có tổng các chữ số chia cho 3 (cho 9) dư m thì số đó chia cho 3 (cho 9) cũng dư m.

Ví dụ 6. Tổng (hiệu) sau có chia hết cho 3, cho 9 không?

a) 10²⁰ + 2

b) 10¹⁰⁰ – 1

Hướng dẫn giải

a) Ta có: 10²⁰ + 2 = 100…00 + 2 = 100…02 có tổng các chữ số bằng 3 nên 10²⁰ + 2 chia hết cho 3 và không chia hết cho 9.

b) Ta có: 10¹⁰⁰ – 1 = 100…00 – 1 = 99…99 chia hết cho cả 3 và 9.

Nhận xét:

Dựa vào dấu hiệu chia hết cho 3 và cho 9, ta cần tính xem tổng (hiệu) trên có tổng các chữ số bằng bao nhiêu?

Lưu ý rằng: 10ⁿ = 100…00 có tổng các chữ số bằng 1.

Tổng quát: 10ⁿ – 1 ⋮ 9

Bài tập tự luyện dạng 1

Bài tập cơ bản

Câu 1. Điền dấu “x” vào ô thích hợp:

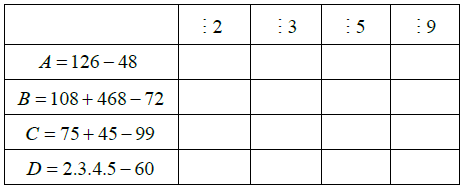
Hướng dẫn giải

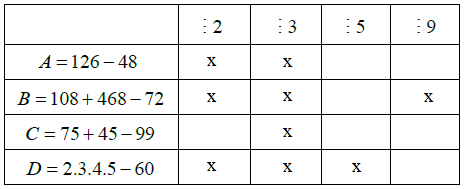
Câu 2. Cho các số: 234; 560; 789; 990; 1045; 2436. Điền số thích hợp vào chỗ chấm.

a) Các số chia hết cho 2 là: ………………………

b) Các số chia hết cho 3 là: ………………………

c) Các số chia hết cho 5 là: ………………………

d) Các số chia hết cho 9 là: ………………………

Hướng dẫn giải

a) Các số chia hết cho 2 là: 234; 560; 990; 2436.

b) Các số chia hết cho 3 là: 234; 789; 990; 2436.

c) Các số chia hết cho 5 là: 560; 990; 1045.

d) Các số chia hết cho 9 là: 234; 990.

Câu 3. Xét xem tổng 66a + 39b + 63c có chia hết cho 3 hay không?

Hướng dẫn giải

Vì 66a ⋮ 3, 39b ⋮ 3, 63c ⋮ 3 nên tổng 66a + 39b + 63c chia hết cho 3.

Câu 4. Áp dụng tính chất chia hết, xét xem tổng (hiệu) nào sau đây chia hết cho 7?

a) 49 + 51 – 7;

b) 1424 – 42;

c) 35 + 84 + 105;

d) 5⋅7 + 56 – 36.

Hướng dẫn giải

a) (49 + 51 – 7) 7 vì có 51 7 .

b) (14⋅24 – 42) ⋮ 7 vì 14⋅24 ⋮ 7 và 42 ⋮ 7

c) (35 + 84 + 105) ⋮ 7 vì cả ba số 35; 84 và 105 đều chia hết cho 7.

d) (5⋅7 + 56 – 36) 7 vì 5⋅7 ⋮ 7; 56 ⋮ 7 và 36 7.

Câu 5. Không thực hiện phép tính, hãy xét xem:

a) 7 + 128 có chia hết cho 7 không?

b) 6 + 24 + 180 + 738 có chia hết cho 6 không?

c) 24 + 18 – 8 có chia hết cho 8 không?

d) 33 + 121 + 144 có chia hết cho 11 không?

Hướng dẫn giải

a) Ta có: 7 + 128 không chia hết cho 7 (vì có 128 7).

b) Ta có: 6 + 24 + 180 + 738 chia hết cho 6 (vì tất cả các số hạng của tổng đều chia hết cho 6).

c) Ta có: 24 + 18 – 8 không chia hết cho 8 (vì 24 ⋮ 8, 8 ⋮ 8 và 18 8).

d) Ta có: 33 + 121 + 144 không chia hết cho 11 (vì 33 ⋮ 11, 121 ⋮ 11 và 144 11).

Câu 6. Điền dấu “x” vào ô trống thích hợp và giải thích:

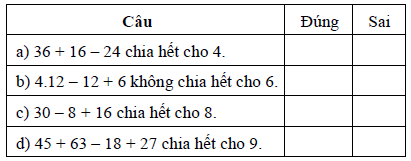
Hướng dẫn giải

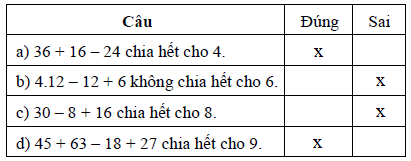
a) Đúng vì các số hạng của tổng đều chia hết cho 4.

b) Sai vì các số hạng của tổng đều chia hết cho 6, nên tổng phải chia hết cho 6.

c) Sai vì 30 8, 8 ⋮ 8 và 16 ⋮ 8.

d) Đúng vì các số hạng của tổng đều chia hết cho 9.

Câu 7. Một số tự nhiên a chia cho 30, được số dư là 18.

a) Hãy biểu diễn số a.

b) Hỏi a có chia hết cho 2, cho 3, cho 5 và cho 6 không?

Hướng dẫn giải

a) Số tự nhiên a chia cho 30, dư 18 có dạng là: a = 30k + 18 (với k ∈ ℕ).

b) Vì 30k chia hết cho 2, cho 3, cho 5 và cho 6. Mà 18 chia hết cho 2, cho 3 và cho 6, nhưng không chia hết cho 5.

Do đó a chia hết cho 2, cho 3 và cho 6, nhưng không chia hết cho 5.

Câu 8. Một số tự nhiên chia cho 45 dư 20. Hỏi số đó có chia hết cho 5 và cho 15 không?

Hướng dẫn giải

Số tự nhiên x chia cho 45 dư 20 có dạng là: x = 45k + 20 (với k ∈ ℕ).

Vì 45k chia hết cho cả 5 và 15, còn 20 chia hết cho 5 nhưng không chia hết cho 15.

Do đó x chia hết cho 5, nhưng không chia hết cho 15.

Câu 9. Gọi m là số dư của a khi chia cho 9. Điền vào ô trống:

Hướng dẫn giải

Bài tập nâng cao

Câu 10. Tổng (hiệu) sau có chia hết cho 3 và cho 9 không?

a) 10²⁰¹⁹ + 3

b) 10²⁰⁰² – 1

Hướng dẫn giải

a) Ta có: 10²⁰¹⁹ + 3 = 100…00 + 3 = 100…03 có tổng các chữ số bằng 4 nên không chia hết cho cả 3 và 9

b) 10²⁰⁰² – 1 = 100…00 – 1 = 99…99 chia hết cho cả 3 và 9.

Câu 11.

a) Tổng 10¹⁵ + 8 có chia hết cho 9 và cho 2 không?

b) Tổng 10²⁰¹⁰ + 8 có chia hết cho 9 không?

c) Tổng 10²⁰²⁰ + 14 có chia hết cho 3 và cho 2 không?

d) Hiệu 10²⁰²⁰ – 4 có chia hết cho 3 không?

Hướng dẫn giải

a) Ta có: 10¹⁵ + 8 = 100…00 + 8 = 100…08 chia hết cho cả 9 và 2 (vì có tổng các chữ số bằng 9 và chữ số tận cùng là 8).

b) Ta có: 10²⁰¹⁰ + 8 = 100…00 + 8 = 100…08 ⋮ 9 (vì có tổng các chữ số bằng 9)

c) Ta có: 10²⁰²⁰ + 14 = 100…00 + 14 = 100…14 chia hết cho cả 2 và 3 (vì có tổng các chữ số bằng 6 và chữ số tận cùng bằng 4).

d) Ta có: 10²⁰²⁰ – 4 = 100…00 – 4 = 99…96 ⋮ 3 (vì có tổng các chữ số chia hết cho 3).

Dạng 2. Lập các số thỏa mãn điều kiện chia hết từ các số cho trước

Phương pháp giải

+) Lập số chia hết cho 2, cần chọn chữ số ở hàng đơn vị là số chẵn (0; 2; 4; 6 hoặc 8).

+) Lập số chia hết cho 5, cần chọn chữ số ở hàng đơn vị là 0 hoặc 5.

+) Lập số chia hết cho 3, cần chọn các chữ số sao cho tổng của chúng chia hết cho 3.

+) Lập số chia hết cho 9, cần chọn các chữ số sao cho tổng của chúng chia hết cho 9.

Ví dụ mẫu

Ví dụ 1. Viết số tự nhiên có hai chữ số giống nhau, biết rằng số đó chia hết cho 2, còn chia 5 thì dư 4.

Hướng dẫn giải

Các số tự nhiên có hai chữ số giống nhau mà chia hết cho 2 là 22; 44; 66; 88.

Trong bốn số trên, số chia cho 5 dư 4 là: 44.

Vậy số cần tìm là: 44.

Ví dụ 2. Từ các chữ số 0; 1; 3; 4; 5, lập được bao nhiêu số có ba chữ số khác nhau chia hết cho 5?

Hướng dẫn giải

+) Chọn 0 làm hàng đơn vị, ta có các số:

130, 310; 140; 410; 150; 510; 340; 430; 350; 530; 450; 540.

+) Chọn 5 làm hàng đơn vị, ta có các số:

105; 305; 405; 135; 315; 145; 415; 345; 435.

Vậy từ các số 0; 1; 3; 4; 5, lập được 21 số có ba chữ số khác nhau chia hết cho 5.

Ví dụ 3. Dùng ba trong bốn chữ số 0; 1; 3; 8, hãy ghép thành các số tự nhiên có ba chữ số, sao cho các số đó:

a) Chia hết cho 9.

b) Chia hết cho 3 mà không chia hết cho 9.

Hướng dẫn giải

a) Ba số có tổng chia hết cho 9 là: 0; 1; 8.

Từ ba chữ số này ta lập được các số có ba chữ số khác nhau là; 180; 810; 108; 801.

b) Ba số có tổng chia hết cho 3 mà không chia hết cho 9 là: 1; 3; 8.

Từ ba chữ số này ta lập được các số có ba chữ số khác nhau là: 138; 183; 318; 381; 813; 831.

Ví dụ 4. Viết số tự nhiên nhỏ nhất có bốn chữ số sao cho số đó:

a) Chia hết cho 3.

b) Chia hết cho 9.

Hướng dẫn giải

a) Vì số cần tìm là số nhỏ nhất có 4 chữ số nên chọn:

+) Hàng nghìn là: 1.

+) Hàng trăm là: 0.

+) Hàng chục là: 0.

Để số đó chia hết cho 3 thì hàng đơn vị là: 2.

Vậy số tự nhiên nhỏ nhất có bốn chữ số chia hết cho 3 là: 1002.

b) Chọn hàng nghìn, hàng trăm và hàng chục giống câu a.

Để số đó chia hết cho 9 thì hàng đơn vị là 8.

Vậy số tự nhiên nhỏ nhất có bốn chữ số chia hết cho 9 là: 1008.

Bài tập tự luyện dạng 2

Câu 1. Dùng ba trong bốn chữ số 0; 4; 5; 6, hãy viết các số có ba chữ số khác nhau sao cho số đó:

a) Chia hết cho 9.

b) Chia hết cho 3 mà không chia hết cho 9.

Hướng dẫn giải

a) Ba số có tổng chia hết cho 9 là: 0; 4; 5.

Từ ba chữ số này ta lập được các số có ba chữ số khác nhau là: 450; 405; 540; 504.

b) Ba số có tổng chia hết cho 3 mà không chia hết cho 9 là: 4; 5; 6.

Từ ba chữ số này ta lập được các số có ba chữ số khác nhau là: 456; 465; 546; 564; 645; 654.

Câu 2. Viết số tự nhiên nhỏ nhất có năm chữ số sao cho số đó

a) Chia hết cho 3.

b) Chia hết cho 9.

Hướng dẫn giải

a) Số tự nhiên nhỏ nhất có năm chữ số chia hết cho 3 là: 10002.

b) Số tự nhiên nhỏ nhất có năm chữ số chia hết cho 9 là: 10008.

Câu 3. Dùng cả ba chữ số 2; 3; 5, hãy ghép thành các số tự nhiên có ba chữ số khác nhau:

a) Lớn nhất và chia hết cho 2.

b) Nhỏ nhất và chia hết cho 5.

Hướng dẫn giải

Từ ba chữ số 2; 3; 5 lập được các số có ba chữ số khác nhau:

a) Lớn nhất và chia hết cho 2 là: 532.

b) Nhỏ nhất và chia hết cho 5 là: 235.

Câu 4. Dùng ba trong bốn chữ số 0; 2; 3; 7, hãy ghép thành các số tự nhiên có ba chữ số sao cho các số đó:

a) Chia hết cho 9.

b) Chia hết cho 3 nhưng không chia hết cho 9.

c) Chia hết cho cả 2 và 5.

Hướng dẫn giải

Dùng ba trong bốn chữ số 0; 2; 3; 7 lập được thành các số tự nhiên có ba chữ số khác nhau và thỏa mãn:

a) Chia hết cho 9 là:

270; 207; 720; 702.

b) Chia hết cho 3, mà không chia hết cho 9 là:

237; 273; 327; 372; 723; 732.

c) Chia hết cho cả 2 và 5 là:

230; 320; 270; 720; 370; 730.

Câu 5. Có bao nhiêu số có ba chữ số:

a) Chia hết cho 2.

b) Chia hết cho 5.

c) Chia hết cho cả 2 và 5.

Hướng dẫn giải

a) Số lớn nhất có ba chữ số chia hết cho 2 là: 998.

Số bé nhất có ba chữ số chia hết cho 2 là: 100.

Khoảng cách giữa hai số liên tiếp chia hết cho 2 là: 2 đơn vị.

Vậy số các số có ba chữ số chia hết cho 2 là:

(998 – 100) : 2 + 1 = 450 số.

b) Số lớn nhất có ba chữ số chia hết cho 5 là: 995.

Số bé nhất có ba chữ số chia hết cho 5 là: 100.

Khoảng cách giữa hai số liên tiếp chia hết cho 5 là: 5 đơn vị.

Vậy số các số có ba chữ số chia hết cho 5 là:

(995 – 100) : 5 + 1 = 180 số.

c) Số chia hết cho cả 2 và 5 thì có tận cùng là 0.

Số lớn nhất chia hết cho cả 2 và 5 là: 990.

Số bé nhất chia hết cho cả 2 và 5 là: 100.

Khoảng cách giữa hai số liên tiếp chia hết cho cả 2 và 5 là: 10 đơn vị.

Vậy số các số có ba chữ số chia hết cho cả 2 và 5 là:

(990 – 100) : 10 + 1 = 90 số.

Dạng 3. Tìm điều kiện để một số chia hết cho một số nào đó

Phương pháp giải

Sử dụng các dấu hiệu chia hết cho 2, cho 3, cho 5, cho 9 và tính chất chia hết của một tổng.

Ví dụ mẫu

Ví dụ 1. Cho A = 15 + 18 + 24 + x, với x ∈ ℕ. Tìm điều kiện của x để:

a) A ⋮ 3;

b) A 3.

Hướng dẫn giải

a) Vì 15 ⋮ 3, 18 ⋮ 3 và 24 ⋮ 3 nên để A ⋮ 3 thì x ⋮ 3.

b) Vì 15 ⋮ 3, 18 ⋮ 3 và 24 ⋮ 3 nên để A 3 thì x 3.

Ví dụ 2. Điền vào dấu * để $\overline {37*}$

a) Chia hết cho 2.

b) Chia hết cho 3.

c) Chia hết cho 5.

d) Chia hết cho 9.

Hướng dẫn giải

Để $\overline {37*}$ chia hết cho 2 thì * ∈ {0; 2; 4; 6; 8}

Để $\overline {37*}$ chia hết cho 3 thì 3 + 7 + * = 10 + * chia hết cho 3, suy ra * ∈ {2; 5; 8}

Để $\overline {37*}$ chia hết cho 5 thì * ∈ {0; 5}

Để $\overline {37*}$ chia hết cho 9 thì 3 + 7 + * = 10 + * chia hết cho 9, suy ra * = 8

Ví dụ 3. Tìm a và b để $\overline {4a6b}$ chia hết cho cả 2; 3; 5 và 9.

Hướng dẫn giải

Để $\overline {4a6b}$ chia hết cho cả 2 và 5 thì b = 0. Ta có số $\overline {4a60}$

Ta thấy $\overline {4a60}$ chia hết cho 9 thì chia hết cho 3 nên ta chỉ cần tìm điều kiện để $\overline {4a60}$ chia hết cho 9.

Suy ra: 4 + a + 6 + 0 = 10 + a chia hết cho 9. Do đó a = 8.

Vậy a = 8; b = 0

Ví dụ 4. Tìm các chữ số a và b sao cho $\overline {a56b} {\text{ }} \vdots {\text{ }}45$

Hướng dẫn giải

Để $\overline {a56b}$ chia hết cho 45 thì $\overline {a56b}$ phải chia hết cho cả 5 và 9.

$\overline {a56b} {\text{ }} \vdots {\text{ }}5 \Rightarrow \left[ \begin{gathered} b = 0 \hfill \\ b = 5 \hfill \\ \end{gathered} \right.$

+) Nếu b = 0 ta có $\overline {a560} {\text{ }} \vdots {\text{ }}9$ thì a + 5 + 6 + 0 = a + 11 chia hết cho 9, suy ra a = 7.

+) Nếu b = 5 ta có $\overline {a560} {\text{ }} \vdots {\text{ }}9$ thì a + 5 + 6 + 5 = a + 16 chia hết cho 9, suy ra a = 2.

Vậy ta có hai cặp số thỏa mãn a = 7, b = 0 hoặc a = 2, b = 5

Ví dụ 5. Cho $A = \overline {7a5} + \overline {8b4}$ . Biết a – b = 6 và A chia hết cho 9. Tìm a và b.

Hướng dẫn giải

Nhận thấy, nếu một số có tổng các chữ số chia hết cho 9 dư m thì số đó chia cho 9 cũng dư m.

Do đó: A ⋮ 9 thì (7 + a + 5) + (8 + b + 4) = 24 + a + b chia hết cho 9.

Mà a, b là các số tự nhiên có một chữ số nên 0 ≤ a + b ≤ 18.

Suy ra: a + b = 3 hoặc a + b = 12

+) Trường hợp 1: Nếu a + b = 3, kết hợp với a – b = 6 thì:

Số lớn là: a = (3 + 6) : 2 = 4 dư 1 (loại)

+) Trường hợp 2: Nếu a + b = 12, kết hợp với a – b = 6 thì:

Số lớn là: a = (12 + 6) : 2 = 9

Số bé là: b = 9 – 6 = 3

Vậy a = 9, b = 3

Ví dụ 6. Điền vào dấu * các chữ số:

$\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{*{\text{ }}*{\text{ }}*{\text{ }}*} \end{array}} \\ {\begin{array}{*{20}{c}} {^ \times }&{}&{}&{_{}^{}{\text{ }}_{}^{}{\text{ }}_{}^{}{\text{ }}9} \end{array}} \\ {\overline {\begin{array}{*{20}{c}} {}&{9{\text{ }}_{}^{}{\text{ }}2{\text{ }}_{}^{}{\text{ }}0{\text{ }}_{}^{}*} \end{array}} } \end{array}$

Hướng dẫn giải

Ta thấy 920* chia hết cho 9 nên 9 + 2 + 0 + * = 11 + * chia hết cho 9. Suy ra * = 7.

Ta được tích bằng 9207.

Thừa số chưa biết là: 9207 : 9 = 1203

Vậy ta có phép nhân:

$\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{1{\text{ }}_{}^{}{\text{ }}0{\text{ }}_{}^{}{\text{ }}2{\text{ }}_{}^{}{\text{ }}3} \end{array}} \\ {\begin{array}{*{20}{c}} {^ \times }&{}&{_{}^{}}&{_{}^{}{\text{ }}_{}^{}{\text{ }}_{}^{}{\text{ }}_{}^{}9} \end{array}} \\ {\overline {\begin{array}{*{20}{c}} {}&{9{\text{ }}_{}^{}{\text{ }}2{\text{ }}_{}^{}{\text{ }}0{\text{ }}_{}^{}{\text{ }}7} \end{array}} } \end{array}$

Bài tập tự luyện dạng 3

Bài tập cơ bản

Câu 1. Cho A = 8 + 12 + x + 16 + 28, với x ∈ ℕ. Tìm điều kiện của x để:

a) A chia hết cho 4.

b) A không chia hết cho 4.

Hướng dẫn giải

Ta thấy các số hạng: 8; 12; 16 và 28 đều chia hết cho 4, do đó:

a) Để A chia hết cho 4 thì x ⋮ 4.

b) Để A không chia hết cho 4 thì x 4.

Câu 2. Điền các chữ số thích hợp vào dấu * để $\overline {182*}$

a) Chia hết cho 2.

b) Chia hết cho 5.

c) Chia hết cho cả 2 và 5.

Hướng dẫn giải

a) * ∈ {0; 2; 4; 6; 8}

b) * ∈ {0; 5}

c) * = 0

Câu 3. Điền vào dấu * để $\overline {34*}$

a) Chia hết cho 2.

b) Chia hết cho 3.

c) Chia hết cho 5.

d) Chia hết cho 9.

Hướng dẫn giải

a) * ∈ {0; 2; 4; 6; 8}

b) * ∈ {2; 5; 8}

c) * ∈ {0; 5}

d) * = 2

Câu 4. Thay a, b bằng các chữ số thích hợp để:

a) $\overline {54a}$ chia hết cho cả 2 và 9.

b) $\overline {341ab}$ chia hết cho cả 5 và 9.

c) $\overline {a18b}$ chia hết cho cả 2; 3; 5 và 9.

Hướng dẫn giải

a) $\overline {54a}$ chia hết cho 9 thì 5 + 4 + a = 9 + a chia hết cho 9, suy ra a = 0 hoặc a = 9.

Mà $\overline {54a}$ chia hết cho 2 nên a = 0.

b) $\overline {341ab}$ chia hết cho 5 thì b = 0 hoặc b = 5.

+) Trường hợp 1: b = 0, ta có: $\overline {341a0} {\text{ }} \vdots {\text{ }}9$ thì 3 + 4 + 1 + a + 0 = 8 + a chia hết cho 9.

Suy ra a = 1.

+) Trường hợp 2: b = 5, ta có: $\overline {341a5} {\text{ }} \vdots {\text{ }}9$ thì 3 + 4 + 1 + a + 5 = 13 + a chia hết cho 9.

Suy ra a = 5.

Vậy ta có hai số thỏa mãn là: 34110 và 34155.

c) $\overline {a18b}$ chia hết cho cả 2 và 5 nên b = 0.

Ta có: $\overline {a180} {\text{ }} \vdots {\text{ }}9$ thì a + 1 + 8 + 0 = a + 9 chia hết cho 9.

Mà a ≠ 0 nên a = 9.

Vậy số thỏa mãn đề bài là: 9180.

Câu 5. Tìm x, y biết:

a) $\overline {23x5y}$ chia hết cho 2, cho 5 và cho 9.

b) $\overline {144xy}$ chia hết cho 3 và cho 5.

Hướng dẫn giải

a) $\overline {23x5y}$ chia hết cho cả 2 và 5 nên y = 0.

Ta có: $\overline {23x50} {\text{ }} \vdots {\text{ }}9$ thì 2 + 3 + x + 5 + 0 = 10 + x chia hết cho 9.

Suy ra x = 8.

Vậy số thỏa mãn đề bài là: 23850.

b) $\overline {144xy}$ chia hết cho 5 suy ra y = 0 hoặc y = 5.

+) Trường hợp 1: y = 0.

Ta có: $\overline {144x0} {\text{ }} \vdots {\text{ 3}}$ thì 1 + 4 + 4 + x + 0 = 9 + x chia hết cho 3.

Suy ra: x ∈ {0; 3; 6; 9}.

+) Trường hợp 2: y = 5.

Ta có: $\overline {144x5} {\text{ }} \vdots {\text{ 3}}$ thì 1 + 4 + 4 + x + 5 = 14 + x chia hết cho 3.

Suy ra: x ∈ {1; 4; 7}.

Vậy các số thỏa mãn là: 14400; 14430; 14460; 14490; 14415; 14445; 14475.

Câu 6.

a) Tìm số tự nhiên có hai chữ số giống nhau, biết rằng số đó chia hết cho 2, còn chia cho 5 thì dư 2.

b) Tìm số tự nhiên có ba chữ số giống nhau, biết rằng số đó chia hết cho 5, còn chia cho 2 thì dư 1.

Hướng dẫn giải

a) 22.

b) 555.

Câu 7.

a) Tìm số có hai chữ số giống nhau, biết rằng số đó chia hết cho 3, còn chia cho 5 thì dư 1.

b) Tìm tập hợp các số tự nhiên n vừa chia hết cho 2, vừa chia hết cho 5 và 132 < n < 178

Hướng dẫn giải

a) Các số có hai chữ số giống nhau mà chia hết cho 3 là; 33; 66; 99.

Trong ba số trên, số chia cho 5 dư 1 là: 66.

Vậy số cần tìm là 66.

b) Số vừa chia hết cho 2, vừa chia hết cho 5 thì có chữ số tận cùng bằng 0.

Tập hợp các số tự nhiên chia hết cho cả 2 và 5 thỏa mãn 132 < n < 178 là: {140; 150; 160; 170}.

Bài tập nâng cao

Câu 8. Tìm các chữ số a và b sao cho b – a = 2 và $\overline {20ab}$ chia hết cho 9.

Hướng dẫn giải

Ta có: $\overline {20ab}$ chia hết cho 9 thì 2 + 0 + a + b = 2 + a + b chia hết cho 9.

Mà a và b là các số tự nhiên có một chữ số nên 0 ≤ a + b ≤ 18.

Suy ra: a + b = 7 hoặc a + b = 16.

+) Trường hợp 1: a + b = 7 kết hợp với b – a = 2.

Số lớn là: b = (7 + 2) : 2 = 4 dư 1 (loại).

+) Trường hợp 2: a + b = 16 kết hợp với b – a = 2.

Số lớn là: b = (16 + 2) : 2 = 9

Số bé là: a = 9 – 2 = 7

Vậy a = 7, b = 9

Câu 9. Tìm các chữ số a và b sao cho a – b = 5 và $\overline {a785b}$ chia hết cho 9.

Hướng dẫn giải

Vì $\overline {a785b}$ chia hết cho 9 nên a + 7 + 8 + 5 + b = a + b + 20 chia hết cho 9.

Do 0 ≤ a, b ≤ 9 và a ≠ 0 nên 1 ≤ a + b ≤ 18

Suy ra a + b = 7 hoặc a + b = 16.

+) Trường hợp 1: a + b = 7 và a – b = 5

Số lớn là: a = (7 + 5) : 2 = 6

Số bé là: b = 6 – 5 = 1

Ta có số cần tìm là 67851.

+) Trường hợp 2: a + b = 16 và a – b = 5

Số lớn là a = (16 + 5) : 2 = 10 dư 1 (loại).

Câu 10. Điền vào dấu * các chữ số thích hợp:

$\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{_{}^{}{\text{ }}_{}^{}{\text{ }}_{}^{}{\text{ }}_{}^{}*{\text{ }}*{\text{ }}*{\text{ }}*} \end{array}} \\ {\begin{array}{*{20}{c}} {^ \times }&{_{}^{}{\text{ }}_{}^{}{\text{ }}}&{_{}^{}{\text{ }}_{}^{}{\text{ }}}&{_{}^{}{\text{ }}_{}^{}{\text{ }}_{}^{}{\text{ }}9} \end{array}} \\ {\overline {\begin{array}{*{20}{c}} {}&{2_{}^{}{\text{ }}_{}^{}{\text{ }}1_{}^{}{\text{ }}_{}^{}{\text{ }}1_{}^{}{\text{ }}_{}^{}{\text{ }}8_{}^{}{\text{ }}_{}^{}{\text{ }}*} \end{array}} } \end{array}$

Hướng dẫn giải

Nhận thấy 2118* chia hết cho 9, khi đó: 2 + 1 + 1 + 8 + * + 12 + * chia hết cho 9.

Suy ra: * = 6.

Ta được thương bằng 21186.

Thừa số chưa biết là: 21186 : 9 = 2354

Vậy ta có phép nhân:

$\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {_{}^{}{\text{ }}_{}^{}{\text{ }}_{}^{}{\text{ }}}&{2_{}^{}{\text{ }}_{}^{}{\text{ }}3_{}^{}{\text{ }}_{}^{}{\text{ }}5_{}^{}{\text{ }}_{}^{}{\text{ }}4} \end{array}} \\ {\begin{array}{*{20}{c}} {^ \times }&{_{}^{}{\text{ }}_{}^{}{\text{ }}}&{_{}^{}{\text{ }}_{}^{}{\text{ }}}&{_{}^{}{\text{ }}_{}^{}{\text{ }}_{}^{}{\text{ }}9} \end{array}} \\ {\overline {\begin{array}{*{20}{c}} {}&{2_{}^{}{\text{ }}_{}^{}{\text{ }}1_{}^{}{\text{ }}_{}^{}{\text{ }}1_{}^{}{\text{ }}_{}^{}{\text{ }}8_{}^{}{\text{ }}_{}^{}{\text{ }}6} \end{array}} } \end{array}$

Dạng 4. Chứng minh tính chất chia hết

Phương pháp giải

Cần lưu ý:

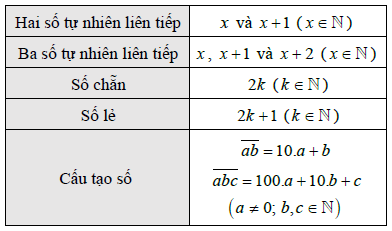
Ví dụ mẫu

Ví dụ 1. Chứng tỏ rằng tổng của ba số tự nhiên liên tiếp là một số chia hết cho 3.

Hướng dẫn giải

Gọi ba số tự nhiên liên tiếp là: x; x + 1; x + 2 (x ∈ ℕ).

Tổng của ba số này là: x + (x + 1) + (x + 2) = 3x + 3 = 3(x + 1) ⋮ 3 (theo định nghĩa).

Vậy tổng của ba số tự nhiên liên tiếp là một số chia hết cho 3.

Ví dụ 2. Chứng minh rằng:

a) Tích của hai số tự nhiên liên tiếp luôn chia hết cho 2.

b) Tổng của bốn số tự nhiên liên tiếp là một số không chia hết cho 4.

Hướng dẫn giải

a) Gọi hai số tự nhiên liên tiếp là x và x + 1 (x ∈ ℕ).

Ta có hai trường hợp sau:

+) Nếu x chia hết cho 2 thì bài toán được giải.

+) Nếu x chia cho 2 dư 1 thì x có dạng x = 2k + 1 (k ∈ ℕ).

Khi đó: x(x + 1)

= (2k + 1)[(2k + 1) + 1]

= (2k + 1)(2k + 2)

= (2k + 1)⋅2⋅(k + 1) ⋮ 2

Vậy tích của hai số tự nhiên liên tiếp luôn chia hết cho 2.

b) Gọi bốn số tự nhiên liên tiếp: x, x + 1, x + 2, x + 3 (x ∈ ℕ).

Ta có: x + (x + 1) + (x + 2) + (x + 3) = 4x + 6

Vì 4x ⋮ 4 nhưng 6 4 nên (4x + 6) 4

Vậy tổng của bốn số tự nhiên liên tiếp là một số không chia hết cho 4.

Nhận xét:

Ta có kết quả tương tự: “Tích của n số tự nhiên liên tiếp chia hết cho n”.

Ví dụ 3. Chứng minh rằng:

a) Số có dạng $\overline {aaa}$ luôn chia hết cho 37.

b) Hiệu $\overline {ab} - \overline {ba}$ (với a ≥ b) luôn chia hết cho 9.

Hướng dẫn giải

Ta có: $\overline {aaa} = a \cdot 111 = a \cdot 3 \cdot 37{\text{ }} \vdots {\text{ }}37$

Vậy số có dạng $\overline {aaa}$ luôn chia hết cho 37.

Ta có: $\overline {ab} - \overline {ba} = \left( {10a + b} \right) - \left( {10b + a} \right)$ $= 9a - 9b = 9\left( {a - b} \right)$

Vậy $\left( {\overline {ab} - \overline {ba} } \right){\text{ }} \vdots {\text{ }}9$

Ví dụ 4. Gọi A = n² + n + 1 (n ∈ ℕ). Chứng tỏ rằng:

a) A không chia hết cho 2.

b) A không chia hết cho 5.

Hướng dẫn giải

a) Ta có: A = n² + n + 1 = (n² + n) + 1 = n(n + 1) + 1

Vì n(n + 1) là tích của hai số tự nhiên liên tiếp nên n(n + 1) ⋮ 2 (theo Ví dụ 2).

Do đó (n + 1) + 1 không chia hết cho 2.

b) Vì n(n + 1) là tích của hai số tự nhiên liên tiếp nên n(n + 1) có tận cùng là 0; 2; 6.

Suy ra n(n + 1) + 1 có tận cùng là 1; 3; 7, không chia hết cho 5.

Vậy A không chia hết cho 5.

Bài tập tự luyện dạng 4

Bài tập cơ bản

Câu 1. Cho x = 180y + 45z, với y, z ∈ ℕ. Chứng minh rằng x chia hết cho 5 và cho 9 với mọi y, z.

Hướng dẫn giải

Ta có: 180y ⋮ 5 và 45z ⋮ 5 nên x cũng chia hết cho 5 với mọi y, z (tính chất chia hết của một tổng).

Tương tự, ta cũng có x chia hết cho 9 với mọi y, z.

Bài tập nâng cao

Câu 2. Chứng tỏ rằng:

a) Trong hai số tự nhiên liên tiếp, luôn có một số chia hết cho 2.

b) Trong ba số tự nhiên liên tiếp, luôn có một số chia hết cho 3.

Hướng dẫn giải

a) Gọi hai số tự nhiên liên tiếp là: a và a + 1 (a ∈ ℕ).

Ta có hai trường hợp sau:

Nếu a chia hết cho 2 thì bài toán được giải.

Nếu a chia 2 dư 1 thì a có dạng x = 2k + 1 (k ∈ ℕ).

Khi đó: a + 1= (2k + 1) + 1 = 2k + 2 = 2(k + 1) ⋮ 2

Vậy trong hai số tự nhiên liên tiếp a và a + 1 luôn có một số chia hết cho 2.

b) Gọi ba số tự nhiên liên tiếp là: x, x + 1, x + 2 (x ∈ ℕ)

Ta có ba trường hợp sau:

Nếu x ⋮ 3 thì bài toán đã được giải.

Nếu x chia cho 3, dư 1. Khi đó x có dạng x = 3k + 1 (với k ∈ ℕ) thì

x + 2 = 3k + 1 + 2 = 3k + 3 = 3(k + 1) ⋮ 3

Nếu x chia cho 3, dư 2. Khi đó x có dạng x = 3k + 2 (với k ∈ ℕ) thì

x + 1 = 3k + 2 + 1 = 3k + 3 = 3(k + 1) ⋮ 3

Vậy trong ba số tự nhiên liên tiếp x, x + 1, x + 2 luôn có một số chia hết cho 3.

Câu 3. Chứng minh rằng:

a) Tích của ba số tự nhiên liên tiếp luôn chia hết cho 6.

b) Tích hai số chẵn liên tiếp chia hết cho 8.

Hướng dẫn giải

a) Áp dụng kết quả của Câu 2, ta có: trong ba số tự nhiên liên tiếp có ít nhất một số chia hết cho 2, và luôn có một số chia hết cho 3.

Do vậy, tích của chúng luôn chia hết cho 6.

b) Gọi hai số chẵn liên tiếp là 2k và 2k + 2

Ta có: 2k⋅(2k + 2) = 2k⋅2⋅(k + 1) = 4k⋅(k + 1) ⋮ 4

Mặt khác: k(k + 1) là tích của hai số tự nhiên liên tiếp nên chia hết cho 2.

Suy ra: 4k⋅(k + 1) ⋮ 8

Vậy tích của hai số chẵn liên tiếp chia hết cho 8.

Câu 4. Chứng tỏ rằng nếu hai số có cùng số dư khi chia cho 7, thì hiệu của chúng cũng chia hết cho 7.

Hướng dẫn giải

Giả sử a và b cùng chia cho 7 có số dư là m.

Khi đó: a = 7x + m và b = 7y + m với x, y ∈ ℕ.

Ta có: a – b = (7x + m) – (7y + m) = 7x – 7y = 7(x – y) ⋮ 7 (đpcm).

Vậy nếu hai số có cùng số dư khi chia cho 7, thì hiệu của chúng cũng chia hết cho 7.

Câu 5. Chứng tỏ rằng:

a) Số có dạng $\overline {aaaaaa}$ luôn chia hết cho 7.

b) Số có dạng $\overline {abcabc}$ luôn chia hết cho 11.

Hướng dẫn giải

a) Ta có: $\overline {aaaaaa} = a \cdot 111111 = a \cdot 7 \cdot 15873{\text{ }} \vdots {\text{ }}7$ (theo định nghĩa).

b) Ta có: $\overline {abcabc} = \overline {abc} \cdot 1000 + \overline {abc}$ $= \overline {abc} \cdot 1001 = \overline {abc} \cdot 11 \cdot 91{\text{ }} \vdots {\text{ }}11$ (theo định nghĩa).

Câu 6. Chứng tỏ rằng với mọi số tự nhiên n thì tích (n + 3)(n + 6) chia hết cho 2.

Hướng dẫn giải

+) Nếu n = 2k (k ∈ ℕ) thì n + 6 = 2k + 6 ⋮ 2

+) Nếu n = 2k + 1 (k ∈ ℕ) thì n + 3 = 2k + 1 + 3 = 2k + 4 ⋮ 2

Vậy (n + 3)(n + 6) ⋮ 2

Thầy Tú dạy toán