Trắc nghiệm số phức – 10 dạng toán đặc trưng nhất

Ở bài viết này, VerbaLearn sẽ giúp bạn đọc tổng hợp lại một số dạng toán trắc nghiệm số phức phổ biến trong chương trình toán lớp 12. Một số dạng toán đặc trưng bao gồm: Phép toán số phức, phần thực phần ảo, module số phức, phương trình bậc nhất, phương trình bậc cao, biểu diễn số phức, …

Dạng 1. Các phép toán số phức

[content_1]

Câu 1. Số phức z thỏa mãn |z| + z = 0. Khi đó:

A. z là số thuần ảo

B. |z| = 1

C. Phần thực của z là số âm

D. z là số thực nhỏ hơn hoặc bằng 0

Lời giải

Chọn D

Đặt z = x + yi (x, y ∈ ℝ)

Theo đề:

Vậy z là số thực nhỏ hơn hoặc bằng 0.

Câu 2. Cho hai số phức z = (a – 2b) – (a – b)i và w = 1 – 2i. Biết z = w.i. Tính S = a + b.

A. S = 7

B. S = –7

C. S = –4

D. S = –3

Lời giải

Chọn B

Ta có z = (a – 2b) – (a – b)i = (1 – 2i).i = 2 + i

Vậy S = a + b = –7

Câu 3. Số phức nghịch đảo của số phức z = 1 + 3i là

A.

B.

C.

D.

Lời giải

Chọn C

Ta có

Câu 4. Tìm số phức z thỏa mãn

A. z = –1 + 3i

B. z = 1 – 3i

C. z = 1 + 3i

D. z = –1 – 3i

Lời giải

Chọn C

Câu 5. Cho số phức . Khi đó:

A.

B.

C.

D.

Lời giải

Chọn A

Câu 6. Gọi a, b lần lượt là phần thực và phần ảo của số phức . Giá trị của a – b là

A. 7

B. –7

C. 31

D. –31

Lời giải

Chọn B

Ta có:

Vậy a – b = 12 – 19 = –7

Câu 7. Cho số phức z thỏa mãn: (1 + 2z)(3 + 4i) + 5 + 6i = 0. Tìm số phức w = 1 + z.

A.

B.

C.

D.

Lời giải

Chọn A

Gọi z = a + bi, với a, b ∈ ℝ.

Ta có:

Câu 8. Cho số phức . Số phức 1 + z + z² bằng.

A.

B. 0

C.

D. 1

Lời giải

Chọn D

Ta có

Câu 9. Cho số phức . Tính số phức

A.

B.

C.

D.

Lời giải

Chọn A

Câu 10. Cho a, b, c là các số thực và . Giá trị của (a + bz + cz²)(a + bz² + cz) bằng

A. 0

B. a + b + c

C. a² + b² + c² – ab – bc – ca

D. a² + b² + c² + ab + bc + ca

Lời giải

Chọn C

Ta có

Và

Khi đó

Câu 11. Cho số phức z = 1 – 3i. Tìm số phức .

A. w = –4 + 4i

B. w = 4 + 4i

C. w = 4 – 4i

D. w = –4 – 4i

Lời giải

Chọn B

Câu 12. Biểu diễn về dạng z = a + bi của số phức là số phức nào?

A.

B.

C.

D.

Lời giải

Chọn C

Ta có

Câu 13. Nếu z = 2i + 3 thì bằng:

A.

B.

C.

D.

Lời giải

Chọn B

Vì z = 2i + 3 = 3 + 2i nên , suy ra:

Dạng 2. Phần thực – Phần ảo của số phức

[content_2]

Câu 1. Cho số phức . Khẳng định nào sau đây là sai?

A. Phần ảo của số phức z là

B. Phần thực của số phức z là 1

C.

D. Điểm biểu diễn của z trên mặt phẳng tọa độ là

Lời giải

Chọn B

Số phức có phần thực là 1, phần ảo là

Câu 2. Cho hai số phức: z₁ = –2 + 3i, z₂ = –1 + i . Phần ảo của số phức w = 2z₁z₂ bằng

A. 5

B. 10

C. –5

D. –10

Lời giải

Chọn D

w = 2z₁z₂ = –2 – 10i

Câu 3. Tổng phần thực và phần ảo của số phức z thoả mãn bằng

A. –6

B. 2

C. –2

D. 6

Lời giải

Chọn D

Đặt z = x + yi (x, y ∈ ℝ).

Khi đó

Suy ra x + y = 6

Câu 4. Nếu số phức z ≠ 1 thỏa mãn |z| = 1 thì phần thực của bằng:

A. 1

B.

C. 2

D. 4

Lời giải

Chọn B

z = x + yi (x, y ∈ ℝ), |z| = 1 ⇔ x² + y² = 1

có phần thực là

Câu 5. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Số phức z = 2 – 3i có phần thực là 2, phần ảo là 3

B. Số phức z = 2 – 3i có phần thực là 2, phần ảo là –3i

C. Số phức z = 2 – 3i có phần thực là 2, phần ảo là 3i

D. Số phức z = 2 – 3i có phần thực là 2, phần ảo là –3

Lời giải

Chọn D

Mỗi số phức z = a + bi có phần thực là a, phần ảo là b .

Câu 6. Xác định phần ảo của số phức z = 18 – 12i.

A. 12

B. –12i

C. –12

D. 18

Lời giải

Chọn C

Phần ảo của số phức z = 18 – 12i là –12

Câu 7. Gọi a, b lần lượt là phần thực và phần ảo của số phức

.

Giá trị của a – b là

A. 31

B. –31

C. 7

D. –7

Lời giải

Chọn D

Ta có:

Vậy a – b = 12 – 19 = –7

Câu 8. Cho số phức z có số phức liên hợp . Tổng phần thực và phần ảo của số phức z bằng

A. –1

B. 1

C. –5

D. 5

Lời giải

Chọn D

Ta có: z = 3 +2i.

Vậy tổng phần thực và phần ảo của số phức z bằng 5.

Câu 9. Cho số phức z₁ = 1 + i và z₂ = 2 – 3i. Tìm số phức liên hợp của số phức w = z₁ + z₂?

A.

B.

C.

D.

Lời giải

Chọn C

Vì z₁ = 1 + i và z₂ = 2 – 3i

Nên w = z₁ + z₂ ⇔ w = (1 + 2) +(1 – 3)i = 3 – 2i

⇒

Câu 10. Tìm phần thực và phần ảo của số phức z = –i.

A. Phần thực là –1 và phần ảo là i

B. Phần thực là 0 và phần ảo là –1

C. Phần thực là 0 và phần ảo là –i

D. Phần thực là –i và phần ảo là 0

Lời giải

Chọn B

Ta có: z = –i = 0 – 1.i nên phần thực là 0, phần ảo là –1

Dạng 3. Số phức liên hợp

[content_3]

Câu 1. Cho số phức . Tìm phần ảo của số phức

A.

B.

C.

D.

Hướng dẫn giải

Chọn C

Ta có:

Câu 2. Cho điểm M là điểm biểu diễn của số phức z. Tìm phần thực và phần ảo của số phức z .

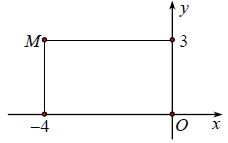
A. Phần thực là 3 và phần ảo là –4

B. Phần thực là –4 và phần ảo là 3i

C. Phần thực là 3 và phần ảo là –4i

D. Phần thực là –4 và phần ảo là 3

Hướng dẫn giải

Chọn D

Câu 3. Cho số phức z = –2 + 3i. Số phức liên hợp của z là

A.

B.

C.

D.

Hướng dẫn giải

Chọn D

Câu 4. Cho số phức z có điểm biểu diễn là điểm A trong hình vẽ bên. Tìm phần thực và phần ảo của số phức .

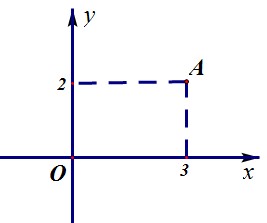
A. Phần thực bằng 3, phần ảo bằng –2

B. Phần thực bằng 3, phần ảo bằng 2

C. Phần thực bằng 2, phần ảo bằng –3i

D. Phần thực bằng 3, phần ảo bằng 2i

Hướng dẫn giải

Chọn A

Từ hình vẽ ta suy ra số phức

Nên số phức có phần thực bằng 3, phần ảo bằng –2

Câu 5. Cho z = 1 – 2i. Phần thực của số phức bằng.

A.

B.

C.

D.

Hướng dẫn giải

Chọn B

Ta có:

. Phần thực là:

Câu 6. Cho số phức z thoả mãn . Số phức liên hợp là.

A.

B.

C.

D.

Hướng dẫn giải

Chọn A

z = (3 + 2i)(1 – i) = 5 – i

Số phức liên hợp

Câu 7. Cho hai số phức z = 1 + 3i, w = 2 – i. Tìm phần ảo của số phức .

A. 5

B. –7i

C. –7

D. 5i

Hướng dẫn giải

Chọn C

Vậy phần ảo của số phức u bằng –7.

Câu 8. Cho số phức z = 3 – 2i. Tìm phần thực và phần ảo của số phức

A. Phần thực bằng 3 và phần ảo bằng –2

B. Phần thực bằng 2 và phần ảo bằng 3

C. Phần thực bằng –3 và phần ảo bằng –2

D. Phần thực bằng 3 và phần ảo bằng 2

Hướng dẫn giải

Chọn D

Câu 9. Số phức z = 2 – 5i có số phức liên hợp là:

A.

B.

C.

D.

Hướng dẫn giải

Chọn A

Ta có

Nên

Câu 10. Tìm số phức liên hợp của số phức z = (2 – 3i)(3 + 2i).

A.

B.

C.

D.

Hướng dẫn giải

Chọn D

Ta có z = (2 – 3i)(3 + 2i) = 6 – 5i – 6i² = 12 – 5i

⇒

Dạng 4. Module số phức

[content_4]

Câu 1. Tìm môđun của số phức

A.

B.

C.

D.

Lời giải

Chọn B

Câu 2. Cho số phức z₁ = –1 + 3i; z₂ = 2 – 2i. Tính mô đun số phức w = z₁ + z₂ – 5.

A.

B.

C.

D.

Lời giải

Chọn D

Ta có: w = z₁ + z₂ – 5 = –1 + 3i + 2 – 2i – 5 = –4 + i

⇒

Câu 3. Cho số phức z thỏa mãn z (1 + i) = 3 – 5i. Tính môđun của z.

A. |z| = 4

B. |z| =

C. |z| = 16

D. |z| = 17

Lời giải

Chọn B

Ta có:

Câu 4. Cho số phức z thỏa mãn điều kiện (2 – i) z = (4 + i) z + 3 – 2i. Số phức liên hợp của z là

A.

B.

C.

D.

Lời giải

Chọn B

Câu 5. Cho số phức z = a + bi, (a, b ∈ ℝ). Tính môđun của số phức .

A.

B.

C.

D.

Lời giải

Chọn C

Do

Câu 6. Cho hai số phức z₁ = 1 + 3i và z₂ = –3 + 2i. Tính mô đun của số phức z₁ + z₂.

A.

B.

C.

D.

Lời giải

Chọn B

Câu 7. Cho hai số phức z₁ = 1 – i và z₂ = –3 + 5i. Môđun của số phức .

A. |w| =

B. |w| = 112

C. |w| =

D. |w| = 130

Lời giải

Chọn A

Ta có:

Khi đó:

Câu 8. Tính môđun của số phức z = (1 – 2i)[2 + i + i(3 – 2i)].

A.

B.

C.

D.

Lời giải

Chọn A

z = (1 – 2i)[2 + i + i(3 – 2i)] = 12 – 4i nên môđun là

Câu 9. Gọi z₁, z₂ là hai nghiệm phức của phương trình z² – 2z + 2 = 0. Tính .

A. T = 2¹⁰¹⁰

B. T = 2²⁰¹⁹

C. T = 1

D. T = 0

Lời giải

Chọn A

Ta có

Khi đó

Và

Vậy

Câu 10. Tính môđun của số phức z = 4 – 3i.

A. |z| = 9

B. |z| = 25

C. |z| = 3

D. |z| = 5

Lời giải

Chọn D

Ta có:

Dạng 5. Phương trình bậc nhất

[content_5]

Câu 1. Cho số phức z thỏa mãn . Tính tích phần thực và phần ảo của số phức z

A. –2

B. –1

C. 2

D. 1

Lời giải

Chọn A

Gọi z = x + yi (với x, y ∈ ℝ), ta có

Theo giả thiết, ta có

Vậy xy = –2

Câu 2. Cho số phức z thỏa mãn (1 + i) z = 11 – 3i. Điểm M biểu diễn cho số phức z trong mặt phẳng tọa độ là

A. M(7; –7)

B. M(14; –14)

C. M(8; –14)

D. M(4; –7)

Lời giải

Chọn D

(1 + i) z = 11 – 3i ⇔ z = 4 – 7i

Điểm M biểu diễn cho số phức z trong mặt phẳng tọa độ là M(4; –7)

Câu 3. Cho số phức z thỏa z = (2 – 5i)(1 + i)⁴. Môđun của số phức z là:

A.

B.

C.

D.

Lời giải

Chọn D

Câu 4. Cho số phức z = a + bi bi thỏa mãn (z – 8)i + z – 6i = 5 + 5i. Giá trị của a + b bằng

A. 14

B. 2

C. 19

D. 5

Lời giải

Chọn C

Ta có (z – 8)i + z – 6i = 5 + 5i ⇔ (1 + i)z = 5 + 19i ⇔ z = 12 + 7i

Mà z = a + bi nên

Câu 5. Gọi z₁, z₂ là hai nghiệm phức của phương trình z² + 2z + 5 = 0. Tính |z₁| + |z₂|.

A. |z₁| + |z₂| =

B. |z₁| + |z₂| = 10

C. |z₁| + |z₂| = 2

D. |z₁| + |z₂| = 5

Lời giải

Chọn A

z² + 2z + 5 = 0 ⇔ z = –1 ± 2i ⇒ |z₁| + |z₂| =

Câu 6. Cho số phức z = a + bi (a, b ∈ ℝ) và thỏa mãn điều kiện . Tính tổng S = a + b.

A. S = –2

B. S = 2

C. S = 8

D. S = –8

Lời giải

Chọn C

Ta có

Khi đó S = a + b = 8

Câu 7. Xét số phức z thỏa mãn . Mệnh đề nào dưới đây đúng?

A.

B.

C.

D.

Lời giải

Chọn C

Ta có

Vậy

Đặt |z|² = a > 0

Câu 8. Tìm số phức z thỏa mãn (1 – i)(z + 1 – 2i) – 3 + 2i = 0

A.

B. z = 4 + 3i

C.

D. z = 4 – 3i

Lời giải

Chọn A

Ta có

Câu 9. Tìm số phức z thỏa mãn

A. z = 5 + i

B. z = 5 – i

C. z = 1 – 5i

D. z = 1 + 5i

Lời giải

Chọn A

Gọi z = a + bi (a, b ∈ ℝ). Suy ra:

Ta có:

Vậy z = 5 + i

Câu 10. Có bao nhiêu số phức z thỏa mãn ?

A. 2

B. 1

C. 4

D. 3

Lời giải

Chọn B

Gọi z = a + bi (a, b ∈ ℝ)

Vậy có một số phức thỏa mãn yêu cầu bài toán.

Dạng 6. Phương trình bậc hai & mối liên hệ giữa hai nghiệm

[content_6]

Câu 1. Gọi z₀ là nghiệm phức có phần ảo âm của phương trình 2z² – 6z + 5 = 0. Tìm iz₀?

A.

B.

C.

D.

Lời giải

Chọn B

Khi đó

Câu 2. Tìm nghiệm phức của phương trình: x² + 2x + 2 = 0.

A. x₁ = 2 – i; x₂ = 2 + i

B. x₁ = –1 – i; x₂ = –1 + i

C. x₁ = 1 – i; x₂ = 1 + i

D. x₁ = –2 – i; x₂ = –2 + i

Lời giải

Chọn B

Ta có: ∆ = 2² – 4.1.2 = –4 suy ra ∆ có một căn bậc hai là 2i, phương trình có hai nghiệm:

Câu 3. Cho các số phức z₁ = 3 + 2i, z₂ = 3 – 2i. Phương trình bậc hai có hai nghiệm z₁, z₂ là

A. z² + 6z – 13 = 0

B. z² – 6z – 13 = 0

C. z² – 6z + 13 = 0

D. z² + 6z + 13 = 0

Lời giải

Chọn C

Do z₁ = 3 + 2i, z₂ = 3 – 2i là hai nghiệm của phương trình nên

(z – z₁)(z – z₂) = 0

⇔ (z – 3 – 2i)(z – 3 + 2i) = 0

⇔ (z – 3)² + 4 = 0

⇔ z² – 6z + 13 = 0

Câu 4. Phương trình 2x² – 5x + 4 = 0 có nghiệm trên tập số phức là.

A.

B.

C.

D.

Lời giải

Chọn D

Phương trình 2x² – 5x + 4 = 0 có ∆ = 5² – 4.2.4 = –7 = 7i²

Vậy phương trình có hai nghiệm là

Câu 5. Gọi z₁, z₂ là hai nghiệm phức của phương trình z² + 6z + 13 = 0 trong đó z₁ là số phức có phần ảo âm. Tìm số phức ω = z₁ + 2z₂.

A. ω = – 9 – 2i

B. ω = 9 – 2i

C. ω = 9 + 2i

D. ω = –9 + 2i

Lời giải

Chọn D

Phương trình z² + 6z + 13 = 0 có hai nghiệm là z₁ = –3 – 2i, z₂ = – 3 + 2i

Vậy ω = –9 + 2i

Câu 6. Gọi z₁ là nghiệm phức có phần ảo âm của phương trình z² – 2z + 5 = 0. Tìm tọa độ điểm biểu diễn số phức trên mặt phẳng phức?

A. M(1; 2)

B. N(1; –2)

C. Q(3; –2)

D. P(3; 2)

Lời giải

Chọn D

Ta có:

Suy ra:

Điểm biểu diễn là P(3; 2)

Câu 7. Biết z là một nghiệm của phương trình . Tính giá trị của biểu thức

A. P = 2

B. P = –2

C. P = 0

D. P = 4

Lời giải

Chọn B

Ta có

Do z ≠ 1 nên z³ + 1 = 0 ⇔ z³ = –1

Vậy P = –2

Câu 8. Phương trình z² – iz + 1 = 0 có bao nhiêu nghiệm trong tập số phức?

A. 0

B. 2

C. Vô số

D. 1

Lời giải

Chọn B

Ta đặt z = a + bi

Khi đó z² – iz + 1 = 0 ⇔ a² – b² – b + 1 + (2ab + a)i = 0

⇔

Trường hợp 1:

Trường hợp 2: vô nghiệm

Câu 9. Gọi z₁; z₂ là hai nghiệm phức của phương trình z² – 2z + 2 = 0. Giá trị của biểu thức bằng

A. 8i

B. 0

C. 8

D. 4

Lời giải

Chọn C

Ta có z² – 2z + 2 = 0

Từ đó suy ra

Vậy

Câu 10. Trong ℂ, phương trình z² + 4 = 0 có nghiệm là:

A.

B.

C.

D.

Lời giải

Chọn A

z² + 4 = 0 ⇔ z² = –4 ⇔ z² = 4i² ⇔ z = ±2i

Dạng 7. Phương trình bậc cao

[content_7]

Câu 1. Cho số phức z thỏa mãn 11z²⁰¹⁸ + 10iz²⁰¹⁷ + 10iz – 11 = 0. Mệnh đề nào sau đây đúng?

A. |z| ∈ [2; 3)

B. |z| ∈

C. |z| ∈ (1; 2)

D. |z| ∈ [0; 1)

Lời giải

Chọn B

Đặt z = x + yi

Trường hợp 1: |z| < 1 ⇔ x² + y² < 1

⇒ 100(x² + y²) + 121 + 220y > 121(x² + y²) + 100 + 220y

⇒ |z| > 1 (sai)

Trường hợp 2: |z| > 1 ⇔ x² + y² > 1

⇒ 100(x² + y²) + 121 + 220y < 121(x² + y²) + 100 + 220y

⇒ |z| < 1 (sai)

Trường hợp 3: |z| = 1 ⇔ x² + y² = 1. Thay vào thấy đúng.

Vậy |z| = 1.

Câu 2. Cho phương trình 3x⁴ – 2x² – 1 = 0 trên tập số phức, khẳng định nào sau đây đúng:

A. Phương trình có 3 nghiệm phức

B. Phương trình chỉ có 2 nghiệm phức

C. Phương trình này có 2 nghiệm thực

D. Phương trình này không có nghiệm phức

Lời giải

Chọn C

Đặt t = x² phương trình thành 3t² – 2t – 1 = 0

Câu 3. Gọi z₁, z₂, z₃ là ba nghiệm của phương trình z³ + z² + 5z – 7 = 0. Tính M = |z₁| + |z₂| + |z₃|.

A.

B.

C.

D.

Lời giải

Chọn D

Ta có: z³ + z² + 5z – 7 = 0 ⇔ (z – 1)(z² + 2z + 7) = 0

Suy ra:

Câu 4. Gọi z₁, z₂, z₃, z₄ là bốn nghiệm phân biệt của phương trình z⁴ + 3z² + 4 = 0 trên tập số phức. Tính giá trị của biểu thức T = |z₁|² + |z₂|² + |z₃|² + |z₄|²

A. T = 2

B. T = 6

C. T = 4

D. T = 8

Lời giải

Chọn D

Ta có

Không mất tính tổng quát giả sử z₁, z₂ là nghiệm của (1) và z₃, z₄ là nghiệm của (2).

Tương tự

Vậy T = 8

Câu 5. Kí hiệu z₁ và z₂ là các nghiệm của phức của phương trình z² – 4z + 5 = 0 và A, B lần lượt là các điểm biểu diễn của z₁ và z₂. Tính

A.

B.

C.

D.

Lời giải

Chọn C

Phương trình

Vậy tọa độ hai điểm biểu diễn z₁ và z₂ là: A(2; 1), B(2; –1)

Ta có:

Câu 6. Gọi z₁, z₂, z₃ là ba nghiệm của phương trình z³ – 2(1 + i) z² + (9 + 4i) z – 18i = 0, trong đó z₁ là nghiệm có phần ảo âm. Tính M = |z₁|

A. M = 4

B. M = 6

C. M = 2

D. M = 3

Lời giải

Chọn D

Ta có: z³ – 2(1 + i) z² + (9 + 4i) z – 18i = 0

⇔ (z – 2i)(z² – 2z + 9) = 0

⇔

Do z₁ là nghiệm có phần ảo âm nên

Câu 7. Trên tập số phức, tính tổng môđun bình phương tất cả các nghiệm của phương trình z⁴ – 16 = 0.

A. 16

B. 8

C. 4

D. 32

Lời giải

Chọn A

Câu 8. Cho số phức z thỏa mãn 11z²⁰¹⁸ + 10iz²⁰¹⁷ + 10iz – 11 = 0. Mệnh đề nào sau đây đúng?

A. 6

B. 3

C. 2

D. 4

Lời giải

Chọn A

Câu 9. Tập nghiệm của phương trình z⁴ – 2z² – 8 = 0 là:

A.

B.

C.

D.

Lời giải

Chọn C

Câu 10. Cho z₁, z₂ là hai nghiệm phức của phương trình z² + 3z + 7 = 0. Tính P = z₁z₂ (z₁ + z₂).

A. P = 21

B. P = 10

C. P= –21

D. P = –10

Lời giải

Chọn C

Áp dụng hệ thức Vi–et ta có:

Vậy P = z₁z₂ (z₁ + z₂) = –21

Dạng 8. Biểu diễn số phức

[content_8]

Câu 1. Cho các điểm A, B, C nằm trong mặt phẳng phức lần lượt biểu diễn các số phức 1+ 3i, –2 + 2i, 1 – 7i. Gọi D là điểm sao cho tứ giác ABCD là hình bình hành. Điểm D biểu diễn số phức nào trong các số phức sau đây?

A. z = 4 + 6i

B. z = 2 + 8i

C. z = –2 – 8i

D. z = 4 – 6i

Lời giải

Chọn D

Ta có: A(1; 3) B(–2; 2), C (1; –7). Gọi D(x_D; y_D)

Vì tứ giác ABCD là hình bình hành

Nên

Câu 2. Mệnh đề nào dưới đây sai?

A. Điểm M(–1; 2) là điểm biểu diễn số phức z = –1 + 2i

B. Số phức là số thuần ảo

C. Mô đun của số phức z = a + bi (a, b ∈ ℝ) là a² + b²

D. Số phức z = 5 – 3i có phần thực là 5, phần ảo –3

Lời giải

Chọn C

Mô đun của số phức z = a + bi (a, b ∈ ℝ) là

Câu 3. Trong hình vẽ bên, điểm M biểu diễn số phức z. Số phức là:

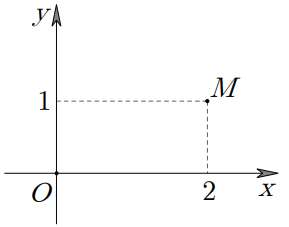
A. 2 + i

B. 2 – i

C. 1 + 2i

D. 1 – 2i

Lời giải

Chọn B

Dựa vào hình vẽ ta có

Câu 4. Điểm M trong hình vẽ bên biểu diễn số phức .

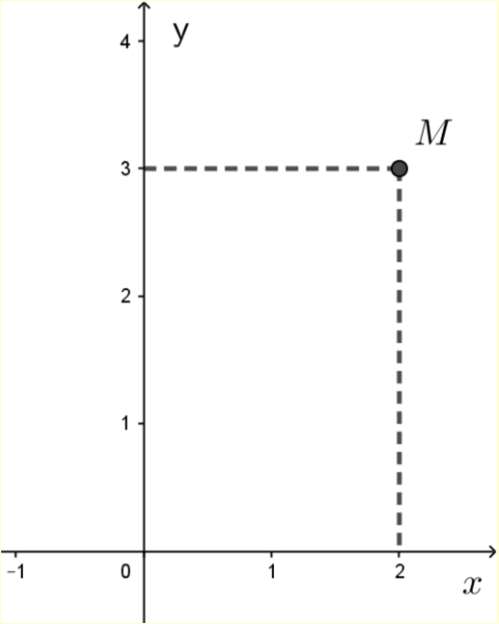
Số phức z bằng

A. 3 + 2i

B. 3 – 2i

C. 2 + 3i

D. 2 – 3i

Lời giải

Chọn D

Từ hình vẽ ta có

Câu 5. Cho số phức z thoả mãn (2 + i)z = 10 – 5i. Hỏi điểm biểu diễn số phức z là điểm nào trong các điểm M, N, P, Q ở hình bên?

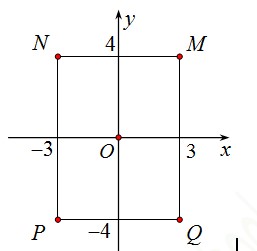
A. Điểm N

B. Điểm M

C. Điểm P

D. Điểm Q

Lời giải

Chọn D

Ta có

Do vậy điểm Q(3; –4) là điểm biểu diễn số phức z.

Câu 6. Hỏi điểm M(3; –1) là điểm biểu diễn số phức nào sau đây?

A. z = 3 – i

B. z = –3 + i

C. z = –1 + 3i

D. z = 1 – 3i

Lời giải

Chọn A

Điểm M(a; b) trong một hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z = a + bi

Do đó điểm M(3; –1) là điểm biểu diễn số phức z = 3 – i

Câu 7. Biểu diễn hình học của số phức z = 2 – 3i là điểm nào trong những điểm sau đây?

A. I(–2; –3)

B. I(–2; 3)

C. I(2; –3)

D. I(2; 3)

Lời giải

Chọn C

Biểu diễn hình học của số phức z = 2 – 3i là điểm I(2; –3)

Câu 8. Điểm A trong hình vẽ bên biểu diễn cho số phức z.

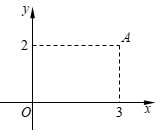
Tìm phần thực và phần ảo của số phức

A. Phần thực là –3 và phần ảo là 2i

B. Phần thực là –3 và phần ảo là 2

C. Phần thực là 3 và phần ảo là –2i

D. Phần thực là 3 và phần ảo là –2

Lời giải

Chọn D

Ta có

Câu 9. Cho số phức z = 5 – 4i. Số phức đối của z có điểm biểu diễn là

A. (–5; 4)

B. (–5; –4)

C. (5; 4)

D. (5; –4)

Lời giải

Chọn A

Ta có số phức z = 5 – 4i nên số phức đối của z là –z = –5 + 4i

Câu 10. Điểm M trong hình vẽ dưới đây biểu thị cho số phức

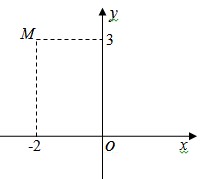
A. 2 – 3i

B. 3 + 2i

C. 3 – 2i

D. –2 + 3i

Lời giải

Chọn D

Hoành độ, tung độ của điểm M là phần thực, phần ảo của số phức ⇔ z = –2 + 3i

Dạng toán 9. Tập hợp điểm biểu diễn số phức

[content_9]

Tập hợp điểm biểu diễn là đường thẳng

Câu 1. Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện là:

A. Trục hoành

B. Trục tung

C. Gồm cả trục hoành và trục tung

D. Đường thẳng y = x

Lời giải

Chọn C

Đặt z = x + yi

Ta có

Suy ra tập các điểm biểu diễn cho số phức z gồm cả trục hoành và trục tung.

Câu 2. Trong mặt phẳng phức tập hợp điểm M(z) thỏa mãn với z₀ = 1 – i là đường thẳng có phương trình.

A. 2x + 2y – 1 = 0

B. –2x + 2y – 1 = 0

C. –2x – 2y – 1 = 0

D. 2x – 2y – 1 = 0

Lời giải

Chọn C

Gọi số phức z = x + yi . Từ điều kiện đề bài.

(hai số phức bằng nhau).

Câu 3. Cho các số phức z thỏa mãn |z + 1 – i| = |z – 1 + 2i|. Tập hợp các điểm biểu diễn các số phức z trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là

A. 4x – 6y – 3 = 0

B. 4x + 6y + 3 = 0

C. 4x – 6y + 3 = 0

D. 4x + 6y – 3 = 0

Lời giải

Chọn A

Gọi z = x + yi. Ta có:

Câu 4. Tìm tập hợp những điểm M biểu diễn số phức z trong mặt phẳng phức, biết số phức z thỏa mãn điều kiện

A. Tập hợp những điểm M là đường thẳng có phương trình 4x + 2y + 3 =0

B. Tập hợp những điểm M là đường thẳng có phương trình 4x – 2y + 3 =0

C. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4y + 3 =0

D. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4y – 3 = 0

Lời giải

Chọn D

Gọi z = x + yi, (x, y ∈ ℝ)

Ta có:

Câu 5. Tập hợp điểm biểu diễn số phức z thỏa mãn |z|² = z² là:

A. Một đường tròn

B. Một điểm

C. Một đường thẳng

D. Một đoạn thẳng

Lời giải

Chọn C

Gọi z = a + bi

Ta có

Suy ra z = a

Vậy tập hợp điểm biểu diễn số phức z thỏa mãn |z|² = z² là một đường thẳng.

Câu 6. Trong mặt phẳng phức với hệ tọa độ Oxy, điểm biểu diễn của các số phức z = 3 + bi với b ∈ ℝ luôn nằm trên đường có phương trình là:

A. y = 3

B. y = x + 3

C. x = 3

D. y = x

Lời giải

Chọn C

Điểm biểu diễn của z = 3 + bi là (3; b) luôn thuộc đường thẳng x = 3

Câu 7. Tìm tập hợp điểm biểu diễn của số phức z biết |z – 1| = |z + 2i|.

A. Hypebol

B. Đường tròn

C. Đường thẳng

D. Parabol

Lời giải

Chọn C

Gọi điểm M(x; y) là điểm biểu diễn số phức z = x + yi, (x, y ∈ ℝ)

Ta có: |z – 1| = |z + 2i|

⇔ |x + yi – 1| = |x + yi + 2i|

⇔ (x – 1)² + y² = x² + (y + 2)²

⇔ 2x + y + 3 = 0

Vậy tập hợp điểm biểu diễn số phức z là đường thẳng 2x + y + 3 = 0

Câu 8. Tìm tập hợp điểm biểu diễn số phức z thỏa mãn |z – i| = |2 – 3i – z|

A. Đường tròn có phương trình x² + y² = 4

B. Elip có phương trình x² + 4y² = 4

C. Đường thẳng có phương trình x – 2y – 3 = 0

D. Đường thẳng có phương trình x + 2y + 1 = 0

Lời giải

Chọn C

Đặt z = x + yi, (x, y ∈ ℝ)

Ta có: |z – i| = |2 – 3i – z|

⇔ |x + yi – i| = |2 – 3i – x – yi|

⇔ x² + (y – 1)² = (2 – x)² + (3 + y)²

⇔ 4x – 8y – 12 = 0 ⇔ x – 2y – 3 = 0

Câu 9. Trong mặt phẳng phức, tập hợp các điểm biểu diễn của số phức z thỏa mãn điều kiện |z + 2| = |i – z| là đường thẳng ∆ có phương trình.

A. 4x – 2y + 3 = 0

B. 4x + 2y + 3 = 0

C. 2x + 4y + 13 = 0

D. –2x + 4y – 13 = 0

Lời giải

Chọn B

Ta có

Câu 10. Tập hợp điểm biểu diễn các số phức z thỏa mãn trong mặt phẳng Oxy là:

A. Đường thẳng ∆: 3x – y + 4 = 0

B. Đường thẳng ∆: x + y + 4 = 0

C. Đường thẳng ∆: 3x + y + 4 = 0

D. Đường thẳng ∆: x + y – 4 = 0

Lời giải

Chọn C

Gọi z = x + yi, (x, y ∈ ℝ)

Khi đó điểm M(x; y) là điểm biểu diễn cho số phức z

Ta có

Vậy tập hợp điểm biểu diễn số phức z là đường thẳng ∆: 3x + y + 4 = 0

Tập hợp điểm biểu diễn là đường tròn

Câu 1. Tập hợp điểm biểu diễn các số phức thỏa |zi + 1| = 1 là một đường tròn. Tìm tâm I của đường tròn đó.

A. I(0; –1)

B. I(0; 1)

C. I(–1; 0)

D. I(1; 0)

Lời giải

Chọn B

Gọi z = x + yi, (x, y ∈ ℝ)

Khi đó |zi + 1| = 1 ⇔ |xi – y + 1| = 1 ⇔ x² + (y – 1)² = 1

Vậy tâm của đường tròn là I(0; 1)

Câu 2. Trên mặt phẳng phức, tập hợp các điểm biểu diễn số phức z thỏa mãn là một đường tròn có bán kính là R. Tính giá trị của R.

A.

B.

C.

D.

Lời giải

Chọn D

Đặt . Ta được:

Câu 3. Biết số phức z thõa mãn |z – 1| ≤ 1 và có phần ảo không âm. Phần mặt phẳng biểu diễn số phức z có diện tích là:

A. 2π

B. π²

C.

D. π

Lời giải

Chọn C

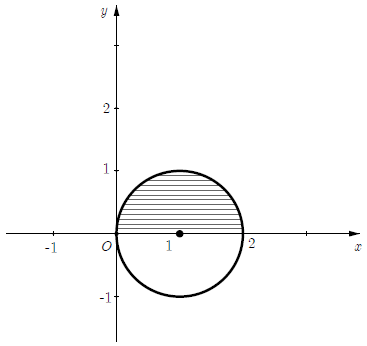
Đặt . Khi đó ta có:

|z – 1| ≤ 1 ⇔ |(x + yi) – 1| ≤ 1

⇔ |(x – 1) + yi| ≤ 1 ⇔ (x – 1)² + y² ≤ 1 (1)

có phần ảo không âm suy ra y ≥ 0 (2)

Từ (1) và (2) ta suy ra phần mặt phẳng biểu diễn số phức z là nửa hình tròn tâm I(1; 0) bán kính r = 1, diện tích của nó bằng (đvdt).

Câu 4. Cho số phức z thỏa mãn |z – 3 + 4i| = 2 và w = 2z + 1 – i. Trong mặt phẳng phức, tập hợp điểm biểu diễn số phức w là đường tròn tâm I, bán kính R. Khi đó:

A. I(–7; 9), R = 4

B. I(7; –9), R = 16

C. I(7; –9), R = 4

D. I(–7; 9), R = 16

Lời giải

Chọn C

Giả sử z = x + yi, (x, y ∈ ℝ)

Từ giả thuyết |z – 3 + 4i| = 2

⇔ |x + yi – 3 + 4i| = 2

⇔ (x – 3)² + (y + 4)² = 4 (*)

Từ w = 2z + 1 – i = 2(x + yi) + 1 – i = (2x + 1) + (2y – 1)i

Giả sử w = a + bi, (a, b ∈ ℝ). Ta có

Thay x, y vào phương trình (*), ta có

Suy ra w chạy trên đường tròn tâm I(7; –9), bán kính R = 4

Câu 5. Tập hợp điểm biểu diễn số phức thỏa điều kiện |z + 1 + 2i| = 1 nằm trên đường tròn có tâm là:

A. I(1; –2)

B. I(–1; 2)

C. I(1; 2)

D. I(–1; –2)

Lời giải

Chọn B

Khi đó ta có |(x + 1) + (2 – y)i| = 1 ⇔ (x + 1)² + (y – 2)² = 1

Vậy tập hợp số phức nằm trên đường tròn có tâm I(–1; 2)

Câu 6. Cho số phức z thỏa mãn điều kiện |z – 3 +4i| ≤ 2. Trong mặt phẳng Oxy tập hợp điểm biểu diễn số phức w = 2z + 1 – i là hình tròn có diện tích

A. S = 9π

B. S = 12π

C. S = 16π

D. S = 25π

Lời giải

Chọn C

Giả sử w = x + yi, (x, y ∈ ℝ)

Khi đó (1) ⇔ (x – 7)² + (y + 9)² ≤ 16

Suy ra tập hợp điểm biểu diễn số phức w là hình tròn tâm I (7; –9), bán kính r = 4.

Vậy diện tích cần tìm là S = π.4² = 16π

Câu 7. Cho số phức z có |z| = 4. Tập hợp các điểm M trong mặt phẳng tọa độ Oxy biểu diễn số phức là một đường tròn. Tính bán kính đường tròn đó.

A. 2

B. 4

C. 5

D. 3

Lời giải

Chọn B

Theo giả thiết ta có:

Do đó: |w – 3i| = 4

Vậy tập hợp các điểm M biểu diễn cho số phức w là đường tròn có bán kính bằng 4.

Câu 8. Tìm tập hợp điểm biểu diễn số phức z thỏa |z – 2 + i| = 2

A. Tập hợp điểm biểu diễn số phức z là đường tròn x² + y² – 4x – 2y – 4 = 0

B. Tập hợp điểm biểu diễn số phức z là đường tròn x² + y² – 4x – 2y + 1 = 0

C. Tập hợp điểm biểu diễn số phức z là đường tròn x² + y² – 4x + 2y – 4 = 0

D. Tập hợp điểm biểu diễn số phức z là đường tròn x² + y² – 4x + 2y + 1 = 0

Lời giải

Chọn D

Gọi z = x + yi, (x, y ∈ ℝ)

Ta có: |z – 2 + i| = 2

⇔ (x – 2)² + (y + 1)² = 4

⇔ x² + y² – 4x + 2y + 1 = 0

Câu 9. Trong mặt phẳng phức Oxy, tập hợp biểu diễn số phức Z thỏa 1 ≤ |z + 1 – i| ≤ 2 là hình vành khăn. Chu vi P của hình vành khăn là bao nhiêu?

A. P = 2π

B. P = 3π

C. P = 4π

D. P = π

Lời giải

Chọn A

Gọi M(x; y) là điểm biểu diễn số phức z = x + yi, (x, y ∈ ℝ)

Gọi A(–1; 1) là điểm biểu diễn số phức –1 + i

1 ≤ |z + 1 – i| ≤ 2 ⇔ 1 ≤ MA ≤ 2

Tập hợp điểm biểu diễn là hình vành khăn giới hạn bởi 2 đường tròn đồng tâm có bán kính lần lượt là R₁ = 2; R₂ = 1

⇔ P = P₁ – P₂ = 2π (R₁ – R₂) = 2π

Lưu ý cần nắm vững lý thuyết và hình vẽ của dạng bài này khi học trên lớp tránh nhầm lẫn sang tính diện tích hình tròn.

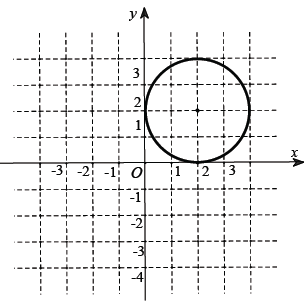
Câu 10. Biết tập hợp tất cả các điểm biểu diễn số phức z là đường tròn cho bởi hình vẽ bên. Hỏi tập hợp tất cả các điểm biểu diễn số phức z – 3 – 4i được thể hiện bởi đường tròn trong hình vẽ nào trong bốn hình vẽ dưới đây?

A.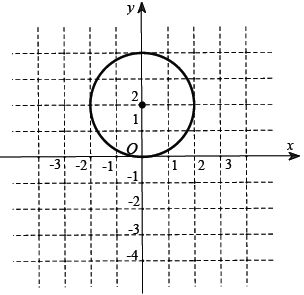

B.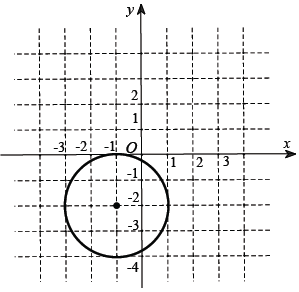

C.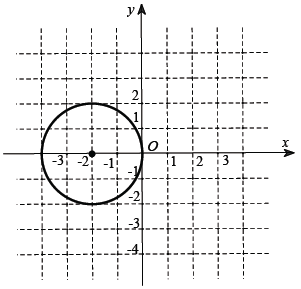

D.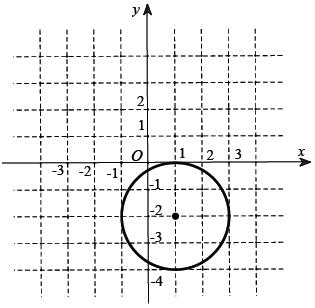

Lời giải

Chọn B

Dựa vào hình vẽ, tập hợp tất cả các điểm M(x; y) biểu diễn số phức z trên mặt phẳng tọa độ là đường tròn có phương trình: (x – 2)² + (y – 2)² = 4

Ta có: z – 3 – 4i = (x – 3) + (y + 4)i có điểm M’(x – 3; y – 4) biểu diễn trên mặt phẳng tọa độ

Ta biểu diễn: (x – 2)² + (y – 2)² = 4

⇔ [(x – 3) + 1]² + [(y – 4) + 2]² = 4

⇒ M’ ∈ (C’): (x + 1)² + (y + 2)² = 4

Với phương trình như vậy, ta thấy đáp án B thỏa mãn.

Tập hợp điểm biểu diễn là đường Coníc

Câu 1. Tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10.

A. Đường tròn (x – 2)² + (y + 2)² = 10

B. Elip

C. Đường tròn (x – 2)² + (y + 2)² = 100

D. Elip

Lời giải

Chọn B

Gọi M(x; y) là điểm biểu diễn số phức z = x + yi, (x, y ∈ ℝ)

Gọi A là điểm biểu diễn số phức 2

Gọi B là điểm biểu diễn số phức –2

Ta có: |z + 2| + |z – 2| = 10 ⇔ MA + MB = 10

Ta có: AB = 4. Suy ra tập hợp điểm M biểu diễn số phức z là Elip với tiêu điểm là A(2; 0), B(–2; 0), tiêu cự AB = 4 = 2c, độ dài trục lớn là 10 = 2a, độ dài trục bé là

Vậy tập hợp là Elip có phương trình

Câu 2. Tập hợp các điểm biểu diễn số phức z thỏa mãn trên mặt phẳng tọa độ là một

A. parabol

B. hypebol

C. đường thẳng

D. đường tròn

Lời giải

Chọn A

Giả sử

Bài ra ta có

Do đó tập hợp các điểm biểu diễn số phức z thỏa mãn trên mặt phẳng tọa độ là một parabol.

Câu 3. Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện là:

A. Một elip

B. Một parabol

C. Một đường tròn

D. Một đường thẳng

Lời giải

Chọn B

Đặt

Ta có:

Câu 4. Tìm tập hợp các điểm M biểu diễn hình học số phức z trong mặt phẳng phức, biết số phức z thỏa mãn điều kiện: |z + 4| + |z – 4| = 10.

A. Tập hợp các điểm cần tìm là những điểm M(x; y) trong mặt phẳng Oxy thỏa mãn phương trình

B. Tập hợp các điểm cần tìm là đường elip có phương trình

C. Tập hợp các điểm cần tìm là đường tròn có tâm O(0; 0) và có bán kính R = 4

D. Tập hợp các điểm cần tìm là đường elip có phương trình

Lời giải

Chọn B

Ta có: Gọi M(x; y) là điểm biểu diễn của số phức z = x + yi

Gọi A(4; 0) là điểm biểu diễn của số phức z = 4

Gọi B(–4; 0) là điểm biểu diễn của số phức z = –4

Khi đó: |z + 4| + |z – 4| = 10 ⇔ MA + MB = 10 (*)

Hệ thức trên chứng tỏ tập hợp các điểm M là elip nhận A, B là các tiêu điểm

Gọi phương trình của elip là

Từ (*) ta có: 2a = 10 ⇔ a = 5

AB = 2c ⇔ 8 = 2c ⇔ c = 4 ⇒ b² = a² – c² = 9

Vậy quỹ tích các điểm M là elip: (E):

Câu 5. Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10

A. Elip

B. Đường tròn (x – 2)² + (y + 2)² = 10

C. Elip

D. Đường tròn (x – 2)² + (y + 2)² = 100

Lời giải

Chọn C

Gọi M(x; y) là điểm biểu diễn của số phức z = x + yi, (x, y ∈ ℝ)

Gọi A là điểm biểu diễn số phức 2

Gọi B là điểm biểu diễn số phức –2

Ta có: |z + 2| + |z – 2| = 10 ⇔ MA + MB = 10

Ta có AB = 4. Suy ra tập hợp điểm M biểu diễn số phức z là Elip với 2 tiêu điểm là A(2; 0), B(–2; 0), tiêu cự AB = 4 = 2c, độ dài trục lớn là 10 = 2a, độ dài trục bé là

Vậy, tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z + 2| + |z – 2| = 10 là Elip có phương trình

Câu 6. Tập hợp các điểm trong mặt phẳng tọa độ biểu diễn số phức z thỏa mãn điều kiện là hình gì?

A. Một đường Elip

B. Một đường thẳng

C. Một đường tròn

D. Một đường Parabol

Lời giải

Chọn D

Đặt điểm biểu diễn của z là M(x, y). Ta có:

Vậy tập hợp các điểm biểu diễn số phức z là một đường Parabol.

Câu 7. Tập hợp các điểm biểu diễn các số phức z thỏa mãn là

A. Một điểm

B. Một đường thẳng

C. Một đường tròn

D. Một Parabol

Lời giải

Chọn D

Gọi

Vậy tập hợp các điểm biểu diễn các số phức z thỏa mãn là một Parabol (P) có phương trình:

Câu 8. Cho số phức z = a + a²i với a ∈ ℝ. Khi đó điểm biểu diễn của số phức z nằm trên:

A. Parabol y = x²

B. Parabol y = –x²

C. Đường thẳng y = 2x

D. Đường thẳng y = –x + 1

Lời giải

Chọn A

Ta có z = a + a²i ⇒ M(a; a²) là điểm biểu diễn của số phức z

Khi đó y = x² là tập hợp các điểm biểu diễn của số phức z

Câu 9. Cho số phức z thỏa mãn điều kiện |z + 4| + |z – 4| = 10. Tập hợp các điểm M biểu diễn cho số phức z là đường có phương trình.

A.

B.

C.

D.

Lời giải

Chọn D

Gọi M(x; y) là điểm biểu diễn của số phức z = x + yi (x, y ∈ ℝ)

Từ giả thiết ta có

với F₁(–4;0), F₂(4; 0)

Vậy tập hợp các điểm M biểu diễn cho số phức z là đường Elip có phương trình

Câu 10. Gọi M là điểm biểu diễn của số phức z thỏa mãn . Tìm tập hợp tất cả những điểm M như vậy.

A. Một đường tròn

B. Một đường thẳng

C. Một parabol

D. Một elip

Lời giải

Chọn C

Gọi số phức z = x + yi có điểm biểu diễn là M(x; y) trên mặt phẳng tọa độ:

Theo đề bài ta có:

Vậy tập hợp các điểm M(x; y) biểu diễn số phức z theo yêu cầu của đề bài là một parabol

Dạng 10. Max – Min của module số phức

[content_10]

Câu 1. Trong các số phức thỏa mãn điều kiện |z + 3i| = |z + 2 – i|. Tìm số phức có môđun nhỏ nhất?

A.

B.

C.

D.

Lời giải

Chọn B

Giả sử z = x + yi (x, y ∈ ℝ)

Suy ra khi

Vậy

Câu 2. Trong các số phức z thỏa mãn |z – 2 – 4i| = |z – 2i|. Số phức z có môđun nhỏ nhất là

A. z = 3 + 2i

B. z = –1 + i

C. z = –2 + 2i

D. z = 2 + 2i

Lời giải

Chọn D

Đặt z = a + bi.

Khi đó |z – 2 – 4i| = |z – 2i|

⇔ |(a – 2) + (b – 4)i| = |a + (b – 2)i|

⇔ (a – 2)² + (b – 4)² = a² + (b – 2)²

⇔ a + b = 4 (1)

Mà và

Đẳng thức xảy ra

Từ (1) và (2)

Câu 3. Cho số phức z thỏa mãn |z – 1| = |z – i|. Tìm mô đun nhỏ nhất của số phức w = 2z + 2 – i.

A.

B.

C.

D.

Lời giải

Chọn A

Giả sử

Khi đó |z – 1| = |z – i|

⇔ |a – 1 + bi| = |a + (b – 1)i|

⇔ (a – 1)² + b² = a² + (b – 1)²

⇔ a – b = 0

Khi đó w = 2z + 2 – i = 2(a + ai) + 2 – i = (2a + 2) + i(a – 1)

Vậy mô đun nhỏ nhất của số phức w là

Câu 4. Cho số phức z thỏa mãn |z – 3 – 4i| = 1. Tìm giá trị nhỏ nhất của |z|.

A. 6

B. 4

C. 3

D. 5

Lời giải

Chọn B

Ta có: 1 = |z – (3 + 4i)| ≥ |3 + 4i| – |z| = 5 – |z|

⇔ |z| ≥ 5 – 1 = 4

Câu 5. Cho hai số phức z₁, z₂ thỏa mãn |z₁ – 3i + 5| = 2 và |iz₂ – 1 + 2i| = 4. Tìm giá trị lớn nhất của biểu thức T = |2iz₁ + 3z₂|.

A.

B.

C.

D.

Lời giải

Chọn A

Ta có |z₁ – 3i + 5| = 2 ⇔ |2iz₁ + 6 + 10i| = 4 (1)

|iz₂ – 1 + 2i| = 4 ⇔ |–(3z₂) – 6 – 3i| = 12 (2)

Gọi A là điểm biểu diễn số phức 2iz₁, B là điểm biểu diễn số phức –3z₂

Từ (1) và (2) suy ra điểm A nằm trên đường tròn tâm I₁(–6; –10) và bán kính R₁ = 4; điểm B nằm trên đường tròn tâm I₂(6; 3) và bán kính R₂ = 12

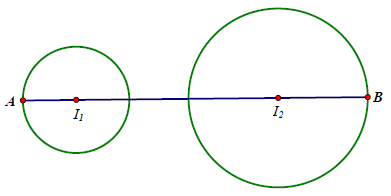
Ta có

Vậy

Câu 6. Trong các số phức z thỏa mãn điều kiện , hãy tìm phần ảo của số phức có môđun nhỏ nhất.

A.

B.

C. –2

D.

Lời giải

Chọn A

Gọi z = a + bi (a, b ∈ ℝ)

Suy ra z có môđun nhỏ nhất khi

Câu 7. Xét các số phức z₁ = 3 – 4i và z₂ = 2 + mi (m ∈ ℝ) . Giá trị nhỏ nhất của môđun số phức bằng?

A.

B. 2

C. 3

D.

Lời giải

Chọn A

Hoặc dùng công thức:

Câu 8. Số phức z nào sau đây có môđun nhỏ nhất thỏa

A.

B.

C.

D.

Lời giải

Chọn A

Gọi

Trong các đáp án, có đáp án và thỏa (*)

Ở đáp án :

Ở đáp án :

Chọn đáp án:

Câu 9. Có tất cả bao nhiêu giá trị nguyên của m để có đúng hai số phức z thỏa mãn và

A. 66

B. 130

C. 131

D. 63

Lời giải

Chọn A

Đặt z = x + yi (x, y ∈ ℝ)

Từ giả thiết , do đó tập hợp các điểm M biểu diễn số phức z là đường tròn (T) có tâm I (m – 1; –1), bán kính R = 8 .

Từ giả thiết

Hay M nằm trên đường thẳng ∆: 2x + 8y – 11 = 0

Yêu cầu bài toán ⇔ ∆ cắt (T) tại 2 điểm phân biệt

Do m ∈ ℤ nên m ∈ {–22; –21; …; 42; 43}

Vậy có tất cả 66 giá trị của m thỏa mãn yêu cầu bài toán.

Câu 10. Cho các số phức z thoả mãn |z| = 2. Đặt w = (1 + 2i)z – 1 + 2i. Tìm giá trị nhỏ nhất của |w|.

A. 2

B.

C.

D.

Lời giải

Chọn D

Gọi số phức z = a + bi (a, b ∈ ℝ)

Ta có:

Mà số phức w = (1 + 2i)z – 1 + 2i

⇔ w = (1 + 2i)(a + bi) – 1 + 2i

⇔ w = (a – 2b – 1) + (2a + b + 2)i

Giả sử số phức w = x + yi (x, y ∈ ℝ)

Khi đó:

Ta có: (x + 1)² + (y – 2)² = (a – 2b)² + (2a + b)²

⇔ (x + 1)² + (y – 2)² = a² + 4b² – 4ab + 4a² + b² + 4ab

⇔ (x + 1)² + (y – 2)² = 5(a² + b²)

⇔ (x + 1)² + (y – 2)² = 20 (theo (*))

Tập hợp các điểm biểu diễn số phức w là đường tròn tâm I(–1; 2), bán kính

Điểm M là điểm biểu diễn của số phức w thì |w| đạt giá trị nhỏ nhất khi và chỉ khi OM nhỏ nhất.

Ta có:

Mặt khác:

Do vậy w nhỏ nhất bằng .