Tổng hợp các phương pháp tìm m để hàm số đồng biến, nghịch biến trên khoảng và các bài tập bám sát chương trình 12 có lời giải chi tiết. Đây là một trong những dạng toán tham số phổ biến khi học về tính đồng biến, nghịch biến. Ở các cấp học nhỏ hơn, dạng toán này tồn tại dưới hình thức là một bài toán khó. Tuy nhiên, đến với chương trình toán THPT thì dạng toán này trở nên phổ biến.

Lý thuyết
Định nghĩa đồng biến, nghịch biến
Cho hàm số y = f(x) xác định trên K , trong đó K là một khoảng, đoạn hoặc nữa khoảng.
a) Hàm số y = f(x) đồng biến trên K nếu mọi x₁, x₂ ∊ K, x₁ < x₂ ⇒ f(x₁) < f(x₂).
b) Hàm số y = f(x) nghịch biến trên K nếu mọi x₁, x₂ ∊ K, x₁ < x₂ ⇒ f(x₁) > f(x₂).
Định lí
Cho hàm số y = f(x) có đạo hàm trên K .
a) Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K .
b) Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K .
c) Nếu f’(x) = 0 với mọi x thuộc K thì hàm số f(x) không đổi trên K .
Chú ý: Nếu hàm số f liên tục trên đoạn [a;b] và có đạo hàm f’(x) > 0 trên khoảng (a;b) thì hàm số f đồng biến trên đoạn [a;b]. Nếu hàm số f liên tục trên đoạn [a;b] và có đạo hàm f’(x) < 0 trên khoảng (a;b) thì hàm số f nghịch biến trên đoạn [a;b].
Định lí mở rộng
Cho hàm số y = f(x) có đạo hàm trên K.
a) Nếu f’(x) ≥ 0 với mọi x thuộc K và f’(x) = 0 xảy ra tại một số hữu hạn điểm của K thì hàm số f(x) đồng biến trên K.
b) Nếu f’(x) ≤ 0 với mọi x thuộc K và f’(x) = 0 xảy ra tại một số hữu hạn điểm của K thì hàm số f(x) nghịch biến trên K.
Qui tắc xét tính đơn điệu của hàm số
Bước 1: Tìm tập xác định.
Bước 2: Tính đạo hàm f’(x). Tìm các điểm xᵢ (i = 1, 2, …,n) mà tại đó đạo hàm bằng 0 hoặc không xác định.
Bước 3: Sắp xếp các điểm xᵢ theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Phân dạng bài tập
Chúng ta sẽ tìm hiểu 6 dạng toán tìm m để hàm đơn điệu trên khoảng để có cái nhìn tổng quan nhất về các bài tập biện luận tham số m liên quan đến tính đồng biến và nghịch biến trên khoảng của hàm số.
Dạng 1. Tìm m để hàm số bậc 3 đồng biến, nghịch biến trên khoảng
Phương pháp giải
Hàm số đồng biến trên ℝ thì y’ ≥ 0, ∀ x ∊ ℝ ⇔ hoặc suy biến
Hàm số nghịch biến trên ℝ thì y’ ≤ 0, ∀ x ∊ ℝ ⇔ hoặc suy biến
Bài tập vận dụng
Câu 1. Tìm tất cả các giá trị thực của tham số m sao cho hàm số giảm trên nửa khoảng [1; +∞)?
A.
B.
C.
D.
Lời giải
Chọn A
Tập xác định D = ℝ, yêu cầu của bài toán đưa đến giải bất phương trình
mx2 + 14mx + 14 ≤ 0, ∀ x ≥ 1 tương đương với
Dễ dàng có được g(x) là hàm tăng ∀ x ∊ [1; +∞), suy ra
Kết luận:
Câu 2. Xác định các giá trị của tham số m để hàm số y = x3 – 3mx2 – m nghịch biến trên khoảng (0;1)?
A. m ≥ 0
B.
C. m ≤ 0
D.
Lời giải
Chọn D
y’ = mx2 – 6mx = 0
Hàm số y = x3 – 3mx2 – m nghịch biến trên khoảng (0;1) ⇔ 2m ≥ 1 ⇔ m ≥ ½
Câu 3. Tìm tất cả các giá trị của tham số m để hàm số y = x3 + 3x2 – mx + 1 đồng biến trên khoảng (-∞;0).
A. m ≤ 0
B. m ≥ -2 .
C. m ≤ -3
D. m ≤ -1
Lời giải
Chọn C
Tập xác định: D = ℝ
Đạo hàm: y’ = 3x2 + 6x – m
Hàm số đồng biến trên khoảng (-∞;0) khi và chỉ khi y’ ≥ 0, ∀ x < 0
⇔ 3x2 + 6x – m ≥ 0, ∀ x < 0
Cách 1
3x2 + 6x – m ≥ 0, ∀ x < 0 ⇔ 3x2 + 6x ≥ m, ∀ x < 0.
Xét hàm số f(x) = 3x2 + 6x trên khoảng (-∞;0), ta có:
f’(x) = 6x + 6. Xét f’(x) = 0 ⇔ 6x + 6 = 0 ⇔ x = -1. Ta có f(-1) = -3.
Bảng biến thiên
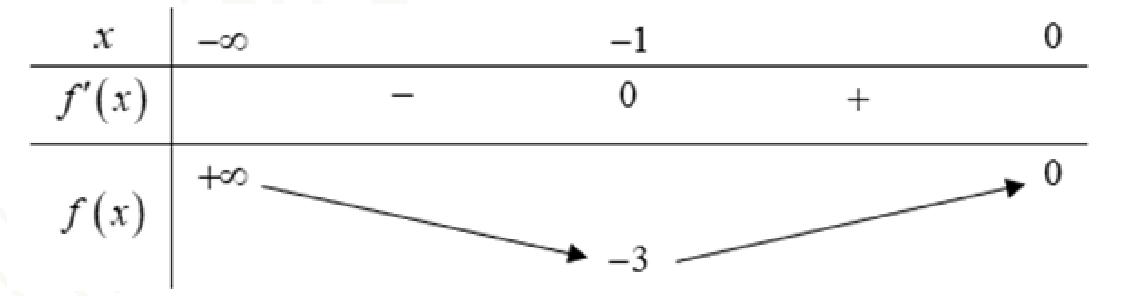
Dựa vào bảng biến thiên, ta có: m ≤ -3 .
Cách 2
Ta có ∆’ = 9 + 3m
Nếu ∆’ ≤ 0 ⇔ m ≤ -3 thì y’ ≥ 0, ∀ x ∊ ℝ ⇒ y’ ≥ 0, ∀ x < 0
Nếu ∆’ > 0 thì y’ có hai nghiệm phân biệt x1, x2. Khi đó để y’ ≥ 0, ∀ x < 0 thì ta phải có 0 ≤ x1 < x2. Điều này không thể xảy ra vì S = x1 + x2 = -2 < 0
Vậy m ≤ -3.
Cách 3
Phương án B: Với m = -3 ta có y = x3 + 3x2 + 3x + 1 = (x + 1)3. Khi đó y’ = 3(x + 1)3 ≥ 0 ∀ x
Suy ra hàm số đồng biến trên khoảng (-∞;0). Vậy B là đáp án đúng.
Câu 4. Tìm tất cả các giá trị thực của tham số m để hàm số y = x3 – 3mx2 – 9m2x nghịch biến trên khoảng (0;1).
A.
B.
C. m < -1
D. hoặc m ≤ -1
Lời giải
Chọn D
Tập xác định D = ℝ
y’ = 3x2 – 6mx -9m2
y’ = 0 ⇔ 3x2 – 6mx -9m2 = 0 ⇔ x2 – 2mx -3m2 = 0
Nếu –m = 3m ⇔ m = 0 thì y’ ≥ 0, ∀ x ∊ ℝ nên hàm số không có khoảng nghịch biến.
Nếu –m < 3m ⇔ m > 0 thì hàm số nghịch biến trên khoảng (-m; 3m).
Do đó hàm số nghịch biến trên khoảng (0;1)
Kết hợp với điều kiện ta được
Nếu –m > 3m ⇔ m < 0 thì hàm số nghịch biến trên khoảng (3m; -m)
Do đó hàm số nghịch biến trên khoảng (0;1)
Kết hợp với điều kiện ta được m ≤ -1
Vậy hàm số nghịch biến trên khoảng (0;1) khi m ≤ -1 hoặc
Dạng 2. Tìm m để hàm phân thức đồng biến, nghịch biến trên khoảng
Phương pháp giải
Loại 1. Tìm điều kiện của tham số để hàm  đơn điệu trên từng khoảng xác định.
đơn điệu trên từng khoảng xác định.
Tính
- Hàm số đồng biến trên từng khoảng xác định của nó ⇔ y’ > 0 ⇔ ad – cb > 0
- Hàm số nghịch biến trên từng khoảng xác định của nó ⇔ y’ < 0 ⇔ ad – cb < 0
Loại 2. Tìm điều kiện để hàm  đơn điệu trên khoảng
đơn điệu trên khoảng 
Tính
Hàm số đồng biến trên khoảng (m;n):
Hàm số nghịch biến trên khoảng (m;n):
Bài tập vận dụng
Câu 1. Cho hàm số với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S.
A. 4
B. Vô số
C. 3
D. 5
Lời giải
Chọn D
D = ℝ \{m};
Hàm số nghịch biến trên các khoảng xác định khi y’ < 0, ∀ x ∊ D ⇔ m2 – 4m < 0 ⇔ 0 < m < 4
Mà m ∊ ℤ nên có 3 giá trị thỏa mãn.
Câu 2. Có bao nhiêu giá trị nguyên của tham số m để hàm số nghịch biến trên khoảng (10; +∞)?
A. Vô số
B. 4
C. 5
D. 3
Lời giải
Chọn B
Tập xác định D = ℝ \{5m}
Hàm số nghịch biến trên (10; +∞) khi và chỉ khi
Mà m ∊ ℤ nên m ∊ {-2; -1; 0; 1}.
Câu 3. Cho hàm số với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số đồng biến trên các khoảng xác định. Tìm số phần tử của S.
A. Vô số
B. 3
C. 5
D. 4
Lời giải
Chọn B
hàm số đồng biến trên khoảng xác định khi -1 < m < 3 nên có 3 giá trị của m nguyên.
Dạng 3: Tìm m để hàm số đặc biệt đồng biến, nghịch biến trên khoảng
Phương pháp giải
Hàm số khác ở đây ám chỉ các loại hàm đa thức bậc cao. Phương pháp chung là đặt ẩn hoặc biến đổi để về các dạng hàm số cơ bản hoặc tính f’ và lập bảng biến thiên. Từ bảng biến thiên ta dễ dàng tìm được tham số m theo yêu cầu bài toán.
Bài tập vận dụng
Câu 1. Có bao nhiêu giá trị nguyên âm của tham số m để hàm số đồng biến trên khoảng (0; +∞)
A. 0
B. 4
C. 5
D. 3
Lời giải
Chọn B
Hàm số đồng biến trên (0; +∞) khi và chỉ khi
Xét hàm số
Bảng biến thiên
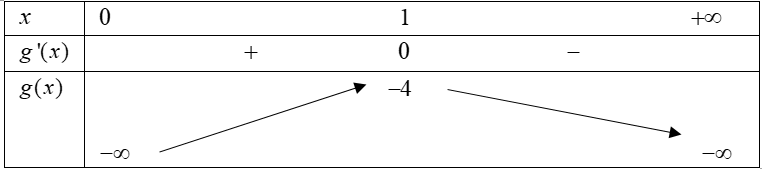
Dựa vào BBT ta có m ≥ -4, suy ra các giá trị nguyên âm của tham số m là -4; -3; -2; -1.
Câu 2. Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên ℝ. Tổng giá trị của tất cả các phần tử thuộc S bằng.
A.
B. -2
C.
D.
Lời giải
Ta có f’(x) = m2x4 – mx2 + 20x – (m2 – m – 20)
= m2(x4 – 1) – m(x2 – 1) + 20(x + 1)
= m2(x – 1)(x + 1)(x2 + 1) – m(x – 1)(x + 1) + 20(x + 1)
= (x + 1)[m2(x – 1)(x2 + 1) – m(x – 1) + 20]
Ta có f’(x) = 0 có một nghiệm đơn là x = -1, do đó nếu (*) không nhận x = -1 là nghiệm thì f’(x) đổi dấu qua x = -1. Do đó để f(x) đồng biến trên ℝ thì f’(x) ≥ 0, ∀ x ∊ ℝ hay (*) nhận x = -1 làm nghiệm (bậc lẻ).
Suy ra: m2 (-1 – 1)(1 + 1) – m(-1 – 1) + 20 = 0 ⇔ -4m2 + 2m + 20 = 0
Tổng các giá trị của m là ½
Câu 3. Tập hợp các giá trị thực của tham số m để hàm số đồng biến trên mỗi khoảng xác định của nó là.
A. [0; 1)
B. (-∞; 0]
C. [0; +∞) \{1}
D. (-∞; 0)
Lời giải
Chọn B
Tập xác định: D = ℝ \{2}
Hàm số đã cho đồng biến trên mỗi khoảng xác định của nó khi và chỉ khi:
y’ ≥ 0, ∀ x ∊ D
⇔ m ≤ (x – 2)2, ∀ x ∊ D
Xét hàm số f(x) = (x – 2)2 ta có:
f’(x) = 2x – 4 ⇒ f’(x) = 0 ⇔ x = 2
Bảng biến thiên
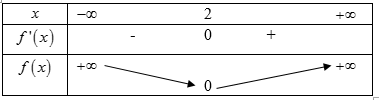
Vậy, để hàm số đã cho đồng biến trên mỗi khoảng xác định của nó thì m ≤ 0 .
Câu 4. Tìm tất cả các giá trị thực của tham số để hàm số nghịch biến trên khoảng
A.
B.
C. m ≤ 3
D. m < 3
Lời giải
Chọn A
Điều kiện: cos x ≠ m.
Ta có:
Vì x ∊ ⇒ sin x > 0, (cos x – m)2 > 0, ∀ x ∊
; cos x ≠ m.
Để hàm số nghịch biến trên khoảng ⇔ y’ < 0 ∀ x ∊
Chú ý : Tập giá trị của hàm số y = cos x, ∀ x ∊ là (-1; 0)
Câu 5. Cho hàm số . Có bao nhiêu giá trị nguyên của m trong khoảng (-10; 10) sao cho hàm số đồng biến trên (-8; 5)?
A. 14
B. 13
C. 12
D. 15
Lời giải
Đặt vì x ∊ (-8; 5)
và
đồng biến trên (-8; 5)
Hàm số trở thành tập xác định D = ℝ \{m}
Để hàm số đồng biến trên khoảng
⇒ m ∊ {-9; -8; -7; -6; -5; -4; -1; 0; 4; 5; 6; 7; 8; 9} có 14 giá trị.
Dạng 4: Tìm m để hàm số đồng biến nghịch biến trên R
Phương pháp giải
Xét hàm số y = ax3 + bx2 + cx + d ⇒ y’ = 3ax2 + 2bx +c
TH1: a = 0 (nếu có tham số)
TH2: a ≠ 0
Hàm số đồng biến trên ℝ ⇔
Hàm số nghịch biến trên ℝ ⇔
Bài tập vận dụng
Câu 1. Cho hàm số y = ⅓ x3 + mx2 + (3m – 2) x + 1. Tìm tất cả giá trị của m để hàm số nghịch biến trên ℝ.
A. (-2; -1)
B. [-2; -1]
C. (-∞; -2) ∪ (-1; +∞)
D. (-∞; -2] ∪ [-1; +∞)
Lời giải
Ta có: y’ = -x2 + 2mx + 3m – 2
Hàm số nghịch biến trên ℝ
⇔ m2 – 3m + 2 ≤ 0 ⇔ m ∊ [-2; -1]
Đáp án B
Câu 2. Cho hàm số y = ⅓ (m – 1)x3 – (m – 1)x2 – x + 1. Tìm m để hàm số nghịch biến trên ℝ.
A. -3 ≤ m ≤ 1
B. 0 ≤ m ≤ 1
C. (0; 1]
D. [0; 1)
Lời giải
Ta có: y’ = (m – 1)x2 – 2(m – 1)x – 1
TH1: m – 1 = 0 ⇒ m = 1 ⇒ y’ = -1 < 0. Hàm số nghịch biến trên ℝ.
TH2: m ≠ 1. Hàm số nghịch biến trên ℝ khi:
⇔ m ∊ [0; 1)
Đáp án D
Câu 3. Tìm m để hàm số y = x3 + 2(m + 1) x2 – 3mx + 5m – 2 đồng biến trên ℝ.
A.
B.
C.
D.
Lời giải
y’ = 3x2 + 4(m + 1) x – 3m
Để hàm số đồng biến trên ℝ thì:
Đáp án A
Dạng 5: Tìm m để hàm số cho bởi đồ thị hàm F(x) đồng biến nghịch biến trên khoảng
Phương pháp giải
Định nghĩa 1
Giả sử K là một khoảng, một đoạn hoặc một nửa khoảng và y = f(x) là một hàm số xác định trên K. Ta nói:
- Hàm số y = f(x) được gọi là đồng biến (tăng) trên K nếu ∀ x₁, x₂ ∊ K, x₁ < x₂ ⇒ f(x₁) < f(x₂).
- Hàm số y = f(x) được gọi là nghịch biến (giảm) trên K nếu ∀ x₁, x₂ ∊ K, x1 < x₂ ⇒ f(x₁) > f(x₂)
- Hàm số đồng biến hoặc nghịch biến trên K gọi chung là đơn điệu trên K.
Nhận xét 1
Nếu hàm số f(x) và g(x) cùng đồng biến (nghịch biến) trên D thì hàm số f(x) + g(x) cũng đồng biến (nghịch biến) trên D. Tính chất này có thể không đúng đối với hiệu f(x) – g(x).
Nhận xét 2
Nếu hàm số f(x) và g(x) là các hàm số dương và cùng đồng biến (nghịch biến) trên D thì hàm số f(x) ∙ g(x) cũng đồng biến (nghịch biến) trên D. Tính chất này có thể không đúng khi các hàm số f(x), g(x) không là các hàm số dương trên D.
Nhận xét 3
Cho hàm số u = u(x), xác định với x ∊ (a;b) và u(x) ∊ (c;d). Hàm số f [u(x)] cũng xác định với x ∊ (a;b). Ta có nhận xét sau:
- Giả sử hàm số u = u(x) đồng biến với x ∊ (a;b). Khi đó, hàm số f [u(x)] đồng biến với x ∊ (a;b) ⇔ f(u) đồng biến với u ∊ (c;d)
- Giả sử hàm số u = u(x) nghịch biến với x ∊ (a;b). Khi đó, hàm số f [u(x)] nghịch biến với x ∊ (a;b) ⇔ f(u) nghịch biến với u ∊ (c;d)
Định lý 1
Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:
a) Nếu hàm số đồng biến trên khoảng K thì f’(x) ≥ 0, ∀ x ∊ K
b) Nếu hàm số nghịch biến trên khoảng K thì f’(x) ≤ 0, ∀ x ∊ K
Định lý 2
Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:
a) Nếu f’(x) > 0, ∀ x ∊ K thì hàm số f đồng biến trên K.
b) Nếu f’(x) < 0, ∀ x ∊ K thì hàm số f nghịch biến trên K.
c) Nếu f’(x) = 0, ∀ x ∊ K thì hàm số f không đổi trên K.
Chú ý
Chú ý: Khoảng K trong định lí trên ta có thể thay thế bởi đoạn hoặc một nửa khoảng. Khi đó phải có thêm giả thuyết “Hàm số liên tục trên đoạn hoặc nửa khoảng đó”. Chẳng hạn:
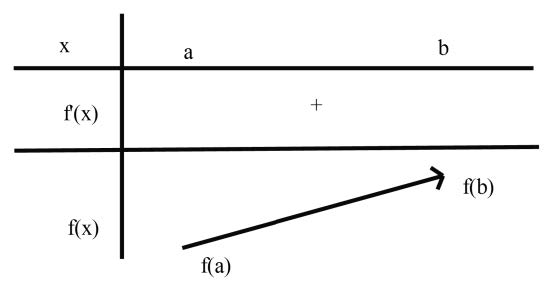
Nếu hàm số f liên tục trên đoạn [a;b] và f’(x) > 0, ∀ x ∊ K thì hàm số f đồng biến trên đoạn [a;b]
Định lý 3
Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:
a) Nếu f’(x) ≥ 0, ∀ x ∊ K và f’(x) = 0 chỉ tại hữu hạn điểm thuộc K thì hàm số f đồng biến trên K.
b) Nếu f’(x) ≤ 0, ∀ x ∊ K và f’(x) = 0 chỉ tại hữu hạn điểm thuộc K thì hàm số f nghịch biến trên K.
Quy tắc xét tính đơn điệu của hàm sốGiả sử hàm số f có đạo hàm trên K
– Nếu f’(x) ≥ 0 với mọi x ∊ K và f’(x) = 0 chỉ tại hữu hạn điểm x ∊ K thì hàm số f đồng biến trên K.
– Nếu f’(x) ≤ 0 với mọi x ∊ K và f’(x) = 0 chỉ tại hữu hạn điểm x ∊ K thì hàm số f nghịch biến trên K.
Bài tập vận dụng
Câu 1. Cho hàm số f(x). Hàm số y = f’(x) có đồ thị như hình sau. Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số g(x) = 4f(x – m) + x2 – 2mx + 2020 đồng biến trên khoảng (1; 2).
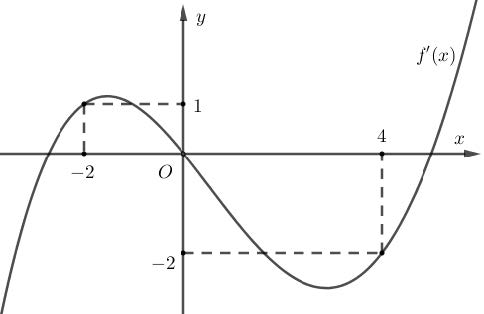
A. 2
B. 3
C. 0
D. 1
Ý tưởng: Phát triển thành bài toán chứa tham số.
Lời giải
Chọn A
Ta có g’(x) = 4f’(x – m) + 2x – 2m
g’(x) ≥ 0 ⇔
Đặt t = x – m thì (*) ⇔
Vẽ đường thẳng trên cùng hệ trục Oxy với đồ thị y = f’(x) như hình vẽ sau:
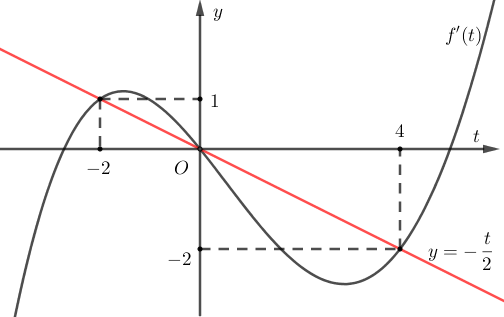
Từ đồ thị ta có
Hàm số g(x) đồng biến trên khoảng (1; 2) ⇔ g’(x) ≥ 0 ∀ x ∊ (1; 2)
Vì m nguyên dương nên m ∊ {2; 3}
Vậy có hai giá trị nguyên dương của m để hàm số g(x) đồng biến trên khoảng (1; 2).
Dạng 6: Tìm m để hàm giá trị tuyệt đối đồng biến, nghịch biến trên khoảng
Phương pháp giải
Hàm số y = |f(x)| đồng biến trên [α;+∞) khi và chỉ khi:
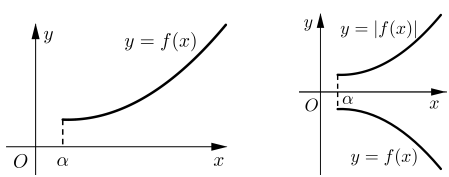
Hàm số y = |f(x)| đồng biến trên (α; β) khi và chỉ khi:
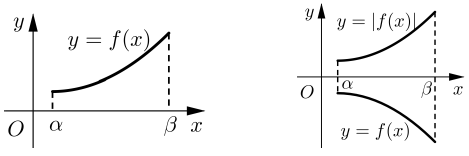
Các dạng đồng biến y = |f(x)| trên [α;+∞), (α; β) ta thực hiện tương tự.
Hàm số hỏi nghịch biến làm ngược lại.
Loại 1: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số dạng đa thức đồng biến, nghịch biến trên tập D cho trước.
Câu 1. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = |x5 – 5x2 + 5(m – 1)x – 8| nghịch biến trên khoảng (-∞;1)?
A. 2
B. 0
C. 4
D. 1
Lời giải
Chọn D
Xét hàm số
f(x) = x5 – 5x2 + 5(m – 1)x – 8
TH1: f(x) = 0 có nghiệm x0 ∊ (-∞;1) thì hàm số y = |f(x)| không thể nghịch biến trên khoảng (-∞;1).
TH2: f(x) = 0 không có nghiệm x0 ∊ (-∞;1)
Ta có: f’(x) = 5x4 – 10x + 5(m – 1)
Khi đó y = |x5 – 5x2 + 5(m – 1)x – 8| = |f(x)| =
Nên
Hàm số nghịch biến trên (-∞;1) khi và chỉ khi y’ ≤ 0 với ∀ x ∊ (-∞;1)
Mà m ∊ ℤ nên m = 3
Câu 2. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = |2x3 – mx + 1| đồng biến trên khoảng (1; +∞)?
A. 2
B. 6
C. 3
D. 4
Lời giải
Chọn C
Xét hàm số
f(x) = 2x3 – mx + 1
TH1: f(x) = 0 có nghiệm x0 ∊ (1;+∞) thì hàm số y = |f(x)| không thể nghịch biến trên khoảng (1;+∞).
TH2: f(x) = 0 không có nghiệm x0 ∊ (1;+∞)
Ta có: f’(x) = 6x2 – m
Khi đó y = |2x3 – mx + 1| = |f(x)| =
Nên
Hàm số nghịch biến trên khoảng (1;+∞) khi và chỉ khi y’ ≥ 0 với ∀ x ∊ (1;+∞)
⇒ m ∊ {1; 2; 3}
Câu 3. Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để hàm số y = |3x4 – 4x3 – 12x2 + m| nghịch biến trên khoảng (-∞; -1)?
A. 6
B. 4
C. 3
D. 5
Lời giải
Chọn D
Xét hàm số f(x) = 3x4 – 4x3 – 12x2 + m ⇒ f’(x) = 12x3 – 12x2 – 24x = 12x (x2 – x – 2)
⇒ f’(x) = 0
BBT:
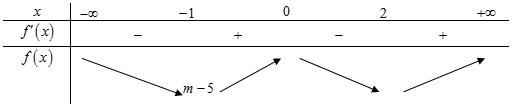
Nhận thấy: Hàm số y = |f(x)| nghịch biến trên khoảng (-∞; -1) ⇔ m – 5 > 0 ⇔ m ≥ 5.
Lại do ⇒ m ∊ {5; 6; 7; 8; 9}
Vậy có 5 giá trị của m thỏa mãn yêu cầu bài toán.
Loại 2: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số dạng phân thức hữu tỉ đồng biến, nghịch biến trên tập D cho trước.
Câu 1. Tính tổng S tất cả các giá trị nguyên của tham số m trong đoạn [-10; 10] để hàm số đồng biến trên (1; +∞).
A. S = 55
B. S = 54
C. S = 3
D. S = 5
Lời giải
Chọn B.
Xét hàm số với x ≠ -m – 2, có
Hàm số đồng biến (1; +∞) khi xảy ra một trong hai trường hợp sau:
TH1:
TH2:
Vậy m ∊ (1; +∞), lại do suy ra m ∊ {2; 3; 4; 5; 6; 7; 8; 9; 10}
Vậy S = 54
Câu 2. Tìm m để hàm số đồng biến trên (1;+∞)
A.
B.
C.
D.
Lời giải
Chọn B
Đặt . ĐK: x ≠ -m
Khi đó
Để hàm số đồng biến trên (1;+∞) ⇔
hoặc
Ta có
Vậy ⅓ < m ≤ 1
Câu 3. Có bao nhiêu số nguyên của tham số m để hàm số đồng biến trên [3; +∞)?
A. 4
B. 5
C. Vô số
D. 6
Lời giải
Chọn A
Tập xác định: D = ℝ \{1}
Xét hàm số
Có
Khi đó
Hàm số đồng biến trên [3; +∞) ⇔ y’ ≥ 0, ∀ x ∊ [3; +∞)
Vì m ∊ ℤ ⇒ m ∊ {-2; -1; 0; 1}
Vậy có 4 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.
Loại 3: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số chứa căn đồng biến, nghịch biến trên tập D cho trước.
Câu 1. Cho hàm số . Có bao nhiêu giá trị m nguyên để hàm số nghịch biến trên (0;1).
A. 4
B. 2
C. 3
D. 5
Lời giải
Chọn A
Đặt
Ta có
Do hàm số liên tục tại x = 0; x = 1 nên để hàm số nghịch biến trên (0;1) ta xét 2 trường hợp sau:
Trường hợp 1:
Trường hợp 2:
(vô nghiệm)
Do m nguyên nên m nhận các giá trị sau -3; -2; -1; 0
Câu 2. Có bao nhiêu giá trị nguyên của tham số m ∊ (-5; 5) để hàm số nghịch biến trên (2; 3)?
A. 2
B. 3
C. 5
D. 9
Lời giải
Chọn B
Xét hàm số
Ta có
Cho f’(x) = 0
Ta thấy f’(x) < 0, ∀ x ∊ (2; 3) nên hàm số f(x) nghịch biến trên (2; 3)
Để nghịch biến trên (2; 3) thì
f(3) ≥ 0
Do m ∊ (-5; 5) nên m = {-2; -3; -4}
Câu 3. Có bao nhiêu giá trị nguyên của tham số m ∊ [0; 10] để hàm số đồng biến trên khoảng (1;+∞)?
A. 11
B. 10
C. 12
D. 9
Lời giải
Chọn A
Tập xác định D = ℝ
Xét hàm số
Hàm số đồng biến trên khoảng (1;+∞)
TH1:
f’(x) ≥ 0, ∀ x ∊ (1;+∞)
Đặt t = x – 1, t > 0
Xét
Bảng biến thiên:
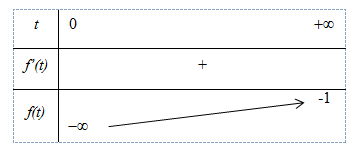
Từ BBT ta có
TH2:
f’(x) ≤ 0, ∀ x ∊ (1;+∞)
Đặt t = x – 1, t > 0
Mà nên với mỗi giá trị của m luôn có giá trị của t dương đủ nhỏ để VT của (*) lớn hơn 0.
Suy ra không có giá trị nào của m để TH2 thỏa mãn.
Vậy có 11 giá trị nguyên của m thỏa mãn là {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10}
Loại 4: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số lượng giác đồng biến, nghịch biến trên tập D cho trước.
Câu 1. Có bao nhiêu giá trị m nguyên để hàm số y = |f(x)| = |x3 – 3x2 +3(m2 + 5) x + (12 – 3m2) cosx| đồng biến trên (0; π)
A. 3
B. 5
C. 4
D. Vô số
Lời giải
Chọn B
Đặt h(x) = x3 – 3x2 + 3(m2 + 5) x + (12 – 3m2) cosx.
Ta có h’(x) = 3x2 – 6x + 3(m2 + 5) – (12 – 3m2) sinx.
⇔ h’(x) = 3(x – 1)2 + 12(1 – sinx) + 3m2(1 + sinx) ≥ 0, ∀ x ∊ (0; π)
Vậy hàm số h(x) luôn đồng biến trên (0; π).
Để y = f(x) đồng biến trên (0; π). Thì h(0) ≥ 0 ⇔ (12 – 3m2) ≥ 0 ⇔ m ∊ [-2; 2]
Kết luận: có 5 giá trị m nguyên thỏa mãn.
Câu 2. Các giá trị của tham số m để hàm số y = |sinx – cosx + m| đồng biến trên khoảng là.
A.
B.
C. m > 1
D. m ≥ 1
Lời giải
Chọn B
Xét hàm số f(x) = sinx – cosx + m =
Khi đó y = |sinx – cosx + m| = |f(x)| = . Nên
Hàm số y = |sinx – cosx + m| đồng biến trên khoảng ⇔ y’ ≥ 0, ∀ x ∊
Với
Nên (1) ⇔ f(x) > 0, ∀ x ∊
Câu 3. Cho hàm số y = |sin3x – m.sinx + 1|. Gọi S là tập hợp tất cả các số tự nhiên m sao cho hàm số đồng biến trên . Tính số phần tử của S .
A. 1
B. 2
C. 3
D. 0
Lời giải
Chọn A
Trên khoảng , hàm số y = sinx đồng biến
Đặt t = sin x, x ∊ ⇒ t ∊ (0;1)
Khi đó hàm số y = |sin3x – m.sinx + 1| đồng biến trên khoảng khi và chỉ khi
y = g(t) = |t3 – mt + 1| đồng biến trên (0;1)
Xét hàm số y = f(t) = t3 – mt + 1 trên khoảng (0;1) có f’(t) = 3t2 – m.
+) Khi m = 0
f’(t) = 3t2 > 0, ∀ t ⇒ y = f(t) = t3 + 1 đồng biến trên (0;1) và đồng thời y = f(t) = t3 + 1 cắt trục hoành tại điểm duy nhất t = -1
⇒ y = g(t) = |t3 – mt + 1| đồng biến trên (0;1) ⇒ m = 0 thỏa mãn
+) Khi m > 0
f’(t) = 0 có 2 nghiệm phân biệt
Hàm số y = f(t) = t3 – mt + 1 đồng biến trên các khoảng và
TH1: ⇔ 0 < m < 3
Hàm số y = f(t) = t3 – mt + 1 nghịch biến trên khoảng và đồng biến trên khoảng
⇒ Không có giá trị của m để y = g(t) = |t3 – mt + 1| đồng biến trên (0;1)
TH2: ⇔ m ≥ 3
Để y = g(t) = |t3 – mt + 1| đồng biến trên (0;1) thì t3 – mt + 1 ≤ 0, ∀ x ∊ (0;1)
⇔ mt ≤ t3 + 1, ∀ x ∊ (0;1)
⇒ Không có giá trị của m thỏa mãn
Vậy chỉ có giá trị m = 0 thỏa mãn
Câu 4. Có bao nhiêu giá trị nguyên của m thuộc [-5;5] để hàm số y = |cos3x – 3m2cosx| nghịch biến trên .
A. 1
B. 11
C. 5
D. 6
Lời giải
Chọn B
Đặt t = cos x, vì x ∊ ⇒ t ∊ (0;1)
Vì t =cos x là hàm số nghịch biến trên nên yêu cầu bài toán trở thành tìm m nguyên thuộc [-5;5] để hàm số y = |t3 – 3m2t| đồng biến trên (0;1).
Xét f(t) = t3 – 3m2t, t ∊ (0;1) ⇒ f’(t) = 3t2 – 3m2
TH1: Nếu m = 0 ⇒ f’(t) > 0, ∀ t ∊ (0;1) ⇒ f(t) luôn đồng biến trên (0;1)
Mà f (0) = 0 ⇒ y = |f(t)| luôn đồng biến trên (0; +∞)
⇒ y = |f(t)| luôn đồng biến trên (0;1)
Do đó m = 0 thỏa mãn bài toán (1)
TH2: m ≠ 0 ⇒ f’(t) = 0
*) Với m > 0 , ta có BBT sau:
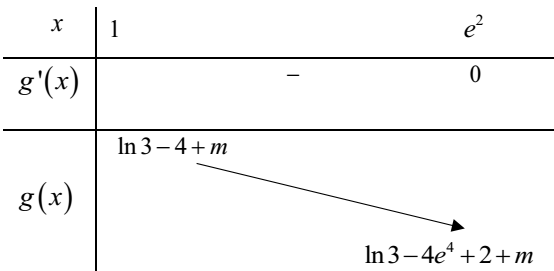
Từ BBT suy ra hàm số y = |f(t)| luôn đồng biến trên (0; m)
YCBT tương đương (0;1) ⊂ (0; m) ⇔ m ≥ 1 (2)
*) Với m < 0 , ta có BBT sau:
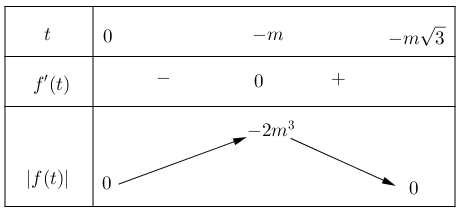
Từ BBT suy ra hàm số y = |f(t)| luôn đồng biến trên (0; -m)
YCBT tương đương (0;1) ⊂ (0; -m) ⇔ m ≤ -1 (3)
Từ (1), (2) và (3) vậy có 11 giá trị nguyên của m thỏa mãn bài toán.
Loại 5: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số mũ đồng biến, nghịch biến trên tập D cho trước.
Câu 1. Có bao nhiêu giá trị nguyên dương của m để y = |9x + 3x – m + 1| đồng biến trên đoạn [0;1]
A. 1
B. 4
C. 3
D. 6
Lời giải
Chọn C
Đặt 3x = t ⇒ t ∊ [1;3] vì t ∊ [0;1]
⇒ t = |t2 + t – m + 1| =
Để hàm số đồng biến trên đoạn t ∊ [1;3] thì
Với mọi giá trị của t ∊ [1;3] thì 2t + 1 > 0 nên
Để y’ ≥ 0, ∀ t ∊ [1;3] thì t2 + t – m + 1 ≥ 0, ∀ t ∊ [1;3]
⇒ m – 1 ≤ t2 + t = g(t) , ∀ t ∊ [1;3]
Vậy có 3 giá trị nguyên {1; 2; 3} thỏa mãn yêu cầu bài toán.
Câu 2. Có bao nhiêu giá trị m nguyên dương và nhỏ hơn 2020 để hàm số y = |4x + m.2x+1 + m + 2| đồng biến trên khoảng (0;1)?
A. 2018
B. 2019
C. 2
D. 3
Lời giải
Chọn A
Xét hàm số f(x) = 4x + m.2x+1 + m + 2 (1) trên khoảng (0;1)
Đặt t = 2x ⇒ t ∊ (1;2)
Hàm số (1) trở thành h(t) = t2 – 2mt + m + 2 trên khoảng (1;2).
Suy ra h’(t) = 2t – 2m
Ta có y = |f(x)| đồng biến trên khoảng (0;1) 
Vì hàm số t = 2x đồng biến trên khoảng (0;1) 
Do đó,
Vậy có 2018 số nguyên dương nhỏ hơn 2020 thỏa ycbt.
Câu 3. Cho hàm số (1). Có bao nhiêu giá trị nguyên dương của tham số m để hàm số nghịch biến trên khoảng (2;4)?
A. 234
B. Vô số
C. 40
D. Không tồn tại m
Lời giải
Chọn C
Đặt
Ta có ⇒ t ∊ (e2; e3), đồng thời x và t sẽ ngược chiều biến thiên.
Khi đó hàm số trở thành y = |t2 + 3t – 2m + 5| = (2)
Ta có:
Hàm số (1) nghịch biến trên khoảng (2;3) ⇔ hàm số (2) đồng biến trên khoảng (e2; e3)
∀ x ∊ (e2; e3)
⇔ t2 + 3t – 2m + 5 > 0 ∀ x ∊ (e2; e3)
∀ x ∊ (e2; e3)
Có ∀ x ∊ (e2; e3)
Với điều kiện m là số nguyên dương ta tìm được 40 giá trị của m.
Câu 4. Có bao nhiêu giá trị nguyên dương m ∊ (-2019; 2020), để hàm số y = |e-x2 + ex2 – m| nghịch biến trên (1;e)?
A. 401
B. 0
C. 2019
D. 2016
Lời giải
Chọn A
Đặt f(x) = e-x2 + ex2 – m ⇒ f’(x) = -2xe-x2 + 2ex2
Ta có y = |f (x)| =
Yêu cầu bài toán ⇔ y’ ≤ 0, ∀ x ∊ (1;e) (*)
Vì x ∊ (1;e) nên -2xe-x2 + 2ex2 = , ∀ x ∊ (1;e)
Khi đó, (*) ⇔ f(x) ≤ 0, ∀ x ∊ (1;e)
⇔ e-x2 + ex2 – m ≤ 0, ∀ x ∊ (1;e)
⇔ e-x2 + ex2 ≤ m, ∀ x ∊ (1;e)
Ta có giá trị lớn nhất của hàm số y = e-x2 + ex2 ∀ x ∊ (1;e) là e-x2 + ex2
Nên m ≥ e-x2 + ex2 ≈ 1618,18
Vậy có 401 giá trị nguyên dương m thỏa mãn.
Loại 6: Tìm điều kiện tham số m để hàm y = |f(x)| với f(x) là hàm số logarit đồng biến, nghịch biến trên tập D cho trước.
Câu 1. Có bao nhiêu giá trị nguyên thuộc khoảng (-100; 100) của tham số m để hàm số y = |ln3x – 4x2 + m| đồng biến trên đoạn [1;e2]?
A. 101
B. 102
C. 103
D. 100
Lời giải
Chọn B
y = |ln3x – 4x2 + m|. Điều kiện x > 0
Xét hàm số g(x) = ln3x – 4x2 + m trên [1;e2]
⇒ g(x) nghịch biến trên [1;e2]

⇒ Hàm số y = |g(x)| = |ln3x – 4x2 + m| đồng biến trên đoạn [1;e2]
⇔ ln3 – 4 + m ≤ 0 ⇔ m ≤ 4 – ln3
Mà m nguyên thuộc khoảng (-100; 100) nên m ∊ {-99; -98;…; -1; 0; 1; 2}
Vậy có 102 giá trị m nguyên thỏa mãn yêu cầu bài toán.
Câu 2. Có bao nhiêu số nguyên m < 2020 để hàm số y = |ln(mx) – x + 2| nghịch biến trên (1;4)?
A. 2018
B. 2019
C. 1
D. Vô số.
Lời giải
Chọn A
Xét f(x) = ln(mx) – x + 2.
Dễ thấy ∀ x ∊ (1;4): mx > 0 ⇔ m > 0
Khi đó
Do đó f(x) luôn nghịch biến trên (1;4)
Yêu cầu bài tóan tương đương với f(4) ≥ 0 ⇔ ln(4m) – 2 ≥ 0
Vậy m ∊ [2; 2019] có 2018 số nguyên thỏa mãn.
Câu 3. Có bao nhiêu số nguyên m thuộc (-2020; 2020) để hàm số y = |ln(x2 + 2x – m) – 2mx2 – 1| luôn đồng biến trên (0;10)?
A. 4038
B. 2020
C. 2017
D. 2018
Lời giải
Chọn C
Ta xét hàm số f(x) = ln(x2 + 2x – m) – 2mx2 – 1 trên (0;10)
Điều kiện hàm số có nghĩa là x2 + 2x – m > 0, ∀ x ∊ (0;10)
⇔ x2 + 2x > m, ∀ x ∊ (0;10) (1)
Ta lại có x2 + 2x = x.(x + 2) > 0 với ∀ x ∊ (0;10) nên điều kiện (1) cho ta m ≤ 0 (2)
Đạo hàm do m ≤ 0 và x ∊ (0;10) nên
Suy ra f’(x) > 0 hàm số đồng biến trên (0;10).
Từ đó để hàm số y = |ln(x2 + 2x – m) – 2mx2 – 1| = |f(x)| đồng biến trên (0;10) điều kiện đủ là f(x) ≥ 0 với ∀ x ∊ (0;10) (3)
+) TH1: Xét m = 0
Khi đó f(x) = ln(x2 + 2x) – 1 có không thỏa mãn (3)
+) TH2: Xét m < 0
Do hàm số f(x) đồng biến nên ta chỉ cần f(0) ≥ 0 ⇔ ln(-m) – 1 ≥ 0 ⇔ -m ≥ e ⇔ m ≤ -e
Từ đó ta được:
⇔ m ∊ {-2019; -2018; -2017;…; -3} có 2017 giá trị m thỏa mãn bài toán.
Câu 4. Có bao nhiêu số nguyên của tham số m trong đoạn [-3;3] để hàm số y = |ln(x3 + mx + 2)| đồng biến trên nửa khoảng [1;3)?
A. 7
B. 4
C. 6
D. 5
Lời giải
Chọn C
Điều kiện xác định: x3 + mx + 2 > 0
Xét hàm số f(x) = ln(x3 + mx + 2)
Ta có:
Hàm số đồng biến trên nửa khoảng [1;3)
Trường hợp 1:
Trường hợp 2:
Từ hai trường hợp trên suy ra m ≥ -2
Mà m ∊ [-3;3] ⇒ m ∊ {-2; -1; 0; 1; 2; 3}
Vậy có 6 số nguyên m thỏa mãn YCBT.