Các bài toán về hình lăng trụ và thể tích khối lăng trụ đều là những bài toán có nhiều hướng phát triển và tư duy. Mật độ xuất hiện của dạng toán này cũng ngày một nhiều. Bài viết sau đây sẽ giúp bạn đọc tìm hiểu chi tiết về công thức tính thể tích khối lăng trụ và các dạng toán thường gặp nhất.
Khái niệm lình lăng trụ
[content_1]Định nghĩa
Cho hai mặt song song (α) và (α’). Trên (α) ta lấy đa giác lồi A1A2…An qua các đỉnh này ta dựng các đường thẳng song song cắt (α’) tại A’1A’2…, A’n. Hình bao gồm hai đa giác A1A2…An, A’1A’2…A’n và các hình bình hành A1A2 A’2A’1,… Được gọi là hình lăng trụ. Kí hiệu là: A1A2…An.A’1A’2…A’n.
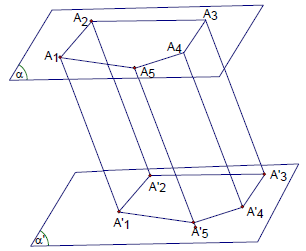
Tính chất
– Các mặt bên của hình lăng trụ bằng nhau và song song với nhau
– Các mặt bên là các hình bình hành
– Hai đáy hình lăng trụ là hai đa giác bằng nhau
Các dạng hình lăng trụ
Định nghĩa
– Hình lăng trụ đứng là hình lăng trụ có cạnh bên vuông góc với đáy. Độ dài cạnh bên được gọi chiều cao của hình lăng trụ. Lúc đó các mặt bên của hình lăng trụ đứng là các hình chữ nhật
– Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều. Các mặt bên của lăng trụ đều là các hình chữ nhật bằng nhau. Ví dụ: hình lăng trụ tam giác đều, tứ giác đều… thì ta hiểu là hình lăng trụ đều
– Hình hộp là hình lăng trụ có đáy là hình bình hành
– Hình hộp đứng là hình lăng trụ đứng có đáy là hình bình hành
– Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật
– Hình lập phương là hình lăng trụ đứng có đáy là hình vuông và các mặt bên đều là hình vuông được gọi là hình lập phương (hay hình chữ nhật có ba kích thước bằng nhau được gọi là hình lập phương)
Tính chất
– Hình hộp chữ nhật ⇒ Hình lăng trụ đứng (Có tất cả các mặt là hình chữ nhật)
– Hình lập phương ⇒ Hình lăng trụ đều (tất cả các cạnh bằng nhau)
– Hình hộp đứng ⇒ Hình lăng trụ đứng (mặt bên là hình chữ nhật, mặt đáy là hình bình hành)
So sánh khối lăng trụ đứng và khối lăng trụ đều
Khối lăng trụ đứng
– Định nghĩa: Hình lăng trụ đứng là hình lăng trụ có cạnh bên vuông góc với mặt đáy
– Tính chất:
- Các mặt bên hình lăng trụ đứng là hình chữ nhật
- Các mặt bên hình lăng trụ đứng vuông góc với mặt đáy
- Chiều cao là cạnh bên
Khối lăng trụ đều
– Định nghĩa: Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều
– Tính chất:
- Các mặt bên của hình lăng trụ đều là các hình chữ nhật bằng nhau
- Chiều cao là cạnh bên
Thể tích khối lăng trụ
[content_2]Công thức tính thể tích khối lăng trụ là: V = B.h, trong đó B là diện tích đáy và h là chiều cao
Phân dạng bài tập
Dạng 1. Bài toán về khối lăng trụ đứng
[content_3]Câu 1.: Cho hình lăng trụ đứng ABC.A’B’C’ có thể tích là V. Trong các khối chóp dưới đây, khối chóp có thể tích là:
A. A.A’B’C’
B. C’.ABC
C. A’.BCC’B’
D. I.ABB’A’
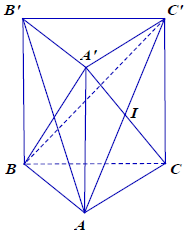
Hướng dẫn giải
Ta có: VABC.A’B’C’ = VA’.BCC’B’ + VA’.ABC.
Mà
⟹ Chọn C
Câu 2.: Cho hình hộp đứng có các cạnh AB = 3a; AD = 2a; AA’ = 2a như hình vẽ. Thể tích của khối A’.ACD’ là:
A. a3
B. 2a3
C. 3a3
D. 6a3
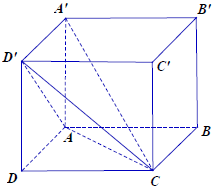
Hướng dẫn giải
Ta có:
⟹ Chọn B
Câu 3.: Cho hình lăng trụ đứng ABC.A’B’C’ có , đường thẳng B’C tạo với mặt phẳng (ABB’A’) một góc α thỏa mãn
. Thể tích khối lăng trụ ABC.A’B’C’ là:
A.
B.
C.
D.
Hướng dẫn giải
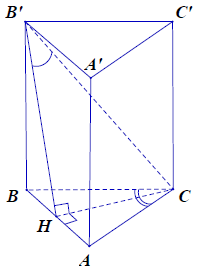
Ta có
Kẻ CH ⊥ AB ⇒ CH ⊥ (ABB’A’) nên B’H là hình chiếu vuông góc của B’C lên (ABB’A’)
⇒ (B’C, (ABB’A’)) = (B’C, B’H) = CB’H = α
Xét ∆BB’C vuông tại B có:
Do đó
Chọn đáp án A
Câu 4.: Khối lập phương có độ dài đường chéo bằng d thì thể tích của khối lập phương là:
A. V = d3
B. V =
C. V = 3d3
D. V =
Hướng dẫn giải
Khối lập phương có cạnh là .
Do đó khối lập phương có thể tích là .
⟹ Chọn D
Câu 5.: Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác cân, AB = AC = a, BAC = 120°. Mặt phẳng (AB’C’) tạo với mặt đáy góc 60°. Tính thể tích lăng trụ ABC.A’B’C’.
A.
B.
C.
D.
Hướng dẫn giải
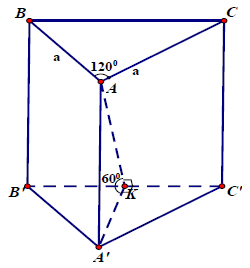
Xác định góc giữa (AB’C’) và mặt đáy là AKA’ ⇒ AKA’ = 60°.
Tính
⟹ Chọn B
Câu 6.: Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân tại A, BC = a, và
. Tính thể tích hình lăng trụ ABC.A’B’C’.
A.
B.
C.
D.
Hướng dẫn giải
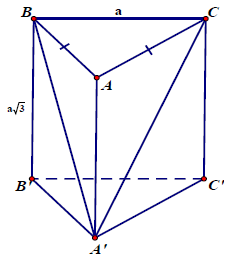
Đặt AB = x thì A’B2 = A’C2 = x2 + 2a2
Áp dụng định lí hàm số cosin trong ∆A’BC, ta có:
Suy ra ∆ABC đều nên
Vậy thể tích hình lăng trụ ABC.A’B’C’ là
⟹ Chọn A
Câu 7.: Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, BAD = 45°, . Thể tích của khối lăng trụ ABCD.A’B’C’D’ là
A.
B.
C.
D.
Hướng dẫn giải
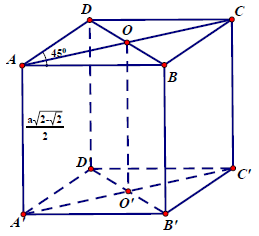
Ta có: SABCD = 2SABD
Do ABCD.A’B’C’D’ là hình lăng trụ đứng nên
→ Vậy chọn đáp án D.
Câu 8.: Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B. Biết AB = 3cm, cm. Thể tích khối lăng trụ đã cho là
A. 27 (cm3)
B. (cm3)
C. (cm3)
D. (cm3)
Hướng dẫn giải
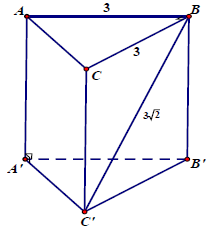
Diện tích đáy của khối lăng trụ:
Chiều cao của khối lăng trụ:
Thể tích của khối lăng trụ đã cho:
⟹ Chọn C
Câu 9.: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi M và N theo thứ tự là trung điểm của A’B’ và B’C’. Tính tỉ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’
A.
B.
C.
D.
Hướng dẫn giải
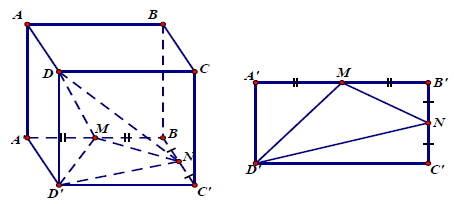
Thể tích khối chóp D’.DMN bằng thể tích khối chóp D.D’MN
Ta có
Thể tích khối chóp D’.DMN là:
Thể tích của khối hộp chữ nhật ABCD.A’B’C’D’ là V = abc
. Vậy chọn đáp án C.
Câu 10. Cho hình lăng trụ đứng ABC.A’B’C’, có đáy ABC là tam giác cân tại A, AB = AC = a, BAC = α. Gọi M là trung điểm của AA’, tam giác C’MB vuông. Thể tích của khối lăng trụ ABC.A’B’C’ là
A.
B.
C.
D.
Hướng dẫn giải
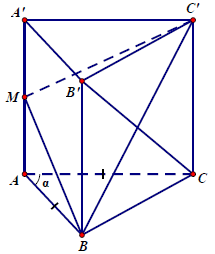
Diện tích đáy của khối lăng trụ là:
Đặt A’A = x. Ta có:
Trong đó: . Tam giác C’MB vuông tại M, ta có:
Thể tích của khối lăng trụ là
⟹ Chọn A
Dạng 2. Bài toán về khối lăng trụ đều
[content_4]Câu 1.: Cho khối lăng trụ tam giác đều ABC.A’B’C’. Mặt phẳng (A’BC) chia khối lăng trụ thành hai phần. Tỉ số thể tích của hai phần đó bằng:
A.
B.
C.
D.
Hướng dẫn giải
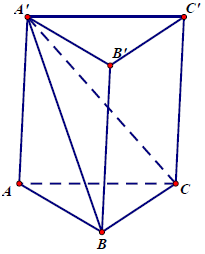
Mặt phẳng (A’BC) chia khối lăng trụ ABC.A’B’C’ thành hai phần là A’.ABC và A’B’C’BC
Ta có:
Suy ra tỉ số thể tích của hai phần đó bằng .
⟹ Chọn A
Câu 2.: Cho khối lăng trụ tam giác đều ABC.A’B’C’. Gọi M là trung điểm cạnh AA’. Mặt phẳng (MBC) chia khối lăng trụ thành hai phần. Tỉ số thể tích của hai phần đó bằng:
A.
B.
C.
D.
Hướng dẫn giải
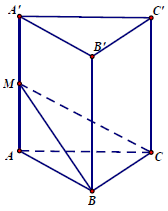
Mặt phẳng (MBC) chia khối lăng trụ thành hai phần M.ABC và MA’B’C’BC.
Ta có:
Suy ra:
Tỉ số thể tích của hai phần đó bằng
⟹ Chọn B
Câu 3.: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và chiều cao bằng . Thể tích khối tứ diện ACA’B’ là
A.
B.
C.
D.
Hướng dẫn giải
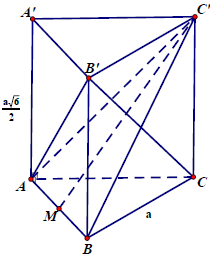
Ta có CM ⊥ AB (vì tam giác ABC là tam giác đều)
⇒ CM ⊥ (AA’B’B) hay CM ⊥ (AA’B’)
⇒ CM = d(C, (AA’B’))
⟹ Chọn A
Câu 4.: Cho khối lăng trụ tứ giác đều ABCD.A’B’C’D’ có khoảng cách giữa hai đường thẳng AB và A’D bằng 2 và độ dài đường chéo của mặt bên bằng 5. Vẽ AK ⊥ A’D (K ∈ A’D). Lúc đó độ dài AK là
A. 1
B. 2
C. 3
D. 4
Hướng dẫn giải
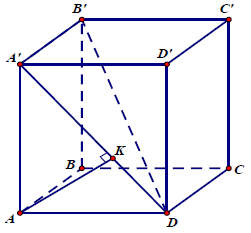
AB // A’B’ ⇒ AB // (A’B’D)
⇒ d(A, (A’B’D)) = d(AB, A’D)
Ta có A’B’ ⊥ (AA’D’D)
⇒ A’B’ ⊥ AK
Ta còn có A’D ⊥ AK (giả thiết)
⇒ AK ⊥ (A’B’D)
Vậy AK = d(A, (A’B’D)) = d(AB, A’D) = 2.
⟹ Chọn B
Câu 5.: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a. Mặt phẳng (ABC’) hợp với mặt phẳng (BCC’B’) một góc α. Diện tích xung quanh của khối lăng trụ là
A.
B.
C.
D.
Hướng dẫn giải
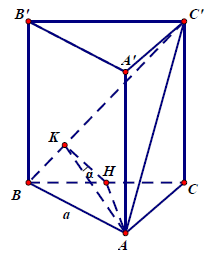
Gọi H, K lần lượt là hình chiếu của A lên BC, BC’.
Ta có AH ⊥ (BCC’B’) ⇒ AH ⊥ BC’
Do đó (AKH) ⊥ (BC’) ⇒ α = AKH
Tam giác AKH vuông tại H và nên
Đặt AA’ = x. Xét tam giác C’AB có:
Nên từ ta tính được
Diện tích xung quanh của khối lăng trụ .
⟹ Chọn C
Câu 6.: Cho lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh bên bằng 4a và đường chéo 5a. Tính thể tích khối lăng trụ này
A. 8a3
B. 9a3
C. 18a3
D. 21a3
Hướng dẫn giải
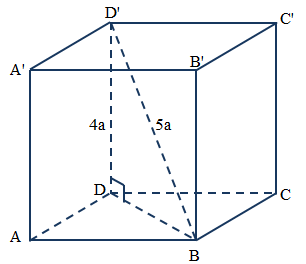
ABCD.A’ B’C’D’ là lăng trụ đứng nên BD2 = BD’2 − DD’2 = 9a2 ⇒ BD = 3a
ABCD là hình vuông
Suy ra
Vậy V = B.h = SABCD . AA’ = 18a3
⟹ Chọn C
Câu 7.: Cho lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy a và mặt phẳng (BDC’) hợp với đáy (ABCD) một góc 60°. Tính thể tích khối hộp chữ nhật.
A.
B.
C.
D.
Hướng dẫn giải
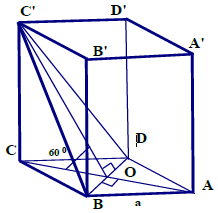
Gọi O là tâm của ABCD. Ta có ABCD là hình vuông nên OC ⊥ BD
CC’ ⊥(ABCD) nên OC’ ⊥ BD (đl 3 ⊥).
Vậy góc [(BDC’); (ABCD)] = COC’ = 60°
Ta có V = B.h = SABCD.CC’
ABCD là hình vuông nên SABCD = a2
∆OCC’ vuông nên . Vậy
⟹ Chọn A
Câu 8.: Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có chiều cao bằng h và góc của hai đường chéo của hai mặt bên kề nhau phát xuất từ một đỉnh là α. Tính thể tích của lăng trụ theo h và α là
A.
B.
C.
D.
Hướng dẫn giải
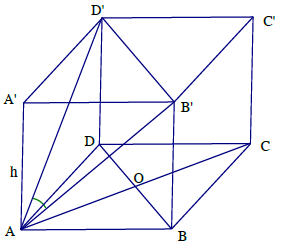
Gọi x là cạnh của đáy, ta có
∆AB’D’:
Vậy
⟹ Chọn C
Câu 9.: Tính thể tích lăng trụ đều ABC.A’B’C’ biết (ABC’) hợp với đáy góc 60° và diện tích tam giác ABC bằng
A.
B.
C.
D.
Hướng dẫn giải
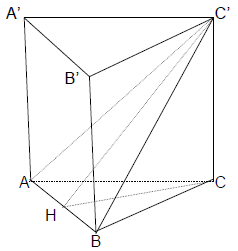
Gọi H là trung điểm AB
⇒
⇒ ((ABC’), (ABC)) = (CH, C’H) = CHC’ = 60°
Xét ∆HCC’ vuông tại C:
Từ (1), (2) ⇒
(đvtt)
⟹ Chọn C
Dạng 3. Bài toán về khối lăng trụ xiêng
[content_5]Câu 1.: Gọi V là thể tích khối hộp ABCD.A’B’C’D’ và V1 là thể tích của khối tứ diện có cùng đáy và chiều cao với khối hộp. Hệ thức nào sau đây là đúng:
A. V = 6V1
B. V = 5V1
C. V = 4V1
D. V = 3V1
Hướng dẫn giải
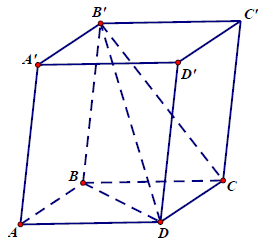
Ta có:
Hay V = 6V1.
⟹ Chọn A
Câu 2.: Cho khối lăng trụ tam giác ABC.A’B’C’ có thể tích V. Trên đáy A’B’C’ lấy điểm M bất kỳ. Thể tích khối chóp M.ABC tính theo V bằng
A.
B.
C.
D.
Hướng dẫn giải
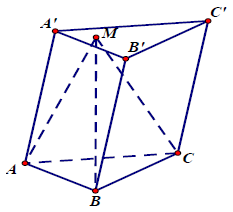
Ta có:
Vậy chọn đáp án C
Câu 3.: Cho hình lăng trụ ABC.A’B’C’, đáy ABC có , BC = 3a, ACB = 30°. Cạnh bên hợp với mặt phẳng đáy góc 60° và mặt phẳng (A’BC) vuông góc với mặt phẳng (ABC). Điểm H trên cạnh BC sao cho HC = 3BH và mặt phẳng (A’AH) vuông góc với mặt phẳng (ABC). Thể tích khối lăng trụ ABC.A’B’C’ là
A.
B.
C.
D.
Hướng dẫn giải
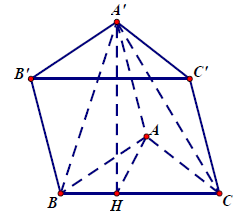
Suy ra A’AH = 60°
AH2 = AC2 + HC2 − 2AC.HC.cos30° = a2 ⇒ AH = a
⟹ Chọn B
Câu 4.: Cho hình lăng trụ ABC.A’B’C’, ∆ABC đều có cạnh bằng a, AA’ = a và đỉnh A’ cách đều A, B, C. Gọi M là trung điểm của cạnh BC. Thể tích khối lăng trụ ABC.A’B’C’ là
A.
B.
C.
D.
Hướng dẫn giải
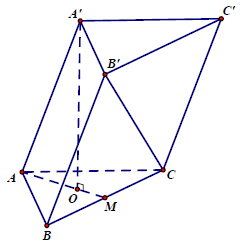
Gọi O là tâm tam giác đều ABC ⇒ A’O ⊥ (ABC)
Ta có
Thể tích khối lăng trụ ABC.A’B’C’:
⟹ Chọn B
Câu 5.: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB = a, ACB = 30°; M là trung điểm cạnh AC. Góc giữa cạnh bên và mặt đáy của lăng trụ bằng 60°. Hình chiếu vuông góc của đỉnh A’ lên mặt phẳng (ABC) là trung điểm H của BM. Thể tích khối lăng trụ ABC.A’B’C’ là
A.
B.
C.
D.
Hướng dẫn giải
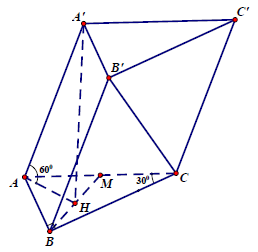
A’H ⊥ (ABC) ⇒ A’H là đường cao của hình lăng trụ.
AH là hình chiếu vuông góc của AA’ lên (ABC) ⇒ A’AH = 60°
VABC.A ‘B’C’ = A’H.SABC
AC = 2a, MA = MB = AB = a
⟹ Chọn A
Câu 6.: Cho hình lăng trụ ABC.A’B’C’ có AB = 2a, AC = a, , BAC = 120°. Hình chiếu vuông góc của C’ lên mặt phẳng (ABC) là trung điểm của cạnh BC. Tính thể tích khối lăng trụ ABC.A’B’C’ theo a và tính số đo góc giữa hai mặt phẳng (ABC) và (ACC’A’).
A.
B.
C.
D.
Hướng dẫn giải
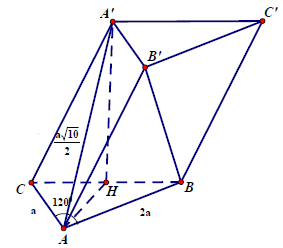
Gọi H là trung điểm BC. Từ giả thiết suy ra C’H ⊥ (ABC). Trong ∆ABC ta có:
Suy ra thể tích lăng trụ
⟹ Chọn B
Câu 7.: Cho hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh bằng a. Hình chiếu vuông góc của điểm A’ trên mặt phẳng ABCD là trung điểm I của cạnh AB. Biết A’C tạo với mặt phẳng đáy một góc α với . Thể tích khối chóp A’.ICD là
A.
B.
C.
D.
Hướng dẫn giải
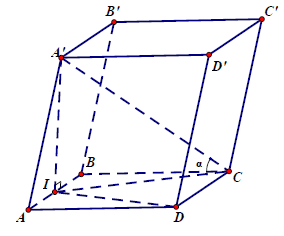
Theo bài ra ta có IC là hình chiếu vuông góc của A’C trên mặt phẳng (ABCD). Suy ra (A’C, (ABCD)) = (A’C, CI) = A’CI = α
Xét tam giác vuông A’IC:
Thể tích khối chóp A’.ICD là:
(đvtt)
⟹ Chọn A
Câu 8.: Cho khối lăng trụ tam giác ABC.A’B’C’ mà mặt bên ABB’A’ có diện tích bằng 4. Khoảng cách giữa cạnh CC’ và mặt (ABB’A’) bằng 7. Thể tích khối lăng trụ là
A. 10
B. 12
C. 14
D. 16
Hướng dẫn giải
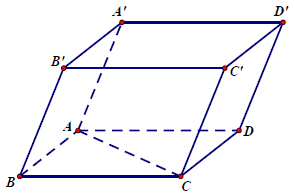
Dựng khối hộp ABCD.A’B’C’D’ ta có:
Xem khối hộp ABCD.A’B’C’D’ là khối lăng trụ có hai đáy là ABB’A’ và DCC’D’.
Vậy VABCD.A’B’C’D’ = SABB’A’.h
Trong đó: h = d((CDD’C’), (ABB’A’)) = d(CC’, (ABB’A’)) = 7
và SABB’A’ = 4 ⇒ .
⟹ Chọn C
Câu 9.: Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, và . Thể tích khối lăng trụ ABC.A’B’C’ theo a là
A.
B.
C.
D.
Hướng dẫn giải
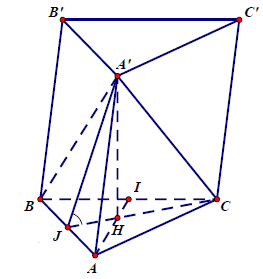
Gọi H là hình chiếu của A trên (ABC)
Vì A’A = A’B = A’C nên HA = HB = HC, suy ra H là tâm của tam giác đều ABC. Gọi I, J lần lượt là trung điểm của BC, AB.
Thể tích khối lăng trụ ABC.A’B’C’ là:
⟹ Chọn B
Câu 10. Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác cân AB = AC = a, BAC = 120° và AB’ vuông góc với đáy (A’B’C’). Mặt phẳng (AA’C’) tạo với mặt phẳng (ABC) một góc 30°. Thể tích khối lăng trụ ABC.A’B’C’ là
A.
B.
C.
D.
Hướng dẫn giải
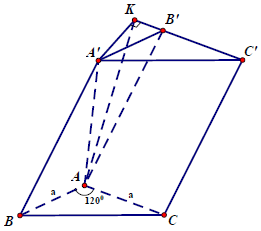
Ta có BC2 = AB2 + AC2 − 2AB.AC.cos A = 3a2
⇒
Gọi K là hình chiếu của B’ lên A’C’, suy ra A’C’ ⊥ (AB’K)
Do đó:
AKB’ = ((A’ B’C’), (AA’C’)) = 30°
Trong tam giác A’KB’ có KA’B’= 60°, AB’ = a nên .
Suy ra
Thể tích khối lăng trụ:
⟹ Chọn C