Trong chương trình toán lớp 12, khối đa diện chiếm một phần lớn kiến thức. Ở bài viết này, VerbaLearn sẽ giúp bạn hiểu thêm về khái niệm một số khối đa diện thường gặp, công thức tính thể thích từng khối đa diện và một số dạng bài tập vận dụng từ cơ bản đến nâng cao.
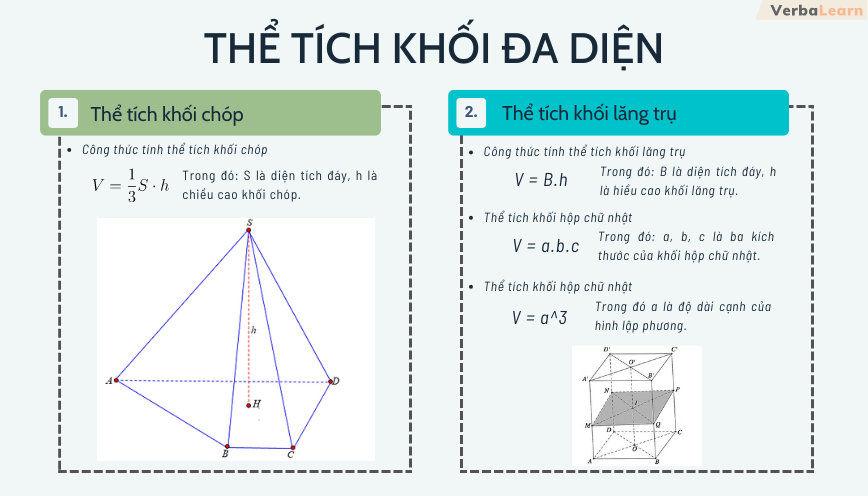
Khái niệm các khối đa diện
[content_1]Hình lăng trụ
– Hình lăng trụ là hình có hai đáy là hai đa giác bằng nhau nằm trên hai mặt phẳng song song với nhau và các mặt bên đều là các hình bình hành.
Hình lăng trụ đứng
Định nghĩa: Hình lăng trụ đứng là hình lăng trụ có cạnh bên vuông góc với mặt đáy.
Tính chất: Các mặt bên của hình lăng trụ đứng là các hình chữ nhật và vuông góc với mặt đáy.
Hình lăng trụ đều
Định nghĩa: Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều.
Tính chất: Các mặt bên của hình lăng trụ đều là các hình chữ nhật bằng nhau và vuông góc với mặt đáy.
Hình hộp
– Hình hộp là hình lăng trụ có đáy là hình bình hành.
Hình hộp đứng
Định nghĩa: Hình hộp đứng là hình hộp có cạnh bên vuông góc với mặt đáy.
Tính chất: Hình hộp đứng có 2 đáy là hình bình hành, 4 mặt xung quanh là 4 hình chữ nhật.
Hình hộp chữ nhật
Định nghĩa: Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật. Tính chất. Hình hộp chữ nhật có 6 mặt là 6 hình chữ nhật.
Hình lập phương
Định nghĩa: Hình lập phương là hình hộp chữ nhật 2 đáy và 4 mặt bên đều là hình vuông Tính chất. Hình lập phương có 6 mặt đều là hình vuông.
Hình chóp
– Hình chóp là hình có đáy là một đa giác và các mặt bên là các tam giác có chung một đỉnh.
Thể tích khối đa diện
[content_2]Thể tích khối chóp
Trong đó: S là diện tích đáy, h là chiều cao khối chóp.
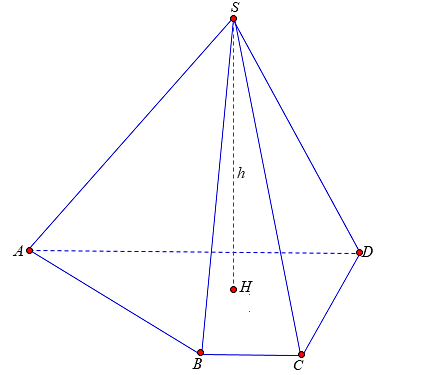
Chú ý: Nếu khối chóp cần tính thể tích chưa biết chiều cao thì ta phải xác định được vị trí chân đường cao trên đáy.
– Chóp có cạnh bên vuông góc chiều cao chính là cạnh bên.
– Chóp có hai mặt bên vuông góc đáy đường cao là giao tuyến của hai mặt bên vuông góc đáy.
– Chóp có mặt bên vuông góc đáy chiều cao của mặt bên vuông góc đáy.
– Chóp đều chiều cao hạ từ đỉnh đến tâm đa giác đáy.
– Chóp có hình chiếu vuông góc của một đỉnh lên xuống mặt đáy thuộc cạnh mặt đáy đường cao là từ đỉnh tới hình chiếu.
Thể tích khối lăng trụ
Công thức tính thể tích khối lăng trụ là: V = B.h
Trong đó: B là diện tích đáy, h là hiều cao khối lăng trụ.
Thể tích khối hộp chữ nhật
– Thể tích khối hộp chữ nhật: V = a.b.c
Trong đó: a, b, c là ba kích thước của khối hộp chữ nhật.
Thể tích khối lập phương
– Thể tích khối lập phương: V = a3
Trong đó a là độ dài cạnh của hình lập phương.
Tỉ số thể tích
Cho khối chóp S.ABC và A’, B’, C’ là các điểm tùy ý lần lượt thuộc SA, SB, SC, ta có:
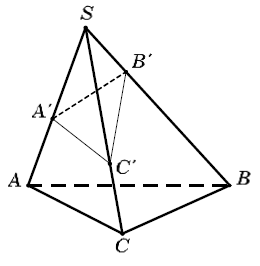
Công thức tỉ số thể tích: (hay gọi là công thức Simson)
Phương pháp này được áp dụng khi khối chóp không xác đinh được chiều cao một cách dễ dàng hoặc khối chóp cần tính là một phần nhỏ trong khối chóp lớn và cần chú ý đến một số điều kiện sau:
- Hai khối chóp phải cùng chung đỉnh.
- Đáy hai khối chóp phải là tam giác.
- Các điểm tương ứng nằm trên các cạnh tương ứng.
Định lý Menelaus
Cho ba điểm thẳng hàng với DEF là một đường thẳng cắt ba đường thẳng BC, CA, AB lần lượt tại D, E, F.
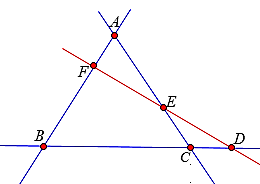
Công thức tính nhanh thể thích khối đa diện
[content_3]Công thức 1: Thể tích tứ diện đều cạnh a:
Công thức 2: Với tứ diện ABCD có AB = a, AC = b, AD = c đôi một vuông góc thì thể tích của nó là
Công thức 3: Với tứ diện ABCD có AB = CD = a, BC = AD = b, AC = BD = c thì thể tích của nó là
Công thức 4: Cho khối chóp S.ABC có SA = a, SB = b, SC = c, BSC = α, CSA = β, ASB = γ thì thể tích của nó là
Công thức 5: Mặt phẳng cắt các cạnh của khối lăng trụ tam giác ABC.A’B’C’ lần lượt tại M, N, P sao cho thì ta có
Công thức 6: Mặt phẳng cắt các cạnh của khối hộp ABCD.A’B’C’D’ lần lượt tại M, N, P, Q sao cho thì ta có
và x + z = y + t
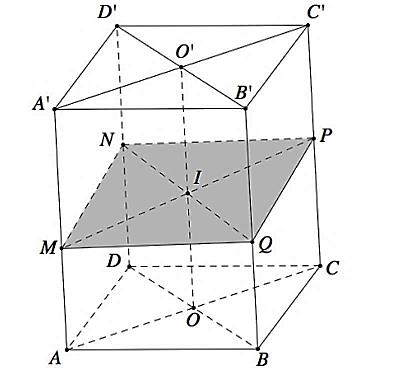
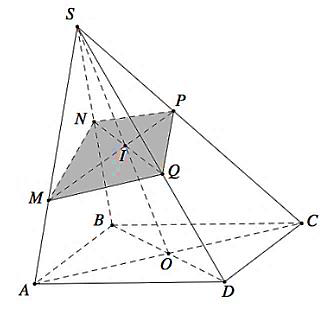
Công thức 7: Mặt phẳng cắt các cạnh của khối chóp tứ giác S.ABCD có đáy là hình bình hành lần lượt tại M, N, P, Q sao cho thì ta có công thức sau đây
và
.
Bài tập vận dụng
[content_4]Câu 1. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, có BC = a. Mặt phẳng (SAC) vuông góc với mặt đáy, các mặt bên còn lại đều tạo với mặt đáy một góc 45°. Tính thể tích khối chóp S.ABC.
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn A
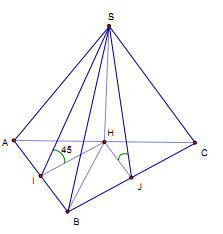
Kẻ SH ⊥ BC vì (SAC) ⊥ (ABC) nên SH ⊥ (ABC).
Gọi I, J là hình chiếu của H trên AB và BC.
⇒ SJ ⊥ AB, SJ ⊥ BC.
Theo giả thiết SIH = SJH = 45°.
Ta có: ∆SHI = ∆SHJ ⇒ HI ⊥ HJ nên BH là đường phân giác của ∆ABC từ đó suy ra H là trung điểm của AC.
Câu 2. Cho hình chóp S.ABCD với đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên . Tam giác SAD là tam giác đều cạnh 2a và nằm trong mặt phẳng vuông góc với đáy hình chóp. Gọi H là trung điểm cạnh AD, khoảng cách từ B tới mặt phẳng (SHC) bằng
. Tính thể tích V của khối chóp S.ABCD?
A.
B.
C.
D.
Hướng dẫn giải
Chọn D
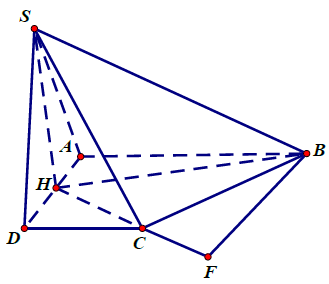
Ta có
Ta có nên
Đặt AB = x nên
Vậy
Câu 3. Cho khối chóp S.ABC có góc khối chóp S.ABC. ASB = BSC = CSA = 60° và SA = 2, SB = 3, SC = 4. Thể tích khối chóp S.ABC.
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn C
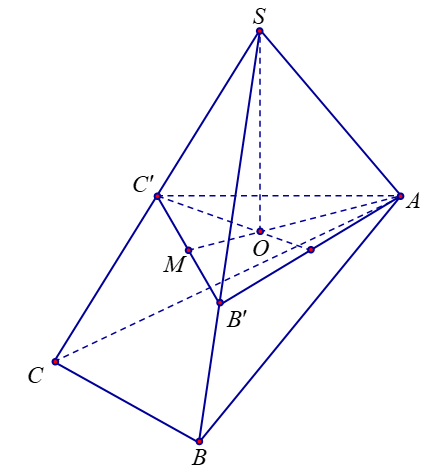
Gọi B’ trên SB sao cho và C’ trên SC sao cho
Khi đó SA = SB’ = SC’ = 2 ⇒ S.AB’C’ là khối tứ diện đều.
Ta có:
Nên và
Khi đó mà
Cách khác: Áp dụng công thức 4
Câu 4. Cho hình chóp S.ABC có AB = 5 cm, BC = 6 cm, CA = 7 cm. Hình chiếu vuông góc của S xuống mặt phẳng (ABC) nằm bên trong tam giác ABC. Các mặt phẳng (SAB), (SBC), (SCA) đều tạo với đáy một góc 60°. Gọi AD, BE, CF là các đường phân giác của tam giác ABC với D ∈ BC, E ∈ AC, F ∈ AB. Thể tích S.DEF gần với số nào sau đây?
A. 3,7 cm3
B. 3,4 cm3
C. 2,9 cm3
D. 4,1 cm3
Hướng dẫn giải
⟹ Chọn B
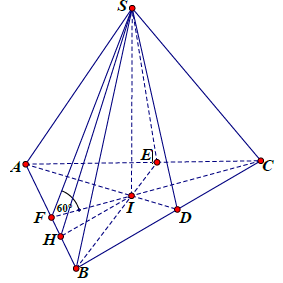
Vì các mặt phẳng (SAB), (SBC), (SCA) đều tạo với đáy một góc 60° và hình chiếu vuông góc của S xuống mặt phẳng (ABC) nằm bên trong tam giác ABC nên ta có hình chiếu của S chính là tâm I của đường tròn nội tiếp tam giác ABC.
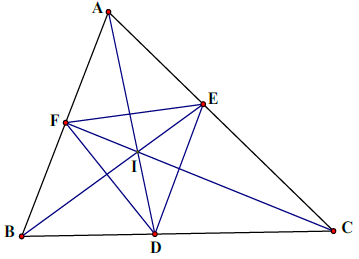
Gọi p là nửa chu vi tam giác ABC thì
Ta có: và
Suy ra chiều cao của hình chóp là:
Vì BE là phân giác của góc B nên ta có:
Tương tự:
Khi đó:
Tương tự:
Do đó với BC = a, AC = b, AB = c
Câu 5. Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh bằng a. Hình chiếu vuông góc của đỉnh S lên mặt phẳng (ABCD) là trung điểm của cạnh OC. Góc giữa mặt phẳng (SAB)
và mặt phẳng (ABCD) bằng 60°. Tính theo a thể tích V của hình chóp S.ABCD.
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn D
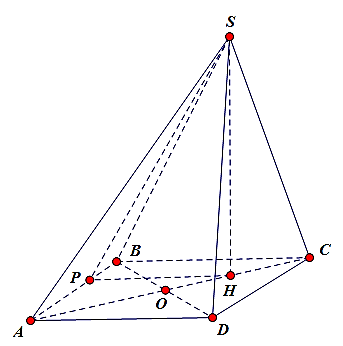
Gọi H là trung điểm của cạnh OC ⇒ SH ⊥ (ABCD).
Kẻ HP ⊥ AB (P ∈ AB)
Ta có
Do đó ((SAB); (ABCD)) = SPH = 60°.
Trên (ABCD),
Câu 6. Cho lăng trụ tam giác ABC.A’B’C’ có BB’ = a, góc giữa đường thẳng BB’ và (ABC)
bằng 60°, tam giác ABC vuông tại C và góc BAC 60°. Hình chiếu vuông góc của điểm B’ lên (ABC) trùng với trọng tâm của ∆ABC. Thể tích của khối tứ diện A’.ABC theo a bằng
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn C
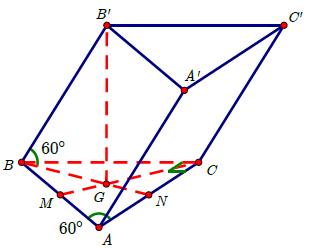
Gọi M, N là trung điểm của AB, AC và G là trọng tâm của ∆ABC.
B’G ⊥ (ABC) ⇒ (BB’, (ABC)) = B’BG = 60°.
Xét ∆B’BG vuông tại G, có B’BG = 60°
(nửa tam giác đều)
Đặt AB = 2x. Trong ∆ABC vuông tại C có BAC = 60°
⇒ tam giác ABC là nửa tam giác đều ⇒
Do G là trọng tâm ∆ABC ⇒ . Trong ∆BNC vuông tại C: BN2 = NC2 + BC2
Vậy
Câu 7. Cho khối tứ diện đều ABCD có thể tích V. Gọi M, N, P lần lượt là trọng tâm các tam giác ABC, ACD, ADB và V là thể tích khối tứ diện AMNP. Tính tỉ số
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn B
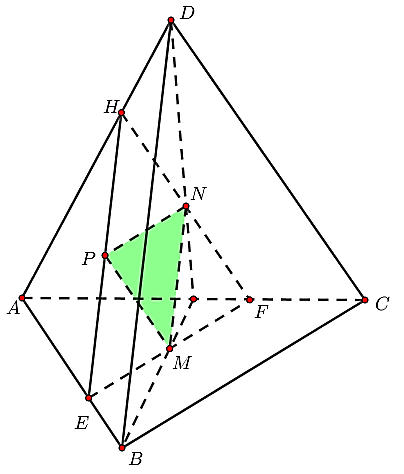
TYPS: Hai khối đa diện đồng dạng với tỷ số k thì ta có . Áp dụng vào bài toán sau đây
Ta có mặt phẳng (MNP) cắt các mặt của tứ diện theo các đoạn giao tuyến EF, FH và HE do vậy
thiết diện là tam giác EFH. Ta dễ có (MNP) // (BCD) và
Ta cũng có
Do đó
Câu 8. Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng 2020. Gọi M, N lần lượt là trung điểm của AA’; BB’ và điểm P nằm trên cạnh CC’ sao cho PC = 3PC. Thể tích của khối đa diện lồi có các đỉnh là các điểm A, B, C, M, N, P bằng
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn D
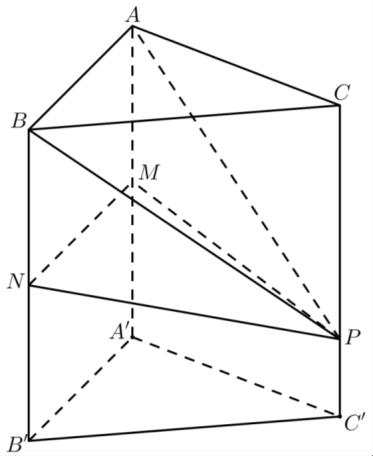
Giả sử V = VABC.A’B’C’= 2020.
Ta có
Ta lại có:
Mặt khác
Mà
Suy ra . Vậy
Cách 2: Dùng công thức giải nhanh
Ta có:
Câu 9. Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, góc giữa cạnh bên với mặt phẳng đáy bằng 60° và A cách đều 3 điểm A, B, C. Gọi M là trung điểm của AA’; N ∈ BB’ thỏa mãn NB = 4NB và P ∈ CC’ sao cho PC = 3PC. Thể tích của khối đa diện lồi có các đỉnh là các điểm A, B, C, M, N, P bằng
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn B
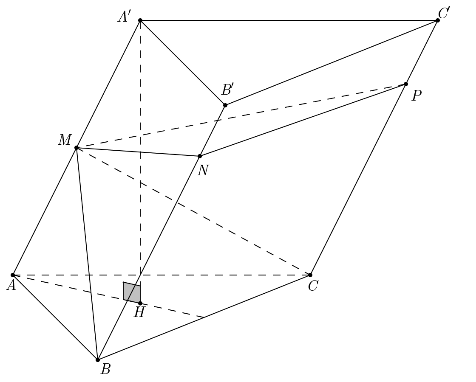
Gọi V là thể tích của khối đa diện có các đỉnh là các điểm A, B, C, M, N, P.
V1 là thể tích của khối lăng trụ ABC.A’B’C’. Gọi H là trọng tâm của tam giác ABC. Vì điểm A cách đều các điểm A, B, C nên A’H ⊥ (ABC).
Hơn nữa: AA’ ⋂ (ABC) = A nên (AA’, (ABC)) = A’AH = 60°.
Suy ra . Do đó
Mà
Từ
Suy ra
Và (vì M là trung điểm của AA’)
Vậy thể tích cần tìm là
Cách 2: Dùng công thức giải nhanh
Ta có:
Câu 10. Cho lăng trụ ABC.A’B’C’ diện tích đáy bằng 3 và chiều cao bằng 5. Gọi M, N, P lần lượt là trung điểm của AA’, BB’, CC’. G, G’ lần lượt là trọng tâm của hai đáy ABC, A’B’C’. Thể tích của khối đa diện lồi có các đỉnh là các điểm G, G’, M, N, P bằng
A. 10
B. 3
C. 5
D. 6
Hướng dẫn giải
⟹ Chọn C
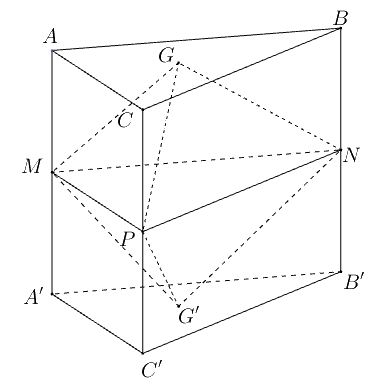
Ta có: VABC.A’B’C’ = 3.5 = 15 (đvtt).
Ta có VGG’MNP = VG.MNP + VG’.MNP
Do M, N, P lần lượt là trung điểm của AA’, BB’, CC’ nên mp (MNP) chia khối lăng trụ
ABC.A’B’C’ thành hai khối lăng trụ bằng nhau ABC.MNP và MNP.A’B’C’.
Lại có G ∈ (ABC) nên
Tương tự ta có
Do đó