Bài viết dưới đây sẽ giúp bạn tìm hiểu chi tiết lý thuyết và hơn 20 dạng bài tập phương trình mặt phẳng trong không gian. Với mỗi dạng bài đều sẽ có phương pháp giải chi tiết và bài tập vận dụng có hướng dẫn giải. Từ đó, giúp độc giả nhanh chóng hiểu cũng như ứng dụng vào các dạng bài tập tương tự.
Tổng quan lý thuyết
Tích có hướng của hai vectơ
Trong không gian Oxyz, cho hai vectơ và
khi đó tích có hướng của 2 vectơ
và
là một vectơ kí hiệu là
và có tọa độ
cùng phương
Ba vectơ đồng phẳng khi và chỉ khi
A, B, C, D tạo thành tứ diện
Diện tích hình bình hành ABCD:
Diện tích tam giác ABC:
Thể tích hình hộp:
Thể tích hình tứ diện:
Vectơ pháp tuyến của mặt phẳng
Định nghĩa: Cho mặt phẳng (α). Nếu khác
và có giá vuông góc với mặt phẳng (α) thì
được gọi là vectơ pháp tuyến của (α).
Chú ý: Nếu là vectơ pháp tuyến của một mặt phẳng thì
với k ≠ 0, cũng là vectơ pháp tuyến của mặt phẳng đó.
Khái niệm 1: Hai vectơ đều khác
và không cùng phương với nhau được gọi là cặp vectơ chỉ phương của (α) nếu giá của chúng song song hoặc nằm trên (α).
Khái niệm 2: Trong không gian Oxyz, cho hai vectơ không cùng phương và
. Khi đó vectơ
được gọi là tích có hướng (hay tích vectơ) của hai vectơ
, kí hiệu
hoặc
Phương trình tổng quát của mặt phẳng trong không gian
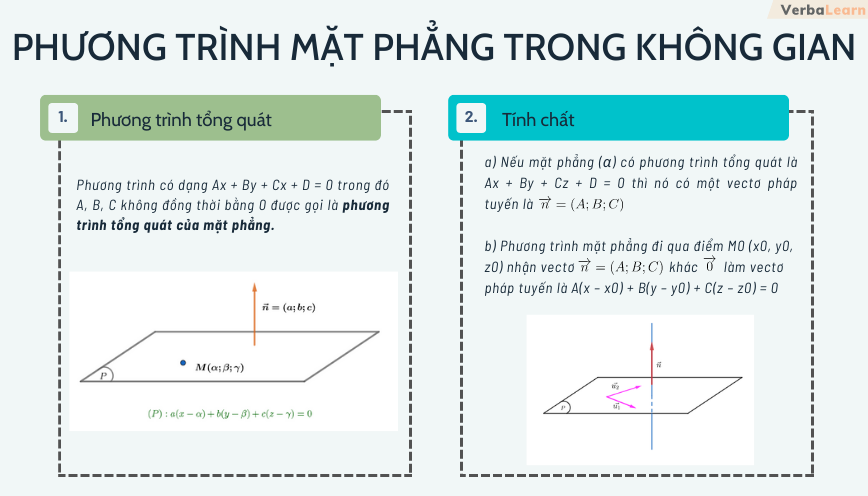
Định nghĩa: Phương trình có dạng Ax + By + Cx + D = 0 trong đó A, B, C không đồng thời bằng 0 được gọi là phương trình tổng quát của mặt phẳng.
Chú ý:
a) Nếu mặt phẳng (α) có phương trình tổng quát là Ax + By + Cz + D = 0 thì nó có một vectơ pháp tuyến là
b) Phương trình mặt phẳng đi qua điểm M0 (x0, y0, z0) nhận vectơ khác
làm vectơ pháp tuyến là A(x – x0) + B(y – y0) + C(z – z0) = 0
Phân dạng bài tập
Dạng 1. Sự đồng phẳng của ba vectơ, bốn điểm đồng phẳng
Phương pháp giải
Trong không gian Oxyz, cho ba vectơ đều khác vectơ
– Ba vectơ đồng phẳng khi và chỉ khi
– Ngược lại, ba vectơ không đồng phẳng khi và chỉ khi
Trong không gian Oxyz, cho bốn điểm A, B, C, D phân biệt
– Bốn điểm A, B, C, D đồng phẳng khi và chỉ khi các vectơ đồng phẳng hay
= 0
– Ngược lại, bốn điểm A, B, C, D không đồng phẳng khi và chỉ khi các vectơ không đồng phẳng hay
Bài tập vận dụng
Câu 1. Trong hệ tọa độ Oxyz, xét sự đồng phẳng của các vectơ sau:
a)
b)
Hướng dẫn giải
a) Ta có:
Vì nên ba vectơ
không đồng phẳng
b) Ta có:
Vì nên ba vectơ
đồng phẳng
Câu 2. Trong không gian Oxyz, xét sự đồng phẳng của các điểm sau đây:
a) A(−4; 4; 0), B(2; 0; 4), C(1; 2; −1) và D(7; −2; 3)
b) M(6; −2; 3), N(0; 1; 6), P(2; 0; −1) và Q(4; 1; 0)
Hướng dẫn giải
a) Ta có:
Khi đó
Vì nên các vectơ
đồng phẳng hay bốn điểm A, B, C, D đồng phẳng.
b) Ta có:
Khi đó
Vì nên các vectơ
không đồng phẳng hay bốn điểm A, B, C, D không đồng phẳng.
Câu 3. Trong không gian với hệ trục tọa độ , cho các điểm A(1; −4; 5); B(2; 1; 0) và hai vectơ
. Chứng minh rằng ABCD là một tứ diện.
Hướng dẫn giải
Ta có: A(1; −4; 5), B(2; 1; 0), C(−2; −1; 1) và D(−3 ; 0 ; −2)
Lại có
Vì nên A, B, C, D không đồng phẳng hay ABCD là một tứ diện
Câu 4. Trong hệ tọa độ Oxyz, cho các vectơ . Tìm giá trị của m để ba vectơ
đồng phẳng
Hướng dẫn giải
Ta có:
Ba vectơ đồng phẳng khi:
(m – 2) (2m + 1) + 2(−m2 – m + 2) = 0
⇔ −5m + 2 = 0 ⇔
Vậy là giá trị thỏa mãn yêu cầu bài toán
Câu 5. Xét sự đồng phẳng của ba vectơ với
Hướng dẫn giải
Ta có:
Do đó không đồng phẳng
Câu 6. Tìm m để các vectơ đồng phẳng
Hướng dẫn giải
Ta có
đồng phẳng khi
Câu 7. Xét sự đồng phẳng của các điểm A = (0; 2; 5); B = (−1; −3; 3); C = (2; −5; 1); D = (8; 0; 2)
Hướng dẫn giải
Ta có:
Vậy A, B, C, D không đồng phẳng.
Câu 8. Tìm m để các A = (−2; 2; 1); B = (3; 0; 2); C = (2; −4; 1); D = (7; m + 3; 2) đồng phẳng
Hướng dẫn giải
Ta có
Vậy A, B, C, D đồng phẳng khi và chỉ khi m = –18
Câu 9. Cho các điểm A = (2; 5; −1); B = (5; 0; 1); C = (1; −4; 0); D = (2; 3; −2). Chứng minh rằng AB và CD chéo nhau.
Hướng dẫn giải
Ta có
Vậy A, B, C, D không đồng phẳng. Do đó AB và CD chéo nhau.
Dạng 2. Diện tích của tam giác
Phương pháp giải
Sử dụng công thức
Bài tập vận dụng
Câu 1. Trong không gian cho
và A’(4; 1; −7)
a) Tính diện tích tam giác ABC
b) Tính diện tích tam giác A’BC
Hướng dẫn giải
Từ đề bài ta có A(2; 1; −3), B(4; 3; −2) ; C(6; −4; −1)
a) Ta có
Vậy diện tích tam giác ABC là
b) Ta có
Vậy diện tích tam giác A’BC là
Dạng 3. Thể tích khối chóp
Phương pháp giải
Áp dụng công thức tính thể tích tứ diện ABCD là
Bài tập vận dụng
Câu 1. Trong không gian Oxyz cho A(3; −2; 1); B(−1; 0; 2); C(3; 4; −5); D(0; 0; 1). Tính thể tích khối tứ diện ABCD.
Hướng dẫn giải
Ta có
Vậy
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Các đỉnh của khối chóp có tọa độ là A(2; 1; –3) ; B = (4; 3; −2); C(6; −4; −1); S(2; 1; −5). Tính thể tích khối chóp S.ABCD.
Hướng dẫn giải
Ta có . Mà:
Vậy
Dạng 4. Thể tích khối hộp
Phương pháp giải
Áp dụng công thức sau tính thể tích hình hộp ABCD. A’B’C’D’ là
Bài tập vận dụng
Đề bài: Trong không gian Oxyz cho các điểm B(1; 3; 1) ; C(0; 1; −1) ; D(−2; 0; 1) ; A’(2; 1; 1). Tính thể tích khối hộp ABCD. A’B’C’D’.
Hướng dẫn giải
Gọi thể tích khối hộp ABCD. A’B’C’D’ là V
Vậy
Vì ABCD là hình bình hành nên . Mà
Vậy
Dạng 5. Lập phương trình mặt phẳng đi qua một điểm và có vectơ pháp tuyến cho trước
Phương pháp giải
Cho mặt phẳng (α) đi qua điểm M(x0; y0; z0) và có vectơ pháp tuyến là
Khi đó (α): A(x – x0) + B(y – y0) + C(z – z0) = 0
Bài tập vận dụng
Câu 1. Viết phương trình mặt phẳng (P) đi qua điểm M(3; 1; 1) và có vectơ pháp tuyến .
Hướng dẫn giải
Ta có phương trình mặt phẳng (P) là:
−1.(x −3) + 1.(y – 1) + 2.(z – 1) = 0 ⇔ −x + y + 2z = 0 ⇔ x – y − 2z = 0
Dạng 6. Lập phương trình mặt phẳng trung trực của đoạn thẳng
Phương pháp giải
Mặt phẳng trung trực của đoạn thẳng AB đi qua trung điểm của AB và có vectơ pháp tuyến
Bài tập vận dụng
Câu 1. Viết phương trình mặt phẳng trung trực của đoạn thẳng AB với A(2; 1; 1) và B(2; −1; −1)
Hướng dẫn giải
Gọi I là trung điểm của AB, khi đó
Mặt khác ta có
Vậy mặt phẳng trung trực đi qua điểm I(2; 0; 0) và có vectơ pháp tuyến nên có phương trình là
0.(x − 2) – 2.(y – 0) – 2.(z − 0) = 0 ⇔ y + z = 0
Dạng 7. Lập phương trình mặt phẳng đi qua một điểm và có cặp vectơ chỉ phương cho trước
Phương pháp giải
Mặt phẳng có một vectơ pháp tuyến là
Bài tập vận dụng
Đề bài: Viết phương trình mặt phẳng (α) đi qua điểm M(1; 2; −3) và có cặp vectơ chỉ phương
Hướng dẫn giải
Ta có vectơ pháp tuyến của (α) là
Mặt phẳng (α) đi qua điểm M(1; 2; −3) và có vectơ pháp tuyến nên có phương trình là
−5.(x − 1) + 8.(y – 2) + 1.(z + 3) = 0 ⇔ 5x – 8y – z + 8 = 0
Dạng 8. Lập phương trình mặt phẳng đi qua một điểm và song song mặt phẳng cho trước
Phương pháp giải
Cho điểm M(x0; y0; z0) và mặt phẳng (β): Ax + By + Cz + D = 0
Gọi (α) là mặt phẳng đi qua M và song song với (β)
Khi đó vectơ pháp tuyến của (α) là
Bài tập vận dụng
Đề bài: Viết phương trình mặt phẳng (α) đi qua điểm M(1; −2; 1) và song song với mặt phẳng (β): 2x – y + 3 = 0
Hướng dẫn giải
Ta có:
Vậy phương trình mặt phẳng (α) là
2.(x – 1) – 1.(y + 2) + 0.(z – 1) = 0 ⇔ 2x – y – 4 = 0
Dạng 9. Lập phương trình mặt phẳng đi qua ba điểm phân biệt không thẳng hàng
Phương pháp giải
Cho ba điểm A, B, C phân biệt không thẳng hàng
Khi đó mặt phẳng (ABC) có một vectơ pháp tuyến là
Bài tập vận dụng
Đề bài: Viết phương trình mặt phẳng (ABC) có A(1; −2; 4), B(3; 2; −1) và C(−2; 1; −3)
Hướng dẫn giải
Ta có
Do đó . Vậy phương trình mặt phẳng (ABC) là
−13.(x – 1) + 29.(y + 2) + 18.(z – 4) = 0 ⇔ 13x – 29y – 18z + 1 = 0
Dạng 10. Lập phương trình mặt phẳng di qua một điểm và vuông góc với đường thẳng đi qua hai điểm cho trước
Phương pháp giải
Cho điểm M và đường thẳng d đi qua hai điểm phân biệt A, B
Khi đó mặt phẳng (α) đi qua điểm M và vuông góc với đường thẳng d có
Bài tập vận dụng
Đề bài: Viết phương trình mặt phẳng (α) đi qua điểm M(1; −2; 4) và vuông góc với đường thẳng đi qua hai điểm A(3;2; −1) ; B(−2; 1; −3).
Hướng dẫn giải
Ta có
Vậy phương trình mặt phẳng (α) là
−5.(x – 1) – 1.(y + 2) – 2.(z – 4) = 0 ⇔ 5x + y + 2z – 11 = 0
Dạng 11. Lập phương trình mặt phẳng đi qua một điểm và vuông góc với hai mặt phẳng cắt nhau cho trước
Phương pháp giải
Cho điểm M và hai mặt phẳng cắt nhau (β) và (γ).
Khi đó mặt phẳng (α) đi qua điểm M, vuông góc với mặt phẳng (β) và (γ) có
Bài tập vận dụng
Đề bài: Viết phương trình mặt phẳng (α) đi qua điểm M(1; 2; –1) và vuông góc với hai mặt phẳng (β): x + y – 2z + 1 = 0; (γ): 2x – y + z = 0.
Hướng dẫn giải
Ta có
Do đó
Vậy phương trình mặt phẳng (α) là
–1.(x – 1) – 5.(y – 2) – 3.(z + 1) = 0 ⇔ x + 5y + 3z – 8 = 0
Dạng 12. Lập phương trình mặt phẳng đi qua hai điểm và vuông góc với một mặt phẳng cắt nhau cho trước
Phương pháp giải
Cho hai điểm A, B và mặt phẳng (β).
Khi đó mặt phẳng (α) đi qua hai điểm A, B và vuông góc với mặt phẳng (β) có
Bài tập vận dụng
Đề bài: Viết phương trình mặt phẳng (α) đi qua hai điểm A(3; 1; –1); B(2; –1; 4) và vuông góc với mặt phẳng (β): 2x – y + 3z – 1 = 0.
Hướng dẫn giải:
Ta có
Do đó
Vậy phương trình mặt phẳng (α) là
–1.(x – 3) + 13.(y – 1) + 5.(z + 1) = 0 ⇔ x – 13y – 5z + 5 = 0
Dạng 13. Lập phương trình mặt phẳng tiếp xúc với mặt cầu tại điểm cho trước
Phương pháp giải
Cho mặt cầu (S) có tâm I
Khi đó mặt phẳng (α) tiếp xúc với mặt cầu (S) tại điểm H có
Bài tập vận dụng
Đề bài: Viết phương trình mặt phẳng (α) tiếp xúc với mặt cầu (S): (x – 3)2 + (y – 1)2 + (z + 2)2 = 24 tại điểm M(–1; 3; 0).
Hướng dẫn giải
Ta có tâm của mặt cầu (S) là I(3; 1; –2)
Khi đó
Vậy phương trình mặt phẳng (α) là
–4.(x + 1) + 2.(y – 3) + 2.(z – 0) = 0 ⇔ 2x – y – z + 5 = 0
Dạng 14. Viết phương trình của mặt phẳng liên quan đến mặt cầu và khoảng cách
Phương pháp giải
Kiến thức cần nhớ
– Khoảng cách từ điểm đến mặt.
– Vị trí tương đối của mặt phẳng với mặt cầu.
Viết phương trình mặt phẳng liên quan đến mặt cầu
Bài tập vận dụng
Câu 1. Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng (Q): x + 2y – 2z + 1 = 0 và tiếp xúc với mặt cầu (S): x2 + y2 + z 2 + 2x – 4y – 2z – 3 = 0.
Hướng dẫn giải
Mặt cầu (S) có tâm I(–1; 2; 1) và bán kính
Do (P) song song với mặt phẳng (Q) nên phương trình của mặt phẳng (P) có dạng:
x + 2y – 2z + D = 0, D ≠ 1
Vì (P) tiếp xúc với mặt cầu (S) nên
Vậy có hai mặt phẳng thảo mãn yêu cầu bài toán: x + 2y – 2z – 10 = 0 và x + 2y – 2z + 8 = 0
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình: x2 + y2 + z 2 −2x + 6y – 4z – 2 = 0. Viết phương trình mặt phẳng (P) song song với giá của vectơ , vuông góc với mặt phẳng (α): x + 4y + z – 11 = 0 và tiếp xúc với (S).
Hướng dẫn giải
Mặt cầu (S) có tâm I(1; −3; 2) và bán kính R = 4
Vectơ pháp tuyến của mặt phẳng (α) là
Suy ra vectơ pháp tuyến của mặt phẳng (P) là
Phương trình của (P) có dạng: 2x – y + 2z + m = 0
Vì (P) tiếp xúc với (S) nên
Vậy phương trình mặt phẳng (P): 2x – y + 2z + 3 = 0 hoặc (P): 2x – y + 2z – 21 = 0
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x2 + y2 + z 2 + 2x – 4y – 4 = 0 và mặt phẳng (P): x + z – 3 = 0. Viết phương trình mặt phẳng (Q) đi qua điểm M(3; 1; –1) vuông góc với mặt phẳng (P) và tiếp xúc với mặt cầu (S).
Hướng dẫn giải
Mặt cầu (S) có tâm I(–1; 2; 0) và bán kính R = 3, mặt phẳng (P) có vectơ pháp tuyến
Phương trình mặt phẳng (Q) đi qua M có dạng:
A.(x – 3) + B.(y – 1) + C.(z + 1) = 0; A2 + B2 + C 2 ≠ 0
Mặt phẳng (Q) tiếp xúc với (S) ⇔ (*)
Mặt khác (Q) ⊥ (P) ⇔ (**)
Từ (*), (**) ⇒
Với A = 2B, chọn B = 1; A = 2; C = –2 suy ra phương trình mặt phẳng (Q): 2x + y – 2z – 9 = 0
Với 7A = – 4B, chọn B = –7; A = 4; C = –4 suy ra phương trình mặt phẳng (Q): 4x – 7y – 4z – 9 = 0
Câu hỏi tương tự:
Với (S): x2 + y2 + z 2 – 2x + 4y + 5 = 0; (P): 2x + y – 6z + 5 = 0; M(1; 1; 2)
ĐS: (Q): 2x + 2y + z – 6 = 0 hoặc (Q): 11x – 10y + 2z – 5 = 0
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x2 + y2 + z 2 – 2x + 4y – 2z – 3 = 0. Viết phương trình mặt phẳng (P) chứa trục Ox và cắt mặt cầu (S) theo một đường tròn có bán kính r = 3.
Hướng dẫn giải
Mặt cầu (S) có tâm I(1; –2; –1), bán kính R = 3
Mặt phẳng (P) chứa Ox, nên phương trình mặt phẳng (P) có dạng: ay + bz = 0
Mặt khác đường tròn thiết diện có bán kính bằng 3 cho nên (P) đi qua tâm I.
Suy ra: –2a – b = 0 ⇔ b = –2a (a ≠ 0) ⇒ (P): y – 2z = 0
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x2 + y2 + z 2 + 2x – 2y + 2z –1 = 0 và đường thẳng d là giao tuyến của hai mặt phẳng x – y – 2 = 0; 2x – z – 6 = 0. Viết phương trình mặt phẳng (P) chứa d và cắt mặt cầu (S) theo một đường tròn có bán kính r = 1.
Hướng dẫn giải
Mặt cầu (S) có tâm I(–1; 1; –1), bán kính R = 2
Phương trình mặt phẳng (P) có dạng:
ax + by + cz + d = 0, (a2 + b2 + c 2 ≠ 0)
Chọn M(2; 0; −2); N(3; 1; 0) ∈ d
Ta có
Với (1) ⇒ (P): x + y – z – 4 = 0
Với (2) ⇒ (P): 7x – 17y + 5z – 4 = 0
Câu 6. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x2 + y2 + z 2 – 2x + 4y – 6z – 11 = 0 và mặt phẳng (α) có phương trình 2x + 2y – z + 17 = 0. Viết phương trình mặt phẳng (β) song song với (α) và cắt mặt cầu (S) theo giao tuyến là đường tròn có chu vi bằng 2p = 6π.
Hướng dẫn giải
Do (α) // (β) nên mặt phẳng (β) có phương trình 2x + 2y – z + D = 0 (với D ≠ 17)
Mặt cầu (S) có tâm I(1; – 2; 3), bán kính R = 5
Đường tròn giao tuyến có chu vi 6π nên có bán kính r = 3.
Khoảng cách từ I tới (β) là
Do đó
Vậy (β) có phương trình: 2x + 2y – z – 7 = 0
Câu hỏi tương tự:
Mặt cầu (S): x2 + y2 + z 2 + 2x + 4y – 6z – 11 = 0 và (α): 2x + y – 2z + 19 = 0 ; p = 8π
ĐS: (β): 2x + y – 2z + 1 = 0
Dạng 15. Viết phương trình mặt phẳng liên quan đến khoảng cách
Câu 1. Trong hệ trục tọa độ Oxyz, cho các điểm A(1; 0; 0), B(0; b; 0), C(0; 0; c) trong đó b, c dương và mặt phẳng (P): y – z + 1 = 0. Viết phương trình mặt phẳng (ABC) biết mặt phẳng (ABC) vuông góc với mặt phẳng (P) và khoảng cách từ điểm O đến mặt phẳng (ABC) bằng .
Hướng dẫn giải
Phương trình mặt phẳng (ABC) có dạng
Vì mặt phẳng (ABC) ⊥ (P) ⇒
Khi đó phương trình mặt phẳng (ABC): bx + y + z – b = 0
Do
Vậy phương trình mặt phẳng (ABC): x + 2y + 2z = 1
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): x + y + z – 3 = 0 và (Q): x – y + z – 1 = 0. Viết phương trình mặt phẳng (R) vuông góc với (P) và (Q) sao cho khoảng cách từ O đến (R) bằng .
Hướng dẫn giải
Vectơ pháp tuyến của mặt phẳng (P), (Q) lần lượt là
Suy ra vectơ pháp tuyến của mặt phẳng
Suy ra phương trình mặt phẳng (R) có dạng x – z + m = 0
Ta có
Vậy (R): x – x ± 2 = 0
Câu 3. Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng (Q): x + 2y – 2z + 1 = 0 và cách (Q) một khoảng bằng 3.
Hướng dẫn giải
Trên mặt phẳng (Q): x + 2y – 2z + 1 = 0 chọn điểm M(–1; 0; 0)
Do (P) song song với mặt phẳng (Q) nên phương trình của mặt phẳng (P) có dạng:
x + 2y – 2z + D = 0; D ≠ 1
Vì
Vậy có hai mặt phẳng thõa mãn yêu cầu bài toán: x + 2y – 2z – 8 = 0 và x + 2y – 2z + 10 = 0
Câu 4. Trong không gian hệ tọa độ Oxyz, viết phương trình (P) đi qua O, vuông góc với mặt phẳng (Q): x + y + z = 0 và cách điểm M(1; 2; –1) và một khoảng bằng .
Hướng dẫn giải
Mặt phẳng (P) qua O nên có dạng: Ax + By + Cz = 0 (với A2 + B2 + C 2 ≠ 0)
Vì (P) ⊥ (Q) nên 1․A + 1․B + 1․C = 0 ⇔ C = –A – B (1)
(2)
Từ (1) và (2) ta được:
Từ (3): B = 0 ⇒ C = –A chọn A = 1 ⇒ C = –1. Do đó (P): x – z = 0
Từ (4): 8A + 5B = 0 chọn A = 5, B = –8 ⇒ C = 3. Do đó (P): 5x – 8y + 3z = 0
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình : x2 + y2 + z2 – 4x – 4y – 4z = 0 và điểm A(4; 4; 0). Viết phương trình mặt phẳng (OAB) biết B thuộc (S) và tam giác OAB đều.
Hướng dẫn giải
Gọi B(a, b, c). Vì tam giác OAB dều nên ta có hệ
Mà B ∈ (S) nên: a2 + b2 + c2 – 4a – 4b – 4c = 0
⇔ (4 – b)2 + b2 + 16 – 2b2 + 8b – 4(4 – b) – 4b – 4c = 0 ⇔ c = 4
⇔
Do đó B(4; 0; 4) hoặc B(0; 4; 4).
Với B(4; 0; 4) ta có nên phương trình (OAB): x – y + z = 0
Với B(0; 4; 4) ta có nên phương trình (OAB): x – y – z = 0
Câu 6. Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(0; – 1; 2) và N(– 1; 1; 3). Viết phương trình mặt phẳng (P) đi qua M, N sao cho khoảng cách từ điểm K(0; 0; 2) đến mặt phẳng (P) là lớn nhất.
Hướng dẫn giải
Phương trình mặt phẳng (P) có dạng:
Ax + B(y + 1) + C(z – 2) = 0 ⇔ Ax + By + Cz + B – 2C = 0 với (A2 + B2 + C 2 ≠ 0)
Vì N(–1; 1; 3) ∈ (P) ⇔ –A + B + 3C + B – 2C = 0 ⇔ A = 2B + C
⇒ (P): (2B + C)x + By + Cz + B – 2C = 0
Lại có
Nếu B =0 thì d(K, (P)) = 0 (loại)
Nếu B ≠ 0 thì
Dấu “=” xảy ra khi B = – C = 1. Khi đó phương trình mặt phẳng (P): x + yz + 3 = 0
Dạng 16. Viết phương trình mặt phẳng liên quan đến góc hoặc liên quan đến tam giác
Phương pháp giải
Giải bài toán viết phương trình mặt phẳng liên quan đến góc hoặc liên quan đến tam giác thường phải sử dụng công thức góc giữa hai mặt phẳng và phương trình mặt phẳng theo đoạn chắn dưới đây:
– Giả sử (α): Ax + By + Cz + D = 0 và (β): A’x + B’y + C’z + D’ = 0 có các vectơ pháp tuyến tương ứng là và
. Khi đó góc α giữa hai mặt phẳng (α) và (β) được tính theo công thức:
– Phương trình mặt phẳng (P) đi qua ba điểm A(a; 0; 0), B(0; b; 0) và C(0; 0; c) (với abc ≠ 0) có dạng
Bài tập vận dụng
Câu 1. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α): 2x – y + 3z – 5 = 0 và A(3; –2; 1). Viết phương trình mặt phẳng (P) qua A và song song với (α).
Hướng dẫn giải
(P) // (α) ⇒ là vectơ pháp tuyến của (P).
Suy ra phương trình của (P) là 2(x – 3) – 1(y + 2) + 3(z – 1) = 0 ⇔ 2x – y + 3z – 11 = 0
Câu 2. Trong không gian cho hệ tọa độ Oxyz, cho hai điểm A(3; 1; –1), B(2; –1; 4) và (α): x – 2y + 3z – 1 = 0. Viết phương trình mặt phẳng (α) qua hai điểm A, B và vuông góc với mặt phẳng (α)
Hướng dẫn giải
(α) có vectơ pháp tuyến
Suy ra (β) có một vectơ pháp tuyến và đi qua A (3; 1; – 1)
Vậy phương trình của (β): 1(x – 3) + 2(y – 1) + 1(z + 1) = 0 ⇔ x + 2y + z – 4 = 0
Câu 3. Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (α) chứa trục Ox và tạo với mặt phẳng (P): một góc bằng 60°
Hướng dẫn giải
Vectơ pháp tuyến của (P) là , vectơ đơn vị của Ox là
Giả sử , a2 + b2 + c2 ≠ 0 là vectơ pháp tuyến của (α)
(α) chứa Ox ⇒ . Suy ra
(α) tạo với (P) một góc 60°
Với c = 0 ⇒ b = 0 (loại do a2 + b2 + c 2 ≠ 0)
Với c ≠ 0, chia hai vế phương trình cho c2, ta được
TH1: , chọn b = 3, c = 1 ⇒
. Suy ra phương trình của (α): 3y + z = 0
TH2: , chọn b = 1, c = –3 ⇒
. Suy ra phương trình của (α): y – 3z = 0
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho (P): 5x – 2y + 5z – 1= 0 và (Q): x – 4y – 8z + 12 = 0. Lập phương trình mặt phẳng (α) đi qua gốc tọa độ O, vuông góc với mặt phẳng (P) và hợp với mặt phẳng (Q) một góc 45°.
Hướng dẫn giải
(P) có vectơ pháp tuyến là
(Q) có vectơ pháp tuyến là
Gọi , a2 + b2 + c2 ≠ 0 là vectơ pháp tuyến của (α)
(α) ⊥ (P) ⇒ (*)
(α) tạo với (Q) góc 45°
Thế (*) vào phương trình trên ta có:
Nếu c = 0 ⇒ a = 0 ⇒ b = 0 (loại a2 + b2 + c 2 ≠ 0)
Nếu c ≠ 0, chia cả hai vế của phương trình cho c2, ta được
Với , chọn a = 1, c = –1 ⇒ b = 0 ⇒
(α) qua O(0; 0; 0) ⇒ (α): x – z = 0
Với , chọn a = 1, c = 7 ⇒ b = 20 ⇒
(α) qua O(0; 0; 0) ⇒ (α): x + 20y + 7z = 0
Câu 5. Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (α) đi qua hai điểm A(3; 0; 0), C(0; 0; 1) và cắt trục Oy tại điểm B sao cho tam giác ABC có diện tích bằng
Hướng dẫn giải
B ∈ Oy ⇒ B(0; b; 0)
Nếu b = 0 ⇒ B ≡ 0 ⇒ S∆ABC = (trái với giả thiết). Vậy b ≠ 0.
Suy ra (α):
Ta có:
Suy ra
Do đó
Vậy hoặc
Dạng 17. Các dạng khác về viết phương trình mặt phẳng
Phương pháp giải
Phương trình mặt phẳng theo đoạn chắn
Giả sử mặt phẳng (P) cắt ba trục tọa độ tại A(a; 0; 0), B(0; b; 0), C(0;0; c)
(P) cắt tia Ox ⇒ a > 0, (P) cắt tia đối của tia Ox ⇒ a < 0
OA = |a|; OB = |b|; OC = |c|
Một số bất đẳng thức cơ bản
Bất đẳng thức Cauchy
Cho 2 số thực không âm x, y. Khi đó . Dấu bằng xảy ra khi x = y.
Cho 3 số thực không âm x, y, z. Khi đó . Dấu bằng xảy ra khi x = y = z.
Bất đẳng thức B–C–S (Bunyakovski)
Cho các số thực x, y, z, a, b, c. Khi đó
(ax + by + cz)2 ≤ (a2 + b2 + c 2) (x2 + y2 + z 2).
Dấu bằng xảy ra khi
Bài tập vận dụng
Câu 1. Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(1; 2; 1); N(−1; 0; −1). Viết phương trình mặt phẳng (P) đi qua M, N cắt trục Ox, Oy, Oz lần lượt tại A, B, C khác gốc tọa độ O sao cho .
Hướng dẫn giải
Giả sử (P) cắt Ox, Oy, Oz lần lượt tại A(a; 0; 0), B(0; b; 0), C(0; 0; c)
Vì (P) đi qua M, N nên
Mặt khác
Với
Với (vô nghiệm)
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho các điểm B(0; 3; 0), M(4; 0; –3). Viết phương trình mặt phẳng (P) chưa B, M và cắt các tia Ox, Oz lần lượt tại A, C sao cho thể tích khối tứ diện OABC bằng 3.
Hướng dẫn giải
Gọi A(a; 0; 0) ∈ Ox, C(0; 0; c) ∈ Oz. Vì (P) cắt các tia Ox, Oz nên a, c > 0.
Vì B(0; 3; 0) ∈ Oy nên phương tình mặt phẳng theo đoạn chắn
Vì M(4; 0; –3) ∈ (P) nên (1)
Thể tích tứ diện OABC là
Theo giải thiết V = 3 ⇔ ac = 6 (2)
Từ (1) và (2) suy ra
Vậy
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho điểm M(2; 4; 1). Viết phương trình mặt phẳng (P) qua M và cắt Ox, Oy, Oz tại A, B, C sao cho 4OA = 2OB = OC.
Hướng dẫn giải
Gải sử (P) cắt các tia Ox, Oy, Oz lần lượt tại A(a; 0; 0), B(0; b; 0), C(0; 0; c) với a, b, c > 0.
Vì 4OA = 2OB = OC nên
Phương trình mặt phẳng (P) là
Vì M(2; 4; 1) ∈ (P) nên
⇒ (P): 4x + 2y + z – 17 = 0
Câu 4. Trong không gian với hệ tọa Oxyz, gọi (P) là mặt phẳng đi qua điểm M(1; 2; 3) cắt các tia Ox, Oy, Oz lần lượt A, B, C sao cho biểu thức có giá trị nhỏ nhất. Viết phương trình mặt phẳng (P).
Hướng dẫn giải
Gọi A(a; 0; 0), B(0; b; 0), C(0; 0; c) với a, b, c > 0.
Phương trình mặt phẳng (P) có dạng .
Vì M(1; 2; 3) ∈ (P) ⇒
Ta có
Áp dụng bất đẳng thức B–C–S, ta có:
Dấu “=” xảy ra khi
Vậy phương trình mặt phẳng (P): x + 2y + 3z – 14 = 0.
Câu 5. Trong không gian với hệ tọa độ Oxyz, gọi (P) là mặt phẳng đi qua điểm M(1; 4; 9), cắt các tia Ox, Oy, Oz lần lượt tại A, B, C sao cho biểu thức OA + OB + OC có giá trị nhỏ nhất. Viết phương trình mặt phẳng (P).
Hướng dẫn giải
Gọi A(a; 0; 0), B(0; b; 0), C(0; 0; c) với a, b, c > 0.
Suy ra OA = a, OB = b, OC = c
Phương tình mặt phẳng (P) có dạng
Vì M(1; 4; 9) ∈ (P)
Dấu “=” xảy ra khi
Vậy phương trình mặt phẳng (P): 6x + 3y + 2z – 36= 0.
Dạng 18. Vị trí tương đối của hai mặt phẳng
Phương pháp giải
Cho hai mặt phẳng (P1): A1x + B1y + C1z + D1 = 0 và A2x + B2y + C2z + D2 = 0
Khi đó ta có ba trường hợp
(P1) ≡ (P2) ⇔
(P1) // (P2) ⇔
(P1) cắt (P2) ⇔ A1 : B1 : C1 ≠ A2 : B2 : C2
Lưu ý: A1.A2 + B1 B2 + C1 C2 = 0 ⇔ (P1) ⊥ (P2).
Bài tập vận dụng
Câu 1. Xét vị trí tương đối của mặt phẳng (P): x + y + z – 1= 0 và (Q): 2x – 1 = 0
Hướng dẫn giải
Cách 1:
Ta có:
Ta thấy ⇒ (P) cắt (Q)
Cách 2:
Ta thấy (P) luôn cắt các mặt phẳng tọa độ, mặt khác mặt phẳng (Q) song song với mặt phẳng (Oyz)
Vậy (P) và (Q) cắt nhau.
Câu 2. Xét vị trí tương đối của mặt phẳng (P): 2x – 3y + 5z – 1 = 0 và (Q): x – y – z + 2 = 0
Hướng dẫn giải
Cách 1:
Ta có:
Ta thấy ⇒ (P) cắt (Q)
Cách 2:
Ta thấy ⇒ (P) ⊥ (Q) ⇒ (P) cắt (Q).
Câu 3. Cho (P): (m + 1)x + (n + 3)y + 2z – 1 = 0 và (Q) x + 2y + z + 3 = 0. Tìm m, n ∈ ℝ để (P) song song với (Q).
Hướng dẫn giải
Ta có (P) // (Q) ⇔
Câu 4. Cho (P): (m + 2n)x + (2n2 + 3)y + z – 8 = 0 và (Q): x – my + (n2 – 5m + 15)z – 3 = 0. Chứng tỏ (P) và (Q) cắt nhau.
Hướng dẫn giải
Xét m = 0
Khi đó ta có
⇒ (P) cắt (Q)
Xét m ≠ 0
Ta thấy
⇔ m2 + 2n․m + 2n2 + 3 = 0 ⇔ (m + n)2 + n2 + 3 = 0 (vô lý).
Vậy (P) luôn cắt (Q).
Câu 5. Viết phương trình mặt phẳng (P) qua A(1; 2; 3) và song song với mặt phẳng (Q): x + 2y – 3z + 3 = 0.
Hướng dẫn giải
Vì (P) // (Q) nên ta có (P): x +2y – 3z + m = 0, m ≠ 3
Ta có A(1 ; 2 ; 3) ∈ (P) ⇒ m = – 3 ≠ 3
Vậy (P): x + 2y – 3z – 3 = 0
Dạng 19. Vị trí tương đối của mặt phẳng và mặt cầu
Phương pháp giải
Cho mặt cầu S(I; R) và mặt phẳng (P). Ta có ba trường hợp
– d(I, (P)) = R ⇔ (P) tiếp xúc (S).
– d(I, (P)) < R ⇔ (P) cắt (S) theo đường tròn (𝒞)
– d(I, (P)) > R ⇔ (P) không cắt (S).
Bài tập vận dụng
Câu 1. Cho mặt cầu (S): (x – 1)2 + (y – 2)2 + (z – 3)2 = 16 và mặt phẳng (P): x + 2y + 2z + 1 = 0. Xác định vị trí tương đối của (S) và (P).
Hướng dẫn giải
Ta thấy mặt cầu (S) có tâm I(1; 2; 3) và bán kính R = 4
Ta có
Vậy mặt phẳng (P) tiếp xúc với mặt cầu (S).
Câu 2. Cho (P): 3x + 4y + 4 = 0 và A(1; 2; 3). Viết phương trình mặt cầu tâm A cắt mặt phẳng (P) theo đường tròn giao tuyến (C) có chu vi bằng 8π.
Hướng dẫn giải
Ta có chu vi đường tròn (C) bằng 8π ⇒ bán kính đường tròn (C) bằng 4.
Ta có
Ta có bán kính mặt cầu
Vậy (S): (x – 1)2 + (y – 2)2 + (z – 3)2 = 52
Câu 3. Cho mặt phẳng (P) : x + y + 2z + 3 = 0 và (Q) : 2x – y – z + 3 = 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành,đồng thời giao tuyến của (S) với các mặt phẳng (P), (Q) là các đường tròn có bán kính lần lượt là , r. Xác định r sao cho có đúng một mặt cầu thõa mãn yêu cầu bài toán.
Hướng dẫn giải
Gọi I(m; 0; 0) ∈ Ox là tâm mặt cầu (S).
Ta có
Vì có đúng một mặt thỏa mãn bài toán nên (*) phải có nghiệm duy nhất.
Vậy r = 4.
Câu 4. Cho A(a; 0; 0), B(0; b; 0, C(0; 0; c); a, b, c > 0 thõa mãn a + 2b + 3c =4. Xác định phương trình mặt phẳng chứa đường tròn lớn của mặt cầu ngoại tiếp hình chóp OABC độc lập với a, b, c.
Hướng dẫn giải
Gọi là tâm mặt cầu ngoại tiếp tam diện vuông OABC.
Ta có
⇒ I ∈ (α): x + 2y + 3x – 2 = 0
Vậy phương trình mặt phẳng cần tìm (α) x + 2y + 3z – 2 =0
Dạng 20. Tính khoảng cách từ một điểm đến một mặt phẳng. Tìm hình chiếu của một điểm trên mặt phẳng. Tìm điểm đối xứng của một điểm qua mặt phẳng
Phương pháp giải
– Khoảng cách từ điểm M(x0; y0; z0) đến mặt phẳng (P) có phương trình Ax + By + Cz + D = 0 là
– Khoảng cách giữa hai mặt phẳng song song: Chọn một điểm trên mặt phẳng (cho y = z = 0). Tính khoảng cách từ điểm đó đến mặt phẳng kia.
Bài tập vận dụng
Câu 1. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x – 2y + 2z =0 và điểm M(1; 2; 3). Tính khoảng cách từ M đến (P).
Hướng dẫn giải
Khoảng cách từ điểm M đến mặt phẳng (P) là:
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho các điểm A(2; 0; 0), B(0; –1; 0, C(0; 0; 3). Tính khoảng cách từ gốc tọa độ đến mặt phẳng (ABC).
Hướng dẫn giải
Phương trình mặt phẳng (ABC) có dạng
Khoảng cách từ điểm O đến mặt phẳng (ABC) là
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng song song (P): x +2y – 2z + 7 = 0 và (Q): x + 2y – 2z – 4 = 0. Tính khoảng cách giữa hai mặt phẳng.
Hướng dẫn giải
Lấy điểm M(0; 0; –2) ∈ (Q)
Câu 4. Trong không gian với hệ tọa độ Oxyz, tìm điểm thuộc trục Ox sao cho khoảng cách đến mặt phẳng (α): x – y + z + 1 = 0 bằng
Hướng dẫn giải
Gọi M(a; 0; 0) ∈ Ox
Vậy M(2; 0; 0) hoặc M(–4; 0; 0)
Câu 5. Trong không gian với hệ tọa độ Oxyz, tìm điểm thuộc trục Oy cách đều điểm A(1; 1; −1) và mặt phẳng (α): x + y + z – 5 = 0
Hướng dẫn giải
Gọi M(0; b; 0) ∈ Oy
Vậy M(0; 2; 0) hoặc M(0; −4; 0).
Câu 6. Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1; 0; 0), B(0; b; 0), C(0; 0; c). Biết b, c > 0, phương trình mặt phẳng (P): y − z + 1 = 0. Biết rằng mặt phẳng (ABC) vuông góc với mặt phẳng (P) và khoảng cách từ O đến mặt phẳng (ABC) bằng . Tìm tọa độ các điểm B và C.
Hướng dẫn giải
Mặt phẳng (P) có vectơ pháp tuyến là
Phương trình mặt phẳng (ABC)có dạng
Do
Giải hệ ta được
Vậy
Dạng 21. Tìm tọa độ hình chiếu của điểm trên mặt phẳng. Điểm đối xứng qua mặt phẳng
Phương pháp giải
– Để tình hình chiếu H của điểm A trên mặt phẳng (P):
Gọi H(x; y; z). Tính vectơ . Sử dụng điều kiện
và H ∈ (P)
– Để tìm tọa độ điểm B đối xứng với A qua (P):
Sử dụng điều kiện H là trung điểm AB.
Bài tập vận dụng
Câu 1. Cho A(1; −1; 1) và mặt phẳng (P): 2x – 2y + z + 4 = 0
a) Tìm tọa độ điểm H là hình chiếu vuông góc của điểm A trên mặt phẳng (P).
b) Tìm tọa độ điểm A’ là điểm đối xứng của điểm A qua mặt phẳng (P).
Hướng dẫn giải
- a) Mặt phẳng (P) có vtpt
. Gọi H(x, y, z), vì H là hình chiếu vuông góc của A trên (P) nên
⇒ 2(1 + 2k) – 2(–1 – 2k) + k + 1 + 4 = 0 ⇒ k = –1 ⇒ H(–1; 1; 0)
b) Gọi A’(xA’, yA’, zA’). Có H là trung điểm của AA’ suy ra
Vậy A’(–3; 3; –1)
Câu 2. Trong không gian với hệ tọa độ Oxyz cho điểm A(1; −1; 1), B(0; 1; −2). Tìm tọa độ điểm M thuộc mặt phẳng (Oxy) sao cho |MA – MB| đạt giá trị lớn nhất.
Hướng dẫn giải
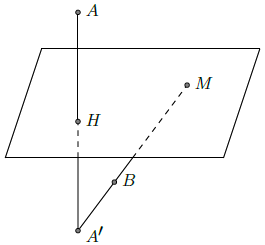
Phương trình mặt phẳng (Oxy) là z = 0
Do zA > 0, zB < 0 ⇒ A, B nằm về hai phía mặt phẳng (Oxy).
Gọi H là hình chiếu vuông góc của A lên (Oxy). Gọi A’ là điểm đối xứng của A qua (Oxy,ta có:
|MA – MB| = |MA’ – MB’| ≤ A’B. Dấu “=” xảy ra khi A’, B, M thẳng hàng
Có H(1; –1; 0), A’(1; –1; –1),
Gọi M(x; y; z) ⇒ . Ta có