Bài học giúp bạn tìm hiểu các dạng phương trình đường thẳng trong không gian, cách tìm phương trình theo mỗi dạng và một số tài liệu học tập tốt chuyên đề này. Qua đó, tạo tiền đề lớn giúp độc giả làm quen và nắm bắt hầu hết các biến thể bài tập. Giúp giải quyết các bài toán một cách nhanh chóng nhất theo cả xu hướng trắc nghiệm và tự luận.
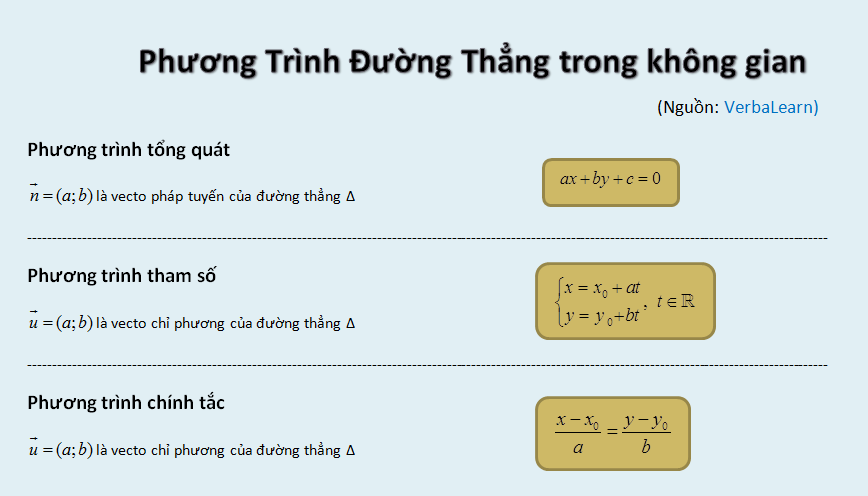
Tổng quan lý thuyết
[content_1]Phương trình đường thẳng trong không gian biểu thị bởi 3 dạng: Phương trình tổng quát, phương trình tham số và phương trình chính tắc. Ứng với mỗi loại phương trình sẽ có một công thức và một số dạng toán khác nhau được khai thác trong các đề thi.
Phương trình tổng quát
Định nghĩa
Cho đường thẳng ∆. Vectơ gọi là vectơ pháp tuyến (VTPT) của ∆ nếu giá của
vuông góc với ∆.
Nhận xét
– Nếu là VTPT của ∆ thì
(k ≠ 0) cũng là VTPT của ∆.
Phương trình tổng quát của đường thẳng
Cho đường thẳng ∆ đi qua M0 (x0; y0) và có VTPT .
Khi đó M (x; y) ∈ ∆ ⇔ ⇔ a(x − x0) + b(y – y0) = 0
⇔ ax + by + c = 0 (c = −ax0 – by0) (1)
(1) gọi là phương trình tổng quát của đường thẳng ∆.
Chú ý
– Nếu đường thẳng ∆: ax + by + c = 0 thì là VTPT của ∆.
Các dạng đặc biệt của phương trình tổng quát
– ∆ song song hoặc trùng với trục Ox ⇔ ∆: by + c = 0
– ∆ song song hoặc trùng với trục Oy ⇔ ∆: ax + c = 0
– ∆ đi qua gốc tọa độ ⇔ ∆: ax + by = 0
– ∆ đi qua hai điểm A(a; 0), B(0; b) ⇔ ∆: với (ab ≠ 0)
– Phương trình đường thẳng có hệ số góc k là y = kx + m với k = tan α, α là góc hợp bởi tia Mt của ∆ ở phía trên trục Ox và tia Mx
Phương trình tham số
Định nghĩa vectơ chỉ phương
Cho đường thẳng ∆. Vectơ gọi là vectơ chỉ phương (VTCP) của đường thẳng ∆ nếu giá của nó song song hoặc trùng với ∆.
Nhận xét
– Nếu là VTCP của ∆ thì
cũng là VTCP của ∆.
– VTPT và VTCP vuông góc với nhau. Do vậy nếu ∆ có VTCP thì
là một VTPT của ∆.
Phương trình tham số của đường thẳng
Cho đường thẳng ∆ đi qua M0(x0; y0) và là VTCP.
Khi đó M (x; y) ∈ ∆ (1)
Hệ (1) gọi là phương trình tham số của đường thẳng ∆, t gọi là tham số
Nhận xét tổng quát
Nếu ∆ có phương trình tham số là (1) khi đó A ∈ ∆ ⇔ A(x0 + at; y0 + bt)
Phương trình chính tắc
Định nghĩa
Cho đường thẳng ∆ đi qua M0(x0; y0) và (với a ≠ 0, b ≠ 0) là vectơ chỉ phương thì phương trình
được gọi là phương trình chính tắc của đường thẳng ∆.
Vị trí tương đối của hai đường thẳng
Cho hai đường thẳng d1: a1x + b1y + c1 = 0; d2: a2x + b2y + c2 = 0
– d1 cắt d2 khi và chỉ khi
– d1 // d2 khi và chỉ khi và
hoặc
và
– d1 ≡ d2 khi và chỉ khi
Chú ý
Với trường hợp a2.b2.c2 ≠ 0 khi đó
– Nếu thì hai đường thẳng cắt nhau.
– Nếu thì hai đường thẳng song song nhau.
– Nếu thì hai đường thẳng trùng nhau.
Phân dạng bài tập
Dạng 1. Viết phương trình đường thẳng
[content_2]Phương pháp giải
– Đường thẳng d đi qua điểm M0(x0; y0; z0) và có vectơ chỉ phương có phương trình tham số là
– Đường thẳng d đi qua hai điểm A, B: Một vectơ chỉ phương của d là
– Đường thẳng d đi qua điểm M0(x0; y0; z0) và song song với đường thẳng ∆ cho trước: Vì d // ∆ nên vectơ chỉ phương của ∆ cũng là vectơ chỉ phương của d.
– Đường thẳng d đi qua điểm M0(x0; y0; z0) và vuông góc với mặt phẳng (P) cho trước: Vì d // (P) nên vectơ pháp tuyến của (P) cũng là vectơ chỉ phương của d.
Đường thẳng d là giao tuyến của hai mặt phẳng (P), (Q).
Cách 1: Tìm một điểm và một vectơ chỉ phương
– Tìm tọa độ một điểm A ∈ d bằng cách giải hệ phương trình mặt phẳng của (P), (Q) với việc chọn giá trị cho một ẩn.
– Tìm một vectơ chỉ phương của d:
Cách 2: Tìm hai điểm A, B thuộc d rồi viết phương trình đường thẳng đi qua hai điểm đó.
– Đường thẳng d đi qua điểm M0(x0; y0; z0) và vuông góc với hai đường thẳng d1, d2: Vì
d ⊥ d1, d ⊥ d2 nên một vectơ chỉ phương của d là:
Bài tập vận dụng
Câu 1. Trong không gian Oxyz, cho tam giác ABC có A(2; 1; −1), B (−2; 3; 1) và C (0; −1; 3). Gọi d là đường thẳng đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với mặt phẳng (ABC). Phương trình đường thẳng d là
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn B
Ta có:
Vậy tam giác ABC đều nên tâm đường tròn ngoại tiếp là trọng tâm G (0; 1; 1).
Ta có
Đường thẳng d đi qua G(0; 1; 1) và có vectơ chỉ phương cùng phương với , do đó chọn
Phương trình đường thẳng d là .
Với t = −1, ta có điểm A(−1; 0; 0) ∈ d.
Vậy đường thẳng d đi qua A(1; 0; 0) và có vectơ chỉ phương .
Câu 2. Trong không gian Oxyz, cho hai M(1; 2; 3), N(3; 4; 5) và mặt phẳng (P): x + 2y + 3z − 14 = 0. Gọi ∆ là đường thẳng thay đổi nằm trong mặt phẳng (P), các điểm H, K lần lượt là hình chiếu vuông góc của M, N trên ∆. Biết rằng khi MH = NK thì trung điểm của HK luôn thuộc một đường thẳng d cố định, phương trình của đường thẳng d là
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn A
Gọi I là trung điểm của HK.
Do MH = NK nên ∆HMI = ∆KNI ⇒ IM = IN. Khi đó I thuộc mặt phẳng (Q) là mặt phẳng trung trực của đoạn MN.
Ta có (Q) đi qua trung điểm của MN là điểm J(2; 3; 4) và nhận làm vectơ pháp tuyến nên có phương trình là (Q): x + y + z − 9 = 0.
Mà I ∈ A ⊂ (P). Suy ra I ∈ d = (P) ∩ (Q):
Tìm được (0; 13; −4) ∈ d và vectơ chỉ phương của d là (1; −2; 1).
Vậy d:
Câu 3. Trong không gian Oxyz. Cho điểm E(1; 1; 1), mặt cầu (S): x2 + y2 + z2 = 4 và mặt phẳng (P): x − 3y + 5z − 3 = 0. Gọi ∆ là đường thẳng đi qua E, nằm trong (P) và cắt (S) tại hai điểm A, B sao cho ∆OAB là tam giác đều. Phương trình tham số của ∆ là
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn C
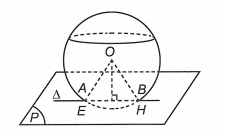
Gọi là một vectơ chỉ phương của ∆ với a2 + b2 + c2 > 0.
Ta có
Vì ∆ ⊂ (P) nên (1)
Mặt cầu (S) có tâm O(0; 0; 0) và bán kính R = 2.
Gọi H là hình chiếu vuông góc của O trên AB
Ta có ∆OAB là tam giác đều cạnh R nên .
Suy ra khoảng cách từ O đến đường thẳng ∆ bằng . .
Khi đó (2)
⇔ (a2 – b2) + (b – c)2 + (c – a)2 = 3(a2 + b2 + c2)
⇔ (a + b + c)2 = 0 ⇔ a + b + c = 0 (2)
Thay (1) vào (2) ta được: 3b – 5c + b + c = 0 ⇔ b = c ⇒ a = −2c.
Thay c = −1 thì b = −1 và a = 2.
Ta được một vectơ chỉ phương của ∆ là
Vậy phương trình của đường thẳng ∆ là:
Dạng 2. Viết phương trình đường thẳng bằng phương pháp tham số hóa
[content_3]Phương pháp giải
– Viết phương trình đường thẳng d đi qua điểm M0(x0; y0; z0), vuông góc và cắt đường thẳng ∆.
Cách 1: Gọi H là hình chiếu vuông góc của M0 trên đường thẳng ∆. Khi đó H ∈ ∆, .
Khi đó đường thẳng d là đường thẳng đi qua M0, H.
Cách 2: Gọi (P) là mặt phẳng đi qua M0 và vuông góc với d. (Q) là mặt phẳng đi qua M0 và chứa d. Khi đó d = (P) ∩ (Q)
– Viết phương trình đường thẳng d đi qua điểm M0(x0; y0; z0) và cắt hai đường thẳng d1, d2.
Cách 1: Gọi M1 ∈ d1 ∩ d, M2 = d2 ∩ d. Suy ra M0, M1, M2 thẳng hàng. Từ đó tìm được M1, M2 và suy ra phương trình đường thẳng d.
Cách 2: Gọi (P) là mặt phẳng đi qua M0 và chứa d1; (Q) là mặt phẳng đi qua M0 và chứa d2.
Khi đó d = (P) ∩ (Q). Do đó một vectơ chỉ phương của d có thể chọn là .
– Đường thẳng d nằm trong mặt phẳng (P) và cắt cả hai đường thẳng d1, d2: Tìm các giao điểm A = d1 ∩ (P), B = d2 ∩ (P). Khi đó d chính là đường thẳng AB.
– Đường thẳng d song song với ∆ và cắt cả hai đường thẳng d1, d2: Viết phương trình mặt phẳng (P) song song với ∆ và chứa d1, mặt phẳng (Q) song song với ∆ và chứa d2. Khi đó d = (P) ∩ (Q).
– Đường thẳng d là đường vuông góc chung của hai đường thẳng d1, d2 chéo nhau:
Cách làm: Gọi M ∈ d1, N ∈ d2. Từ điều kiện , ta tìm được M, N. Viết phương trình đường thẳng MN chính là đường vuông góc chung của d1, d2.
Bài tập vận dụng
Câu 1. Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): x + y − z − 1 = 0 và đường thẳng d: . Phương trình đường thẳng d’ là hình chiếu vuông góc của d trên mặt phẳng (P) là
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn B
Đường thẳng d có phương trình tham số là (t ∈ ℝ)
Lấy điểm M = d ∩ (P) ⇒ M(4 − 2t; −2 + 2t; −1 + t) ∈ d.
Thay đổi tọa độ điểm M vào phương trình mặt phẳng (P) ta được:
4 − 2t − 2 + 2t + 1− t = 0 ⇔ t = 2.
Suy ra M (0; 2; 1).
Do đó d ∩ (P) = M(0; 2; 1).
Lấy A(4; −2; −1) ∈ d. Gọi H là hình chiếu vuông góc của A lên mặt phẳng (P).
Đường thẳng AH đi qua A(4; −2; −1) và nhận làm vectơ chỉ phương nên AH có phương
trình là .
Suy ra H(4 + t1; −2 + t1; −1 – t1).
Thay tọa độ H vào phương trình mặt phẳng (P) được:
MH là hình chiếu của d lên mặt phẳng (P), MH đi qua M(0; 2; 1) và nhận là vectơ chỉ phương nên có phương trình là
.
Câu 2. Cho các đường thẳng d1: và đường thẳng d2:
. Phương trình đường thẳng ∆ đi qua A(1; 0; 2), cắt d1 và vuông góc với d2 là:
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn C
Gọi I = d1 ∩ ∆, I(1+ t, −1 + 2t, −t) ⇒ là một vectơ chỉ phương của ∆.
Do là một vectơ chỉ phương của đường thẳng d2 và ∆ ⊥ d2.
Suy ra
Vậy . Phương trình đường thẳng ∆ cần tìm là
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 3x + y − 2z = 0 và hai đường thẳng d1: và d2:
. Đường thẳng vuông góc với (P) cắt cả hai đường thẳng d1 và d2 có phương trình là
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn A
M ∈ d1 ⇔ M(−1− t; 6 + 2t; t).
N ∈ d1 ⇔ N(1− 3t’; 2 – t’; −4 + 4t’).
(P): 3x + y − 2z = 0 có vectơ pháp tuyến .
Đường thẳng (d) vuông góc với (P) cắt cả hai đường thẳng d1 tại M và cắt d2 tại N suy ra
t = −2 ⇒ M (1; 2; −2)
Do (d) ⊥ (P) nên .
Phương trình đường thẳng d là
Chọn s = −1 ⇒ A(–2; 1; 0) ∈ d ⇒
Câu 4. Viết phương trình đường thẳng d qua A(1; 2; 3) cắt đường thẳng và song song với mặt phẳng (P): x + y − z − 2 = 0.
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn C
Do d ∩ d1 = B ⇒ B(2m; m; m + 2) ⇒
d song song với mặt phẳng (P) nên
Vậy phương trình đường thẳng .
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x − y + z −10 = 0, điểm A(1; 3; 2) và đường thẳng d: . Tìm phương trình đường thẳng ∆ cắt (P) và d lần lượt tại M và N sao cho A là trung điểm của MN.
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn A
Ta có N = ∆ ∩ d ⇒ N(−2 + 2t; 1 + t; 1 – t).
A là trung điểm của MN ⇒ M(4 − 2t; 5 − t; 3 + t).
Mà M ∈ (P) nên tọa độ M thỏa phương trình (P), ta được:
2(4 − 2t) − (5 − t) + (3 + t) − 10 = 0 ⇔ t = −2 ⇒ N(−6; −1; 3), M(8; 7; 1).
Suy ra
Đường thẳng ∆ đi qua hai điểm M và N nên có một vectơ chỉ phương nên có phương trình là
Câu 6. Trong không gian tọa độ Oxyz, cho điểm A(−3; 3; −3) thuộc mặt phẳng (α): 2x − 2y + z + 15 = 0 và mặt cầu (S): (x – 2)2 + (y – 3)2 + (z – 5)2 = 100. Đường thẳng ∆ qua A, nằm trên mặt phẳng (α) cắt (S) tại M, N. Để độ dài MN lớn nhất thì phương trình đường thẳng ∆ là
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn A
Mặt cầu (S) có tâm I(2; 3; 5) và bán kính R = 10.
Mặt phẳng (α) có vectơ pháp tuyến
Gọi H, K lần lượt là hình chiếu vuông góc của I lên ∆ và mặt phẳng (α).
⇒ IK ⊥ (α) nên phương trình đường thẳng IK đi qua I và vuông góc với mặt phẳng (α) là
Tọa độ điểm K là nghiệm hệ phương trình
Vì ∆ ⊂ (α) nên IH ≥ IK. Do đó IH nhỏ nhất khi H trùng với K.
Để MN lớn nhất thì IH phải nhỏ nhất.
Khi đó đường thẳng ∆ cần tìm đi qua A và K. Ta có
Đường thẳng ∆ có phương trình là:
Câu 7. Trong không gian Oxyz, cho ∆ABC có A(2; 3; 3), phương trình đường trung tuyến kẻ từ B là d: , phương trình đường phân giác trong của góc C là ∆:
. Đường thẳng AB có một vectơ chỉ phương là
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn C
Ta có phương trình tham số của ∆ là:
Gọi M là trung điểm của AC nên
Vì M ∈ d nên
Suy ra C(4; 3; 1).
Phương trình mặt phẳng (P) đi qua A và vuông góc với ∆ là: 2x − y − z + 2 = 0. Gọi H là giao điểm của (P) và ∆ ⇒ H(2; 4; 2).
Gọi A’ là điểm đối xứng với A qua đường phân giác ∆, suy ra H là trung điểm AA’ ⇒ A’(2; 5; 1).
Do A’ ∈ BC nên đường thẳng BC có vectơ chỉ phương là
Suy ra phương trình của đường thẳng BC là
Vì B = BM ∩ BC ⇒ B(2; 5; 1) = A’.
Đường thẳng AB có một vectơ chỉ phương là
Câu 8. Trong không gian hệ tọa độ Oxyz, cho đường thẳng ∆: và hai điểm A(4; −2; 4), B(0; 0; −2). Gọi d là đường thẳng song song và cách ∆ một khoảng bằng
, gần đường thẳng AB nhất. Đường thẳng d cắt mặt phẳng (Oxy) tại điểm nào dưới đây?
A. (2; 1; 0)
B.
C. (3; 2; 0)
D. (0; 0; 0)
Hướng dẫn giải
⟹ Chọn D
Phương trình tham số của đường thẳng AB có dạng:
Để đường thẳng d thỏa mãn bài toán thì ta có hình vẽ tương ứng
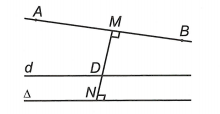
Đoạn vuông góc chung của hai đường thẳng AB và ∆ là MN với M(0; −5; 1), N(3; 1; 1).
Để d gần đường thẳng AB nhất thì d phải đi qua điểm D nằm trên đoạn MN mà .
Do đó
Vectơ chỉ phương của đường thẳng d là
Suy ra phương trình tham số của d là
Đường thẳng d cắt (Oxy) tại điểm có
Vậy giao điểm của d và (Oxy) là (0; 0; 0).
Câu 9. Trong không gian với hệ tọa độ Oxyz, cho bốn đường thẳng
Biết không tồn tại đường thẳng nào trong không gian mà cắt được đồng thời cả bốn đường thẳng trên. Giá trị của
biểu thức T = a − 2b bằng
A. −2
B. −3
C. 2
D. 3
Hướng dẫn giải
⟹ Chọn A
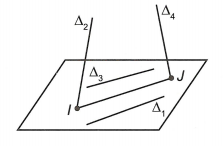
Ta có: ∆1 //∆3.
Gọi (P) là mặt phẳng chứa ∆1 và ∆3 ⇒ (P): x + 2y − z + 3 = 0.
Gọi I = ∆2 ∩ (P) ⇒ I(0; −1; 1).
Gọi J = ∆4 ∩ (P) ⇒
Để thỏa mãn yêu cầu bài toán thì phải cùng phương với
Suy ra
Dạng 3. Góc giữa đường thẳng với mặt phẳng
[content_4]Phương pháp giải
Cho đường thẳng (∆): và mặt phẳng (α): Ax + By +Cz + D = 0.
Gọi φ là góc giữa hai mặt phẳng (∆) và (α) ta có công thức:
Chú ý: A, B, C và a, b, c không đồng thời bằng 0.
Bài tập vận dụng
Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng ∆: và mặt phẳng (α): 3x + 4y + 5z + 8 = 0. Tính góc tạo bởi ∆ và (α).
Hướng dẫn giải
∆ có vectơ chỉ phương
(α) có vectơ pháp tuyến
Ta có:
Suy ra
Bài tập vận dụng
Câu 1. Trong không gian Oxyz, cho hai đường thẳng ∆: và mặt phẳng (P): x + y − 2z + 6 = 0. Biết ∆ cắt mặt phẳng (P) tại A, M thuộc ∆ sao cho
. Tính khoảng cách từ M tới mặt phẳng (P).
A.
B. 2
C.
D. 3
Hướng dẫn giải
⟹ Chọn B
Đường thẳng ∆: có vectơ chỉ phương
Mặt phẳng (P): x + y − 2z + 6 = 0 có vectơ chỉ phương
Suy ra
Dạng 4. Góc giữa hai đường thẳng
[content_5]Phương pháp giải
Cho hai đường thẳng:
.
Gọi φ là góc giữa hai đường thẳng (∆1) và (∆2)
Ta có:
Bài tập vận dụng
Đề bài
Trong không gian Oxyz, cho hai đường thẳng
Tính góc giữa hai đường thẳng trên.
Hướng dẫn giải
Vectơ chỉ phương của ∆1 là
Vectơ chỉ phương của ∆2 là
Vậy góc giữa hai đường thẳng đã cho là 45°.
Bài tập vận dụng
Câu 1. Trong không gian Oxyz, cho đường thẳng (d) là giao tuyến của hai mặt phẳng (P): x − z.sinα + cosα = 0; (Q): y − z.cosα − sinα = 0; . Góc giữa (d) và trục Oz là:
A. 30°
B. 45°
C. 60°
D. 90°
Hướng dẫn giải
⟹ Chọn B
Mặt phẳng (P) có vectơ pháp tuyến là
Mặt phẳng (Q) có vectơ pháp tuyến là
(d) là giao tuyến của (P) và (Q) nên vectơ chỉ phương của (d) là:
Vectơ chỉ phương của (Oz) là
Suy ra
Vậy góc giữa (d) và trục (Oz) là 45°.
Câu 2. Trong không gian Oxyz, d là đường thẳng đi qua điểm A(1; −1; 2), song song với mặt phẳng (P): 2x − y − z + 3 = 0, đồng thời tạo với đường thẳng ∆: một góc lớn nhất. Phương trình đường thẳng d là
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn D
Mặt phẳng (P): 2x − y − z + 3 = 0 có một vectơ pháp tuyến là
Đường thẳng ∆: có một vectơ chỉ phương là
Giả sử đường thẳng d có vectơ chỉ phương là
Do 0° ≤ (d, ∆) ≤ 90° mà theo giả thiết d tạo ∆ góc lớn nhất nên (d, ∆) = 90° ⇒
Lại có d // (P) nên . Do đó chọn
Vậy phương trình đường thẳng d là
Câu 3. Trong không gian Oxyz, cho đường thẳng d: và mặt phẳng (P): 2x − y + 2z +1 = 0. Đường thẳng ∆ đi qua E(−2; 1; −2), song song với (P) có một vectơ chỉ phương
, đồng thời tạo với d góc bé nhất. Tính T = m2 − n2.
A. T = −5
B. T = 4
C. T = 3
D. T = −4
Hướng dẫn giải
⟹ Chọn D
Mặt phẳng (P) có vectơ pháp tuyến là ; đường thẳng d có vectơ chỉ phương là
∆ // (P) ⇒
Mặt khác ta có:
Vì nên
bé nhất khi và chỉ khi
lớn nhất.
Xét hàm số
Bảng biến thiên:
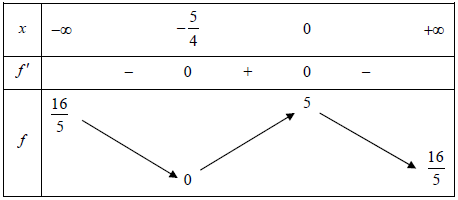
Dựa vào bảng biến thiên ta có: max f(t) = f(0) = 5.
Suy ra bé nhất khi m = 0 ⇒ n = 2.
Do đó T = m2 − n2 = −4.
Dạng 5. Khoảng cách từ một điểm đến đường thẳng
[content_6]Phương pháp giải
Cho đường thẳng (∆) đi qua điểm M0(x0, y0, z0) và có vectơ chỉ phương . Khi đó khoảng cách từ điểm M1 đến (∆) được tính bởi công thức:
Bài tập vận dụng
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: . Tính khoảng cách từ M(−2; 1; −1) tới d.
Hướng dẫn giải
Ta có: A(1; 2; −2) ∈ d ⇒
Khoảng cách từ điểm M đến đường thẳng d là:
Bài tập vận dụng
Câu 1. Viết phương trình đường thẳng d đi qua điểm A(1; 1; −1) cho trước, nằm trong mặt phẳng (P): 2x − y − z −2 = 0 và cách điểm M(0; 2; 1) một khoảng lớn nhất.
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn C
Ta gọi B là hình chiếu của M lên đường thẳng d khi đó MB ≤ MA.
Suy ra MBmax = MA nên đường thẳng d đi qua điểm A và vuông góc với MA.
Đồng thời đường thẳng d nằm trong mặt phẳng (P) nên ta có
Câu 2. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(2; 1; −2), B(5; 1; 1) và mặt cầu (S): x2 + y2 + z2 + 6y +12z + 9 = 0. Xét đường thẳng d đi qua A và tiếp xúc với (S) sao cho khoảng cách từ B đến d nhỏ nhất. Phương trình của đường thẳng d là
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn C
Mặt cầu (S): x2 + y2 + z2 + 6y +12z + 9 = 0 có tâm I(0; −3; −6) bán kính R = 6.
IA = 6 = R ⇒ A ∈ (S), nên B nằm ngoài (S).
Đường thẳng d đi qua A và tiếp xúc với (S) nên d nằm trong mặt phẳng (P) tiếp xúc với mặt cầu (S) tại A.
Mặt phẳng (P) đi qua A và nhận làm vectơ pháp tuyến có phương trình là x + 2y + 2z = 0.
Gọi H là hình chiếu của B lên (P) thì tọa độ của H(4; −1; −1).
Ta có: d(B; d) ≥ d(B; (P)) = BH.
Vậy khoảng cách từ B đến d nhỏ nhất khi d đi qua H. Ta có
Suy ra phương trình đường thẳng d là:
Dạng 6. Khoảng cách giữa hai đường thẳng chéo nhau
[content_7]Phương pháp giải
Trong không gian Oxyz, cho hai đường thẳng chéo nhau: ∆1 có vectơ chỉ phương và đi qua
M0(x0; y0; z0); ∆2 có vectơ chỉ phương và đi qua M’0(x’0; y’0; z’0)
Khi đó khoảng cách giữa ∆1 và ∆2 được tính bởi công thức
Nếu ∆1 // ∆2 ( và
cùng phương và M0 ∉ ∆2) thì d(∆1, ∆2) = d(M0, ∆2)
Bài tập vận dụng
Đề bài
Trong không gian Oxyz, tính khoảng cách giữa hai đường thẳng d1: và d2:
Hướng dẫn giải
Đường thẳng d1 đi qua điểm M(1; −2; 0) và có một vectơ chỉ phương
Đường thẳng d2 đi qua điểm N(1; −1; 2) và có một vectơ chỉ phương
Do cùng phương với
và M ∉ d2 nên d1 // d2.
Suy ra
Ta có
Suy ra
Vậy
Bài tập vận dụng
Câu 1. Cho phương trình mặt phẳng (P): 2x + y + z − 3 = 0, đường thẳng d’: và điểm A(0; 2; 1). Viết phương trình đường thẳng d đi qua A, nằm trong (P) sao cho khoảng cách d và d’ đạt giá trị lớn nhất.
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn A
Gọi d1 là đường thẳng đi qua A và song song với d’.
Phương trình của d1 là:
Trên đường thẳng d1 lấy điểm B(1; 0; 0).
Gọi (Q) là mặt phẳng chứa d và d1.
Ta có d(d, d’) = d(d’, (Q)) = d(B, (Q)).
Do d1 cố định cho nên d(d, d’) = d(B, (Q)) ≤ d(B, d1).
Đẳng thức xảy ra khi và chỉ khi trong đó H là hình chiếu của B lên d1.
Ta tìm được nên
.
Ta có
Vậy phương trình của đường thẳng d là
Lưu ý: Vì đường thẳng d đi qua A nên ta có thể loại đáp án bằng cách thay đổi tọa độ điểm A vào các đáp án trong bài.
Dạng 7. Vị trí tương đối giữa đường thẳng và mặt phẳng
[content_8]Phương pháp giải
Trong không gian Oxyz, xét đường thẳng (∆) có vectơ chỉ phương là và đi qua M0(x0, y0, z0) và mặt phẳng (α): Ax + By + Cz + D = 0 có vectơ pháp tuyến
– (∆) cắt (α) ⇔
– (∆) // (α) ⇔
– (∆) ⊂ (α) ⇔
– (∆) ⊥ (α) ⇔ và
cùng phương ⇔ a1 : a2 : a3 = A : B : C
Ta có thể biện luận vị trí tương đối dựa vào số nghiệm của phương trình đường thẳng (∆) và mặt phẳng (α)
Bài tập vận dụng
Câu 1. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: và mặt phẳng (P): 3x − 3y + 2z − 6 = 0. Mệnh đề nào dưới đây đúng?
A. d cắt và không vuông góc với (P)
B. d song song với (P)
C. d vuông góc với (P)
D. d nằm trong (P)
Hướng dẫn giải
⟹ Chọn A
Đường thẳng d nhận làm một vectơ chỉ phương.
Mặt phẳng (P) nhận làm một vectơ pháp tuyến.
Do và hai vectơ này không cùng phương nên đường thẳng d cắt và không vuông góc với (P).
Câu 2. Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng có phương trình d: và mặt phẳng (P): x + my + (m2 − 1)z − 7 = 0 với m là tham số thực. Tìm m sao cho đường thẳng d song song với mặt phẳng (P).
A. m = 1
B. m = −1
C.
D. m = 2
Hướng dẫn giải
⟹ Chọn B
Đường thẳng d có vectơ chỉ phương là và mặt phẳng (P) có vectơ pháp tuyến là
d // (P)
Thử lại ta thấy với m = −2 thì d ⊂ (P) (loại). Vậy m = −1.
Câu 3. Trong không gian Oxyz, cho đường thẳng d: và mặt phẳng (α): x − y + 2z – 5 = 0, mệnh đề nào dưới đây là đúng?
A. d // (α)
B. d ⊂ (α)
C. d cắt (α) và không vuông góc với (α)
D. d ⊥ (α)
Hướng dẫn giải
⟹ Chọn B
Ta có d:
Xét hệ phương trình:
Thay (1), (2), (3) vào (*) ta được 1 + 2t – (2 + 4t) + 2(3 + t) − 5 = 0. Phương trình này có vô số nghiệm.
Do đó, đường thẳng d nằm trong mặt phẳng (α).
Câu 4. Trong không gian Oxyz, cho hai mặt phẳng (P): x + 2y − z − 1 = 0, (Q): 2x + y − z + 2 = 0 và hai đường thẳng . Đường thẳng ∆ song song với hai mặt phẳng (P), (Q) và cắt ∆1, ∆2 tương ứng tại H, K. Độ dài đoạn HK bằng
A.
B.
C. 6
D.
Hướng dẫn giải
⟹ Chọn A
Ta có
Gọi H(2t; 1+ t; −1 + 2t); K(m; 2 − m;1 + 2m)
⇒
Vì ∆ song song với 2 mặt phẳng (P), (Q) nên nên
Tính ra được . Suy ra
.
Câu 5. Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): 2(m2 + m + 2)x + (m2 – 1)y + (m + 2)z + m2 + m +1 = 0 luôn chứa đường thẳng ∆ cố định khi m thay đổi. Khoảng cách từ gốc tọa độ đến ∆ là?
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn C
Ta có: 2(m2 + m + 2)x + (m2 – 1)y + (m + 2)z + m2 + m +1 = 0, ∀ m ∈ ℝ
⇔ m2(2x + y + 1) + m(2x + z + 1) + 4x − y + 2z + 1 = 0, ∀ m ∈ ℝ
Vậy (P) luôn chứa đường thẳng (∆) cố định:
Đường thẳng ∆ đi qua và có vectơ chỉ phương
Vậy khoảng cách từ gốc tọa độ đến ∆ là:
Dạng 8. Vị trí tương đối giữa hai đường thẳng
[content_9]Phương pháp giải
Trong không gian Oxyz, cho hai đường thẳng d1: đi qua M1(x0; y0; z0) có vectơ chỉ phương
và d2:
đi qua M2(x’0; y’0; z’0) có vectơ chỉ phương
.
Để xét vị trí tương đối của d1 và d2, ta sử dụng phương pháp sau:
– d1 trùng d2
– d1 // d2 hoặc
– d1 cắt d2
– d1 chéo d2 ⇔
Bài tập vận dụng
Câu 1. Trong không gian tọa độ Oxyz, cho hai đường thẳng
d1: và d2:
(m ≠ 0).
Tập hợp các giá trị m thỏa mãn d1 //d2 có số phần tử là:
A. 1
B. 0
C. 3
D. 2
Hướng dẫn giải
⟹ Chọn B
Đường thẳng d1 đi qua A(1; −1; 2) và có vectơ chỉ phương là
Đường thẳng d2 đi qua B(−3; −9; −2) và có vectơ chỉ phương là
Đường thẳng d1 // d2 khi và chỉ khi cùng phương với
và hai đường thẳng d1 và d2 không trùng nhau.
Vì nên B nằm trên đường thẳng d1.
Do đó hai đường thẳng này luôn có điểm chung là B nên hai đường thẳng không thể song song.
Câu 2. Trong không gian tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng
A. ∆1 song song với ∆2
B. ∆1 chéo với ∆2
C. ∆1 cắt ∆2
D. ∆1 trùng với ∆2
Hướng dẫn giải
⟹ Chọn C
Vì nên vectơ chỉ phương
của đường thẳng ∆1 không cùng phương với vectơ chỉ phương
của ∆2.
Suy ra ∆1 chéo với ∆2 hoặc ∆1 cắt ∆2.
Lấy M(1; −1; 0) ∈ ∆1, N(3; 3; −2) ∈ ∆2. Ta có
Khi đó
Suy ra đồng phẳng.
Vậy ∆1 cắt ∆2.
Dạng 9. Vị trí tương đối giữa đường thẳng và mặt cầu
[content_10]Phương pháp giải
Cho đường thẳng d: và mặt cầu (S): (x – a)2 + (y – b)2 + (z – c)2 = R2 có tâm I(a; b; c), bán kính R.
Bước 1: Tính khoảng cách từ tâm I của mặt cầu (S) đến đường thẳng d là
Bước 2: So sánh d(I, d) với bán kính R của mặt cầu:
– Nếu d(I, d) > R thì d không cắt (S).
– Nếu d(I, d) = R thì d tiếp xúc (S).
– Nếu d(I, d) < R thì d cắt (S) tại hai điểm phân biệt M, N và MN vuông góc với đường kính (bán kính) mặt cầu (S).
Bài tập vận dụng
Câu 1. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x2 + y2 + (z + 2)2 = 25 và đường thẳng d có phương trình . Chứng minh d luôn cắt (S) tại hai điểm phân biệt.
Hướng dẫn giải
Mặt cầu (S) có tâm I(0; 0; −2) và bán kính R = 5
Đường thẳng d đi qua M(−2; 2; −3) và có vectơ chỉ phương là
Ta có
Vì h < R nên d cắt mặt cầu (S) tại hai điểm phân biệt.
Phương pháp đại số
Thế (1), (2), (3) vào phương trình (S) và rút gọn đưa về phương trình bậc hai theo t (*).
– Nếu phương trình (*) vô nghiệm thì d không cắt (S).
– Nếu phương trình (*) có một nghiệm thì d tiếp xúc (S).
– Nếu phương trình (*) có hai nghiệm thì d cắt (S) tại hai điểm phân biệt M, N.
Chú ý: Để tìm tọa độ M, N ta thay giá trị t vào phương trình đường thẳng d.
Câu 2. Trong không gian Oxyz, mặt cầu (S): x2 + y2 + (z + 2)2 = 17 cắt trục Oz tại hai điểm A, B. Tìm độ dài đoạn AB.
Hướng dẫn giải
Gọi M là giao điểm của (S) với trục Oz.
Ta có M ∈ Oz nên M(0; 0; t).
Mà M ∈ (S) nên 02 + 02 + (t + 2)2 = 17
Suy ra tọa độ các giao điểm là .
Bài tập vận dụng
Câu 1. Trong không gian tọa độ Oxyz, cho điểm A(0; 0; −2) và đường thẳng ∆ có phương trình là . Phương trình mặt cầu tâm A, cắt ∆ tại hai điểm B và C sao cho BC = 8 là
A. (x + 2)2 + (y – 3)2 + (z + 1)2 = 16
B. x2 + y2 + (z + 2)2 = 25
C. (x + 2)2 + y2 + z2 = 25
D. x2 + y2 + (z + 2)2 = 16
Hướng dẫn giải
⟹ Chọn B
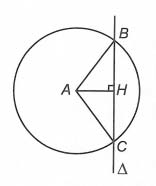
Gọi (S) là mặt cầu tâm A(0; 0; −2) và có bán kính R.
Đường thẳng ∆ đi qua M(−2; 2; −3) có vectơ chỉ phương .
Gọi H là trung điểm BC nên AH ⊥ BC
Ta có
Với
Bán kính mặt cầu (S) là:
Vậy phương trình mặt cầu (S) là: x2 + y2 + (z + 2)2 = 25.
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x − 1)2 + (y + 1)2 + (z − 2)2 = 9 và điểm M(1; 3; −1). Biết rằng các tiếp điểm của các tiếp tuyến kẻ từ M tới mặt cầu đã cho luôn thuộc một đường tròn (C) có tâm J(a; b; c). Giá trị 2a + b + c bằng
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn C
Ta có mặt cầu (S) có tâm I(1; −1; 2) và bán kính R = 3.
Khi đó IM = 5 > R ⇒ M nằm ngoài mặt cầu.
Phương trình đường thẳng MI là
Tâm J(a; b; c) nằm trên MI nên J(1; −1 + 4t; 2 − 3t).
Xét ∆MHI vuông tại H có
Mặt khác
Suy ra hoặc
– Với thì
(nhận)
– Với thì
(loại)
Vậy nên
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình là và đường thẳng d có phương trình
. Gọi A(x0; y0; z0), x0 > 0 là điểm nằm trên đường thẳng d sao cho từ A kẻ được ba tiếp tuyến đến mặt cầu (S) có các tiếp điểm B, C, D sao cho ABCD là tứ diện đều. Giá trị của biểu thức P = x0 + y0 + z0 là
A. 6
B. 16
C. 12
D. 8
Hướng dẫn giải
⟹ Chọn C
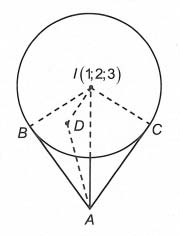
I là tâm mặt cầu thì I(1; 2; 3).
Gọi O là giao điểm của mặt phẳng (BCD) và đoạn AI.
Vì theo giả thiết AB = AC = AD và nên AI vuông góc với mặt phẳng (BCD) tại O. Khi đó O là tâm đường tròn ngoại tiếp ∆BCD.
Đặt
Ta có
Do ABCD là tứ diện đều nên
A ∈ d nên A(4 + 3t; 4 + 2t; 4 + t).
Suy ra
Do x0 > 0 nên điểm A có tọa độ A(4; 4; 4).
Suy ra P = 12.
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho ba điểm P, Q, R lần lượt di động trên ba trục tọa độ Ox, Oy, Oz (không trùng với gốc tọa độ O) sao cho . Biết mặt phẳng (PQR) luôn tiếp xúc với mặt cầu (S) cố định. Đường thẳng (d) thay đổi nhưng luôn đi qua
và cắt (S) tại hai điểm A, B phân biệt. Diện tích lớn nhất của ∆AOB là
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn D
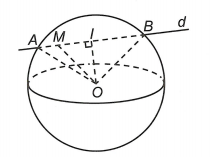
Gọi H là hình chiếu vuông góc của điểm O trên mặt phẳng (PQR).
Dễ thấy
Khi đó (PQR) luôn tiếp xúc với mặt cầu (S) tâm O, bán kính .
Ta có nên điểm M nằm trong mặt cầu (S).
Gọi I là trung điểm của AB, do ∆OAB cân tại O nên
Đặt OI = x. Vì OI ≤ OM nên 0 < x ≤ 1 và
Ta có
Xét hàm số f(x) = 8x2 – x4, 0 < x ≤ 1.
Vì f ‘(x) = 4x(4 − x2) > 0 với mọi x ∈ (0;1) nên f(x) ≤ f(1) = 7.
Suy ra diện tích của ∆OAB lớn nhất bằng đạt được khi M là trung điểm của AB.
Dạng 10. Một số bài toán cực trị
[content_1]Bài tập vận dụng
Câu 1. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm M(−2; −2; 1), A(1; 2; −3) và đường thẳng d: . Tìm một vectơ chỉ phương
của đường thẳng ∆ đi qua M, vuông góc với đường thẳng d đồng thời cách điểm A một khoảng bé nhất.
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn C
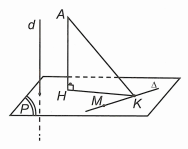
Xét (P) là mặt phẳng qua M và (P) ⊥(d).
Mặt phẳng (P) qua M(−2; −2; 1) và có vectơ pháp tuyến nên có phương trình: 2x + 2y − z + 9 = 0.
Gọi H, K lần lượt là hình chiếu của A lên (P) và ∆.
Khi đó AK ≥ AH = const nên AK đạt giá trị nhỏ nhất khi và chỉ khi K ≡ H.
Đường thẳng AH đi qua A(1; 2; −3) và có vectơ chỉ phương nên AH có phương trình tham số là
Vì H ∈ AH nên H(1 + 2t; 2 + 2t; −3 – t).
Lại H ∈ (P) nên 2(1 + 2t) + 2(2 + 2t) – (−3 – t) + 9 = 0 ⇔ t = −2 ⇒ H(−3; −2; −1)
Vậy
Câu 2. Trong không gian Oxyz, cho mặt cầu (S) có phương trình x2 + y2 + z2 − 4x + 2y − 2z − 3 = 0 và điểm A(5; 3; −2). Một đường thẳng d thay đổi luôn đi qua A và luôn cắt mặt cầu tại hai điểm phân biệt M, N. Tính giá trị nhỏ nhất của biểu thức S = AM + 4AN.
A. Smin = 30
B. Smin = 20
C. Smin =
D. Smin =
Hướng dẫn giải
⟹ Chọn C
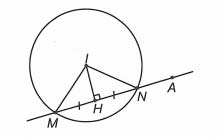
Mặt cầu (S) có tâm I(2; −1; 1), bán kính
Ta có: > R nên A nằm ngoài mặt cầu (S).
Ta lại có: S = AM + 4AN.
Đặt
Mà
Do đó: với
Ta có: với
Do đó:
Dấu “=” xảy ra ⇔ A, M, N, I thẳng hàng và
Câu 3. Trong không gian Oxyz, cho hai điểm A(9; 6; 11), B(5; 7; 2) và điểm M di động trên mặt cầu (S): (x – 1)2 + (y – 2)2 + (z – 3)2 = 36. Giá trị nhỏ nhất của AM + 2MB bằng
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn C
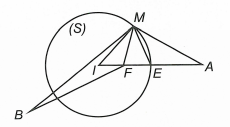
Mặt cầu (S): (x – 1)2 + (y – 2)2 + (z – 3)2 = 36 có tâm I(1; 2; 3) và bán kính R = 6 .
Ta có IA = 12 = 2R.
Gọi E là giao điểm của IA và mặt cầu (S) suy ra E là trung điểm của IA nên E(5; 4; 7).
Gọi F là trung điểm của IE suy ra F(3; 3; 5).
Xét ∆MIF và ∆AIM có chung và
Suy ra ∆MIF ∽ ∆AIM (c.g.c) ⇒
Do đó (theo bất đẳng thức tam giác).
Dấu “=” xảy ra khi M là giao điểm FB và mặt cầu (S).