Tổng hợp chi tiết lý thuyết hàm số mũ, hàm số logarit và các dạng bài tập đặc trưng. Chuyên đề thuộc chương trình toán học lớp 12. Bài giảng kèm bộ tài liệu có hướng dẫn giải chi tiết nhất do VerbaLearn tổng hợp và biên soạn.

Đạo hàm hàm số mũ, hàm số logarit
Tổng hợp các công thức đạo hàm hàm số mũ, hàm số logarit chi tiết nhất. Đây là những công thức được sử dụng phổ biến khi làm bài tập và bắt buộc phải ghi nhớ.
1. Hàm số mũ
1.
2.
3.
4.
Với u = u(x) là hàm hợp theo biến x
2. Hàm số logarit
1.
2.
3.
4.
Với u = u(x) là hàm hợp theo biến x.
Khảo sát hàm số mũ và hàm số logarit
1. Hàm số mũ
a > 1
– Tập xác định: D = ℝ
– Tập giá trị: T = (0; +∞)
– Tính đơn điệu: ⟹ Hàm số đồng biến trên ℝ
– Giới hạn đặc biệt: ⟹ y = 0 là tiệm cận ngang.
– Bảng biến thiên
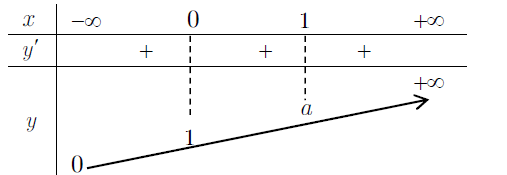
– Đồ thị
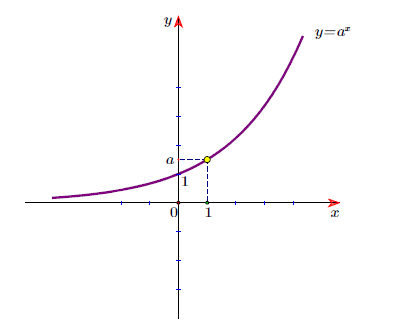
0 < a <1
– Tập xác định: D = ℝ
– Tập giá trị: T = (0; +∞)
– Tính đơn điệu: ⟹ Hàm số nghịch biến trên ℝ
– Giới hạn đặc biệt: là tiệm cận nang
– Bảng biến thiên
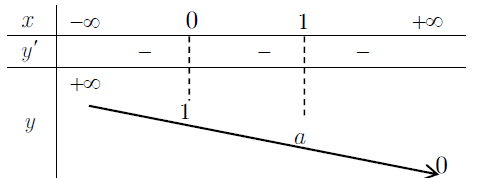
– Đồ thị
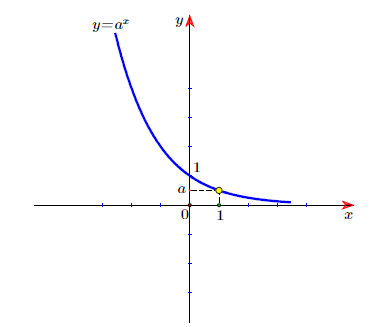
⟹ Đồ thị hàm số luôn đi qua 2 điểm A(0;1), B(1;a) và nhận trục hoành làm tiệm cận ngang.
2. Hàm số logarit 
Với a > 1
– Tập xác định: D = (0; +∞)
– Tập giá trị T = ℝ
– Tính đơn điệu:
– Hàm số đồng biến trên (0; +∞)
– Giới hạn đặc biệt:
⟹ x = 0 là tiệm cận đứng
– Bảng biến thiên
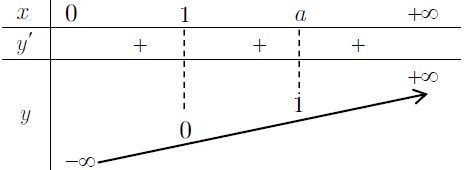
– Đồ thị
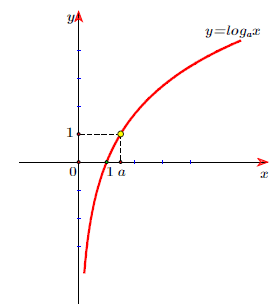
Với 0 < a < 1
– Tập xác định: D = (0; +∞)
– Tập giá trị: T = ℝ
– Tính đơn điệu
⟹ Hàm số nghịch biến trên (0; +∞)
– Giới hiện đặc biệt
⟹ x = 0 là tiệm cận đứng
– Bảng biến thiên
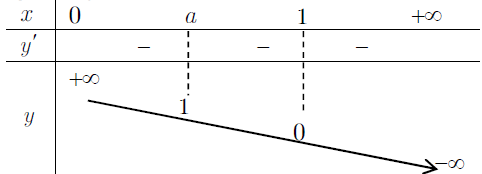
– Đồ thị
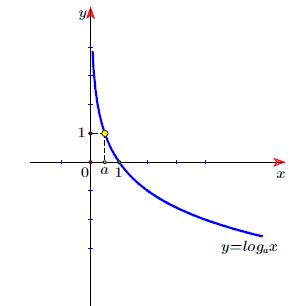
⟹ Đồ thị hàm số luôn đi qua 2 điểm A(1;0), B(a;1) và nhận trục tung làm tiệm cận đứng.
3. So sánh đồ thị hàm số lũy thừa, hàm số logarit
⟹ Đặc điểm chung của đồ thị hàm số y = ax và y = logax khi vẽ trên cùng hệ trục tọa độ: Hai đồ thị của hàm số luôn đối xứng nhau qua đường thẳng y = x ( Đường phân giác của góc phần tư thứ nhất và thứ ba).
Với a > 1
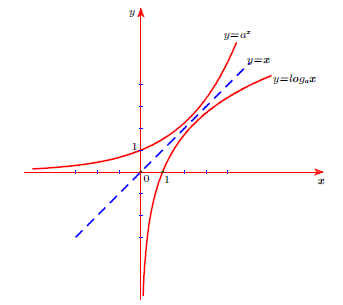
Với 0 < a <1
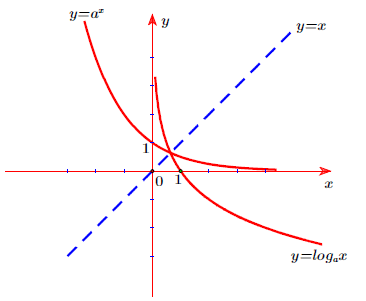
Phân dạng bài tập
Dạng 1. Tìm tập xác định của hàm số logarit
Phương pháp giải
Hàm số logarit y = loga f(x) xác định .
Theo tính đơn điệu của hàm số mũ và hàm số logarit ta luôn có:
Với a > 1 thì .
Với 0 < a < 1 thì .
Hàm số y = loga f(x) xác định trên tập K ⇔ f(x) > 0, ∀x ∊ K.
Bài tập vận dụng
Câu 1. Tập xác định của hàm số là
A. D = (1; 3)
B. D = (–1; 1)
C. D = (–∞; 3)
D. D = (1; +∞)
Hướng dẫn giải
Hàm số xác định . Vậy TXĐ: D = (1; 3).
⟹ Chọn A
Câu 2. Tìm tập xác định của hàm số .
A.
B.
C.
D.
Hướng dẫn giải
Hàm số xác định . Vậy TXĐ:
.
⟹ Chọn A
Câu 3. Tập xác định của hàm số là
A. D = (–3; e)
B. D = (0; 1)
C. D = (–∞; 1)
D. D = (0; +∞)
Hướng dẫn giải
Hàm số xác định .
Vậy TXĐ: D = (0; 1).
⟹ Chọn B
Câu 4. Tập xác định của hàm số là
A. D = (–1; 1]
B. D = (–1; 0)
C. D = [1; +∞)
D. D = (–∞; 1]
Hướng dẫn giải
HSXĐ
Vậy TXĐ: D = (–1; 0).
⟹ Chọn B
Câu 5. Tìm giá trị nguyên âm lớn nhất của tham số m để hàm số y = log2020 (x3 – 3x2 + 2 – m) luôn xác định trên khoảng (–2; +∞).
A. –1
B. –19
C. –18
D. –5
Hướng dẫn giải
Hàm số xác định trên (–2; +∞) ⇔ x3 – 3x2 + 2 – m >0, ∀x ∊ (–2; +∞)
⇔ m < f(x) = x3 – 3x2 + 2, ∀x ∊ (–2; +∞)
Ta có .
BBT:
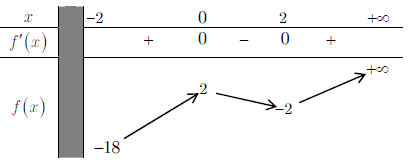
Dựa vào BBT, suy ra: m ≤ –18. Vậy giá trị nguyên âm lớn nhất của m là –18.
⟹ Chọn C
Câu 6. Tìm tất cả các giá trị của tham số m để hàm số có tập xác định là ℝ
A.
B.
C.
D.
Hướng dẫn giải
Hàm số xác định trên ℝ .
.
⟹ Chọn A
Dạng 2. Đạo hàm và đồ thị của hàm số mũ – logarit
Phương pháp giải giải
Ghi nhớ công thức hàm số mũ
– (ax)’ = ax. ln a
– (au)’ = u’. au. ln a
– (ex)’ = ex
– (eu)’ = u’. eu
Với u = u(x) là hàm hợp theo biến x.
Ghi nhớ công thức hàm số logarit
–
–
–
–
Với u = u(x) là hàm hợp theo biến x.
– Sử dụng máy tính cầm tay để tính đạo hàm của hàm số tại một điểm
– Để tính đạo hàm của hàm số tại 1 điểm x0 cho trước ta có thể sử dụng chức năng
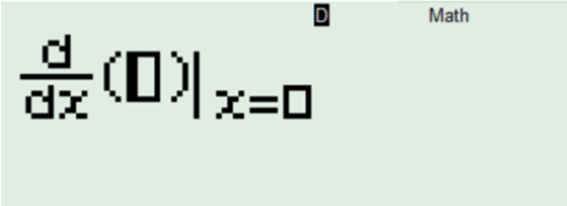 Với u = u(x) là hàm hợp theo biến x.
Với u = u(x) là hàm hợp theo biến x.
– Bước 1: Bấm tổ hợp shift + ![]()
– Bước 2: Nhập hàm số và giá trị x0 cần tính đạo hàm.
Bài tập vận dụng
Câu 1. Trong các hàm số sau, hàm số nào đồng biến trên ℝ?
A.
B.
C.
D.
Hướng dẫn giải
Hàm số đồng biến trên ℝ vì
.
⟹ Chọn A
Câu 2. Trong các hàm số sau, hàm số nào đồng biến trên tập xác định của nó?
A. y = log x
B.
C.
D. y = ln (x2 + 1)
Hướng dẫn giải
Hàm số y = log x đồng biến trên tập xác định của nó vì cơ số 10 > 1.
⟹ Chọn A
Câu 3. Cho 4 hàm số f(x) = ln x, ,
,
. Có bao nhiêu hàm số đồng biến trên khoảng (0; + ∞)?
A .1
B. 2
C. 3
D. 4
Hướng dẫn giải
Hàm số f(x) = ln x đồng biến trên (0; +∞) vì cơ số e > 1
Hàm số nghịch biến trên ℝ vì cơ số
.
Hàm số xác định với ∀x ∊ ℝ và
nên hàm số đồng biến trên (0; +∞).
Hàm số xác định với ∀x ∊ ℝ và
nên hàm số đồng biến trên (0; +∞).
⟹ Chọn C
Câu 4. Đạo hàm của hàm số y = ecos2x tại bằng
A.
B.
C.
D.
Hướng dẫn giải
y’ = (cos2x)’. ecos2x = –2 sin2x. ecos2x
⟹ Chọn B
Câu 5. Phát biểu nào sau đây sai?
A. Hai hàm số y = ax và y = loga x với a > 1 có cùng tính đơn điệu trên tập xác định.
B. Đồ thị hàm số y = ax với 0 < a ≠ 1 luôn nằm trên trục hoành.
C. Đồ thị hàm số y = loga x với 0 < a ≠ 1 luôn nằm bên phải trục tung.
D. Hai hàm số y = ax và y = loga x (0 < a < 1) đều có đồ thị nằm phía trên trục hoành.
Hướng dẫn giải
Căn cứ vào tính chất của đồ thị hàm số mũ ta rút ra kết quả là đáp án D
Hai hàm số y = ax và y = loga x với a > 1 cùng đồng biến trên TXĐ.
y = ax nên đồ thị luôn nằm trên trục hoành.
y = loga x có TXĐ D = (0; +∞) nên đồ thị luôn nằm bên phải trục tung.
⟹ Chọn D
Câu 6. Cho hàm số f(x) = 2ex – x. Đồ thị của hàm số y = f’(x) có thể là hình vẽ nào sau đây?
A. 
B. 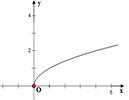
C. 
D. 
Hướng dẫn giải
Ta có f’(x) = 2ex – 1. Xét hàm số g(x) = 2ex – 1.
g’(x) = 2. ex > 0, ∀x ∊ ℝ. Do đó hàm số luôn đồng biến và đi qua điểm M (0; 1).
⟹ Chọn D
Câu 7. Nếu và
thì ta kết luận gì về a, b?
A. 0 < a, b < 1
B. 0 < a < 1, b > 1
C. a > 1, 0 < b < 1
D. a, b > 1
Hướng dẫn giải
Ta có và
.
⟹ Chọn B
Câu 8. Hình bên dưới là đồ thị của ba hàm số y = loga x, y = logb x, y = logc x với 0 < a, b, c ≠ 1 được vẽ trên cùng một hệ trục tọa độ.
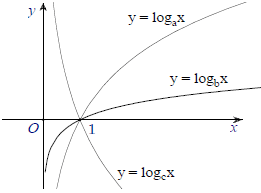
Khẳng định nào sau đây đúng?
A. a > c > b
B. a > b > c
C. b > c > a
D. b > a > c
Hướng dẫn giải
Vì đồ thị hàm số y = logc x nghịch biến trên (0; +∞) nên 0 < c < 1.
Đồ thị hàm số y = loga x, y = logb x đồng biến trên (0; +∞) nên a, b > 1.
Dựng đường thẳng y = 1 cắt hai đồ thị hàm y = loga x, y = logb x lần lượt tại A (a; 1), B (b; 1) nên b > a. Vậy b > a > c.
⟹ Chọn D
Câu 9. Hình bên dưới là đồ thị của ba hàm số y = ax, y = bx, y = cx với 0 < a, b, c ≠ 1 được vẽ trên cùng một hệ tọa độ.
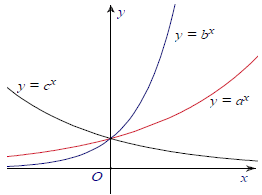
Khẳng định nào sau dây đúng?
A. a > c > b
B. a > b > c
C. b > c > a
D. b > a > c
Hướng dẫn giải
Vì đồ thị hàm số y = cx nghịch biên trên ℝ nên 0 < c < 1.
Đồ thị hàm số y = ax, y = bx đồng biến trên ℝ nên a, b > 1.
Dựng đường thẳng x = 1 cắt 2 đồ thị hàm y = ax, y = bx lần lượt tại A (1; a), B (1; b) nên b > a. Vậy b > a > c.
⟹ Chọn D
Câu 10. Đạo hàm của hàm số y = log7 (x2 – 3x + 4) là
A. y’ = (2x – 3). log7 (x2 – 3x + 4)
B.
C.
D.
Hướng dẫn giải
⟹ Chọn C
Ta có .
Câu 11. Cho hàm số . Tính giá trị f’ (0).
A.
B. 2 ln 2
C. 2
D. ln 2
Hướng dẫn giải
Ta có . Vậy f’ (0) = 2. 2–1. ln 2 = ln 2.
⟹ Chọn D
Câu 12. Đạo hàm của hàm số .
A.
B.
C.
D.
Hướng dẫn giải
Ta có .
Tổng quát: với a > 0.
⟹ Chọn D
Câu 13. Tính tổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số f(x) = x – ln (x + 1) trên [0; 2].
A. 0
B. 1 – ln 2
C. 2 – ln 3
A. 2 + ln 3
Hướng dẫn giải
Ta có .
Vây .
⟹ Chọn C
Câu 14. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn
. Khi đó giá trị của biểu thức
bằng
A.
B.
C.
D.
Hướng dẫn giải
Ta có .
. Vậy
.
⟹ Chọn C
Câu 15. Cho hàm số . Tìm mệnh đề đúng trong các mệnh đề sau
A. xy’ – 1 = –ey
B. xy’ – 1 = ey
C. xy’ + 1 = ey
D. xy’ + 1 = –ey
Hướng dẫn giải
TXĐ: D = (1; +∞).
Ta có .
. Mà
nên xy’ + 1 = ey.
⟹ Chọn C
Câu 16. Cho hàm số . Tìm tất cả các giá trị thực của tham số m để hàm số m đã cho luôn nghịch biến trên ℝ.
A.
B.
C.
D.
Hướng dẫn giải
HS luôn NB trên ℝ .
.
⟹ Chọn A
Câu 17. Có bao nhiêu giá trị nguyên dương của m để hàm số đông biến trên khoảng (0; +∞)?
A. 1
B. 2
C. 3
D. 4
Hướng dẫn giải
Ta có .
YCBT
Xét hàm số trên (0; +∞). Ta có
Bảng biến thiên
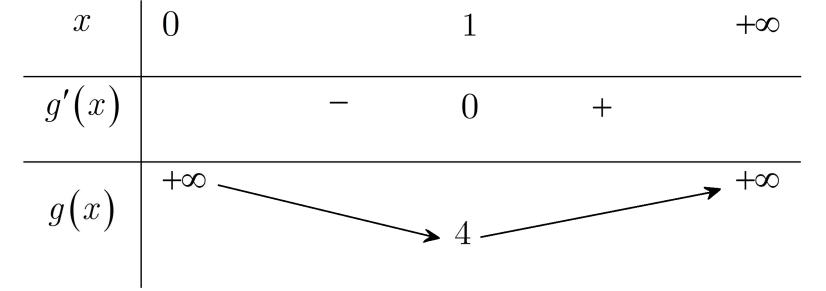
Dựa vào bảng biến thiên suy ra 2 (m – 1) ≤ 4 ⇔ m ≤ 3.
Do m nguyên dương nên m ∊ {1; 2; 3}. Vậy có 3 giá trị m nguyên dương thỏa mãn.
⟹ Chọn C
Dạng 3. Các bài toán thực tế về hàm số mũ
Phương pháp giải
Bài toán 1: (Lãi kép) Một người gửi vào ngân hàng số tiền A đồng, với lãi suất là r% trên một kì hạn. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi kì hạn, số tiền lãi được nhập vào vốn ban đầu, sau n kì hạn, số tiền cả vốn lẫn lãi nhận dược là:
Tn = A (1 + r%) (kì hạn ở đây có thể là một năm; 1 tháng hoặc k tháng)
Chứng minh
Số tiền nhận được (gồm cả gốc và lãi) sau kì hạn thứ nhất là T1 = A + A. r% = A (1 + r%)
Số tiền nhận được (gồm cả gốc và lãi) sau kì hạn thứ 2 là T2 = T1 + T1. r% = T1 (1 + r%) = A (1+ r%)2
………
Số tiền nhận được (gồm cả gốc và lãi) sau kì hạn thứ n là
Tn = Tn – 1 + Tn – 1. r% = Tn – 1. (1 + r%) = A (1 + r%) n
Bài toán 2: (Gửi tiết kiệm) Hàng tháng một người gửi vào ngân hàng số tiền là A đồng (gửi đầu tháng). Biết lãi suất hàng tháng là r%. Tổng tiền nhận được sau n tháng là:
Chứng minh
Số tiền có được (gồm cả gốc và lãi) vào cuối thứ nhất là T1 = A + A. r% = A (1 + r%).
Số tiền có được (gồm cả gốc và lãi) vào cuối thứ hai là
T2 = T1 + A + (T1 + A). r% = (T1 + A) (1 + r%) = A (1 + r%)2 + A (1 + r%).
Số tiền có được (gồm cả gốc và lãi) vào cuối thứ ba là
T3 = T2 + A + (T2 + A). r% = (T2 + A) (1 + r%) = A (1 + r%)3 + A (1 + r%)2 + A (1 + r%).
…….
Số tiền nhận được (gồm cả gốc và lãi) vào cuối tháng thứ n là
Tn = A (1 + r%) n + A (1+ r%) n – 1 +… + A (1 + r%) = A [(1 + r%) + (1 + r%)2 +… + (1 + r%) n – 1 + (1 + r%) n]
Theo công thức tính tổng n số hạng đầu tiên của CSN ta suy ra:
Bài toán 3: (Vay trả góp) Một người vay ngân hàng A đồng, với lãi suất là r% trên một tháng, sau đúng một tháng kể từ ngày vay, bắt đầu hoàn nợ, hai lần hoàn nợ cách nhau đúng một tháng, mỗi lần hoàn nợ trả a đồng. Số tiền còn nợ ngân hàng sau n tháng là:
Chứng minh:
Số tiền còn nợ ngân hàng vào cuối thứ nhất là T1 = A (1 + r%) – a.
Số tiền còn nợ ngân hàng vào cuối thứ hai là:
T2 = T1 (1 + r%) – a = [A (1 + r%) – a] (1 + r%) – a = A (1 + r%)2 – a (1 + r%) – a
Số tiền còn nợ ngân hàng vào cuối thứ ba là:
T3 = T2 (1 + r%) – a = [A (a + r%)2 – a (1 + r%) – a] (1 + r%) – a = A (1 + r%)3 – a (1 + r%)2 – a (1 + r%) – a
…..
Số tiền còn nợ ngân hàng vào cuối tháng thứ n là:
Tn = Tn – 1 (1 + r%) – a = A (1 + r%) n – a (1 + r%) n – 1 – a (1 + r%) n – 2 – … – a (1 + r%) – a
⇔ Tn = A (1 + r%) n – a [(1 + r%) n – 1 + (1 + r%) n – 2 + …+ (1 + r%) + 1]
Theo công thức tính tổng n số hạng đầu tiên của CSN ta suy ra:
Chú ý: Để trả hết nợ cho Tn = 0 ta sẽ tìm ra được thời gian trả hết số tiền đã vay.
Bài toán: (Gửi tiết kiệm và rút hàng tháng) Một người gửi ngân hàng A đồng, với lãi suất là r% trên một tháng. Mỗi tháng vào ngày ngân hàng tính lãi, người này rút ra một số tiền là a để sử dụng. Sau n tháng thì số tiền còn lại trong ngân hàng là:
Bài tập vận dụng
Câu 1. Một người gửi tiết kiệm số tiền 100.000.000 VNĐ vào ngân hàng với lãi suất 8% / năm và lãi suất hàng năm được nhập vào vốn. Hỏi sau 15 năm số tiền người ấy nhận về là bao nhiêu? (làm tròn đến đơn vị nghìn đồng):
A .117.217.000 VNĐ
B. 417.217.000 VNĐ
C. 317.217.000 VNĐ
D. 217.217.000 VNĐ
Hướng dẫn giải
Theo công thức ở bài toán 1 ta có: T15 = 108 (1 + 8%) 15 = 317.216.911.
⟹ Chọn C
Câu 2. Một người gửi tiết kiệm vào ngân hàng với lãi suất 8,4% / năm và tiền lãi hàng năm được nhập vào tiền vốn. Tính số năm tối thiểu người đó cần gửi để số tiền thu được nhiều hơn 2 lần số tiền gửi ban đầu.
A. 10 năm
B. 9 năm
C. 8 năm
D. 11 năm
Hướng dẫn giải
Gọi số tiền gửi ban đầu là A và số năm tối thiểu thỏa ycbt là n.
Ta có A (1 + 8,4%) n = 2A ⇔ 1,084n = 2 ⇔ n = log1,084 2 = 8,59.
Vậy số năm tối thiểu là 9 năm.
⟹ Chọn B
Câu 3. Theo thông tin trên internet, lãi suất tiền gửi của ngân hàng TP Bank là 6,2%/ năm. Tại thời điểm ngày 01/01/2020 anh Nguyễn Văn A dự định vào ngày 01/01/2021 sẽ mua một chiếc laptop trị giá 20.000.000 đồng nên đã quyết định gửi ngân hàng trên một số tiền là T triệu đồng. Theo em anh Nguyễn Văn A nên gửi số tiền gần với số tiền nào sau đây?
A. 18.832.391 đồng
B. 15.832.391 đồng
C. 17.832.391 đồng
D. 16.832.391 đồng
Hướng dẫn giải
Số tiền anh A nhận được sau 12 tháng được tính bởi công thức:
T1 = T. (1 +r%)1 ⇔ 20.000.000 = T (1 + 6,2%) ⇒
⟹ Chọn A
Câu 4. Một người gửi tiết kiệm với số tiền gửi là A đồng với lãi suất 6% một năm, biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính gốc cho năm tiếp theo. Sau 10 năm người đó rút ra được số tiền gốc lẫn lãi nhiều hơn số tiền ban đầu là 100 triệu đồng? Hỏi người đó phải gửi số tiền A bằng bao nhiêu?
A. 145.037.058 đồng
B. 55.839.478 đồng
C. 126.446.589 đồng
D. 111.321.564 đồng
Hướng dẫn giải
Từ công thức lãi kép ta có A n = A (1 + r) n.
Theo đề bài ta có
⟹ Chọn C
Câu 5. Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền T theo hình thức lãi kép với lãi suất 0,6% mỗi tháng. Biết sau 15 tháng, người đó có số tiền là 10 triệu đồng. Hỏi số tiền T gần với số tiền nào nhất trong các số sau.
A. 635.000 đồng
B. 645.000 đồng
C. 613.000 đồng
D. 535.000 đồng
Hướng dẫn giải
Với số tiền T gửi đều đặn mỗi tháng theo hình thức lãi kép với lãi suất r% mỗi tháng, ta có
Sau một tháng, số tiền của người đó là A1 = T (1 + r) đồng.
Sau hai tháng, số tiền của người đó là A2 = [T (1 + r) + T] (1 + r) = T [(1 + r)2 + (1 + r)] đồng.
Sau ba tháng, số tiền của người đó là
A3 = {T [(1 + r)2 + (1 + r)] + T} (1 + r) = T [(1 + r)3 + (1 + r)2 + (1 + r)] đồng.
….
Sau mười lăm tháng, số tiền của người đó là
đồng.
Theo đề thì sau 15 tháng người đó có số tiền là 10 triệu đồng nên
đồng.
⟹ Chọn A
Câu 6. Anh Nam dự điịnh sau 8 năm (kể từ lúc gửi tiết kiệm lần đầu) sẽ có đủ 2 tỉ đồng để mua nhà. Mỗi năm anh phải gửi tiết kiệm bao nhiêu (số tiền mỗi năm gửi như nhau ở thời điểm cách lần gửi trước 1 năm)? Biết lãi suất là 8% / năm, lãi hàng năm được nhập vào vốn và sau kỳ gửi cuối cùng anh đợi đúng 1 năm để có đủ 2 tỉ đồng.
A. tỉ đồng
B. tỉ đồng
C. tỉ đồng
D. tỉ đồng
Hướng dẫn giải
Gọi M là số tiền anh Nam phải gửi hàng năm.
Để sau 8 năm (kể từ lúc gửi tiết kiệm làn đầu) sẽ có đủ 2 tỉ đồng, tính luôn cả thời gian anh đợi để rút tiền ra thì anh gửi tất cả 8 lần.
Ta có công thức
tỉ đồng.
⟹ Chọn A
Câu 7. Một người vay ngân hàng 100 triệu đồng với lãi suất là 0,7% / tháng, theo thỏa thuận cứ mỗi tháng người đó sẽ trả cho ngân hàng 5 triệu đồng và cứ trả hàng tháng như thế cho đến khi hết nợ (tháng cuối cùng có thể trả dưới 5 triệu). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng.
A. 21
B. 22
C. 23
D. 24
Hướng dẫn giải
Theo công thức ở bài toán 3, số tiền mà người đó còn nợ sau n tháng là:
.
Sau n tháng thì người đó sẽ trả hết nợ thì
Vậy sau tháng thứ 22 thì người đó sẽ trả hết nợ.
⟹ Chọn B
Câu 8. Năm 1992, người ta đã biết số p = 2756839 – 1 là một nguyên tố (số nguyên tố lớn nhất được biết cho đến lúc đó). Hãy tìm số các chữ số của p khi viết trong hệ thập phân.
A. 227830 chữ số
B. 227834 chữ số
C. 227832 chữ số
D. 227831 chữ số
Hướng dẫn giải
2756839 có chữ số tận cùng khác 0 nên 2756839 và p = 2756839 – 1 có các chữ số bằng nhau.
Số các chữ số của p khi viết trong hệ thập phân của p = 2756839 – 1 là:
[log 2756839] + 1 = [756839 log2] + 1 = [227831,2409] + 1 = 227832Suy ra p = 2756839 – 1 khi viết trong hệ thập phân là số có 227832 chữ số.
⟹ Chọn C
Câu 9. Dân số thế giới được dự đoán theo công thức P(t) = a. ebt, trong đó a, b là các hằng số, t là năm tính dân số. Theo số liệu thực tế, dân số thế giới năm 1950 là 2560 triệu người; dân số thế giới năm 1980 là 3040 triệu người. Hãy dự đoán dân số thế giới năm 2020?
A. 3823 triệu
B. 5360 triệu
C. 3954 triệu
D. 4017 triệu
Hướng dẫn giải
Từ giả thiết ta có hệ phương trình:
.
Suy ra: .
Vậy dân số thế giới năm 2020 là .
⟹ Chọn A
Câu 10. Sự tăng trưởng của một loại vi khuẩn tuân theo công thức S = A. ert, trong đó A là số vi khuẩn ban đầu, r là tỉ lệ tăng trưởng, t là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ có 300 con. Để số lượng vi khuẩn ban đầu tăng gấp đôi thì thời gian tăng trưởng t gần với kết quả nào sau đây nhất?
A. 3 giờ 9 phút
B. 3 giờ 2 phút
C. 3 giờ 30 phút
D. 3 giờ 18 phút
Hướng dẫn giải
Ta có . Khi đó
giờ.
⟹ Chọn A
Dạng 4. Cực trị hàm số mũ – logarit và min max hàm nhiều biến
Bài tập vận dụng
Câu 1. Tìm giá trị cực tiểu của hàm số
A. x = 0
B. y = 1
C. x = 1
D. y = 0
Hướng dẫn giải
Tập xác định: D = ℝ \ {–1}.
Ta có .
Lập BBT, suy ra hàm số đạt cực tiểu tại x = 0 và yCT = y (0) = 1.
⟹ Chọn B
Câu 2. Tìm điểm cực tiểu của hám số y = x2 lnx.
A.
B.
C. x = e
D.
Hướng dẫn giải
TXĐ: D = (0; +∞).
Ta có
Bảng biến thiên

Dựa vào bảng biến thiên suy ra hàm số đạt cực tiểu tại .
⟹ Chọn B
Câu 3. Tọa độ điểm cực đại của đồ thị hàm số là
A.
B.
C.
D.
Hướng dẫn giải
TXĐ: D = ℝ.
Ta có
Bảng xét dấu của y’

Vậy hàm số đã cho đạt cực đại tại
Tọa đồ điểm cực đại của đồ thị hàm số đã cho là .
⟹ Chọn B
Câu 4. Cho hàm số y = f’ (x – 1) có đồ thị như hình vẽ

Hàm số y = π2 f(x) – 4x đạt cực tiểu tại điểm nào?
A. x = 2
B. x = –1
C. x = 1
D. x = 0
Hướng dẫn giải
Ta có y’ = [2 f’(x) – 4] π2 f(x) – 4x ln π = 0 ⇔ 2 f’(x) – 4 = 0 ⇔ f’(x) = 2.
Đặt x = t – 1 ta có f’ (t – 1) = 2.
Dựa vào đồ thị ta có
Như vậy .
Do x = –2 và x = 1 là nghiệm bội chẵn nên ta có bảng biến thiên sau:
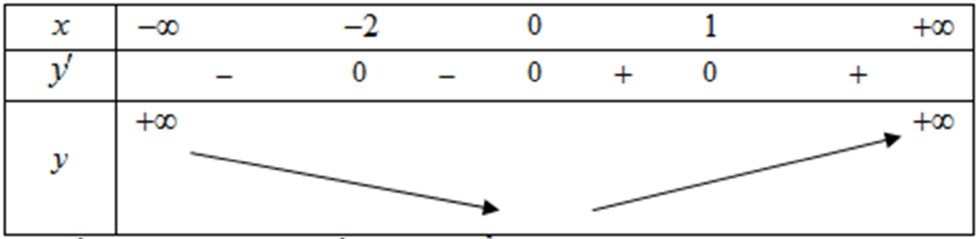
Từ bảng biến thiên ta có hàm số đạt cực tiểu tại x = 0.
⟹ Chọn D
Câu 5. Cho , với a > 1, b > 1 và P = loga2 b + 16 logb a. Tìm m sao cho P đạt giá trị nhỏ nhất.
A. m = 1
B.
C. m = 4
D. m = 2
Hướng dẫn giải
Ta có .
Vì a, b > 1 nên .
Khi đó: .
Dấu “=” xảy ra khi . Vậy min P = 12 ⇔ m = 1.
⟹ Chọn A
Câu 6. Cho biểu thức với
và M, m lần lượt là giá trị lớn nhất và nhỏ nhất của P. Tính S = 4M – 3m.
A.
B.
C. 42
D. 38
Hướng dẫn giải
Ta có .
Đặt t = log3 a. Do nên t ∊ [–3; 1].
Khi đó với t ∊ [–3; 1].
. Vậy 4M – 3m = 42.
⟹ Chọn C
Câu 7. Xét các số thực 0 < x, y < 1 thỏa mãn . Tìm giá trị nhỏ nhất Pmin của biểu thức P = x + y
A.
B.
C.
D.
Hướng dẫn giải
Ta có
⇔ f (3 – xy) = f (x + 2y) (*)
Xét hàm số f (t) = log3 t + t, t > 0
. Suy ra hàm số f (t) đồng biến trên (0; + ∞).
Khi đó (*) . Suy ra:
.
Ta có: . Vậy
.
⟹ Chọn D
Câu 8. Cho ba số thực dương a, b, c và đồ thị các hàm số y = ax, y = (ab)x, y = (c + 1) x được cho như hình vẽ dưới đây
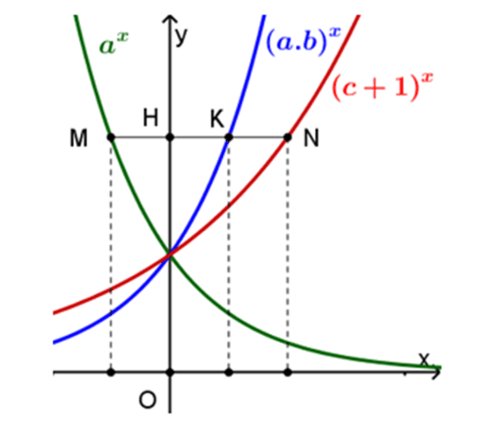
Biết rằng MH = HK = KN. Giá trị nhỏ nhất của biểu thức bằng
A. 0
B. 2
C. –1
D. 1
Hướng dẫn giải
Đặt MH = HK = KN = m > 0 ⇒ xK = m, xM = –m, xN = 2m.
Khi đó:
Do đó:
Dấu bằng xảy ra khi và chỉ khi (thỏa mãn điều kiện a < 1).
Vậy giá trị nhỏ nhất của T bằng 0.
⟹ Chọn A
Câu 9. Xét các số thực dương a, b, x, y thỏa mãn a > 1, b > 1 và . Giá trị nhỏ nhất của biểu thức P = x. y là
A.
B.
C. P = 1
D.
Hướng dẫn giải
Ta có
Vì a, b > 1 ⇒ loga b > 0, logb a > 0
Vì x > 0, y > 0 ⇒ xy ≥ 1. Dấu bằng xảy ra khi và chỉ khi a = b. Vậy min P = 1 ⇔ a = b.
⟹ Chọn C
Câu 10. Cho hàm số thực dương a, b > 1 và sao cho luôn tồn tại số thực 0 < x ≠ 1 thỏa mãn hệ thức . Giá trị lớn nhất của biểu thức T = 10 log ab – log2 a – log2 b bằng
A. 36
B.
C. 45
D. 18
Hướng dẫn giải
Ta có: .
Có a, b > 1 ⇒ logb a > 0. Nên ta có: (logb a)2 = 4 ⇔ logb a = 2 ⇔ a = b2.
Suy ra: T = 10 logab – log2a – log2b = 10. logb3 – log2 (b2) – log2 b = 30 log b – 5 log2 b
T = 5. (6. log b – log2 b) = 45 – 5 (log b – 3)2 ≤ 45.
Dấu “=” xảy ra khi log b = 3 ⇔ b = 103 ⇒ a = 106.
Vậy giá trị lớn nhất của biểu thức T là Tmax = 45.
⟹ Chọn C
Dạng 5. Toán tìm tham số m để hàm số xác định
Phương pháp giải
– Sử dụng điều kiện xác định của hàm số trên dạng 1.
– Casio: Table
Bài tập vận dụng
Câu 1. Tìm tất cả các giá trị của tham m để hàm số y = log2 (x2 – 2x + m) có tập xác định ℝ.
A. m ≥ 1
B. m ≤ 1
C. m > 1
D. m < –1
Hướng dẫn giải
Hàm số có tập xác định là ℝ ⇔ x2 – 2x +m > 0, ∀x ∊ ℝ.
Tam thức vế trái có hệ số bậc hai dương nên để thỏa mãn yêu cầu bài toán thì
∆’ < 0 ⇔ 1 – m < 0 ⇔ m > 1.
Vậy m > 1.
⟹ Chọn C
Câu 2. Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số xác định trên khoảng (2; 3)?
A. 1
B. 2
C. 4
D. 3
Hướng dẫn giải
Hàm số y xác định trên khoảng (2; 3)
Vậy có 2 giá trị nguyên dương của m thỏa mãn yêu cầu bài toán.
⟹ Chọn B
Câu 3. Hàm số y = ln (x2 – 2mx + 4) có tập xác định D = ℝ khi các giá trị của tham số m là
A. m < 2
B. m < –2 hoặc m > 2
C. m = 2
D. –2 < m < 2
Hướng dẫn giải
Hàm số y = ln (x2 – 2mx + 4) có tập xác định ℝ khi x2 – 2mx + 4 > 0, ∀x ∊ ℝ (1)
.
⟹ Chọn D
Câu 1. Hàm số y = ln (x2 + mx + 1) xác định với mọi giá trị của x khi.
A.
B. m > 2
C. –2 < m < 2
D. m < 2
Hướng dẫn giải
Yêu cầu bài toán ⇔ x2 + mx + 1 > 0, ∀x ∊ ℝ ⇔ m2 – 4 < 0 ⇔ –2 < m < 2.
⟹ Chọn C
Câu 2. Tìm tất cả các giá trị của m để hàm số y = log3 (–x2 + mx + 2m + 1) xác định với mọi x ∊ (1; 2).
A.
B.
C.
D.
Hướng dẫn giải
Yêu cầu bài toán ⇔ –x2 + mx + 2m + 1 > 0, ∀x ∊ (1; 2)
Xét hàm số , với x ∊ (1; 2)
.
⇒ f’(x) > 0, ∀x ∊ (1; 2),
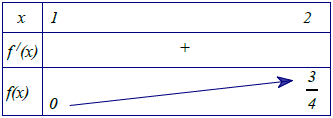
Dựa vào bảng biến thiên có , ∀∊ (1; 2), nêm
.
Vậy .
⟹ Chọn B
Câu 3. Tìm tất cả các giá trị của tham số m để hàm số y = ln [(m – 1) x – m + 2] xác định trên đoạn [0; 2]
A. 0 < m < 2
B. 1 ≤ m < 2
C. m > 2
D. m ≤ 1
Hướng dẫn giải
Yêu cầu bài toán ⇔ (m – 1) x – m + 2 > 0, ∀x ∊ [0; 2]
Bài toán tương đương với tìm m để đồ thị hàm số nằm phía trên trục Ox
ĐK hàm số y = (m – 1) x – m + 2, 0 ≤ x ≤ 2 có hai đầu mút y (0) > 0 và y (2) > 0.
.
⟹ Chọn A
Câu 4. Tìm tất cả các giá trị của tham số m để hàm số y = log (x2 – 2mx + 4) có tập xác định là ℝ
A. m > 2 ∨ m < –2
B. m = 2
C. m < 2
D. –2 < m < 2
Hướng dẫn giải
Điều kiện xác định của hàm số: x2 – 2mx + 4 > 0.
Để hàm số có tập xác định là ℝ thì x2 – 2mx + 4 > 0, ∀x ∊ ℝ ⇔ m2 – 4 < 0 ⇔ –2 < m < 2.
⟹ Chọn D
Câu 5. Số các giá trị nguyên của tham số m để hàm số y = log (mx – m + 2) xác định trên là
A. 4
B. 5
C. Vô số
D. 3
Hướng dẫn giải
YCBT ⇔ mx – m + 2 > 0 thỏa
Vì m ∊ ℤ nên m ∊ {0; 1; 2; 3}.
⟹ Chọn A
Câu 6. Số các giá trị nguyên của tham số m để hàm số y = log (mx – m + 2) xác định trên là
A. 4
B. 5
C. Vô số
D. 3
Hướng dẫn giải
YCBT ⇔ mx – m + 2 > 0 thỏa
Vì m ∊ ℤ nên m ∊ {0; 1; 2; 3}.
⟹ Chọn A
Câu 7. Tìm tất cả các giá trị của m để hàm số xác định với mọi giá trị x thuộc [0; + ∞)
A. m > 9
B. m < 1
C. m < 2
Hướng dẫn giải
Hàm số đã cho xác định ∀x ∊ [0; + ∞)
Đặt
f’(x) = 2018x ln (2018) – 1 – x
f’’(x) = 2018x (ln2018)2 – 1
Có 2018x (ln2018)2 – 1 > 0, ∀x ∊ [0; + ∞) ⇒ f’’(x) > 0
Bảng biến thiên
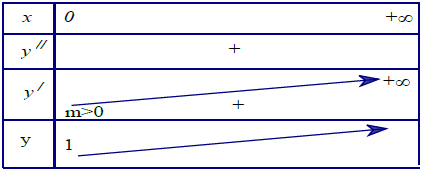
Có y’’ > 0. Suy ra y’ = f’ (x) đồng biến trong [0; + ∞), có f’ (0) = ln (2018) – 1 > 0
Suy ra y = f(x) đồng biến trong [0; + ∞), có f (0) = 1
Dựa vào BBT để có (1) ⇔ m < 1.
⟹ Chọn B
Câu 8. Tìm tất cả các giá trị thực của tham số m để hàm số y = log (x2 – 2mx + 4) có tập xác định là ℝ
A. –2 ≤ m ≤ 2
B. –2 < m < 2
C.
D. m = 2
Hướng dẫn giải
Điều kiện để hàm số y = log (x2 – 2mx + 4) xác định trên ℝ là
.
⟹ Chọn B