Khi chương trình chuyển sang hình thức thi trắc nghiệm thì các công thức giải nhanh bắt đầu phát huy tác dụng. Bài viết dưới đây sẽ trình bày đến bạn đọc toàn bộ các công thức giải nhanh toán 12 theo từng chuyên đề của chương trình học.

Phần 1. Công thức giải nhanh khảo sát hàm số
1. Hàm số bậc 3
Hàm bậc ba: y = ax3 + bx2 + cx + d (a ≠ 0) có đạo hàm y’ = 3ax2 + bx + c
TXĐ: D = ℝ
Cách 1: Tính y’, giải pt: y’ = 0. Lập bảng biến thiên hoặc bảng xét dấu của y’ rồi từ đó suy ra khoảng đồng biến; khoảng nghịch biến. Chú ý: Nếu phương trình y’ = 0 vô nghiệm hoặc có 1 nghiệm kép thì nếu a > 0 ta kết luận hàm số đồng biến trên ℝ. Còn a < 0 ta kết luận hàm số nghịch biến trên ℝ
Cách 2: Bấm Mode 7 thử đáp án (Chú ý nếu (a; b) thì Start a + 0,001; And b − 0,001;
Cách 3: thử nhiều giá trị. Nếu dương thì đồng biến, âm thì nghịch biến.
– Tìm điểm cực trị (điểm cực đại, điểm cực tiểu) của hàm số là tìm xCĐ, xCT: Tính đạo hàm y’, giải phương trình y = 0 tìm x, lập BBT suy ra luận hàm số không có cực trị xCĐ, xCT. Nếu phương trình: y = 0 vô nghiệm hoặc có 1 nghiệm kép thì ta kết luận hàm số không có cực trị.
– Tìm giá trị cực trị (giá trị cực đại, giá trị cực tiểu) của hàm số là tìm yCĐ, yCT: Tính đạo hàm y’, giải phương trình y’ = 0 tìm x, rồi suy ra y (y có giá trị lớn là yCĐ, y có giá trị bé là yCT)
– Tìm điểm cực trị (điểm cực đại, điểm cực tiểu) của đồ thị hàm số là tìm cặp số (xCĐ; yCĐ), (xCT; yCT): Tính đạo hàm y’, giải phương trình y’ = 0 tìm x, rồi suy ra y, rồi suy ra cặp số cần tìm.
– Tìm điểm uốn hay tâm đối xứng: tính y’, tính y”, giải pt: y” = 0 ⇒ x = … ⇒ y = … ⇒ cặp số (x; y)
– Tìm m để hàm số y = ax3 + bx2 + cx + d (a > 0) đồng biến trên ℝ: Tính y’, tính ∆y’, cho ∆y’ ≤ 0 ⇒ m…
– Tìm m để hàm số y = ax3 + bx2 + cx + d (a < 0) nghịch biến trên ℝ: Tính y’, tính ∆y’, cho ∆y’ ≤ 0 ⇒ m…
– Tìm m để đồ thị hàm số y = ax3 + bx2 + cx + d (a ≠ 0) có cực trị (có CĐ, CT): Tính ∆y’, cho ∆y’ > 0 ⇒ m…
– Tìm m để đồ thị hàm số y = ax3 + bx2 + cx + d (a ≠ 0) không có cực trị (không có CĐ, CT): Tính ∆y’, cho ∆y’ ≤ 0 ⇒ m…
– Hàm số đạt cực đại tại ; Đạt cực tiểu tại
Hàm số đạt cực trị tại
– Đồ thị hàm số y = ax3 + bx2 + cx + d (a ≠ 0) có tính chất:
a) Luôn cắt trục hoành.
b) Luôn có tâm đối xứng (điểm uốn).
c) Không có tiệm cận.
– Sự tương giao (số nghiệm là số giao điểm)
a) Giao với trục hoành (Ox): cho y = 0, bấm máy giải pt: ax3 + bx2 + cx + d = 0 ⇒ x = …
b) Giao với trục tung (Oy): cho x = 0 ⇒ y = d
c) Giao với y = g(x): cho ax3 + bx2 + cx + d = g(x) ⇒ x = …
– Tìm m để đường thẳng y = m cắt đồ thị hàm số y = ax3 + bx2 + cx + d (a ≠ 0)
Ta tính yCĐ, yCT của hàm số y = ax3 + bx2 + cx + d (a ≠ 0)
– Cắt nhau tại 3 điểm phân biệt khi yCT < m < yCĐ
– Cắt nhau tại 1 điểm phân biệt khi m < yCT hoặc m > yCĐ
– Tiếp xúc nhau hay có 2 điểm chung khi m = yCT hoặc m = yCĐ
– Nhận dạng đồ thị. Nhận dạng đồ thị theo thứ tự dựa vào: hình dạng đồ thị thuộc hàm loại nào → dấu của hệ số a → Cực trị (nghiệm phương trình y’) → giao điểm với trục tung Oy → giao điểm với trục hoành Ox… (Đồ thị luôn đi từ trái qua phải. Đi lên thì đồng biến, đi xuống thì nghịch biến.)
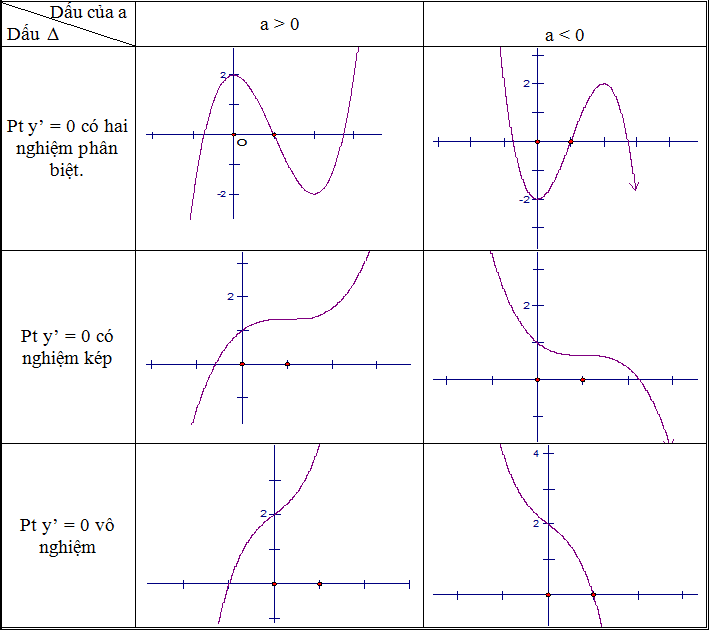
– Cho đồ thị hàm số: y = f (x)
Đồ thị hàm số y = f (|x|) là phần bên phải của đồ thị hàm số y = f (x) và phần đối xứng của nó qua trục Oy.
Đồ thị hàm số y = f (|x|) là phần trên trục hoành của đồ thị hàm số y = f (x) và phần đối xứng của phần dưới trục hoành của đồ thị hàm số y = f (x) qua trục hoành Ox.
2. Hàm số trùng phương
Hàm bậc 4 trùng phương y = ax4 + bx2 + c (a ≠ 0)
TXĐ: D = ℝ
– Tìm khoảng đồng biến, nghịch biến: (Bấm máy giống hàm bậc 3)
Lập bảng biến thiên hoặc bảng xét dấu của y’ rồi từ đó suy ra khoảng đồng biến; khoảng nghịch biến.
– Tìm điểm cực trị (điểm cực đại, điểm cực tiểu) của hàm số là tìm xCĐ, xCT: Tính đạo hàm y’, giải phương trình y’ = 0 tìm x, lập Bảng biến thiên rồi suy ra xCĐ, xCT.
– Tìm giá trị cực trị (giá trị cực đại, giá trị cực tiểu) của hàm số là tìm yCĐ, yCT: Tính đạo hàm y’, giải phương trình y’ = 0 tìm x, rồi suy ra y (y có giá trị lớn là yCĐ, y có giá trị bé là yCT)
– Tìm điểm cực trị (điểm cực đại, điểm cực tiểu) của đồ thị hàm số là tìm cặp số (xCĐ; yCĐ), (xCT; yCT): Tính đạo hàm y’, giải phương trình y’= 0 tìm x, rồi suy ra y, rồi suy ra cặp số cần tìm.
– Tìm điểm uốn: tính y’, tính y”, giải pt: y” = 0 ⇒ x = … ⇒ y = … ⇒ cặp số (x; y)
– Tìm m để hàm số y = ax4 + bx2 + c (a ≠ 0) có 3 cực trị (có CĐ, CT): cho a.b < 0 ⇒ m…
– Tìm m để hàm số y = ax4 + bx2 + c (a ≠ 0) có 1 cực trị: cho a.b ≥ 0 ⇒ m…
– Tìm m để hàm số ax4 + bx2 + c (a ≠ 0) (có 1 CĐ, 2 CT): cho ⇒ m…
– Tìm m để hàm số ax4 + bx2 + c (a ≠ 0) có 3 CT tạo thành 1∆ vuông cân ⇒ 8a + b3 = 0 ⇒ m…
– Tìm m để hàm số ax4 + bx2 + c (a ≠ 0) có 3 CT tạo thành 1∆ đều ⇒ 24a + b3 = 0 ⇒ m…
– Tìm m để hàm số ax4 + bx2 + c (a ≠ 0) (có 2 CĐ, 1 CT): cho ⇒ m…
– Tìm m để đồ thị hàm số y = ax4 + bx2 + c (a ≠ 0) có 2 điểm uốn: cho a.b < 0 ⇒ m…
– Tìm m để đồ thị hàm số y = ax4 + bx2 + c (a ≠ 0) không có điểm uốn: cho a.b ≥ 0 ⇒ m…
– Đồ thị hàm số y = ax4 + bx2 + c (a ≠ 0) có tính chất:
a) Luôn có cực trị.
b) Nhận trục tung Oy làm trục đối xứng (không có tâm đối xứng).
c) Không có tiệm cận.
– Sự tương giao (Số nghiệm là số giao điểm)
a) Giao với trục hoành (Ox): cho y = 0, bấm máy giải pt: ax4 + bx2 + c = 0 xem x2 là t bấm máy phương trình bậc hai với ẩn t. Chú ý chỉ nhận những t ≥ 0.
b) Giao với trục tung (Oy): cho x = 0 ⇒ y = c
c) Giao với y = g(x): cho ax4 + bx2 + c = g(x) ⇒ x = …
– Tìm m để đường thẳng y = m cắt đths y = ax4 + bx2 + c (a ≠ 0)
Ta tính yCĐ, yCT của hàm số y = ax4 + bx2 + c (a ≠ 0)
– Cắt nhau tại 4 điểm phân biệt yCT < m < yCĐ
– Cắt nhau tại 2 điểm phân biệt m < yCT nếu a < 0; còn m > yCĐ nếu a > 0
– Tiếp xúc nhau hay có 3 điểm chung khi m = yCT hoặc m = yCĐ
– Đths y = ax4 + bx2 + c (a ≠ 0) nằm phía trên trục hoành khi yCT > 0 (không cắt trục hoành)
– Đths y = ax4 + bx2 + c (a ≠ 0) nằm phía dưới trục hoành khi yCĐ < 0 (không cắt trục hoành)
– Nhận dạng đồ thị. Nhận dạng đồ thị theo thứ tự dựa vào: hình dạng đồ thị thuộc hàm loại nào → dấu của hệ số a → nghiệm phương trình y’ → giao điểm với trục tung Oy → giao điểm với trục hoành…
(Đồ thị luôn đi từ trái qua phải. Đi lên thì đồng biến, đi xuống thì nghịch biến.)
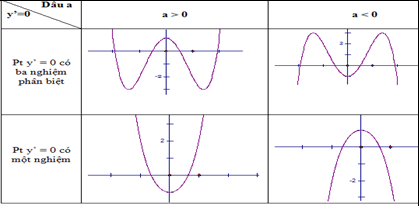
3. Hàm nhất thức
Hàm nhất thức Có đạo hàm
. TXĐ:
– Tìm khoảng đồng biến, nghịch biến của hàm số : Tính
Nếu ad − bc > 0 ⇒ y’ = 0 suy ra hàm số đồng biến trên các khoảng
Nếu ad − bc < 0 ⇒ y’ = 0 suy ra hàm số nghịch biến trên các khoảng
– Đồ thị hàm số có các đường tiệm cận khi ad − bc ≠ 0 ⇒ m…
Đồ thị hàm số có đường tiệm cận đứng ; đường tiệm cận ngang
– Đồ thị hàm số có tâm đối xứng
– Tìm m để hàm số đồng biến trên từng khoảng xác định: Tính
cho ad − bc > 0 ⇒ m…
– Tìm m để hàm số nghịch biến trên từng khoảng xác định: Tính
cho ad − bc < 0 ⇒ m…
– Tìm m để hàm số đồng biến trên khoảng (x0; +∞): cho
⇒ m…
– Tìm m để hàm số đồng biến trên khoảng (−∞; x0): cho
⇒ m…
– Tìm m để hàm số nghịch biến trên khoảng (x0; +∞): cho
⇒ m…
– Tìm m để hàm số nghịch biến trên khoảng (−∞; x0): cho
⇒ m…
– Đồ thị hàm số có tính chất:
a) Không có cực trị.
b) Có tâm đối xứng
– Sự tương giao (Số nghiệm là số giao điểm)
a) Giao với trục hoành (Ox): cho y = 0, bấm máy giải pt:
b) Giao với trục tung (Oy): cho
c) Giao với y = g(x): cho
– Tìm m để đường thẳng y = m cắt đths : cho
hoặc
; Không cắt thì cho
– Tìm m hoặc n để đường thẳng y = mx + n cắt đths tại 2 điểm phân biệt: Lập pt:
Đưa về phương trình bậc 2 chứa tham số. Cho ∆ > 0 ⇒ m = … Chú ý: không phải là nghiệm của pt.
– Nhận dạng đồ thị: Nhận dạng đồ thị theo thứ tự dựa vào: hình dạng đồ thị thuộc hàm loại nào → dấu y’ (dấu ad − bc) → giao điểm với trục tung Oy → giao điểm với trục hoành Ox…
4. Xét khoảng đồng biến, nghịch biến
Cho hàm số y = f (x) có đạo hàm trên (a; b)
– Nếu f‘(x) > 0 ∀x ∈ (a, b) thì f (x) đồng biến trên khoảng đó. Nếu f‘(x) < 0, ∀x ∈ (a, b) thì f (x) nghịch biến trên (a, b).
– Nếu f‘(x) > 0 ∀x ∈ (a, b) thì f (x) đồng biến trên khoảng đó. Nếu f‘(x) > 0 ∀x ∈ (a, b) thì f (x) nghịch biến trên (a, b).
Chú ý: Dấu bằng chỉ xảy ra tại một số hữu hạn điểm.
Hướng dẫn sử dụng máy tính
– Tìm khoảng đồng biến và nghịch biến của hàm số y = f (x) trên TXĐ
Cách 1: Bấm Mode 7 thử đáp án (Chú ý nếu (a; b) thì start a + 0,001; and b − 0,001; )
Nếu f (x) tăng thì đồng biến, f (x) giảm thì đồng biến.
Cách 2: Bấm thử giá trị ở từng khoảng.
Nếu dương thì đồng biến, âm thì nghịch biến. Nên bấm CALC thử nhiều giá trị.
5. Tìm GTLN – GTNN của hàm số
– Số M được gọi là GTLN của hàm số y = f (x) trên D ⇔
– Số m được gọi là GTNN của hàm số y = f (x) trên D ⇔
Hướng dẫn sử dụng máy tính
– Tìm GTLN – GTNN của hàm số y = f (x) trên đoạn [a; b]
Bấm MODE sau đó chọn 7 (TABLE) → Nhập biểu thức f (x) vào máy → “=” nhập Start = a; End = b; → Dò kết quả.
– Tìm GTLN – GTNN của hàm số y = f (x) trên khoảng (a; b)
Bấm MODE sau đó chọn 7 (TABLE) → Nhập biểu thức f (x) vào máy → “=” nhập Start a + 0,001; And b − 0,001; → Dò kết quả.
6. Tìm các đường tiệm cận của đồ thị hàm số y = f (x)
là TCN của đồ thị hàm số y = f (x) (Nhập hàm bấm CALC 1010)
là TCN của đồ thị hàm số y = f (x) (Nhập hàm bấm CALC −1010)
là TCĐ của đồ thị hàm số y = f (x) (Nhập hàm bấm CALC (x0 + 0,001))
là TCĐ của đồ thị hàm số y = f (x) (Nhập hàm bấm CALC (x0 − 0,001))
(Chú ý: Tìm TCĐ ta thường cho mẫu bằng 0, giải pt đc: x = x0. Thay x = x0 vào tử nếu tử bằng 0 hoặc không xác định thì x = x0 không phải là TCĐ. Nếu tử xác định khác 0 thì x = x0 là TCĐ của đồ thị hàm số.)
7. Hàm số y = (f (x))α
Đạo hàm: y’ = f ‘(x) (f (x))α−1
– Nếu α nguyên dương: → ĐK là: f (x) xác định.
f (x) xác định nghĩa là hàm căn thì biểu thức trong căn ≥ 0. Hàm phân thức thì mẫu ≠ 0.
– Nếu α nguyên âm: → ĐK là: f (x) ≠ 0.
– Nếu α không nguyên: → ĐK là: f (x) > 0.
– Nếu α < 0 thì đồ thị hàm số nhận trục Ox làm tiệm cận ngang. Nhận trục Oy làm tiệm cận đứng.
– α > 0 thì hàm số luôn đồng biến. α < 0 thì hàm số luôn nghịch biến.
– Đồ thị hàm số luôn đi qua điểm (1;1).
8. Hàm số y = ax (0 < a ≠ 1)

Hàm số y = logax (0 < a ≠ 1)

– Đồ thị hàm số y = ax và y = logax (0 < a ≠ 1) đối xứng nhau qua đường thẳng y = x.
– ĐK của hàm số y = loga f (x) ; y = ln f (x) và y = log f (x) là: f (x) > 0.
– Công thức đạo hàm:
(uα)’ = u’.α.uα−1
(eu)’ = u’.eu
(au)’ = u’.au. ln a
(sin u)’ = u’. cos u
(cos u)’ = −u’. sin u
– Chú ý: af (x) = b ⇔ f (x) = logab
loga f (x) = b ⇔ f (x) = ab
Phần 2. Công thức tính nhanh Mũ – Logarit
1. Công thức lũy thừa
– Cho a > 0, b > 0 và m, n ∈ ℝ. Khi đó
am. an = am+n
(am)n = am.n
(ab)n = an. bn
– af (x) = ag(x) ⇔ f (x) = g(x) (a > 0)
– Nếu a > 1 thì af (x) > ag(x) ⇔ f (x) > g(x)
– Nếu 0 < a < 1 thì af (x) > ag(x) ⇔ f (x) < g(x)
2. Công thức logarit
– Với các điều kiện 0 < a ≠ 1; b > 0; m > 0; n > 0 ta có:
logab = α ⇔ aα = b
loga1 = 0
logaa = 1
loga aα = α
alogab = b
logabα = α logab
loga (m.n) = loga m + loga n
– loga f (x) = loga g(x) ⇔ f (x) = g(x) với 0 < a ≠ 1.
– Nếu a > 1 thì loga f (x) > loga g(x) ⇔ f (x) > g(x)
– Nếu 0 < a < 1 thì loga f (x) > loga g(x) ⇔ f (x) < g(x)
3. Phương trình mũ
Phương pháp đưa về cùng cơ số: af (x) = ag(x) ⇔ f (x) = g(x)
4. Phương trình logarit
Phương pháp đưa về cùng cơ số:
– Bất phương trình mũ, bất phương trình logarit: Sử dụng máy tính Casio
5. Hướng dẫn sử dụng máy tính
Tìm tập xác định của hàm số y = loga f (x)
Tương tự cho các hàm số: y = ln f (x); y = log f (x)
A. (a; b)
B. [a; b)
C. (a; +∞)
D. (−∞; b]
– Thử A: Nhập loga f (x) rồi ấn CALC 1 giá trị lớn hơn a, 1 giá trị bé hơn b, CALC 1 giá trị ở giữa a và b.
– Thử B: Nhập loga f (x) rồi ấn CALC giá trị a, CALC 1 giá trị bé hơn b, và CALC 1 giá trị ở giữa a và b.
– Thử C: Nhập loga f (x) rồi ấn CALC 1 giá trị lớn hơn a, CALC giá trị 1000, và 1 giá trị ở giữa chúng.
– Thử D: Nhập loga f (x) rồi ấn CALC giá trị −1000, CALC giá trị b, và CALC 1 giá trị ở giữa chúng.
Chú ý: Đáp án nào có chỉ cần có 1 giá trị mà máy không xử lý ra kết quả thì loại.
Giải bất phương trình mũ hoặc logarit dạng: f (x) ≥ g(x)
B1: Chuyển vế về f (x) − g(x) ≥ 0 (Luân chuyển để vế phải là 0)
B2: Nhập hàm f (x) − g(x) rồi bấm CALC thử giống mục 1.
Chú ý: do BPT ≥ 0 nên chọn đáp án nào mà kết quả bấm CALC ra đều ≥ 0.
Tương tự: Nếu BPT > 0 thì chọn đáp án nào mà kết quả bấm CALC ra đều > 0.
Nếu BPT ≤ 0 thì chọn đáp án nào mà kết quả bấm CALC ra đều ≤ 0.
Nếu BPT < 0 thì chọn đáp án nào mà kết quả bấm CALC ra đều < 0.
Phần 3. Công thức tính nhanh nguyên hàm – tích phân
1. Công thức nguyên hàm
Nguyên hàm của hàm số cơ bản
∫dx = x + C
∫ex dx = ex + C
∫cosx.dx = sinx + C
∫sinx.dx = –cosx + C
Nguyên hàm mở rộng
∫a.dx = ax + C, a ϵ ℝ
Công thức tích phân
F (x) là một nguyên hàm của hàm số f (x) trên đoạn [a; b] thì
Phương pháp đổi biến số
Nhớ: Đổi biến thì phải đổi cận.
Dạng 1: Tính
Đặt t = φ(x) ⇒ dt = φ'(x).dx
Đổi cận:
Ví dụ: Nếu cho yêu cầu:
a) Tính thì ta đặt
và đổi cận ta sẽ được
b) Tính thì ta đặt
và đổi cận ta sẽ được
* Chú ý: Thông thường các ta đặt t là căn, mũ, mẫu.
Phương pháp tích phân từng phần
Công thức tính:
Đặt
Ta thường gặp hai loại tích phân từng phần như sau: (Với P(x) là đa thức bậc n)
* Loại 1:
* Loại 2:
Chú ý: f (x) là hàm số chẵn thì f (−x) = f (x)
Còn f (x) là hàm số lẻ thì f (−x) = −f (x)
Do đó: f (x) là hàm số chẵn thì
Còn f (x) là hàm số lẻ thì
Tính chất tích phân
Tính chất 1:
Tính chất 2: , với k là hằng số
Tính chất 3:
Tính chất 4:
Tính chất 5:
Tính chất 6: Nếu f (x) > 0, ∀x ∈ [a; b] thì ; Nếu f (x) > g(x), ∀x ∈ [a; b] thì
Diện tích hình phẳng
Lưu ý: Diện tích là những giá trị dương.
Dạng 1: Cho hàm số y = f (x) liên tục trên [a; b]. Khi đó diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f (x), trục Ox và hai đường thẳng x = a và x = b là: → Bấm máy
– f (x) = 0 vô nghiệm trên (a; b) thì
– f (x) = 0 có 1 nghiệm c ∈ (a; b) thì
Dạng 2: Cho hai hàm số y = f (x) và y = g(x) liên tục trên [a; b]. Khi đó diện tích của hình phẳng giới hạn bởi đồ thị hai hàm số y = f (x), y = g(x) và hai đường thẳng x = a, x = b là: → Bấm máy
Dạng 3: Cho hai hàm số y = f (x) và y = g(x) liên tục. Khi đó diện tích của hình phẳng giới hạn bởi đồ thị hai hàm số f (x), g(x) là → Bấm máy (với x1 < x2 là hai nghiệm của pt f (x) = g(x))
Thể tích vật thể tròn xoay
Lưu ý: Thể tích là giá trị dương.
Dạng 1: Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi các đường y = f (x), trục Ox và hai đường thẳng x = a, x = b quay xung quanh trục Ox là: → Bấm máy
Dạng 2: Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi các đường y = f (x), y = g(x) trục Ox và hai đường thẳng x = a, x = b quay xung quanh trục Ox là: → Bấm máy
Dạng 3: Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi các đường y = f (x), y = g(x) quay xung quanh trục Ox là: → Bấm máy
(với x1 < x2 là hai nghiệm của phương trình f (x) = g(x))
Dạng 4: Thể tích vật thể của một vật nằm giữa 2 mặt phẳng x = a, x = b, biết thiết diện của vật bị cắt bởi mp vuông góc với trục Ox tại điểm x(a ≤ x ≤ b) có diện tích S(x) là: → Bấm máy
Hướng dẫn sử dụng máy tính
– Hàm số y = f (x) đạt cực trị tại điểm x = x0 thì đạo hàm tại x = x0 sẽ bằng 0
Bấm ; Muốn biết điểm x = x0 là CĐ hay CT ta bấm
CALC x0 nếu bằng 0 thì x = x0 có khả năng là cực trị, khác 0 thì loại. Rồi bấm tiếp CALC x0 + 0,001 và x0 − 0,001 nếu lần lượt được + và – thì x = x0 là cực đại. Còn lần lượt được – và + thì x = x0 là cực tiểu.
– Tính đạo hàm của hàm số y = f (x) tại điểm x = x0
Bấm (Trừ đi kết quả ở đáp án A nếu thử đáp án A) rồi ấn “=”
– Tính đạo hàm của hàm số y = f (x)
A. f1 (x)
B. f2 (x)
C. f3 (x)
D. f4 (x)
Bấm (Đề bài trừ đáp án)
(Trừ đi kết quả ở đáp án A nếu thử đáp án A) rồi ấn CALC 1 giá trị rồi Ấn “=” (CALC thử 2 đến 3 giá trị). Đáp án nào ra kết quả = 0 hoặc gần bằng 0 (..,…×10(mũ âm)) thì chọn đáp án đó.
– Tìm nguyên hàm của hàm số y = f (x) hay ∫f (x) dx
A. F1(x) + C
B. F2(x) + C
C. F3(x) + C
D. F4(x) + C
Cách 1: Bấm (Đáp án trừ đề bài)
(Nhập biểu thức ở đáp án A nếu thử A) rồi ấn CALC 1 giá trị rồi Ấn “=” (chú ý CALC thử 2 đến 3 giá trị) Đáp án nào ra kết quả = 0 hoặc gần bằng 0 (..,…×10(mũ âm)) thì chọn đáp án đó.
Cách 2: Ấn Với a, b là hai số bất kìa gần nhau thỏa mãn f (x) liên tục.
Đáp án nào ra kết quả = 0 thì chọn đáp án đó.
– Tính tích phân
Bấm (Nhập kết quả ở đáp án A nếu thử đáp án A)
– Tìm x0 để tích phân
A. b1
B. b2
C. b3
D. b4
Bấm (CALC thử từng đáp án ra = 0 đúng, khác 0 thì sai).
Tương tự cho dạng toán tìm x0 để tích phân
Phần 4. Công thức tính nhanh Số Phức
1. Công thức tính nhanh
– Số phức: z = a + bi, a, b ∈ ℝ; i2 = −1
– Phần thực của z là a; phần ảo của z là b (chú ý là b chứ không phải là bi)
– Nếu b = 0 thì z = a gọi là số thực.
Nếu a = 0; b ≠ 0 thì z = bi gọi là số ảo hoặc số thuần ảo.
– Số phức liên hợp:
Số phức nghịch đảo là
– Môđun của số phức: . Môđun của số phức là một số thực không âm (≥ 0)
Tính chất:
– Điểm biểu diễn của số phức z = a + bi, a, b ∈ ℝ là điểm M(a; b)
– Hai số phức bằng nhau (phần thực = phần thực; phần ảo = phần ảo)
– Phép toán trên tập số phức:
(a + bi) + (c + di) = (a + c) + (b + d)i
(a + bi)(c + di) = (ac − bd) + (ad + bc)i
(a + bi) − (c + di) = (a − c) + (b − d)i
– Căn bậc hai của số thực a âm là:
– Phương trình bậc hai trên tập số phức az2 + bz + c = 0 (a ≠ 0):
Nếu ∆ = 0 thì phương trình có một nghiệm kép (thực)
Nếu ∆ > 0 thì phương trình có hai nghiệm thực
Nếu ∆ < 0 thì phương trình có hai nghiệm phức
Chú ý:
– Nếu quỹ tích của số phức z là đường tròn (x – a)2 + (x – b)2 = R2 tâm I(a; b) và bán kính là R thì: còn
– Nếu tập hợp số phức z thỏa mãn(x – a)2 + (x – b)2 ≤ R2 thì quỹ tích là hình tròn tâm I(a; b) và bán kính là R.
2. Hướng dẫn sử dụng máy tính
Số phức: Bấm mode 2 màn hình hiện CMPLX
Cộng trừ nhân chia nhập tính bình thường
Tính môđun nhập shift hyp
Số phức liên hợp bấm shift 2 2 (xuất hiện conjg (…))
Phần 5. Công thức tính nhanh thể tích khối đa diện
1. Hệ thức lượng trong tam giác vuông
Cho ∆ABC vuông ở A ta có:
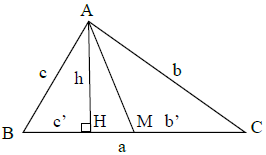
– Định lý Pitago: BC2 = AB2 + AC2
– BA2 = BH. BC; CA2 = CH.CB
– AB. AC = BC. AH
–
– AH2 = BH.CH
– BC = 2AM
–
– b = a.sinB = a.cosC
– c = a.sinC = a.cosB
–
– b = c.tan B = c.cot C
* Định lý hàm số Cosin: a2 = b2 + c2 − 2bc.cosA
2. Công thức tính diện tích, thể tích
a) Công thức tính diện tích tam giác:
Hoặc với
với a, b, c là độ dài 3 cạnh của tam giác
Đặc biệt:
– ∆ABC vuông ở A:
– ∆ABC đều cạnh a:
b) Diện tích hình vuông: S = cạnh × cạnh
c) Diện tích hình chữ nhật: S = dài x rộng
d) Diện tích hình thoi: (chéo dài x chéo ngắn)
e) Diện tích hình bình hành: S = đáy × chiều cao
f) Diện tích hình thang: (đáy lớn + đáy nhỏ) × chiều cao
g) Diện tích hình tròn: S = πr2
Chu vi đường tròn: C = 2πr
h) Thể tích khối tứ diện đều cạnh a:
k) Thể tích khối chóp tam giác đều cạnh đáy a: (α là góc giữa cạnh bên và mặt đáy)
i) Thể tích khối chóp tam giác đều cạnh đáy a: (β là góc giữa mặt bên và mặt đáy)
j) Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng a:
m) Thể tích khối chóp tứ giác đều cạnh đáy a: (α là góc giữa mặt bên và mặt đáy)
n) Thể tích khối chóp tứ giác đều cạnh đáy a: (β là góc giữa mặt bên và mặt đáy)
l) Thể tích khối lăng trụ tam giác đều có tất cả các cạnh bằng a:
Chú ý:
– Đường chéo của hình vuông cạnh a là:
Tam giác vuông cân thì hai cạnh góc vuông bằng nhau và bằng cạnh huyền chia
Đường chéo của hình lập phương cạnh a là:
Đường chéo của hình hộp chữ nhật có 3 kích thước a, b, c là:
– Đường cao của tam giác đều cạnh a là:
– Hình chóp đều là hình chóp có đáy là đa giác đều và các cạnh bên bằng nhau và tạo với mp đáy 1 góc bằng nhau, các mặt bên là các tam giác đều và tạo với mp đáy 1 góc bằng nhau, hình chiếu của đỉnh xuống mp đáy trùng với tâm của đáy (Hình chóp tam giác đều thì đáy là tam giác đều, hình chóp tứ giác đều thì đáy là hv)
– Lăng trụ đứng là lăng trụ có các mặt bên là các hình chữ nhật
– Lăng trụ đều là lăng trụ đứng có đáy là đa giác đều. Lăng trụ tam giác đều là lăng trụ đứng.
– Góc giữa cạnh bên và mặt đáy là góc hợp bởi 3 điểm: (Đỉnh, Điểm chung; Chân đường cao)
– Góc giữa mặt bên và mặt đáy là góc hợp bởi 3 điểm: (Đỉnh, Điểm M; Chân đường cao). Với M là giao điểm của đường thẳng kẻ từ chân đường cao vuông góc với giao tuyến của mặt bên và mặt đáy.
3. Các công thức thể tích của khối đa diện
Thể tích khối lăng trụ
V = Sđáy × h
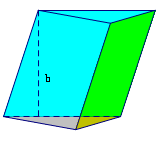
Thể tích khối hộp chữ nhật
Đường chéo
V = a.b.c (a, b, c là ba kích thước)
Thể tích khối lập phương
Đường chéo
V = a3 (a là độ dài cạnh)
Thể tích khối chóp
V = Sđáy × h (h là chiều cao)
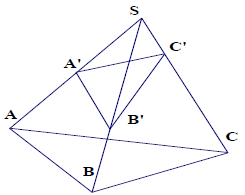
Tỉ số thể tích tứ diện
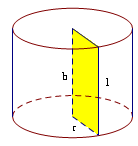
Khối nón
V = Sđáy × h =
πr2h
Stp = Sxq + Sđáy = πrl + πr2
Liên hệ (l2 = h2 + r2)
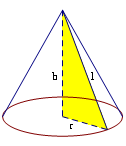
Khối trụ
V = Sđáy × h = πr2h
Sxq = 2πrl = 2πrh
Stp = Sxq + Sđáy = πrl + πr2
Liên hệ (h = l)
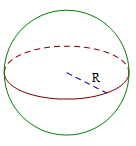
Khối cầu
V = πR3
S = 4πR2
Phần 6. Công thức tính nhanh hệ tọa độ trong không gian
Một số phép toán vectơ
–
–
–
–
–
–
–
–
–
–
–
–
(Tính tích có hướng: Bấm M0DE 8, bấm 1 chọn (vectơ A), bấm 1 chọn 1:3, sau đó nhập tọa độ vectơ A vào, rồi bấm SHIFT 5 2 2 chọn (vectơ B), bấm 1 chọn 1:3, sau đó nhập tọa độ vectơ B vào, bấm AC, rồi bấm shift 5, bấm 3 chọn (vectơ A), bấm dấu nhân x, bấm shift 5, bấm 4 chọn (vectơ B), bấm dấu bằng =, ta được kết quả)
– M là trung điểm A ⇒
– G là trọng tâm tam giác ABC ⇒
– G’ là trọng tâm tứ diện ABCD ⇒
– Các tính chất và ứng dụng của tích có hướng:
và
cùng phương ⇔
và
không cùng phương ⇔
và
đồng phẳng ⇔
và
đồng phẳng ⇔
(ABCD là hình bình hành)
(Với: klt là khối lăng trụ; ktd là khối tứ diện; kh là khối hộp)
Phương trình mặt phẳng
– Phương trình mp (α) qua M(x0; y0; z0) có vtpt là: A(x – x0) + B(y – y0) + C(z – z0) = 0
Nếu mp (α) có phương trình: Ax + By + Cz + D = 0 thì ta có vtpt
– Phương trình mặt phẳng theo đoạn chắn đi qua A(a, 0, 0); B(0, b, 0); C(0, 0, c) là:
Chú ý: Muốn viết phương trình mặt phẳng ta cần xác định tọa độ điểm đi qua và 1 vectơ pháp tuyến.
– Vị trí tương đối của hai mp (α1) và (α2):
(α) cắt (β) ⇔ A1 : B1 : C1 ≠ A2 : B2 : C2
(α) // (β) ⇔
(α) ≡ (β) ⇔
(α) ⊥ (β) ⇔ A1A2 + B1B2 + C1C2 = 0
– Khoảng cách từ M(x0, y0, z0) đến (α): Ax + By + Cz + D = 0 là:
Chú ý: mp Oxy có pt: z = 0
mp Oxz có pt: y = 0
mp Oyz có pt: x = 0.
– Góc giữa hai mặt phẳng:
Phương trình đường thẳng
– Phương trình tham số của đường thẳng d qua M(x0; y0; z0) có vtcp là:
– Phương trình chính tắc của d:
Chú ý: Trục Ox, Oy, Oz đi qua O và lần lượt có vectơ chỉ phương:
– Góc giữa 2 đường thẳng: Gọi φ là góc giữa d và d’ là:
– Vị trí tương đối của 2 đường thẳng d, d’: Ta thực hiện hai bước
Tìm quan hệ giữa 2 vtcp
Tìm điểm chung của d, d’ bằng cách xét hệ:

Một số dạng toán thường gặp
Dạng 1: Chứng minh A, B, C là ba đỉnh tam giác
A, B, C là ba đỉnh tam giác ⇔ không cùng phương
Dạng 2: Tìm D sao cho ABCD là hình bình hành:
ABCD là hình bình hành ⇔
Dạng 3: Chứng minh ABCD là một tứ diện:
– Viết phương trình (BCD)
– Thay tọa độ A vào phương trình mp (BCD) và chứng minh A ∉ (BCD).
Dạng 4: Tìm hình chiếu của điểm M.
– H là hình chiếu của M trên mp (α)
Viết phương trình đường thẳng d qua M và vuông góc (α): ta có
Gọi H = d ∩ (α) ⇒ H (theo t) ∈ d. mà H ∈ (α) ⇒ t = ? ⇒ tọa độ H
– H là hình chiếu của M trên đường thẳng d
d có vtcp
Gọi H (theo t) ∈ d, Tính . Ta có:
⇒ tọa độ H
Dạng 5: Điểm đối xứng.
Điểm M’ đối xứng với M qua mp (α)
– Tìm hình chiếu H của M trên mp (α) (dạng 4.a)
– M’ đối xứng với M qua (α) ⇔ H là trung điểm của MM’ ⇒
Điểm M’ đối xứng với M qua đường thẳng d:
– Tìm hình chiếu H của M trên d (dạng 4.b)
– M’ đối xứng với M qua d ⇔ H là trung điểm của MM’ ⇒
Dạng 6: Khoảng cách
a) Khoảng cách từ điểm A đến đường thẳng ∆:
– Viết phương trình mp (α) chứa A và ⊥ ∆.
– Tìm giao điểm H của ∆ và (α).
– Tính d(A, ∆) = AH
Chú ý: Có thể sử dụng công thức: với M ∈ (∆).
b) Khoảng cách giữa đường thẳng ∆ và (α) với ∆ // (α):
– Lấy M trên ∆
– d(∆, (α)) = d(M, (α))
c) Khoảng cách giữa 2 đường thẳng chéo nhau ∆, ∆’:
– Viết phương trình mặt phẳng (α) chứa ∆’ và // ∆
– Lấy M trên ∆
– d(∆, ∆’) = d(M, (α))
Chú ý: Có thể sử dụng công thức: Với M ∈ (∆); M’ ∈ (∆’).
Phương trình mặt cầu
a) Phương trình mặt cầu tâm I (a; b; c), bán kính R:
(S): (x – a)2 + (y – b)2 + (z – c)2 = R2
Nếu mặt cầu có phương trình (S): x2 + y2 + z2 − 2ax − 2by − 2cz + d = 0 với (a2 + b2 + c2 − d > 0)
Ta có: Tâm I (a; b; c) và
b) Vị trí tương đối của mặt phẳng và mặt cầu
Cho (S): (x – a)2 + (y – b)2 + (z – c)2 = R2 và (α): Ax + By + Cz + D = 0
Gọi d = d(I, (α)): khoảng cách từ tâm mặt cầu (S) đến mp (α).
– d > R: (S) ∩ (α) = ∅
– d = R: (α) tiếp xúc (S) tại H (H: tiếp điểm, (α): tiếp diện)
Tìm tiếp điểm H (là hình chiếu vuông góc của tâm I trên mp (α))
– Viết phương trình đường thẳng d qua I và vuông góc mp (α): ta có
– H = d ∩ (α). Gọi H (theo t) ∈ d. Ta có H ∈ (α) ⇒ t = ? ⇒ tọa độ H
d < R: (α) cắt (S) theo đường tròn (C):
Tìm bán kính r và tâm H của đường tròn giao tuyến:
– Bán kính
– Tìm tâm H (là hình chiếu vuông góc của tâm I trên mp (α))