Bài viết sau đây, VerbaLearn sẽ giúp bạn đọc tổng hợp các dạng toán về bất phương trình mũ, bất phương trình logarit và cách giải từng dạng toán một cách chi tiết nhất. Mảng kiến thức thuộc chương trình toán 12 và xuất hiện nhiều trong đề thi THPT Quốc Gia môn toán.
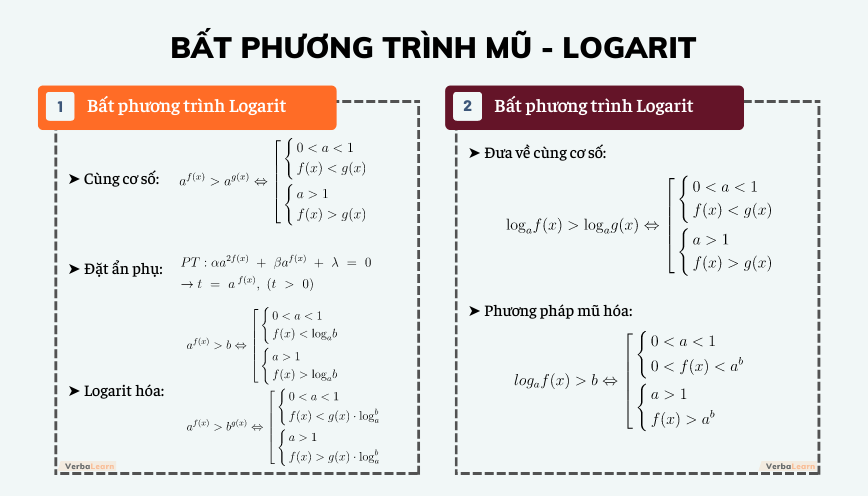
Cách giải bất phương trình mũ
1. Đưa về cùng cơ số
2. Đặt ẩn phụ
αa2f(x) + βaf(x) + λ = 0. Đặt t = a f(x), (t > 0)
3. Phương pháp logarit hóa
Cách giải bất phương trình logarit
1. Đưa về cùng cơ số
2. Phương pháp mũ hóa
Phân loại và phương pháp giải bài tập
Dạng 1. Phương pháp biến đổi tương đương đưa về cùng cơ số
Phương pháp giải
Bất phương trình mũ cơ bản
– Bất phương trình hoặc
– Bất phương trình
– Bất phương trình
Bất phương trình logarit cơ bản
– Bất phương trình hoặc
– Bất phương trình
– Bất phương trình
Bài tập vận dụng
Câu 1. Cho bất phương trình log7 (x2 + 2x + 2) + 1 > log7 (x2 + 6x + 5 + m). Có bao nhiêu giá trị nguyên của tham số m để bất phương trình trên có tập ngiệm chứa khoảng (1; 3)?
A. 35
B. 36
C. 34
D. 33
Hướng dẫn giải
BPT
, với f(x) = –x2 – 6x – 5; g(x) = 6x2 + 8x + 9
Xét sự biến thiên của hai hàm số f(x) và g(x)
f’(x) = –2x – 6 < 0, ∀ x ∈ (1; 3) ⇒ f(x) luôn nghịch biến trên khoảng (1; 3)
g’(x) = 12x + 8 > 0, ∀ x ∈ (1; 3) ⇒ g(x) luôn đồng biến trên khoảng (1; 3)
Khi đó –12 < m < 23
Mà m ∈ ℤ nên m ∈ {–11; –10; …; 22}
Vậy có tất cả 34 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
⟹ Chọn C
Câu 2. Gọi S là tập tất cả các giá trị nguyên của tham số m để bất phương trình log2 (7x2 + 7) ≥ log2 (mx2 + 4x + m) có tập nghiệm là ℝ. Tổng các phần tử của S là
A. 10
B. 11
C. 12
D. 13
Hướng dẫn giải
⟹ Chọn C
BPT có tập nghiệm ℝ
, ∀ x ∈ ℝ
Ta có:
Ta có:
Do đó
Mà m ∈ ℤ nên m ∈ {3; 4; 5}
Vậy S = 3 + 4 + 5 = 12.
Câu 3. Bất phương trình có tập nghiệm là
. Hỏi M = a + b bằng?
A. M = 12
B. M = 8
C. M = 9
D. M = 10
Hướng dẫn giải
Ta có
Nên ⇒ M = a + b = 1 + 9 = 10
⟹ Chọn C
Câu 4. Tập nghiệm của bất phương trình là:
A.
B.
C.
D.
Hướng dẫn giải
ĐKXĐ:
Bất phương trình
Kết hợp điều kiện ta được:
⟹ Chọn B
Câu 5. Bất phương trình ln (2x2 + 3) > ln (x2 + ax + 1) nghiệm đúng với mọi số thực x khi:
A.
B.
C. 0 < a < 2
D. –2 < a < 2
Hướng dẫn giải
ln (2x2 + 3) > ln (x2 + ax + 1) nghiệm đúng với mọi số thực x
⟹ Chọn D
Câu 6. Bất phương trình (3x – 1)(x2 + 3x – 4) có bao nhiêu nghiệm nguyên nhỏ hơn 6?
A. 9
B. 5
C. 7
D. Vô số
Hướng dẫn giải
Kết hợp điều kiện nghiệm nguyên nhỏ hơn 6 ta thấy các giá trị thỏa là {–3; –2; –1; 2; 3; 4; 5}
⟹ Chọn C
Câu 7. Nghiệm của bất phương trình là
A.
B.
C. (–1; 0)
D.
Hướng dẫn giải
Do nên
⟹ Chọn D
Câu 8. Số nghiệm nguyên của bất phương trình là
A. 1
B. 0
C. 9
D. 11
Hướng dẫn giải
Vậy tập tất cả các nghiệm nguyên của bất phương trình đã cho là {5; 6; 7; 8; 9; 10; 11; 12; 13}.
⟹ Chọn C
Câu 9. Tìm tập nghiệm S của bất phương trình logm (2x2 + x + 3) ≤ logm (3x2 – x) với m là tham số thực dương khác 1, biết x = 1 là một nghiệm của bất phương trình đã cho.
A. (–2; 0) ∪
B. [–1; 0] ∪
C. S = (–1; 0) ∪ (1; 3]
D. S = [–1; 0) ∪
Hướng dẫn giải
Do x = 1 là nghiệm nên ta có logm 6 ≤ logm 2 ⇒ 0 < m < 1.
Bất phương trình tương đương với
Vậy S = [–1; 0) ∪
⟹ Chọn D
Câu 10. Tìm tất cả các giá trị của tham số m để bất phương trình: 1 + log5 (x2 + 1) ≥ log5 (mx2 + 4x + m) thỏa mãn với mọi x ∈ ℝ.
A. –1 < m ≤ 0
B. –1 < m < 0
C. 2 < m ≤ 3
D. 2 < m < 3
Hướng dẫn giải
Ta có:
1 + log5 (x2 + 1) ≥ log5 (mx2 + 4x + m) ⇔ log5 (5x2 + 5) ≥ log5 (mx2 + 4x + m)
Để bất phương trình đã cho thỏa mãn với x ∈ ℝ điều kiện là cả (1) và (2) đều thỏa mãn với mọi x ∈ ℝ.
Điều kiện là
⟹ Chọn C
Câu 11. Bất phương trình ln (2x2 + 3) > ln (x2 + ax + 1) nghiệm đúng với mọi số thực x khi:
A.
B.
C. 0 < a < 2
D. –2 < a < 2
Hướng dẫn giải
Ta có ln (2x2 + 3) > ln (x2 + ax + 1) nghiệm đúng với mọi số thực x
⟹ Chọn D
Câu 12. Gọi S là tập tất cả các giá trị nguyên không dương của m để phương trình có nghiệm. Tập S có bao nhiêu tập con?
A. 1
B. 2
C. 3
D. 4
Hướng dẫn giải
Ta có:
Do đó phương trình có nghiệm khi và chỉ khi
Mà m là số nguyên không dương nên m ∈ {–1; 0}. Suy ra S = {–1; 0}.
Vậy số tập con của S bằng 22 = 4 .
Chú ý:
Các tập con của S là: ∅, {–1}, {0}, S
Một tập hợp có n phần tử thì số tập con của nó là n = 2 .
⟹ Chọn D
Câu 13. Tìm các giá trị thực của tham số m để bất phương trình log0,02 (log2 (3x +1)) > log0,02 m có nghiệm với mọi x ∈ (–∞; 0)
A. m > 9
B. m < 2
C. 0 < m < 1
D. m ≥ 1
Hướng dẫn giải
log0,02 (log2 (3x +1)) > log0,02 m
TXĐ: D = ℝ
ĐK tham số m: m > 0
Ta có: log0,02 (log2 (3x +1)) > log0,02 m ⇔ log2 (3x + 1) < m
Xét hàm số f(x) = log2 (3x + 1), ∀ x ∈ (–∞; 0) có H57, ∀ x ∈ (–∞; 0)
Bảng biến thiên f(x):
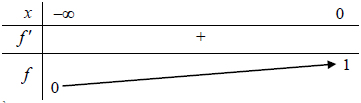
Khi đó với yêu cầu bài toán thì m ≥ 1.
⟹ Chọn D
Câu 14. Nghiệm của bất phương trình là
A.
B.
C. x ≤ 1
D.
Hướng dẫn giải
Điều kiện
Ta có
⟹ Chọn A
Câu 15. Có bao nhiêu giá trị nguyên của tham số m để bất phương trình sau nghiệm đúng với mọi x thuộc ℝ: 1 + log6 (x2 + 1) ≥ log6 (mx2 + 2x + m).
A. 2
B. 3
C. 4
D. 5
Hướng dẫn giải
Điều kiện: mx2 + 2x + m > 0
Ta có: 1 + log6 (x2 + 1) ≥ log6 (mx2 + 2x + m)
⇔ log6 [6(x2 + 1)] ≥ log6 (mx2 + 2x + m)
⇔ 6(x2 + 1) ≥ mx2 + 2x + m
⇔ (m – 6)x2 + 2x + m – 6 ≤ 0
Điều kiện bài toán
Giải (1): Do m = 0 không thỏa (1) nên
Giải (2): Do m = 6 không thỏa (2) nên:
Suy ra 1 < m ≤ 5 .
Vậy có 4 giá trị nguyên của m.
⟹ Chọn C
Dạng 2. Phương pháp đặt ẩn phụ
Phương pháp
Bất phương trình mũ
Tổng quát:
Ta thường gặp các dạng:
– m․a2f(x) + n․af(x) + p = 0
– m․af(x) + n․bf(x) + p = 0, trong đó a․b = 1. Đặt t = af(x), t > 0. Suy ra
– m․a2f(x) + n․(a․b)f(x) + p․b2f(x) = 0. Chia hai vế cho b2f(x) và đặt
Bất phương logarit
– Tổng quát:
Bài tập vận dụng
Câu 1. Tìm số các nghiệm nguyên của bất phương trình
A. 10
B. 9
C. 8
D. 11
Hướng dẫn giải
Điều kiện: x > 0
Phương trình
Đặt thì phương trình trở thành:
Do đó
Số các nghiệm nguyên của bất phương trình là 8.
⟹ Chọn C
Câu 2. Xét bất phương trình . Tìm tất cả các giá trị của tham số m để bất phương trình có nghiệm thuộc khoảng
.
A. m ∈ (0; +∞)
B.
C.
D. m ∈ (–∞; 0)
Hướng dẫn giải
Điều kiện: x > 0
⇔ (1 + log2 x)2 – 2(m + 1) log2 x – 2 < 0 (1)
Đặt t = log2 x .Vì x ∈ nên
. Do đó t ∈
(1) thành (1 + t)2 – 2(m + 1) t – 2 < 0 ⇔ t2 – 2mt – 1 <0 (2)
Cách 1: Yêu cầu bài toán tương đương tìm m để bpt (2) có nghiệm thuộc
Xét bất phương trình (2) có: ∆’ = m2 + 1 > 0, ∀ m ∈ ℝ
f(t) = t2 – 2mt – 1 = 0 có ac < 0 nên (2) luôn có 2 nghiệm phân biệt t1 < 0 < t2
Khi đó cần
Cách 2: t2 – 2mt – 1 < 0
Khảo sát hàm số f(t) trong (0; +∞) ta được
⟹ Chọn C
Câu 3. Cho bất phương trình: 9x + (m – 1)․3x + m > 0 (1). Tìm tất cả các giá trị của tham số m để bất phương trình (1) nghiệm đúng ∀ x > 1 .
A.
B.
C.
D.
Hướng dẫn giải
Đặt t = 3x
Vì x > 1 ⇒ t > 3 Bất phương trình đã cho thành: t2 + (m – 1)․t + m > 0 nghiệm đúng ∀ t ≥ 3
nghiệm đúng ∀ t > 3
Xét hàm số
Hàm số đồng biến trên [3; +∞) và
Yêu cầu bài toán tương
⟹ Chọn A
Câu 4. Có bao nhiêu giá trị nguyên của tham số m ∈ [0; 10] để tập nghiệm của bất phương trình chứa khoảng (256; +∞)
A. 7
B. 10
C. 8
D. 9
Hướng dẫn giải
Điều kiện:
Với điều kiện trên bất phương trình trở thành H95
Đặt t = log2 x thì t > 8 vì x ∈ (256; +∞)
Đặt
Yêu cầu bài toán
Xét hàm số trên khoảng (8; +∞)
Ta có
⇒ f(t) luôn nghịch biến trên khoảng (8; +∞)
Do đó
Mà m ∈ [0; 10] nên m ∈ {3; 4; …; 10}.
Vậy có 8 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.
⟹ Chọn C
Câu 5. Tìm tất cả các giá trị thực của tham số m để bất phương trình log2 (5x – 1)․log2 (2.5x – 2) ≥ m có nghiệm với mọi x ≥ 1.
A m ≥ 6
B m > 6
C m ≤ 6
D m < 6
Hướng dẫn giải
Điều kiện của bất phương trình: x > 0
Ta có log2 (5x – 1)․log2 (2.5x – 2) ≥ m ⇔ log2 (5x – 1)․[1+ log2 (5x – 1)] ≥ m (1)
Đặt t = log2 (5x – 1), với x ≥ 1 ta có t ≥ 2. Khi đó (1) trở thành m ≤ t2 + t (2)
Xét hàm số f(t) = t2 + t trên [2; +∞) ta có f’(t) = 2t + 1 > 0, ∀ t ∈ [2; +∞).
Do đó để bất phương trình đã cho có nghiệm với mọi t ≥ 2 thì hay m ≤ 6.
⟹ Chọn C
Câu 6. Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình có nghiệm?
A. 6
B. 4
C. 9
D. 1
Hướng dẫn giải
Điều kiện x2 – 3x + m ≥ 0 (*)
Do m nguyên dương nên m = 1 thỏa mãn (*).
⟹ Chọn D
Câu 7. Bất phương trình có bao nhiêu nghiệm nguyên dương nhỏ hơn 10.
A. 7
B. 8
C. 9
D. 6
Hướng dẫn giải
Điều kiện của bất phương trình là x > 0.
Khi đó:
Đặt t = log2 x. Ta có:
Trả lại ẩn ta có .
Kết hợp với điều kiện x > 0 ta có hoặc
hoặc x > 2
Khi đó bất phương trình có 7 nghiệm nguyên dương nhỏ hơn 10.
⟹ Chọn A
Câu 8. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình m․4x + (m – 1)․2x+2 + m – 1 > 0 nghiệm đúng ∀ x ∈ ℝ?
A. m ≤ 3
B. m ≥ 1
C. –1 ≤ m ≤ 4
D. m ≥ 0
Hướng dẫn giải
Bất phương trình ⇔ m․4x + 4(m – 1)․2x + m – 1 > 0 ⇔ m(4x + 4․2x + 1) > 1 + 4․2x
⇔
Đặt 2x = t (t > 0). Khi đó .
Để bất phương trình ban đầu nghiệm đúng ∀ x ∈ ℝ thì bất phương trình nghiệm đúng ∀ t > 0.
Đặt
Hàm số nghịch biến trên (0; +∞). Khi đó , ∀ t > 0 khi và chỉ khi m ≥ f (0) = 1
⟹ Chọn B
Câu 9. Tìm tất cả các giá trị của tham số m bất phương trình 4x–1 – m(2x + 1) > 0 có nghiệm ∀ x ∈ ℝ
A. m ∈ (–∞; 0]
B. m ∈ (0; +∞)
C. m ∈ (0; 1)
D. m ∈ (–∞; 0) ∪ (1; +∞)
Hướng dẫn giải
Ta có:
Đặt 2x = t (t > 0). Yêu cầu bài toán tương đương với , ∀ t ∈ (0; +∞)
Đặt
Bảng biến thiên
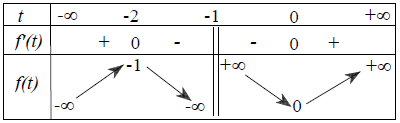
Dựa vào bảng biến thiên có m ≤ 0.
⟹ Chọn A
Câu 10. Xét bất phương trình . Tìm tất cả các giá trị của tham số m để bất phương trình có nghiệm thuộc khoảng
.
A. m ∈ (0; +∞)
B.
C.
D. m ∈ (–∞; 0)
Hướng dẫn giải
Điều kiện: x > 0
⇔ (1 + log2 x)2 – 2(m – 1) log2 x – 2 < 0 (1)
Đặt t = log2 x. Vì nên
. Do đó t ∈
(1) thành (1 + t)2 – 2(m + 1) t – 2 < 0 ⇔ t2 – 2mt – 1 < 0 (2)
Cách 1: Yêu cầu bài toán tương đương tìm m để bpt (2) có nghiệm thuộc
Xét bất phương trình (2) có: ∆’ = m2 + 1 > 0, ∀ m ∈ ℝ
f(t) = t2 – 2mt – 1 = 0 có ac < 0 nên (2) luôn có 2 nghiệm phân biệt t1 < 0 < t2
Khi đó cần
Cách 2: t2 – 2mt – 1 < 0
Khảo sát hàm số f(t) trong (0; +∞) ta được
⟹ Chọn C
Câu 11. Tìm giá trị gần đúng tổng các nghiệm của bất phương trình sau:
A. 12,3
B. 12
C. 12,1
D. 12,2
Hướng dẫn giải
Điều kiện: 0 < x ≠ 1.
Ta có 24x6 – 2x5 + 27x4 – 2x3 + 1997x2 + 2016
= (x3 – x2)2 + (x3 – 1)2 + 22x6 + 26x4 +1997x2 + 2015 > 0, ∀x
Do đó bất phương trình đã cho tương đương với
Đặt , ta có bất phương trình
Đặt . Ta có
Dấu bằng xảy ra khi
⟹ Chọn C
Câu 12. Tìm tất cả giá trị thực của tham số m để bất phương trình 4x – m․2x+1 + 3 – 2m ≤ 0 có nghiệm thực.
A. m ≥ 2
B. m ≤ 3
C. m ≤ 5
D. m ≥ 1
Hướng dẫn giải
Ta có 4x – m․2x+1 + 3 – 2m ≤ 0 ⇔ (2x)2 – 2m․2x + 3 – 2m ≤ 0
Đặt 2x = t (t > 0)
Ta có bất phương trình tương đương với
Xét trên (0; +∞)
Bảng biến thiên
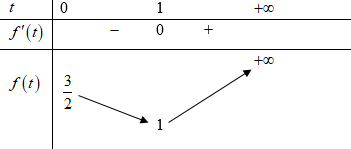
Vậy để bất phương trình có nghiệm thực thì m ≥ 1.
⟹ Chọn D
Câu 13. Tìm tất cả các giá trị thực của tham số m để bất phương trình nghiệm đúng với mọi giá trị x ∈ (1; 64).
A. m ≤ 0
B. m ≥ 0
C. m < 0
D. m > 0
Hướng dẫn giải
Ta có
Đặt log2 x = t, khi x ∈ (1; 64) thì t ∈ (0; 6)
Khi đó, ta có t2 + t + m ≥ 0 ⇔ m ≥ –t2 –t (*)
Xét hàm số f(t) = –t2 –t với t ∈ (0; 6)
Ta có f’(t) = –2t – 1 < 0, ∀ t ∈ (0; 6)
Ta có bảng biến thiên:
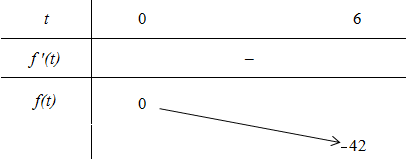
Bất phương trình đã cho đúng với mọi x ∈ (1; 64) khi và chỉ khi bất phương trình (*) đúng với mọi t ∈ (0; 6) ⇔ m ≥ 0.
⟹ Chọn B
Câu 14. Có bao nhiêu giá trị dương của tham số thực m để bất phương trình có nghiệm duy nhất thuộc [32; +∞)?
A. 2
B. 1
C. 3
D. 0
Hướng dẫn giải
Điều kiện xác định
Hàm số xác định trên [32; +∞)
Đặt t = log2 x. Khi x ≥ 32, ta có miền giá trị của t là [5; +∞).
Bất phương trình có dạng:
Xét hàm số trên [5; +∞) có
nên hàm số nghịch biến trên [5; +∞)
Do và f (5) = 3 nên ta có 1 < f(t) ≤ 3
Do với mỗi t có duy nhất một giá trị x nên để bất phương trình đãcho có nghiệm duy nhất thuộc [32; +∞) khi và chỉ bất phương trình có nghiệm duy nhất trên [5; +∞)
Khi đó: . Do đó không có số nguyên dương m thỏa mãn.
⟹ Chọn D
Câu 15. Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình có nghiệm?
A. 6
B. 4
C. 9
D. 1
Hướng dẫn giải
Điều kiện: x2 + 3x + m ≥ 0 (*)
Do m nguyên dương nên m = 1 thỏa mãn (*).
⟹ Chọn D
Câu 16. Tìm tất cả các giá trị thực của tham số m để bất phương trình log2 (5x – 1)․log2 (2․5x – 2) ≥ m có nghiệm với mọi x ≥ 1.
A. m ≥ 6
B. m > 6
C. m ≤ 6
D. m < 6
Hướng dẫn giải
Điều kiện của bất phương trình: x > 0
Ta có log2 (5x – 1)․log2 (2․5x – 2) ≥ m ⇔ log2 (5x – 1)․[1 + log2 (5x – 1)] ≥ m (1)
Đặt t = log2 (5x – 1), với x ≥ 1 ta có t ≥ 2. Khi đó (1) trở thành m ≤ t2 + t (2)
Xét hàm số f(t) = t2 + t trên [2; +∞) ta có f’(t) = 2t + 1 > 0, ∀ t ∈ [2; +∞)
Do đó để bất phương trình đã cho có nghiệm với mọi t ≥ 2 thì hay m ≤ 6
⟹ Chọn C
Câu 17. Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình m․4x + (m – 1)․2x+2 + m – 1 > 0 nghiệm đúng ∀ x ∈ ℝ?
A. m ≤ 3
B. m ≥ 1
C. –1 ≤ m ≤ 4
D. m ≥ 0
Hướng dẫn giải
Bất phương trình ⇔ m․4x + 4(m – 1)․2x + m – 1 > 0 ⇔ m (4x + 4․2x + 1) > 1 + 4․2x
⇔
Đặt 2x = t (Điều kiện t > 0 ).
Khi đó
Để bất phương trình ban đầu nghiệm đúng ∀ x ∈ ℝ thì bất phương trình nghiệm đúng ∀ t > 0
Đặt
Hàm số nghịch biến trên (0; +∞). Khi đó , ∀ t > 0 khi và chỉ khi m ≥ f (0) = 1
⟹ Chọn B
Câu 18. Tìm tất cả các giá trị của tham số m bất phương trình 4x–1 – m(2x + 1) > 0 có nghiệm ∀ x ∈ ℝ
A. m ∈ (–∞; 0]
B. m ∈ (0; +∞)
C. m ∈ (0; 1)
D. m ∈ (–∞; 0) ∪ (1; +∞)
Hướng dẫn giải
Ta có:
Đặt t = 2x, t > 0. Yêu cầu bài toán tương đương với , ∀ t ∈ (0; +∞)
Đặt
Bảng biến thiên
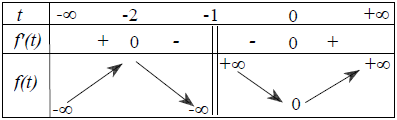
Dựa vào bảng biến thiên có m ≤ 0.
⟹ Chọn A
Dạng 3: Phương pháp Logarit hóa
Phương pháp
Với bất phương trình
Bài tập vận dụng
Câu 1. Nghiệm của bất phương trình là
A.
B.
C.
D.
Hướng dẫn giải
Ta có
⟹ Chọn D
Câu 2. Bất phương trình có tập nghiệm là (–∞; –b) ∪ (–a; a). Khi đó b – a bằng
A. log2 5
B.
C. 1
D. 2 + log2 5
Hướng dẫn giải
Ta có
Bảng xét dấu:

Từ bảng xét dấu ta có
Do đó
⟹ Chọn A
Câu 3. Có bao nhiêu số nguyên dương m trong đoạn [–2018; 2018] sao cho bất phương trình sau đúng với mọi x ∈ (1; 100):
A. 2018
B. 4026
C. 2013
D. 4036
Hướng dẫn giải
Do x ∈ (1; 100) ⇒ log x ∈ (0; 2). Do đó
Đặt t = log x , t ∈ (0; 2)
Xét hàm số
Do đó
Để đúng với mọi x ∈ (1; 100) thì
Do đó hay có 2018 số thỏa mãn.
Dạng 4. Phương pháp sử dụng tính đơn điệu
Phương pháp giải
– Nếu hàm số y = f(x) luôn đồng biến trên D thì f(u) > f(v) ⇔ u > v, ∀ u,v ∈ D
– Nếu hàm số y = f(x) luôn nghịch biến trên D thì f(u) > f(v) ⇔ u < v, ∀ u,v ∈ D
Bài tập vận dụng
Câu 1. Tìm số nghiệm nguyên của bất phương trình
A. 6
B. 4
C. 5
D. 3
Hướng dẫn giải
Đặt a = 2x2 – 15x + 100; b = x2 + 10x – 50 ta có bất phương trình:
2a – 2b + a – b < 0 ⇔ 2a + a < 2b + b ⇔ a < b
(do hàm số y = 2x + x là hàm số đồng biến trên ℝ)
Với a < b ⇔ 2x2 – 15x + 100 < x2 + 10x – 50 ⇔ x2 – 25x + 150 < 0 ⇔ x ∈ (10; 15).
Vậy bất phương trình có 4 nghiệm nguyên.
⟹ Chọn B
Câu 2. Tìm số nguyên m nhỏ nhất để bất phương trình log3 (x2 + x + 1) + 2x3 ≤ 3x2 + log3 x + m – 1 (ẩn x) có ít nhất hai nghiệm phân biệt.
A. m = 3
B. m = 2
C. m = 1
D. m = –1
Hướng dẫn giải
log3 (x2 + x + 1) + 2x3 ≤ 3x2 + log3 x + m – 1 (1)
Điều kiện x > 0
Xét , với x > 0
Với x ∈ (0; 1) ⇒ f’(x) < 0; với x ∈ (1; +∞) ⇒ f’(x) > 0
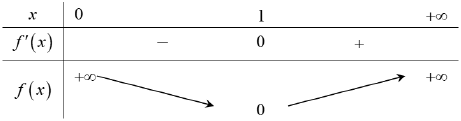
Vậy bất phương trình có ít nhất hai nghiệm ⇔ m – 1 > 0 ⇔ m > 1. Vậy m = 2.
⟹ Chọn B
Câu 3. Gọi a là số thực lớn nhất để bất phương trình x2 – x + 2 + a․ln (x2 – x + 1) ≥ 0 nghiệm đúng với mọi x ∈ ℝ. Mệnh đề nào sau đây đúng?
A. a ∈ (2; 3]
B. a ∈ (8; +∞)
C. a ∈ (6; 7]
D. a ∈ (–6; –5]
Hướng dẫn giải
Đặt suy ra
Bất phương trình x2 – x + 2 + a․ln (x2 – x + 1) ≥ 0 ⇔ t + a․ln t + 1 ≥ 0 ⇔ a․ln t ≥ –t – 1
Trường hợp 1: t = 1 khi đó a․ln t ≥ –t – 1 luôn đúng với mọi a.
Trường hợp 2:
Ta có
Xét hàm số
Do đó
Trường hợp 3: t > 1
Ta có
Xét hàm số
Xét hàm số
Vậy g(t) = 0 có tối đa một nghiệm.
Vì g (1) = –2; vậy g(t) = 0 có duy nhất một nghiệm trên (1; +∞)
Do đó f’(t) = 0 có duy nhất một nghiệm là t0 . Khi đó suy ra f (t0) = –t0
Bảng biến thiên
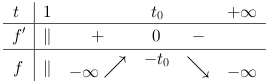
Vậy
Vậy
Vậy số thực a thỏa mãn yêu cầu bài toán là: a ∈ (6; 7]
⟹ Chọn C
Câu 4. Biết tập hợp tất cả các giá trị của tham số m để bất phương trình có nghiệm là
với a, b là các số nguyên dương và
tối giản. Tổng S = a + b là:
A. S = 13
B. S = 15
C. S = 9
D. S = 11
Hướng dẫn giải
Ta có:
Xét
Do nên
hay
Dấu đẳng thức xảy ra khi cos2 x = 1 ⇔ sin x = 0 ⇔ x = kπ
Vậy .
Bất phương trình có nghiệm khi và chỉ khi hay
⟹ Chọn A
Câu 5. Với giá trị nào của tham số m thì bất phương trình có nghiệm?
A. m ≤ 4
B. m ≥ 4
C. m ≤ 1
D. m ≥ 1
Hướng dẫn giải
Chia hai vế của bất phương trình cho , ta được
Xét hàm số là hàm số nghịch biến.
Ta có: 0 ≤ sin2 x ≤ 1 nên 1 ≤ y ≤ 4
Vậy bất phương trình có nghiệm khi m ≤ 4. Chọn đáp án A.
⟹ Chọn A
Câu 6. Tìm số nguyên m nhỏ nhất để bất phương trình log3 (x2 + x + 1) + 2x3 ≤ 3x2 + log3 x + m – 1 (ẩn x) có ít nhất hai nghiệm phân biệt.
A. m = 3
B. m = 2
C. m = 1
D. m = –1
Hướng dẫn giải
log3 (x2 + x + 1) + 2x3 ≤ 3x2 + log3 x + m – 1 (1)
Điều kiện x > 0
Xét , với x > 0
Với x ∈ (0; 1) ⇒ f’(x) < 0; với x ∈ (1; +∞) ⇒ f’(x) > 0.
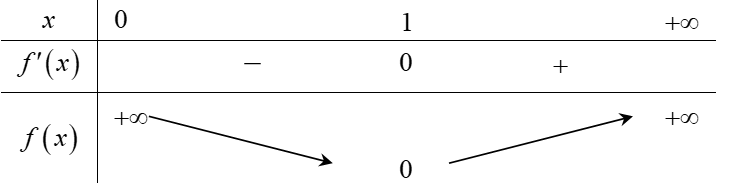
Vậy bất phương trình có ít nhất hai nghiệm ⇔ m – 1 > 0 ⇔ m > 1. Vậy m = 2.
⟹ Chọn B
Câu 7. Biết tập nghiệm của bất phương trình là (a; b). Khi đó tổng a + 2b bằng?
A. 3
B. 4
C. 2
D. 1
Hướng dẫn giải
Xét hàm số
Dễ đánh giá
Bảng biến thiên:
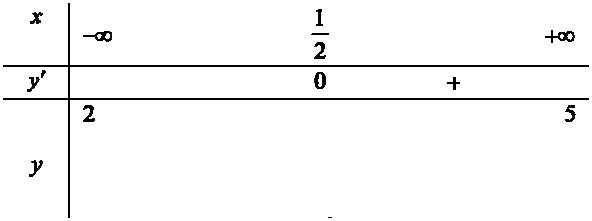
Có f (0) = f (1) = 3 và dựa vào bảng biến thiên ta có f(x) < 3 ⇔ x ∈ (0; 1)
Vậy a = 0; b = 1, suy ra a + 2b = 2
⟹ Chọn C
Câu 8. Tìm tất cả các giá trị thực của tham số a (a > 0) thỏa mãn
A. 0 < a < 1
B. 1 < a < 2017
C. a ≥ 2017
D. 0 < a ≤ 2017
Hướng dẫn giải
Ta có
Xét hàm số
Ta có
Nên y = f(x) là hàm giảm trên (0; +∞)
Do đó f (a) ≤ f (2017), (a > 0) khi 0 < a ≤ 2017
⟹ Chọn D
Câu 9. Tìm tất cả các giá trị thực của tham số m để bất phương trình nghiệm đúng với mọi giá trị x ∈ (1; 64).
A. m ≤ 0
B. m ≤ 0
C. m < 0
D. m > 0
Hướng dẫn giải
Ta có ⇔ (log2 x)2 + log2 x + m ≥ 0
Đặt log2 x = t, khi x ∈ (1; 64) thì t ∈ (0; 6)
Khi đó, ta có t2 + t + m ≥ 0 ⟺ m ≥ –t2 – t (*)
Xét hàm số f(t) = –t2 –t với t ∈ (0; 6)
Ta có f’(t) = –2t – 1 < 0, ∀ t ∈ (0; 6)
Ta có bảng biến thiên:
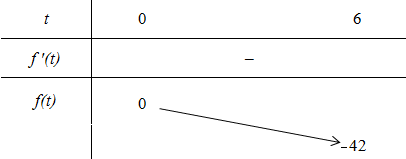
Bất phương trình đã cho đúng với mọi x ∈ (1; 64) khi và chỉ khi bất phương trình (*) đúng với mọi t ∈ (0; 6) ⇔ m ≥ 0.
⟹ Chọn B
Câu 10. Giả sử S = (a; b] là tập nghiệm của bất phương trình . Khi đó b – a bằng?
A.
B.
C.
D. 2
Hướng dẫn giải
Điều kiện:
Giải hệ (I):
Giải (1):
Xét hàm số với x ∈ (0; 3]
Ta có , ∀ x ∈ (0; 3]
Lập bảng biến thiên
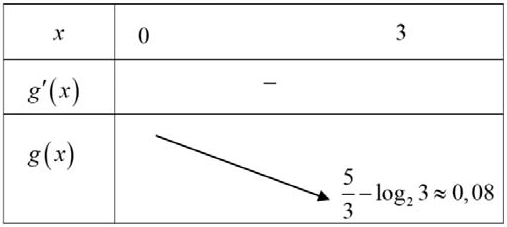
Vậy , ∀ x ∈ (0; 3]
Xét bất phương trình (2):
Vậy nghiệm của hệ (I) là
Hệ (II) vô nghiệm.
Vậy
⟹ Chọn A
Câu 11. Có bao nhiêu giá trị nguyên thuộc khoảng (-9; 9) của tham số m để bất phương trình có nghiệm thực?
A. 6
B. 7
C. 10
D. 11
Hướng dẫn giải
Điều kiện:
Bất phương trình đã cho tương đương
Áp dụng bất đẳng thức cô si ta có
Vì vậy
Khảo sát hàm số trên (0; 1) ta được
Vậy m có thể nhận được các giá trị {2; 3; 4; 5; 6; 7; 8}.
⟹ Chọn B