Ở bài viết này, VerbaLearn giúp bạn đọc tổng hợp một số dạng bài tập nguyên hàm đặc trưng theo chương trình toán lớp 12. Từ đó giúp các bạn học sinh có thêm nguồn tài liệu tham khảo quan trọng để làm chủ chuyên đề này.
Dạng 1.Tính nguyên hàm bằng bảng nguyên hàm
Phương pháp giải
Bài toán 1. Tìm nguyên hàm F(x) của hàm số f(x) (giả sử điều kiện được xác định)
Một số công thức thường sử dụng
∫kdx = kx + C
∫kf(x)dx = k.∫f(x)dx
∫|f(x) ± g(x)|dx = ∫f(x)dx ± ∫g(x)dx
Bài tập vận dụng
Câu 1. Tìm họ nguyên hàm của f(x) = 4x3 + x + 5
Hướng dẫn giải
Ta có:
Câu 2. Tìm họ nguyên hàm của f(x) = 3x2 – 2x
Hướng dẫn giải
Ta có: F(x) = ∫f(x)dx = ∫(3x2 – 2x)dx = x3 – x2 + C
Câu 3. Tìm họ nguyên hàm của
Hướng dẫn giải
Ta có:
Câu 4. Tìm họ nguyên hàm của
Hướng dẫn giải
Ta có:
Câu 5. Tính I = ∫(x2 – 3x)(x + 1)dx
Hướng dẫn giải
Phân phối được:
Câu 6. Tính I = ∫(x – 1)(x2 + 2)dx
Hướng dẫn giải
Phân phối được
Câu 7. Tính I = ∫(2x + 1)5dx (công thức mở rộng)
Hướng dẫn giải
Câu 8. Tính I = ∫(2x – 10)2020dx
Hướng dẫn giải
Câu 9. Tìm một nguyên hàm F(x) của hàm số f(x) = 4×3 – 4x + 5 thỏa mãn F(1) = 3
A. F(x) = x4 – 2x2 + 5x – 1
B. F(x) = x4 – 4x2 + 5x + 1
C. F(x) = x4 – 2x2 + 5x + 3
D. F(x) = x4 – 2x2 + 5x + 5
Hướng dẫn giải
Ta có: F(x) = ∫f(x)dx = ∫(4x3 – 4x + 5)dx = x4 – 2x2 + 5x – C
Theo đề bài, ta có: F(1) = 3 ⇔ 14 – 2.12 + 5.1 + C = 3 ⇔ C = –1
Do đó: F(x) = x4 – 2x2 + 5x – 1
Lưu ý. Nếu đề bài yêu cầu tìm F(a) ta chỉ cần thế x = a vào F(x) sẽ tìm được F(a). Chẳng hạn, tính F(2), ta thế x = 2 vào F(x), nghĩa là F(2) = 24 – 2.22 + 5.2 – 1 = 17
⟹ Chọn A
Câu 10. Tìm một nguyên hàm F(x) của hàm số f(x) = 3x2 + 2x + 5 thỏa mãn F(1) = 4
A. F(x) = x3 – x2 + 5x – 3
B. F(x) = x3 + x2 + 5x – 3
C. F(x) = x3 + x2 – 5x + 3
D. F(x) = x3 + x2 + 5x + 3
Hướng dẫn giải
∫f(x)dx = ∫(3x2 + 2x + 5)dx = x3 + x2 + 5x + C
F(1) = 4 ⇒ 7 + C = 4 ⇔ C = –3
Vậy F(x) = x3 + x2 + 5x – 3
⟹ Chọn B
Câu 11. Hàm số f(x) = –5x4 + 4x2 – 6 có một nguyên hàm F(x) thỏa F(3) = 1. Tính F(–3)
A. F(–3) = 226
B. F(–3) = –225
C. F(–3) = 451
D. F(–3) = 225
Hướng dẫn giải
Do đó F(–3) = 451
⟹ Chọn C
Câu 12. Hàm số f(x) = x3 + 3x + 2 có một nguyên hàm F(x) thỏa F(2) = 14. Tính F(–2)
A. F(–2) = 6
B. F(–2) = –14
C. F(–2) = –6
D. F(–2) = 14
Hướng dẫn giải
Do đó F(–2) = 6
⟹ Chọn A
Câu 13. Hàm số f(x) = (2x + 1)3 có một nguyên hàm F(x) thỏa . Tính
A. P = 32
B. P = 34
C. P = 18
D. P = 30
Hướng dẫn giải
Do đó
⟹ Chọn B
Dạng 2. Nguyên hàm của hàm số hữu tỷ
Bài tập vận dụng
Câu 1. Tìm
Hướng dẫn giải
Ta có
Câu 2. Tìm
Hướng dẫn giải
Ta có
Câu 3. Tìm
Hướng dẫn giải
Ta có
Câu 4. Tìm
Hướng dẫn giải
Ta có
Câu 5. Tìm
Hướng dẫn giải
Ta có
Câu 6. Tìm
Hướng dẫn giải
Ta có
Câu 7. Tìm
Hướng dẫn giải
Ta có
Câu 8. Tìm
Hướng dẫn giải
Ta có
Câu 9. Tìm
Hướng dẫn giải
Ta có
j) Tìm
Hướng dẫn giải
Ta có
Dạng 3. Nguyên hàm từng phần
Phương pháp giải
Định lý
Định lí 1: Nếu ∫f(u) du = F(u) + C và u = u(x) là hàm số có đạo hàm liên tục thì
∫f(u(x)).u’(x)dx = F(u(x)) + C
Hệ quả: Nếu u = ax + b (a ≠ 0) thì ta có
Định lí 2: Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì:
∫u(x).v’(x)dx = u(x)v(x) – ∫u’(x).v(x)dx
Hay ∫udv = uv – ∫vdu
Vận dụng giải toán
Nhận dạng: Tích hai hàm nhân khác nhau, ví dụ: ∫exsinxdx, ∫xlnxdx, …
– Đặt . Suy ra I = ∫udv = uv – ∫vdu
– Thứ tự ưu tiên chọn u: log – đa – lượng – mũ và dv = phần còn lại.
– Lưu ý: Bậc của đa thức và bậc của ln tương ứng với số lần lấy nguyên hàm.
– Dạng mũ nhân lượng giác là dạng nguyên hàm từng phần luân hồi.
Tìm nguyên hàm F(x) của hàm số f(x) (giả sử điều kiện được xác định):
Kỹ năng cơ bản
– Tìm nguyên hàm bằng phương pháp biến đổi trực tiếp.
– Tìm nguyên hàm bằng phương pháp đổi biến số.
– Tìm nguyên hàm bằng phương pháp nguyên hàm từng phần.
Bài tập vận dụng
Câu 1. Tìm I = ∫(x + 1)sinxdx
Hướng dẫn giải
Chọn
Suy ra I = –(x + 1)cosx + ∫cosxdx = –(x + 1)cosx + sinx + C
Câu 2. Tìm I = ∫xlnxdx
Hướng dẫn giải
Chọn
Suy ra
Câu 3. Tìm I = ∫xexdx
Hướng dẫn giải
Chọn
Suy ra I = xex – ∫exdx = xex – ex + C = ex(x – 1) + C
Câu 4. Tìm I = ∫xe–xdx
Hướng dẫn giải
Chọn
Suy ra I = –xe–x – ∫e–xdx = –xe–x – e–x + C = –e–x(x + 1) + C
Câu 5. Tìm
Hướng dẫn giải
Chọn
Suy ra
Câu 6. Tìm
Hướng dẫn giải
Chọn
Suy ra
Cần nhớ:
+) ∫tanxdx = –ln|cosx| + C
+) ∫cotxdx = –ln|sinx| + C
Câu 7. Tìm I = ∫lnxdx
Hướng dẫn giải
Đặt
Câu 8. Tìm I = ∫(2x + 1)lnxdx
Hướng dẫn giải
Đặt
Câu 9. Tìm I = ∫xsinxcosxdx
Hướng dẫn giải
Ta có
Khi đó, đặt
Suy ra
Câu 10. Tìm I = ∫x(2cos2x – 1)dx
Hướng dẫn giải
Ta có I = ∫x(1 + cosx + x)dx = ∫(x2 + x)dx + ∫xcos2xdx
Đặt
Câu 11. Tìm I = ∫exsinxdx
Hướng dẫn giải
Đặt
Đặt
Câu 12. Nguyên hàm của hàm số f(x) = x3 + 3x + 2 là hàm số nào trong các hàm số sau?
A.
B.
C.
D.
Hướng dẫn giải
Sử dụng bảng nguyên hàm.
⟹ Chọn A
Câu 13. Hàm số F(x) = 5x3 + 4x2 – 7x + 120 + C là họ nguyên hàm của hàm số nào sau đây?
A. f(x) = 15x2 + 8x – 7
B. f(x) = 5x2 + 4x + 7
C.
D. f(x) = 5x2 + 4x – 7
Hướng dẫn giải
Lấy đạo hàm của hàm số F(x) ta được kết quả.
⟹ Chọn A
Câu 14. Họ nguyên hàm của hàm số: là
A.
B.
C.
D.
Hướng dẫn giải
Sử dụng bảng nguyên hàm.
⟹ Chọn A
Câu 15. Tìm nguyên hàm của hàm số f(x) = (x + 1)(x + 2)
A.
B.
C.
D.
Hướng dẫn giải
f(x) = (x + 1)(x + 2) = x2 + 3x + 2. Sử dụng bảng nguyên hàm.
⟹ Chọn A
Câu 16. Nguyên hàm F(x) của hàm số là hàm số nào?
A.
B.
C.
D.
Hướng dẫn giải
Sử dụng bảng nguyên hàm.
⟹ Chọn A
Câu 17. Tính F(x) = ∫xsinx dx bằng
A. F(x) = sin x – xcos x + C
B. F(x) = xsin x – cos x + C
C. F(x) = sin x + xcos x + C
D. F(x) = xsin x + xcos x + C
Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần
Phương pháp trắc nghiệm:
Cách 1: Dùng định nghĩa, sử dụng máy tính nhập , CALC ngẫu nhiên tại một số điểm x0 thuộc tập xác định, kết quả xấp xỉ bằng 0 chọn.
Cách 2: Sử dụng phương pháp bảng
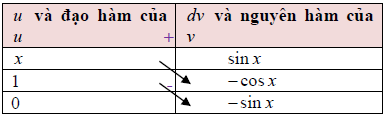
Vậy F(x) = sin x – xcos x + C
⟹ Chọn A
Câu 18. Tính ∫xln2x dx. Chọn kết quả đúng:
A.
B.
C.
D.
Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần 2 lần.
Phương pháp trắc nghiệm
Cách 1: Sử dụng định nghĩa F’(x) = f(x) ⇔ F’(x) – f(x) = 0
Nhập máy tính . CALC x tại một số giá trị ngẫu nhiên x0 trong tập xác định, nếu kết quả xấp xỉ bằng 0 thì chọn.
Cách 2: Sử dụng phương pháp bảng:

Do đó
⟹ Chọn A
Câu 19. Tính F(x) = ∫x sinx cosx dx. Chọn kết quả đúng:
A.
B.
C.
D.
Hướng dẫn giải
Phương pháp tự luận: Biến đổi rồi sử dụng phương pháp nguyên hàm từng phần.
Phương pháp trắc nghiệm:
Cách 1: Sử dụng định nghĩa F’(x) = f(x) ⇔ F’(x) – f(x) = 0
Nhập máy tính . CALC x tại một số giá trị ngẫu nhiên x0 trong tập xác định, nếu kết quả xấp xỉ bằng 0 thì chọn.
Cách 2: Sử dụng phương pháp bảng:
⟹ Chọn A
Câu 20. Tính . Chọn kết quả đúng
A.
B.
C.
D.
Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với
Phương pháp trắc nghiệm:
Cách 1: Sử dụng định nghĩa F’(x) = f(x) ⇔ F’(x) – f(x) = 0
Nhập máy tính . CALC x tại một số giá trị ngẫu nhiên x0 trong tập xác định, nếu kết quả xấp xỉ bằng 0 thì chọn.
Cách 2: Sử dụng phương pháp bảng:
⟹ Chọn A
Câu 21. Tính . Chọn kết quả đúng
A. F(x) = x․tan x + ln|cos x| + C
B. F(x) = –x․cot x + ln|cos x| + C
C. F(x) = –x․tan x + ln|cos x| + C
D. F(x) = –x․cot x – ln|cos x| + C
Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với
Phương pháp trắc nghiệm:
Cách 1: Sử dụng định nghĩa F’(x) = f(x) ⇔ F’(x) – f(x) = 0
Nhập máy tính . CALC x tại một số giá trị ngẫu nhiên x0 trong tập xác định, nếu kết quả xấp xỉ bằng 0 thì chọn.
Cách 2: Sử dụng phương pháp bảng:
⟹ Chọn A
Câu 22. Tính F(x) = ∫x2cos x dx. Chọn kết quả đúng
A. F(x) = (x2 – 2) sin x + 2x cos x + C
B. F(x) = 2x2 sin x – x cos x + sin x + C
C. F(x) = x2 sin x – 2x cos x + 2sin x + C
D. F(x) = (2x + x2) cos x – x sin x + C
Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần 2 lần với u = x2; dv = cosx dx, sau đó u1 = x; dv1 = sinx dx
Phương pháp trắc nghiệm:
Cách 1: Sử dụng định nghĩa F’(x) = f(x) ⇔ F’(x) – f(x) = 0
Nhập máy tính . CALC x tại một số giá trị ngẫu nhiên x0 trong tập xác định, nếu kết quả xấp xỉ bằng 0 thì chọn.
Cách 2: Sử dụng phương pháp bảng:
⟹ Chọn A
Câu 23. Tính F(x) = ∫x sin2x dx. Chọn kết quả đúng
A.
B.
C.
D.
Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với u = x; dv = sin2x dx
Phương pháp trắc nghiệm:
Sử dụng phương pháp bảng hoặc sử dụng máy tính:
Nhập , CALC ngẫu nhiên tại một số điểm x0 bất kỳ, nếu kết quả xấp xỉ bằng 0 thì chọn đáp án đó.
⟹ Chọn A
Câu 24. Hàm số F(x) = x.sin x + cos x + 2017 là một nguyên hàm của hàm số nào?
A. f(x) = x․cos x
B. f(x) = x․sin x
C. f(x) = –x․cos x
D. f(x) = –x․sin x
Hướng dẫn giải
Phương pháp tự luận: Tính F’(x) có kết quả trùng với đáp án chọn.
Phương pháp trắc nghiệm:
Sử dụng định nghĩa F’(x) = f(x) ⇔ F’(x) – f(x) = 0
Nhập máy tính . CALC x tại một số giá trị ngẫu nhiên x0 trong tập xác định, nếu kết quả xấp xỉ bằng 0 thì chọn
⟹ Chọn A
Câu 25. Tính . Khẳng định nào sau đây là sai?
A.
B.
C.
D.
Hướng dẫn giải
Phương pháp tự luận: Sử dụng phương pháp nguyên hàm từng phần với u = 1 + ln (x + 1); hoặc biến đổi rồi đặt u = ln (x + 1);
Phương pháp trắc nghiệm: Sử dụng máy tính kiểm tra bằng định nghĩa.
Dạng 4. Nguyên hàm đổi biến số
Phương pháp giải
Định lí: Cho ∫f(u)du = F(u) + C và u = u(x) là hàm số có đạo hàm liên tục thì
∫f[u(x)].u’(x).dx = F[u(x)] + C
Có sẵn Tách từ hàm Nhân thêm
Một số dạng đổi biến thường gặp
1) , với m, n ϵ ℤ
2) Đặt
3) Đặt
4) Đặt
5) Đặt
6) Đặt
7) Đặt
8) Đặt
9) Đặt
10) Đặt
Lưu ý: Sau khi đổi biến và tính nguyên hàm xong, ta cần trả lại biến cũ ban đầu là x.
Nhóm 1.
, khi m, n ϵ ℤ
Bài tập vận dụng
Câu 1. Tìm I = ∫x(1 – x)2018dx
Hướng dẫn giải
Đặt t = 1 – x ⇒ x = 1 – t ⟶ dx = –dt
Khi đó:
Suy ra
Câu 2. Tìm I = ∫x(1 + x)2019dx
Hướng dẫn giải
Đặt t = 1 + x ⇒ x = t – 1 ⟶ dx = dt
Khi đó:
Suy ra
Câu 3. Tìm I = ∫x(x2 + 1)5dx
Hướng dẫn giải
Đặt
Khi đó:
Suy ra
Câu 4. Tìm I = ∫x2(x – 1)9dx
Hướng dẫn giải
Đặt t = x – 1 ⇒ x = t + 1 ⟶ dx = dt
Khi đó:
Suy ra
Câu 5. Tìm
Hướng dẫn giải
Dạng 5. Tính chất nguyên hàm & nguyên hàm của hàm ẩn
Nhóm 1. Sử dụng định nghĩa F’(x) = f(x).
Câu 1. (THPT Lương Thế Vinh – Hà Nội năm 2019) Gọi F(x) = (ax2 + bx + c).ex là một nguyên hàm của hàm số f(x) = (x – 1)2ex. Giá trị của biểu thức S = a + 2b + c bằng
A. 3
B. –2
C. 0
D. 4
Hướng dẫn giải
Theo định nghĩa F’(x) = f(x), ta có f(x) = F’(x) = [(ax2 + bx + c).ex]’
= (2ax + b)ex + ex(ax2 + bx + c) = [ax2 + (2a + b)x + b + c]ex = (x2 – 2x + 1)ex
Đồng nhất hệ số:
⟹ Chọn B
Câu 2. Biết F(x) = (ax2 + bx + c).e–x là một nguyên hàm của hàm số f(x) = (2x2 – 5x + 2).e–x trên ℝ. Giá trị của biểu thức f [F(0)] bằng.
A. –e–1
B. 9e
C. 20e2
D. 3e
Hướng dẫn giải
Theo định nghĩa F’(x) = f(x), ta có: f(x) = F’(x) = [(ax2 + bx + c).e–x]’
= (2ax + b)e–x – e–x(ax2 + bx + c) = [–ax2 + (2a – b)x + b – c]e–x = (2x2 – 5x + 2)e–x
Đồng nhất hệ số:
⟹ Chọn B
Câu 3. Biết là một nguyên hàm của hàm số
trên khoảng
. Giá trị của biểu thức T = a + b + c bằng.
A. 5
B. 6
C. 7
D. 8
Hướng dẫn giải
Theo định nghĩa F’(x) = f(x), ta có:
Do đó ta có
⟹ Chọn C
Câu 4. Cho hàm số F(x) là một nguyên hàm của f(x) = 2019x(x2 – 4)(x2 – 3x + 2). Khi đó số điểm cực trị của hàm số F(x) là.
A. 5
B. 4
C. 3
D. 2
Hướng dẫn giải
Theo định nghĩa F’(x) = f(x), ta có:
x = 2 là nghiệm bội bậc hai nên f(x) không đổi dấu qua x = 2
Vậy hàm số y = F(x) có hai điểm cực trị.
⟹ Chọn D
Câu 5. Cho F(x) là một nguyên hàm của hàm số . Hàm số F(x2 + x) có bao nhiêu điểm cực trị?
A. 5
B. 4
C. 3
D. 2
Hướng dẫn giải
Ta có
Vậy hàm số F(x2 + x) có 5 điểm cực trị
⟹ Chọn A
Nhóm 2. Sử dụng định nghĩa giải bài toán nguyên hàm của hàm ẩn
Vận dụng tính chất ∫f’(x)dx = f(x) + C, ∫f’’(x)dx = f’(x) + C,… vào các dạng sau:
Câu 1. (HSG Bắc Ninh năm 2019) Cho hàm số y = f(x) có đạo hàm liên tục trên đoạn [1; 2] thỏa mãn f(1) = 4 và f(x) = xf’(x) – 2x3 – 3x2 . Giá trị của f(2) bằng
A. 5
B. 10
C. 15
D. 20
Hướng dẫn giải
Ta có
Do f(1) = 4 ⇒ 4 = 1 + 3 + C ⇒ C = 0 ⇒ f(x) = x3 + 3x2 ⇒ f(2) = 20
⟹ Chọn D
Câu 2. (THPT Yên Định Thanh Hóa năm 2019) Cho hàm số f(x) thỏa mãn f(x).f’(x) = 3x5 + 6x2 và f(0) = 2. Giá trị của f2(2) bằng
A. 144
B. 64
C. 100
D. 81
Hướng dẫn giải
Ta có:
Do f(0) = 2 ⇒ 4 = C ⇒ C = 4 ⇒ f2(2) = 100
⟹ Chọn C
Câu 3. (Đề thi THPT QG năm 2018 – Mã đề 102 – Câu 40) Cho hàm số f(x) thỏa mãn và f’(x) = x[f(x)]2 với mọi x ϵ ℝ. Giá trị của f(1) bằng
A.
B.
C.
D.
Hướng dẫn giải
Ta có
Do
⟹ Chọn B
Câu 4. Cho hàm số f(x) thỏa f2(x) + 2x.f(x).f’(x) = 5x4 với f(1) = 0, f(x) > 0. Hệ số góc tiếp tuyến k của đồ thị hàm số y = f(x) tại điểm có hoành độ x = 2 bằng
A. k = 1
B. k = 2
C. k = 4
D. k = 3
Hướng dẫn giải
Ta có f2(x) + 2x.f(x).f’(x) = 5x4 ⇔ [x.f2(x)]’ = 5x4
⇔ ∫[x.f2(x)]’dx = ∫(5x4)dx ⇔ x.f2(x) = x5 + C
Do f(1) = 0 ⇒ 0 = 15 + C ⇒ C = –1 ⇒ x.f2(x) = x5 – 1
Dạng 6. Nguyên hàm của hàm số lượng giác
Phương pháp giải
Cần nắm vững công thức nguyên hàm đối với các hàm số lượng giác sơ cấp và hàm số lượng giác hợp.
Bài tập vận dụng
Câu 1. Tìm nguyên hàm của hàm số f(x) = sin2x
A.
B.
C. ∫sin2x dx = cos2x + C
D. ∫sin2x dx = –cos2x + C
Hướng dẫn giải
⟹ Chọn A
Câu 2. Tìm nguyên hàm của hàm số
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn A
Câu 3. Tìm nguyên hàm của hàm số
A.
B.
C.
D.
Hướng dẫn giải
nên
⟹ Chọn A
Câu 4. Tìm nguyên hàm của hàm số
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn A
Câu 5. Tìm nguyên hàm của hàm số f(x) = sin3x․cosx
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn A
Dạng 7. Nguyên hàm của hàm số mũ, lôgarit
Phương pháp giải
Ghi nhớ các công thức nguyên hàm của hàm số mũ, logarit để giúp quá trình làm bài tập hoặc suy luận nhanh hơn. Tránh sai sót.
Bài tập vận dụng
Câu 1. Tìm nguyên hàm của hàm số f(x) = ex – e–x
A. ∫f(x) dx = ex + e–x + C
B. ∫f(x) dx = –ex + e–x + C
C. ∫f(x) dx = ex – e–x + C
D. ∫f(x) dx = –ex – e–x + C
Hướng dẫn giải
∫(ex – e–x) dx = ex + e–x + C
⟹ Chọn A
Câu 2. Tìm nguyên hàm của hàm số f(x) = 2x․3–2x
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn A
Câu 3. Họ nguyên hàm của hàm số f(x) = ex (3 + e–x) là
A. F(x) = 3ex + x + C
B. F(x) = 3ex + ex lnex + C
C.
D. F(x) = 3ex – x + C
Hướng dẫn giải
F(x) = ∫ex (3 + e–x) dx = ∫(3ex + 1) dx = 3ex + x + C
⟹ Chọn A
Câu 4. Hàm số F(x) = 7ex – tanx là một nguyên hàm của hàm số nào sau đây?
A.
B.
C.
D.
Hướng dẫn giải
Ta có:
⟹ Chọn A
Câu 5. Tìm nguyên hàm của hàm số
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn A
Dạng 8. Nguyên hàm của hàm số chứa căn thức
Phương pháp giải
Ghi nhớ các công thức nguyên hàm của các hàm số chứa căn thức.
Bài tập vận dụng
Câu 1. Nguyên hàm của hàm số là
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn A
Câu 2. Tìm nguyên hàm của hàm số
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn A
Câu 3. Tìm nguyên hàm của hàm số
A.
B.
C.
D.
Hướng dẫn giải
Đặt
⟹ Chọn A
Câu 4. Tìm nguyên hàm của hàm số
A.
B.
C.
D.
Hướng dẫn giải
Đặt
⟹ Chọn A
Câu 5. Tìm nguyên hàm của hàm số
A.
B.
C.
D.
Hướng dẫn giải
Đặt
Khi đó
⟹ Chọn A
Câu 6. Tìm nguyên hàm của hàm số
A.
B.
C.
D.
Hướng dẫn giải
Đặt
Khi đó
⟹ Chọn A
Câu 7. Tìm nguyên hàm của hàm số
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn A
Câu 8. Hàm số là một nguyên hàm của hàm số nào sau đây?
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn A
Câu 9. Biết một nguyên hàm của hàm số là hàm số F(x) thỏa mãn
. Khi đó F(x) là hàm số nào sau đây?
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn A
Câu 10. Biết là một nguyên hàm của hàm số
. Khi đó giá trị của a bằng
A. –3
B. 3
C. 6
D.
Hướng dẫn giải
⟹ Chọn A
Trên đây là một số bài tập trắc nghiệm nguyên hàm có lời giải chi tiết và phân dạng rõ ràng. Bạn đọc có thể tải thêm một số bài tập dưới dạng file PDF để có được ma trận bài đa dạng hơn. Từ đó tránh bỡ ngỡ trong quá trình thi cử trên trường.