Bài viết giúp bạn đọc tìm hiểu cách tính xác suất thông qua 2 quy tắc cộng và quy tắc nhân. Ngoài ra, các định nghĩa về biến cố trong quá trình tính xác xuất cũng được VerbaLearn trình bày rõ ràng kèm các ví dụ cụ thể.
Quy tắc cộng xác suất
1. Biến cố hợp
Cho hai biến cố A và B. Biến cố “A hoặc B xảy ra”, kí hiệu là A ∪ B được gọi là hợp của hai biến cố A và B. Khi đó ΩA ⊂ ΩB ⊂ Ω.
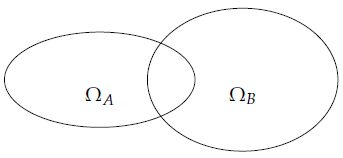 Hình ảnh minh họa 2 biến cố hợp
Hình ảnh minh họa 2 biến cố hợp
Ví dụ: Chọn ngẫu nhiên một bạn học sinh lớp 11 của trường. Gọi A là biến cố:”Bạn đó là học sinh giỏi toán” và B là biến cố: “Bạn đó là học sinh giỏi Lý”. Khi đó A ∪ B là biến cố: “Bạn đó là học sinh giỏi Toán hoặc giỏi Lý”
2. Biến cố xung khắc
Cho hai biến cố A và B. Hai biến cố A và B được gọi là xung khắc nếu biến cố này xảy ra thì biến cố kia không xảy ra. Khi đó ΩA ∩ B = ∅.
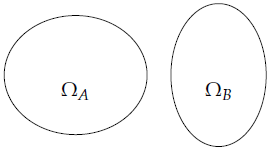 Hình ảnh minh họa biến cố xung khắc
Hình ảnh minh họa biến cố xung khắc
Ví dụ: Chọn ngẫu nhiên một học sinh lớp 11 của trường. Gọi A là biến cố: “Bạn đó là học sinh lớp 11C1” và B biến cố: “Bạn đó là học sinh lớp 11C2”. Khi đó A và B là hai biến cố xung khắc.
3. Quy tắc cộng xác suất hai biến cố xung khắc
+) Nếu A và B là hai biến cố xung khắc thì xác suất biến cố A ∪ B là:
P(A + B) = P(A) + P(B).
+) Cho n biến cố A1, A2, …, An đôi một là các biến cố xung khắc với nhau. Khi đó:
P(A1 ∪ A2 ∪ A3 ∪… ∪ An = P(A1) + P(A2) + P(A3) + … + P(An).
Ví dụ 1. Cho một hộp đựng 4 viên bi xanh và 3 bi đỏ. Lấy ngẫu nhiên 3 viên bi. Tính xác suất để có ít nhất 2 viên bi xanh.
ĐS:
Lời giải
Số phần tử của không gian mẫu là:
Gọi A là biến cố “3 viên bi lấy ra có ít nhất 2 viên bi xanh”. Có các trường hợp sau:
+) Lấy được 2 viên bi xanh và 1 viên bi đỏ, số cách chọn là
+) Lấy được 3 viên bi xanh, số cách chọn là
Theo quy tắc cộng ta có n(A) = 18 + 4 = 22
Vậy xác suất của A là:
Ví dụ 2. Trên một kệ sách có 7 quyển sách Toán, 6 quyển sách Lý và 4 quyển sách Hóa. Lấy ngẫu nhiên từ kệ sách đó ra hai quyển sách. Tính xác suất để lấy được hai quyển sách cùng một môn.
ĐS:
Lời giải
Số phần tử của không gian mẫu là:
Gọi A là biến cố: “Lấy được hai quyển sách cùng một môn”. Có các trường hợp sau:
+) Lấy được 2 quyển sách Toán, có cách
+) Lấy được 2 quyển sách Lý, có cách
+) Lấy được 2 quyển sách Hóa, có cách
Theo quy tắc cộng ta có n(A) = 21 + 15 + 6 = 42
Vậy xác suất của A là:
4. Biến cố đối
Cho là một biến cố. Khi đó biến cố “không
”, kí hiệu là
, được gọi là biến cố đối của
. Ta nói
và
là hai biến cố đối của nhau.
Khi đó:
 Hình ảnh minh họa biến cố đối
Hình ảnh minh họa biến cố đối
Ví dụ 1. Hai biến cố đối nhau có phải là hai biến cố xung khắc?
Lời giải
Hai biến cố đối nhau là hai biến cố xung khắc.
Ví dụ 2. Hai biến cố xung khắc có phải là hai biến cố đối?
Lời giải
Hai biến cố xung khắc không phải là hai biến cố đối.
Ví dụ 3. Một xạ thủ bắn vào bia một viên đạn với xác suất . Khi đó xác suất bắn trượt là bao nhiêu?
ĐS:
Lời giải
Gọi A là biến cố: “Một xạ thủ bắn vào bia một viên đạn” thì .
Khi đó xác suất bắn trượt là:
Ví dụ 4. Từ một hộp có 6 quả cầu trắng và 4 quả cầu xanh, lấy ngẫu nhiên cùng một lúc ra 4 quả. Tính xác suất sao cho:
a) Bốn quả lấy ra cùng màu
ĐS:
b) Bốn quả lấy ra có đủ hai màu
ĐS:
Lời giải
Số phần tử của không gian mẫu là
a) Gọi A là biến cố: “Bốn quả lấy ra cùng màu”. Có hai trường hợp:
+) Bốn quả lấy ra cùng màu trắng, có cách chọn
+) Bốn quả lấy ra cùng màu xanh, có cách chọn
Theo quy tắc cộng thì n(A) = 15 + 1 = 16 cách chọn.
Vậy xác suất của A là:
b) Gọi B là biến cố: “Bốn quả lấy ra có đủ màu” thì
Suy ra:
Quy tắc nhân xác suất
1. Biến cố giao
Cho hai biến cố A và B. Biến cố “A và B cùng xảy ra”, kí hiệu là A ∩ B (hay AB) gọi là giao của hai biến cố A và B.
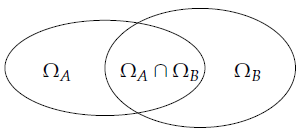 Hình ảnh minh họa biến cố giao
Hình ảnh minh họa biến cố giao
Ví dụ 1. Chọn ngẫu nhiên một học sinh lớp 11 của trường. Gọi A là biến cố: “Bạn đó là học sinh giỏi Toán” và gọi B là biến cố: “Bạn đó là học sinh giỏi Lý”. Khi đó: A ∩ B là biến cố: “Bạn đó là học sinh giỏi Toán và giỏi Lý”
2. Hai biến cố độc lập
Ví dụ 2. Gieo một đồng xu liên tiếp 2 lần. Gọi A là biến cố: “Lần gieo thứ nhất xuất hiện mặt sấp” và gọi B là biến cố: “Lần gieo thứ hai xuất hiện mặt ngửa”. Khi đó A và B là 2 biến cố độc lập.
+) Hai biến cố được gọi là độc lập với nhau nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng xác suất xảy ra của biến cố kia.
+) Nếu hai biến cố A và B độc lập với nhau thì và
,
và
,
và
cũng là độc lập
3. Quy tắc nhân xác suất hai biến cố độc lập
+) Nếu A và B là hai biến cố độc lập với nhau thì ta luôn có: P(AB) = P(A).P(B)
+) Cho n biến cố A1, A2, A3, …, An độc lập với nhau từng đôi một. Khi đó:
hay
Ví dụ 1. Một cầu thủ sút bóng vào cầu môn hai lần. Biết rằng xác suất sút vào cầu môn là . Tính xác suất để cầu thủ đó sút hai lần bóng đều vào được cầu môn
ĐS:
Lời giải
Gọi A là biến cố: “Cầu thủ sút bóng vào cầu môn lần thứ nhất” thì
Gọi B là biến cố: “Cầu thủ sút bóng vào cầu môn lần thứ hai” thì
Suy ra AB là biến cố: “Cầu thủ sút hai lần bóng đều vào được cầu môn”.
Vì A và B là hai biến cố độc lập nên xác suất của AB là:
Ví dụ 2. Có hai xạ thủ bắn bia. Xác suất hạ thủ thứ nhất bắn trúng bia là 0,8. Xác suất xạ thủ thứ hai bắn trúng bia là 0,7. Tính xác suất để:
a) Cả hai xạ thủ đều bắn trúng
ĐS: 0,56
b) Cả hai xạ thủ đều không bắn trúng bia
ĐS: 0,06
c) Có ít nhất một xạ thủ bắn trúng bia
ĐS: 0,94
Lời giải
Gọi A là biến cố: “Xạ thủ thứ nhất bắn trúng” và B là biến cố: “Xạ thủ thứ hai bắn trúng” thì P(A) = 0,8 và P(B) = 0,7.
Ta có A và B là hai biến cố độc lập
a) Biến cố “Cả hai xạ thủ đều bắn trúng” là AB nên P(AB) = P(A).P(B) = 0,8 × 0,7 = 0,56
b) Biến cố “Cả hai xạ thủ đều không bắn trúng bia” là .
Do A và B độc lập nên và
cũng độc lập. Suy ra:
c) Biến cố: “Có ít nhất một xạ thủ bắn trúng bia” là A ∪
P(A ∪ B) = P(A) + P(B) – P(AB) = 0,8 + 0,7 – 0,56 = 0,94
Áp dụng các nguyên tắc tính xác suất để giải bài toán, thường ta làm theo các bước sau:
+) Bước 1: Gọi A là biến cố cần tính xác suất và là các biến cố liên quan đến A sao cho
Biến cố A biểu diễn theo các biến cố Ai, (A1, A2, …, An).
Hoặc xác suất các biến cố Ai tính toán dễ dàng hơn so với A
+) Bước 2: Biểu diễn biến cố A theo các biến cố Ai
+) Bước 3: Xác định mối liên hệ giữa các biến cố và áp dụng các nguyên tắc
Nếu A1, A2 xung khắc (A1 ∩ A2 = ∅) thì P(A1 ∪ A2) = P(A1) + P(A2)
Nếu A1, A2 bất kỳ P(A1 ∪ A2 ) = P(A1) + P(A2) – P(A1. A2)
Nếu A1, A2 độc lập P(A1. A2) = P(A1) . P(A2)
Nếu A1, A2 đối nhau P(A1) = 1 − P(A2)
Bài tập tính xác suất
Câu 1. Một cặp vợ chồng mong muốn sinh bằng được con trai (sinh được con trai rồi thì không sinh nữa, chưa sinh được thì sẽ sinh tiếp). Xác suất sinh được con trai trong mỗi lần sinh là 0,51. Tính xác suất sao cho cặp vợ chồng đó mong muốn sinh được con trai ở lần sinh thứ 2.
ĐS: 0,2499
Lời giải
Xác suất sinh con gái là 1 − 0,51 = 0,49
Xác suất để cặp vợ chồng đó sinh được con trai ở lần thứ 2 là 0,49 × 0,51 = 0,2499
Câu 2. Ba xạ thủ độc lập cùng bắn vào một cái bia. Xác suất bắn trúng mục tiêu của mỗi xạ thủ là 0,6
a) Tính xác suất để trong 3 xạ thủ bắn có đúng một xạ thủ bắn trúng mục tiêu
ĐS: 0,288
b) Muốn mục tiêu bị phá hủy hoàn toàn phải có ít nhất hai xạ thủ bắn trúng mục tiêu. Tính xác suất để mục tiêu bị phá hủy hoàn toàn.
ĐS: 0,648
Lời giải
a) Gọi Xi là xạ thủ thứ i bắn trúng bia.
Khi đó: là xạ thủ thứ i không bắn trúng bia.
Ta có:
Gọi A là biến cố “3 xạ thủ bắn có đúng một xạ thủ bắn trúng mục tiêu”
Ta có:
b) Gọi B là biến cố “ mục tiêu bị phá hủy hoàn toàn”
Câu 3. Hai xạ thủ A và B cùng bắn vào tấm bia mỗi người mỗi phát. Xác suất bắn trúng bia của xạ thủ A là 0,7. Tìm xác suất bắn trúng bia của xạ thủ B. Biết xác suất có ít nhất một người bắn trúng bia là 0,94
ĐS: 0,8
Lời giải
Gọi XA là xạ thủ A bắn trúng bia ⇒ là xạ thủ A không bắn trúng bia ⇒
Gọi XB là xạ thủ B bắn trúng bia ⇒ là xạ thủ B không bắn trúng bia
Gọi E biến cố “có ít nhất một người bắn trúng bia” ⇒ là biến cố “không ai bắn trúng bia” ⇒
⇒
Ta có:
Câu 4. Hai người độc lập nhau cùng bắn mỗi người một viên đạn vào bia. Xác suất bắn trúng bia của họ lần lượt là và
.Tính xác suất của các biến cố sau:
a) A: “Cả hai đều bắn trúng”
ĐS:
b) B: “Cả hai đều bắn trượt”
ĐS:
c) C: “ít nhất một người bắn trúng”
ĐS:
d) D: “Có đúng một người bắn trúng”
ĐS:
Lời giải
a) A: “Cả hai đều bắn trúng”. Khi đó:
b) B: “Cả hai đều bắn trượt”. Khi đó:
c) C: “ít nhất một người bắn trúng”.
Ta có: biến cố B chính là biến cố đối của C. Khi đó:
d) D: “Có đúng một người bắn trúng” tức là người thứ nhất bắn trúng người thứ 2 bắn trật hoặc người thứ nhất bắn trật người thứ hai bắn trúng. Ta có:
Câu 5. Có 3 người cùng đi câu cá; xác suất Câu được cá của người thứ nhất là 0,5; xác suất câu được cá của người thứ hai là 0,4; xác suất câu được cá của người thứ ba là 0,2. Tính xác suất biến cố:
a) Có đúng 1 người câu được cá
ĐS: 0,46
b) Có đúng 2 người câu được cá
ĐS: 0,26
c) Người thứ 3 luôn luôn câu được cá
ĐS: 0,2
d) Có ít nhất 1 người câu được cá
ĐS: 0,76
Lời giải
a) Gọi Xi là người thứ i câu được cá.
Khi đó: là người thứ i không câu được cá. Ta có:
Gọi A biến cố “có đúng 1 người câu được cá”. Ta có:
b) Gọi B là biến cố “có đúng 2 người câu được cá”. Ta có:
c) Gọi C là biến cố “người thứ 3 luôn luôn câu được cá”.
Khi đó: P(D) = P(X3) = 0,2
d) Gọi D là biến cố “có ít nhất 1 người câu được cá” ⇒ là biến cố “không ai câu được cá”. Ta có:
Câu 6. Một xạ thủ bắn vào bia 4 lần độc lập; xác suất bắn trúng một lần là 0,3. Tính xác suất biến cố:
a) Cả 4 lần đều bắn trượt
ĐS: 0,2401
b) Có đúng 3 lần bắn trúng
ĐS: 0,0756
c) Lần thứ 1 bắn trúng, lần thứ 2 bắn trượt
ĐS: 0,21
d) Ít nhất 2 lần bắn trúng
ĐS:0,2601
Lời giải
a) Gọi Xi là xạ thủ bắn trúng bia lần thứ i.
Khi đó: là xạ thủ không bắn trúng bia lần thứ i.
Ta có:
Gọi A là biến cố “Cả 4 lần đều bắn trượt”. Ta có:
b) Gọi B là biến cố “có đúng 3 lần bắn trúng” ⇒ P(B) = 4 × (0,7 × 0,33) = 0,0756
c) Gọi C là biến cố “Lần thứ 1 bắn trúng, lần thứ 2 bắn trượt” ⇒ P(C) = 0,3 × 0,7 = 0,21
d) Gọi D là biến cố “Ít nhất 2 lần bắn trúng”
Câu 7. Có hai hộp đựng thẻ, mỗi hộp đựng 12 thẻ được đánh số từ 1 đến 12. Từ mỗi hộp rút ngẫu nhiên một thẻ. Tính xác suất để trong 2 thẻ rút ra có ít nhất một thẻ đánh số 12
ĐS:
Lời giải
Gọi Xi là từ hộp thứ i rút ra được một thẻ được ghi số 12.
Khi đó: là từ hộp thứ i rút ra được một thẻ không ghi số 12. Ta có:
Gọi A là biến cố “2 thẻ rút ra có ít nhất một thẻ đánh số 12”
⇒ là biến cố “2 thẻ rút ra không có thẻ đánh số 12”. Ta có:
Câu 8. Có ba xạ thủ cùng bắn vào một tấm bia. Xác suất trúng đích lần lượt của mỗi người là 0,6; 0,7 và 0,8. Tính xác suất để có ít nhất một người bắn trúng bia
ĐS: 0,976
Lời giải
Gọi Xi là xạ thủ thứ i bắn trúng bia.
Khi đó: là xạ thủ thứ i không bắn trúng bia. Ta có:
Gọi A là biến cố « có ít nhất một người bắn trúng kia”
⇒ là biến cố không ai bắn trúng bia. Ta có:
Câu 9. Có một xạ thủ mới tập bắn, bắn vào tấm bia. Xác suất trúng đích là 0,2. Tính xác suất để trong ba lần bắn:
a) Ít nhất một lần trúng bia
ĐS: 0,488
b) Bắn trúng bia đúng lần thứ nhất
ĐS: 0,2
Lời giải
a) Gọi Xi là lần thứ i xạ thủ bắn trúng bia.
Khi đó: là lần thứ i xạ thủ không bắn trúng bia. Ta có:
Gọi A là biến cố “ít nhất một lần trúng bia”
⇒ là biến cố không ai bắn trúng bia. Ta có:
b) Gọi B là biến cố “bắn trúng bia đúng lần thứ nhất”.
Ta có: P(B) = P(Xi) = 0,2
Câu 10. Việt và Nam thi đấu với nhau một trận bóng bàn, người nào thắng trước 3 séc thì thắng trận. Xác suất Nam thắng mỗi séc là 0,4 (giả sử không có séc hòa). Tính xác suất Nam thắng trận?
ĐS: 0,11008
Lời giải
Xác suất Nam thắng mỗi séc là 0,4; xác suất Nam không thắng mỗi séc là: 1 – 0,4 = 0,6
Xác suất Nam thắng cả 3 séc đầu: 0,43 = 0,064
Xác suất Nam thắng 3 séc trong 4 séc đầu: 0,43 × 0,6 = 0,0384
Xác suất Nam thắng cả 3 séc trong 5 séc: 0,43 × 0,62 = 0,02304
Vậy xác suất Nam thắng trận là: 0,064 + 0,0384 + 0,02304 = 0,11008
Câu 11. Một nhóm xạ thủ gồm có 10 người trong đó có 3 xạ thủ loại I và 7 xạ thủ loại II. Xác suất bắn trúng đích trong mỗi lần bắn của một xạ thủ loại I và loại II lần lượt là 0,9 và 0,8. Chọn ngẫu nhiên một xạ thủ trong 10 người và cho bắn một viên đạn. Tính xác suất để viên đạn trúng đích?
ĐS: 0,83
Lời giải
Xác suất chọn 1 xạ thủ loại I và trúng là:
Xác suất chọn 1 xạ thủ loại II và bắn trúng là:
Vậy xác suất để viên đạn trúng đích là: 0,27 + 0,56 = 0,83
Câu 12. Có ba lô hàng. Người ta lấy một cách ngẫu nhiên từ mỗi lô hàng một sản phẩm. Biết rằng xác suất để được một sản phẩm có chất lượng tốt ở từng lô hàng lần lượt là 0,5; 0,6 và 0,7. Tính xác suất để trong ba sản phẩm lấy ra có ít nhất một sản phẩm có chất lượng tốt?
ĐS: 0,94
Lời giải
Gọi Xi là biến cố chọn được sản phẩm có chất lượng tốt ở lô hàng thứ i.
Khi đó: là biến cố chọn được sản phẩm có chất lượng chưa tốt ở lô hàng thứ i. Ta có:
Gọi A là biến cố “lấy ra ít nhất một sản phẩm có chất lượng tốt”
⇒ là biến cố “lấy ra có ít nhất một sản phẩm có chất lượng chưa tốt”. Ta có:
Câu 13. Một hộp chứa 11 bi được đánh số từ 1 đến 11. Chọn 6 bi một cách ngẫu nhiên, rồi cộng các số trên 6 bi được rút ra với nhau. Tính xác suất để kết quả thu được là số lẻ
ĐS:
Lời giải
Từ 1 đến 11 có 6 số lẻ, 5 số chẵn.
Số phần tử không gian mẫu:
Gọi A là biến cố chọn 6 bi một cách ngẫu nhiên, rồi cộng các số trên 6 bi được rút ra với nhau được số lẻ.
+) Trường hợp 1: 1 số lẻ, 5 số chẵn
+) Trường hợp 2: 3 số lẻ, 3 số chẵn
+) Trường hợp 3: 5 số lẻ, 1 số chẵn
⇒ n(A) = 6 + 200 + 30 = 236.
Vậy xác suất để kết quả thu được là số lẻ là:
Câu 14. Một hộp có đựng 4 chính phẩm và 2 phế phẩm. Lấy ngẫu nhiên từng sản phẩm một, không bỏ trở lại để kiểm tra cho đến khi lấy ra hai phế thì thôi. Tính xác suất để biến cố việc kiểm tra chỉ dừng lại ở sản phẩm thứ 2.
ĐS:
Lời giải
Xác suất lấy ra được chính phẩm
Xác suất lấy ra được phế phẩm
Vậy: Xác suất của biến cố việc kiểm tra chỉ dừng lại ở sản phẩm thứ 2 là
Câu 15. Một thủ kho có một chùm chìa khóa gồm 10 chiếc hình thức giống nhau nhưng trong đó chỉ có 3 chìa là mở được kho. Anh ta mở ngẫu nhiên từng chìa khóa một kho đến khi mở được kho. Tính xác suất để:
a) Anh ta mở được kho ở lần thứ 3
ĐS: 0,147
b) Anh ta mở được kho mà không quá 3 lần mở
ĐS: 0,657
Lời giải
a) Gọi Xi là biến cố chọn được chìa khóa thứ i mở được kho.
Khi đó: là biến cố được chọn chìa khóa thứ i không mở được kho.
Ta có:
Gọi A là biến cố “mở được kho ở lần thứ 3”
⇒ là biến cố không ai bắn trúng bia. Ta có:
b) Gọi B là biến cố “mở được kho mà không quá 3 lần mở”
Ta có: P(B) = 0,3 + 0,7 × 0,3 + 0,7 × 0,7 × 0,3 = 0,657
Câu 16. Một nồi hơi có 3 van bảo hiểm hoạt động độc lập với xác suất hỏng của van 1, van 2, van 3 trong khoảng thời gian t tương ứng là 0,1; 0,2 và 0,3. Nồi hoạt động an toàn nếu ít nhất một van không hỏng. Tìm xác suất để nồi hơi hoạt động an toàn trong khoảng thời gian t?
ĐS: 0,994
Lời giải
Gọi Xi là biến cố van thứ i bị hỏng.
Khi đó: là biến cố van thứ i không bị hỏng.
Ta có: P(X1) = 0,1; P(X2) = 0,2; P(X3) = 0,3
Gọi A là biến cố “nồi hơi hoạt động an toàn trong khoảng thời gian t”
⇒ là biến cố 3 van bị hỏng. Ta có:
Câu 17. Trong thời gian có dịch bệnh ở vùng dân cư. Cứ 100 người bệnh thì phải có 20 người đi cấp cứu. Xác suất để gặp người đi cấp cứu do mắc phải dịch bệnh của vùng đó là 0,08. Tìm tỉ lệ mắc bệnh của vùng dân cư đó.
ĐS: 0,016
Lời giải
Tỉ lệ mắc bệnh của vùng dân cư đó là:
Câu 18. Một máy bay có 5 động cơ gồm 3 động cơ bên cánh trái và hai động cơ bên cánh phải. Mỗi động cơ bên cánh phải có xác suất bị hỏng là 0,09; mỗi động cơ bên cánh trái có xác suất hỏng là 0,04. Các động cơ hoạt động độc lập với nhau. Máy bay chỉ thực hiện được chuyến bay an toàn nếu ít nhất hai động cơ làm việc. Tính xác suất để máy bay thực hiện được chuyến bay an toàn.
ĐS: 0,9999590464
Lời giải
Gọi A là biến cố máy bay bay an toàn. Khi đó: là biến cố máy bay bay không an toàn.
+) Trường hợp 1: 5 động cơ hỏng 0,093 × 0,042
+) Trường hợp 2: 4 động cơ hỏng 0,093 × 0,04 × 0,96 + 0,092 × 0,91 × 0,042
Câu 19. Ba cầu thủ sút phạt luân lưu 11 mét, mỗi người đá một lần với xác suất làm bàn tương ứng là x; y và 0,6 (với x > y). Biết xác suất để ít nhất một trong ba cầu thủ ghi bàn là 0,976 và xác suất để ba cầu thủ đều ghi bàn là 0,336. Tính xác suất để có đúng hai cầu thủ ghi bàn?
Lời giải
Xác suất để 3 cầu thủ cùng ghi bàn là:
x.y.0,6 = 0,336 ⇔ x.y = 0,56 (1)
Xác suất để không cầu thủ nào ghi bàn là:
(1 – x)(1 – y)(1 − 0,6) = 1 – 0,976 (2)
Từ (1), (2) ta có:
Câu 20. Một bài trắc nghiệm có 10 câu hỏi, mỗi câu hỏi có 4 phương án lựa chọn trong đó có 1 đáp án đúng. Giả sử mỗi câu trả lời đúng được 5 điểm và mỗi câu trả lời sai được trừ 2 điểm. Một học sinh không học bài nên đánh hú họa một câu trả lời. Tìm xác suất để học sinh này nhận điểm dưới 1.
ĐS:
Lời giải
Gọi x là số câu trả lời đúng (0 ≤ x ≤ 10), khi đó số câu trả lời sai là 10 – x.
Để học sinh làm dưới 1 điểm thì số câu trả lời đúng thỏa mãn bất phương trình:
5x + (10 – x)(–2) < 1
⇔ 7x < 21
⇔ x < 3 ⇒ x ∈ {0; 1; 2}
+) x = 0 không có câu đúng
+) x = 1 có 1 câu đúng
+) x = 2 có 2 câu đúng
Vậy xác suất để học sinh này nhận điểm dưới 1 là:
Câu 21. Trong một lớp học có 60 sinh viên, trong đó có 40 sinh viên học tiếng Anh, 30 sinh viên học tiếng Pháp và 20 sinh viên học cả tiếng Anh và Pháp. Chọn ngẫu nhiên một sinh viên. Tính xác suất của các biến cố sau:
+) A: “Sinh viên được chọn học tiếng Anh”
ĐS:
+) B: “Sinh viên được chọn học tiếng Pháp”
ĐS:
+) C: “Sinh viên được chọn học cả tiếng Anh lẫn tiếng Pháp”
ĐS:
+) D: “Sinh viên được chọn không học tiếng Anh và tiếng Pháp”
ĐS:
Lời giải
+) Theo đề số học sinh học tiếng Anh là 40, số học sinh học tiếng Pháp là 30, số học sinh học cả 2 môn Anh, Pháp là 20, số học sinh không học môn Anh, Pháp là 60 – (40 + 30 – 20) = 10
Xác suất chọn được sinh viên học tiếng Anh là
+) Xác suất chọn được sinh viên học tiếng Pháp là
+) Xác suất chọn được sinh viên học cả tiếng Anh lẫn tiếng Pháp là
+) Xác suất chọn được sinh viên không học tiếng Anh và tiếng Pháp là
Câu 22. Trong kì kiểm tra chất lượng ở hai khối lớp, mỗi khối có 25% học sinh trượt Toán, 15% trượt Lý, 10% trượt cả Lý lẫn Toán. Từ mỗi khối chọn ngẫu nhiên một học sinh. Tính xác suất sao cho:
+) Hai học sinh đó trượt Toán
ĐS:
+) Hai học sinh đó đều trượt một môn nào đó
ĐS:
+) Hai học sinh không bị trượt môn nào
ĐS:
+) Có ít nhất một trong hai học sinh bị trượt ít nhất một môn
ĐS:
Lời giải
Kí hiệu A1, A2, A3 lần lượt là các biến cố: Học sinh được chọn từ khối I trượt Toán, Lí Hóa; B1, B2, B3 lần lượt là các biến cố: Học sinh được chọn từ khối II trượt Toán, Lí Hóa. Rõ ràng với mọi (i; j), các biến cố Ai và Bj độc lập.
+) Ta có:
+) Xác suất cần tính là:
+) Đặt A = A1 ∪ A2 ∪ A3 , B = B1 ∪ B2 ∪ B3
Cần tính . Do
độc lập, ta có:
+) Cần tính P(A ∪ B). Ta có:
Câu 23. Trong kì thi THPT Quốc Gia, bạn X làm đề thi trắc nghiệm môn Hóa. Đề thi gồm 50 câu hỏi, mỗi câu có 4 phương án trả lời, trong đó chỉ có 1 phương án đúng, trả lời đúng mỗi câu được 0,2 điểm. Bạn X trả lời hết các câu hỏi và chắc chắn đúng 45 câu, 5 câu còn lại X chọn ngẫu nhiên. Tính xác suất để điểm thi Hóa của X không dưới 9,5 điểm.
ĐS:
Lời giải
Thí sinh X không dưới 9,5 điểm khi và chỉ khi trong 5 câu trả lời ngẫu nhiên có ít nhất 3 câu đúng.
Xác suất trả lời đúng 1 câu hỏi là , trả lời sai là
. Ta có các trường hợp:
+) Xác suất thí sinh X trả lời đúng 3 trên 5 câu là
+) Xác suất thí sinh X trả lời đúng 4 trên 5 câu là
+) Xác suất thí sinh X trả lời đúng 5 trên 5 câu là
Vậy xác suất cần tính:
Câu 24. Trong kì thi THPT Quốc Gia, bạn X dự thi hai môn trắc nghiệm môn Hóa và Lí. Đề thi gồm 50 câu hỏi, mỗi câu có 4 phương án lựa chọn, trong đó chỉ có 1 phương án đúng, làm đúng mỗi câu được 0,2 điểm. Mỗi môn thi bạn X làm hết các câu hỏi và chắc chắn đúng 45 câu, 5 câu còn lại X chọn ngẫu nhiên. Tính xác suất để tổng hai môn thi của X không dưới 19 điểm
ĐS:
Lời giải
Thí sinh X không dưới 19 điểm khi và chỉ khi trong 10 câu trả lời ngẫu nhiên ở cả hai môn Hóa và Lí có ít nhất 5 câu đúng.
Xác suất trả lời đúng 1 câu hỏi là , trả lời sai là
. Ta có các trường hợp:
+) Xác suất thí sinh X trả lời đúng 5 trên 10 câu là
+) Xác suất thí sinh X trả lời đúng 6 trên 10 câu là
+) Xác suất thí sinh X trả lời đúng 7 trên 10 câu là
+) Xác suất thí sinh X trả lời đúng 8 trên 10 câu là
+) Xác suất thí sinh X trả lời đúng 9 trên 10 câu là
+) Xác suất thí sinh X trả lời đúng 10 trên 10 câu là
Vậy xác suất cần tính là: