Theo lý thuyết xác suất thì biến cố là tập các kết quả đầu ra (tập con không gian mẫu) mà tương ứng với đó người ta sẽ gán kèm với một số thực (xác suất). Nếu không gian mẫu hữu hạn thì bất cứ tập hợp con nào của không gian mẫu cũng được xem là một biến cố.
Trong bài viết này, VerbaLearn sẽ giúp bạn đọc tìm hiểu chi tiết định nghĩa về xác suất của biến cố. Từ đó ứng dụng vào giải một số bài toán xác suất cơ bản và nâng cao theo chương trình.
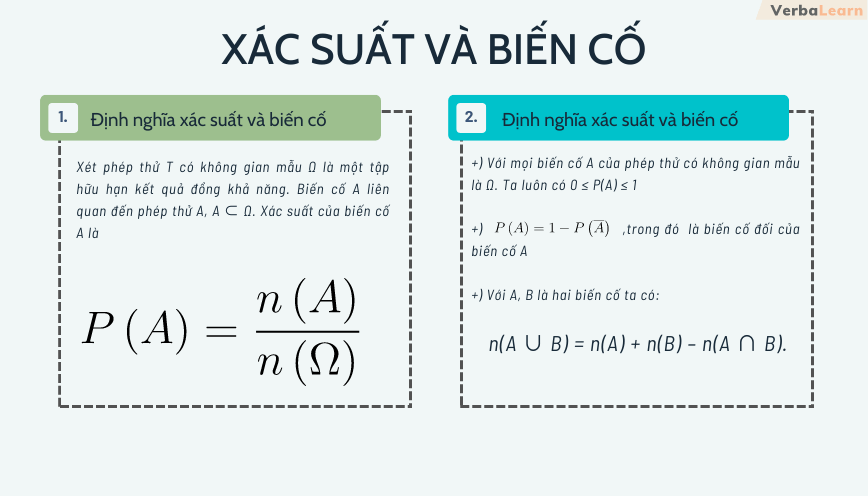
Xác suất của biến cố
[content_1]Xét phép thử T có không gian mẫu Ω là một tập hữu hạn kết quả đồng khả năng. Biến cố A liên quan đến phép thử A, A ⊂ Ω. Xác suất của biến cố A là
– Với mọi biến cố A của phép thử có không gian mẫu là Ω. Ta luôn có 0 ≤ P(A) ≤ 1
– , trong đó
là biến cố đối của biến cố A
– Với A, B là hai biến cố ta có n(A ∪ B) = n(A) + n(B) – n(A ∩ B).
Ví dụ 1: Xét phép thử T “Gieo đồng thời hai con súc sắc cân đối và đồng chất”. Tập các kết quả là tập hợp gồm tất cả các cặp số bởi bảng sau
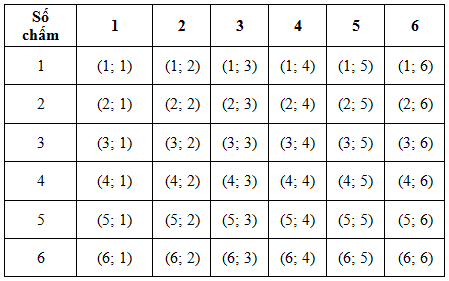
Không gian mẫu của phép thử là:
– Số phần tử của không gian mẫu là 36
– Biến cố A: “Tổng số chấm xuất hiện trên mặt bằng 7”
Ta có: A = {(1; 6); (2; 5); (3; 4); (4; 3); (5; 2); (6; 1)}
⇒ n(A) = 6
Xác suất của biến cố A là:
Ví dụ 2: Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất. Tính xác suất của các biến cố
– A: “Mặt có số chấm lẻ xuất hiện”
ĐS:
– B: “Mặt xuất hiện có số chấm chia hết cho 3”
ĐS:
– C: “Mặt xuất hiện có số chấm lớn hơn 2”
ĐS:
Hướng dẫn giải
– A: “Mặt có số chấm lẻ xuất hiện”
Số phần tử của không gian mẫu là n(Ω) = 6
Biến cố A = {1; 3; 5} ⇒ n(A) = 3
Xác suất của A là:
– B: “Mặt xuất hiện có số chấm chia hết cho 3”
Biến cố B = {6; 3} ⇒ n(B) = 2
Xác suất của biến cố B là:
– C: “Mặt xuất hiện có số chấm lớn hơn 2”
Biến cố C = {3; 4; 5; 6}
Xác suất của biến cố C là:
Ví dụ 3: Từ một hộp chứa 4 quả cầu trắng, 3 quả cầu đỏ và 2 quả cầu xanh. Lấy ngẫu nhiên một quả cầu từ hộp. Tính xác suất để
– Lấy được quả màu trắng
ĐS:
– Lấy được quả cầu đỏ
ĐS:
Hướng dẫn giải
Số phần tử của không gian mẫu là n(Ω) = 9
– Quả cầu được lấy có màu trắng, số cách lấy là 4
Xác suất lấy quả cầu trắng là
– Quả cầu được lấy có màu đỏ, số cách lấy là 3
Xác suất lấy quả cầu đỏ là
Ví dụ 4: Trong một đợt kiểm tra vệ sinh an toàn thực phẩm của ngành y tế tại chợ X. Ban quản lí chợ lấy ra 15 mẫu thịt lợn trong đó có 4 mẫu ở quầy A, 5 mẫu ở quầy B và 6 mẫu ở quầy C. Mỗi mẫu thịt này có khối lượng như nhau và để trong một hộp kín có kích thước giống hệt nhau, Đoàn kiểm tra lấy ngẫu nhiên ba hộp để phân tích, kiểm tra xem trong thịt lợn có chứa chất tạo nạc (Clenbuterol) hay không. Tính xác suất để cả 3 hộp lấy ra có đủ cả ba loại thịt ở các quầy A, B, C
ĐS:
Hướng dẫn giải
Số phần tử của không gian mẫu là
Gọi X là biến cố “Cả ba cửa hàng đều có mẫu thịt được lấy”
Số phần tử của X là:
Xác suất của là:
Ví dụ 5: Trong một chiếc hộp có chứa 10 quả cầu có kích thước như nhau, được đánh ố từ 1 đến 10. Lấy ngẫu nhiên ra 3 quả cầu trong hộp đó. Tính xác suất để số ghi trên 3 quả cầu lấy được là độ dài ba cạnh của một tam giác vuông
ĐS:
Hướng dẫn giải
Số phần tử của không gian mẫu là
Giả sử 3 số ghi trên các quả cầu được chọn là a, b, c với a < b < c thỏa mãn a2 + b2 = c2
Có hai khả năng (a; b; c) = (3; 4; 5) hoặc (a; b; c) = (6; 8; 10)
Gọi X là biến cố: “3 số ghi trên 3 quả cầu được chọn là độ dài 3 cạnh của một tam giác vuông”
Số phần tử của X là n(X) = 2
Xác suất của biến cố X là:
Ví dụ 6: Trong một chiếc hộp 6 viên bi đỏ, 5 viên bi vàng và 4 viên bi trắng. Lấy ngẫu nhiên trong hộp ra 4 viên bi. Tính xác suất để trong 4 viên lấy ra không đủ cả 3 màu.
ĐS:
Hướng dẫn giải
Số phần tử của không gian mẫu là
Gọi A là biến cố “4 viên lấy ra không đủ ba màu”
Biến cố A xảy ra trong các trường hợp
– Trường hợp 1: 4 viên đúng một màu
Số cách lấy là
– Trường hợp 2: 4 viên có đúng hai màu
Hai màu đỏ – vàng, có
Hai màu đỏ – trắng, có
Hai màu vàng – trắng, có
Tổng số cách lấy 4 viên đúng hai màu có 310 + 194 + 120 = 624
Số phần tử của biến cố A là:
n(A) = 624 + 21 = 645
Xác suất của biến cố A là:
Phân dạng bài tập
Dạng 1. Chọn hoặc sắp xếp đồ vật
[content_2]Phương pháp giải
Phương pháp 1: Tính xác suất theo định nghĩa
Đếm số phần tử của không gian mẫu, số phần tử của biến cố
Phương pháp 2: Tính xác suất của biến cố đối
Phương pháp 3: Áp dụng quy tắc cộng và quy tắc nhân xác suất
Kiến thức bổ sung
– Công thức đếm số phần tử của hợp hai tập hợp
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
– Công thức đếm số phần tử của hợp ba tập hợp
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(C ∩ A) + n(A ∩ B ∩ C)
– Phương pháp đặt song ánh 1 – 1
Khi cần đếm một tập A trực tiếp khó khăn ta có thể chỉ ra tập số có sự tương ứng 1 – 1 với tập B và khi đó chỉ cần đếm B
Bài tập vận dụng
Câu 1. Một bình đựng 6 viên bi không giống nhau,trong đó có 2 xanh, 2 vàng và 2 đỏ. Lấy ngẫu nhiên 2 viên bi. Tính xác suất để lấy được.
– 2 viên bi xanh
ĐS:
– 2 viên bi khác màu
ĐS:
Hướng dẫn giải
– Xác suất lấy được 2 viên bi xanh
Số phần tử của không gian mẫu là
Gọi A là biến cố “2 viên bi lấy được là bi xanh”
Số phần tử của biến cố A là:
Xác suất của biến cố A là:
– Xác suất lấy được hai viên bi khác màu
Gọi B là biến cố “2 viên bi lấy được khác màu”
Biến cố B xảy ra khi 2 viên bi lấy được là 1 xanh – 1 vàng; 1 xanh − 1 đỏ; 1 vàng – 1 đỏ
Số phần tử của B là:
Xác suất của biến cố B là:
Câu 2. Một chiếc hộp đựng 6 quả cầu trắng, 4 quả cầu đỏ, 2 quả cầu đen, các quả cầu khác nhau. Chọn ngẫu nhiên 6 quả cầu. Tính xác suất để chọn được 3 quả cầu trắng, 2 quả cầu đỏ và 1 quả đầu đen
ĐS:
Hướng dẫn giải
Số phần tử của không gian mẫu
Gọi A là biến cố “Lấy được 3 quả cầu trắng, 2 quả cầu đỏ và 1 quả cầu đen”
Số phần tử của biến cố A là:
Xác suất của biến cố A là:
Câu 3. Cho một hộp đựng 12 viên bi, trong đó có 7 viên bi đỏ, 5 viên bi xanh. Lấy ngẫu nhiên mỗi lần 3 viên bi. Tính xác suất trong 2 trường hợp
– Lấy được 3 viên bi màu đỏ
ĐS:
– Lấy được ít nhất 2 viên bi màu đỏ
ĐS:
Hướng dẫn giải
– Xác suất lấy được 3 viên bi màu đỏ
Số phần tử của không gian mẫu
Gọi A là biến cố “Lấy được 3 viên bi màu đỏ”
Số phần tử của biến cố A là:
Xác suất của biến cố A là:
– Xác suất lấy được ít nhất 2 viên bi màu đỏ
Gọi B là biến cố “Lấy được ít nhất hai viên bi màu đỏ”
Số phần tử của biến cố B là:
Xác suất của biến cố B là:
Câu 4. Một hộp chứa các quả cầu kích thước khác nhau gồm 3 quả cầu đỏ, 6 quả cầu xanh và 9 quả cầu vàng. Chọn ngẫu nhiên 2 quả cầu. Tính xác suất để hai quả cầu được chọn là khác màu.
ĐS:
Hướng dẫn giải
Số phần tử của không gian mẫu
Gọi A là biến cố “Hai quả cầu được chọn không cùng màu”
Biến cố đối của A là “2 viên bi được lấy cùng màu”
Ta có:
Xác suất của biến cố A là:
Có thể tính trực tiếp:
Câu 5. Một hộp đựng 15 viên bi, trong đó có 7 viên bi xanh và 8 viên bi đỏ. Lấy ngẫu nhiên 3 viên bi. Tính xác suất để trong 3 viên bi lấy ra có ít nhất một viên bi đỏ.
ĐS:
Hướng dẫn giải
Số phần tử của không gian mẫu
Gọi A là biến cố “Có ít nhất một viên bi màu đỏ được lấy”
Biến cố đối của A là “3 viên bi được lấy đều màu xanh”
Số phần tử của là:
Xác suất của biến cố A là:
Câu 6. Một hộp đựng 20 viên bi, trong đó có 7 viên bi xanh và 8 viên bi đỏ và 5 viên bi vàng. Lấy ngẫu nhiên 9 viên bi. Tính xác suất trong các trường hợp
– 9 viên bi lấy được có đúng 2 màu
ĐS:
– 9 viên bi lấy được có đủ màu
ĐS:
Hướng dẫn giải
– Xác suất 9 viên bi lấy được có đúng 2 màu
Số phần tử của không gian mẫu:
Gọi A là biến cố “9 viên bi được lấy có đúng 2 màu”
Do số viên bi của các màu đều nhỏ hơn 9 nên ta có
Số cách lấy 9 viên có đúng hai màu xanh – đỏ là
Số cách lấy 9 viên có đúng hai màu xanh – vàng là
Số cách lấy 9 viên có đúng hai màu đỏ – vàng là
Do đó số phần tử của biến cố A là:
Xác suất của biến cố A là:
– Xác suất 9 viên bi lấy được có đủ 3 màu
Gọi B là biến cố “9 viên bi được lấy có đủ 3 màu”
Do số viên bi của các màu đều nhỏ hơn 9 nên không thể xảy ra trường hợp 9 viên một màu
Do đó số phần tử của B là n(B) = n(Ω) – n(A) = 162020
Xác suất của B là
Dạng 2. Chọn hoặc sắp xếp người
[content_3]Câu 1. Một lớp có 30 học sinh, trong đó có 8 em giỏi, 15 em khá và 7 em trung bình. Chọn ngẫu nhiên 3 em đi dự đại hội. Tính xác suất để:
– Cả 3 em đều là học sinh giỏi
ĐS:
– Có ít nhất 1 học sinh giỏi
ĐS:
– Không có học sinh trung bình
ĐS:
Hướng dẫn giải
Gọi Ω là không gian mẫu:
– Gọi A là biến cố: “Cả 3 em được chọn đều là học sinh giỏi”, ta có:
Vậy xác suất của biến cố A là:
– Gọi B là biến cố “Trong cả 3 em được chọn có ít nhất 1 học sinh giỏi”
Suy ra là biến cố “Trong cả 3 em được chọn không có học sinh giỏi”, ta có:
Vậy xác suất của biến cố B là:
– Gọi C là biến cố “Trong cả 3 em được chọn không có học sinh trung bình”, ta có:
Vậy xác suất của biến cố C là:
Câu 2. Một đội ngũ cán bộ khoa học gồm 8 nhà toán học nam, 5 nhà vật lý nữ và 3 nhà hóa học nữ. Chọn ra từ đó 4 người đi công tác. Tính xác suất trong 4 người được chọn phải có nữ và có đủ cả ba bộ môn
ĐS:
Hướng dẫn giải
Gọi Ω là không gian mẫu:
Gọi A là biến cố: “Trong 4 người được chọn phải có nữ và có đủ ba bộ môn”
Trường hợp 1: Số cách chọn 4 người trong đó có 2 nhà toán học, 1 nhà vật lý, 1 nhà hóa học là:
Trường hợp 2: Số cách chọn 4 người trong đó có 1 nhà toán học, 2 nhà vật lý, 1 nhà hóa học là:
Trường hợp 3: Số cách chọn 4 người trong đó có 1 nhà toán học, 1 nhà vật lý, 2 nhà hóa học là:
Số phần tử của biến cố A là:
Vậy:
Câu 3. Một lớp có 20 nam sinh và 15 nữ sinh. Giáo viên gọi ngẫu nhiên 4 học sinh lên bảng giải bài tập. Tính xác suất để 4 học sinh được gọi có cả nam và nữ
ĐS:
Hướng dẫn giải
Gọi Ω là không gian mẫu:
Gọi A là biến cố: “4 học sinh được gọi lên bảng có cả nam và nữ”
Trường hợp 1: Số cách chọn 4 học lên bảng trong đó có 3 bạn học sinh nam và 1 học sinh nữ là
Trường hợp 2: Số cách chọn 4 học lên bảng trong đó có 2 bạn học sinh nam và 2 học sinh nữ là
Trường hợp 3: Số cách chọn 4 học lên bảng trong đó có 1 bạn học sinh nam và 3 học sinh nữ là
Số phần tử của biến cố A là:
Vậy:
Câu 4. Một đội văn nghệ có 15 người gồm 9 nam và 6 nữ. Chọn ngẫu nhiên 8 người đi hát đồng ca. Tính xác suất để trong 8 người được chọn có số nữ nhiều hơn số nam
ĐS:
Hướng dẫn giải
Gọi Ω là không gian mẫu:
Gọi A là biến cố: “8 người được chọn có số nữ nhiều hơn số nam”
Trường hợp 1: 2 bạn học sinh nam và 6 học sinh nữ được chọn:
Trường hợp 2: 3 bạn học sinh nam và 5 học sinh nữ được chọn:
Số phần tử của biến cố A là:
Vậy:
Câu 5. Cần chọn ngẫu nhiên 5 học sinh trong một lớp học có 15 nam và 10 nữ để tham gia đồng diễn. Tính xác suất sao cho 5 học sinh được chọn có cả nam lẫn nữ và số học sinh nữ ít hơn số học sinh nam
ĐS:
Hướng dẫn giải
Gọi Ω là không gian mẫu:
Gọi A là biến cố: “5 học sinh được chọn có cả nam lẫn nữ và số học sinh nữ ít hơn số học sinh nam”
Trường hợp 1: 1 bạn học sinh nữ và 4 học sinh nam được chọn:
Trường hợp 2: 2 bạn học sinh nữ và 3 học sinh nữ được chọn:
Số phần tử của biến cố A là:
Vậy:
Dạng 3. Chọn hoặc sắp xếp số
[content_4]Phương pháp giải
Một số kiến thức liên quan
– Cho m ∈ ℕ, ta có m ⋮ 2 ⇔ chữ số hàng đơn vị của m là chữ số chẵn
– Cho m ∈ ℕ, ta có m ⋮ 5 ⇔ chữ số hàng đơn vị của m bằng 0 hoặc bằng 5
– Cho m ∈ ℕ, ta có m ⋮ 4 ⇔ hai chữ số cuối tạo thành số chia hết cho 4
– Cho m ∈ ℕ, ta có m ⋮ 3 ⇔ tổng các chữ số của m chia hết cho 3
– Cho m ∈ ℕ, ta có m ⋮ 9 ⇔ tổng các chữ số của m chia hết cho 9
– Cho m ∈ ℕ, ta có m ⋮ 11 ⇔ tổng các chữ số ở hàng chẵn bằng tổng các chữ số ở hàng lẻ (tính từ trái sang phải)
– Cho m ∈ ℕ, m được phân tích thành thừa số nguyên tố dạng
Khi đó mỗi ước số của m ứng với một bộ (j1; j2; …; jn) trong đó 0 ≤ j1 ≤ i1; …; 0 ≤ jn ≤ in
– Số nghiệm nguyên dương của phương trình
x1 + x2 + …xn = m (m, n ∈ ℕ, n ≤ m)
là
– Mỗi bộ n số thực luôn có duy nhất một cách sắp xếp thứ tự từ bé đến lớn
– Cho n là số tự nhiên khác 0, tập số tự nhiên ℕ được phân lớp thành các tập:
X0 gồm các số chia m hết cho n, m = k, k ∈ ℕ
X1 gồm các số tự nhiên m chia n dư 1, m = k. n + 1, k ∈ ℕ
…
Xn−1 gồm các số tự nhiên m chia n dư n − 1, m = k(n – 1), k ∈ ℕ
Bài tập vận dụng
Câu 1. Cho tập hợp A gồm tất cả các sô tự nhiên có ba chữ số khác nhau đôi một được lập từ các số 1; 2; 3; 4; 5; 6. Chọn ngẫu nhiên một phần tử của A. Tính xác suất để phần tử đó là số chẵn
ĐS:
Hướng dẫn giải
Gọi là số thuộc vào tập A, ta có
số như vậy
Vậy số cách tùy ý một số từ tập A là 120 cách
Gọi là các số chẵn thuộc vào tập A, ta có
số như vậy
Suy ra xác suất để chọn được số thỏa mãn bài toán là
Câu 2. Gọi S là tập hợp tất cả các số tự nhiên gồm ba chữ số phân biệt được chọn từ các chữ số 1; 2; 3; 4; 5; 6; 7. Xác định số phần tử của S. Chọn ngẫu nhiên một số từ S, tính xác suất để chọn được là số chẵn
ĐS:
Hướng dẫn giải
Gọi là số thuộc vào tập S, ta có
số như vậy
Vậy số cách tùy ý một số từ tập S là 210 cách
Gọi là các số thỏa mãn yêu cầu bài toán và thuộc vào tập S, ta có
số như vậy
Suy ra xác suất để chọn được số thỏa mãn bài toán là
Câu 3. Cho tập hợp A gồm tất cả các số tự nhiên có bốn chữ số đôi một khác nhau được lập từ các chữ số 1; 2; 3; 4; 5; 6. Chọn ngẫu nhiên từ A hai phần tử. Tính xác suất để hai phần tử được lấy ra từ A có một số chẵn và một số lẻ
ĐS:
Hướng dẫn giải
Gọi là số thuộc vào tập A, ta có
số như vậy
Vậy số cách chọn tùy ý hai số tùy ý từ tập A là cách
Gọi là các số lẻ thuộc vào tập A, ta có
số, vậy có 720 – 300 = 420 số chẵn trong tập A
Suy ra xác suất để chọn được số thỏa mãn bài toán là
Câu 4. Từ một hộp chứa 16 thẻ được đánh số từ 1 đến 16, chọn ngẫu nhiên 4 thẻ. Tính xác suất để 4 thẻ được chọn đều được đánh số chẵn.
ĐS:
Hướng dẫn giải
Số cách chọn tùy ý 4 thẻ là
Do có 8 số chẵn trong các số từ 1 đến 16 nên để chọn được 4 thẻ đánh số chẵn, ta có
Suy ra xác suất để chọn được 4 thẻ mang số chẵn là
Câu 5. Gọi X là tập hợp các số gồm hai chữ số khác nhau được lấy từ 0; 1; 2; 3; 4; 5; 6. Lấy ngẫu nhiên hai phần tử của X. Tính xác suất để hai số lấy được đều là số chẵn
ĐS:
Hướng dẫn giải
Gọi là số thuộc vào tập X, ta có 6 × 6 = 36 số như vậy
Vậy số cách chọn tùy ý hai số từ tập X là
Gọi là các số chẵn thuộc vào tập X
– TH1: Số có dạng , ta có 6 số như vậy
– TH2: Xét d ≠ 0, ta có 3 × 5 = 15 số như vậy
Vậy có 6 + 15 = 21 số chẵn trong tập hợp X
Suy ra xác suất để chọn được hai số chẵn từ tập X là
Câu 6. Gọi S là tập hợp các số tự nhiên gồm có 2 chữ số. Chọn ngẫu nhiên một số từ S. Tính xác suất để số được chọn có chữ số hàng đơn vị và hàng chục đều là chữ số chẵn.
ĐS:
Hướng dẫn giải
Gọi là số thuộc vào tập S, ta có 9 × 10 = 90 số như vậy
Vậy số cách chọn tùy ý một số từ tập S là 90 cách
Gọi là các số thỏa mãn yêu cầu bài toán và thuộc vào tập S, ta có 4 × 5= 20 số như vậy
Suy ra xác suất để chọn được số thỏa mãn bài toán là
Câu 7. Cho E là tập hợp các số có 3 chữ số khác nhau đôi một được lấy từ: 0; 1; 2; 3; 4; 5. Chọn ngẫu nhiên 1 phần tử của E. Tính xác suất để phần tử được chọn là số có 3 chữ số đều chẵn.
ĐS:
Hướng dẫn giải
Gọi Ω là không gian mẫu của phép thử “chọn ngẫu nhiên 1 phần tử của E”.
Gọi A là biến cố “số được chọn là số có 3 chữ số đều chẵn”.
Giả sử số có ba chữ số thuộc E có dạng , ta có
– a có 5 cách chọn, b có 5 cách chọn, c có 4 cách chọn. Do đó, số phần tử của không gian mẫu là nΩ = 5 × 5 × 4 = 100
– Số được chọn có 3 chữ số đều chẵn lấy từ các số {0, 2, 4}. Do đó a có 2 cách chọn, b có 2 cách chọn và c có 1 cách chọn. Số kết quả thuận lợi của biến cố A là nA = 2 × 2 × 1 = 4
Suy ra, xác suất cần tìm là:
Vậy xác suất để chọn được số có 3 chữ số đều chẵn từ E là
Câu 8. Có 20 thẻ đựng trong 2 hộp khác nhau, mỗi hộp chứa 10 thẻ được đánh số liên tiếp từ 1 đến 10. Lấy ngẫu nhiên 2 thẻ từ 2 hộp (mỗi hộp 1 thẻ). Tính xác suất lấy được hai thẻ có tích hai số ghi trên hai thẻ là một số chẵn
ĐS:
Hướng dẫn giải
Gọi Ω là không gian mẫu của phép thử “lấy ngẫu nhiên 2 thẻ từ 2 hộp (mỗi hộp 1 thẻ)”. Gọi A là biến cố “lấy được hai thẻ có tích hai số trên hai thẻ là số chẵn”. Để có thể lấy được hai thẻ có tích hai số ghi trên hai thẻ là một số chẵn, ta có các trường hợp sau đây:
– Hai thẻ lấy ra đều là thẻ chẵn, có 5 × 5= 25 (cách)
– Thẻ lấy ra ở hộp thứ nhất là thẻ chẵn, hộp thứ hai là thẻ lẻ, có 5 × 5= 25 (cách)
– Thẻ lấy ra ở hộp thứ nhất là thẻ lẻ, hộp thứ hai là thẻ chẵn, có 5 × 5= 25 (cách)
– Do vậy, số kết quả thuận lợi của biến cố A là nA = 25 + 25 + 25 = 75
Lại có, số phần tử của không gian mẫu là nΩ = 10 × 10 = 100
Suy ra, xác suất cần tìm:
Vậy xác suất để lấy được hai thẻ có tích hai số ghi trên hai thẻ là một số chẵn là
Câu 9. Một chiếc hộp gồm có 9 thẻ được đánh số liên tiếp từ 1 đến 9. Rút ngẫu nhiên hai thẻ (không kể thứ tự), rồi nhân hai số ghi trên thẻ lại với nhau. Tính xác suất để kết quả nhận được là một số chẵn.
ĐS:
Hướng dẫn giải
Gọi Ω là không gian mẫu của hai phép thử “rút ngẫu nhiên hai thẻ (không kể thứ tự), rồi nhân hai số ghi trên hai thẻ lại với nhau”. Gọi A là biến cố “lấy được hai thẻ có tích các số ghi trên hai thẻ là số chẵn”. Ta có
– Số phần tử của không gian mẫu là
Trong hai thẻ lấy ra, ta xét các trường hợp sau đây:
– Một thẻ lẻ và một thẻ chẵn, có (cách)
– Hai thẻ đều mang số chẵn, có (cách)
– Do vậy, số kết quả thuận lợi của biến cố A là nA = 26
Suy ra, xác suất cần tìm là:
Câu 10. Gọi S là tất cả các số tự nhiên gồm 2 chữ số khác nhau lập từ 0; 1; 2; 3; 4; 5; 6. Chọn ngẫu nhiên 2 số từ tập S. Tích xác suất để tích 2 số được chọn là số chẵn
ĐS:
Hướng dẫn giải
Gọi Ω là không gian mẫu của hai phép thử “chọn ngẫu nhiên 2 số từ tập S”. Gọi A là biến cố “tích 2 số được chọn là số chẵn”. Giả sử số có hai chữ số thuộc S có dạng , ta có:
– Số phần tử của S là nS = 6 × 6 = 36
– Số phần tử của không gian mẫu là
– Số các số chẵn thuộc S (xét trường hợp b = 0 và b ≠ 0) là 6 + 5 × 3 = 21
– Số các số lẻ thuộc S là 36 – 21 = 15
Trong hai số được chọn, ta xét trường hợp sau:
– Có một số chẵn và một số lẻ, có (cách)
– Có hai số chẵn, có (cách)
– Do đó, số kết quả thuận lợi của biến cố A là nA = 315 + 210 = 525
Xác suất cần tìm là: