Trong bài viết này, VerbaLearn sẽ giới thiệu đến độc giả định nghĩa về số trung bình cộng, số trung vị và mốt theo chương trình toán lớp 10. Ứng với mỗi định nghĩa sẽ có các ví dụ và dạng toán đi kèm, giúp bạn đọc nắm vững lý thuyết cũng như cách áp dụng vào trường hợp cụ thể.
Tổng hợp lý thuyết
[content_1]Số trung bình cộng
Định nghĩa: Số trung bình cộng (số trung bình) của một dãy gồm n số liệu x1, x2, …, xn kí hiệu là ![\[\overline x \]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-1.svg)
và được tính theo công thức:
![\[\overline x = \frac{{{x_1} + {x_2} + \cdots + {x_n}}}{n}\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-2.svg)
– Trường hợp bảng phân bố tần số và tần suất
Số trung bình cộng được tính theo công thức:
![\[\begin{gathered} \overline x {\text{ }} = \frac{{{n_1}{x_1} + {n_2}{x_2} + \cdots + {n_k}{c_k}}}{n} \hfill \\ \begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \hfill \\ \end{gathered} &{ = {f_1}{x_1} + {f_2}{x_2} + \cdots + {f_k}{x_k}} \end{array} \hfill \\ \end{gathered} \]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-2a.svg)
Trong đó: ni, fi lần lượt là tần số, tần suất của giá trị xi (i = 1, 2, …, k) và n là số các số liệu thống kê (n = n1 + n2 + ··· + nk).
– Trường hợp bảng phân bố tần số và tần suất ghép lớp
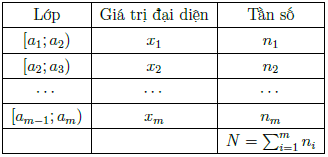
Số trung bình cộng được tính theo công thức:
![\[\begin{gathered} \overline x {\text{ }} = \frac{{{n_1}{c_1} + {n_2}{c_2} + \cdots + {n_k}{c_k}}}{n} \hfill \\ \begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \hfill \\ \end{gathered} &{ = {f_1}{c_1} + {f_2}{c_2} + \cdots + {f_k}{c_k}} \end{array} \hfill \\ \end{gathered} \]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-3.svg)
Trong đó: ni, ci, fi lần lượt là giá trị đại diện, tần số, tần suất của lớp thứ i (i = 1, 2, …, k) và n là số các số liệu thống kê (n = n1 + n2 + ··· + nk).
Số trung vị
[content_2]Định nghĩa: Sắp thứ tự các số liệu thống kê thành dãy không giảm (hoặc không tăng). Số trung vị (của các số liệu thống kê đã cho) kí hiệu Me là số đứng giữa dãy nếu số phần tử là lẻ và là trung bình cộng của hai số đứng giữa dãy nếu số phần tử là chẵn.
Số trung vị được xác định như sau:
– ![\[{M_e} = {x_{\frac{{n + 1}}{2}}}\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-4.svg)
nếu n là số lẻ.
– ![\[{M_e} = \frac{1}{2}\left( {{x_{\frac{n}{2}}} + {x_{\frac{{n + 1}}{2}}}} \right)\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-5.svg)
nếu n là số chẵn.
Mốt
[content_3]Định nghĩa: Mốt của một bảng phân bố tần số là giá trị có tần số lớn nhất và được kí hiệu là MO.
Chú ý:
– Số trung bình của mẫu số liệu được dùng làm đại diện cho các số liệu của mẫu.
– Nếu các số liệu trong mẫu có sự chênh lệch quá lớn thì dùng số trung vị làm đại diện cho các số liệu của mẫu.
– Nếu quan tâm đến giá trị có tần số lớn nhất thì dùng mốt làm đại diện. Một bảng phân bố tần số có thể có hai hay nhiều mốt.
Phân dạng bài tập
[content_4]Dạng 1. Số trung bình
Phương pháp giải
Áp dụng công thức số trung bình cho bảng số tần số, tần suất và tần số, tần suất ghép lớp.
Bài tập vận dụng
Câu 1. Khối lượng 30 chi tiết máy được cho bởi bảng sau:
Tính số trung bình (làm tròn đến chữ số thứ hai sau dấu phẩy) của bảng nói trên.
Hướng dẫn giải
Áp dụng công thức tính số trung bình cho bảng tần số ta có:
![\[\begin{gathered} \overline x {\text{ }} = \frac{{250 \cdot 4 + 300 \cdot 4 + 350 \cdot 5 + 400 \cdot 6 + 450 \cdot 4 + 500 \cdot 7}}{{30}} \hfill \\ \begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \hfill \\ \end{gathered} &{ \approx 388,33\left( {gam} \right)} \end{array} \hfill \\ \end{gathered} \]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-6.svg)
Câu 2. Chiều cao của 20 cây giống được cho bởi bảng sau:
Tính số trung bình (làm tròn đến chữ số thứ hai sau dấu phẩy) của bảng nói trên.
Hướng dẫn giải
Bảng tần số ghép lớp của bảng nói trên là
Áp dụng công thức tính số trung bình cho bảng tần số ghép lớp ta có:
![\[\begin{gathered} \overline x {\text{ }} = \frac{{42 \cdot 2 + 47 \cdot 5 + 52 \cdot 3 + 57 \cdot 4 + 62 \cdot 3 + 67 \cdot 3}}{{20}} \hfill \\ \begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \hfill \\ \end{gathered} &{ \approx 54,5\left( {cm} \right)} \end{array} \hfill \\ \end{gathered} \]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-7.svg)
Dạng 2. Số trung vị
[content_5]Phương pháp giải
Áp dụng định nghĩa của số trung vị. Lưu ý có hai trường hợp khác nhau là mẫu số liệu có kích thước lẻ và mẫu số liệu có kích thước chẵn.
Bài tập vận dụng
Câu 1. Điều tra số học sinh của 30 lớp học, ta được bảng số liệu như sau:
Tính số trung vị của bảng nói trên.
Hướng dẫn giải
Ta có: N = 30 là số chẵn. Số liệu thứ 15 và 16 lần lượt là 46, 48.
Vậy số trung vị là ![\[{M_e} = \frac{{46 + 48}}{2} = 47\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-8.svg)
(học sinh).
Câu 2. Điểm học kì một của một học sinh được cho bởi bảng số liệu sau (Đơn vị: điểm)
Tính số trung vị của bảng nói trên.
Hướng dẫn giải
Ta có: N = 9 là số lẻ.
Số liệu thứ ![\[\frac{{N + 1}}{2} = 5\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-9.svg)
là số trung vị.
Do đó số trung vị là Me = 7 (điểm).
Câu 3. Bảng số liệu sau đây thống kê thời gian nảy mầm một loại hạt mới trong các điều kiện khác nhau:
Tính giá trị trung bình (làm tròn đến hai chữ số sau dấu phẩy) về thời gian nảy mầm loại hạt mới nói trên.
Hướng dẫn giải
Áp dụng công thức tính số trung bình cho bảng tần số ta có:
![\[\begin{gathered} \overline x {\text{ }} = \frac{{4208 + 44017 + 45018 + 48016 + 50011 + 54010}}{{80}} \hfill \\ \begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \hfill \\ \end{gathered} &{ = 469} \end{array} \hfill \\ \end{gathered} \]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-10.svg)
Câu 4. Điều tra số học sinh giỏi khối 10 của 15 trường cấp ba trên địa bản tỉnh A, ta được bảng số liệu như sau:
Tính số trung vị của bảng nói trên.
Hướng dẫn giải
Ta có: N = 15 là số lẻ. Số liệu thứ ![\[\frac{{15 + 1}}{2} = 8\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-11.svg)
.
Vậy số trung vị là Me = 8 (Học sinh).
Câu 5. Tốc độ phát triển của một loại Vi-rút trong 10 ngày với các điểu kiện khác nhau (đơn vị nghìn con) được thống kê như sau:
Trong trường hợp này ta chọn số nào dưới đây làm giá trị đại diện là tốt nhất? Tính giá trị đại diện đó.
Hướng dẫn giải
Ta chọn số trung vị làm đại diện là tốt nhất vì có sự chênh lệch lớn giữa các số liệu trong mẫu.
Sắp xếp lại số liệu mẫu:
Kích thước mẫu là N = 10. Số liệu thứ 5 và 6 lần lượt là 60, 100.
Vậy giá trị đại diện cho bảng số liệu là ![\[{M_e} = \frac{{60 + 100}}{2} = 80\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-12.svg)
(nghìn con).
Câu 6. Một cửa hàng bán 3 loại hoa quả nhập khẩu: Bưởi, Dưa vàng và Lê với số liệu tính toán được cho bởi bảng (trong một quý) sau khi giảm giá mỗi loại lần lượt là x, y, z trên 1 kg.
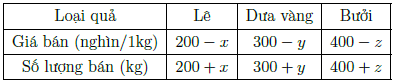
Biết rằng x + y + z = 90 (nghìn). Tính giá trị x; y; z để lợi nhuận bình quân của một 1 kg hoa quả đạt được cao nhất.
Hướng dẫn giải
Do khối lượng hoa quả bán được là 200 + x + 300 + y + 400 + z = 990 là cố định, vì thế bình quân mỗi kg hoa quả có giá cao nhất khi tổng số tiền thu được là cao nhất.
Tổng số tiền thu được là:
P = (200 − x)(200 + x) + (300 − y)(300 + y) + (400 − z) + (400 + z)
= 290000 − (x2 + y2 + z2)
Ta có bất đẳng thức sau:
x2 + y2 + z2 ≥ ![\[\frac{1}{3}\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-13.svg)
(x + y + x)2 = 2700
Từ đó P ≤ 287300.
Vậy P lớn nhất khi dấu bằng xảy ra tức là x = y = z = 30 (nghìn)
Câu 7. Để đảm bảo bảng số liệu được phân bố đồng đều người ta điều chỉnh các giá trị x, y sao cho số trung bình cộng và số trung vị bằng nhau. Khi đó bảng số liệu được cho như sau:
Biết rằng x ≤ 0. Tìm x?
Hướng dẫn giải
Số trung bình của bảng số liệu bằng:
![\[\overline x {\text{ }} = \frac{{\left( {60 + x} \right)\left( {60 - x} \right) + \left( {90 - y} \right)\left( {90 + y} \right) + 2300}}{{200}}\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-14.svg)
Và số trung vị là ![\[{M_e} = \frac{{30 + 60 - x}}{2}\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-15.svg)
Ta có: 20 + 30 + 60 – x + 90 – x = 200 ⇔ x + y = 0
Ta giải phương trình 2 giá trị này bằng nhau rồi lấy số nguyên gần nhất với nghiệm.
![\[\frac{{\left( {60 + x} \right)\left( {60 - x} \right) + \left( {90 - y} \right)\left( {90 + y} \right) + 2300}}{{200}} = \frac{{40 + 50 - x}}{2}\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-16.svg)
Do đó ![\[x = 25 - 25\sqrt 5 \]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-17.svg)
hoặc ![\[x = 25 + 5\sqrt {21} \]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-18.svg)
, vì x ≤ 0 nên ta lấy nghiệm thứ nhất, số nguyên gần với nó nhất là ![\[25 - 25\sqrt 5 \]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-19.svg)
.
Dạng 3. Mốt
[content_6]Phương pháp giải
Áp dụng định nghĩa về Mốt của bảng số liệu thống kê.
Bài tập vận dụng
Câu 1. Tuổi thọ của 30 bóng đèn được thắp thử (đơn vị: giờ) được cho bởi bảng số liệu thống kê dưới đây
Hãy tính mốt của bảng số liệu thống kê trên.
Hướng dẫn giải
Từ bảng số liệu trên ta suy ra bảng phân bố tần số các giá trị tuổi thọ của 30 bóng đèn như sau:
Ta thấy giá trị 1170 có tần số bằng 12 là lớn nhất.
Do đó mốt của bảng số liệu là: MO = 1170.
Câu 2. Kết quả kiểm tra chất lượng đầu năm (thang điểm 30) của 41 học sinh của một lớp được cho bởi bảng số liệu thống kê dưới đây:
Hãy tính mốt của bảng số liệu thống kê trên.
Hướng dẫn giải
Ta thấy điểm 11 và điểm 18 có tần số bằng 7 là lớn nhất.
Do đó bảng số liệu có hai mốt là: ![\[M_O^{\left( 1 \right)} = 11\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-20.svg)
và ![\[M_O^{\left( 2 \right)} = 18\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-21.svg)
Câu 3. Một bác sĩ mắt ghi lại tuổi của 30 bệnh nhân mắc bệnh đau mắt hột. Kết quả thu được mẫu số liệu như sau:
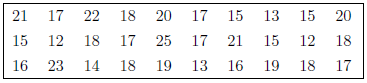
Tính mốt MO của bảng số liệu đã cho.
Hướng dẫn giải
Từ bảng số liệu trên ta suy ra bảng phân bố tần số tuổi của 30 bệnh nhân đau mắt hột như sau:
Ta thấy tuổi 17 và 18 có tần số bằng 5 là lớn nhất.
Do đó bảng số liệu có hai mốt là: ![\[M_O^{\left( 1 \right)} = 17\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-22.svg)
và
Câu 4. Điểm bài kiểm tra một tiết môn toán của 40 học sinh lớp 11A1 được thống kê bằng bảng số liệu dưới đây:
Trong đó: n ∈ ℕ, n ≥ 4. Tính mốt của bảng số liệu thống kê đã cho.
Hướng dẫn giải
Vì tổng các số liệu thống kê bằng 40 nên ta có:
5n + 15 = 40 ⇔ n = 5.
Với n = 5 ta có bảng phân bố tần số:
Vậy mốt của bảng số liệu là: MO = 6.
Câu 5. Cho bảng phân bố tần số sau:
Tìm tất cả các số tự nhiên n để MO = x3 là mốt duy nhất của bảng phân bố tần số đã cho.
Hướng dẫn giải
Từ giả thiết MO = x3 là mốt duy nhất của bảng số liệu thống kê đã cho nên ta có:
![\[\left\{ \begin{gathered} {n^2} > 16 \hfill \\ {n^2} > 6n - 5 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} \left[ \begin{gathered} n < - 4 \hfill \\ n > 4 \hfill \\ \end{gathered} \right. \hfill \\ \left[ \begin{gathered} n < 1 \hfill \\ n > 5 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} n < - 4 \hfill \\ n > 5 \hfill \\ \end{gathered} \right.\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-23.svg)
Vì n là số tự nhiên nên các giá trị n thỏa mãn là n > 5.
Câu 6. Cho bảng phân bố tần số sau:
Tìm các số tự nhiên n để MO = x4 là mốt duy nhất của bảng số liệu thống kê đã cho.
Hướng dẫn giải
Từ giả thiết MO = x4 là mốt duy nhất của bảng số liệu thống kê đã cho nên ta có:
![\[\left\{ \begin{gathered} 20 - n > 8 \hfill \\ 20 - n > n \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} n < 12 \hfill \\ n < 10 \hfill \\ \end{gathered} \right. \Leftrightarrow n < 10\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-25.svg)
Vì n là số tự nhiên nên các giá trị n thỏa mãn là: 0 ≤ n < 10.
Câu 7. Cho bảng phân bố tần số sau:
Gọi S là tập hợp tất cả các số n nguyên dương sao cho MO = x2 và MO = x4 là hai mốt của bảng phân bố tần số đã cho. Tính số phần tử của tập hợp S.
Hướng dẫn giải
Từ giả thiết x2 và x4 là các mốt của bảng số liệu thống kê đã cho, ta có:
![\[\left\{ \begin{gathered} {n^2} + 3 = 7n - 9 \hfill \\ 7n - 9 > n + 1 \hfill \\ 7n - 9 > 7 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} {n^2} - 7n + 12 = 0\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ n > \frac{5}{3} \hfill \\ n > \frac{{16}}{7}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} n = 3 \hfill \\ n = 4 \hfill \\ \end{gathered} \right.\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-26.svg)
Vì n là số nguyên dương nên n = 3 và n = 4 thỏa mãn.
Vậy tập hợp S có 2 phần tử.
Câu 8. Quan sát 9 con chuột chạy qua một mê hồn trận và ghi lại thời gian (tính bằng phút) của chúng trong bảng sau:
a) Tính số trung bình, số trung vị và mốt của thời gian chuột ra khỏi mê hồn trận?
b) Trong trường hợp này nên chọn đại lượng nào để thể hiện xu thế trung bình của mẫu?
Hướng dẫn giải
a) Số trung bình:
![\[\overline x = \frac{{1 + 2,5 + \cdots + 30}}{9} \approx 4,79\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-27.svg)
Sắp xếp dãy số liệu theo thứ tự không giảm ta được:
0,9; 1; 1; 1,25; 1,5; 2; 2,5; 3; 30
Số trung vị: Me = x5 = 1,5.
Mốt: MO = 1.
b) Trong trường hợp này ta nên chọn số trung vị để thể hiện xu thế trung bình của mẫu.
Câu 9. Trong kỳ thi Tiếng Anh cấp chứng chỉ B1 theo chuẩn Châu u của trường Đại học Cần Thơ, điểm thi của 32 thí sinh (thang điểm 100) như sau:
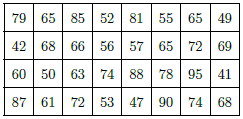
a) Lập bảng phân bố tần số ghép lớp của mẫu số liệu trên với các lớp [40; 50), [50; 60), …, [90; 100).
b) Tính số trung bình của mẫu số liệu theo bảng phân bố tần số ghép lớp (chính xác đến hàng phần trăm).
c) Tính số trung vị.
Hướng dẫn giải
a) Bảng phân bố tần số ghép lớp của mẫu số liệu:
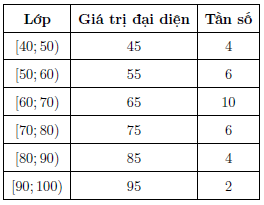
b) Số trung bình
![\[\overline x = \frac{{45 \cdot 4 + 55 \cdot 6 + \cdots + 95 \cdot 2}}{9} \approx 66,88\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-28.svg)
c) Vì có 32 số liệu nên số trung vị là
![\[{M_e} = \frac{{{x_{16}} + {x_{17}}}}{2}\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-29.svg)
Nhìn vào bảng trên ta thấy x16, x17 thuộc lớp [60; 70), từ đó ta có: x16 = 65, x17 = 66.
Vậy ![\[{M_e} = \frac{{{x_{16}} + {x_{17}}}}{2} = \frac{{65 + 66}}{2} = 65,5\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-30.svg)
Câu 10. Điểm kiểm tra của Darell (thang điểm 100) trong giai đoạn đầu tiên được biểu diễn bởi dãy số liệu sau:
78, 83, 84, 86, 87, 90, 92, 92
Darell có thể miêu tả điểm của mình với bố mẹ như thế nào? Dùng số trung bình, số trung vị hay mốt? Liệu số liệu này có cho phép đưa đến một sự miêu tả đúng hay không?
Hướng dẫn giải
Số trung bình:
![\[\overline x = \frac{{78 + 83 + 84 + 86 + 87 + 90 + 92 + 92}}{8} = 86,5\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-31.svg)
Số trung vị: Me = 86.5.
Mốt: MO = 92.
Do mốt có giá trị lớn nhất nên Darell có thể dùng nó để môt tả cho điểm kiểm tra của anh ấy.
Tuy nhiên, trong trường hợp này mốt không phải là giá trị đại diện tốt cho điểm kiểm tra của anh ấy vì tất cả các điểm còn lại đều nhỏ hơn 92.
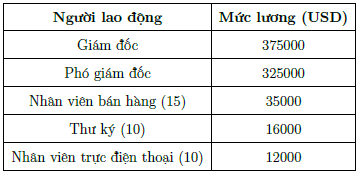
Câu 11. Nói về tiền lương, Amara đang tham gia phỏng vấn tìm việc làm tại một công ty kỹ thuật. Cô ấy nói rằng mức lương trung bình của 37 công nhân tại đây là nhiều hơn 40000 USD. Sử dụng những thông tin có trong bảng cho biết liệu Amara có nên mong đợi mức lương hơn 40000 USD nếu cô làm việc cho công ty này. Hãy giải thích tại sao?
Hướng dẫn giải
Công ty có 37 nhân viên, nhưng chỉ có hai nhân viên có mức lương trên 40000 USD là giám đốc và phó giám đốc.
Do đó, Amara không nên mong đợi một mức lương cao hơn 40000 USD khi vào làm việc cho công ty này.
Nói cách khác, con số trung bình về mức lương trên 40000 USD là một số không đại diện tốt cho các số liệu trên.
Câu 12. Cho bảng phân bố tần số:
Với x, y là các số tự nhiên. Tìm tất cả các cặp số (x; y) để x5 là mốt của bảng số liệu đã cho.
Hướng dẫn giải
Điều kiện để x5 là mốt của bảng số liệu đã cho là:
![\[\left\{ \begin{gathered} 0 \leqslant x + y \leqslant 6{\text{ }}\left( 1 \right) \hfill \\ 0 \leqslant 2x - y \leqslant 6{\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right.\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-32.svg)
Từ (1) suy ra y ≤ 6 − x và x ≤ 6 − y.
Từ (2) suy ra 2x − 6 ≤ y và ![\[\frac{y}{2} \leqslant x\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-33.svg)
.
Do đó: ![\[\left\{ \begin{gathered} 2x - 6 \leqslant 6 - x\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \frac{y}{2} \leqslant 6 - y \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} 0 \leqslant x \leqslant 4 \hfill \\ 0 \leqslant y \leqslant 4 \hfill \\ \end{gathered} \right.\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-34.svg)
Từ đó tìm được 14 cặp số thỏa mãn là:
(0; 0), (1; 0), (1; 1), (1; 2), (2; 0), (2; 1), (2; 2)
(3; 0), (3; 1), (3; 2), (3; 3), (4; 2), (2; 3), (2; 4).
Câu 13. Cho bảng phân bố tần số
Với x, y là các số tự nhiên. Tìm tất cả các cặp số (x; y) để bảng số liệu thống kê đã cho có mốt là 3 giá trị khác nhau.
Hướng dẫn giải
Trường hợp 1: Các giá trị x1, x2, x3 là mốt khi
![\[\left\{ \begin{gathered} 3x + y = 6 \hfill \\ 3y - 3x = 6 \hfill \\ x + y < 6 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x = 1 \hfill \\ y = 3 \hfill \\ x + y < 6 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x = 1 \hfill \\ y = 3 \hfill \\ \end{gathered} \right.\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-35.svg)
Trường hợp 2: Các giá trị x1, x2, x4 là mốt khi
![\[\left\{ \begin{gathered} 3x + y = 6 \hfill \\ x + y = 6 \hfill \\ 3y - 3x < 6 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x = 0 \hfill \\ y = 6 \hfill \\ y - x < 2 \hfill \\ \end{gathered} \right.\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-36.svg)
Hệ vô nghiệm vì ![\[\left\{ \begin{gathered} x = 0 \hfill \\ y = 6 \hfill \\ \end{gathered} \right.\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-37.svg)
không thỏa mãn bất phương trình y − x < 2.
Trường hợp 3: Các giá trị x1, x3, x4 là mốt khi
![\[\left\{ \begin{gathered} x + y = 6 \hfill \\ 3y - 3x = 6 \hfill \\ 3x + y < 6 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x = 2 \hfill \\ y = 4 \hfill \\ 3x + y < 6 \hfill \\ \end{gathered} \right.\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-38.svg)
Hệ vô nghiệm vì ![\[\left\{ \begin{gathered} x = 2 \hfill \\ y = 4 \hfill \\ \end{gathered} \right.\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-39.svg)
không thỏa mãn bất phương trình 3x + y < 6.
Trường hợp 4: các giá trị x2, x3, x4 là mốt khi
![\[\left\{ \begin{gathered} 3x + y = 3y - 3x \hfill \\ 3x + y = x + y \hfill \\ x + y > 6 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x = 0 \hfill \\ y = 0 \hfill \\ x + y > 6 \hfill \\ \end{gathered} \right.\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-40.svg)
Hệ vô nghiệm vì ![\[\left\{ \begin{gathered} x = 0 \hfill \\ y = 0 \hfill \\ \end{gathered} \right.\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-41.svg)
không thỏa mãn bất phương trình x + y > 6.
Vậy chỉ có ![\[\left\{ \begin{gathered} x = 1 \hfill \\ y = 3 \hfill \\ \end{gathered} \right.\]](http://verbalearn.org/wp-content/uploads/2023/03/so-trung-binh-cong-so-trung-vi-mot-42.svg)
thỏa mãn yêu cầu của bài toán.
