Tổng hợp toàn bộ lý thuyết & bài tập giúp tìm hiểu 3 quy tắc đếm trong toán học: Quy tắc cộng, quy tắc nhân và quy tắc bù trừ. Nắm rõ bản chất từng quy tắc sẽ giúp cho bạn đọc hiểu hơn về chuyên đề hoán vị, chỉnh hợp, tổ hợp và tránh sự nhầm lẫn qua lại giữa các quy tắc.
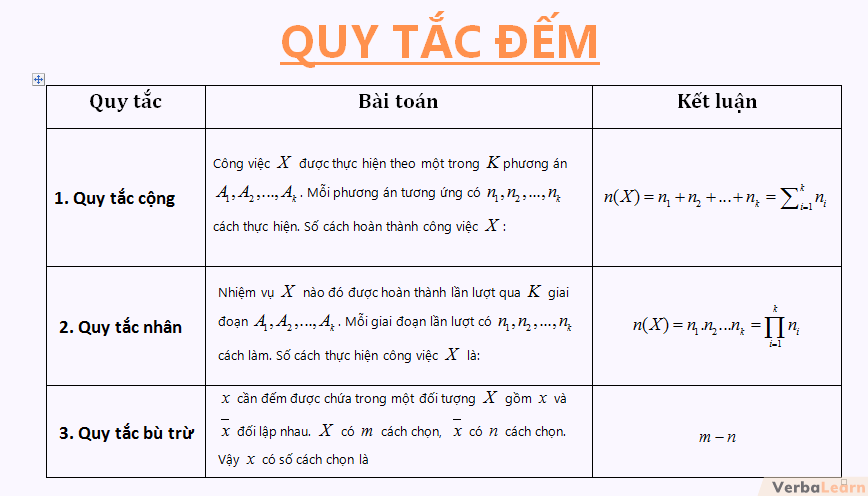
Lý thuyết quy tắc đếm
[content_1]Định nghĩa
Đếm trong toán học hay ngoài thực tế đều là tìm số phần tử của một tập hợp hữu hạn các đối tượng. Ngoài việc đếm truyền thống thì việc áp dụng các quy tắc đếm sẽ giúp quy trình đếm trở nên nhanh chóng và chính xác hơn, áp dụng được nhiều tình huống phức tạp của một bài toán. Bài viết này sẽ giúp bạn đọc hiểu rõ 3 quy tắc đếm là nền tảng cho phần toán học tổ hợp.
Quy tắc cộng
Trong toán tổ hợp, quy tắc cộng (hay còn gọi là quy tắc tổng) là một nguyên tắc đếm cơ bản. Nói một cách đơn giản, đó là ý tưởng trực quan rằng nếu chúng ta có A cách để làm một việc gì đó và B cách để làm một việc khác và chúng ta không thể làm cả hai cùng một lúc, thì có A + B cách để chọn một trong số các hành động. [1]WikiPedia, Rule of sum, 13/03/2022 Ta có thể diễn tả chi tiết bằng bài toán nhỏ dưới đây:
Một công việc X được thực hiện theo một trong k phương án A1, A2, …, Ak, trong đó:
– Phương án A1 có n1 cách thực hiện
– Phương án A2 có n2 cách thực hiện
– …
– Phương án Ak có nk cách thực hiện
Khi đó số cách hoàn thành công việc X là cách. [2]W. Somerset Maugham, The Basic Rules of Counting, 2018
Quy tắc nhân
Quy tắc nhân nói rằng nếu có A cách làm điều gì đó, và B cách làm khác đi. Tổng quan lại sẽ có A*B cách thực hiện cả hai hành động này. Nói cách khác, khi chọn một tùy chọn cho A và một tùy chọn cho B, sẽ có A*B các cách khác nhau để thực hiện cả hai hành động. Ta có thể diễn tả chi tiết bằng bài toán nhỏ dưới đây:
Giả sử một nhiệm vụ X nào đó được hoàn thành lần lượt qua k giai đoạn A1, A2, …, Ak:
– Giai đoạn A1 có n1 cách làm;
– Giai đoạn A2 có n2 cách làm;
– . . .
– Giai đoạn Ak có nk cách làm.
Khi đó công việc X có số cách thực hiện là cách. [3]Kim Seward, Tutorial 55: The Fundamental Counting Principle, 20/12/2014
Quy tắc bù trừ
Đối tượng x cần đếm được chứa trong một đối tượng X gồm x và đối lập nhau. Nếu X có m cách chọn,
có n cách chọn. Vậy x có (m − n) cách chọn
Về mặt thực hành, đề cho đếm những đối tượng thỏa a và b. Ta cần làm:
– Bài toán 1: Đếm những đối tượng thỏa a.
– Bài toán 2: Đếm những đối tượng thỏa a, không thỏa b.
Do đó, kết quả bài toán = kết quả bài toán 1 – kết quả bài toán 2.
– Nếu bài toán chia ra từng trường hợp không trùng lặp để hoàn thành công việc thì dùng quy tắc cộng, nếu bài toán chia ra từng giai đoạn thực hiện thì ta dùng quy tắc nhân. Trong nhiều bài toán, không chỉ kết hợp giữa hai quy tắc này lại với nhau để giải mà cần phân biệt khi nào cộng, khi nào nhân, khi nào trừ.
– “Nếu cho tập hợp hữu hạn bất kỳ A và B giao nhau khác rỗng. Khi đó thì số phần tử của A ∪ B bằng số phần tử của A cộng với số phần tử của B rồi trừ số phần tử của A ∩ B, tức là n (A ∪ B) = n(A) + n(B) – n(A ∩ B)”. Đó là quy tắc cộng mở rộng. Do đó khi giải các bài toán đếm liên quan đến tìm số sao cho số đó là số chẵn, số lẻ, số chia hết ta nên ưu tiên việc thực hiện (chọn) chúng trước và nếu chứa số 0 nên chia 2 trường hợp nhằm tránh trùng lặp với nhau.
– Dấu hiệu chia hết:
Gọi là số tự nhiên có n + 1 chữ số (an ≠ 0). Khi đó:
+ N ⋮ 2 ⇔ a0 ⋮ 2 ⇔ a0 ∈ {0; 2; 4; 6; 8}.
+ N ⋮ 5 ⇔ a0 ⋮ 5 ⇔ a0 ∈ {0; 5}.
+ N ⋮ 4 (hay 25) ⇔ (hay 25).
+ N ⋮ 8 (hay 125) ⇔ (hay 125).
+ N ⋮ 3 (hay 9) ⇔ a0 + a1 + … + an ⋮ 3 (hay 9).
Phân dạng bài tập sử dụng quy tắc đếm
[content_2]Dạng 1. Bài toán sử dụng quy tắc cộng
Câu 1. Trong một cuộc thi tìm hiểu về đất nước Việt Nam, ban tổ chức công bố danh sách các đề tài bao gồm: 8 đề tài về lịch sử, 7 đề tài về thiên nhiên, 10 đề tài về con người và 6 đề tài về văn hóa. Hỏi mỗi thí sinh có bao nhiêu cách chọn đề tài?
Đáp số: 31
Hướng dẫn giải
Mỗi thí sinh có các 4 phương án chọn đề tài:
– Chọn đề tài về lịch sử có 8 cách chọn
– Chọn đề tài về thiên nhiên có 7 cách chọn
– Chọn đề tài về con người có 10 cách chọn
– Chọn đề tài về văn hóa có 6 cách chọn
Theo quy tắc cộng, có 8 + 7 + 10 + 6 = 31 cách chọn đề tài.
Câu 2. Giả sử từ tỉnh A đến tỉnh B có thể đi bằng các phương tiện: ô tô, tàu hỏa hoặc máy bay. Mỗi ngày có 10 chuyến ô tô, 5 chuyến tàu hỏa và 3 chuyến máy bay. Hỏi có bao nhiêu cách lựa chọn chuyến đi từ tỉnh A đến tỉnh B?
Đáp số: 18
Hướng dẫn giải
Để đi từ A đến B có 3 phương án lựa chọn:
– Đi bằng ô tô có 10 cách chọn
– Đi bằng tàu hỏa có 5 cách chọn
– Đi bằng máy bay có 3 cách chọn
Theo quy tắc cộng, có 10 + 5 + 3 = 18 cách chọn
Dạng 2. Bài toán sử dụng quy tắc nhân
[content_3]Câu 1. An đến nhà Bình để cùng Bình đến chơi nhà Cường. Từ nhà An đến nhà Bình có 4 con đường đi, từ nhà Bình đến nhà Cường có 6 con đường đi. Hỏi An có bao nhiêu cách chọn đường đi từ nhà mình đến nhà Cường?
Đáp số: 24
Hướng dẫn giải
Để đi từ nhà An đến nhà Cường cần thực hiện 2 giai đoạn
– Đi từ nhà An đến nhà Bình có 4 cách.
– Đi từ nhà Bình đến nhà Cường có 6 cách.
Theo quy tắc nhân, có 4 × 6 = 24 cách chọn đường đi.
Câu 2. Lớp 11A có 30 học sinh. Tập thể lớp muốn bầu ra một lớp trưởng, một lớp phó và một thủ quỹ. Hỏi có bao nhiêu cách chọn một ban cán sự lớp như trên, biết rằng một bạn chỉ có thể làm tối đa một vai trò?
Đáp số: 24360
Hướng dẫn giải
Để bầu một ban cán sự lớp cần thực hiện 3 giai đoạn
– Bầu lớp trưởng có 30 cách
– Bầu phó có 29 cách
– Bầu thủ quỹ có 28 cách
Theo quy tắc nhân, có 30 × 29 × 28 = 24360 cách chọn.
Dạng 3: Bài toán sử dụng quy tắc bù trừ
[content_4]Câu 1. Có bao nhiêu số tự nhiên gồm năm chữ số khác nhau mà không bắt đầu bởi 12?
Đáp số: 26880
Hướng dẫn giải
Gọi a1a2a3a4a5 là số cần lập
Để lập được số tự nhiên có 5 chữ số khác nhau, ta thực hiện các bước lần lượt
– Chọn a1 có 9 cách.
– Chọn a2 có 9 cách.
– Chọn a3 có 8 cách.
– Chọn a4 có 7 cách.
– Chọn a5 có 6 cách.
Do đó có 9 × 9 × 8 × 7 × 6 = 27216 so có năm chữ số khác nhau. Để lập được số tự nhiên có 5 chữ số khác nhau bắt đầu bằng 12, ta thực hiện các bước lần lượt:
– Chọn a1a2 có 1 cách.
– Chọn a3 có 8 cách.
– Chọn a4 có 7 cách.
– Chọn a5 có 6 cách.
Do đó có 1 × 8 × 7 × 6 = 336 số có năm chữ số khác nhau. Theo quy tắc bù trừ, có 27216 – 336 = 26880 số có năm chữ số khác nhau không bắt đầu bởi 12.
Câu 2. Trong một hộp có 6 bi đỏ, 5 bi trắng và 4 bi vàng. Có bao nhiêu cách lấy 3 viên bi từ hộp này sao cho chúng không đủ ba màu?
Đáp số: 335
Hướng dẫn giải
Số cách lấy 3 bi bất kỳ từ 15 bi là C315 = 455.
Số cách lấy 3 bi từ 15 bi mà đủ ba màu là 6 × 5 × 4 = 120.
Theo quy tắc bù trừ, số cách lấy 3 viên bi không đủ ba màu là 455 − 120 = 335.
Bài tập vận dụng quy tắc đếm
Câu 1. Một hộp có 12 viên bi trắng, 10 viên bi xanh và 8 viên bi đỏ. Một em bé muốn chọn 1 viên bi để chơi. Hỏi có bao nhiêu cách chọn?
Đáp số: 30 cách
Hướng dẫn giải
Để chọn 1 viên bi để chơi có các phương án
– Chọn 1 viên bi trắng có 12 cách.
– Chọn 1 viên bi xanh có 10 cách.
– Chọn 1 viên bi đỏ có 8 cách.
Theo quy tắc cộng, số cách để chọn 1 viên bi để chơi là 12 + 10 + 8 = 30 cách.
Câu 2. Chợ Bến Thành có 4 cổng ra vào. Hỏi một người đi chợ:
a) Có mấy cách vào và ra chợ?
Đáp số: 16
b) Có mấy cách vào và ra chợ bằng 2 cổng khác nhau?
Đáp số: 12
Hướng dẫn giải
a) Để vào và ra chợ ta thực hiện liên tiếp các bước
– Vào chợ có 4 cách.
– Ra chợ có 4 cách
Theo quy tắc nhân, có 4 × 4 = 16 cách vào và ra chợ.
b) Để vào và ra chợ bằng 2 cổng khác nhau ta thực hiện liên tiếp các bước
– Vào chợ có 4 cách.
– Ra chợ bằng cổng khác có 3 cách
Theo quy tắc nhân, có 4 × 3 = 12 cách vào và ra chợ bằng hai cổng khác nhau.
Câu 3. Có 8 quyển sách Toán, 7 quyển sách Lí, 5 quyển sách Hóa. Một học sinh chọn 1 quyển trong bất kỳ 3 loai trên. Hỏi có bao nhiêu cách chọn?
Đáp số: 20 cách
Lời giải
Để chọn 1 quyển sách trong 3 loai sách, ta có các phương án
– Chọn 1 quyển sách Toán có 8 cách.
– Chọn 1 quyển sách Lí có 7 cách.
– Chọn 1 quyển sách Hóa có 5 cách.
Theo quy tắc cộng, số cách để chọn 1 viên bi để chơi là 8 + 7 + 5 = 20 cách.
Câu 4. Cho sơ đồ mạch điện như hình vẽ dưới đây. Hỏi có bao nhiêu cách đóng – mở 5 công tắc để có được dòng điện đi từ A đến B.
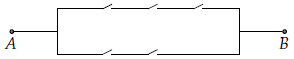
Đáp số: 12 cách
Hướng dẫn giải
Để dòng điện đi tù A đến B có 2 phương án:
– Phương án 1: 3 công tắc phía trên đóng. Khi đó có 22 = 4 trạng thái của các công tắc phía dưới.
– Phương án 2: 2 công tắc phía dưới đóng. Khi đó có 23 = 8 trạng thái của các công tắc phía trên.
Theo quy tắc cộng, có 4 + 8 = 12 cách để dòng điện đi từ A đến B.
Câu 5. Đề thi học kỳ môn Hóa gồm hai phần: trắc nghiệm và tự luận. Trong ngân hàng đề thi có 15 để trắc nghiệm và 8 đề tự luận. Hỏi có bao nhiêu cách ra đề?
Đáp số: 120 cách
Hướng dẫn giải
Để tạo được một đề thi, cần thực hiện hai bước liên tiếp
– Chọn đề trắc nghiệm có 15 cách.
– Chọn đề tự luận có 8 cách.
Theo quy tắc nhân, có 15 × 8 = 120 cách ra đề.
Câu 6. Một ca sĩ có 30 cái áo và 20 cái quần, trong đó có 18 cái áo màu xanh và 12 cái áo màu đỏ; 12 quần xanh và 8 quần đỏ. Có bao nhiêu cách chọn một bộ quần áo khác màu để người ca sĩ này đi trình diễn?
Đáp số: 240 cách
Hướng dẫn giải
Để chọn một bộ quần áo khác màu, ta có các phương án
Áo màu xanh và quần màu đỏ có 18 × 8 = 144 cách.
Áo màu đỏ và quần màu xanh có 12 × 8 = 96 cách.
Theo quy tắc cộng, số cách chọn quần áo là 144 + 96 = 240 cách.
Câu 7. Trong lớp 11A có 39 học sinh trong đó có học sinh tên Chiến, lớp 11B có 32 học sinh trong đó có học sinh tên Tranh. Có bao nhiêu cách chọn một số gồm 2 học sinh khác lớp mà không có mặt Chiến và Tranh cùng lúc?
Đáp số: 1247 cách
Hướng dẫn giải
Để chọn một số gồm 2 sinh khác lớp, có 39 × 32 = 1248 cách.
Trong đó có 1 cách chọn tổ có mặt cả Chiến và Tranh.
Do đó số cách chọn một tổ không có mặt Chiến và Tranh cùng lúc là 1248 − 1 = 1247 cách.
Câu 8. Trong lớp 11A có 50 học sinh, trong đó có 2 học sinh tên Ưu và Tiên. Có bao nhiêu cách chọn ra 2 học sinh đi thi mà trong đó có mặt ít nhất 1 trong 2 học sinh tên Ưu và tên Tiên?
Đáp số: 97 cách
Hướng dẫn giải
Có 3 phương án chọn
– Phương án 1: Chọn chỉ có Ưu 1 cách, chọn một bạn khác Tiên có 48 cách nên có 1 × 48 = 48 cách trong trường hợp này
– Phương án 2: Chọn chỉ có Tiên 1 cách, chọn một bạn khác Tiên có 48 cách nên có 1 × 48 = 48 cách trong trường hợp này
– Phương án 3: Có cả Ưu và Tiên: 1 cách trong trường hợp này.
Vậy số cách chọn thỏa yêu cầu đề bài là 48 + 48 + 1 = 97 cách thỏa yêu cầu.
Câu 8. Có 20 bông hoa trong đó có 8 bông hồng, 7 bông cúc, 5 bông đào. Chọn ngẫu nhiên 4
bông, hỏi có bao nhiêu cách chọn để trong đó hoa đưa chọn có đủ cả ba loai?
Đáp số: 2380 cách
Hướng dẫn giải
Có 3 phương án chọn.
– Phương án 1: Chọn 2 bông hồng, 1 bông cúc, 1 bông đào có cách trong trường hợp này.
– Phương án 2: Chọn 1 bông hồng, 2 bông cúc, 1 bông đào có cách trong trường hợp này.
– Phương án 3: Chọn 1 bông hồng, 1 bông cúc, 2 bông đào có cách trong trường hợp này.
Vậy số cách chọn thỏa yêu cầu đề bài là 980 + 840 + 560 = 2380 cách thỏa yêu cầu.
Câu 10. Có 12 học sinh giỏi gồm 3 học sinh khối 12; 4 học sinh khối 11; 5 học sinh khối 10. Hỏi có bao nhiêu cách chọn ra 6 học sinh sao cho mỗi khối có ít nhất 1 học sinh?
Đáp số: 805 cách
Hướng dẫn giải
Có 4 phương án chọn.
– Số cách chọn 6 học sinh bất kỳ từ 12 học sinh có cách.
– Số cách chọn 6 học sinh trong đó không có học sinh lớp 12 có cách.
– Số cách chọn 6 học sinh trong đó không có học sinh lớp 11 có cách.
– Số cách chọn 6 học sinh trong đó không có học sinh lớp 10 có cách.
Do đó số cách chọn thỏa mãn yêu cầu là 924 − (84 + 28 + 7) = 805 cách.
Câu 11. Có bao nhiêu biển số xe gồm hai chữ cái ở đầu (26 chữ cái) và 4 chữ số theo sau (chữ số đầu không nhất thiết khác 0 và chữ số cuối khác 0), sao cho:
1) Chữ cái tùy ý và bốn chữ số tùy ý tạo thành một số chia hết cho 2 theo sau.
Đáp số: 2704000 cách
2) Chữ cái khác nhau và 4 chữ số đôi một khác nhau tạo thành một số chia hết cho 5 tiếp theo sau.
Đáp số: 291200 cách
Hướng dẫn giải
Có 3 bước chọn.
– Chọn 2 chữ cái 262 cách.
– Chọn 3 chữ số tiếp theo có 103 cách.
– Chọn chữ số cuối cùng thuộc {2; 4; 6; 8} có 4 cách.
Vậy có tất cả 262 × 103 × 4 = 2704000 cách. Có 3 bước chọn.
– Chọn 2 chữ cái có 26 × 25 = 650 cách. Chữ số cuối có 1 cách chọn số 5.
– Chọn 3 chữ số còn lại 8 × 8 × 7 = 448 cách. Vậy có tất cả 26 × 25 × 1 × 8 × 8 × 7 = 291200 cách.
Câu 12. Người ta có thể ghi nhãn cho những chiếc ghế trong một giảng đường Đại học bằng một chữ cái (26 chữ cái) và một số nguyên dương theo sau mà không vượt quá 100. Bằng cách ghi như vậy, nhiều nhất có bao nhiêu chiếc ghế có thể được ghi nhãn khác nhau?
Đáp số: 2600 cách
Hướng dẫn giải
Có 26 chữ cái và 100 số thỏa mãn.
Vậy số cách ghi nhiều nhất là 26 × 100 = 2600 cách.
Câu 13. Cho tập hợp A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}. Có bao nhiêu số tự nhiên gồm năm chữ số được lấy từ tập A, sao cho các chữ số này:
– Tùy ý.
Đáp số: 90000 số
– Khác nhau từng đôi một.
Đáp số: 27216 số
– Khác nhau từng đôi một và năm chữ số này tạo thành một số lẻ.
Đáp số: 13440 số
– Khác nhau từng đôi một và năm chữ số này tạo thành một số chia hết cho 5.
Đáp số: 5712 số
– Khác nhau từng đôi một và năm chữ số này tạo thành một số chia hết cho 2.
Đáp số: 13776 số
Hướng dẫn giải
Gọi là số cần tìm.
– Tùy ý.
a có 9 cách chọn.
b có 10 cách chọn.
c có 10 cách chọn.
d có 10 cách chọn.
e có 10 cách chọn.
Vậy có 9 × 10 × 10 × 10 × 10 = 90000 số thỏa yêu cầu.
– Khác nhau từng đôi một.
a có 9 cách chọn.
b có 9 cách chọn..
c có 8 cách chọn.
d có 7 cách chọn.
e có 6 cách chọn.
Vậy có 9 × 9 × 8 × 7 × 6 = 27216 số thỏa mãn yêu cầu.
– Khác nhau từng đôi một và năm chữ số này tạo thành một số lẻ.
e có 5 cách chọn.
a có 8 cách chọn.
b có 8 cách chọn.
c có 7 cách chọn.
d có 6 cách chọn.
Vậy có 5 × 8 × 8 × 7 × 6 = 13440 số thỏa mãn yêu cầu.
– Khác nhau từng đôi một và năm chữ số này tạo thành một số chia hết cho 5.
Có 2 trường hợp:
Trường hợp 1:
e = 0 có 1 cách chọn.
a có 9 cách chọn.
b có 8 cách chọn.
c có 7 cách chọn.
d có 6 cách chọn.
Vậy có 9 × 8 × 7 × 6 × 1 = 3024 số trong trường hợp này.
Trường hợp 2:
e = 5 có 1 cách chọn.
a có 8 cách chọn.
b có 8 cách chọn.
c có 7 cách chọn.
d có 6 cách chọn.
Vậy có 8 × 8 × 7 × 6 × 1 = 2688 số trong trường hợp này.
Vậy có tất cả: 3024 + 2688 = 5712 số thỏa mãn yêu cầu.
– Khác nhau từng đôi một và năm chữ số này tạo thành một số chia hết cho 2.
Có 2 trường hợp:
Trường hợp 1:
e = 0 có 1 cách chọn.
a có 9 cách chọn.
b có 8 cách chọn.
c có 7 cách chọn.
d có 6 cách chọn.
Vậy có 9 × 8 × 7 × 6 × 1 = 3024 số trong trường hợp này.
Trường hợp 2:
e ∈ {2; 4; 6; 8} có 4 cách chọn.
a có 8 cách chọn.
b có 8 cách chọn.
c có 7 cách chọn.
d có 6 cách chọn.
Vậy có 8 × 8 × 7 × 6 × 4 = 10752 số trong trường hợp này.
Vậy có tất cả 3024 + 10752 = 13776 số thỏa mãn yêu cầu.
Câu 14. Từ các chữ số 0, 1, 2, …, 9 có thể lập được bao nhiêu số tự nhiên chẵn gồm năm chữ số khác nhau đôi một và chữ số chính giữa luôn là số 2?
Đáp số: 1218 số
Hướng dẫn giải
Gọi (a ≠ 0).
– Xét , a bất kì, d ∈ {0; 4; 6; 8}
Có 4 cách chọn d, 8 cách chọn a, 7 cách chọn b, 6 cách chọn c, nên có 4 × 8 × 7 × 6 = 1344 cách.
– Xét , d ∈ {4; 6; 8} và a = 0.
Có 3 cách chọn d, 7 cách chọn b, 6 cách chọn c, nên có 3 × 7 × 6 = 126 cách.
Vậy số cách chọn thỏa yêu cầu bài toán là 1344 − 126 = 1218 số.
Câu 15. Cho tập hợp X = {0; 1; 2; 3; 4; 5; 6; 7}. Có thể lập được bao nhiêu số tự nhiên gồm năm chữ số khác nhau đôi một từ X, sao cho một trong ba chữ số đầu tiên phải bằng 1.
Đáp số: 2280 số
Hướng dẫn giải
Đặt số cần tìm là (a ≠ 0).
– Xét trường hợp a bất kỳ.
Xếp số 1 vào một trong ba vị trí a, b, c có 3 cách.
Xếp các số còn lại lần lượt vào vị trí tiếp theo có 7, 6, 5, 4 cách.
Do đó có 3 × 7 × 6 × 5 × 4 = 2520 cách xếp.
– Xét trường hợp a = 0.
Xếp số 1 vào một trong hai vị trí b, c có 2 cách.
Xếp các số còn lại lần lượt vào vị trí tiếp theo có 6, 5, 4 cách.
Do đó có 2 × 6 × 5 × 4 = 240 cách.
Vậy có tất cả 2520 − 240 = 2280 số xếp thỏa yêu cầu.
Câu 16. Cho sáu chữ số 1; 2; 3; 4; 5; 6. Có thể tạo ra bao nhiêu số gồm bốn chữ số khác nhau? Trong đó có bao nhiêu số chia hết cho 5?
Đáp số: 360 số và 60 số
Hướng dẫn giải
Gọi số cần tìm là
a có 6 cách chọn.
b có 5 cách chọn.
c có 4 cách chọn.
d có 3 cách chọn.
Do đó có tất cả 6 × 5 × 4 × 3 = 360 số có 4 chữ số khác nhau.
Trong đó, các số chia hết cho 5 có dạng .
d có 1 cách chọn.
a có 5 cách chọn.
b có 4 cách chọn.
c có 3 cách chọn.
Do đó có 1 × 5 × 4 × 3 = 60 số thỏa yêu cầu.
Câu 17. Cho tập A = {0; 1; 2; 3; 4; 5; 6; 7}. Có bao nhiêu số gồm sáu chữ số có nghĩa đôi một khác nhau chia hết cho 5 và luôn có chữ số 0 được lấy từ tập A?
Đáp số: 4680 số
Hướng dẫn giải
Gọi
– Xét số x có dạng có 1 × 7 × 6 × 5 × 4 × 3 = 2520 số.
– Xét số x có dạng
Xếp số 0 vào 1 trong 5 vị trí có 5 cách.
Xác vị trí còn lại lần lượt có 6, 5, 4, 3 cách.
Do đó có 5 × 6 × 5 × 4 × 3 = 1800 cách.
– Xét số x dạng có 6 × 5 × 4 × 3 = 360 cách.
Vậy có tất cả 2520 + 1800 − 360 = 3960 số thỏa mãn yêu cầu.
Câu 18. Có bao nhiêu số tự nhiên gồm năm chữ số đôi một khác nhau, trong đó chữ số 1 phải có mặt một trong hai vị trí đầu?
Đáp số: 5712 số
Hướng dẫn giải
Gọi số cần tìm là
+ Xét x dạng có 1 × 9 × 8 × 7 × 6 = 3024 số.
+ Xét x dạng
Với a bất kỳ có 9 × 1 × 8 × 7 × 6 = 3024 số.
Với a = 0 có 1 × 1 × 8 × 7 × 6 = 336 số.
Do đó có 3024 − 336 = 2688 số.
Vậy có tất cả 3024 + 2688 = 5712 số thỏa mãn yêu cầu.
Câu 19. Có bao nhiêu số tự nhiên gồm ba chữ số mà trong đó có hai chữ số chẵn đúng liền nhau, còn chữ số còn lại lẻ?
Đáp số: 225 số
Hướng dẫn giải
Gọi số cần tìm là
TH1: a, b chẵn, c lẻ có 4 × 5 × 5 = 100 số.
TH2: a lẻ, b, c chẵn có 5 × 5 × 5 = 125 số.
Vậy có tất cả 100 + 125 = 225 số thỏa yêu cầu.
Câu 20. Từ các chữ số 1; 2; 3; 4; 5 có thể lập được bao nhiêu số có ba chữ số khác nhau nằm trong khoảng (300; 500)?
Đáp số: 24 số
Hướng dẫn giải
Gọi số cần tìm là
– a có 2 cách chọn. (a = 4 hoặc a = 3).
– b có 4 cách chọn.
– c có 3 cách chọn.
Vậy có 2 × 3 × 4 = 24 số thỏa mãn yêu cầu.
Câu 21. Cho các chữ số 1; 2; 5; 7; 8, có bao nhiêu cách lập ra một số gồm ba chữ số khác nhau từ năm chữ số trên sao cho số tạo thành là một số nhỏ hơn 278?
Đáp số: 20 số
Hướng dẫn giải
Gọi số cần tìm là .
Trường hợp 1:
a = 1 có 1 cách chọn.
b có 4 cách chọn..
c có 3 cách chọn.
Vậy có 4 × 3 × 1 = 12 số trong trường hợp này.
Trường hợp 2:
a = 2 có 1 cách chọn.
b < 7 có 2 cách chọn.
c có 3 cách chọn.
Vậy có 1 × 2 × 3 = 6 số trong trường hợp này.
Trường hợp 3:
a = 2 có 1 cách chọn.
b = 7 có 1 cách chọn.
c ∈ {1; 5} có 2 cách chọn.
Vậy có 1 × 1 × 2 = 2 số trong trường hợp này.
Vậy có tất cả 12 + 6 + 2 = 20 số thỏa mãn yêu cầu.
Câu 22. Từ các chữ số 0; 1; 2; 3; 4; 5; 6 có thể lập được bao nhiêu số lẻ có ba chữ số khác nhau nhỏ hơn 400?
Đáp số: 35 số
Hướng dẫn giải
Gọi số cần tìm là: (a ∈ 1; 2; 3).
Trường hợp 1:
– a ∈ {1; 3} có 2 cách chọn.
– c có 2 cách chọn.
– b có 5 cách chọn.
Vậy có 2 × 2 × 5 = 20 số trong trường hợp này.
Trường hợp 2:
a = 2 có 1 cách chọn.
c có 3 cách chọn.
b có 5 cách chọn.
Vậy có 3 × 5 × 1 = 15 số trong trường hợp này.
Vậy có tất cả 20 + 15 = 35 số thỏa mãn yêu cầu.
Câu 23. Có bao nhiêu số tự nhiên chẵn có năm chữ số khác nhau và nhỏ hơn 34000?
Đáp số: 3570 số
Hướng dẫn giải
Trường hợp 1: Số được lập bắt đầu bởi một trong các giá trị sau: 13; 15; 17; 19; 31.
– Có 5 cách chọn hai chữ số đầu tiên.
– Có 5 cách chọn chữ số hàng đơn vị.
– Có 7 cách chọn chữ số hàng chục.
– Có 6 cách chọn chữ số hàng trăm.
Vậy có 5 × 5 × 7 × 6 = 1050 số có 5 chữ số thoả mãn trong trường hợp này.
Trường hợp 2: Số được lập bắt đầu bởi một trong các giá trị sau: 10; 12; 14; 16; 18; 21; 23; 25; 27; 29; 30; 32.
– Có 12 cách chọn hai chữ số đầu tiên.
– Có 4 cách chọn chữ số hàng đơn vị.
– Có 7 cách chọn chữ số hàng chục.
– Có 6 cách chọn chữ số hàng trăm.
Vậy có 12 × 4 × 7 × 6 = 2016 số có 5 chữ số thỏa mãn trong trường hợp này.
Trường hợp 3: Số được lập bắt đầu bởi một trong các giá trị sau: 20; 24; 26; 28.
– Có 4 cách chọn hai chữ số đầu tiên.
– Có 3 cách chọn chữ số hàng đơn vị.
– Có 7 cách chọn chữ số hàng chục.
– Có 6 cách chọn chữ số hàng trăm.
Vậy có 4 × 3 × 7 × 6 = 504 số có 5 chữ số thỏa mãn trong trường hợp này.
Vậy có tổng cộng 1050 + 2016 + 504 = 3570 số có 5 chữ số thỏa mãn.
Câu 24. Có bao nhiêu số tự nhiên gồm năm chữ số khác nhau mà không bắt đầu bởi 12?
Đáp số: 26880 số
Hướng dẫn giải
Trước hết ta đếm số các số tự nhiên có 5 chữ số khác nhau.
– Có 9 cách chọn chữ số hàng chục nghìn.
– Có 9 cách chọn chữ số hàng nghìn.
– Có 8 cách chọn chữ số hàng trăm.
– Có 7 cách chọn chữ số hàng chục.
– Có 6 cách chọn chữ số hàng đơn vị.
Vậy có tất cả 9 × 9 × 8 × 7 × 6 = 27216 số tự nhiên có 5 chữ số khác nhau.
Tiếp theo, ta đếm số các số tự nhiên có 5 chữ số khác nhau mà bắt đầu bởi 12.
– Có 8 cách chọn chữ số hàng trăm.
– Có 7 cách chọn chữ số hàng chục.
– Có 6 cách chọn chữ số hàng đơn vị.
Vậy có tất cả 8 × 7 × 6 = 336 số tự nhiên có 5 chữ số khác nhau mà bắt đầu bởi 12.
Vậy có 27216 − 336 = 26880 số tự nhiên gồm 5 chữ số khác nhau mà không bắt đầu bởi 12.
Câu 25. Cho tập A = {0; 1; 2; 3; 4; 5; 6}. Có bao nhiêu số tự nhiên gồm năm chữ số khác nhau đôi một được lấy từ tập A và trong đó có chứa chữ số 4?
Đáp số: 1560 số
Hướng dẫn giải
Trường hợp 1: Chữ số 4 ở vị trí hàng chục nghìn.
– Có 6 cách chọn chữ số hàng nghìn.
– Có 5 cách chọn chữ số hàng trăm.
– Có 4 cách chọn chữ số hàng chục.
– Có 3 cách chọn chữ số hàng đơn vị.
Vậy có 6 × 5 × 4 × 3 = 360 số thỏa mãn trong trường hợp này.
Trường hợp 2: Chữ số 4 không nằm ở vị trí hàng chục nghìn.
– Có 4 cách chọn vị trí cho chữ số 4.
– Có 5 cách chọn chữ số hàng chục nghìn.
– Có 5 cách chọn chữ số thứ ba.
– Có 4 cách chọn chữ số thứ tư.
– Có 3 cách chọn chữ số thứ năm.
Vậy có 4 × 5 × 5 × 4 × 3 = 1200 số thỏa mãn trong trường hợp này.
Vậy có tổng cộng 360 + 1200 = 1560 số có 5 chữ số thỏa mãn.
Câu 26. Hỏi từ 10 chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9 có thể lập được bao nhiêu số gồm 6 chữ số khác nhau, sao cho trong các chữ số đó có mặt số 0 và số 1?
Đáp số: 50400 số
Hướng dẫn giải
– Có 6 cách chọn vị trí cho chữ số 0.
– Có 5 cách chọn vị trí cho chữ số 1.
– Có 8 cách chọn giá trị cho chữ số thứ ba.
– Có 7 cách chọn giá trị cho chữ số thứ tư.
– Có 6 cách chọn giá trị cho chữ số thứ năm.
– Có 5 cách chọn giá trị cho chữ số thứ sáu.
Vậy có 6 × 5 × 8 × 7 × 6 × 5 = 50400 số có 6 chữ số khác nhau thỏa mãn.
Câu 27. Từ các chữ số 0; 1; 2; 3; 6; 7; 8; 9 có thể lập được bao nhiêu số tự nhiên gồm có sáu chữ số đôi một khác nhau, trong đó phải có mặt chữ số 7?
Đáp số: 13320 số
Hướng dẫn giải
Trường hợp 1: Chữ số 7 ở vị trí hàng trăm nghìn.
– Có 7 cách chọn chữ số hàng chục nghìn.
– Có 6 cách chọn chữ số hàng nghìn.
– Có 5 cách chọn chữ số hàng trăm.
– Có 4 cách chọn chữ số hàng chục.
– Có 3 cách chọn chữ số hàng đơn vị.
Vậy có 7 × 6 × 5 × 4 × 3 = 2520 số thỏa mãn trong trường hợp này.
Trường hợp 2: Chữ số 7 không nằm ở vị trí hàng trăm nghìn.
– Có 5 cách chọn vị trí cho chữ số 7.
– Có 6 cách chọn chữ số hàng trăm nghìn.
– Có 6 cách chọn chữ số thứ ba.
– Có 5 cách chọn chữ số thứ tư.
– Có 4 cách chọn chữ số thứ năm.
– Có 3 cách chọn chữ số thứ sáu.
Vậy có 5 × 6 × 6 × 5 × 4 × 3 = 10800 số thỏa mãn trong trường hợp này.
Vậy có tổng cộng 2520 + 10800 = 13320 số có 6 chữ số thỏa mãn.
Câu 28. Cho tập hợp A = {0; 1; 2; 3; 4; 5}, từ A có thể lập được bao nhiêu số tự nhiên gồm năm chữ số khác nhau, trong đó nhất thiết phải có chữ số 0 và 3?
Đáp số: 480 số
Hướng dẫn giải
– Có 5 cách chọn vị trí cho chữ số 0.
– Có 4 cách chọn vị trí cho chữ số 3.
– Có 4 cách chọn giá trị% cho chữ số thứ ba.
– Có 3 cách chọn giá trị cho chữ số thứ tư.
– Có 2 cách chọn giá trị cho chữ số thứ năm.
Vậy có 5 × 4 × 4 × 3 × 2 = 480 số có 5 chữ số khác nhau thoả mãn.
Câu 29. Cho tập hợp A = {0; 1; 2; 3; 4; 5}, từ các chữ số thuộc tập A lập được bao nhiêu số tự nhiên có năm chữ số và số đó chia hết cho 3?
Đáp số: 216 số
Hướng dẫn giải
Vì số được lập chia hết cho 3 nên các chữ số của số đó là 1; 2; 3; 4; 5 hoặc 0; 1; 2; 4; 5.
Trường hợp 1: Các chữ số của số được lập là 1; 2; 3; 4; 5.
– Có 5 cách chọn chữ số hàng chục nghìn.
– Có 4 cách chọn chữ số hàng nghìn.
– Có 3 cách chọn chữ số hàng trăm.
– Có 2 cách chọn chữ số hàng chục.
– Có 1 cách chọn chữ số hàng đơn vị.
Vậy có 5 × 4 × 3 × 2 × 1 = 120 số thoả mãn trong trường hợp này.
Trường hợp 2: Các chữ số của số được lập là 0; 1; 2; 4; 5.
– Có 4 cách chọn chữ số hàng chục nghìn.
– Có 4 cách chọn chữ số hàng nghìn.
– Có 3 cách chọn chữ số hàng trăm.
– Có 2 cách chọn chữ số hàng chục.
– Có 1 cách chọn chữ số hàng đơn vị.
Vậy có 4 × 4 × 3 × 2 × 1 = 96 số thỏa mãn trong trường hợp này.
Vậy có tổng cộng 120 + 96 = 216 số có 5 chữ số thỏa mãn.
Câu 30. Từ các chữ số 0; 1; 2; . . . ; 9 có thể lập được bao nhiêu số tự nhiên chẵn gồm năm chữ số khác nhau đôi một và chữ số chính giữa luôn là số 2?
Đáp số: 1218 số
Hướng dẫn giải
Trường hợp 1: Chữ số hàng đơn vị là 0.
– Có 1 cách chọn chữ số hàng đơn vị.
– Có 1 cách chọn chữ số hàng trăm.
– Có 8 cách chọn chữ số hàng chục nghìn.
– Có 7 cách chọn chữ số hàng nghìn.
– Có 6 cách chọn chữ số hàng chục.
Vậy có 1 × 1 × 8 × 7 × 6 = 336 số thỏa mãn trong trường hợp này.
Trường hợp 2: Chữ số hàng đơn vị khác 0.
– Có 3 cách chọn chữ số hàng đơn vị.
– Có 1 cách chọn chữ số hàng trăm.
– Có 7 cách chọn chữ số hàng chục nghìn.
– Có 7 cách chọn chữ số hàng nghìn.
– Có 6 cách chọn chữ số hàng chục.
Vậy có 3 × 1 × 7 × 7 × 6 = 882 số thoả mãn trong trường hợp này.
Vậy có tổng cộng 336 + 882 = 1218 số có 5 chữ số thỏa mãn.
Câu 31. Trong một trường THPT A, khối 11 mỗi học sinh tham gia một trong hai câu lạc bộ Toán và Tin học. Có 160 em tham gia câu lạc bộ Toán, 140 em tham gia câu lạc bộ Tin học, 50 em tham gia cả hai câu lạc bộ. Hỏi khối 11 có bao nhiêu học sinh?
Đáp số: 250 học sinh
Hướng dẫn giải
Số học sinh khối 11 là 160 + 140 − 50 = 250 học sinh.
Câu 32. Một lớp có 40 học sinh, đăng ký chơi ít nhất một trong hai môn thể thao là bóng đá và cầu lông. Có 30 em đăng ký môn bóng đá, 25 em đăng ký môn cầu lông. Hỏi có bao nhiêu em đăng ký cả hai môn thể thao?
Đáp số: 15 học sinh
Hướng dẫn giải
Số em học sinh đăng ký cả hai môn thể thao là 30 + 25 − 40 = 15 học sinh.
Câu 33. Có 5 học sinh, trong đó có An và Bình. Hỏi có bao nhiêu cách sắp xếp 5 học sinh này lên một đoàn tàu gồm 8 toa, biết rằng:
a) 5 học sinh lên cùng một toa.
Đáp số: 8 cách
b) 5 học sinh lên 5 toa đầu và mỗi toa một người.
Đáp số: 120 cách
c) 5 học sinh lên 5 toa khác nhau.
Đáp số: 6720 cách
d) An và Bình lên cùng toa đầu tiên.
Đáp số: 512 cách
e) An và Bình lên cùng một toa, ngoài ra không có học sinh nào khác lên toa này.
Đáp số: 2744 cách
Hướng dẫn giải
a) 5 học sinh lên cùng một toa.
Có 8 cách chọn toa tàu để cả 5 học sinh cùng lên toa tàu đó. Vậy có 8 cách sắp xếp để 5 học sinh lên cùng một toa.
b) 5 học sinh lên 5 toa đầu và mỗi toa một người.
– Có 5 cách chọn học sinh lên toa đầu tiên.
– Có 4 cách chọn học sinh lên toa thứ hai.
– Có 3 cách chọn học sinh lên toa thứ ba.
– Có 2 cách chọn học sinh lên toa thứ tư.
– Có 1 cách chọn học sinh lên toa thứ năm.
Vậy có 5 × 4 × 3 × 2 × 1 = 120 cách sắp xếp để 5 học sinh lên 5 toa đầu và mỗi toa một người.
c) 5 học sinh lên 5 toa khác nhau.
– Có 8 cách chọn toa tàu cho học sinh đầu tiên.
– Có 7 cách chọn toa tàu cho học sinh thứ hai.
– Có 6 cách chọn toa tàu cho học sinh thứ ba.
– Có 5 cách chọn toa tàu cho học sinh thứ tư.
– Có 4 cách chọn toa tàu cho học sinh thứ năm.
Vậy có 8 × 7 × 6 × 5 × 4 = 6720 cách sắp xếp để 5 học sinh lên 5 toa khác nhau.
d) An và Bình lên cùng toa đầu tiên.
– Có 1 cách chọn toa tàu cho An và Bình.
– Có 8 cách chọn toa tàu cho học sinh thứ ba.
– Có 8 cách chọn toa tàu cho học sinh thứ tư.
– Có 8 cách chọn toa tàu cho học sinh thứ năm.
Vậy có 1 × 8 × 8 × 8 = 512 cách sắp xếp để An và Bình lên cùng toa đầu tiên.
e) An và Bình lên cùng một toa, ngoài ra không có học sinh nào khác lên toa này.
– Có 8 cách chọn toa tàu cho An và Bình.
– Có 7 cách chọn toa tàu cho học sinh thứ ba.
– Có 7 cách chọn toa tàu cho học sinh thứ tư.
– Có 7 cách chọn toa tàu cho học sinh thứ năm.
Vậy có 8 × 7 × 7 × 7 = 2744 cách sắp xếp để An và Bình lên cùng một toa, ngoài ra không có học sinh nào khác lên toa này.
Câu 34. Có bao nhiêu số tự nhiên có đúng năm chữ số, sao cho trong mỗi số đó chữ số đứng sau lớn hơn chữ số đứng liền trước? ĐS: 126 số
Hướng dẫn giải
Vì chữ số đứng sau lớn hơn chữ số đứng liền trước nên các chữ số phải khác 0. Trước tiên ta sẽ đếm số các số có 5 chữ số đôi một khác nhau và khác 0.
– Có 9 cách chọn chữ số hàng chục nghìn.
– Có 8 cách chọn chữ số hàng nghìn.
– Có 7 cách chọn chữ số hàng trăm.
– Có 6 cách chọn chữ số hàng chục.
– Có 5 cách chọn chữ số hàng đơn vị.
Vậy có 9 × 8 × 7 × 6 × 5 = 15120 có 5 chữ số đôi một khác nhau và khác 0.
Nhận thấy, với một bộ 5 chữ số nào đó thì sẽ có 5 × 4 × 3 × 2 × 1 = 120 cách sắp xếp vị trí cho các chữ số đó, tuy nhiên chỉ có 1 cách xếp các chữ số thỏa mãn.
Vậy số các số thỏa mãn bài toán là số.
Câu 35. Có 20 thẻ đựng trong hai hộp khác nhau, mỗi hộp chứa 10 thẻ được đánh số liên tiếp từ 1 đến 10. Có bao nhiêu cách chọn hai thẻ (mỗi hộp một thẻ) sao cho tích hai số ghi trên hai thẻ là một số chẵn.
Đáp số: 75 cách
Hướng dẫn giải
Có 10 cách chọn tấm thẻ ở hộp thứ nhất và có 10 cách chọn tấm thẻ ở hộp thứ hai
Nên có 10 × 10 = 100 cách chọn hai thẻ, mỗi hộp một thẻ.
Có 5 cách chọn tấm thẻ ở hộp thứ nhất và có 5 cách chọn tấm thẻ ở hộp thứ hai
Nên có 5 × 5 = 25 cách chọn hai thẻ, mỗi hộp một thẻ và tích hai số ghi trên hai thẻ là một số lẻ.
Vậy có 100 − 25 = 75 cách chọn hai thẻ, mỗi hộp một thẻ và tích hai số ghi trên hai thẻ là một số chẵn.
Câu 36. Gọi S là tập hợp tất cả các số tự nhiên gồm hai chữ số phân biệt khác nhau được lấy từ tập A = {0; 1; 2; 3; 4; 5; 6}. Hỏi S có bao nhiêu phần tử? Có bao nhiêu cách lấy hai phần tử từ tập S sao cho tích của hai phần tử này là một số chẵn?
Đáp số: 1050 cách
Hướng dẫn giải
– Có 6 cách chọn chữ số hàng chục.
– Có 6 cách chọn chữ số hàng đơn vị.
Vậy tập S có 6 × 6 = 36 phần tử
Ta sẽ đếm xem trong tập S có bao nhiêu số lẻ.
– Có 3 cách chọn chữ số hàng đơn vị.
– Có 5 cách chọn chữ số hàng chục.
Vậy trong tập S có 3 × 5 = 15 số lẻ.
Có 36 × 35 = 1260 cách chọn ra hai số từ tập S và có 15 × 14 = 210 cách chọn ra hai số từ tập S có tích là số lẻ
Nên có 1260 − 210 = 1050 cách chọn ra hai số từ tập S có tích là số chẵn.
Câu 37. Có bao nhiêu số tự nhiên gồm tám chữ số phân biệt sao cho tổng của tám chữ số này chia hết cho 9.
Đáp số: 181440 số
Hướng dẫn giải
Vì số được lập chia hết cho 9 nên tổng hai chữ số không xuất hiện trong số được lập phải bằng 9.
Trường hợp 1: Hai chữ số 0 và 9 không xuất hiện trong số được lập.
– Có 8 cách chọn chữ số hàng chục triệu.
– Có 7 cách chọn chữ số hàng triệu.
– Có 6 cách chọn chữ số hàng trăm nghìn.
– Có 5 cách chọn chữ số hàng chục nghìn.
– Có 4 cách chọn chữ số hàng nghìn.
– Có 3 cách chọn chữ số hàng trăm.
– Có 2 cách chọn chữ số hàng chục.
– Có 1 cách chọn chữ số hàng đơn vị.
Vậy có 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 40320 số có 8 chữ số thỏa mãn trong trường hợp này.
Trường hợp 2: Hai chữ số không xuất hiện trong số được lập là (1; 8) hoặc (2; 7) hoặc (3; 6) hoặc (4; 5).
– Có 4 cách chọn hai chữ số không xuất hiện.
– Có 7 cách chọn chữ số hàng chục triệu.
– Có 7 cách chọn chữ số hàng triệu.
– Có 6 cách chọn chữ số hàng trăm nghìn.
– Có 5 cách chọn chữ số hàng chục nghìn.
– Có 4 cách chọn chữ số hàng nghìn.
– Có 3 cách chọn chữ số hàng trăm.
– Có 2 cách chọn chữ số hàng chục.
– Có 1 cách chọn chữ số hàng đơn vị.
Vậy có 4 × 7 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 141120 số có 8 chữ số thỏa mãn trong trường hợp này.
Vậy có tổng cộng 40320 + 141120 = 181440 số có 8 chữ số thỏa mãn.
Tài liệu về quy tắc đếm
Thông tin tài liệu
| Thông tin | |
| Tên tài liệu | 252 Bài Tập Quy Tắc Đếm Ôn Thi THPT QG |
| Tác giả | Tiêu Phước Thừa |
| Số trang | 62 |
Mục lục
– Dạng 1: Quy tắc cộng
– Dạng 2: Quy tắc nhân
– Dạng 3: Bài toán kết hợp quy tắc cộng và quy tắc nhân
Xem tài liệu
[content_5]

























































Nguồn tham khảo
Website chỉ sử dụng các nguồn tài liệu toán học uy tín.
Câu hỏi thường gặp
Quy tắc đếm là gì?
Đếm trong toán học hay ngoài thực tế đều là tìm số phần tử của một tập hợp hữu hạn các đối tượng. Ngoài việc đếm truyền thống thì việc áp dụng các quy tắc đếm sẽ giúp quy trình đếm trở nên nhanh chóng và chính xác hơn, áp dụng được nhiều tình huống phức tạp của một bài toán.
Quy tắc cộng là gì?
Trong toán tổ hợp, quy tắc cộng (hay còn gọi là quy tắc tổng) là một nguyên tắc đếm cơ bản. Nói một cách đơn giản, đó là ý tưởng trực quan rằng nếu chúng ta có A cách để làm một việc gì đó và B cách để làm một việc khác và chúng ta không thể làm cả hai cùng một lúc, thì có A + B cách để chọn một trong số các hành động.
Quy tắc nhân là gì?
Quy tắc nhân nói rằng nếu có A cách làm điều gì đó, và B cách làm khác đi. Tổng quan lại sẽ có A*B cách thực hiện cả hai hành động này. Nói cách khác, khi chọn một tùy chọn cho A và một tùy chọn cho B, sẽ có A*B các cách khác nhau để thực hiện cả hai hành động.