Bài viết này VerbaLearn trình bày đến bạn đọc các điểm lý thuyết về góc lượng giác, bảng dấu giá trị lượng giác, mối liên hệ của 2 góc bù nhau – phụ nhau, hệ thức lượng giác cơ bản và giá trị lượng giác của các góc đặc biệt từ 0° đến 180° theo chương trình toán lớp 10. Từ đó vận dụng vào việc giải một số dạng toán như tính giá trị biểu thức, chứng minh đẳng thức lượng giác hoặc các bài toán rút gọn.

Lý thuyết góc lượng giác
[content_1]Định nghĩa
Trong mặt phẳng tọa độ Oxy.Với góc α (0° ≤ α ≤ 180°), ta xác định được duy nhất điểm M trên trên đường nửa đường tròn đơn vị tâm O, sao cho , biết M(x; y).
Khi đó:
Các số sin α, cos α, tan α, cot β được gọi là giá trị lượng giác của góc α.

Chú ý: Với 0° ≤ α ≤ 180° ta có 0 ≤ sin ≤ 1; –1 ≤ cos ≤ 1.
Bảng dấu của giá trị lượng giác
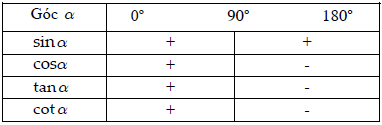
Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau
sin (180° – α) = sin α
cos (180° – α) = –cos α
tan (180° – α) = –tan α
cot (180° – α) = –cot α
Mối quan hệ giữa các giá trị lượng giác của hai góc phụ nhau
sin (90° – α) = cos α
cos (90° – α) = sin α
tan (90° – α) = cot α
cot (90° – α) = tan α
Giá trị lượng giác của các góc đặc biệt
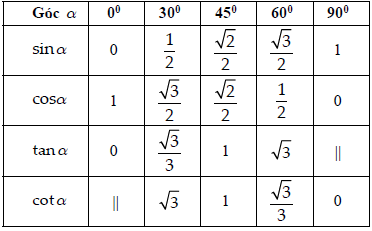
Các hệ thức lượng giác cơ bản
Phân dạng bài tập
[content_2]Dạng 1. Tính các giá trị biểu thức lượng giác
Phương pháp giải
– Sử dụng định nghĩa giá trị lượng giác của một góc
– Sử dụng tính chất và bảng giá trị lượng giác đặc biệt
– Sử dụng các hệ thức lượng giác cơ bản
Bài tập vận dụng
Câu 1. Tính giá trị các biểu thức sau:
a) A = a2 sin 90° + b2 cos 90° + c2 cos 180°
b) B = 3 – sin2 90° + 2cos2 60° – 3tan2 45°
c) C = sin2 45° – 2sin2 50° + 3cos2 45° – 2sin2 40° + 4tan 55°⋅tan 35°
Hướng dẫn giải
a) A = a2 sin 90° + b2 cos 90° + c2 cos 180°
= a2⋅1 + b2⋅0 + c2⋅(–1) = a2 – c2
b) B = 3 – sin2 90° + 2cos2 60° – 3tan2 45°
=
= 1
c) C = sin2 45° – 2sin2 50° + 3cos2 45° – 2sin2 40° + 4tan 55°⋅tan 35°
=
=
= 4
Câu 2. Tính giá trị các biểu thức sau:
a) A = sin2 3° + sin2 15° + sin2 75° + sin2 87°
b) B = cos 0° + cos 20° + cos 40° + … + cos 160° + cos 180°
c) C = tan 5°⋅tan 10°⋅tan 15°… tan 80°⋅tan 85°
Hướng dẫn giải
a) A = (sin2 3° + sin2 87°) + (sin2 15° + sin2 75°)
= (sin2 3° + cos2 3°) + (sin2 15° + cos2 15°)
= 1 + 1 = 2
b) B = (cos 0° + cos 180°) + (cos 20° + cos 160°) + … + (cos 80° + cos 100°)
= (cos 0° – cos 0°) + (cos 20° – cos 20°) + … + (cos 80° – cos 80°)
= 0
c) C = (tan 5°⋅tan 85°)(tan 15°⋅tan 75°) … (tan 45°⋅tan 45°)
= (tan 5°⋅cot 5°)(tan 15°⋅cot 5°) … (tan 45°⋅cot 5°)
= 1
Câu 3. Giá trị của cos 60° + sin 30° bằng bao nhiêu?
A.
B.
C.
D. 1
Hướng dẫn giải
Ta có:
⟹ Chọn D
Câu 4. Giá trị của tan 30° + cot 30° bằng bao nhiêu?
A.
B.
C.
D. 2
Hướng dẫn giải
⟹ Chọn A
Câu 5. Trong các đẳng thức sau đây, đẳng thức nào sai?
A. sin 0° + cos 0° = 1
B. sin 90° + cos 90° = 1
C. sin 180° + cos 180° = –1
D. sin 60° + cos 60° = 1
Hướng dẫn giải
Giá trị lượng giác của góc đặc biệt.
⟹ Chọn D
Câu 6. Trong các khẳng định sau, khẳng định nào sai?
A. cos 60° = sin 30°
B. cos 60° = sin 120°
C. cos 30° = sin 120°
D. sin 60° = –cos 120°
Hướng dẫn giải
Giá trị lượng giác của góc đặc biệt.
⟹ Chọn B
Câu 7. Đẳng thức nào sau đây sai?
A. sin 45° + cos 45° =
B. sin 60° + cos 150° = 0
C. sin 30° + cos 60° = 1
D. sin 120° + cos 30° = 0
Hướng dẫn giải
Giá trị lượng giác của góc đặc biệt.
⟹ Chọn D
Câu 8. Giá trị sin 45° + cos 45° bằng bao nhiêu?
A. 1
B.
C.
D. 0
Hướng dẫn giải
Ta có: sin 45° + cos 45° =
⟹ Chọn B
Câu 9. Trong các đẳng thức sau, đẳng thức nào đúng?
A. sin (180° – α) = –cos α
B. sin (180° – α) = –sin α
C. sin (180° – α) = sin α
D. sin (180° – α) = cos α
Hướng dẫn giải
⟹ Chọn C
Câu 10. Trong các đẳng thức sau, đẳng thức nào sai?
A. sin 0° + cos 0° = 0
B. sin 90° + cos 90° = 1
C. sin 180° + cos 180° = –1
D. sin 60° + cos 60° =
Hướng dẫn giải
Ta có: sin 0° + cos 0° = 1
⟹ Chọn A
Câu 11. Cho α là góc tù. Điều khẳng định nào sau đây là đúng?
A. sin α < 0
B. cos α > 0
C. tan α < 0
D. cot α > 0
Hướng dẫn giải
Góc tù có điểm biểu diễn thuộc góc phần tư thứ II, có giá trị sin α > 0, còn cos α, tan α và cot α đều nhỏ hơn 0.
⟹ Chọn C
Câu 12. Giá trị của E = sin 36°cos 6°sin 126°cos 84° là
A.
B.
C. 1
D. –1
Hướng dẫn giải
E = sin 36°cos 6°sin (90° + 36°)cos (90° – 6°)
= sin 36°cos 6° – cos 36°sin 6°
= sin 30° =
⟹ Chọn A
Câu 13. Giá trị của biểu thức A = sin2 51° + sin2 55° + sin2 39° + sin2 35° là
A. 3
B. 4
C. 1
D. 2
Hướng dẫn giải
A = (sin2 51° + sin2 39°) + (sin2 55° + sin2 35°)
= (sin2 51° + cos2 51°) + (sin2 55° + cos2 55°)
= 2
⟹ Chọn D
Câu 14. Giá trị của biểu thức A = tan 1°tan 2°tan 3°… tan 88°tan 89° là
A. 0
B. 2
C. 3
D. 1
Hướng dẫn giải
A = (tan 1°tan 89°)(tan 2°tan 88°) … (tan 44°tan 46°)tan 45° = 1
⟹ Chọn D
Câu 15. Tổng sin2 2° + sin2 4° + sin2 6° + … + sin2 84° + sin2 86° + sin2 88° bằng
A. 21
B. 23
C. 22
D. 24
Hướng dẫn giải
A = sin2 2° + sin2 4° + sin2 6° + … + sin2 84° + sin2 86° + sin2 88°
= (sin2 2° + sin2 88°) + (sin2 4° + sin2 86°) +… + (sin2 44° + sin2 46°)
= (sin2 2° + cos2 2°) + (sin2 4° + cos2 4°) + … + (sin2 44° + cos2 44°)
= 22
⟹ Chọn C
Câu 16. Giá trị của A = tan 5°tan10°tan15°… tan 80°tan 85° là
A. 2
B. 1
C. 0
D. –1
Hướng dẫn giải
A = (tan 5°tan 85°)(tan 10°tan 80°) … (tan 40°tan 50°)tan 45° = 1
⟹ Chọn B
Câu 17. Giá trị của B = cos2 73° + cos2 87° + cos2 3° + cos2 17° là
A.
B. 2
C. –2
D. 1
Hướng dẫn giải
B = (cos2 73° + cos2 17°) + (cos2 87° + cos2 3°)
= (cos2 73° + sin2 73°) + (cos2 87° + sin2 87°)
= 2
⟹ Chọn B
Dạng 2. Tính giá trị của một biểu thức lượng giác, khi biết trước một giá trị lượng giác
[content_3]Phương pháp giải
– Dựa vào các hệ thức lượng giác cơ bản
– Dựa vào dấu của giá trị lượng giác
– Sử dụng các hằng đẳng thức đáng nhớ
Bài tập vận dụng
Câu 1. Cho với 90° < α < 180°. Tính cos α và tan α
Hướng dẫn giải
Vì 90° < α < 180° nên cos α < 0
Mặt khác: sin2 α + cos2 α = 1 suy ra
Do đó:
Câu 2. Cho và sin α > 0. Tính sin α và cot α
Hướng dẫn giải
Vì sin2 α + cos2 α = 1 và sin α > 0, nên
Câu 3. Cho . Tính giá trị lượng giác còn lại.
Hướng dẫn giải
Vì
Mặt khác:
Nên
Ta có:
Câu 4. Cho với 0° < α < 90°. Tính
.
Hướng dẫn giải
Ta có:
Suy ra:
Câu 5. Cho . Tính
.
Hướng dẫn giải
Suy ra:
Câu 6. Biết sin x + cos x = m.
a) Tìm |sin4 x – cos4 x|
b) Chứng minh rằng |m| ≤
Hướng dẫn giải
a) Ta có: (sin x + cos x)2
= sin2 x + 2sin x⋅cos x + cos2 x
= 1 + 2sin x⋅cos x (*)
Mặt khác: sin x + cos x = m nên m2 = 1 + 2sin α⋅cos α hay
Đặt A = |sin4 x – cos4 x|. Ta có:
Vậy:
b) Ta có: 2sin x⋅cos x ≤ sin2 x + cos2 x = 1
Kết hợp với (*) suy ra (sin x + cos x)2 ≤ 2
⇒ |sin x + cos x| ≤
Câu 7. Cho cos x = . Tính biểu thức P = 3sin2 x + 4cos2 x.
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn A
Câu 8. Biết cos α = . Giá trị đúng của biểu thức P = sin2 α + 3cos2 α là:
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn C
Câu 9. Cho biết tan α = . Tính cot α.
A. cot α = 2
B. cot α =
C. cot α =
D. cot α =
Hướng dẫn giải
⟹ Chọn A
Câu 10. Cho biết cos α = và
. Tính tan α.
A.
B.
C.
D.
Hướng dẫn giải
Do ⇒ tan α < 0. Ta có:
⟹ Chọn D
Câu 11. Cho α là góc tù và sin α = . Giá trị của biểu thức 3sin α + 2cos α là?
A. 3
B.
C. –3
D.
Hướng dẫn giải
Ta có:
Do α là góc tù nên cos α < 0, từ đó cos α =
Như vậy:
⟹ Chọn B
Câu 12. Cho biết sin α + cos α = a. Giá trị của sin α⋅cos α bằng bao nhiêu?
A. sin α⋅cos α = a
B. sin α⋅cos α = 2a
C. sin α⋅cos α =
D. sin α⋅cos α =
Hướng dẫn giải
⟹ Chọn D
Câu 13. Cho biết cos α = . Tính giá trị của biểu thức
?
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn B
Câu 14. Cho biết cot α = 5. Tính giá trị của E = 2cos2 α + 5sin α⋅cos α + 1?
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn D
Câu 15. Cho cos α = . Giá trị của biểu thức
là?
A.
B. –13
C.
D. 13
Hướng dẫn giải
⟹ Chọn D
Câu 16. Cho biết cos α = . Giá trị của biểu thức
bằng bao nhiêu?
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn C
Câu 17. Biết sin a + cos a = . Hỏi giá trị của sin4 a + cos4 a bằng bao nhiêu?
A.
B.
C. –1
D. 0
Hướng dẫn giải
Ta có: sin a + cos a =
⇒ (sin a + cos a)2 = 2
⇒ sin a⋅cos a =
⟹ Chọn B
Câu 18. Cho tan α + cot α = m. Tìm m để tan2 α + cot2 α = 7.
A. m = 9
B. m = 3
C. m = −3
D. m = ±3
Hướng dẫn giải
7 = tan2 α + cot2 α = (tan α + cot α)2 – 2
⇒ m2 = 9 ⇔ m = ±3
⟹ Chọn D
Câu 19. Cho biết 3cos α – sin α = 1, 0° < α < 90°. Giá trị của tan α bằng?
A. tan α =
B. tan α =
C. tan α =
D. tan α =
Hướng dẫn giải
Ta có:
– sin α = –1: không thỏa mãn vì 0° < α < 90°
–
⟹ Chọn A
Câu 20. Cho , 0° < α < 90°. Tính giá trị của cot α.
A. cot α =
B. cot α =
C. cot α =
D. cot α =
Hướng dẫn giải
Ta có:
– cos α = 1: không thỏa mãn vì 0° < α < 90°
–
⟹ Chọn C
Câu 21. Cho biết cos α + sin α = . Giá trị của
bằng bao nhiêu?
A.
B.
C.
D.
Hướng dẫn giải
Ta có:
Ta có:
⟹ Chọn B
Câu 22. Cho biết cos α – sin α = . Giá trị của
bằng bao nhiêu?
A.
B.
C.
D.
Hướng dẫn giải
Ta có:
⟹ Chọn B
Dạng 3. Chứng minh các đẳng thức, rút gọn các biểu thức lượng giác
[content_4]Phương pháp giải
– Sử dụng các hệ thức lượng giác cơ bản
– Sử dụng tính chất của giá trị lượng giác
– Sử dụng các hằng đẳng thức đáng nhớ.
Bài tập vận dụng
Câu 1. Chứng minh các đẳng thức sau (giả sử các biểu thức sau đều có nghĩa)
a) sin4 x + cos4 x = 1 – 2sin2 x⋅cos2 x
b)
c)
Hướng dẫn giải
a) sin4 x + cos4 x
= sin4 x + cos4 x + 2sin2 x⋅cos2 x – 2sin2 x⋅cos2 x
= (sin2 x + cos2 x)2 – 2sin2 x⋅cos2 x
= 1 – 2sin2 x⋅cos2 x
b)
c)
Câu 2. Cho tam giác ABC. Chứng minh:
Hướng dẫn giải
Vì A + B + C = 180° nên
Suy ra điều phải chứng minh.
Câu 3. Đơn giản các biểu thức sau (giả sử các biểu thức sau đều có nghĩa)
a) A = sin(90° – x) + cos(180° – x) + sin2 x(1 + tan2 x) – tan2 x
b)
Hướng dẫn giải
a)
b)
Câu 4. Chứng minh biểu thức sau không phụ thuộc vào x.
Hướng dẫn giải
Vậy P không phụ thuộc vào x.
Câu 5. Trong các hệ thức sau hệ thức nào đúng?
A. sin2 α + cos α2 = 1
B. sin2 α + cos2 2α = 1
C. sin α2 + cos α2 = 1
D. sin2 2α + cos2 2α = 1
Hướng dẫn giải
Công thức lượng giác cơ bản.
⟹ Chọn D
Câu 6. Trong các hệ thức sau hệ thức nào đúng? α
A. sin2 α + cos α2 = 1
B. sin2 α + cos2 2α = 1
C. sin α2 + cos α2 = 1
D. sin2 α + cos2 α = 1
Hướng dẫn giải
Công thức lượng giác cơ bản.
⟹ Chọn D
Câu 7. Trong các hệ thức sau hệ thức nào đúng?
A. sin α + cos 2α = 1
B. sin α2 + cos α2 = 1
C. sin2 α + cos α2 = 1
D. sin2 α + cos2 α = 1
Hướng dẫn giải
Công thức lượng giác cơ bản.
⟹ Chọn D
Câu 8. Rút gọn biểu thức sau:
P = (tan x + cot x)2 – (tan x – cot x)2
A. P = 4
B. P = 1
C. P = 2
D. P = 3
Hướng dẫn giải
P = (tan2 x + 2tan x⋅cot x + cot2 x) – (tan2 x – 2tan x⋅cot x + cot2 x) = 4
⟹ Chọn A
Câu 9. Đơn giản biểu thức
G = (1 – sin2 x)cot2 x + 1 – cot2 x
A. sin2 x
B. cos2 x
C. sin x
D. cos x
Hướng dẫn giải
G = [(1 – sin2 x) – 1]cot2 x + 1
= – sin2 x⋅cot2 x + 1
= 1 – cos2 x = sin2 x
⟹ Chọn A
Câu 10. Khẳng định nào sau đây là sai?
A. sin2 α + cos2 α = 1
B.
C. tan α⋅cot α = –1 (sin α⋅cos α ≠ 0)
D.
Hướng dẫn giải
⟹ Chọn C
Câu 11. Rút gọn biểu thức
A. P = tan x
B. P = cot x
C. P = 2cot x
D. P = 2tan x
Hướng dẫn giải
⟹ Chọn B
Câu 12. Đẳng thức nào sau đây là sai?
A. (cos x + sin x)2 + (cos x – sin x)2 = 2,∀x
B. tan2 x – sin2 x = tan2 x⋅sin2 x, ∀x ≠ 90°
C. sin4 x + cos4 x = 1 – 2sin2 x⋅cos2 x, ∀x
D. sin6 x – cos6 x = 1 – 3sin2 x⋅cos2 x, ∀x
Hướng dẫn giải
sin6 x – cos6 x = (sin2 x – cos2 x)(1 – sin2 x⋅cos2 x)
⟹ Chọn D
Câu 13. Đẳng thức nào sau đây là sai?
A. (x ≠ 0°; 180°)
B. (x ≠ 0°; 90°; 180°)
C. (x ≠ 0°; 90°; 180°)
D. sin2 2x + cos2 2x = 2
Hướng dẫn giải
sin2 2x + cos2 2x = 1
⟹ Chọn D
Câu 13. Biểu thức tan2 x⋅sin2 x – tan2 x + sin2 x có giá trị bằng
A. –1
B. 0
C. 2
D. 1
Hướng dẫn giải
⟹ Chọn B
Câu 14. Biểu thức (cot a + tan a)2 bằng
A.
B. cot2 a + tan2 a – 2
C.
D. cot2 a⋅tan2 a + 2
Hướng dẫn giải
⟹ Chọn C
Câu 15. Đơn giản biểu thức
A. sin x
B.
C.
D. cos x
Hướng dẫn giải
⟹ Chọn C
Câu 16. Rút gọn biểu thức sau
A. A = 1
B. A = 2
C. A = 3
D. A = 4
Hướng dẫn giải
⟹ Chọn A
Câu 17. Biểu thức f(x) = 3(sin4 x + cos4 x) – 2(sin6 x + cos6 x) có giá trị bằng:
A. 1
B. 2
C. –3
D. 0
Hướng dẫn giải
sin4 x + cos4 x = 1 – 2sin2 x⋅cos2 x
sin6 x + cos6 x = 1 – 3sin2 x⋅cos2 x
f(x) = 3(1 – 2sin2 x⋅cos2 x) – 2(1 – 3sin2 x⋅cos2 x) = 1
⟹ Chọn A
Câu 18. Biểu thức: f(x) = cos4 x + cos2 x⋅sin2 x + sin2 x có giá trị bằng
A. 1
B. 2
C. –2
D. –1
Hướng dẫn giải
f(x) = cos2 x(cos2 x + sin2 x) + sin2 x
= cos2 x + sin2 x = 1
⟹ Chọn A
Câu 19. Trong các mệnh đề sau, mệnh đề nào sai?
A. (sin x⋅cos x)2 = sin2 x⋅cos2 x
B. sin4 x + cos4 x = 1 – 2sin2 x⋅cos2 x
C. (sin x + cos x)2 = 1 + 2sin x⋅cos x
D. sin6 x + cos6 x = 1 + sin2 x⋅cos2 x
Hướng dẫn giải
Ta có: sin6 x + cos6 x
= (sin2 x)3 + (cos2 x)3
= (sin2 x + cos2 x)3 – 3(sin2 x + cos2 x)sin2 x⋅cos2 x
= 1 – 3sin2 x⋅cos2 x
⟹ Chọn D