Bội chung và bội chung nhỏ nhất
+) Số tự nhiên n được gọi là bội chung của hai số a và b nếu n vừa là bội của a vừa là bội của b.
+) Số nhỏ nhất khác 0 trong các bội chung của a và b được gọi là bội chung nhỏ nhất của a và b.
+) Ta kí hiệu: tập hợp các bội chung của a và b là: BC(a; b)
tập hợp các bội chung nhỏ nhất của a và b kí hiệu: BCNN(a; b)
Ví dụ: BC(4; 5) = {0; 20; 40; 60;…}, BCNN(4; 5) = {20}.
Chú ý: Bội chung của nhiều số là bội của bội chung nhỏ nhất của chúng.
Nếu các số đã cho từng đôi một nguyên tố cùng nhau thì BCNN của chúng là tích của các số đó.
Cách tìm BCNN
Bước 1: Phân tích các số ra thừa số nguyên tố
Bước 2: Chọn ra các thừa số chung và riêng
Bước 3: Lập tích các thừa số đã chọn. mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.
+) Nhận xét:
BCNN(a) = {a,1}
BCNN(a; b; 1) = BCNN(a; b)
Phân dạng bài tập
Dạng 1. Tìm bội chung nhỏ nhất của các số cho trước
Phương pháp giải.
Bước 1. Phân tích mỗi số ra thừa số nguyên tố
Bước 2. Chọn ra các thừa số nguyên tố chung và các thừa số nguyên tố riêng
Bước 3. Với mỗi thừa số nguyên tố chung và riêng, ta chọn lũy thừa với số mũ lớn nhất
Bước 4. Lấy tích của các lũy thừa đã chọn, ta nhận được BCNN cần tìm
Bài toán.
Bài 1. Tìm:
a) BCNN(15; 18)
b) BCNN(84; 108)
c) BCNN(33; 44; 55)
d) BCNN(8; 18; 30)
Hướng dẫn giải
a) Ta có: 15 = 3⋅5; 18 = 2⋅32
BCNN(15; 18) = 2⋅32⋅5 = 90
b) Ta có: 84 = 22⋅3⋅7; 108 = 22⋅33
BCNN(84; 108) = 22⋅33⋅7 = 756
c) Ta có: 33 = 3⋅11; 44 = 4⋅11; 55 = 5⋅11
BCNN(33; 44; 55) = 3⋅4⋅5⋅11 = 660
d) Ta có: 8 = 23; 18 = 2⋅32; 30 = 2⋅3⋅5
BCNN(8; 18; 30) = 23⋅32⋅5 = 240
Bài 2. Tìm:
a) BCNN(10; 12)
b) BCNN(24; 10)
c) BCNN(4; 14; 26)
d) BCNN(6; 8; 10)
Hướng dẫn giải
a) Ta có: 10 = 2⋅5; 12 = 22⋅3
BCNN(10; 12) = 22⋅3⋅5 = 60
b) Ta có: 24 = 23⋅3; 10 = 2⋅5
BCNN(24; 10) = 23⋅3⋅5 = 120
c) Ta có: 4 = 22; 14 = 2⋅7; 26 = 2⋅13
BCNN(4; 14; 26) = 22⋅7⋅13 = 364
d) Ta có: 6 = 2⋅3; 8 = 23; 10 = 2⋅5
BCNN(6; 8; 10) = 23⋅3⋅5 = 120
Dạng 2. Tìm bội chung của hai hay nhiều số thỏa mãn điều kiện cho trước
Phương pháp giải.
Bước 1. Tìm BCNN của các số đó
Bước 2. Tìm các bội của BCNN này
Bước 3. Chọn trong các số đó các bội thỏa mãn điều kiện đã cho
Bài toán.
Bài 1. Tìm các bội chung của 8 và 10 thông qua BCNN
Hướng dẫn giải
Ta có: BCNN(8; 10) = {40}.
Vậy BC(8; 10) = {0; 40; 80; 120…}
Bài 2. Tìm các bội chung của 8; 12 và 15 thông qua BCNN
Hướng dẫn giải
Ta có BCNN(8; 12; 15) = {120}.
Vậy BC(8; 12; 15) = {0; 120; 240; 360;…}
Bài 3. Tìm số tự nhiên x thỏa mãn x ⋮ 4; x ⋮ 6 và 0 < x < 50
Hướng dẫn giải
Vì x ⋮ 4; x ⋮ 6 nên x ∈ BC(4; 6) = {0; 12; 24; 36; 48; 60;…}
Mà 0 < x < 50 nên x ∈ {0; 12; 24; 36; 48}
Bài 4. Tìm số tự nhiên x thỏa mãn x ⋮ 20; x ⋮ 35 và x < 500.
Hướng dẫn giải
Vì x ⋮ 20; x ⋮ 35 nên x ∈ BC(20; 35) = {0; 140; 280; 420; 560;…}
Mà x < 500 nên x ∈ {0; 140; 280; 420}
Bài 5. Tìm các bội chung của 7; 9 và 6 thông qua BCNN
Hướng dẫn giải
Ta có: BCNN(7; 9; 6) = {122}.
Vậy BC(7; 9; 6) = {0; 122; 244; 366…}
Dạng 3. Tìm các số tự nhiên thỏa mãn điều kiện cho trước
Phương pháp giải.
Sử dụng định nghĩa về BCNN.
Khi tìm hai số biết ƯCLN và BCNN thì tích của hai số là tích của BCNN và ƯCLN.
Bài toán.
Bài 1. Tìm số tự nhiên a,b biết rằng
a) a – b = 5 và BCNN(a; b) = 60
b) ƯCLN(a; b) = 5 và BCNN(a; b) = 60
Hướng dẫn giải
a) BCNN(a; b) = 60 ⇒ 60 ⋮ a; 60 ⋮ b.
Hay a, b là ước tự nhiên của 60.
Các ước tự nhiên của 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
Vì a – b = 5 nên a > b
Ta xét bảng sau:
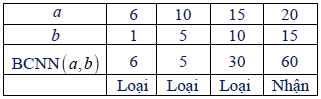
Vậy cặp số tự nhiên cần tìm là 20 và 15.
b) ƯCLN(a; b) = 5 ⇒ a = 5a1; b = 5b1 và (a1; b1) = 1
Ta có: a⋅b = 5⋅60 = 300 ⇒ a1⋅b1 = 12
Ta có bảng sau:
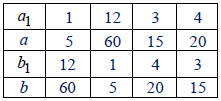
Vậy các cặp số tự nhiên (a; b) cần tìm là:
(5; 60), (60; 5), (15; 20), (20; 15)
Bài 2. Tìm số tự nhiên a, b biết rằng
a) a – b = 4 và BCNN(a; b) = 60
b) ƯCLN(a; b) = 5 và BCNN(a; b) = 150
Hướng dẫn giải
a) BCNN(a; b) = 60 ⇒ 60 ⋮ a, 60 ⋮ b. Hay a, b là ước tự nhiên của 60.
Các ước tự nhiên của 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
Vì a – b = 4 nên a > b.
Ta xét bảng sau

Vậy không tìm được cặp số tự nhiên thỏa mãn đề bài.
b) ƯCLN(a; b) = 5⇒ a = 5a1; b = 5b1 và (a1; b1) = 1
Ta có: a⋅b = 5⋅150 = 750 ⇒ a1⋅b1 = 30
Ta có bảng sau:

Vì vai trò của a, b như nhau nên ta có các cặp đảo ngược vị trí.
Vậy các cặp số tự nhiên (a; b) cần tìm là:
(5; 150), (150; 5), (10; 75), (75; 10), (15; 50), (50; 15), (25; 30) (30; 25)
Bài 3. Tìm số tự nhiên a, b biết rằng
a) ab = 180 và BCNN(a; b) = 60
b) và BCNN(a; b) = 140
Hướng dẫn giải
a) Gọi ƯCLN(a; b) = k ⇒ a = ka1; b = kb1 với (a1; b1) = 1
Ta có: ab = k2a1b1 = 180
Mà BCNN(a; b) = ka1b1 = 60
Suy ra k = 3; a1b1 = 20
Ta có bảng sau:
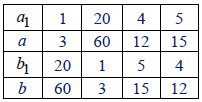
Vậy các cặp số tự nhiên (a; b) cần tìm là: (3; 60), (60; 3), (12; 15), (15; 12)
b) Gọi ƯCLN(a; b) = k
Vì mà (4; 5) = 1 nên a = 4k, b = 5k
BCNN(a; b) = 4⋅5⋅k = 140 ⇒ k = 7
Vậy a = 28, b = 35
Bài 4. Tìm số tự nhiên a, b biết rằng a + b = 42 và BCNN(a; b) = 72.
Hướng dẫn giải
Gọi ƯCLN(a; b) = k. Nên a = ka1; b = kb1
Ta có: a + b = 42 ⇒ k (a1 + b1) = 42 (1)
BCNN(a; b) = ka1b1 = 72 (2)
Từ (1) và (2) suy ra 42 ⋮ k; 72 ⋮ k hay k ∈ ƯC(42; 72) ⇒ k ∈ {1; 2; 3; 6}.
Thay k lần lượt các trường hợp trên ta thấy k = 3 hoặc k = 6
Khi đó: tìm được các cặp (a; b) là (6; 36), (18; 24).
Dạng 4: Bài toán có lời văn
Phương pháp giải.
Bước 1. Gọi ẩn, đặt đơn vị, điều kiện cho ẩn
Bước 2. Dựa vào đề bài biểu diễn các dữ kiện theo ẩn.
Bước 3. Tìm ẩn, so sánh điều kiện
Bước 4. Trả lời và kết luận
Bài toán.
Bài 1. Một số sách khi xếp thành từng bó 10 cuốn, 12 cuốn, 18 cuốn đều vừa đủ. Tìm tổng số sách biết số sách trong khoảng 200 đến 500.
Hướng dẫn giải
Gọi số sách cần tìm là x quyển, (x ∈ ℕ, 200 ≤ x ≤ 500)
Vì khi xếp thành từng bó 10 cuốn, 12 cuốn, 18 cuốn đều vừa đủ nên x ⋮ 10, x ⋮ 12, x ⋮ 18 suy ra x ∈ BC(10; 12; 18).
BCNN(10; 12; 18) = 360
BC(10; 12; 18) = {0; 360; 720;…}.
Suy ra x ∈ {0; 360; 720;…}, mà 200 ≤ x ≤ 500 nên x = 360 (thỏa mãn điều kiện)
Vậy số quyển sách cần tìm là 360 quyển.
Bài 2. Hai bạn A và B cùng học chung một trường nhưng ở hai lớp khác nhau. A cứ 10 ngày lại trực nhật, B cứ 12 ngày lại trực nhật. Lần đầu tiên hai bạn trực nhật vào một ngày. Hỏi sau ít nhất bao nhiêu ngày hai bạn lại cùng trực nhật.
Hướng dẫn giải
Do cứ 10 ngày A trực nhật một lần nên ngày trực của A là B(10).
Do cứ 12 ngày B trực nhật một lần nên ngày trực của B là B(12).
Lần đầu tiên hai bạn trực cùng 1 ngày, để đến lần gần nhất trực cùng nhau thì sẽ là: BCNN(10; 12) = 60
Vậy sau ít nhất 60 ngày hai bạn lại cùng trực nhật.
Bài 3. Số học sinh khối 6 của một trường trong khoảng từ 300 đến 400. Biết rằng nếu xếp hàng 5, 8, 12 thì thiếu 1 em. Tính số học sinh khối 6 của trường.
Hướng dẫn giải
Gọi số học sinh khối 6 của trường cần tìm là x học sinh, (x ∈ ℕ, 300 ≤ x ≤ 400)
Vì khi xếp thành 5, 8, 12 thì thiếu 1 em nên x = 5k – 1, x = 8t – 1, x = 12m – 1 suy ra x là 1 bội chung của 5, 8, 12 trừ 1.
BCNN(5; 8; 12) = 120
BC(5; 8; 12) = {0; 120; 240; 360; 480; 600…}.
Suy ra: x + 1 ∈ {0; 120; 240; 360; 480; 600…}
Mà 300 ≤ x ≤ 400 ⇒ 301 ≤ x + 1 ≤ 401
Nên x + 1 = 360 ⇒ x = 359 (thỏa mãn điều kiện)
Vậy số học sinh khối 6 là 359 học sinh.
Bài 4. Tìm số tự nhiên nhỏ nhất sao cho khi chia cho 3 thì dư 2, khi chia cho 7 thì dư 6 khi chia cho 25 thì dư 24.
Hướng dẫn giải
Gọi x là số cần tìm.
Vì x chia 3 dư 2, chia cho 7 thì dư 6, chia cho 25 thì dư 24.
Nên x + 1 chia hết cho 3, 7, 25.
Do đó: x + 1 = BCNN(3; 7; 25) = 525.
Vậy số cần tìm là 525 – 1 = 524.
Bài 5. Có ba chiếc hộp hình vuông: Hộp màu đỏ cao 8 cm, hộp màu xanh cao 7 cm, hộp màu vàng cao 12 cm. Người ta xếp thành ba chồng bằng nhau, mỗi chồng một màu. Hỏi chiều cao nhỏ nhất của chồng hộp đó.
Hướng dẫn giải
Gọi chiều cao nhỏ nhất của chồng hộp là x (cm).
Ta có: x = BCNN(7; 8; 12) = 23⋅3⋅7 = 168
Vậy chiều cao nhỏ nhất của chồng hộp là 168 (cm)
Bài 6. Tìm số tự nhiên x. Biết số đó chia hết cho 7 và khi chia cho 2, cho 3, cho 4, cho 5, cho 6 đều dư 1 và x < 400.
Hướng dẫn giải
Ta có: x – 1 = BC(2; 3; 4; 5; 6).
⇒ x – 1 ∈ {60; 120; 180; 240; 300; 360}
⇒ x ∈ {61; 121; 181; 241; 301; 361}
Do x chia hết cho 7 nên x = 301.
Bài 7. Một liên đội thiếu niên khi xếp hàng 2, hàng 3, hàng 4, hàng 5 đều thừa 1 người. Tính số đội viên của liên đội biết rằng số đó trong khoảng từ 100 đến 150.
Hướng dẫn giải
Gọi số đội viên của liên đội là x (đội viên).
Vì xếp thành hàng 2, hàng 3, hàng 4, hàng 5 đều thừa 1 người nên: x – 1 ∈ BC(2; 3; 4; 5).
BCNN(2; 3; 4; 5) = 22⋅3⋅5 = 60
BC(2; 3; 4; 5) = {0; 60; 120; 180; 240;…}.
Mà số đội viên trong khoảng từ 100 đến 150.
Nên x – 1 = 120 ⇒ x = 121 đội viên.
Bài 8. Một bộ phận của máy có hai bánh răng cửa khớp với nhau, bánh một có 18 răng cưa, bánh xe hai có 12 răng cưa. Người ta đánh dấu “x” vào hai răng cửa khớp với nhau. Hỏi mỗi bánh xe phải quay ít nhất bao nhiêu răng cưa để hai răng cưa đánh dấu ấy lại khớp với nhau ở vị trí giống lần trước? Khi đó mỗi bánh xe đã quay được bao nhiêu vòng.
Hướng dẫn giải
Gọi số răng cưa phải tìm là x (răng).
Ta có: x ⋮ 12; x ⋮ 8.
Vì x nhỏ nhất nên x là BCNN(8; 12) = 22⋅32 = 36
Vậy mỗi bánh xe phải quay ít nhất 36 răng cưa để hai răng cưa đánh dấu ấy lại khớp với nhau ở vị trí giống lần trước. Khi đó:
Bánh xe thứ nhất quay được 36 : 18 = 2 vòng
Bánh xe thứ hai quay được 36 : 12 = 3 vòng.