Tính chất chia hết của một tích

Phương pháp giải

Để xét một tích có chia hết cho một số hay không, ta làm như sau:

Cách 1. Xét xem có thừa số nào của tích chia hết cho số đó hay không. Nếu tồn tại thì thì tích đã cho chia hết cho số đó.

Cách 2. Tính tích của các thừa số và xét tích đó có chia hết cho số đã cho hay không.

Bài toán.

Bài 1. Các tích sau đây có chia hết cho 7 không?

a) 7⋅2018

b) 2020⋅56

c) 4⋅23⋅16

d) 12⋅8⋅721

Hướng dẫn giải

a) Tích 7⋅2018 chia hết cho 7 vì 7 ⋮ 7

b) Tích 2020⋅56 chia hết cho 7 vì 56 ⋮ 7.

c) Tích 4⋅23⋅16 không chia hết cho 7 vì 4⋅23⋅16 = 1472

d) Tích 12⋅8⋅721 chia hết cho 7 vì 721 ⋮ 7

Bài 2. Các tích sau đây có chia hết cho 3 không?

a) 218⋅3

b) 45⋅121

c) 279⋅7⋅13

d) 37⋅4⋅16

Hướng dẫn giải

a) Tích 218⋅3 chia hết cho 3 vì 3 ⋮ 3.

b) Tích 45⋅121 chia hết cho 3 vì 45 ⋮ 3.

c) Tích 279⋅7⋅13 chia hết cho 3 vì 279 ⋮ 3.

d) Tích 37⋅4⋅16 không chia hết cho 3 vì 37⋅4⋅16 = 2368

Bài 3. Tích A = 1⋅2⋅3⋅4⋅…⋅10 có chia hết cho 100 không?

Hướng dẫn giải

A chia hết cho 100 vì 2⋅5⋅10 = 100 ⋮ 100

Bài 4. Tích B = 2⋅4⋅6⋅8⋅…⋅20 có chia hết cho 30 không?

Hướng dẫn giải

Tích B = 2⋅4⋅6⋅8⋅…⋅20 chia hết cho 30 vì 6⋅20 = 120 ⋮ 30

Bài 5. Cho A = 2⋅4⋅6⋅8⋅10⋅12 – 40. Hỏi A có chia hết cho 6; cho 8; cho 20 không? Vì sao?

Hướng dẫn giải

Ta có tích 2⋅4⋅6⋅8⋅10⋅12 ⋮ 6 nhưng 40 không chia hết cho 6

⇒ A không chia hết cho 6

Ta có tích 2.4.6.8.10.12 6 và 40 ⋮ 8

⇒ số A chia hết cho 8

Ta có tích 2⋅4⋅6⋅8⋅10⋅12 ⋮ 2 và 10

⇒ Tích 22⋅4⋅6⋅8⋅10⋅12 ⋮ 20 và 40 ⋮ 20

⇒ Số A chia hết cho 20

Bài 6. Khi chia số tự nhiên a cho 36 ta được số dư 12. Hỏi a có chia hết cho 4; cho 9 không vì sao?

Hướng dẫn giải

a: 36 được thương là k và dư 12 ⇒ a = 36k + 12

Ta có: 36k ⋮ 4 và 12 ⋮ 4 ⇒ Số a chia hết cho 4

Ta có: 36k ⋮ 4 và 12 không chia hết cho 4 ⇒ Số a không chia hết cho 4

Bài 7. Điền dấu X và ô thích hợp:

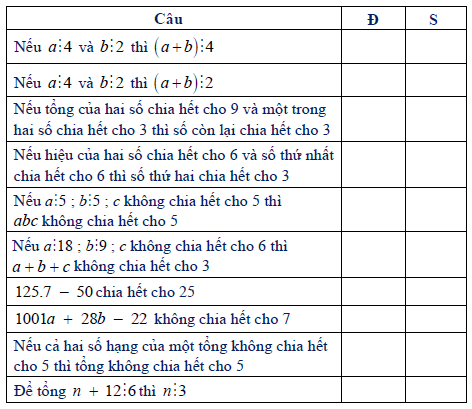
Hướng dẫn giải

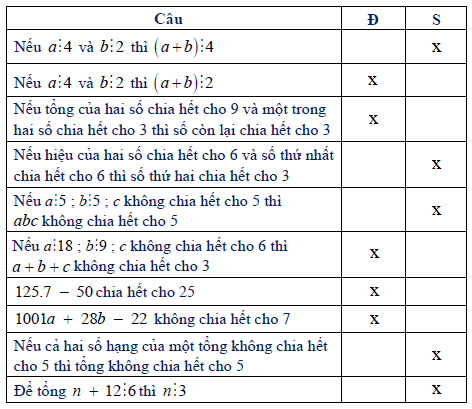
Bài 8. Chứng minh rằng tổng của ba số tự nhiên liên tiếp luôn chia hết cho 3.

Hướng dẫn giải

Gọi ba số tự nhiên liên tiếp là: a, a + 1, a + 2

Tổng của ba số tự nhiên liên tiếp là:

a + a + 1 + a + 2 = (3a + 3) ⋮ 3 (Tính chất chia hết của một tổng).

Bài 9. Tổng của 4 số tự nhiên liên tiếp có chia hết cho 4 hay không?

Hướng dẫn giải

Gọi 4 số tự nhiên liên tiếp là: a, a + 1, a + 2, a + 3

Tổng của 4 số tự nhiên liên tiếp là:

a + a + 1 + a + 2 + a + 3 = 4a + 6

Do 4 chia hết cho 4 nên 4a chia hết cho 4 mà 6 không chia hết cho 4 nên (4a + 6) không chia hết cho 4.

⇒ Tổng của 4 số tự nhiên liên tiếp không chia hết cho 4.

Kết luận: Vậy không phải lúc nào tổng n số tự nhiên liên tiếp cũng chia hết cho n

Bài 10. Khi chia một số cho 255 ta được số dư là 170. Hỏi số đó có chia hết cho 85 không? Vì sao?

Hướng dẫn giải

Gọi số đó là a (a là số tự nhiên).

Vì a chia cho 255 có số dư là 170 nên a = 255k + 170 (k ∈ ℕ)

Ta có: 255 ⋮ 85 nên 255k ⋮ 85; 170 ⋮ 85.

⇒ (255k + 170) ⋮ 85 (Tính chất chia hết của một tổng).

Do vậy a chia hết cho 85.

Bài 11. Tìm x ∈ ℕ sao cho:

a) 6 chia hết cho x

b) 8 chia hết cho x + 1

c) 10 chia hết cho x + 2

Hướng dẫn giải

a) Vì 6 ⋮ x

⇒ x ∈ {1; 2; 3; 6}

b) Vì 8 ⋮ (x + 1)

⇒ x + 1 ∈ {1; 2; 4; 8}

⇒ x ∈ {0; 1; 3; 7}

c) Vì 10 ⋮ (x – 2)

⇒ x – 2 ∈ {1; 2; 5; 10}

⇒ x ∈ {3; 4; 7; 12}

Bài 12. Tìm x ∈ ℕ sao cho:

a) x + 6 chia hết cho x

b) x + 9 chia hết cho x + 1

c) 2x + 1 chia hết cho x – 1

Hướng dẫn giải

a) Vì x ⋮ x nên (x + 6) ⋮ x khi 6 ⋮ x

⇒ x ∈ {1; 2; 3; 6}

b) Ta có: x + 9 = (x + 1) + 8

Vì (x + 1) ⋮ (x + 1) nên (x + 9) ⋮ (x + 1) khi 8 ⋮ (x + 1)

⇒ x + 1 ∈ {1; 2; 4; 8}

Từ đó tìm được: x ∈ {0; 1; 3; 7}

c) Ta có: 2x + 1 = 2(x + 1) – 1

Vì 2(x + 1) ⋮ (x + 1) nên (2x + 1) ⋮ (x + 1) khi 1 ⋮ (x + 1)

⇒ (x + 1) ∈ {1}

Từ đó tìm được: x ∈ {0}

Bài 13. Biết a – b chia hết cho 6. Chứng minh rằng các biểu thức sau cũng chia hết cho 6:

a) a + 5b

b) a – 13b

Hướng dẫn giải

a) Ta có: a + 5b = a – b + 6b

Mà a – b ⋮ 6; 6b ⋮ 6. Nên (a – b + 6b) ⋮ 6

Vậy a + 5b ⋮ 6 (đpcm).

b) Ta có: a – 13b = a – b – 12b

Mà a – b ⋮ 6; 12b ⋮ 6. Nên (a – b – 12b) ⋮ 6

Vậy a – 13b ⋮ 6 (đpcm).

Bài 14. Tìm số tự nhiên n để (3n + 14) chia hết cho (n + 2)

Hướng dẫn giải

Ta có: 5n + 14 = 5(n + 2) + 4

Mà 5(n + 2) ⋮ (n + 2)

Do đó: (5n + 14) ⋮ (n + 2) ⇔ 4 ⋮ (n + 2)

⇔ (n + 2) là Ư(4)

⇔ (n + 2) ∈ {1; 2; 4}

⇒ n ∈ {0; 2}

Vậy với n ∈ {0; 2} thì (5n + 14) ⋮ (n + 2)

Bài 15. Cho các chữ số 0, a, b. Hãy viết tất cả các số có ba chữ số tạo bởi ba số trên. Chứng minh rằng tổng tất cả các số đó chia hết cho 211.

Hướng dẫn giải

Tất cả các số có ba chữ số tạo bởi ba chữ 0, a, b là:

Tổng của các số đó là:

Thầy Tú dạy toán