Bài viết này sẽ giúp bạn?
+) Nhận biết được tập hợp và hiểu được khái niệm phần tử của tập hợp.
+) Nhận biết được một đối tượng cụ thể, thuộc hay không thuộc một tập hợp cho trước.
+) Biết biểu diễn tập hợp bằng cách: liệt kê các phần tử, chỉ ra tính chất đặc trưng và dùng biểu đồ Ven.
+) Biết sử dụng đúng các kí hiệu ∈ và ∉.
Lí thuyết trọng tâm
Tập hợp
Khái niệm tập hợp thường gặp trong toán học và cả trong đời sống.
Cách viết các kí hiệu
Cách biểu diễn tập hợp
Người ta thường dùng chữ cái in hoa để đặt tên tập hợp.
A là tập hợp các số tự nhiên nhỏ hơn 4. Ta viết A = {0; 1; 2; 3}. Các số 0; 1; 2; 3 là các phần tử của tập hợp A.
Các kí hiệu ∈ và ∉
Số 1 là một phần tử của tập hợp A. Ta viết 1 ∈ A, đọc là 1 thuộc A.
Số 5 không là một phần tử của tập hợp A. Ta viết 5 ∉ A, đọc là 5 không thuộc A.
Cách viết một tập hợp
Để viết một tập hợp, thường có hai cách:
+) Liệt các phần tử của tập hợp.
+) Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó. Ngoài ra, người ta còn minh họa tập hợp bằng một vòng kín gọi là biểu đồ Ven, mỗi phần tử của tập hợp được biểu diễn bởi một dấu chấm bên trong vòng kín đó.
Ví dụ.
Tập hợp các học sinh của lớp 6A.
Tập hợp các chữ cái a, b, c.
Chú ý:
Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, cách nhau bởi dấu “;” (nếu có phần tử là số) hoặc dấu “,”.
Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.
Ví dụ.
A = {0; 2; 4; 6; 8}
A = {x ∈ ℕ| x ⋮ 2, x ≤ 8}
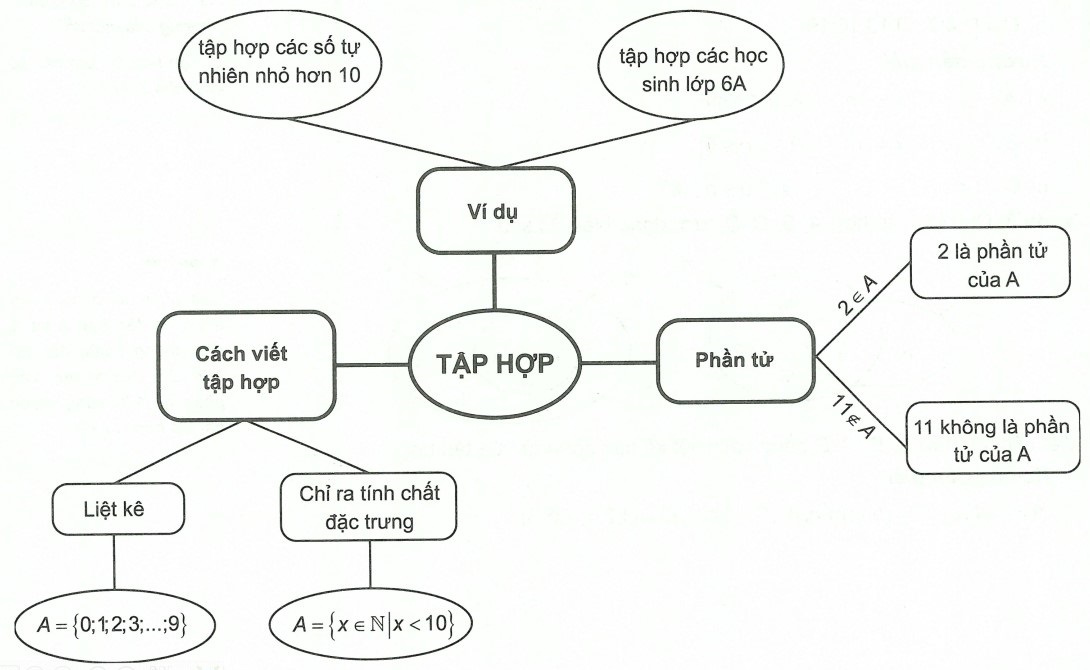
Sơ đồ hệ thống hóa
Phân dạng bài tập
Dạng 1. Biểu diễn một tập hợp cho trước
Ví dụ mẫu
Ví dụ 1. Cho A là tập hợp các số lẻ không lớn hơn 9. Viết tập hợp A bằng hai cách. Minh họa tập hợp A bằng biểu đồ Ven.
Hướng dẫn giải
Cách 1. Liệt kê các phần tử: A = {1; 3; 5; 7; 9}
Cách 2. Chỉ ra tính chất đặc trưng: A = {x ∈ ℕ| x = 2n + 1, 0 ≤ n ≤ 4}.
Minh họa bằng biểu đồ Ven:
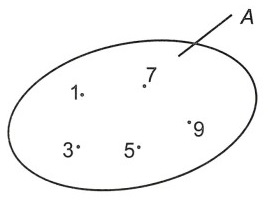
Nhận xét:
Các số lẻ có dạng x = 2n + 1. Vì 1 ≤ x ≤ 9 nên 0 ≤ n ≤ 4.
Ví dụ 2. Viết các tập hợp sau đây bằng cách chỉ ra tính chất đặc trưng cho các phần tử của nó.
a) A = {0; 4; 8; 12; 16; 20; 24}
b) B = {1; 4; 9; 16; 25}
c) C = {1; 4; 7; 10; 13; 16; 19}
Hướng dẫn giải
a) A = {x ∈ ℕ| x = 4n, n ∈ ℕ, 0 ≤ n ≤ 6}
b) B = {x ∈ ℕ| x = n2, n ∈ ℕ, 1 ≤ n ≤ 5}
c) C = {x ∈ ℕ| x = 3n + 1, n ∈ ℕ, 0 ≤ n ≤ 6}
Nhận xét:
a) Tập hợp A gồm các số chia hết cho 4.
b) Tập hợp B gồm các số viết được dưới dạng bình phương của một số.
c) Tập hợp C gồm các số chia cho 3 dư 1.
Ví dụ 3. Cho các tập hợp A, B, C, D dưới dạng biểu đồ sau:
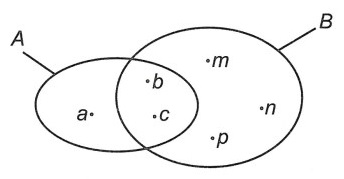
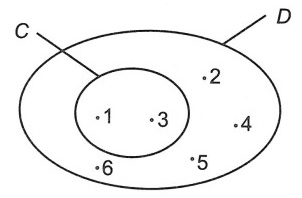
Viết các tập hợp A, B, C, D bằng cách liệt kê các phần tử của tập hợp.
Hướng dẫn giải
A = {a; b; c}
B = {b; c; m; n; p}
C = {1; 3}
D = {1; 2; 3; 4; 5; 6}
Nhận xét:
Các phần tử b, c nằm trong hai tập hợp A và B nên chúng thuộc hai tập hợp đó. Tương tự, các phần tử 1; 3 cũng thuộc hai tập hợp C và D.
Bài tập tự luyện dạng 1
Bài tập cơ bản
Câu 1. Viết các tập hợp sau bằng hai cách: liệt kê các phần tử của tập hợp và chỉ ra tính chất đặc trưng của các phần tử.
a) Tập hợp A gồm các số tự nhiên chẵn nhỏ hơn 10.
b) Tập hợp B gồm các số tự nhiên lẻ lớn hơn 3 và nhỏ hơn 15.
Hướng dẫn giải
a) Liệt kê các phần tử: A = {0; 2; 4; 6; 8}
Chỉ ra tính chất đặc trưng:
A = {x ∈ ℕ| x ⋮ 2, x < 10}
b) Liệt kê các phần tử: B = {5; 7; 9; 11; 13}
Chỉ ra tính chất đặc trưng:
B = {x ∈ ℕ| x = 2n + 1, 3 < x < 15} = {x ∈ ℕ| 1 < x < 7}
Câu 2. Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của nó và biểu diễn bằng biểu đồ Ven.
a) A là tập hợp các số tự nhiên lớn hơn 4 và nhỏ hơn 10;
b) B là tập hợp các ngày trong tuần;
c) C là tập hợp các chữ cái trong từ “HA NOI”.
Hướng dẫn giải
a) A = {5; 6; 7; 8; 9}
b) B = {thứ hai; thứ ba; thứ tư; thứ năm; thứ sáu; thứ bảy; chủ nhật}
c) C = {H; A; N; O; I}
Học sinh tự vẽ biểu đồ Ven.
Câu 3. Nhìn các hình vẽ dưới đây và viết các tập hợp A, B, X, Y.
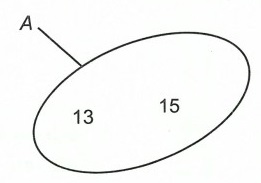
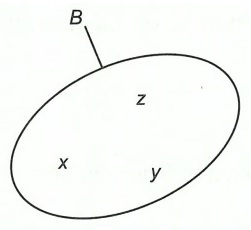
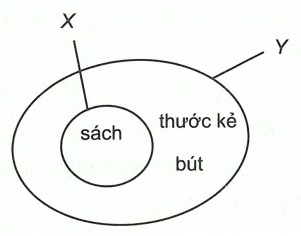
Hướng dẫn giải
A = {13; 15}
B = {x; y; z}
X = {sách}
Y = {thước kẻ; sách; bút}
Câu 4. Viết các tập hợp sau bằng cách chỉ ra tính chất đặc trưng của các phần tử thuộc tập hợp đó.
a) A = {0; 1; 2; 3; …; 30}
b) B = {1; 3; 5; 7; 9; …; 49}
c) C = {11; 22; 33; 44; 55; …; 99}
Hướng dẫn giải
a) A = {x ∈ ℕ| 0 ≤ x ≤ 30}
b) B = {x ∈ ℕ| x = 2n + 1; n ∈ ℕ, 0 ≤ n ≤ 24}
c) C = {x ∈ ℕ| x = 11n, n ∈ ℕ, 1 ≤ n ≤ 9}
Câu 5. Viết các tập hợp sau đây bằng cách chỉ ra tính chất đặc trưng cho các phần tử của nó.
a) A = {0; 1; 2; 3; …; 20}
b) B = {2; 5; 8; 11; 17; 20}
c) C = {1; 8; 27; 64; 125}
d) D = {2; 6; 12; 20; 20; 42; 56}
Hướng dẫn giải
a) A = {x ∈ ℕ| x < 21}
b) B = {x ∈ ℕ| x = 3n + 2; n ∈ ℕ, 0 ≤ n ≤ 6}
c) C = {x ∈ ℕ| x = n3, n ∈ ℕ, 1 ≤ n ≤ 5}
d) D = {x ∈ ℕ| x = n(n + 1), n ∈ ℕ, 1 ≤ n ≤ 7}
Câu 6. Viết các tập hợp sau đây bằng cách liệt kê các phần tử của nó.
a) Tập hợp các số tự nhiên không lớn hơn 6.
b) Tập hợp các số tự nhiên có hai chữ số không nhỏ hơn 90.
c) Tập hợp các số tự nhiên lớn hơn 30, nhỏ hơn 50 và chia hết cho 3.
d) Tập hợp các số tự nhiên thỏa 4 : x = 2
e) Tập hợp các số tự nhiên thỏa x + 3 < 7
Hướng dẫn giải
a) A = {0; 1; 2; 3; 4; 5; 6}
b) B = {90; 91; 92; 93; 94; 95; 96; 97; 98; 99}
c) C = {33; 36; 39; 42; 45; 48}
d) D = {2}
e) E = {0; 1; 2; 3}
Câu 7. Cho ba con đường a1, a2, a3 đi từ A đến B và có hai con đường b1, b2 đi từ B đến C. Viết tập hợp các con đường đi từ A đến C.
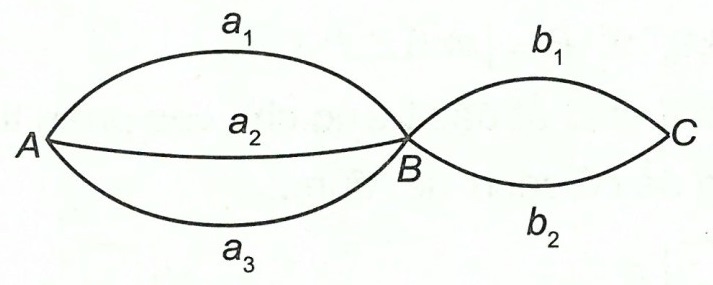
Hướng dẫn giải
Tập hợp các con đường đi từ A đến C là:
X = {a1b1; a1b2; a2b1; a2b2; a3b1; a3b2}
Câu 8. Cho hai tập hợp:
A = {3; 6; 9; 12; 15; 18; 24}
B = {4; 8; 12; 16; 20; 24}
a) Viết tập hợp A và B dưới dạng chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.
b) Tìm tập hợp C gồm các phần tử vừa thuộc tập A vừa thuộc tập B.
c) Biểu diễn ba tập hợp bằng biểu đồ Ven.
Hướng dẫn giải
a) A = {x ∈ ℕ| x = 3n; 1 ≤ n ≤ 8}
B = {x ∈ ℕ| x = 4n; 1 ≤ n ≤ 6}
b) C = {12; 24}
c)
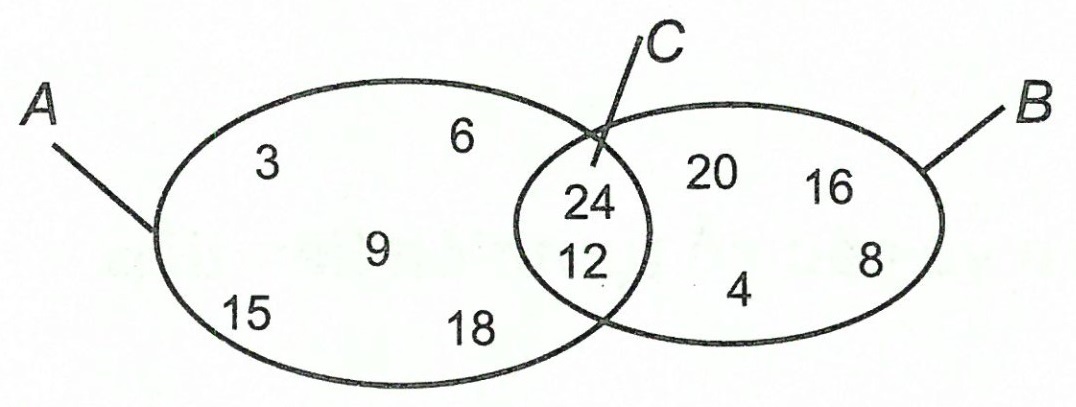
Bài tập nâng cao
Câu 9. Viết mỗi tập hợp bằng cách chỉ ra tính chất đặc trưng cho các phần tử của mỗi tập hợp đó.
a) A = {0; 3; 8; 15; 24; 35}
b) ![\[B = \left\{ {\frac{1}{2};\frac{1}{6};\frac{1}{{12}};\frac{1}{{20}};\frac{1}{{30}}} \right\}\]](https://danchuyentoan.com/wp-content/uploads/2024/03/tap-hop-1.svg)
c) ![\[C = \left\{ {\frac{2}{3};\frac{3}{8};\frac{4}{{15}};\frac{5}{{24}};\frac{6}{{35}}} \right\}\]](https://danchuyentoan.com/wp-content/uploads/2024/03/tap-hop-2.svg)
Hướng dẫn giải
a) Ta thấy mỗi số thuộc tập hợp A cộng thêm 1 đều là bình phương của một số.
Từ đó ta có thể viết:
A = {n2 – 1| n ∈ ℕ, 1 ≤ n ≤ 6}
b) ![\[B = \left\{ {\left. {\frac{1}{{n\left( {n + 1} \right)}}} \right|n \in \mathbb{N},1 \leqslant n \leqslant 5} \right\}\]](https://danchuyentoan.com/wp-content/uploads/2024/03/tap-hop-3.svg)
c) ![\[C = \left\{ {\left. {\frac{n}{{{n^2} - 1}}} \right|n \in \mathbb{N},2 \leqslant n \leqslant 6} \right\}\]](https://danchuyentoan.com/wp-content/uploads/2024/03/tap-hop-4.svg)
Dạng 2. Quan hệ phần tử và tập hợp
Ví dụ mẫu
Ví dụ 1. Cho A là tập hợp các số tự nhiên lớn hơn 12 và nhỏ hơn 20. Điền kí hiệu ∈ và ∉ vào ô trống.
12 
A; 15 A; 23 A.
Hướng dẫn giải
Do A là tập hợp các số tự nhiên lớn hơn 12 và nhỏ hơn 20 nên
A = {13; 14; 15; 16; 17; 18; 19}
Do vậy 12 
A; 15 A; 23 A
Nhận xét:
Viết tập hợp A. Từ đó nhận xét xem 12; 15 và 23 có là các phần tử của A hay không.
Ví dụ 2. Cho A = {1; 3; 4; 5}; B = {4; 5; 6}. Dùng kí hiệu ∈ và ∉ để ghi các phần tử:
a) Thuộc A và thuộc B.
b) Thuộc A nhưng không thuộc B.
c) Thuộc B nhưng không thuộc A.
Hướng dẫn giải
a) 4 ∉ A; 4 ∉ B; 5 ∉ A; 5 ∉ B
b) 1 ∉ A; 1 ∉ B; 3 ∉ A; 3 ∉ B
c) 6 ∉ B; 6 ∉ A
Bài tập tự luyện dạng 2
Câu 1. Cho hai tập hợp:
A = {a; b; c}; B = {c; m; n}
Điền kí hiệu {∈, ∉} thích hợp vào ô vuông:
a) m A
b) c A
c) c B
d) b B
Hướng dẫn giải
a) m A
b) c 
A
c) c B
d) b B
Câu 2. Cho hai tập hợp:
A = {5; 6; 7; 8; 9; 10}
B = {m; 5; 6; 7; n}
a) Viết tập hợp A bằng cách chỉ ra tính chất đặc trưng cho các phần tử của nó.
b) Điền kí hiệu ∈ và ∉ vào ô trống để có cách viết đúng.
5 A; 7 B; 10 B
Hướng dẫn giải
a) A = {x ∈ ℕ| 5 ≤ x ≤ 10}
b) 5 A; 7 B; 10 B
Câu 3. Cho tập hợp:
A = {n ∈ ℕ| 13 < n ≤ 20}
a) Liệt kê các phần tử của tập hợp A theo thứ tự tăng dần.
b) Cho biết các phần tử sau đây có thuộc tập hợp A không?
1; 13; 15; 19; 20
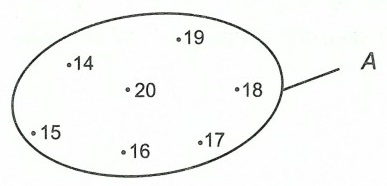
c) Biểu diễn tập hợp A bằng biểu đồ Ven.
Hướng dẫn giải
a) A = {14; 15; 16; 17; 18; 19; 20}
b) 1 ∉ A; 13 ∉ A; 15 ∈ A; 19 ∈ A; 20 ∈ A
c)
