Bài viết này sẽ giúp bạn?
+) Trình bày được định lí về quan hệ giữa góc và cạnh đối diện trong một tam giác.
+) Áp dụng được định lí về quan hệ giữa góc và cạnh đối diện trong một tam giác để so sánh độ dài các cạnh, số đo góc của tam giác đó.
+) Biết vận dụng các định lí để giải quyết bài toán.
+) Vận dụng vẽ hình theo đúng yêu cầu bài toán, nhận biết được các tính chất qua hình vẽ.
Quan hệ giữa góc và cạnh trong một tam giác
+) Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.
+) Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
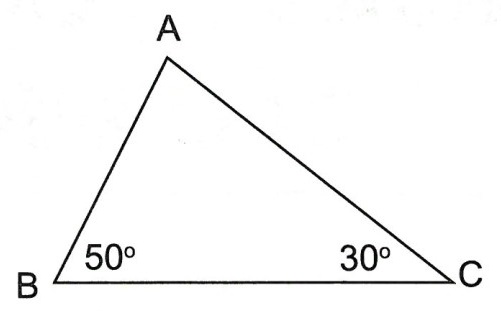
nên AB < AC
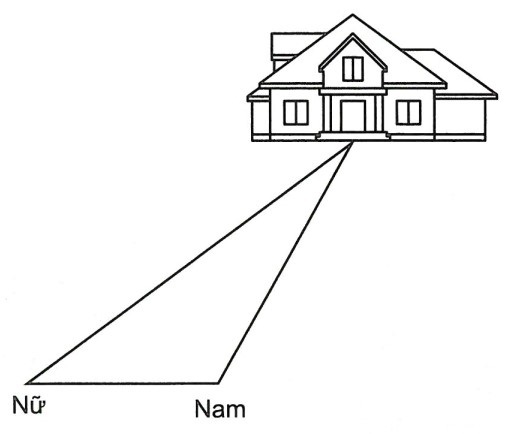
Bạn nữ đi xa hơn bạn nam
Phân dạng bài tập
Dạng 1. So sánh hai góc trong một tam giác
Phương pháp giải
+) Để so sánh hai góc trong một tam giác, ta so sánh hai cạnh đối diện với hai góc đó.
+) Sử dụng định lí: “Trong một tam giác, góc có cạnh đối diện lớn hơn thì lớn hơn”.
Ví dụ: Cho tam giác ABC có AB = 8 cm, AC = 10 cm. So sánh và
.
Hướng dẫn giải
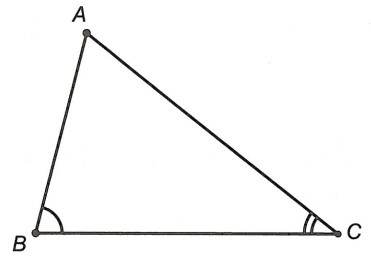
Xét △ABC, có:
AB = 8 cm, AC = 10 cm
⇒ AC > AB ⇒
Ví dụ mẫu
Ví dụ 1. Cho tam giác ABC vuông tại A, AB = 3 cm, BC = 5 cm. Hãy so sánh góc và góc
. Hướng dẫn giải
Vì △ABC vuông tại A, áp dụng định lí Pi-ta-go, ta có:
BC2 = AB2 + AC2
⇒ AC2 = BC2 – AB2 = 25 – 9 = 16
⇒ AC = 4
⇒ AC > AB
Do đó:
Ví dụ 2. Cho tam giác ABC, đường cao AH, biết BH = 5 cm, CH = 7cm. Hãy so sánh hai góc và
.
Hướng dẫn giải
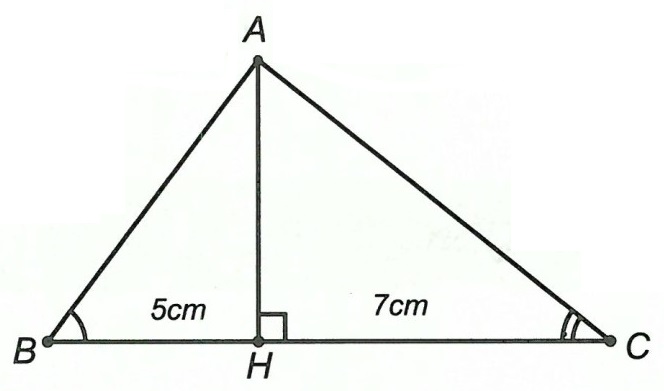
Vì △HAB vuông tại H và △HAC vuông tại H nên áp dụng định lí Pi-ta-go, ta có:
AB2 = BH2 + AH2 = 25 + AH2
AC2 = CH2 + AH2 = 49 + AH2
⇒ AC2 > AB2 ⇒ AC > AB
Xét △ABC có AC > AB nên
Ví dụ 3. Cho tam giác ABC, tia phân giác của góc cắt BC tại D, biết BD = 2DC. Chứng minh rằng:
Hướng dẫn giải
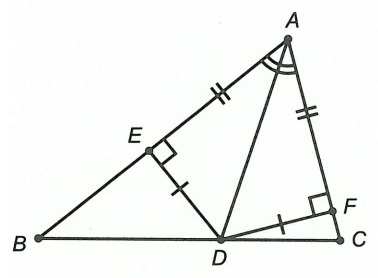
Kẻ DE ⊥ AB, DF ⊥ AC (E ∈ AB, F ∈ AC)
Xét △ADE và △ADF, có:
,
AD chung,
(do AD là tia phân giác).
Do đó: △ADE = △ADF (cạnh huyền – góc nhọn)
⇒ AE = AF, DE = DF (hai cạnh tương ứng)
Xét △EBD có: . Áp dụng định lí Pi-ta-go ta có:
BE2 = BD2 – ED2 = (2DC)2 – DF2 = 4DC2 – DF2 (1)
Xét △FDC có: . Áp dụng định lí Pi-ta-go ta có:
DC2 = DF2 + CF2 ⇒ CF2 = DC2 – DF2 (2)
Từ (1) và (2) suy ra BE > CF
Mặt khác: AB = BE + AE; AC = AF + FC
Và AE = AF
Nên AB > AC
Do đó: (điều phải chứng minh).
Bài tập tự luyện dạng 1
Câu 1. Cho tam giác ABC có AB = 23 cm, AC = 25 cm và BC = 30 cm. So sánh các góc của tam giác ABC.
Hướng dẫn giải
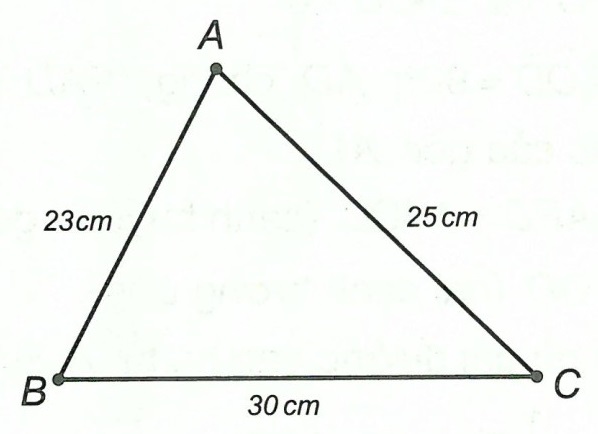
Xét △ABC, có:
AB = 23 cm, AC = 25 cm, BC = 30 cm
⇒ AB < AC < BC
⇒
Câu 2. Cho tam giác ABC cân ở A có chu vi bằng 20cm, cạnh đáy BC = 6 cm. So sánh các góc của tam giác ABC.
Hướng dẫn giải
Vì △ABC cân tại A nên AB = AC
Theo đề bài, ta có: AB + AC + BC = 20 cm
⇒ 2AB + BC = 20 (cm)
Mặt khác: BC = 6 cm nên AB = AC = 7 (cm)
⇒ AB = AC > BC
⇒
Câu 3. Cho tam giác ABC có AB = 6 cm, AC = 8 cm, tia phân giác của góc cắt cạnh BC tại D. Chứng minh rằng:
Hướng dẫn giải

Trên AC lấy E sao cho AE = AB = 6 cm.
Vì AC = 8 cm > AE nên E nằm giữa A và C.
Xét △ABD và △AED, có:
AB = AE
(Vì AD là phân giác
)
AD chung
Do đó: △ABD = △AED (c.g.c)
⇒ (hai góc tương ứng)
Mặt khác E nằm giữa A và C nên
⇒ (đpcm)
Câu 4. Cho tam giác ABC, biết AB = 6 cm, BC = 7 cm và diện tích tam giác là 21 cm2. Hãy so sánh các góc của tam giác.
Hướng dẫn giải
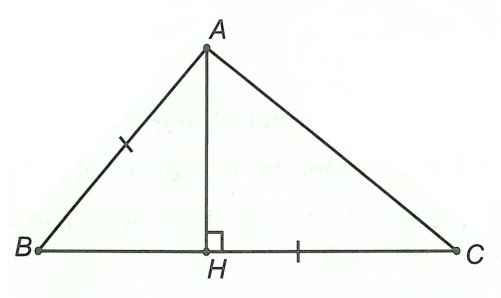
Kẻ đường cao CH (H ∈ BC)
Ta có:
⇒ △ABC vuông tại B
⇒ CA là cạnh huyền
⇒ AC > BC > AB
⇒
Câu 5. Cho tam giác ABC, có AH ⊥ BC (H ∈ BC) và AB = HC. Hãy so sánh độ lớn của góc và góc
trong tam giác ABC.
Hướng dẫn giải
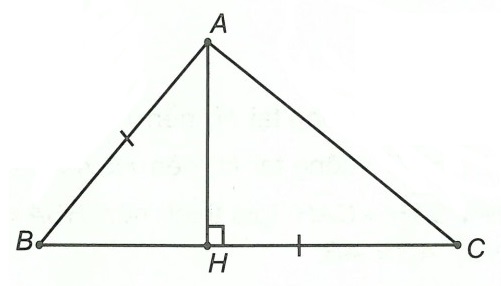
Xét △HAC vuông tại H nên AC là cạnh huyền
⇒ AC > HC
Mà HC = AB nên AC > AB ⇒
Câu 6. Cho tam giác ABC, M là trung điểm của BC, . Hãy so sánh góc
và
.
Hướng dẫn giải
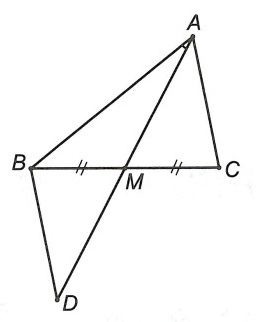
Trên tia đối của tia MA, lấy điểm D sao cho MD = MA
Xét △MAC và △MDB, có:
MB = MC (do M là trung điểm của BC)
(hai góc đối đỉnh)
MA = MD
Do đó: △MAC = △MDB (c.g.c)
⇒ và BD = AC
Xét △ABD, có:
⇒ AB > BD ⇒ AB > AC
⇒
Câu 7. Cho tam giác ABC, tia phân giác của góc cắt cạnh BC tại D, biết BD = 3 cm, DC = 5cm. Hãy so sánh độ lớn góc
và góc
của tam giác ABC.
Hướng dẫn giải
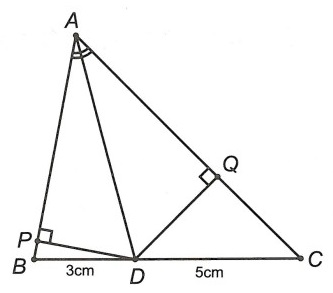
Từ D hạ DP ⊥ AB tại P, DQ ⊥ AC tại Q
Xét △APD và △AQD, có:
AD chung
(do AD là phân giác của góc
)
Do đó: △APD = △AQD (cạnh huyền – góc nhọn)
⇒ PD = QD (hai cạnh tương ứng)
Gọi h là độ dài đường cao hạ từ A xuống BC
Dạng 2. So sánh hai cạnh trong một tam giác
Phương pháp giải
+) Để so sánh hai cạnh trong một tam giác, ta so sánh hai góc đối diện với hai cạnh đó.
+) Sử dụng định lí: “Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn”.
Ví dụ: Cho tam giác ABC có . Hãy so sánh các cạnh của tam giác ABC.
Hướng dẫn giải

Xét △ABC ta có
Mặt khác: (giả thiết)
Mà nên
Ví dụ mẫu
Ví dụ 1. Cho △ABC, biết
a) So sánh các cạnh của △ABC
b) Tia phân giác của góc cắt BC ở D. So sánh độ dài các đoạn BD và CD.
Hướng dẫn giải
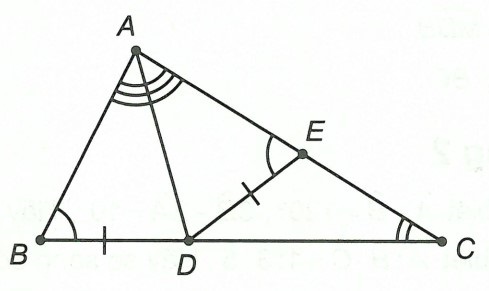
a) Từ giả thiết, ta có:
Mặt khác:
Do đó: BC > AC > AB
b) Trên cạnh AC lấy điểm E sao cho AE = AB
Xét △ABD và △AED, có:
AB = AE,
(vì AD là tia phân giác của góc
),
AD chung.
Do đó: △ABD = △AED (c.g.c)
⇒ (hai góc tương ứng); BD = DE (hai cạnh tương ứng).
Ta có: (hai góc kề bù)
Xét △DEC có nên DC > DE
Mà BD = DE. Do đó DC > BD
Ví dụ 2. Cho tam giác ABC, biết . So sánh các cạnh của tam giác.
Hướng dẫn giải
Theo giả thiết ta có:
Áp dụng tính chất dãy tỷ số bằng nhau, ta có:
Vậy nên BC < AC < AB
Ví dụ 3. Cho tam giác ABC cân ở A. Trên cạnh AB lấy điểm M, trên tia đối của tia CA lấy điểm N sao cho BM = CN. Từ C kẻ tia Cx // MN, từ M kẻ tia My // CN. Hai tia Cx và My cắt nhau tại D. So sánh BC và CD.
Hướng dẫn giải
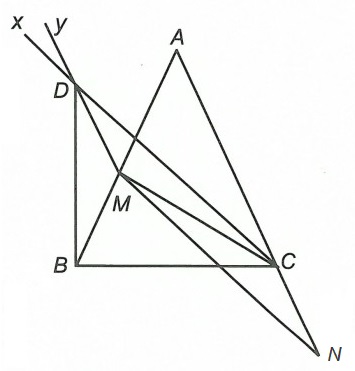
Xét △MDC và △CNM, có:
MC chung,
(hai góc so le trong do MD // CN),
(hai góc so le trong do CD // MN).
Do đó: △MDC = △CNM (g.c.g)
⇒ (hai góc tương ứng), DM = CN (hai cạnh tương ứng).
Mà CN = BM nên DM = BM
Ta có: (góc ngoài tại đỉnh C của △CMN )
⇒
Mà (do △ABC cân tại A) nên
Xét △MBD, có: BM = DM
⇒ △MBD cân tại M
⇒
⇒
Hay
Bài tập tự luyện dạng 2
Câu 1. Cho tam giác ABC, biết . Hãy so sánh độ dài các cạnh trong tam giác ABC.
Hướng dẫn giải
Theo giả thiết, ta có:
Ta có:
Câu 2. Cho tam giác ABC, biết . Hãy so sánh độ dài các cạnh của tam giác ABC.
Hướng dẫn giải
Theo giả thiết, ta có:
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Câu 3. Cho tam giác ABC, H là chân đường cao hạ từ đỉnh A, H nằm giữa B và C, . Hãy so sánh độ dài các cạnh AB và AC của tam giác ABC.
Hướng dẫn giải
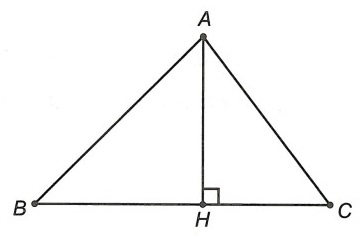
Vì △HAB vuông tại H nên
△HAC vuông tại H nên
Mà (giả thiết) nên
hay
⇒ AC < AB
Câu 4. Cho tam giác ABC vuông tại A, điểm M nằm giữa A và C. So sánh độ dài BM và BC.
Hướng dẫn giải
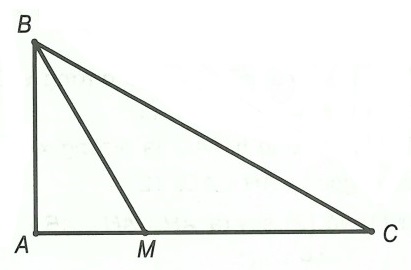
Xét △MBC, có:
(tính chất góc ngoài của tam giác)
⇒ △MBC có là góc tù
⇒
⇒ BC > BM
Câu 5. Cho tam giác ABC, hai đường cao BD và CE. Chứng minh rằng AC – AB > CE – BD
Hướng dẫn giải
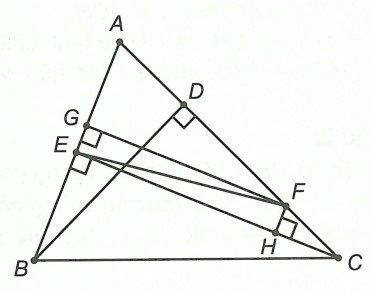
Vì ⇒ AC > AB
Trên AC lấy F sao cho AF = AB, từ F kẻ FG ⊥ AB tại G; kẻ FH ⊥ CE tại H.
Ta có: CE ⊥ AB, GF ⊥ AB ⇒ GF // CE
⇒ (hai góc so le trong)
Xét △AGF và △ADB, có:
chung
AB = AF
Do đó: △AGF = △ADB (cạnh huyền – góc nhọn)
⇒ GF = BD (hai cạnh tương ứng)
Xét △GFE và △HEF, có:
EF chung
Do đó: △GFE = △HEF (cạnh huyền – góc nhọn)
⇒ GF = EH (hai cạnh tương ứng)
Xét △HFC có: FC là cạnh huyền nên FC > HC
AC – AF > EC – HE
⇒ AC – AB > CE – BD (do AB = AF)