Quan hệ giữa ba cạnh của một tam giác

Bài viết này sẽ giúp bạn?

+) Phát biểu được định lí và hệ quả của bất đẳng thức tam giác.

+) Vận dụng được định lí và hệ quả của bất đẳng thức tam giác trong các bài toán.

Quan hệ giữa ba cạnh của một tam giác

Định lí

Trong tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.

Cho △ABC ta có các bất đẳng thức sau:

AB + AC > BC

AB + BC > AC

AC + BC > AB

Hệ quả

Trong một tam giác, độ dài của một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh còn lại.

AB – AC < BC < AB + AC

Phân dạng bài tập

Dạng 1. Sử dụng điều kiện tồn tại một tam giác dựa vào yếu tố độ dài ba cạnh

Phương pháp giải

+) Ba đoạn thẳng a, b, c lập thành một tam giác nếu

$\left\{ \begin{gathered} a < b + c \hfill \\ b < a + c \hfill \\ c < a + b \hfill \\ \end{gathered} \right.$ hoặc $\left| {b - c} \right| < a < b + c$

+) Trong trường hợp xác định được a là số lớn nhất trong ba số a, b, c thì điều kiện tồn tại tam giác chỉ cần a < b + c

Bước 1. Dựa vào bất đẳng thức tam giác xét các trường hợp

$\left\{ \begin{gathered} a < b + c \hfill \\ b < a + c \hfill \\ c < a + b \hfill \\ \end{gathered} \right.$ hoặc $\left| {b - c} \right| < a < b + c$

Bước 2. Lựa chọn giá trị thích hợp.

Ví dụ: Cho tam giác ABC có BC = 1 cm, AC = 7 cm. Tìm độ dài cạnh AB, biết độ dài này là một số nguyên (cm).

Hướng dẫn giải

Gọi độ dài cạnh AB là x (cm) (x > 0)

Theo bất đẳng thức trong tam giác ABC, ta có:

|BC – AC| < AB < BC + AC

⇒ |1 – 7| < x < 1 + 7

⇒ 6 < x < 8

Vì x là số nguyên nên x = 7.

Vậy độ dài cạnh AB = 7 cm.

Ví dụ mẫu

Ví dụ. Cho tam giác ABC cân. Tính AC, BC biết chu vi tam giác ABC là 23cm và AB = 5 cm.

Hướng dẫn giải

+) Nếu AB là cạnh bên và △ABC cân tại A, ta có AB = AC = 5 cm.

Do chu vi tam giác ABC bằng 23cm nên

BC = 23 – (AB + AC) = 23 – (5 + 5) = 13 (cm)

BC – AB = 13 – 5 = 8 > 5 = AC hay BC – AB > AC

(không thỏa mãn bất đẳng thức tam giác).

+) Nếu AB là cạnh bên và △ABC cân tại B ta có AB = BC = 5 cm ⇒ AC = 13 cm.

Lại có: AC – AB > BC (13 – 5 > 5) (không thỏa mãn bất đẳng thức tam giác).

+) Nếu AB là cạnh đáy thì △ABC cân tại C.

Suy ra: AC = BC = (23 – 5) : 2 = 9 cm (thỏa mãn bất đẳng thức tam giác).

Vậy AC = BC = 9 cm

Bài tập tự luyện dạng 1

Câu 1. Bộ ba độ dài sau đây có thể là ba cạnh của một tam giác?

a) 3cm; 4cm; 5cm.

b) 2m; 3m; 6m.

Hướng dẫn giải

a) Xét bộ ba cạnh 3cm; 4cm; 5cm.

Ta có 5cm là số lớn nhất mà 3 + 4 > 5 (thỏa mãn) nên bộ ba cạnh 3cm; 4cm; 5cm lập thành một tam giác

b) Xét bộ ba cạnh 2m; 3m; 6m.

Ta có 6m là số lớn nhất mà 2 + 3 < 6 (không thỏa mãn bất đẳng thức tam giác) nên bộ ba cạnh 2m; 3m; 6m không lập thành một tam giác

Câu 2. Cho tam giác MNP với MN = 1 cm, NP = 3 cm. Hãy tìm độ dài cạnh MP, biết rằng độ dài này là một số nguyên (cm). Tam giác MNP là tam giác gì?

Hướng dẫn giải

Gọi độ dài cạnh MP là x (cm) (x > 0)

Theo bất đẳng thức trong △MNP, ta có:

|MN – NP| < MP < MN + NP

⇒ |1 – 3| < x < 1 + 3

⇒ 2 < x < 4

Vì x là số nguyên nên x = 3

Vậy độ dài cạnh MP = 3 cm

Ta có: MP = NP = 3 cm nên △MNP cân tại P

Câu 3. Tính chu vi của tam giác cân ABC biết

a) AB = 7 cm, AC = 13 cm

b) AB = 5 m, AC = 12 m

Hướng dẫn giải

a) Gọi độ dài cạnh BC là x (cm) (x > 0)

Xét △ABC, ta có:

|AB – AC| < BC < AB + AC (bất đẳng thức tam giác)

⇒ |7 – 13| < x < 7 + 13

⇒ 6 < x < 20

Tam giác ABC là tam giác cân ⇒ BC = 7 cm hoặc BC = 13 cm

Nếu BC = 7 cm thì chu vi tam giác ABC là:

AB + AC + BC = 7 + 13 + 7 = 27 (cm)

Nếu BC = 13 cm thì chu vi tam giác ABC là:

AB + AC + BC = 7 + 13 + 13 = 33 (cm)

b) Gọi độ dài cạnh BC là x (cm) (x > 0)

Xét △ABC, ta có:

|AB – AC| < BC < AB + AC (bất đẳng thức tam giác)

⇒ |5 – 12| < x < 5 + 12

⇒ 7 < x < 17

△ABC là tam giác cân nên BC = 12 cm

Chu vi tam giác ABC là:

AB + AC + BC = 5 + 12 + 12 = 29 (cm)

Dạng 2. Chứng minh các bất đẳng thức về độ dài

Phương pháp giải

+) Sử dụng bất đẳng thức tam giác và các biến đổi về bất đẳng thức.

+) Cộng cùng một số vào hai vế của bất đẳng thức

a < b ⇒ a + c < b + c

+) Cộng từng vế hai bất đẳng thức cùng chiều

$\left. \begin{gathered} a < b \hfill \\ c < d \hfill \\ \end{gathered} \right\} \Rightarrow a + c < b + d$

Ví dụ: Cho tam giác ABC, điểm N thuộc cạnh AB.

a) So sánh NC với AN + AC

b) Chứng minh: NB + NC < AB + AC

Hướng dẫn giải

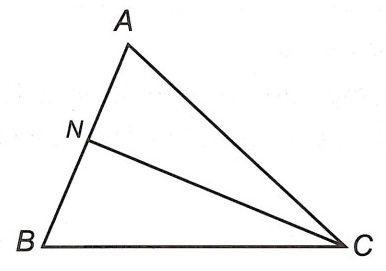
a) Xét △ANC, ta có:

NC < AN + AC (bất đẳng thức tam giác).

b) Theo câu a) ta có:

NC < AN + AC ⇒ NB + NC < NB + AN + AC

⇒ NB + NC < AB + AC (điều phải chứng minh).

Ví dụ mẫu

Ví dụ. Cho △ABC có M là trung điểm của BC. Chứng minh rằng:

$\left| {\frac{{AB - AC}}{2}} \right| < AM < \frac{{AB + AC}}{2}$

Hướng dẫn giải

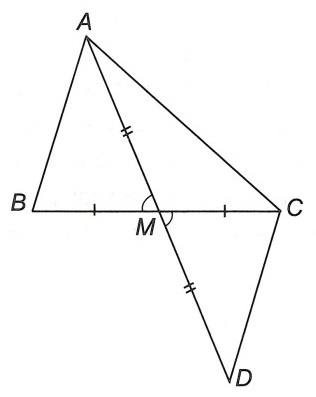
Trên tia AM lấy điểm D sao cho AM = MD.

Xét △AMB và △DMC, có:

AM = MD

$\widehat {AMB} = \widehat {DMC}$ (đối đỉnh)

BM = MC (giả thiết)

Do đó: △AMB = △DMC (c.g.c)

⇒ AB = DC (hai cạnh tương ứng)

Xét △ACD, có:

|DC – AC| < AD < AC + DC (bất đẳng thức tam giác).

Do AB = DC (chứng minh trên); AD = 2AM, nên ta có:

|AB – AC| < 2AM < AB + AC

Vậy $\left| {\frac{{AB - AC}}{2}} \right| < AM < \frac{{AB + AC}}{2}$

Bài tập tự luyện dạng 2

Câu 1. Cho tam giác OBC cân tại O. Trên tia đối của tia CO lấy điểm A. Chứng minh AB > AC.

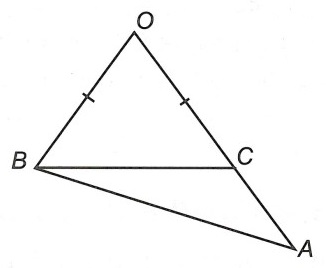
Hướng dẫn giải

Xét tam giác OBA, có:

AO – OB < AB (bất đẳng thức tam giác)

⇒ AC + OC – OB < AB.

Lại có: OB = OC (△OBC cân tại O)

⇒ AC = AB (điều phải chứng minh).

Câu 2. Cho góc $\widehat {xOy}$ nhọn, trên Ox lấy hai điểm A và B (điểm A nằm giữa hai điểm O và B). Trên Oy lấy hai điểm C và D (điểm C nằm giữa O và D). Chứng minh AB + CD < AD + BC .

Hướng dẫn giải

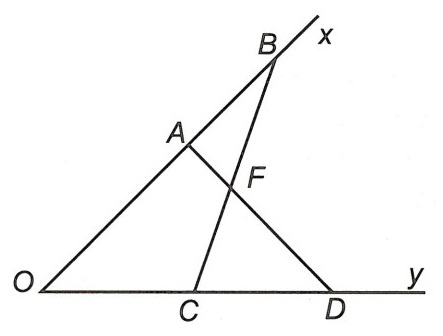
Gọi F là giao điểm của AD và BC.

Xét △AFB, ta có AB < AF + FB (bất đẳng thức tam giác) (1)

Xét △CFD, ta có CD < CF + FD (bất đẳng thức tam giác) (2)

Từ (1), (2) có: AB + CD < AF + FB + CF + FD = AD + BC hay AB + CD < AD + BC (đpcm).

Câu 3. Cho tam giác ABC, điểm M bất kỳ nằm trong tam giác. Chứng minh:

$MA + MB + MC > \frac{{AB + BC + CA}}{2}$

Hướng dẫn giải

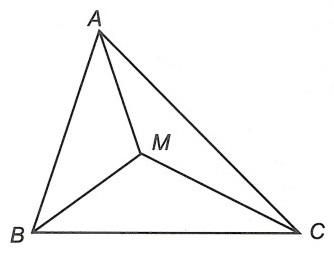
Xét △AMB, ta có:

MA + MB > AB (bất đẳng thức tam giác) (1)

Xét △AMC, ta có:

MA + MC > AC (bất đẳng thức tam giác) (2)

Xét △BMC, ta có:

MB + MC > BC (bất đẳng thức tam giác) (3)

Cộng từng vế (1), (2) và (3) ta được:

MA + MB + MA + MC + MB + MC = AB + AC + BC

⇒ 2(MA + MB + MC) > AB + AC + BC

Vậy $MA + MB + MC > \frac{{AB + BC + CA}}{2}$ (đpcm)

Câu 4. Cho tam giác ABC có (AB < AC) và AD là phân giác góc A (D ∈ BC). Gọi E là một điểm bất kỳ thuộc cạnh AD (E khác A). Chứng minh AC – AB > EC – EB.

Hướng dẫn giải

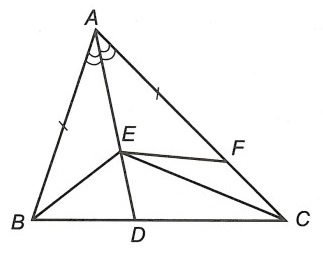
Trên cạnh AC lấy điểm F sao cho AF = AB

Xét △ABE và △AFE, có:

AB = AF (cách vẽ)

$\widehat {BAE} = \widehat {FAE}$ (giả thiết)

AE chung.

Do đó: △ABE = △AFE (c.g.c)

⇒ BE = EF (hai cạnh tương ứng)

Xét △EFC có FC > EC – EF (bất đẳng thức tam giác).

Mà BE = EF nên FC > EC – EB (1)

Lại có: FC = AC – AF mà AF = AB

Nên FC = AC – AB (2)

Từ (1) và (2) suy ra AC – AB > EC – EB .

Câu 5. Cho tam giác ABC vuông tại A có AB = 3; AC = 4. Gọi I là trung điểm của AC, d là đường trung trực của đoạn AC và điểm M tùy ý trên d.

a) Chứng minh rằng: MA + MB ≥ 5.

b) Xác định vị trí của M để tổng MA + MB nhỏ nhất. Tìm giá trị nhỏ nhất đó.

Hướng dẫn giải

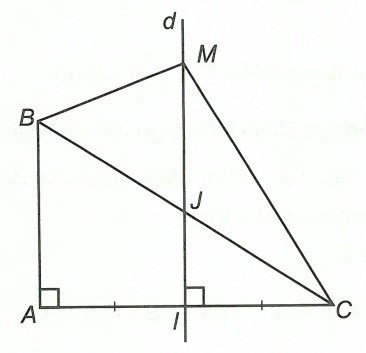
a) Xét △ABC vuông tại A, ta có:

AB² + AC² = BC² (định lí Pi-ta-go)

⇒ BC² = 3² + 4² = 5²

⇒ BC = 5

Xét △AMI và △CMI, có:

$\widehat {MIA} = \widehat {MIC} = 90^\circ$ (MI là trung trực của AC)

AI = CI (giả thiết)

MI là cạnh chung

Do đó: △AMI = △CMI (hai cạnh góc vuông)

⇒ MA = MC (hai cạnh tương ứng)

⇒ MA + MB = MC + MB.

Áp dụng bất đẳng thức tam giác trong △BMC, ta có:

MB + MC ≥ BC ⇒ MA + MB ≥ 5

b) Vì MA + MB ≥ 5 (chứng minh trên) nên MA + MB nhỏ nhất khi và chỉ khi MA + MB = BC. Điều này xảy ra khi và chỉ khi M nằm trên đoạn BC

⇒ M ≡ J, với J là giao điểm của d và BC.

Câu 6. Cho hai điểm A và B nằm về hai phía của đường thẳng d. Tìm điểm C thuộc đường thẳng d sao cho tổng AC + CB là nhỏ nhất.

Hướng dẫn giải

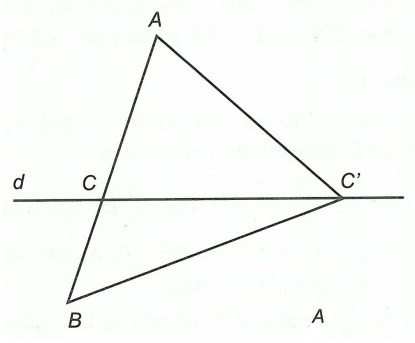
Giả sử C là giao điểm của đoạn thẳng AB với đường thẳng d.

Vì C nằm giữa A và B nên AC + CB = AB (1)

Lấy điểm C’ bất kỳ trên d (C’ ≠ C). Nối AC’, BC’

Sử dụng bất đẳng thức tam giác vào △ABC’, ta có: AC’ + BC’ > AB (2)

Từ (1) và (2) suy ra AC’ + BC’ > AC + CB.

Vậy C là điểm cần tìm.

Câu 7. Cho đường thẳng d và hai điểm A, B nằm cùng về một phía của d và AB không song song với d. Một điểm H di động trên d. Tìm vị trí của H sao cho |HA – HB| là lớn nhất.

Hướng dẫn giải

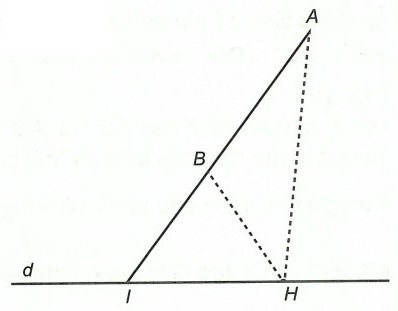
Vì AB không song song với d nên AB cắt d tại I.

Với điểm H bất kì thuộc d mà H không trùng với I thì ta có tam giác HAB.

Xét tam giác HAB, có: |HA – HB| < AB

Khi H ≡ I thì |HA – HB| = AB

Vậy |HA – HB| lớn nhất là bằng AB, khi đó H ≡ I là giao điểm của hai đường thẳng d và AB.

Thầy Tú dạy toán