Định nghĩa tam giác cân

Tam giác cân là tam giác có hai cạnh bằng nhau.
Tam giác ABC có AB = AC được gọi là tam giác ABC cân đỉnh A, trong đó:
+) AB, AC là cạnh bên và BC là cạnh đáy.
+) ,
là các góc ở đáy;
là góc ở đỉnh.
Tính chất
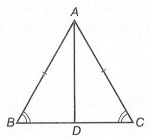
Định lý 1: Trong một tam giác cân, hai góc ở đáy bằng nhau. Nếu △ABC cân đỉnh A thì
Định lý 2: Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân. Nếu △ABC có thì △ABC cân đỉnh A.
Tam giác vuông cân
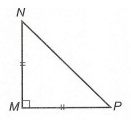
Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.
Nếu △MNP có MN = MP và MN ⊥ MP thì △MNP là tam giác vuông cân tại M.
Tam giác đều
Định nghĩa
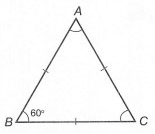
Tam giác đều là tam giác có ba cạnh bằng nhau.
Tính chất
+) Trong một tam giác đều, mỗi góc bằng 60°.
△ABC là tam giác đều thì
+) Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.
+) Nếu một tam giác cân có một góc bằng 60° thì tam giác đó là tam giác đều.
Phân dạng bài tập
Dạng 1: Nhận biết tam giác cân, tam giác đều
Phương pháp giải
Dựa vào dấu hiệu nhận biết của tam giác cân, tam giác đều.
Một tam giác là tam giác cân nếu:
+) Tam giác có hai cạnh bằng nhau.
+) Tam giác có hai góc bằng nhau.
Một tam giác là tam giác đều nếu:
+) Tam giác có ba cạnh bằng nhau.
+) Tam giác có ba góc bằng nhau.
+) Tam giác cân có một góc bằng 60°.
Bước 1. Xác định cặp cạnh (góc) bằng nhau của tam giác cần chứng minh thông qua phân tích dữ kiện bài toán.
Bước 2. Chứng minh cặp cạnh (góc) tương ứng bằng nhau và kết luận.
Quá trình chứng minh, có thể cần dựng thêm đường phụ.
Ví dụ: Cho tam giác ABC cân đỉnh A. Gọi BD, CE lần lượt là phân giác trong góc ,
của tam giác ABC. Chứng minh rằng tam giác ADE là tam giác cân.
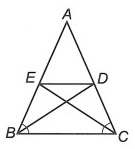
Hướng dẫn giải
Phân tích: Có hai cách để chứng minh △ADE cân là ta chứng minh AD = AE hoặc
Ta có thể chứng minh cặp góc (cạnh) bằng nhau qua việc xét cặp tam giác bằng nhau.
+) Nếu chứng minh AD = AE ta có thể ghép vào cặp tam giác △ADB và △AEC.
+) Cách còn lại khó khăn hơn vì chỉ là góc của △ADE.
Ta có: (do BD là phân giác của
)
(do CE là phân giác của
)
Mà △ABC cân đỉnh A nên AB = AC và
Xét △ADB và △AEC, có:
(góc chung)
AB = AC
Do đó: △ADB = △AEC (g.c.g)
Suy ra: AD = AE (cặp cạnh tương ứng).
Vậy △ADE cân tại A.
Ví dụ mẫu
Ví dụ 1. Cho tam giác ABC có AD là đường phân giác trong góc A (D ∈ BC). Trên cạnh AB lấy điểm I, trên cạnh AC lấy điểm H sao cho AI = AH. Chứng minh rằng △IDH là tam giác cân.
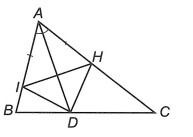
Hướng dẫn giải
Do AD là phân giác trong góc A nên
Xét △ADI và △ADH, có:
AI = AH (giả thiết),
(chứng minh trên),
AD chung.
Do đó: △ADI = △ADH (c.g.c)
⇒ DI = DH (cặp cạnh tương ứng).
Vậy tam giác DHI là tam giác cân đỉnh D.
Ví dụ 2. Cho tam giác ABC có . Trên tia phân giác của góc
, lấy điểm D sao cho AD = AB + AC. Chứng minh rằng △BCD đều.
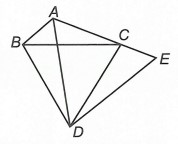
Hướng dẫn giải
Do AD là phân giác trong góc A nên
Trên tia AC lấy điểm E sao cho AE = AD.
Do AD = AB + AC (giả thiết) nên ta có AE = AB + AC
⇒ AE = AC hay C nằm giữa A và E.
Khi đó, ta có AC + EC = AB + AC ⇒ EC = AB
Xét △ADE có: AD = AE và
⇒ △DAE đều
Suy ra: DA = DE = AE và
Xét △ABD và △ECD, có:
AB = EC (chứng minh trên)
DA = DE (chứng minh trên)
Do đó: △ABD = △ECD (c.g.c)
Suy ra: DB = DC (hai cạnh tương ứng),
(hai góc tương ứng) (1)
Theo chứng minh trên, ta có:
Do đó từ (1), ta có:
Vậy △BCD có DB = DC và nên △BCD đều.
Định hướng:
Cần chứng minh:
Bài tập tự luyện dạng 1
Câu 1: Tam giác cân là tam giác
A. Có hai đường cao bằng nhau.
B. Có hai đường trung tuyến bằng nhau.
C. Có hai cạnh bằng nhau.
D. Có hai tia phân giác trong bằng nhau.
Hướng dẫn giải
Chọn C
Câu 2: Cho tam giác ABC cân đỉnh A có các đường trung tuyến BD, CE. Tam giác nào dưới đây là tam giác cân?
A. △ABD
B. △BCE
C. △ADE
D. △BDE
Hướng dẫn giải
Chọn C

Xét △ADE, có: AE = AB, AD =
AC
Mà AB = AC (do △ABC cân) nên AE = AD
Vậy △ADE cân tại A
Câu 3: Cho tam giác ABC có
a) Chứng minh rằng tam giác ABC cân.
b) Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Chứng minh rằng △BCD là tam giác vuông.
Hướng dẫn giải
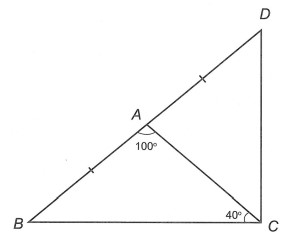
a) Xét △ABC, có:
Do đó △ABC cân đỉnh A
b) ABC cân tại A nên AB = AC
Mà AB = AD (giả thiết)
⇒ AC = AD
⇒ △ACD cân đỉnh A
Xét △ACD có là góc ngoài đỉnh A
Vậy
Khi đó:
Do đó: △BCD vuông tại C
Câu 4: Cho tam giác nhọn ABC có AD là phân giác trong góc A (D ∈ BC). Đường thẳng qua D song song với AB cắt AC tại I, đường thẳng qua D song song với AC cắt AB tại K. Chứng minh rằng △IDK là tam giác cân.
Hướng dẫn giải
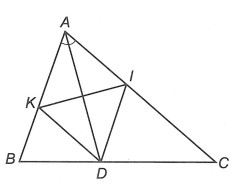
Ta có: (tính chất đường phân giác)
Mà (hai góc so le trong)
(hai góc so le trong)
Suy ra:
Xét △ADI và △ADK, có:
AD chung
Do đó: △ADI = △ADK (g.c.g)
⇒ DI = DK (hai cạnh tương ứng)
Do đó: △IDK cân tại D
Dạng 2: Tính số đo góc, chứng minh các góc bằng nhau
Phương pháp giải
+) Sử dụng tính chất của tam giác cân, tam giác đều.
+) Sử dụng tính chất tổng ba góc trong một tam giác.
Bước 1. Xác định cặp góc bằng nhau qua tính chất của tam giác cân.
Bước 2. Sử dụng tính chất tổng ba góc trong tam giác để tính góc tương ứng.
Ví dụ: Cho tam giác ABC cân tại A. Tính số đo các góc còn lại của tam giác ABC nếu
a)
b)
Hướng dẫn giải
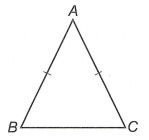
Do tam giác ABC cân đỉnh A nên ta có
Mà ta luôn có
a) Với ta có:
b) Do nên
. Suy ra:
Ví dụ mẫu
Ví dụ. Cho tam giác ABC vuông tại A. Biết AB = BC. Tính số đo các góc của tam giác ABC.
Hướng dẫn giải
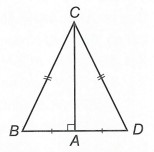
Trên tia đối của tia AB lấy điểm D sao cho DA = BA.
Suy ra: BD = DA + AB = 2AB = BC (1)
Xét △CAB và △CAD, có:
AB = AD
CA chung
Do đó: △CAB = △CAD (c.g.c)
⇒ CD = CB (hai cạnh tương ứng) (2)
Từ (1) và (2) ta có: BC = CD = DB nên △BCD là tam giác đều.
Suy ra hay
Mà △ABC vuông tại A nên
Vậy
Bài tập tự luyện dạng 2
Câu 1: Tam giác ABC là tam giác gì nếu biết và
?
Hướng dẫn giải
Xét △ABC có (tổng ba góc trong tam giác)
Vì nên
Theo giả thiết, ta có:
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Vậy nên △ABC cân đỉnh B
Câu 2: Cho tam giác nhọn ABC. Kẻ AD ⊥ BC (D ∈ BC) và BE ⊥ AC (E ∈ AC). Gọi H là giao điểm của AD và BE. Biết rằng AH = BC, tính số đo .
Hướng dẫn giải
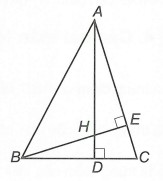
Ta có: (do △ADC vuông tại D)
(do △BCE vuông tại E)
Xét △AHE và △BCE, có:
AH = BC (giả thiết)
(chứng minh trên)
Do đó: △AHE = △BCE cạnh huyền – góc nhọn)
⇒ AE = BE (hai cạnh tương ứng)
Xét △ABE, có: AE = BE,
Suy ra △AEB là tam giác vuông cân tại E.
Do đó:
Câu 3: Tam giác ABC là tam giác gì nếu
và
Hướng dẫn giải
Ta có:
Mà
Suy ra:
Vậy △ABC có , suy ra △ABC là tam giác đều
Dạng 3: Chứng minh đoạn thẳng bằng nhau
Phương pháp giải
+) Sử dụng tính chất: Tam giác cân có hai cạnh bên bằng nhau (dành cho hai đoạn thẳng có một đầu mút chung).
+) Gắn các đoạn thẳng cần chứng minh vào hai cạnh tương ứng của hai tam giác bằng nhau (có thể áp dụng với mọi cặp đoạn thẳng).
Bước 1. Xác định phương pháp chứng minh tương ứng đối với hai đoạn thẳng.
Bước 2. Lập luận và chứng minh.
Ví dụ: Cho tam giác ABC cân tại A. Trên các cạnh AB, AC lần lượt lấy các điểm M, N sao cho AM = AN. Chứng minh rằng: CM = BN.
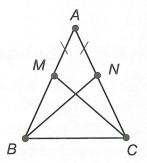
Hướng dẫn giải
Do CM và BN là hai đoạn thẳng không có đầu mút chung nên ta sẽ chứng minh CM = BN thông qua hai tam giác bằng nhau.
Vì △ABC cân đỉnh A nên AB = AC và .
Suy ra: AM + MB = AN + NC
Lại có AM = AN nên BM = CN.
Xét △BCM và △CBN, có:
BM = CN (chứng minh trên),
(chứng minh trên),
BC là cạnh chung
Do đó: △BCM = △CBN (c.g.c)
Suy ra: CM = BN (hai cạnh tương ứng).
Ví dụ mẫu
Ví dụ. Cho tam giác ABC vuông tại A, M là trung điểm của cạnh huyền BC. Chứng minh rằng: MA = MB = MC = BC.
Hướng dẫn giải
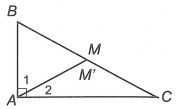
Gọi M’ là điểm nằm trên cạnh BC thỏa mãn M’B = M’A
Khi đó △M’AB cân đỉnh M’
hay
Do △ABC vuông tại A nên ta có:
Từ (1) và (2), ta được:
Suy ra: hay
Do đó △M’AC cân đỉnh M’, suy ra M’A = M’C
Kết hợp với M’B = M’A (cách dựng), ta có M’B = M’C = M’A nên M’ là trung điểm của đoạn BC.
Vậy M’ ≡ M nên ta chứng minh được MB = MC = MA.
Phân tích: Ta cần thiết lập mối quan hệ giữa MA và MB. Vì vậy, ta sẽ chứng minh bài toán dựa trên ý tưởng: Gọi điểm M’ thỏa mãn M’ ∈ BC và M’A = M’B sau đó ta chứng minh M’ ≡ M.
Bình luận: Bạn đọc có thể tự chứng minh chiều ngược của bài toán trên: “Cho tam giác MAB cân đỉnh M. Trên tia đối của tia MB, lấy điểm C sao cho M là trung điểm của BC. Chứng minh rằng tam giác ABC là tam giác vuông”.
Bài tập tự luyện dạng 3
Câu 1: Cho tam giác ABC cân tại A có . Tia phân giác góc B cắt cạnh AC tại điểm D. Chứng minh rằng DA = DB = BC.
Hướng dẫn giải
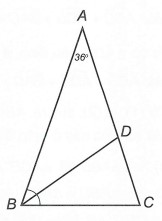
Ta có: AB = AC, (do △ABC cân đỉnh A)
Mà (tổng ba góc trong một tam giác)
Do BD là tia phân giác góc nên
Xét △ABD, có nên △ABD cân đỉnh D ⇒ DB = DA (1)
Có là góc ngoài đỉnh D của △ABD nên
Xét △BCD, có nên △BCD cân đỉnh B ⇒ BD = BC (2)
Từ (1) và (2) suy ra: DA = DB = BC.
Câu 2: Cho tam giác ABC cân đỉnh A, gọi M là trung điểm của BC. Trên cạnh AB lấy điểm D. Từ D kẻ đường vuông góc với AM tại K và kéo dài cắt cạnh AC tại E. Chứng minh: AD = AE.
Hướng dẫn giải
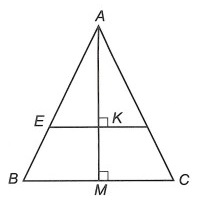
Ta có: △ABC cân đỉnh A nên AB = AC,
Xét △ABM và △ACM, có:
AB = AC
BM = CM (giả thiết)
AM chung
Do đó: △ABM = △ACM (c.c.c)
⇒ (hai góc tương ứng)
Mà
Nên
⇒ AM ⊥ BC
Ta có: DE ⊥ AM (giả thiết)
⇒ DE // BC (cùng vuông góc với AM)
⇒ (các góc đồng vị)
Mà nên
Suy ra △ADE cân đỉnh A. Suy ra AD = AE
Dạng 4: Các bài toán tổng hợp
Phương pháp giải
Sử dụng kết hợp tính chất của tam giác cân, quan hệ song song và một số kết quả đã được chứng minh trong các dạng trước đó.
Ví dụ mẫu
Ví dụ. Cho tam giác ABC cân đỉnh A có M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng MN // BC và MN = BC.
Hướng dẫn giải
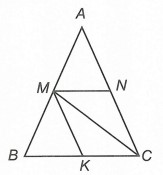
Do ABC cân đỉnh A nên AB = AC và
Lại do M, N lần lượt là trung điểm của AB, AC nên
AM = BM = AB
AN = CN = AC
Do đó AM = AN ⇒ △AMN cân đỉnh A
⇒
Mà △AMN, có:
⇒
Mặt khác:
⇒
Suy ra:
Mà hai góc ở vị trí đồng vị nên MN // BC.
Qua M dựng đường thẳng song song với AC, cắt cạnh BC tại điểm K.
⇒ (đồng vị)
Mà nên
Xét △MBK có nên △MBK cân đỉnh M
⇒ MK = MB.
Ta có: MK = MB = MA = AN = CN.
Lại có: MK // AC nên (đồng vị).
Xét △AMN và △MBK, có:
Do đó: △AMN = △MBK (g.c.g)
⇒ MN = BK (hai cạnh tương ứng) (1)
Xét △MNC và △CKM, có:
(do MN // BC)
CM chung
(do MK // AC)
Do đó: △MNC = △CKM (g.c.g)
⇒ MN = CK (hai cạnh tương ứng) (2)
Từ (1)và (2) suy ra MN = BK = CK.
Mà BK + CK = BC nên K là trung điểm của BC.
Do đó: MN = BK = CK = BC (điều phải chứng minh).
Hướng tư duy:
+) Chứng minh quan hệ song song có thể sử dụng mối quan hệ về góc (ưu tiên). Do đó ta chứng minh cặp góc so le trong hoặc đồng vị bằng nhau.
+) Chứng minh hai góc bằng nhau qua tính chất của tam giác cân hoặc hai đường thẳng song song.
+) Chứng minh quan hệ độ dài đoạn thẳng có thể sử dụng các đoạn thẳng tương ứng trong hai tam giác bằng nhau.
Bình luận: Đây là bài toán điển hình trong việc sử dụng các mối quan hệ từ tam giác cân cho đến các đường thẳng song song. Có thể mở rộng kết quả của bài toán này cho tam giác ABC bất kỳ:
Gọi M, N lần lượt là trung điểm của AB, AC.
Khi đó ta có: MN // BC, MN = BC
Lưu ý việc chứng minh song song (MN // BC) có thể thực hiện thông qua việc dựng đường thẳng MN’ // BC với N’ ∈ BC. Sau đó, ta tìm cách chỉ ra N’ ≡ N.
Bài tập tự luyện dạng 4
Câu 1: Cho tam giác ABC có BC = 2AB, M là trung điểm của cạnh BC, D là trung điểm của BM. Chứng minh rằng AC = 2AD.
Hướng dẫn giải
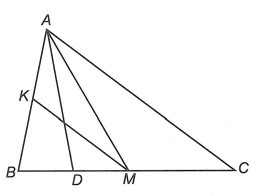
Do M là trung điểm của BC nên BM = CM = BC = AB
Gọi K là trung điểm của AB nên AK = BK = AB
Ta có: D là trung điểm của BM nên BD = MD = BM
Suy ra: AK = BK = BD = MD
Xét △ABD và △MBK, có:
AB = MB
chung
BD = BK.
Do đó: △ABD = △MBK (c.g.c).
Suy ra: AD = MK (hai cạnh tương ứng).
Lại có: MK = AC (áp dụng kết quả phần ví dụ).
Suy ra: AD = AC hay AC = 2AD
Câu 2: Cho tam giác ABC cân tại A có kẻ BD vuông góc với AC. Trên cạnh AB lấy điểm E sao cho AE = AD. Chứng minh rằng:
a) DE // BC
b) CE ⊥ AB
Hướng dẫn giải
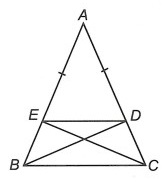
a) Do △ABC cân đỉnh A nên
Mà
Ta có: △ADE cân đỉnh A (do AD = AE) nên
Mà
Từ (1) và (2) suy ra:
Mà hai góc này ở vị trí đồng vị nên DE // BC.
b) Xét △ABD và △ACE, có:
AB = AC
chung
AD = AE
Do đó: △ABD = △ACE (c.g.c)
⇒ (hai góc tương ứng)
⇒ CE ⊥ AB (đpcm)