Tính chất 3 đường phân giác của tam giác

Tính chất đường phân giác của tam giác

Kiến thức cơ bản

Định lý

Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.

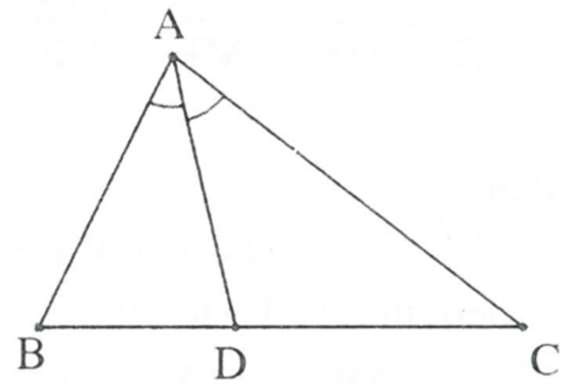
$\left. \begin{gathered} \begin{array}{*{20}{c}} {}&{} \end{array}\Delta ABC \hfill \\ \widehat {BAD} = \widehat {CAD} \hfill \\ \end{gathered} \right\} \Rightarrow \frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}$

Chú ý:

+) Định lý vẫn đúng với đối với đường phân giác góc ngoài của tam giác.

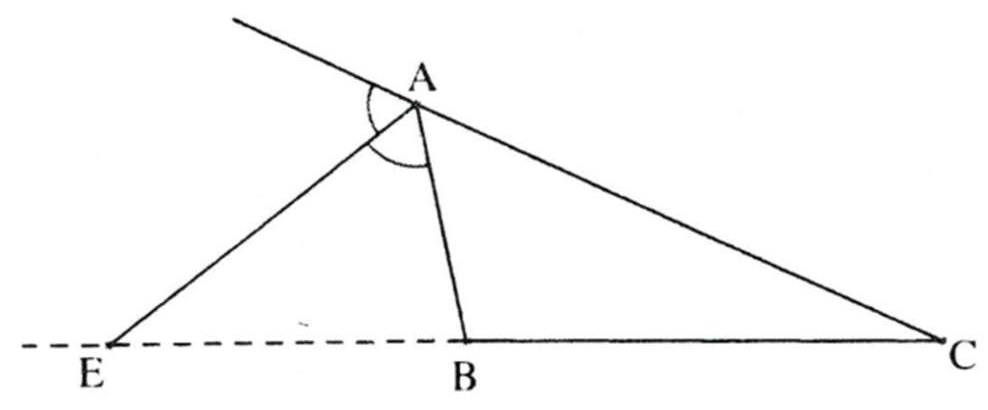
$\left. \begin{gathered} \Delta ABC\left( {AB \ne AC} \right) \hfill \\ \widehat {BAE} = \widehat {CAE} \hfill \\ \end{gathered} \right\} \Rightarrow \frac{{EB}}{{EC}} = \frac{{AB}}{{AC}}$

+) Các định lý trên có định lý đảo:

$\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}$ ⇒ AD là đường phân giác trong của tam giác.

$\frac{{EB}}{{EC}} = \frac{{AB}}{{AC}}$ ⇒ AE là đường phân giác ngoài của tam giác.

Phân dạng bài tập

Dạng 1. Tính độ dài đoạn thẳng

Phương pháp giải

+) Áp dụng tính chất đường phân giác, lập tỉ lệ thức giữa các đoạn thẳng và sử dụng kĩ thuật đại số hóa hình học.

+) Áp dụng định lí Py-ta-go.

Ví dụ

Ví dụ 1. Cho tam giác ABC có AB = 5 cm, BC = 7 cm và CA = 6 cm. Tia phân giác của góc $\widehat {BAC}$ cắt cạnh BC ở E. Tính các đoạn EB, EC.

Hướng dẫn giải

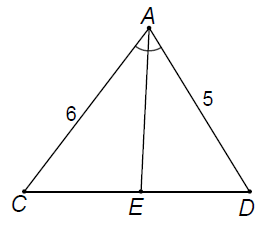
Áp dụng tính chất của đường phân giác AD vào tam giác ABC và tính chất của dãy tỉ số bằng nhau, ta có:

$\frac{{EB}}{{BA}} = \frac{{EC}}{{CA}} = \frac{{EB + EC}}{{BA + CA}} = \frac{{BC}}{{BA + CA}}$

Hay $\frac{{EB}}{5} = \frac{{EC}}{6} = \frac{7}{{11}}$

$\Rightarrow EB = \frac{{35}}{{11}}\left( {cm} \right);{\text{ }}EC = \frac{{42}}{{11}}\left( {cm} \right)$

Ví dụ 2. Cho tam giác ABC vuông ở A, đường phân giác BD. Tính AB, BC biết AD = 4 cm và DC = 5 cm.

Hướng dẫn giải

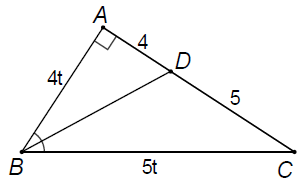
Áp dụng tính chất của đường phân giác BD vào tam giác ABC, ta được:

$\frac{{AB}}{{BC}} = \frac{{DA}}{{DC}} = \frac{4}{5} \Rightarrow \left\{ \begin{gathered} AB = 4t \hfill \\ BC = 5t \hfill \\ \end{gathered} \right.{\text{ }}\left( {t > 0} \right)$

Áp dụng định lí Py-ta-go vào tam giác ABC vuông ở A, ta được:

BC² = CA² + AB²

⇔ (5t)² = 9² + (4t)²

⇔ (3t)² = 9²

⇔ 3t = 9

⇔ t = 3 (vì t > 0)

Ví dụ 3. Cho tam giác ABC có BC = 24 cm, AC = 3AB. Tia phân giác của góc ngoài tại A cắt đường thẳng BC ở E. Tính độ dài EB.

Hướng dẫn giải

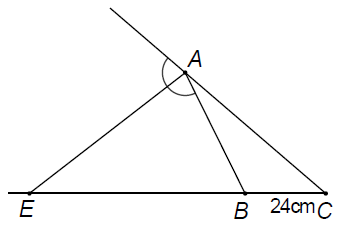
Áp dụng tính chất của đường phân giác ngoài AE vào tam giác ABC, ta được:

$\frac{{EB}}{{EC}} = \frac{{BA}}{{CA}} = \frac{{BA}}{{3BA}} = \frac{1}{3} \Rightarrow \frac{{EB}}{1} = \frac{{EC}}{3}$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

$\frac{{EB}}{1} = \frac{{EC}}{3} = \frac{{EC - EB}}{{3 - 1}} = \frac{{BC}}{2} = \frac{{24}}{2} = 12\left( {cm} \right)$

Vậy EB = 12 cm

Dạng 2. Tính tỉ số độ dài, tỉ số diện tích hai tam giác

Phương pháp giải

+) Áp dụng tính chất đường phân giác, lập tỉ lệ thức giữa các đoạn thẳng.

+) Sử dụng kĩ thuật đại số hóa hình học. Công thức và kết quả thu được từ công thức tính diện tích tam giác.

Ví dụ

Ví dụ 1. Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của góc $\widehat {AMB}$ cắt cạnh AB ở D, tia phân giác của góc $\widehat {AMC}$ cắt các cạnh AC ở E. Chứng minh rằng: DE // BC.

Hướng dẫn giải

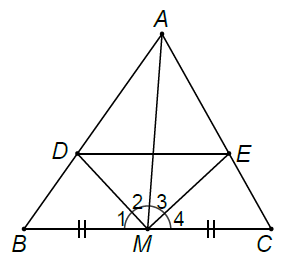
Từ giả thiết AM là trung tuyến, đặt BM = MC = a.

Áp dụng tính chất của đường phân giác MD và ME vào △AMB và △AMC, ta được:

$\left\{ \begin{gathered} \frac{{AB}}{{DB}} = \frac{{AM}}{{MB}} = \frac{{AM}}{a}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \frac{{AE}}{{EC}} = \frac{{AM}}{{MC}} = \frac{{AM}}{a}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right. \Rightarrow \frac{{AB}}{{DB}} = \frac{{AE}}{{EC}}$

Điều này chứng tỏ đường thẳng DE cắt hai cạnh AB và AC của △ABC và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ, nên DE // BC (theo định lí Ta-lét đảo).

Ví dụ 2.

a\ Cho tam giác ABC với đường trung tuyến AM và phân giác AD. Tính diện tích tam giác ADM biết AB = m, AC = n (n > m).

b\ Cho n = 7 cm, m = 3 cm. Hỏi diện tích tam giác ADM chiếm bao nhiêu phần trăm diện tích tam giác ABC?

Hướng dẫn giải

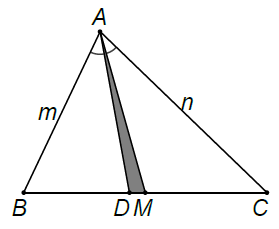
a\ Ta có: $\frac{{{S_{ADM}}}}{{{S_{ABC}}}} = \frac{{DM}}{{BC}}$ hay ${S_{ADM}} = \frac{{DM}}{{BC}} \cdot S$

(vì chung chiều cao kẻ từ A đến BC, với S = S_ABC).

Ta còn phải tính tỉ số DM ∶ BC.

Áp dụng tính chất của đường phân giác AD vào tam giác ABC, ta được:

$\frac{{DB}}{{DC}} = \frac{{BA}}{{CA}} = \frac{m}{n} \Rightarrow \left\{ \begin{gathered} DB = mt \hfill \\ DC = nt \hfill \\ \end{gathered} \right.{\text{ }}\left( {t > 0} \right)$

Do đó: $BC = DB + DC = \left( {m + n} \right)t$ , nên:

$\begin{gathered} BM = \frac{1}{2}BC = \frac{{\left( {m + n} \right)t}}{2}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \Rightarrow DM = BM - BD = \frac{{\left( {m + n} \right)t - mt}}{2} = \frac{{\left( {n - m} \right)t}}{2} \hfill \\ \end{gathered}$

Suy ra tỉ số:

$DM:BC = \frac{{\left( {n - m} \right)t}}{2}:\left( {m + n} \right)t = \frac{{n - m}}{{2\left( {m + n} \right)}}$

Vậy ${S_{ADM}} = \frac{{n - m}}{{2\left( {m + n} \right)}} \cdot S$

b\ Với n = 7 cm, m = 3 cm thì

${S_{ADM}} = \frac{{7 - 3}}{{2\left( {7 + 3} \right)}} \cdot S = 0,2 \cdot S = 20\% S$

Điều này chứng tỏ diện tích tam giác ADM chiếm 20% diện tích tam giác ABC.

Ví dụ 3. Cho tam giác ABC, các đường phân giác BD và CE. Biết $\frac{{AD}}{{BC}} = \frac{2}{3};\frac{{EA}}{{EB}} = \frac{5}{6}$ . Tính các cạnh của tam giác ABC, biết chu vi tam giác bằng 45cm.

Hướng dẫn giải

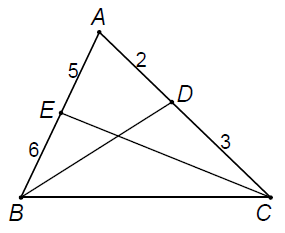
Áp dụng tính chất của các đường phân giác BD và CE vào tam giác ABC, ta được:

$\begin{gathered} \frac{{AB}}{{BC}} = \frac{{AD}}{{BC}} = \frac{2}{3} = \frac{4}{6} \Rightarrow \left\{ \begin{gathered} AB = 4t \hfill \\ BC = 6t \hfill \\ \end{gathered} \right.{\text{ }}\left( {t > 0} \right) \hfill \\ \frac{{AC}}{{BC}} = \frac{{AE}}{{EB}} = \frac{5}{6} \Rightarrow \left\{ \begin{gathered} AC = 5t \hfill \\ BC = 6t \hfill \\ \end{gathered} \right.{\text{ }}\left( {t > 0} \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Từ giả thiết chu vi của tam giác ABC bằng 45cm, ta có:

45 = AB + BC + CA = 4t + 6t + 5t = 15t ⇔ t = 3

Vậy AB = 12 cm, BC = 18 cm, CA = 15 cm

Phiếu bài tự luyện dạng cơ bản

Bài 1: Tính độ dài x, y trong các hình vẽ sau:

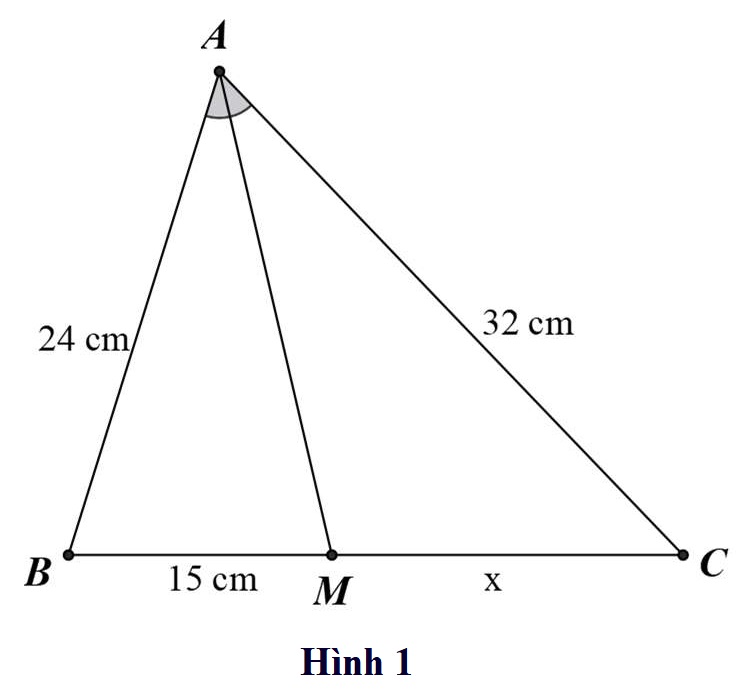
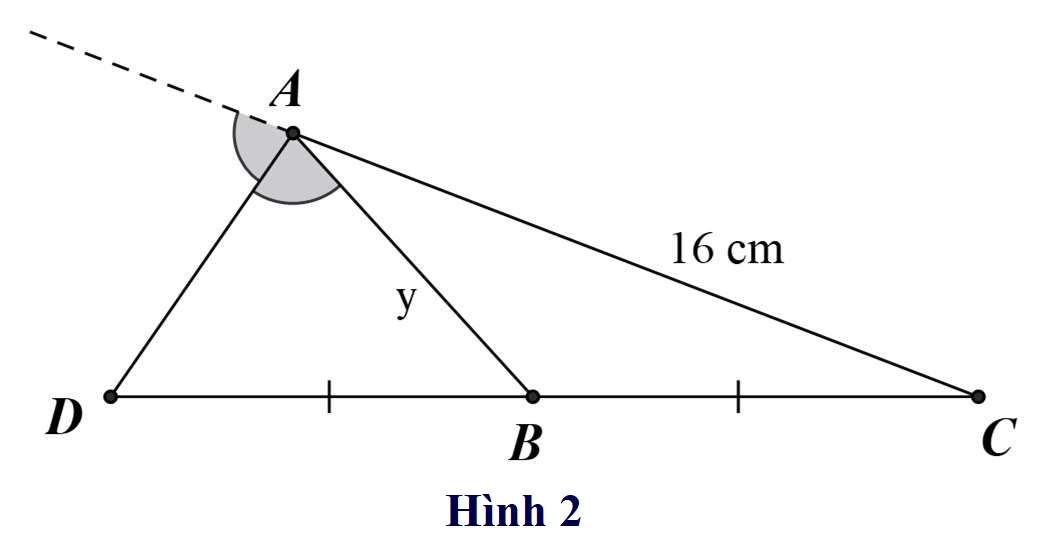
Hướng dẫn giải

a\ Xét △ABC có AM là đường phân giác trong nên:

$\begin{gathered} \frac{{MB}}{{MC}} = \frac{{AB}}{{AC}} \hfill \\ \Rightarrow \frac{{15}}{x} = \frac{{24}}{{32}} = \frac{3}{4}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \Rightarrow x = \frac{{15 \cdot 4}}{3} = 20\left( {cm} \right) \hfill \\ \end{gathered}$

b\ Xét △ABC có AD là đường phân giác ngoài nên: $\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}{\text{ }}\left( 1 \right)$

Mà B là trung điểm của đoạn thẳng DC nên: $\frac{{DB}}{{DC}} = \frac{1}{2}{\text{ }}\left( 2 \right)$

Từ (1) và (2) suy ra: $\frac{1}{2} = \frac{y}{{16}} \Rightarrow y = 8\left( {cm} \right)$

Bài 2: Cho tam giác ABC có AB = 4 cm, AC = 5 cm, BC = 6 cm, các đường phân giác BD và CE cắt nhau ở I.

a\ Tính các độ dài AD, DC.

b\ Tính các độ dài AE, BE.

Hướng dẫn giải

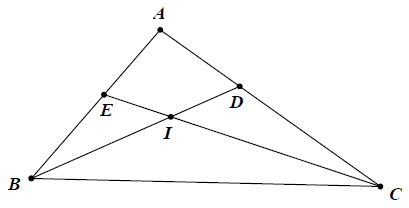
a\ Theo tính chất đường phân giác:

$\frac{{AD}}{{DC}} = \frac{{BA}}{{BC}} = \frac{2}{3} \Rightarrow \frac{{AD}}{2} = \frac{{CD}}{3} = 1$

Do đó: AD = 2 cm, CD = 3 cm

b\ Ta có, theo tính chất đường phân giác:

$\frac{{AE}}{{EB}} = \frac{{CA}}{{CB}} = \frac{5}{6} \Rightarrow \frac{{AE}}{5} = \frac{{EB}}{6} = \frac{4}{{11}}$

Do đó: $AE = \frac{{20}}{{11}}\left( {cm} \right);{\text{ }}BE = \frac{{24}}{{11}}\left( {cm} \right)$

Bài 3: Cho tam giác cân ABC có AB = BC. Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N. Chứng minh: MN // AC.

Hướng dẫn giải

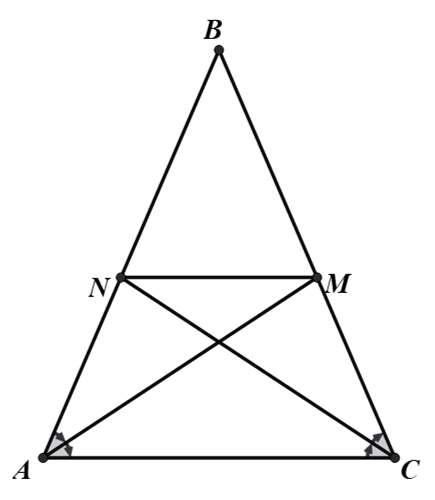
AM là phân giác của $\widehat A$ nên $\frac{{BM}}{{CM}} = \frac{{AB}}{{AC}}$

CN là phân giác của $\widehat C$ nên $\frac{{BN}}{{AN}} = \frac{{BC}}{{AC}}$

Lại có: AB = BC

Suy ra: $\frac{{AB}}{{AC}} = \frac{{BC}}{{AC}} \Rightarrow \frac{{BN}}{{AN}} = \frac{{BM}}{{CM}}$

⇒ MN // AC

Bài 4: Cho △ABC có AD, BE, CF là các đường phân giác. Chứng minh rằng:

$\frac{{AE}}{{EC}} \cdot \frac{{CD}}{{DB}} \cdot \frac{{BF}}{{FA}} = 1$

Hướng dẫn giải

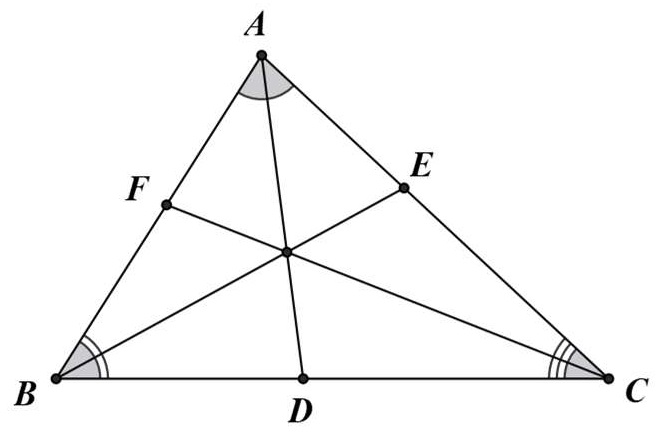
Xét △ABC, áp dụng tính chất đường phân giác ta có:

$\begin{gathered} \frac{{AE}}{{EC}} = \frac{{AB}}{{BC}}{\text{ }}\left( 1 \right) \hfill \\ \frac{{CD}}{{DB}} = \frac{{AC}}{{AB}}{\text{ }}\left( 2 \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \frac{{BF}}{{FA}} = \frac{{BC}}{{AC}}{\text{ }}\left( 3 \right) \hfill \\ \end{gathered}$

Nhân (1), (2), (3) theo vế ta được:

$\frac{{AE}}{{EC}} \cdot \frac{{CD}}{{DB}} \cdot \frac{{BF}}{{FA}} = \frac{{AB}}{{BC}} \cdot \frac{{AC}}{{AB}} \cdot \frac{{BC}}{{AC}} = 1$

Bài 5: Cho hình bình hành ABCD. Phân giác của $\widehat A$ và $\widehat D$ cắt các đường chéo BD và AC lần lượt tại M và N. Chứng minh: MN // AD.

Hướng dẫn giải

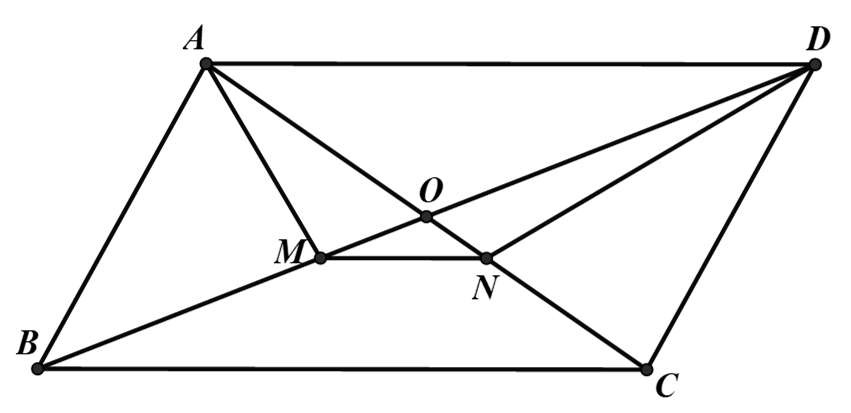
Gọi O là giao điểm BD và AC

Xét △ABD, phân giác AM ta có: $\frac{{AB}}{{AD}} = \frac{{BM}}{{DM}}$

Tương tự: $\frac{{CD}}{{AD}} = \frac{{CN}}{{AN}}$

Mà AB = CD suy ra $\frac{{BM}}{{DM}} = \frac{{CN}}{{AN}}$

Từ đó ta có: $\frac{{BM}}{{DM}} + 1 = \frac{{CN}}{{AN}} + 1$

$\Leftrightarrow \frac{{BD}}{{DM}} = \frac{{CA}}{{AN}} \Leftrightarrow \frac{{DO}}{{DM}} = \frac{{AO}}{{AN}}$

⇒ MN // AD

Bài 6: Cho △ABC có phân giác AD, biết AB = m, AC = n.

a\ Tính tỉ số diện tích của △ABD và △ACD theo m và n.

b\ Vẽ phân giác DE của △ADB và vẽ phân giác DF của △ADC. Chứng minh rằng: AF⋅CD⋅BE = AE⋅BD⋅CF

Hướng dẫn giải

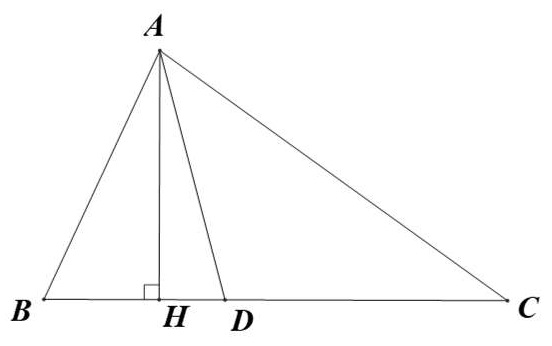
a\ Vẽ đường cao △AH của ABC. Vì △ABC có phân giác AD nên:

$\frac{{BD}}{{CD}} = \frac{{AB}}{{AC}} = \frac{m}{n}$

Vậy $\frac{{{S_{\Delta ABD}}}}{{{S_{\Delta ACD}}}} = \frac{\begin{gathered} \hfill \\ \frac{1}{2}AH \cdot BD \hfill \\ \end{gathered} }{\begin{gathered} \frac{1}{2}AH \cdot CD \hfill \\ \hfill \\ \end{gathered} } = \frac{{BD}}{{CD}} = \frac{m}{n}$

b\ Ta có: $\frac{{AF}}{{CF}} = \frac{{AD}}{{CD}}$ (do DF là phân giác $\widehat {ADC}$ )

$\frac{{BE}}{{AE}} = \frac{{BD}}{{AD}}$ (do DE là phân giác $\widehat {ADB}$ )

$\begin{gathered} \Rightarrow \frac{{AF}}{{CF}} \cdot \frac{{CD}}{{BD}} \cdot \frac{{BE}}{{AE}} = \frac{{AD}}{{CD}} \cdot \frac{{CD}}{{BD}} \cdot \frac{{BD}}{{AD}} = 1\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \Rightarrow AF \cdot CD \cdot BE = AE \cdot BD \cdot CF \hfill \\ \end{gathered}$

Bài 7: Cho △ABC, trung tuyến AM, đường phân giác của $\widehat {AMB}$ cắt AB ở D, đường phân giác của $\widehat {AMC}$ cắt AC ở E.

a\ Chứng minh rằng: DE // BC.

b\ Gọi I là giao điểm của AM và DE. Chứng minh rằng: DI = IE.

c\ Tính DE, biết BC = 30 cm, AM = 10 cm.

d\ △ABC phải thêm điều kiện gì để ta có DE = AM?

e\ Chứng minh rằng △ABC cân nếu biết MD = ME.

Hướng dẫn giải

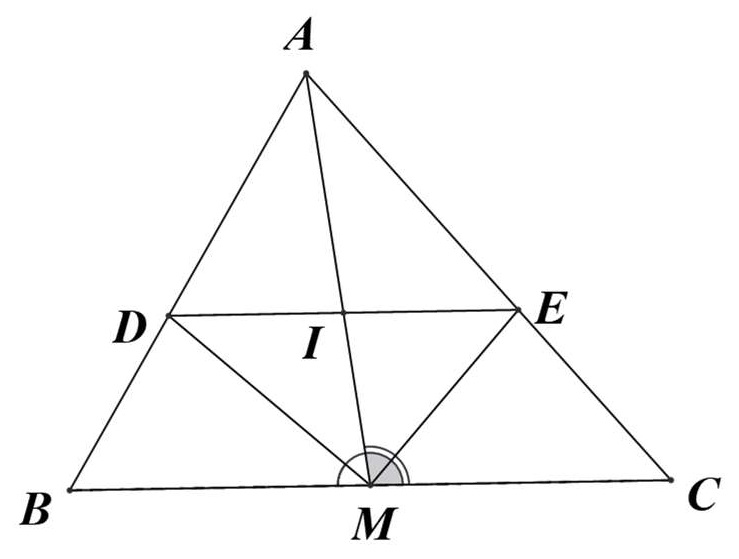
a\ Ta có: $\frac{{BD}}{{AD}} = \frac{{MB}}{{MA}}$ (do MD là phân giác $\widehat {AMB}$ )

$\frac{{CE}}{{AE}} = \frac{{MC}}{{MA}}$ (do ME là phân giác $\widehat {AMC}$ )

Mà MB = MC (M là trung điểm của BC)

$\Rightarrow \frac{{BD}}{{AD}} = \frac{{CE}}{{AE}} \Rightarrow DE\parallel BC$

b\ Xét △ABM và △ACM lần lượt có:

DI // BM và EI // CM

$\frac{{DI}}{{BM}} = \frac{{EI}}{{CM}}\left( { = \frac{{AI}}{{AM}}} \right)$

Mà BM = CM ⇒ DI = EI

c\ Ta có: $\frac{{BD}}{{AD}} = \frac{{MB}}{{MA}}$

Mà $\frac{{BD}}{{AD}} = \frac{{IM}}{{AI}}{\text{ }}\left( {do{\text{ }}DI\parallel BM} \right) \Rightarrow \frac{{BM}}{{AM}} = \frac{{IM}}{{AI}}$

Ta lại có: $\frac{{BM}}{{DI}} = \frac{{AM}}{{AI}}{\text{ }}\left( {do{\text{ }}DI\parallel BM} \right)$

$\begin{gathered} \frac{{BM}}{{DI}} = \frac{{AI + IM}}{{AI}} = 1 + \frac{{IM}}{{AI}} = 1 + \frac{{BM}}{{AM}} = \frac{{AM + BM}}{{AM}} \hfill \\ \Rightarrow DI = \frac{{BM \cdot AM}}{{AM + BM}} = \frac{{15 \cdot 10}}{{10 + 15}} = \frac{{150}}{{25}} = 6\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \Rightarrow ED = 2DI = 2 \cdot 6 = 12{\text{ }}\left( {do{\text{ }}DI = IE = \frac{1}{2}DE} \right) \hfill \\ \end{gathered}$

d\ Để DE = AM ta cần tứ giác ADME là hình chữ nhật

Hay DM // AE, EM // AD, $\widehat {BAC} = 90^\circ$

Khi $\widehat {BAC} = 90^\circ$ thì AM = MB = MC (đường trung tuyến ứng với cạnh huyền BC)

⇒ △ABM, △ACM cân tại M

⇒ MD ⊥ AB, ME ⊥ AC (đường phân giác của tam giác cân đồng thời là đường cao)

Mà: AB ⊥ AC. Suy ra: DM // AE, EM // AD.

Suy ra tứ giác ADME là hình chữ nhật

Vậy △ABC vuông tại A thì DE = AM.

e) Khi DM = EM thì △DME cân tại M có MI là trung tuyến (DI = IE) nên đồng thời là đường cao

⇒ MI ⊥ DE

Mà DE // BC (cmt) nên MI ⊥ BC

△ABC có AI vừa là đường trung tuyến vừa là đường cao nên là tam giác cân.

Bài 8: Cho △ABC vuông cân tại A. Đường cao AH và đường phân giác BE cắt nhau tại I. Chứng minh rằng: CE = 2HI.

Hướng dẫn giải

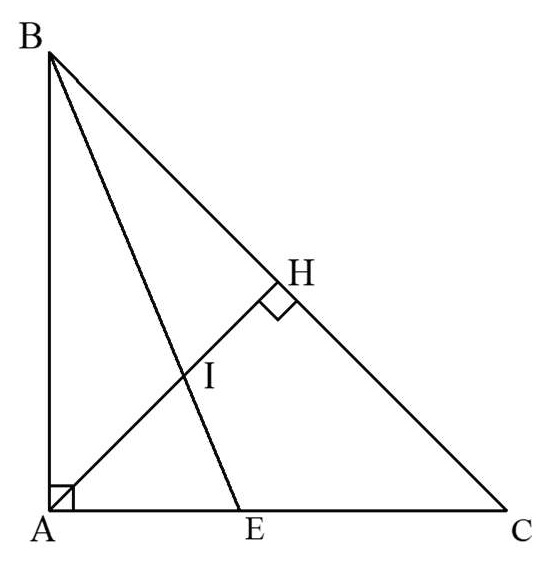
$\begin{gathered} \widehat {AIE} = \widehat {BAH} + \widehat {ABI} = \frac{1}{2}\left( {\widehat A + \widehat B} \right) \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array}{\text{ }} = 45^\circ + \frac{1}{2}\widehat B = 45^\circ + \frac{1}{2}\widehat C = \widehat {AEI}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Suy ra: △AIE cân tại A ⇒ AI = AE (1)

Áp dụng tính chất đường phân giác của △ABH và △BAC ta có:

$\begin{gathered} \frac{{IH}}{{IA}} = \frac{{BH}}{{BA}} \Rightarrow \frac{{AB}}{{AI}} = \frac{{BH}}{{IH}}{\text{ }}\left( 2 \right) \hfill \\ \frac{{EC}}{{EA}} = \frac{{BC}}{{BA}} \Rightarrow \frac{{AB}}{{AE}} = \frac{{BC}}{{EC}}{\text{ }}\left( 3 \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Từ (2) và (3) suy ra: $\frac{{BH}}{{IH}} = \frac{{BC}}{{EC}}{\text{ }}\left( 4 \right)$

Vì △ABC vuông cân tại A nên BC = 2BH.

Từ đó kết hợp với (4) suy ra EC = 2IH

Dạng bài nâng cao

Ví dụ 1. Cho tam giác ABC vuông tại A có G là trọng tâm, BM là đường phân giác. Biết rằng GM ⊥ AC. Chứng minh rằng BM vuông góc với trung tuyến AD.

Hướng dẫn giải

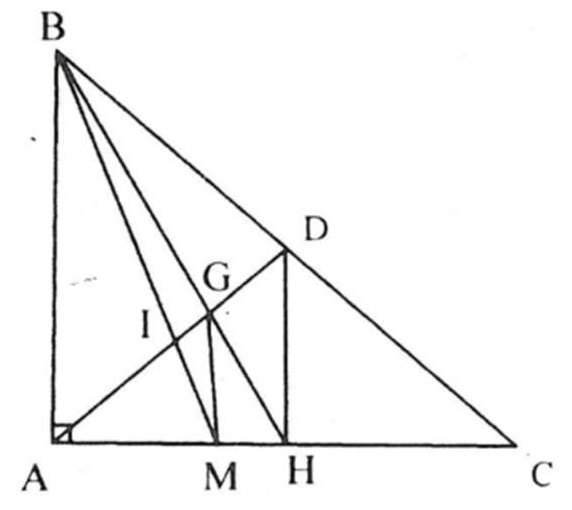
Cách 1: (Không dùng tính chất đường phân giác)

Gọi I là giao điểm của BM và AD, H là trung điểm AC

⇒ DH // AB và DH = $\frac{1}{2}$ AB (vì DH là đường trung bình △ABC)

Lại có: GM // AB (cùng vuông góc với AC)

⇒ GM // DH. Áp dụng hệ quả định lý ta-lét:

Xét △ADH, có GM // DH

$\Rightarrow \frac{{GM}}{{DH}} = \frac{{AG}}{{AD}} = \frac{2}{3} \Rightarrow \frac{{GM}}{{DH}} = \frac{2}{3}$

Xét △ABI, có GM // AB

$\begin{gathered} \Rightarrow \frac{{GI}}{{AI}} = \frac{{GM}}{{AB}} = \frac{{GH}}{{BH}} = \frac{1}{3} \hfill \\ \Rightarrow \frac{{GI + AI}}{{AI}} = \frac{{1 + 3}}{3}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \Rightarrow AI = \frac{3}{4}AG = \frac{3}{4} \cdot \frac{2}{3} \cdot AD \hfill \\ \Rightarrow AI = \frac{{AD}}{2}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

⇒ I là trung điểm của AD.

△ABD có BI vừa là đường phân giác, vừa là đường trung tuyến, suy ra △ABD cân tại B nên BI vừa là đường cao vừa là đường phân giác. Do đó: BM ⊥ AD.

Cách 2: △ADH có GM // DH

$\begin{gathered} \Rightarrow \frac{{AM}}{{AH}} = \frac{{AG}}{{AD}} = \frac{2}{3} \hfill \\ \Rightarrow 3 \cdot AM = 2 \cdot AH = AC = AM + MC\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \Rightarrow MC = 2AM \hfill \\ \end{gathered}$

Áp dụng tính chất đường phân giác trong △ABC, ta có:

$\frac{{BC}}{{AB}} = \frac{{MC}}{{MA}} = 2 \Rightarrow AB = \frac{{BC}}{2} = BD$

Vậy △ABD cân tại B nên BI vừa là phân giác vừa là đường cao.

Do đó: BM ⊥ AD

Ví dụ 2. Cho tam giác ABC có I là giao điểm của ba đường phân giác. Đường thẳng qua I cắt các đường thẳng BC, CA, AB lần lượt tại D, E, F sao cho D, E nằm cùng phía đối với điểm I. Chứng minh rằng: $\frac{{BC}}{{ID}} + \frac{{AC}}{{IE}} = \frac{{AB}}{{IF}}$

Hướng dẫn giải

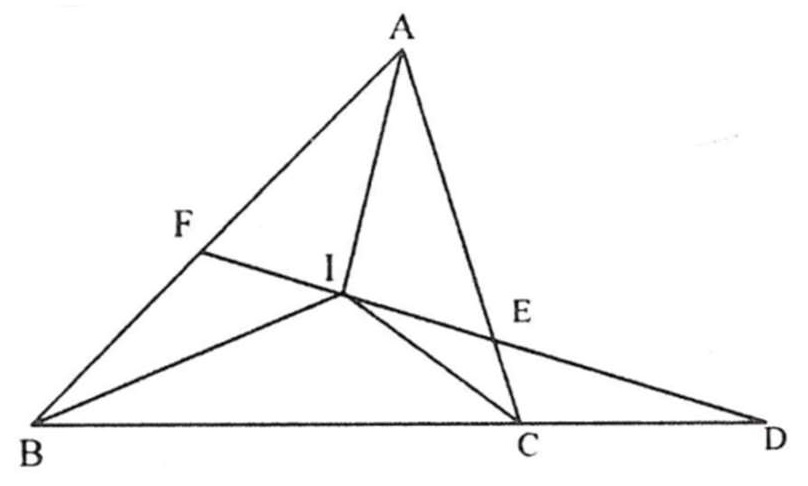
Áp dụng tính chất đường phân giác trong và ngoài của tam giác, ta có:

$\frac{{BD}}{{ID}} = \frac{{BF}}{{IF}};{\text{ }}\frac{{CE}}{{IE}} = \frac{{CD}}{{ID}};{\text{ }}\frac{{AF}}{{IF}} = \frac{{AE}}{{IE}}$

Ta có:

$\begin{gathered} \frac{{BC}}{{ID}} = \frac{{BD}}{{ID}} - \frac{{CD}}{{ID}} = \frac{{BF}}{{IF}} - \frac{{CE}}{{IE}}{\text{ }}\left( 1 \right) \hfill \\ \frac{{AC}}{{IE}} = \frac{{AE}}{{IE}} + \frac{{CE}}{{IE}} = \frac{{AF}}{{IF}} + \frac{{CE}}{{IE}}{\text{ }}\left( 2 \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Từ (1) và (2) cộng vế với vế, suy ra:

$\frac{{BC}}{{ID}} + \frac{{AC}}{{IE}} = \frac{{BF}}{{IF}} + \frac{{AF}}{{IF}} = \frac{{AB}}{{IF}}$

Ví dụ 3. Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. Trên tia HC lấy điểm D sao cho HD = AH. Đường thẳng vuông góc với BC tại D cắt AC tại E. Gọi M là trung điểm của BE, tia AM cắt BC tại G. Chứng minh: $\frac{{BG}}{{BC}} = \frac{{HD}}{{AH + HC}}$

Hướng dẫn giải

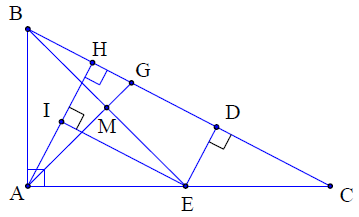
$\begin{gathered} \frac{{BG}}{{BC}} = \frac{{HD}}{{AH + HC}} \hfill \\ \Rightarrow \frac{{BC}}{{BG}} = \frac{{AH + HC}}{{HD}} = 1 + \frac{{HC}}{{HD}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \Rightarrow \frac{{BC}}{{BG}} - 1 = \frac{{HC}}{{HD}} \hfill \\ \Rightarrow \frac{{BC - BG}}{{BG}} = \frac{{HC}}{{HD}}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \Rightarrow \frac{{GC}}{{GB}} = \frac{{HC}}{{HD}} \hfill \\ \end{gathered}$

Ta chứng minh: $\frac{{HC}}{{HD}} = \frac{{GC}}{{GB}}$

Ta có: $DE\parallel AH \Rightarrow \frac{{HC}}{{HD}} = \frac{{AC}}{{AE}}$

Dựng đường thẳng qua E vuông góc AH tại I, suy ra HIED là hình chữ nhật.

$IE = HD = HA;{\text{ }}\widehat {IAE} = \widehat {HBA}$

Do đó hai tam giác vuông IEA và HBA bằng nhau.

$\Rightarrow AE = AB \Rightarrow \frac{{HC}}{{HD}} = \frac{{AC}}{{AE}} = \frac{{AC}}{{AB}}$

Vì M là trung điểm BE, tam giác ABE cân tại A nên AM là tia phân giác góc $\widehat {BAC}$ hay G là chân đường phân giác trong góc $\widehat {BAC}$ trong tam giác ABC.

Từ đó ta có: $\frac{{GC}}{{GB}} = \frac{{AC}}{{AB}}$

Vậy $\frac{{HC}}{{HD}} = \frac{{AC}}{{AE}} = \frac{{AC}}{{AB}} = \frac{{GC}}{{GB}}$

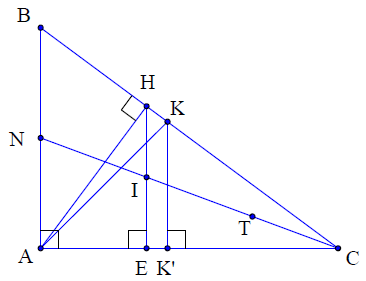
Ví dụ 4. Cho tam giác ABC vuông tại A có AH là đường cao (H ∈ BC), N là trung điểm của AB. Biết AB = 6 cm, AC = 8 cm.

a\ Vẽ AK là tia phân giác của góc $\widehat {BAC}$ (K ∈ BC). Tính AK?

b\ Gọi E là hình chiếu vuông góc của H lên AC và T là điểm đối xứng của N qua I với I là giao điểm của CN và HE. Chứng minh tứ giác NETH là hình bình hành.

Hướng dẫn giải

a\ Theo tính chất chân đường phân giác trong ta có:

$\frac{{KC}}{{KB}} = \frac{{AC}}{{AB}} = \frac{4}{3} \Rightarrow \frac{{CK}}{{CB}} = \frac{4}{7}$

Gọi K’ là hình chiếu vuông góc của K lên AC, suy ra KK’ // AB. Theo định lí Talet ta có:

$\begin{gathered} \frac{{KK'}}{{AB}} = \frac{{CK}}{{CB}} = \frac{4}{7} \hfill \\ \Rightarrow KK' = \frac{4}{7} \cdot AB = \frac{4}{7} \cdot 6 = \frac{{24}}{7}\left( {cm} \right)\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered}$

Mặt khác, tam giác AKK’ vuông cân tại K’ nên:

$AK = KK' \cdot \sqrt 2 = \frac{{24\sqrt 2 }}{7}\left( {cm} \right)$

b\ Ta chứng minh I là trung điểm của HE.

Vì HE ⊥ AC nên HE // BA. Theo định lí Talet ta có:

$\frac{{IE}}{{NA}} = \frac{{CI}}{{CN}} = \frac{{IH}}{{NB}}$

Vì NA = NB nên IE = IH. Do đó I là trung điểm của HE.

Theo giả thiết thì I là trung điểm của NT.

Tứ giác NETH có hai đường chéo NT và EH có chung trung điểm I nên NETH là hình bình hành.

Thầy Tú dạy toán