Tính chất 3 đường trung trực của tam giác

Tính chất ba đường trung trực của tam giác

+) Trong một tam giác, đường trung trực của một cạnh được gọi là một đường trung trực của tam giác đó.

+) Ba đường trung trực của tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó. Điểm này chính là tâm đường tròn đi qua 3 đỉnh của tam giác (ta gọi đường tròn này là đường tròn ngoại tiếp tam giác).

Đường trung trực của tam giác đặc biệt

+) Trong một tam giác cân, đường trung trực ứng với cạnh đáy đồng thời là đường trung tuyến, đường phân giác xuất phát từ đỉnh đối diện.

+) Trong một tam giác, nếu hai trong ba đường (đường trung tuyến, đường phân giác xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của đỉnh này) trùng nhau thì tam giác đó cân.

Ví dụ. Chứng minh ba đường trung trực của tam giác cùng đi qua một điểm:

Gọi O là giao điểm của hai đường trung trực ứng với các cạnh AB và AC của △ABC.

Vì O nằm trên đường trung trực AB nên OA = OB.

Vì O nằm trên đường trung trực của AC nên OA = OC.

Từ (1) và (2), ta có OB = OC = (OA).

Suy ra O nằm trên đường trung trực của cạnh BC (tính chất đường trung trực)

Vậy ba đường trung trực của △ABC cùng đi qua điểm O và OA = OB = OC.

Phân dạng bài tập

Dạng 1. Xác định tâm đường tròn ngoại tiếp tam giác

Phương pháp giải

Sử dụng tính chất

+) Giao điểm các đường trung trực trong tam giác thì cách đều ba đỉnh của tam giác đó.

+) Ba đường trung trực trong tam giác cắt nhau tại một điểm.

Do đó để xác định tâm đường tròn ngoại tiếp tam giác, ta đi xác định giao điểm của hai đường trung trực.

Ví dụ: Cho △ABC có AB = 6 cm, BC = 8 cm. Xác định tâm đường tròn ngoại tiếp △ABC.

Hướng dẫn giải

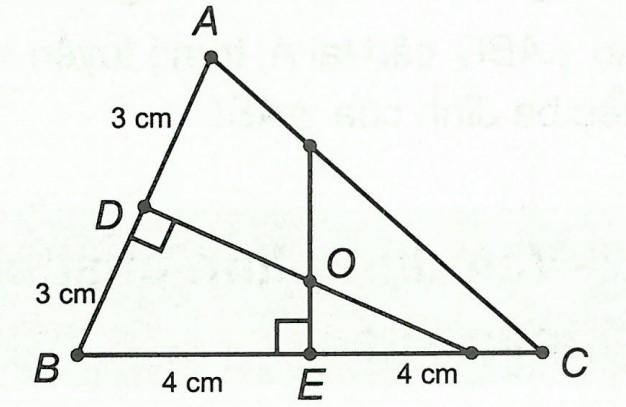
Lấy D là trung điểm của AB ⇒ BD = 3 cm.

Qua D kẻ đường thẳng d₁ ⊥ AB.

Lấy E là trung điểm của BC ⇒ BE = 4 cm.

Qua E kẻ đường thẳng d₂ ⊥ BC.

d₁ cắt d₂ tại O thì O chính là tâm đường tròn ngoại tiếp △ABC.

Ví dụ mẫu

Ví dụ. Chứng minh rằng trong tam giác vuông, giao điểm của ba đường trung trực là trung điểm của cạnh huyền.

Hướng dẫn giải

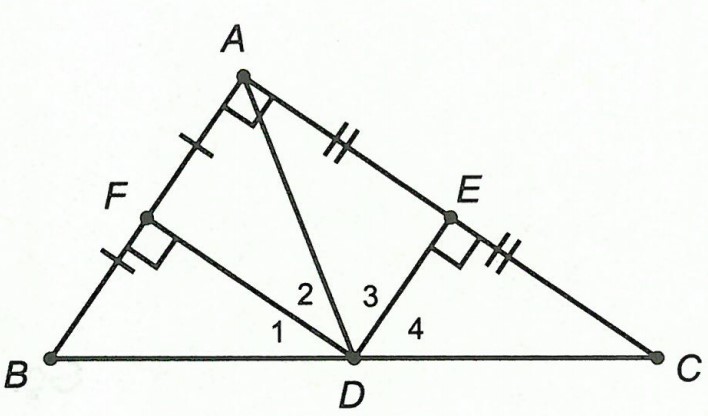
Xét tam giác ABC vuông tại A, ta có: $\widehat B + \widehat C = 90^\circ$

Gọi D là giao điểm của các đường trung trực cạnh AB và AC.

Ta có: EA = EC. Khi đó DE cũng là đường trung tuyến △ADC nên △ADC cân tại D.

$\Rightarrow \widehat {{D_3}} = \widehat {{D_4}} = 90^\circ - \widehat C$ và AD = DC

FA = FB và FD ⊥ AB ⇒ △DAB cân tại D

$\Rightarrow \widehat {{D_1}} = \widehat {{D_2}} = 90^\circ - \widehat B$ và AD = BD

Do đó: $\widehat {{D_1}} + \widehat {{D_2}} + \widehat {{D_3}} + \widehat {{D_4}}$

$\begin{gathered} = 2\left( {90^\circ - \widehat B} \right) + 2\left( {90^\circ - \widehat C} \right) \hfill \\ = 2\left( {180^\circ - \widehat B - \widehat C} \right)\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ = 2\left( {180^\circ - 90^\circ } \right) = 180^\circ \hfill \\ \end{gathered}$

⇒ B, D, C thẳng hàng ⇒ D nằm trên BC.

Mà BD = AD và AD = DC nên BD = DC

⇒ D là trung điểm của BC hay giao điểm của ba đường trung trực của △ABC nằm trên trung điểm cạnh huyền.

Bài tập tự luyện dạng 1

Câu 1. Cho △ABC có $\widehat A$ là góc tù. Các đường trung trực của AB và của AC cắt nhau ở O và cắt BC theo thứ tự ở D và E.

a) Các △ABD, △ACE là tam giác gì?

b) Đường tròn tâm O bán kính OA đi qua những điểm nào trong hình vẽ?

Hướng dẫn giải

a) Gọi M, N lần lượt là trung điểm của AB và AC.

Xét △DAB có DM là trung trực của AB

⇒ △DAB cân tại D

Tương tự ta có △EAC cân tại E.

b) Xét △OAB có OM là trung trực của AB

⇒ △OAB cân tại O

⇒ OA = OB (1)

Tương tự có △OAC cân tại O ⇒ OA = OC (2)

Từ (1) và (2), ta có OA = OB = OC

⇒ Đường tròn tâm O bán kính OA đi qua ba điểm A, B, C.

Câu 2. Cho △ABC vuông tại A. Trên nửa mặt phẳng bờ là BC, khác phía với A lấy điểm D sao cho BD ⊥ CD. Hãy xác định tâm đường tròn ngoại tiếp △ABD.

Hướng dẫn giải

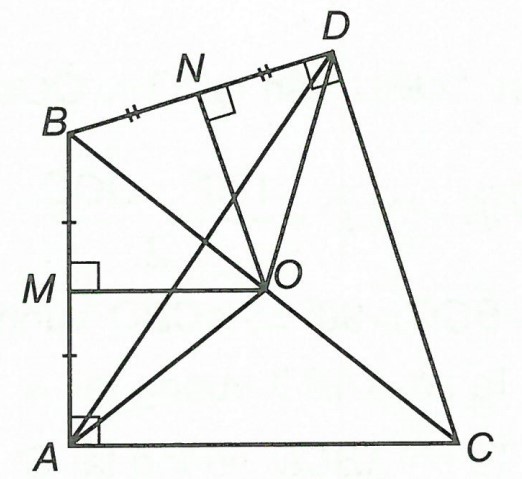
Gọi O là trung điểm của BC.

Xét △ABC, có: $\widehat {BAC} = 90^\circ$

Theo chứng minh ở ví dụ 1 thì O là tâm đường tròn ngoại tiếp △ABC, ta có OA = OB = OC (1)

Xét △DBC, có: $\widehat {BDC} = 90^\circ$ nên OB = OC = OD (2)

Từ (1) và (2), ta có OA = OB = OD

Vậy O là tâm đường tròn ngoại tiếp △ABD.

Câu 3. Cho △ABC cân tại A, trung tuyến AM. Đường trung trực của AB cắt AM ở O. Chứng minh rằng điểm O cách đều ba đỉnh của △ABC.

Hướng dẫn giải

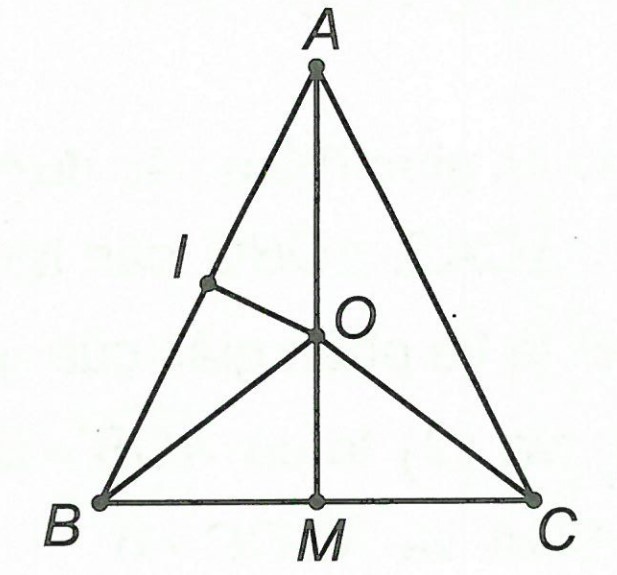
Xét △OAB vì OI là trung trực của AB nên OA = OB (1)

Vì △ABC cân tại A nên đường trung tuyến AM đồng thời là đường trung trực của BC.

Mà đường trung trực của AB cắt AM tại O nên O là giao điểm của 3 đường trung trực.

Vậy O cách đều ba đỉnh của △ABC.

Dạng 2. Vận dụng tính chất ba đường trung trực trong tam giác để giải quyết các bài toán khác

Phương pháp giải

Sử dụng tính chất

Trong một tam giác, giao điểm của hai đường trung trực thuộc đường trung trực còn lại của tam giác đó.

Ví dụ: Cho △ABC đều. Gọi D là điểm nằm giữa A và B, E là điểm nằm giữa A và C sao cho BD = AE. Chứng minh rằng khi D và E thay đổi trên các cạnh AB và AC thì đường trung trực của đoạn thẳng DE luôn đi qua tâm đường tròn ngoại tiếp △ABC.

Hướng dẫn giải

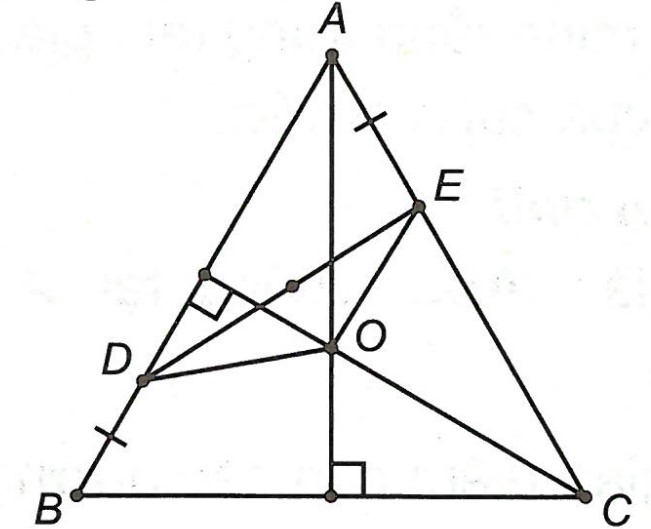
Gọi O là tâm đường tròn ngoại tiếp △ABC

⇒ OA = OB = OC.

Ta có: AO là đường trung trực ứng với cạnh BC đồng thời là đường phân giác của góc $\widehat A$ .

Suy ra: $\widehat {BAO} = \widehat {OAC} = \frac{{60^\circ }}{2} = 30^\circ$

Tương tự, ta có: $\widehat {OCE} = 30^\circ$

Vì △ABC đều nên AB = AC = BC.

Lại có: $\left\{ \begin{gathered} CE = AC - AE \hfill \\ AD = AB - BD \hfill \\ AE = BD \hfill \\ \end{gathered} \right. \Rightarrow CE = AD$

Xét △OAD và △OCE, có:

OA = OC

$\widehat {OAD} = \widehat {OCE} = 30^\circ$

CE = AD (cmt)

⇒ △OAD = △OCE (c.g.c) ⇒ OD = OE

⇒ △ODE cân tại O

Vậy đường trung trực của đoạn DE luôn đi qua điểm cố định O.

Ví dụ mẫu

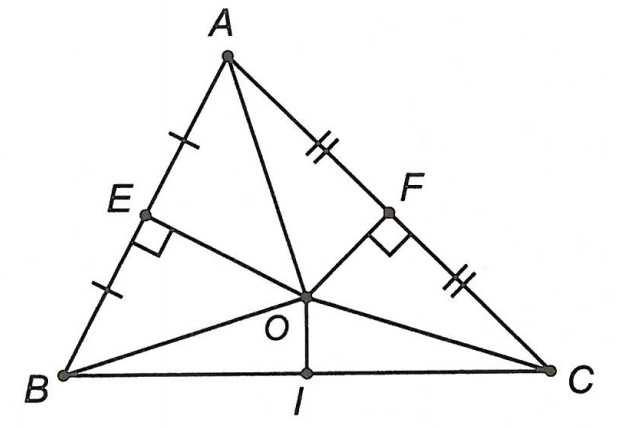
Ví dụ 1. Cho △ABC, M là trung điểm của BC. Các đường trung trực của AB và AC cắt nhau tại O. Tính số đo $\widehat {OMB}$ .

Hướng dẫn giải

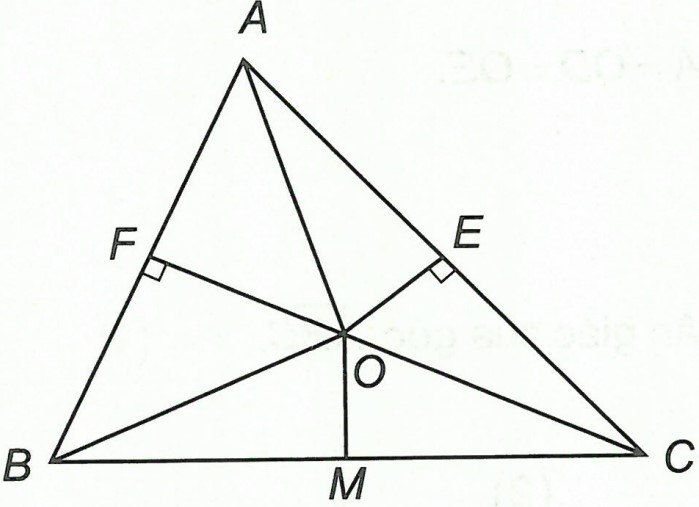
Vì OF là trung trực nên OA = OB.

Vì OE là trung trực nên OA = OC.

Suy ra: OA = OB = OC

⇒ △OBC cân tại O mà M là trung điểm BC

⇒ OM là đường trung trực của △OBC

⇒ OM ⊥ BC ⇒ $\widehat {OMB} = 90^\circ$

Ví dụ 2. Cho △ABC cân tại A, có $\widehat A = 50^\circ$ . Đường trung trực của AB cắt BC ở D.

a) Tính $\widehat {CAD}$

b) Trên tia đối của tia AD lấy điểm M sao cho AM = CD. Chứng minh △BMD là tam giác cân.

Hướng dẫn giải

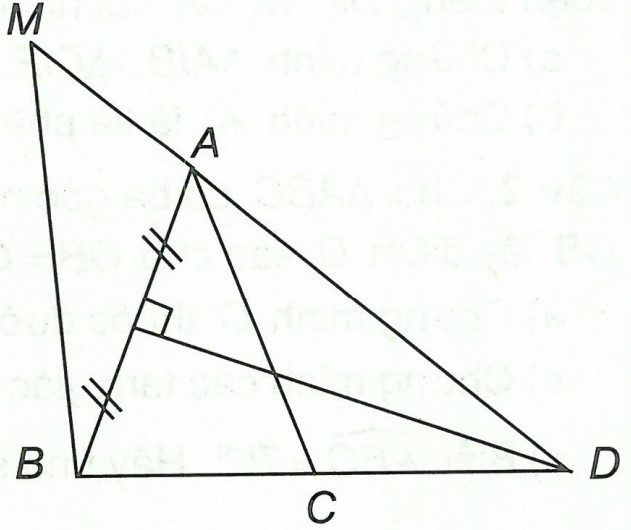
a) Xét △DAB có DH là trung trực của AB nên △DAB cân tại D (H ∈ AB)

⇒ AD = BD và $\widehat {BAD} = \widehat {ABD}$

Ta có △ABC cân tại A có $\widehat A = 50^\circ$

$\begin{gathered} \Rightarrow \widehat {ABC} = \widehat {ACB} = \frac{{180^\circ - \widehat {BAC}}}{2} = \frac{{180^\circ - 50^\circ }}{2} = 65^\circ \hfill \\ \Rightarrow \widehat {BAD} = 65^\circ \begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \Rightarrow \widehat {CAD} = \widehat {BAD} - \widehat {BAC} = 65^\circ - 50^\circ = 15^\circ \hfill \\ \end{gathered}$

b) Xét △BAM và △ACD, có:

AB = AC (do △ABC cân tại A)

$\begin{gathered} \widehat {BAM} = 180^\circ - \widehat {BAD} = 180^\circ - 65^\circ = 115^\circ {\text{ }}\left( 1 \right) \hfill \\ \widehat {DCA} = 180^\circ - \widehat {ACB} = 180^\circ - 65^\circ = 115^\circ {\text{ }}\left( 2 \right)\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered}$

Từ (1) và (2) suy ra: $\widehat {BAM} = \widehat {ACD}$

Lại có: MA = CD.

Do đó: △BAM = △ACD (c.g.c) ⇒ BM = AD.

Mặt khác AD = BD ⇒ BD = BM

⇒ △BMD cân tại B.

Ví dụ 3. Cho △ABC vuông tại A. Trên cạnh BC lấy hai điểm D và E sao cho BD = BA và CE = CA. Chứng minh tâm O của đường tròn ngoại tiếp △ADE là giao điểm của các đường phân giác của △ABC.

Hướng dẫn giải

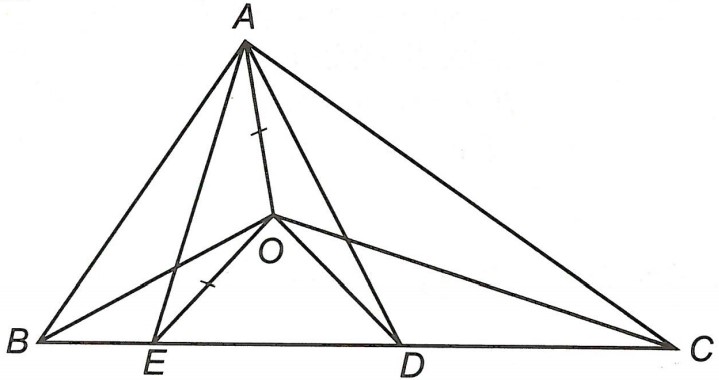
Gọi O là tâm đường tròn ngoại tiếp △ADE

⇒ OA = OD = OE.

Xét △OBA và △OBD, có:

AB = BD; OA = OD; OB chung.

Do đó: △OBA = △OBD (c.c.c)

⇒ $\widehat {OBA} = \widehat {OBD}$ (hai góc tương ứng)

⇒ BO là phân giác của góc $\widehat {ABC}$ (1)

Tương tự ta có: △OAC = △OEC (c.c.c)

⇒ $\widehat {OCA} = \widehat {OCE}$

⇒ CO là phân giác của $\widehat {ACB}$ (2)

Từ (1) và (2), ta có O là giao của ba đường phân giác của △ABC.

Bài tập tự luyện dạng 2

Câu 1. Cho △ABC có AB < AC, lấy E trên cạnh CA sao cho CE = BA, các đường trung trực của các đoạn thẳng BE và CA cắt nhau ở I.

a) Chứng minh: △AIB = △CIE.

b) Chứng minh AI là tia phân giác của góc $\widehat {BAC}$ .

Hướng dẫn giải

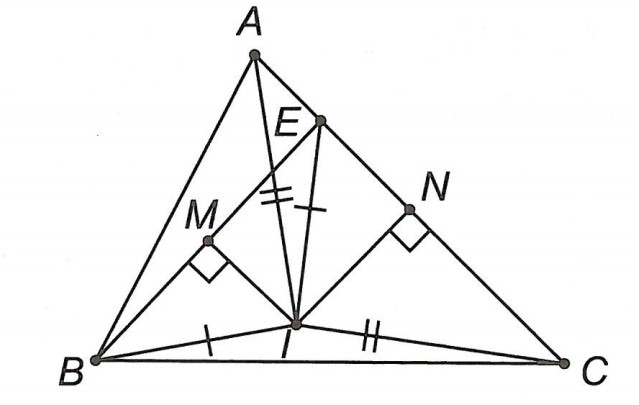
a) Xét △IBE có IM là trung trực của BE

⇒ △IBE cân tại I ⇒ IB = IE

Xét △IAC có IN là trung trực của AC

⇒ △IAC cân tại I ⇒ IA = IC

Xét △AIB và △CIE, có:

IA = IC; AB = CE; IB = IE

Do đó: △AIB = △CIE (c.c.c)

b) Vì △IAC cân tại I nên $\widehat {IAC} = \widehat {ICA}{\text{ }}\left( 1 \right)$

△AIB = △CIE ⇒ $\widehat {IAB} = \widehat {ICE} = \widehat {ICA}{\text{ }}\left( 2 \right)$

Từ (1) và (2) ta có: $\widehat {IAC} = \widehat {IAB}$

⇒ AI là tia phân giác của góc $\widehat {BAC}$

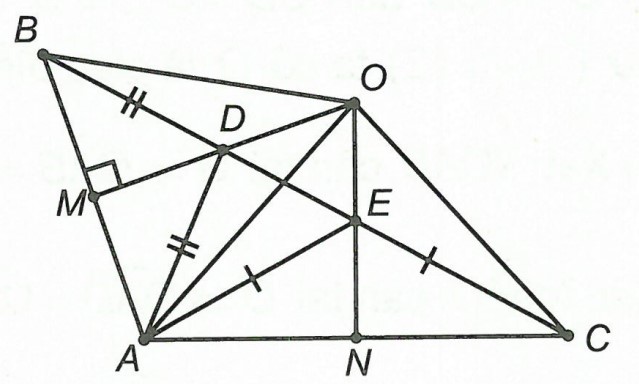
Câu 2. Cho △ABC có ba góc nhọn, O là giao điểm hai đường trung trực của AB và AC. Trên tia đối của tia OB lấy điểm D sao cho OB = OD.

a) Chứng minh O thuộc đường trung trực của AD và CD.

b) Chứng minh các tam giác ABD, CBD vuông.

c) Biết $\widehat {ABC} = 70^\circ$ . Hãy tính số đo góc $\widehat {ADC}$ ?

Hướng dẫn giải

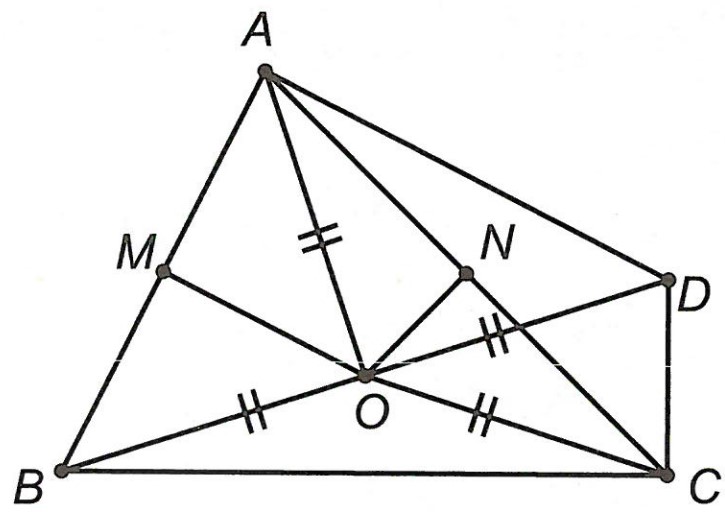
a) Vì O là giao điểm hai đường trung trực của AB và AC nên OA = OB = OC.

Vì OD = OB nên OD = OA

⇒ O thuộc đường trung trực của AD (1)

Vì OD = OB nên OD = OC

⇒ O thuộc đường trung trực của CD (2)

Từ (1) và (2) ta có O là giao điểm của ba đường trung trực tam giác ACD.

b) Xét △OAB cân tại O

$\Rightarrow \widehat {OAB} = \widehat {OBA} = \frac{{180^\circ - \widehat {AOB}}}{2}$

Xét △OAD cân tại O

$\begin{gathered} \Rightarrow \widehat {OAD} = \widehat {ODA} = \frac{{180^\circ - \widehat {AOD}}}{2}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \Rightarrow \widehat {OAB} + \widehat {OAD} = \frac{{180^\circ - \widehat {AOB}}}{2} + \frac{{180^\circ - \widehat {AOD}}}{2} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&{} \end{array}{\text{ }} = 180^\circ - \frac{{\widehat {AOB} + \widehat {AOD}}}{2}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&{} \end{array}{\text{ }} = 180^\circ - \frac{{180^\circ }}{2} = 90^\circ \hfill \\ \Rightarrow \widehat {BAD} = 90^\circ \hfill \\ \end{gathered}$

⇒ △ABD vuông tại A.

Xét △OCD cân tại O

$\Rightarrow \widehat {OCD} = \widehat {ODC} = \frac{{180^\circ - \widehat {DOC}}}{2}$

Xét △OBC cân tại O

$\begin{gathered} \Rightarrow \widehat {OCB} = \widehat {OBC} = \frac{{180^\circ - \widehat {BOC}}}{2}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \Rightarrow \widehat {OCB} + \widehat {OCD} = \frac{{180^\circ - \widehat {DOC}}}{2} + \frac{{180^\circ - \widehat {BOC}}}{2} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&{} \end{array}{\text{ }} = 180^\circ - \frac{{\widehat {DOC} + \widehat {COB}}}{2}\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&{} \end{array}{\text{ }} = 180^\circ - \frac{{180^\circ }}{2} = 90^\circ \hfill \\ \Rightarrow \widehat {BCD} = 90^\circ \hfill \\ \end{gathered}$

⇒ △CBD vuông tại C.

c) Ta có: △ABD vuông tại A nên

$\widehat {ADB} = 90^\circ - \widehat {ABD}$

Ta có: △BCD vuông tại C nên

$\widehat {BDC} = 90^\circ - \widehat {CBD}$

Suy ra:

$\begin{gathered} \widehat {ADO} + \widehat {ODC} = 180^\circ - \left( {\widehat {ABO} + \widehat {CBO}} \right) \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&{ = 180^\circ - \widehat {ABC}\begin{array}{*{20}{c}} {} \\ {} \end{array}} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&{ = 180^\circ - 70^\circ = 110^\circ } \end{array} \hfill \\ \Rightarrow \widehat {ADC} = 110^\circ \begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered}$

Câu 3. Cho △ABC có O là giao điểm các đường trung trực của tam giác. Biết BO là tia phân giác của góc $\widehat {ABC}$ . Chứng minh rằng:

a) △BOA = △BOC

b) BO là đường trung trực của AC

Hướng dẫn giải

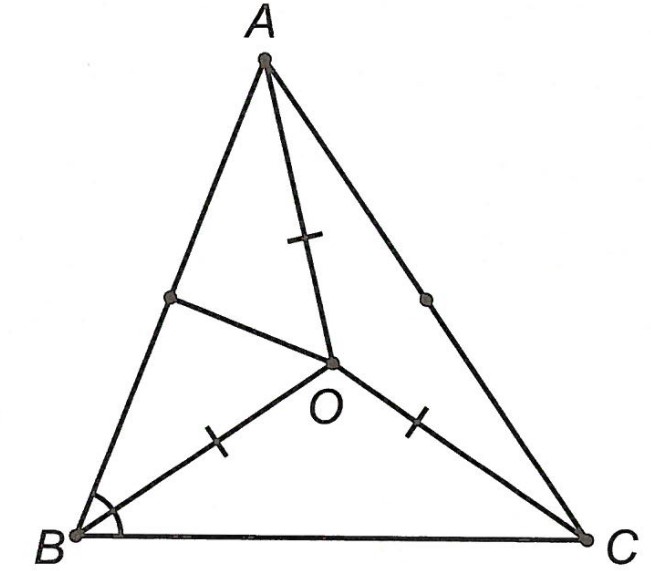
a) Vì O là giao điểm các đường trung trực của △ABC nên OA = OB = OC

Suy ra △OAB, △OBC cân tại O

$\Rightarrow \widehat {OAB} = \widehat {OBA};{\text{ }}\widehat {OBC} = \widehat {OCB}{\text{ }}\left( 1 \right)$

Do OB là tia phân giác của góc $\widehat {ABC}$ nên $\widehat {OBA} = \widehat {OBC}{\text{ }}\left( 2 \right)$

Từ (1) và (2) ta có: $\widehat {AOB} = \widehat {BOC}$

Xét △BOA và △BOC, có:

OA = OC

$\widehat {AOB} = \widehat {BOC}$

OB chung

Do đó: △BOA = △BOC (c.g.c).

b) Vì △BOA = △BOC

⇒ AB = BC (hai cạnh tương ứng)

⇒ △BAC cân tại B

Mà OB là tia phân giác của góc $\widehat {ABC}$ nên OB là trung trực của AC.

Câu 4. Cho △ABC, $\widehat B = 75^\circ ,\widehat C = 45^\circ$ . Vẽ đường trung trực d của BC cắt BC tại M. Gọi E là điểm thuộc d và thuộc nửa mặt phẳng bờ BC chứa điểm A sao cho $\widehat {EBC} = 30^\circ$ . Chứng minh rằng:

a) △BEC cân tại E;

b) $\widehat {BAC} = \widehat {ABE} + \widehat {ACE}$

c) $\widehat {AEB} = 90^\circ$

Hướng dẫn giải

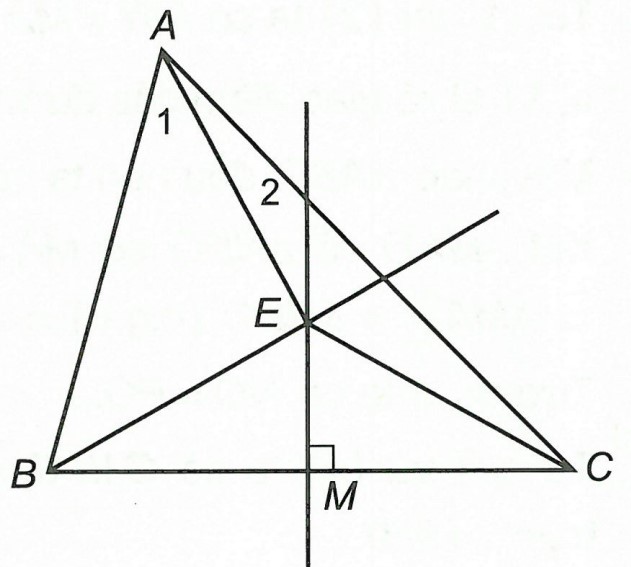
a) Xét △BEC có EM là trung trực của cạnh BC

⇒ EB = EC ⇒ △BEC cân tại E

b) Vì △BEC cân tại E nên $\widehat {EBC} + \widehat {ECB} = 30^\circ$

$\begin{gathered} \widehat {ABE} = \widehat {ABC} - \widehat {EBC} = 75^\circ - 30^\circ = 45^\circ \hfill \\ \widehat {ACE} = \widehat {ACB} - \widehat {ECB} = 45^\circ - 30^\circ = 15^\circ \begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered}$

Trong △ABC ta có:

$\begin{gathered} \widehat {BAC} = 180^\circ - \widehat {ABC} - \widehat {ACB} \hfill \\ \begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \hfill \\ \end{gathered} &{ = 180^\circ - 75^\circ - 45^\circ = 60^\circ } \end{array}} \end{array} \hfill \\ \end{gathered}$

Mà $\widehat {ABE} + \widehat {ACE} = 45^\circ + 15^\circ = 60^\circ$

Nên $\widehat {BAC} = \widehat {ABE} + \widehat {ACE}$

c) Nếu $\widehat {AEB} > 90^\circ$ , trong △ABE, có: $\widehat {ABE} = 45^\circ$

$\begin{gathered} \Rightarrow \widehat {{A_1}} = 180^\circ - \widehat {ABE} - \widehat {AEB} < 180^\circ - 45^\circ - 90^\circ = 45^\circ \hfill \\ \Rightarrow \widehat {{A_1}} < \widehat {ABE} \Rightarrow AE > BE \Rightarrow AE > EC\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered}$

Trong △EAC, có:

$\begin{gathered} AE > EC \Rightarrow \widehat {{A_2}} < \widehat {ACE} = 15^\circ \hfill \\ \Rightarrow \widehat {{A_1}} + \widehat {{A_2}} < 45^\circ + 15^\circ = 60^\circ \begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered}$

Điều này vô lý vì $\widehat {{A_1}} + \widehat {{A_2}} = 60^\circ$ (1)

Nếu $\widehat {AEB} < 90^\circ$ , lập luận tương tự, ta có:

$AE < EC \Rightarrow \widehat {{A_1}} + \widehat {{A_2}} > 45^\circ + 15^\circ = 60^\circ$

Điều này vô lý vì $\widehat {{A_1}} + \widehat {{A_2}} = 60^\circ$ (2)

Từ (1) và (2) suy ra: $\widehat {AEB} = 90^\circ$

Dạng 3. Chứng minh ba đường thẳng đồng quy, ba điểm thẳng hàng

Phương pháp giải

Sử dụng tính chất: “Ba đường trung trực trong tam giác cắt nhau tại một điểm”.

Ví dụ: Cho △ABC cân ở A. Gọi M là trung điểm của BC. Các đường trung trực của AB và AC cắt nhau ở E. Chứng minh rằng ba điểm A, E, M thẳng hàng.

Hướng dẫn giải

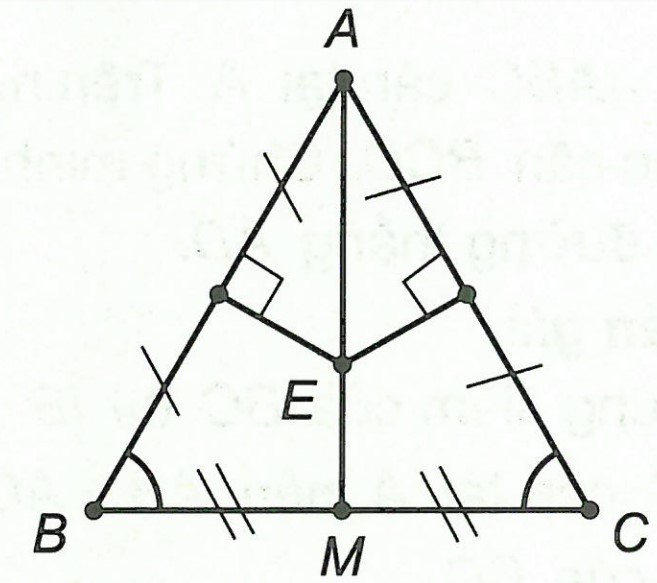
Xét △MAB và △MAC, có:

AB = AC (vì △ABC cân tại A);

BM = MC (vì M là trung điểm BC);

AM chung.

⇒ △MAB = △MAC (c.c.c)

⇒ $\widehat {AMB} = \widehat {AMC}$ (hai góc tương ứng)

Mặt khác: $\widehat {AMB} + \widehat {AMC} = 180^\circ$

⇒ $\widehat {AMB} = \widehat {AMC} = 90^\circ$

⇒ AM ⊥ BC

⇒ AM là trung trực ứng với cạnh BC của △ABC

⇒ Giao điểm E của các đường trung trực phải thuộc AM hay A, E, M thẳng hàng.

Ví dụ mẫu

Ví dụ 1. Cho góc $\widehat {xOy} = \alpha ^\circ$ , A là một điểm di động ở góc trong góc đó. Vẽ các điểm M và N sao cho đường Ox là đường trung trực của AM, đường thẳng Oy là đường trung trực của AN.

a) Chứng minh rằng đường trung trực của MN luôn đi qua một điểm cố định.

b) Tính giá trị của α để O là trung điểm của MN.

Hướng dẫn giải

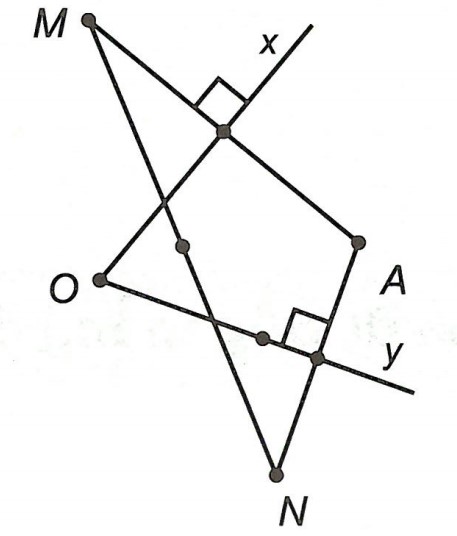
a) Xét △AMN có Ox là trung trực của AM; Oy là trung trực của AN

Vậy O là giao điểm của ba đường trung trực của △AMN.

Trung trực của MN luôn đi qua O cố định khi A di động (vì 3 đường trung trực trong tam giác luôn đồng quy tại một điểm).

b) Vì O thuộc MN nên O, M, N thẳng hàng

$\Rightarrow \widehat {xOM} + \widehat {xOA} + \widehat {yOA} + \widehat {yON} = 180^\circ$

Mặt khác: $\left\{ \begin{gathered} \widehat {xOM} = \widehat {xOA} \hfill \\ \widehat {yON} = \widehat {yOA} \hfill \\ \end{gathered} \right.$

$\begin{gathered} \Rightarrow 2\left( {\widehat {xOA} + \widehat {yOA}} \right) = 180^\circ \hfill \\ \Rightarrow 2\widehat {xOy} = 180^\circ \begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \Rightarrow \widehat {xOy} = 90^\circ \hfill \\ \Rightarrow \alpha = 90^\circ \begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered}$

Bài tập tự luyện dạng 3

Câu 1. Cho △ABC cân tại A. Trên nửa mặt phẳng bờ BC không chứa điểm A, dựng tam giác cân BCD. Chứng minh rằng các đường trung trực của AB và AC đồng quy với đường thẳng AD.

Hướng dẫn giải

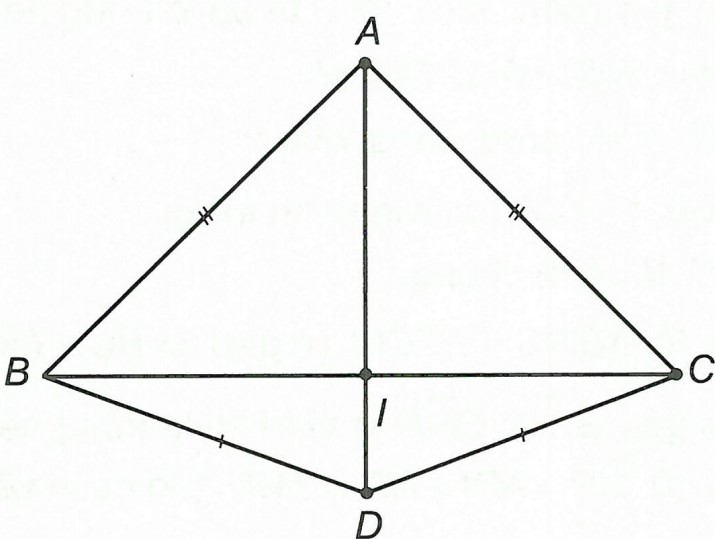
Gọi I là trung điểm của BC thì IB = IC.

Mà △ABC cân tại A nên AB = AC ⇒ AI là trung trực của BC.

Tương tự, ta có: △ABD cân tại D nên DI là trung trực của BC.

⇒ A, D, I thẳng hàng hay AD là trung trực của BC.

Khi đó AD là đường trung trực của △ABC.

Vậy các đường trung trực của AB và AC đồng quy với AD tại O.

Câu 2. Cho △ABC đều. Trên các cạnh AB, BC, CA lấy theo thứ tự ba điểm M, N, P sao cho AM BN CP.

a) Chứng minh tam giác △MNP là tam giác đều.

b) Gọi O là giao điểm các đường trung trực.

Hướng dẫn giải

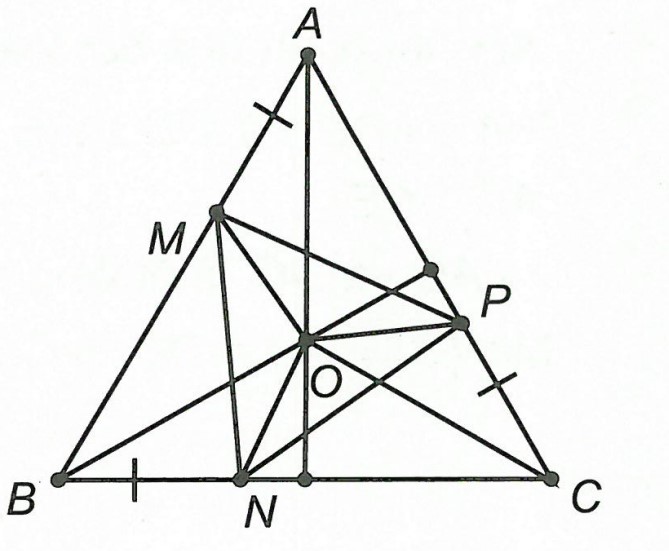
a) △ABC đều nên AB = AC = BC.

Ta có: $\left\{ \begin{gathered} AP = AC - PC \hfill \\ CN = BC - BN \hfill \\ PC = BN \hfill \\ AC = BC \hfill \\ \end{gathered} \right. \Rightarrow AP = CN$