Tam giác vuông bằng nhau
Trường hợp hai cạnh góc vuông
Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (theo trường hợp cạnh – góc – cạnh).
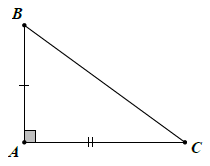
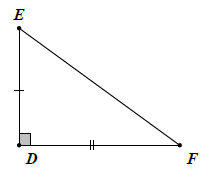
Trường hợp một cạnh góc vuông và một góc nhọn
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (theo trường hợp góc – cạnh – góc).
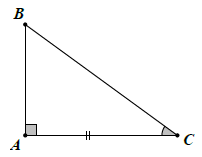

Trường hợp cạnh huyền và một góc nhọn
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (theo trường hợp g.c.g)
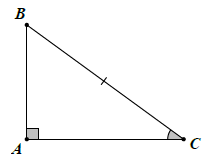
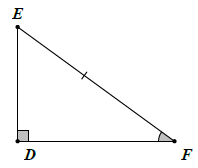
Trường hợp cạnh huyền và cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác đó bằng nhau.
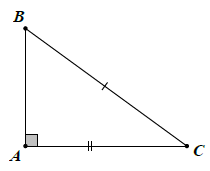

Phân dạng bài tập
Dạng 1. Tìm hoặc chứng minh hai tam giác vuông bằng nhau
Phương pháp giải:
+) Xét hai tam giác vuông.
+) Kiểm tra các điều kiện bằng nhau cạnh – góc – cạnh, góc – cạnh – góc, cạnh huyền – góc nhọn, cạnh huyền – cạnh góc vuông.
+) Kết luận hai tam giác bằng nhau.
Bài toán.
Bài 1. Tìm các tam giác vuông bằng nhau trên hình dưới đây?
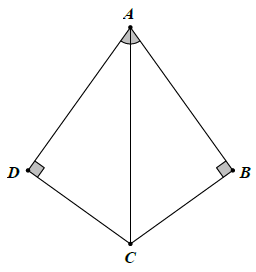
Hướng dẫn giải
Xét △ABC và △ADC, có:
(gt)
AC chung
Do đó: △ABC = △ADC (cạnh huyền – góc nhọn)
Bài 2. Tìm các tam giác vuông bằng nhau trên hình sau:
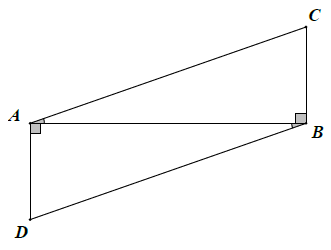
Hướng dẫn giải
Xét △ABC và △BAD, có:
AB chung
(gt)
Do đó: △ABC = △BAD (cạnh góc vuông – góc nhọn)
Bài 3. Tìm các tam giác vuông bằng nhau trên hình dưới đây? B
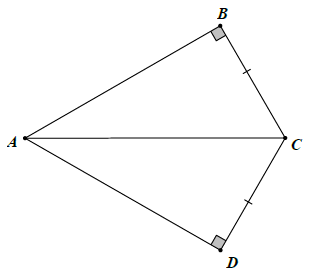
Hướng dẫn giải
Xét △ABC và △ADC, có:
BC = DC (gt)
AC chung
Do đó: △ABC = △ADC (cạnh huyền – cạnh góc vuông)
Bài 4. Tìm các tam giác vuông bằng nhau trên hình sau:
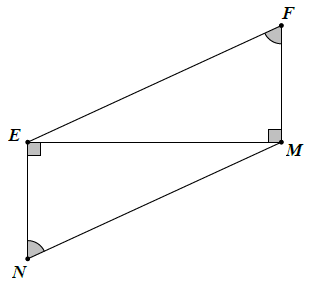
Hướng dẫn giải
Xét △MEF vuông tại M nên:
Xét △EMN vuông tại E nên:
Mà (gt)
Nên
Xét △MEF và △EMN, có:
(chứng minh trên)
ME là cạnh chung
Do đó: △MEF = △EMN (g.c.g).
Bài 5. Cho hình vẽ sau:
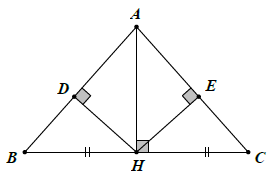
Chứng minh rằng:
a) △ABH = △ACH
b) △ADH = △AEH
c) △DBH = △ECH
Hướng dẫn giải
a) Xét △ABH vuông tại H và △ACH vuông tại H có:
BH = CH (gt)
AH là cạnh chung
Do đó: △ABH = △ACH (2 cạnh góc vuông)
b) Xét △ADH vuông tại D và △AEH vuông tại E có:
AH là cạnh chung
(do △ABH = △ACH)
Do đó: △ADH = △AEH (cạnh huyền – góc nhọn)
c) Xét △DBH vuông tại D và △ECH vuông tại E có:
(do △ABH = △ACH)
BH = CH (gt)
Do đó: △DBH = △ECH (cạnh huyền – góc nhọn)
Bài 6. Cho . Tia Oz là tia phân giác
. Lấy điểm A thuộc tia Oz (A ≠ O). Kẻ AB ⊥ Ox, AC ⊥ Oy (B ∈ Ox, C ∈ Oy). Chứng minh: △OAB = △OAC.
Hướng dẫn giải

Xét △OAB vuông tại B và △OAC vuông tại C có:
OA là cạnh chung
(do Oz là tia phân giác
)
Do đó: △OAB = △OAC (cạnh huyền – góc nhọn)
Bài 7. Cho hình vẽ sau. Tìm các tam giác vuông bằng nhau trên hình?

Hướng dẫn giải
Xét △BFD vuông tại F và △CGE vuông tại G ta có:
BD = CE (gt)
(gt)
Do đó: △BFD = △CGE (cạnh huyền – góc nhọn)
Xét △AFD vuông tại F và △AGE vuông tại G ta có:
AD = AE (gt)
FD = GE (do △BFD = △CGE)
Do đó: △AFD = △AGE (cạnh huyền – cạnh góc vuông)
Bài 8. Cho tam giác ABC có AB = AC. Gọi D là trung điểm của cạnh BC. Kẻ DE ⊥ AB, DF ⊥ AC. Chứng minh:
a) △DEB = △DFC
b) △DEA = △DFA
Hướng dẫn giải
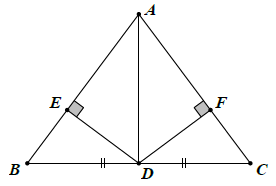
a) Xét △ABD và △ACD, có:
AB = AC (gt)
AD là cạnh chung
DB = DC (D là trung điểm của cạnh BC)
Do đó: △ABD = △ACD (c.c.c)
Nên và
+) Xét △DEB vuông tại E và △DFC vuông tại F ta có:
AD chung
(chứng minh trên)
Do đó: △DEB = △DFC (cạnh huyền – góc nhọn)
b) Xét △DEA vuông tại E và △DFA vuông tại F ta có:
AD là cạnh chung
(chứng minh trên)
Do đó: △DEA = △DFA (cạnh huyền – góc nhọn)
Bài 9. Cho tam giác ABC vuông tại A và AB = AC. Qua A kẻ đường thẳng d cắt BC. Vẽ BM, CN vuông góc với d. Chứng minh rằng: △BAM = △ACN.
Hướng dẫn giải
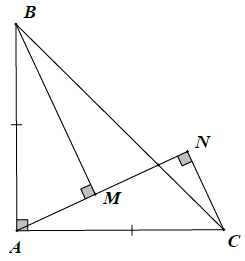
Vì △ABC vuông tại A nên
Và △ANC vuông tại N nên
Do đó:
Xét △BAM vuông tại M và △ACN vuông tại N có:
(cmt)
AB = AC (gt)
Nên △BAM = △ACN (cạnh huyền – góc nhọn).
Bài 10. Cho △ABC có . Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN). Chứng minh rằng: △BME = △CNF.
Hướng dẫn giải
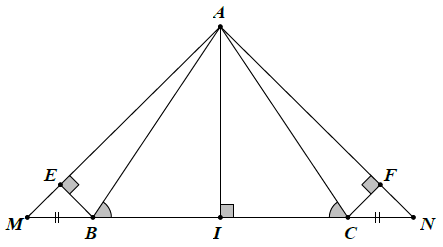
Ta có: ;
(kề bù)
Mà (gt)
Kẻ AI ⊥ BC tại I.
Xét △ABI vuông tại I nên ta có:
Xét △ACI vuông tại I nên ta có:
Mà (gt)
Nên
+) Xét △ABI và △ACI ta có:
AI chung
(chứng minh trên)
Do đó: △ABI = △ACI (g.c.g)
Nên AB = AC
Xét △ABM và △ACN, có:
BM = CN (gt)
(cmt)
AB = AC (cmt)
⇒ △ABM = △ACN (c.g.c)
Nên M N=
+) Xét △BME vuông tại E và △CNF vuông tại F ta có:
BM = CN (gt)
(cmt)
Do đó: △BME = △CNF (cạnh huyền – góc nhọn).
Bài 11. Cho △ABC. Từ A vẽ cung tròn có bán kính bằng BC, từ C vẽ cung tròn có bán kính bằng AB. Hai cung tròn này cắt nhau tại D (D nằm khác phía của B đối với AC). Kẻ AH ⊥ BC (H ∈ BC) và CK ⊥ AD (K ∈ AD)
a) Chứng minh: △AHC = △CKA
b) Chứng minh: △AHB = △CKD
Hướng dẫn giải
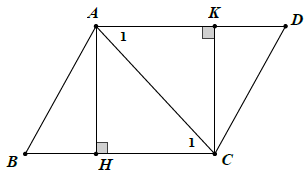
a) Vì cung tròn tâm A bán kính bằng BC cắt cung tròn tâm C có bán kính bằng AB tại D
Nên AD = BC = CD = AB
+) Xét △ABC và △CDA, có:
AC cạnh chung
AD = BC (cmt)
CD = AB (cmt)
Do đó: △ABC = △CDA (c.c.c)
⇒
Xét △AHC vuông tại H và △CKA vuông tại K, có:
(cmt)
AC cạnh chung
Suy ra: △AHC = △CKA (cạnh huyền – góc nhọn)
b) Xét △AHB vuông tại H và △CKD vuông tại K, có:
AH = CK (do △AHC = △CKA)
AB = CD (cmt)
Do đó: △AHB = △CKD (cạnh huyền – cạnh góc vuông)
Dạng 2. Sử dụng các trường hợp bằng nhau của tam giác vuông để chứng minh hai đoạn thẳng bằng nhau, hai góc bằng nhau. Tính độ dài đoạn thẳng, số đo góc.
Phương pháp giải:
+) Chọn hai tam giác vuông có cạnh (góc) là đoạn thẳng (góc) cần tính hoặc chứng minh bằng nhau.
+) Tìm thêm hai điều kiện bằng nhau, trong đó có một điều kiện về cạnh, để kết luận hai tam giác bằng nhau.
+) Suy ra các cạnh (góc) tương ứng bằng nhau và kết luận.
Bài toán.
Bài 1. Cho hình vẽ sau. Chứng minh OK là phân giác của góc .
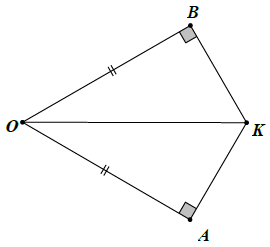
Hướng dẫn giải
Xét △OBK vuông tại B và △OAK vuông tại A, có:
OK chung
OB = OA (gt)
Do đó: △OBK = △OAK (cạnh huyền – góc nhọn)
Suy ra: (cặp góc tương ứng).
Vậy OK là phân giác của góc
Bài 2. Cho △ABC có AB = AC. Kẻ AD ⊥ BC. Chứng minh AD là tia phân giác của .
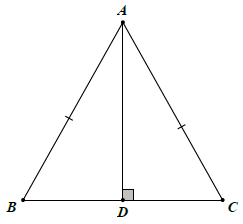
Hướng dẫn giải
Xét △ABD vuông tại D và △ACD vuông tại D có:
OD chung
AB = AC (gt)
Do đó: △ABD = △ACD (cạnh huyền – góc nhọn)
Suy ra: (cặp góc tương ứng).
Vậy AD là phân giác của góc
Bài 3. Cho △ABC có BA = BC. Qua A kẻ đường vuông góc với AB, Qua C kẻ đường vuông góc với CB, chúng cắt nhau ở K. Chứng minh BK là phân giác của góc .

Hướng dẫn giải
Xét △ABK vuông tại A và △CBK vuông tại C, có:
AB = AC (gt)
BK chung
Do đó: △ABK = △CBK (cạnh huyền – cạnh góc vuông)
Nên (hai góc tương ứng)
Hay BK là phân giác của góc
Bài 4. Cho tam giác ABC, M là trung điểm cạnh BC. Vẽ BI, CK vuông góc với AM. Chứng minh BI = CK.
Hướng dẫn giải
Xét △BIM và △CKM, có:
MB = MC (M là trung điểm của BC)
(đối đỉnh)
Do đó: △BIM = △CKM (cạnh huyền – góc nhọn)
Từ đó suy ra: BI = CK (cặp cạnh tương ứng)
Bài 5. Cho tam giác ABC vuông tại A. Tia phân giác góc cắt cạnh AC tại điểm M. Kẻ MD ⊥ BC (D ∈ BC).
a) Chứng minh: BA = BD
b) Gọi E là giao điểm của hai đường thẳng DM và BA. Chứng minh: △ABC = △DBE.
Hướng dẫn giải
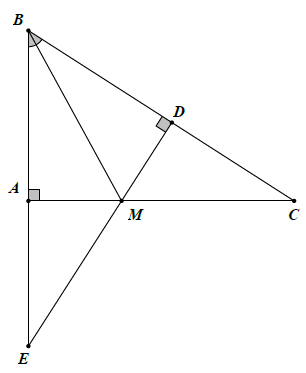
a) Xét △BMA vuông tại A và △BMD vuông tại D ta có:
BM cạnh chung
(do BM là phân giác của góc
)
Do đó: △BMA = △BMD (cạnh huyền – góc nhọn)
Suy ra: BA = BD.
b) Xét △ABC và △DBE, có:
BA = BD (chứng minh trên)
là góc chung
Do đó: △ABC = △DBE (g.c.g)
Bài 6. Cho tam giác ABC có AB = AC. Trên cạnh AB, AC lần lượt lấy các điểm M, N sao cho AM = AN. Các đường thẳng vuông góc với AB, AC tại M, N cắt nhau ở O. AO cắt BC tại H. Chứng minh:
a) △AMO = △ANO
b) HB = HC và AH ⊥ BC.
Hướng dẫn giải
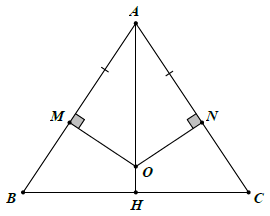
a) Xét △AMO vuông tại M và △ANO vuông tại N, có:
AO là cạnh chung
AM = AN (gt)
⇒ △AMO = △ANO (cạnh huyền – góc nhọn)
b) Xét △AHB và △AHC, có:
AB = AC (gt)
(do △AMO = △ANO)
AH là cạnh chung
⇒ △AHB = △AHC (c.g.c)
⇒ HB = HC (hai cạnh tương ứng)
Và (hai góc tương ứng), mà hai góc này ở vị trí kề bù
Vậy AH ⊥ BC
Bài 7. Cho tam giác ABC có AB = AC. Đường thẳng vuông góc với AB tại B cắt đường thẳng vuông góc với AC tại C ở D. Gọi M là trung điểm cạnh BC. Chứng minh:
a) △DAB = △DAC;
b) A, M, D thẳng hàng.
Hướng dẫn giải
a) Xét △DAB và △DAC, có:
AB = AC (gt)
AD là cạnh chung
Do đó: △DAB = △DAC (cạnh huyền – cạnh góc vuông).
b) Xét △ABM và △ACM, có:
AB = AC (gt)
MB = MC (M là trung điểm cạnh BC)
AM là cạnh chung
Do đó: △ABM = △ACM (c.c.c)
, mà hai góc này ở vị trí kề bù nên
Hay AM ⊥ BC tại M (1)
Xét △DBM và △DCM, có:
DB = DC (△DAB = △DAC)
MB = MC (M là trung điểm cạnh BC)
DM cạnh chung
Do đó: △DBM = △DCM (c.c.c)
, mà hai góc này ở vị trí kề bù nên
Hay DM ⊥ BC tại M (2)
Từ (1) và (2) ta suy ra AM và DM cùng vuông góc với BC nên A, M, D thẳng hàng.
Bài 8. Cho △ABC vuông tại A và AB = AC. Tính số đo góc ,
?
Hướng dẫn giải

Kẻ AD ⊥ BC (D ∈ BC)
+) Xét △ABD vuông tại D và △ACD vuông tại D, có:
AB = AC (gt)
AD chung
Suy ra: △ABD = △ACD (cạnh huyền – cạnh góc vuông)
Do đó: (hai góc tương ứng) (1)
Vì △ABC vuông tại A nên (2)
Từ (1) và (2) suy ra:
Bài 9. Cho △ABC vuông tại A. Từ điểm K trên cạnh AC, vẽ KH ⊥ BC, biết KH = KA. Chứng minh rằng: BK ⊥ AH.
Hướng dẫn giải

Xét △ABK vuông tại A và △HBK vuông tại H, có:
BK chung
KA = KH (gt)
Suy ra: △ABK = △HBK (cạnh huyền – cạnh góc vuông)
⇒
Gọi M là giao điểm của BK và AH.
Xét △ABM và △HBM, có:
AB = BH (chứng minh trên)
(do
)
AM cạnh chung
Suy ra: △ABM = △HBM (c.g.c)
(hai góc tương ứng), mà hai góc này ở vị trí kề bù
Vậy BK ⊥ AH
Bài 10. Cho △ABC vuông tại A (AB < AC) và các điểm M thuộc cạnh AC, H thuộc cạnh BC sao cho MH ⊥ BC và MH = HB. Chứng minh rằng AH là tia phân giác của góc .
Hướng dẫn giải
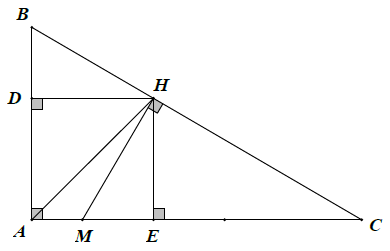
Kẻ HD ⊥ AB (D ∈ AB) và HE ⊥ AC (E ∈ AC)
Xét △DBH và △EMH, có:
HB = HM (gt)
(cùng phụ
)
Suy ra: △DBH = △EMH (cạnh huyền – góc nhọn)
⇒ HE = HD (hai cạnh tương ứng)
Xét △DAH và △EAH, có:
HD = HE (chứng minh trên)
AH là cạnh chung
Suy ra: △DAH = △EAH (cạnh huyền – cạnh góc vuông)
⇒ (hai góc tương ứng)
Vậy AH là tia phân giác của góc .
Bài 11. Cho tam giác ABC. Các tia phân giác của góc và
cắt nhau ở I. Kẻ ID ⊥ AB, IE ⊥ AC (D ∈ AB, E ∈ AC). Chứng minh rằng: AD = AE.
Hướng dẫn giải
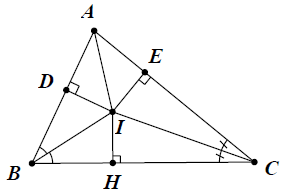
Kẻ HI ⊥ BC
+) Xét △BID vuông tại D và △BIH vuông tại H, có:
(IB là phân giác của góc
)
IB là cạnh chung
Do đó: △BID = △BIH (cạnh huyền – góc nhọn)
Suy ra: ID = IH (hai cạnh tương ứng) (1)
+) Xét △CIE vuông tại E và △CIH vuông tại H, có:
(IC là phân giác của góc
)
IC là cạnh chung
Do đó: △CIE = △CIH (cạnh huyền – góc nhọn)
Suy ra: IE = IH (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra ID = IE.
+) Xét △IAD vuông tại D và △IAE vuông tại E ta có:
ID = IE (chứng minh trên)
IA là cạnh chung
Do đó: △IAD = △IAE (cạnh huyền – cạnh góc vuông)
Suy ra: AD = AE (hai cạnh tương ứng)
Bài 12. Cho △ABC vuông tại A có AB < AC. Vẽ AH ⊥ BC (H ∈ BC). D là điểm trên cạnh AC sao cho AD = AB. Vẽ DE ⊥ BC (E ∈ BC). Chứng minh: HA = HE.
Hướng dẫn giải
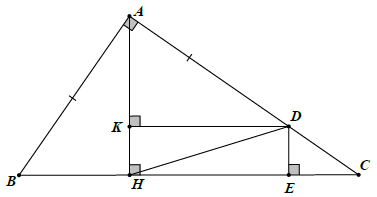
Kẻ DK ⊥ AH (K ∈ AH)
+) Xét △HAB vuông tại H và △KDA vuông tại K, có:
AD = AB (gt)
(cùng phụ với
)
Do đó: △HAB = △KDA (cạnh huyền – góc nhọn)
⇒ HA = KD (hai cạnh tương ứng)
Ta có: KD ⊥ AH (cách vẽ)
Và EH ⊥ AH (do BC ⊥ AH)
⇒ KD // EH
⇒ (hai góc so le trong)
+) Xét △KDH vuông tại K và △EHD vuông tại E, có:
DH cạnh chung
(cmt)
Do đó: △KDH = △EHD (cạnh huyền – góc nhọn)
Suy ra: HA = HE (hai cạnh tương ứng)
Bài 13. Cho tam giác ABC có M là trung điểm của BC và AM là tia phân giác của góc . Chứng minh: AB = AC.
Hướng dẫn giải
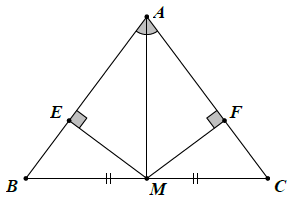
Từ M kẻ ME ⊥ AB, MF ⊥ AC
+) Xét △MEA vuông tại E và △MFA vuông tại F, có:
MA là cạnh chung
(vì AM là tia phân giác của góc
)
Do đó: △MEA = △MFA (cạnh huyền – góc nhọn)
⇒ AE = AF (1) và ME = MF
+) Xét △MEB vuông tại E và △MFC vuông tại F, có:
MB = MC (vì M là trung điểm của BC)
ME = MF (chứng minh trên)
Do đó: △MEB = △MFC (cạnh huyền – cạnh góc vuông)
⇒ BE = CF (2)
Từ (1) và (2) ta suy ra AE + BE = AF + CF hay AB = AC.