Góc tạo bởi một đường thẳng cắt hai đường thẳng.
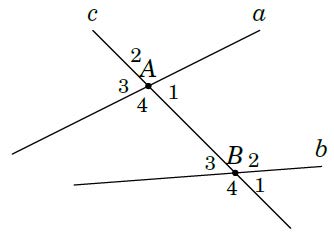
+) Cho đường thẳng c cắt hai đường thẳng a và b tại hai điểm A, B như hình vẽ bên
+) Có hai cặp góc so le trong là A1 và B3; A4 và B2.
+) Có bốn cặp góc đồng vị là: A1 và B1; A2 và B2; A3 và B3; A4 và B4.
+) Có hai cặp góc trong cùng phía là A1 và B2; A4 và B3.
+) Có hai cặp góc so le ngoài là A2 và B4; A3 và B1.
Nhắc lại
+) Hai đường thẳng song song là hai đường thẳng không có điểm chung.
+) Hai đường thẳng phân biệt hoặc cắt nhau hoặc song song.
Dấu hiệu nhận biết hai đường thẳng song song
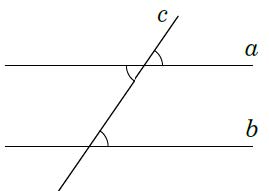
+) Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì a và b song song với nhau.
Phân dạng bài tập
Dạng 1. Xác định cặp góc so le trong, cặp góc đồng vị, cặp góc trong cùng phía, cặp góc so le ngoài trên hình vẽ cho trước. Vẽ hai đường thẳng song song hoặc kiểm tra xem hai đường thẳng có song song với nhau không? Tính số đo góc.
Phương pháp giải
+) Dựa vào vị trí của các cặp góc xác định đúng cặp góc so le trong, cặp góc đồng vị, cặp góc trong cùng phía, cặp góc so le ngoài trên hình vẽ cho trước.
+) Dùng góc nhọn của ê-ke để vẽ hai góc so le trong hoặc hai góc đồng vị bằng nhau.
+) Dùng thước đo góc để kiểm tra xem hai góc so le trong hoặc hai góc đồng vị (các góc tạo bởi một đường thẳng cắt hai đường thẳng cần kiểm tra có song song hay không) có bằng nhau hay không.
Bài toán.
Bài 1. Cho hình sau:
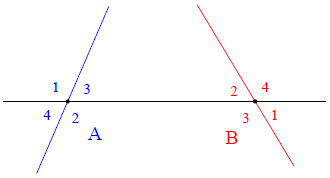
a) Kể tên các góc so le trong.
b) Kể tên các góc đồng vị.
c) Kể tên các góc trong cùng phía.
Hướng dẫn giải
a) Các góc so le trong là: A2 và B2; A3 và B3
b) Các góc đồng vị là: A1 và B2; A3 và B4; A4 và B3; A2 và B1
c) Các góc trong cùng phía là: A3 và B2; A2 và B3
Bài 2. Chỉ ra các cặp góc so le trong, cặp góc đồng vị, cặp góc trong cùng phía, cặp góc so le ngoài trong các hình vẽ sau:
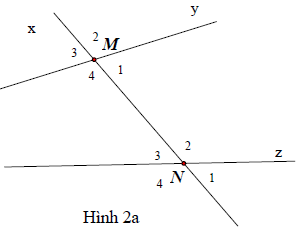
Hướng dẫn giải
Hình 2a:
+) Cặp góc so le trong: M1 và N3; M4 và N2.
+) Cặp góc so le ngoài: M2 và N4; M3 và N1.
+) Cặp góc đồng vị: M4 và N4; M1 và N1; M2 và N2; M3 và N3.
+) Cặp góc trong cùng phía: M4 và N3; M1 và N2.
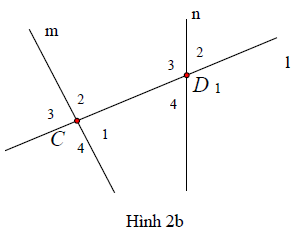
Hình 2b:
+) Cặp góc so le trong: C2 và D4, C1 và D3
+) Cặp góc so le ngoài: C3 và D1, C4 và D2
+) Cặp góc đồng vị: C1 và D1, C2 và D2, C3 và D3, C4 và D4.
+) Cặp góc trong cùng phía: C2 và D3, C1 và D4
Bài 3. Vẽ hai đường thẳng xx′, yy′ sao cho xx′ song song yy′.
Hướng dẫn giải
Sử dụng ê-ke và thước vẽ như các bước ở thực hành 1 hoặc 2 ta được hình vẽ
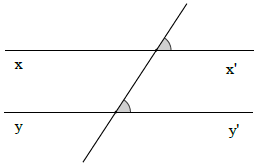
Hình vẽ tham khảo
Bài 4. Cho hai điểm A và B. Hãy vẽ một đường thẳng a đi qua A và đường thẳng b đi qua B sao cho b song song với a.
Hướng dẫn giải
Sử dụng ê-ke và thước vẽ như các bước ở thực hành 1 hoặc 2 ta được hình vẽ
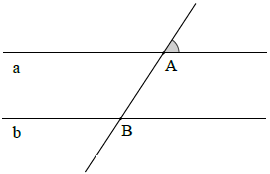
Hình vẽ tham khảo
Bài 5. Chỉ ra các cặp góc so le trong, cặp góc đồng vị trong các hình vẽ bên.
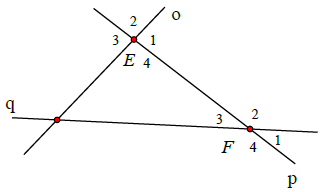
Hướng dẫn giải
+) Cặp góc so le trong: E1 và F3, E4 và F2
+) Cặp góc đồng vị: E4 và F4, E1 và F1, E2 và F2, E3 và F3.
Bài 6. Xem hình bên rồi điền vào chỗ trống (…) trong các câu sau:
a) IPO và POR là một cặp góc …
b) OPI và TNO là một cặp góc …
c) PIO và NTO là một cặp góc …
d) OPR và POI là một cặp góc …
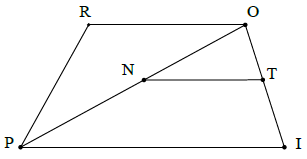
Hướng dẫn giải
a) IPO và POR là một cặp góc so le trong.
b) OPI và TNO là một cặp góc đồng vị.
c) PIO và NTO là một cặp góc đồng vị.
d) OPR và POI là một cặp góc so le trong.
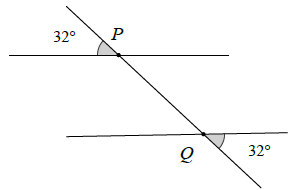
Bài 7. Cho hình sau:
a) Đặt tên cho các góc trong hình.
b) Kể tên các góc bằng nhau có trong hình.
Hướng dẫn giải
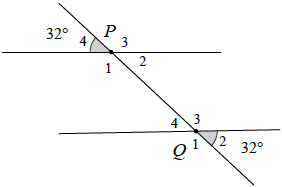
Vì P3 và P4 là 2 góc kề bù nên P3 + P4 = 180°
Ta tính được P3 = 180° – 32° = 148°
Vì P4 và P2 là 2 góc đối đỉnh nên P4 = P2 = 32°
Vì P3 và P1 là 2 góc đối đỉnh nên P3 = P1 = 148°
Tương tự ta có các góc tại đỉnh Q
Q1 = Q3 = 148°; Q2 = Q4 = 32°
Vậy các góc bằng nhau có trong hình là:
P4 = P2 = Q2 = Q4 = 32°
P3 = P1 = Q1 = Q3 = 148°
Bài 8. Cho hình sau.
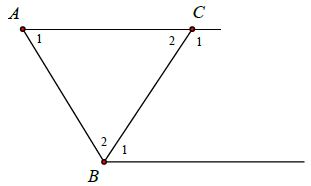
a) Viết tên hai góc trong cùng phía tại A và B.
b) Viết tên các góc so le trong tại B và C.
c) Hai góc C1 và A1 là hai góc gì?
d) Hai góc B2 và C2 là hai góc gì?
Hướng dẫn giải
a) Hai góc trong cùng phía tại A và B: A1 và B2
b) Các góc so le trong tại B và C: C2 và B1, C1 và B2
c) Hai góc C1 và A1 là hai góc đồng vị
d) Hai góc B2 và C2 là hai góc trong cùng phía
Bài 9. Vẽ lại các hình sau và tính số đo các góc còn lại.
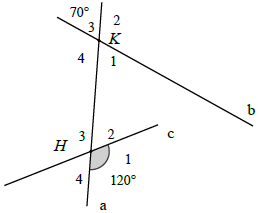
Hướng dẫn giải
Ta có: K2 + K3 = 180° (2 góc kề bù).
Thay số K2 + 70° = 180°.
Suy ra: K2 = 180° – 70° = 110°
Ta có: K1 = K3 = 70° (2 góc đối đỉnh)
K2 = K4 = 110° (2 góc đối đỉnh).
Tương tự: H3 = H1 = 120° (2 góc đối đỉnh)
H1 + H2 = 180° (2 góc kề bù)
Thay số: 120° + H2 = 180°.
Suy ra: H2 = 180° – 120° = 60°
Suy ra: H4 = H2 = 60°
Bài 10. Cho hình vẽ bên:
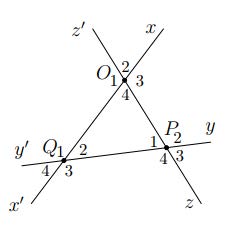
a) Kể tên các cặp góc so le trong, các cặp góc đồng vị và các cặp góc trong cùng phía.
b) Tính số đo các cặp góc còn lại, biết: O1 = 100°, P1 = 60°, Q2 = 40°
Hướng dẫn giải
a) Các cặp góc so le trong: O1 và Q2; O4 và Q1; O3 và P1; O4 và P2, Q2 và P4, Q3 và P1
Các cặp góc đồng vị: O1 và Q4; O2 và Q1; O3 và Q2; P4 và Q3; O1 và P1; O2 và P2; O3 và P3; O4 và P4; Q1 và P1; Q2 và P2; Q3 và P3; Q4 và P4
Các cặp góc trong cùng phía: O1 và Q1; O4 và P1; O3 và P2; Q2 và P1; Q3 và P4
b) Từ Q1 = 100°, suy ra: O3 = 100°; O2 = O4 = 80°
Từ P1 = 60°, suy ra: P3 = 60°; P2 = P4 = 120°
Từ Q2 = 40°, suy ra: Q4 = 40°; Q1 = Q3 = 140°
Bài 11. Cho hình vẽ bên
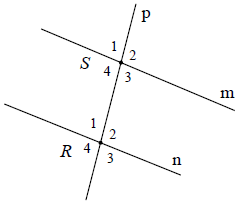
a) Kể tên các cặp góc so le trong, các cặp góc đồng vị và các cặp góc trong cùng phía.
b) Tính số đo các cặp góc còn lại, biết: R4 = S2 = 120°
Hướng dẫn giải
a) Cặp góc so le trong: S4 và R2; S3 và R1
Cặp góc đồng vị: S1 và R1; S2 và R2; S3 và R3; S4 và R4
Cặp góc trong cùng phía: S4 và R1; S3 và R2
b) Ta có: S4 = S2 = 120° (2 góc đối đỉnh).
S2 + S3 = 180° (2 góc kề bù).
Thay số: 120° + S3 = 180°.
Suy ra: S3 = 180° – 120° = 60°
Suy ra: S3 = S1 = 60° (2 góc đối đỉnh)
Tương tự: R2 = R4 = 120° (2 góc đối đỉnh)
R1 + R2 = 180° (2 góc kề bù)
Thay số: R1 + 120° = 180°.
Suy ra: R1 = 180° – 120° = 60°
Suy ra: R3 = R1 = 60°
Bài 12. Cho hình vẽ bên.
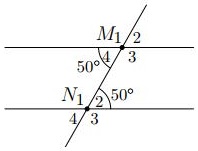
a) Kể tên các cặp góc so le trong, các cặp góc đồng vị và các cặp góc trong cùng phía.
b) Ghi tiếp số đo ứng với các góc còn lại.
c) Tính M3 + N2; M4 + N1
Hướng dẫn giải
a) Cặp góc so le trong: M4 và N2; M3 và N1
Cặp góc đồng vị: M1 và N1; M4 và N4, M3 và N3, M1 và N1
Cặp góc trong cùng phía: M4 và N1, M3 và N2
b) M2 = M4 =50° (2 góc đối đỉnh)
M1 + M2 = 180° (2 góc kề bù)
Suy ra: M1 = 180° – 50° = 130°
Suy ra: M3 = M1 = 130° (2 góc đối đỉnh)
Tương tự: N4 = N2 = 50° (2 góc đối đỉnh)
N1 + N2 = 180° (2 góc kề bù).
Suy ra: N1 = 180° – 50° = 130°
Suy ra: N3 = N1 = 130° (2 góc đối đỉnh)
c) Từ kết quả đã tính ở ý b), ta có:
M3 + N2 = 180°; M4 + N1 = 180°
Dạng 2. Nhận biết hai đường thẳng song song. Vận dụng tính số đo góc.
Phương pháp giải
+) Dựa vào tính chất hai góc kề bù, đối đỉnh để chỉ ra hai góc so le trong hoặc hai góc đồng vị bằng nhau hoặc hai góc trong cùng phía bù nhau.
+) Áp dụng tính chất hai góc kề bù, đối đỉnh để lý luận và biến đổi tính góc.
Bài toán.
Bài 1. Cho hình vẽ bên.
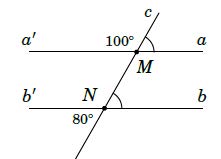
Hai đường thẳng aa′ và bb′ có song song với nhau không? Vì sao?
Hướng dẫn giải
Ta có:
Mà hai góc này ở vị trí đồng vị nên hai đường thẳng aa′và bb′song song với nhau (dhnb).
Bài 2. Cho hình vẽ bên.
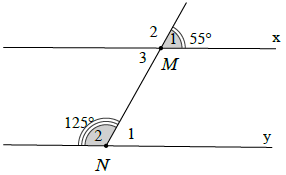
Đường thẳng x, y có song song với nhau không? Tại sao?
Hướng dẫn giải
Ta có: M1 = M3 = 55° (2 góc đối đỉnh).
Suy ra: M3 + N2 = 55° + 125° = 180°
Mà hai góc này ở vị trí hai góc trong cùng phía nên x // y (dhnb).
Bài 3. Cho hình vẽ bên.
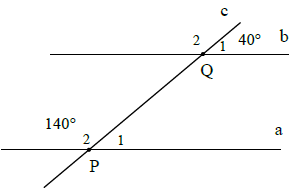
Đường thẳng a, b có song song với nhau không? Tại sao?
Hướng dẫn giải
Ta có: P1 + P2 = 180° (2 góc kề bù).
⇒ P1 = 180° – P2 = 180° – 40° = 40°
⇒ P1 = Q1 = 40°
Mà hai góc này ở vị trí đồng vị nên a // b (dhnb).
Bài 4. Cho hình vẽ bên, biết hai đường thẳng a và b song song với nhau. Tính số đo các góc T1, T2, T3, T4.
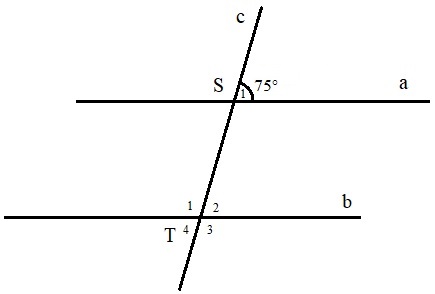
Hướng dẫn giải
Ta có: T2 = S1 = 75° (hai góc đồng vị).
Lại có T1 kề bù với T2 ⇒ T1 = 180° – T2 = 105°
T4 = T2 = 75° (đối đỉnh) và T3 = T1 = 75° (đối đỉnh)
Bài 5. Cho hình vẽ bên, biết hai đường thẳng m và n song song với nhau. Tính số đo các góc B1, B2, B3, B4.
Hướng dẫn giải
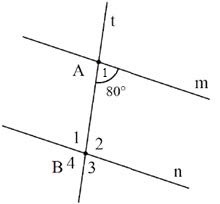
Ta có: B1 = A1 (hai góc so le trong)
Lại có B1 kề bù với B2 ⇒ B1 = 180° – B1 = 120°
B4 = B2 = 120° (đối đỉnh) và B3 = B1 = 80° (đối đỉnh)
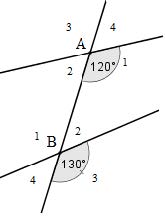
Bài 6. Cho hình vẽ, biết A1 = 120°; B3 = 130° thì hai đường thẳng a và b có song song với nhau không? Muốn a // b thì góc A1 hay B3 phải thay đổi thế nào?
Hướng dẫn giải
Có A1, B3 là hai góc đồng vị
Và A1 ≠ B3 (do 120° ≠ 130°)
Vậy hai đường thẳng a và b không song song với nhau
Muốn a // b thì góc A1 = 130° hoặc B3 = 120°
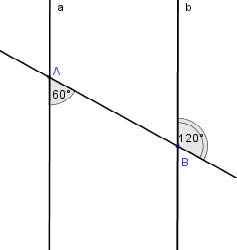
Bài 7. Cho hình vẽ. Hãy chứng tỏ a // b bằng nhiều cách.
Hướng dẫn giải
Có A1 + A2 = 180° (2 góc kề bù)
Hay 60° + A2 = 180°
⇒ A2 = 180° – 60° = 120°
Tương tự ta có: B3 + B2 =180° (2 góc kề bù)
Hay B3 + 120° = 180°
⇒ B3 = 180° – 120° = 60°
Cách 1: Có A1 = B3 = 60°. Và A1, B3 ở vị trí so le trong. Vậy a // b.
Cách 2: Có A2 = B2 = 120°. Và A2, B2 ở vị trí đồng vị. Vậy a // b.
Cách 3: Có A2 + B3 = 120° + 60° = 180°. Và A2, B3 ở vị trí trong cùng phía. Vậy a // b.
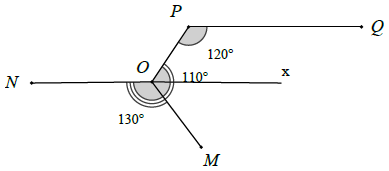
Bài 8. Cho hình vẽ bên.
Đường thẳng PQ và NO có song song với nhau không? Tại sao?
Hướng dẫn giải
Kẻ tia Ox là tia đối của tia ON
Ta có: (2 góc kề bù)
Thay số:
Suy ra
Lại có:
Suy ra:
Khi đó:
Mà hai góc này ở vị trí trong cùng phía nên PQ // Ox hay PQ // NO (dhnb)
Bài 9. Cho hình vẽ. Hãy chứng tỏ AC // BD.
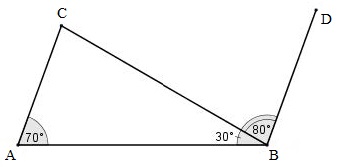
Hướng dẫn giải
Có
Lại có:
Và là hai góc trong cùng phía.
Vậy AC // BC (dhnb).
Bài 10. Cho , A là điểm nằm trên tia Ox. Vẽ đường thẳng d vuông góc với Ox tại A.
Hướng dẫn giải

Ta có:
Mà d ⊥ Ox tại A. Suy ra:
Suy ra:
Mà hai góc này ở vị trí đồng vị nên d // Oy (dhnb)
Bài 11. Cho hình vẽ. Tìm trên hình các đường thẳng song song với OC. Vì sao?
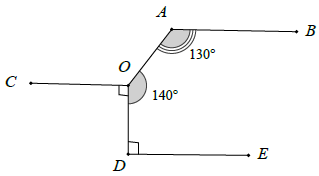
Hướng dẫn giải
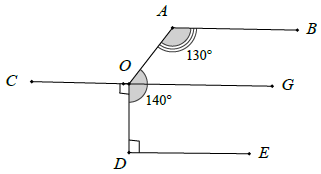
Có . Và
là hai góc so le trong.
Suy ra: OC // DE (dhnb)
Vẽ OG // DE
Ta có: là hai góc kề bù nên
Lại có:
Hay
Nên
Mà là hai góc trong cùng phía.
Nên AB // OG (dhnb)
Suy ra: AB // OC
Vậy OC // DE và OC // AB
Bài 12. Cho hình vẽ. Chứng tỏ rằng AB // CD.
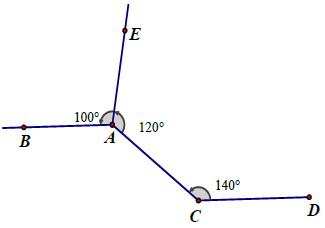
Hướng dẫn giải
Có
Hay
Do đó:
Và là hai góc so le trong.
Vậy AB // CD.