Tập hợp q

Bài viết này sẽ giúp bạn?

+) Nắm được định nghĩa số hữu tỉ, mối quan hệ giữa các tập hợp số đã học với tập số hữu tỉ

+) Nắm được cách biểu diễn số hữu tỉ trên trục số.

+) Nắm được phương pháp so sánh hai số hữu tỉ; khái niệm số hữu tỉ âm, số hữu tỉ dương.

+) Nhận biết số hữu tỉ và biểu diễn được số hữu tỉ trên trục số.

+) Biểu diễn được số hữu tỉ thành nhiều phân số bằng nhau.

+) Biết cách so sánh các số hữu tỉ với nhau.

+) Nhận biết được số hữu tỉ âm, số hữu tỉ dương và tìm điều kiện để số hữu tỉ là số âm (dương) hoặc số nguyên.

Lý thuyết tập hợp q

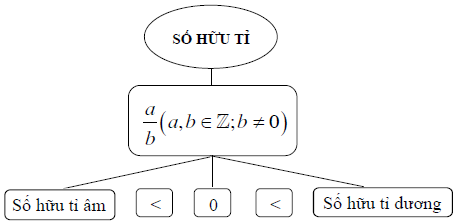
Định nghĩa

Số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b}\left( {a,b \in \mathbb{Z};b \ne 0} \right)$

Tập hợp số hữu tỉ được kí hiệu là ℚ.

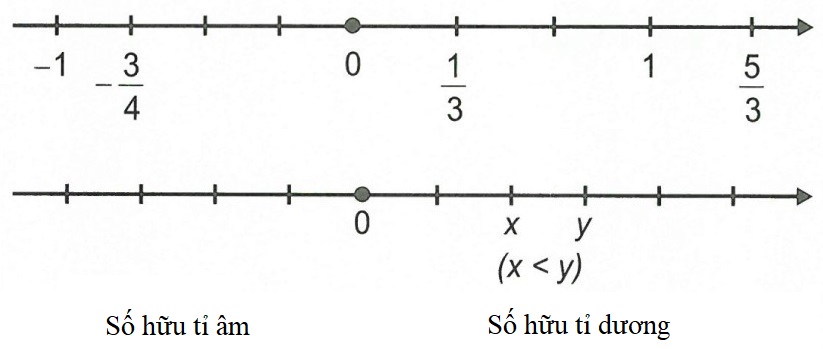
Biểu diễn số hữu tỉ trên trục số

Bất kì số hữu tỉ nào cũng có thể biểu diễn trên trục số dưới dạng phân số có mẫu dương.

Trên trục số, điểm biểu diễn số hữu tỉ x được gọi là điểm x.

So sánh hai số hữu tỉ

Với hai số hữu tỉ x, y ta luôn có hoặc x = y hoặc x < y hoặc x > y. Ta có thể so sánh hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi so sánh hai phân số đó.

+) Nếu x y thì trên trục số, điểm x ở bên trái điểm y.

+) Số hữu tỉ lớn hơn 0 được gọi là số hữu tỉ dương;

+) Số hữu tỉ nhỏ hơn 0 được gọi là số hữu tỉ âm.

Số 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.

Ứng dụng số hữu tỉ

Ở Pháp vào mùa đông, nhiệt độ có khi là âm: –3°C hoặc –10°C, có khi là dương +2°C.

Các số –3; –10; +2 là các số hữu tỉ thể hiện nhiệt độ không khí.

Các số $0; - 2;\frac{1}{2};2\frac{3}{2}$ đều là các số hữu tỉ.

Thật vậy, các số đều được viết dưới dạng $\frac{a}{b}$ như sau:

$0 = \frac{0}{1} - \ldots ; - 2 = \frac{{ - 4}}{2};\frac{1}{2} = \frac{2}{4};2\frac{3}{2} = \frac{7}{2}$

Trên trục số, ta biểu diễn các điểm:

$- 1; - \frac{3}{4};\frac{1}{3};1;\frac{5}{3}$

Sơ đồ hệ thống hóa

Phân dạng bài tập

Dạng 1: Nhận biết quan hệ giữa các tập hợp số

Phương pháp giải

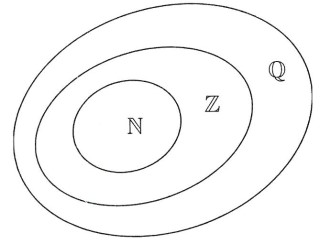
+) Mối quan hệ giữa các tập hợp số đã biết với tập hợp số hữu tỉ: ℕ ⊂ ℤ ⊂ ℚ

+) Sử dụng các kí hiệu ∈, ∉, ⊂, ⊃, ℕ, ℤ, ℚ để biểu diễn mối quan hệ giữa số và tập hợp hoặc giữa các tập hợp với nhau.

Ví dụ. Điền các kí hiệu thích hợp (∈, ∉, ⊂, ⊃, ℕ, ℤ, ℚ) vào ô trống:

–3 ℕ

$\frac{{ - 1}}{2}$ ℚ

$\frac{7}{9}$ ∈

ℕ ℤ ⊂

Hướng dẫn giải

–3 ℕ

$\frac{{ - 1}}{2}$ ℚ

$\frac{7}{9}$ ∈

ℕ ℤ ⊂

Ví dụ mẫu

Ví dụ. Điền các kí hiệu thích hợp (∈, ∉, ⊂, ⊃, ℕ, ℤ, ℚ) vào ô trống:

1 ℕ

–1 ℕ

$- \frac{{10}}{2}$ ℤ

$\frac{3}{{ - 8}}$ ℚ

$\frac{{ - 4}}{9}$ ℤ

$\frac{1}{4}$ ∉

$\frac{2}{5}$ ∈

ℚ ⊃

Hướng dẫn giải

1 ℕ

–1 ℕ

$- \frac{{10}}{2}$ ℤ

$\frac{3}{{ - 8}}$ ℚ

$\frac{{ - 4}}{9}$ ℤ

$\frac{1}{4}$ ∉

$\frac{2}{5}$ ∈

ℚ ⊃

Chú ý:

+) Kí hiệu ∈ là “thuộc”.

+) Kí hiệu ∉ là “không thuộc”.

+) Kí hiệu ⊂ là “tập hợp con”.

+) Kí hiệu ⊃ là “chứa trong” hoặc “chứa”.

+) Kí hiệu ℕ là “tập hợp các số tự nhiên”.

Bài tập tự luyện dạng 1

Câu 1: Điền kí hiệu (∈, ∉, ⊂) thích hợp và ô trống:

–4 ℕ

$\frac{{ - 5}}{3}$ ℚ

–8 ℤ

$\frac{{ - 2}}{9}$ ℤ

$- \frac{1}{{11}}$ ℤ

$- \frac{2}{7}$ ℚ

$- \frac{2}{{19}}$ ℕ

ℕ ℚ

Hướng dẫn giải

–4 ℕ

$\frac{{ - 5}}{3}$ ℚ

–8 ℤ

$\frac{{ - 2}}{9}$ ℤ

$- \frac{1}{{11}}$ ℤ

$- \frac{2}{7}$ ℚ

$- \frac{2}{{19}}$ ℕ

ℕ ℚ

Câu 2: Điền các kí hiệu ℕ, ℤ, ℚ thích hợp vào ô trống (điền tất cả các khả năng có thể):

–6 ∈

22 ∈

$\frac{{ - 2}}{{23}}$ ∈

ℕ ⊂

ℤ ⊂

$\frac{{ - 5}}{7}$ ∉

–21 ∉

$1\frac{3}{4}$ ∉

Hướng dẫn giải

–6 ∈

22 ∈

$\frac{{ - 2}}{{23}}$ ∈

ℕ ⊂

ℤ ⊂

$\frac{{ - 5}}{7}$ ∉

–21 ∉

$1\frac{3}{4}$ ∉

Câu 3: Khẳng định nào dưới đây sai?

A Số 19 là một số tự nhiên.

B Số –5 là một số nguyên âm.

C Số $- \frac{{15}}{{19}}$ là một số hữu tỉ.

D Số 0 là một số hữu tỉ dương.

Hướng dẫn giải

Chọn D

Vì số 0 không là số hữu tỉ âm, cũng không là số hữu tỉ dương.

Câu 4: Viết Đ vào ô có khẳng định đúng và S vào ô có khẳng định sai:

a) Số nguyên là số hữu tỉ;

b) Số nguyên âm không là số hữu tỉ âm;

c) Tập hợp ℚ gồm các số hữu tỉ âm và các số hữu tỉ dương;

d) Số $1\frac{1}{2}$ là số hữu tỉ;

e) Số $\frac{{ - 1}}{{ - 5}}$ không là số hữu tỉ.

Hướng dẫn giải

a) Đ

b) S

c) S

d) Đ

e) S

Dạng 2: Biểu diễn số hữu tỉ

Bài toán 1: Biểu diễn số hữu tỉ trên trục số

Phương pháp giải

Để biểu diễn một số hữu tỉ trên trục số, ta thường làm như sau:

Bước 1. Ta viết số đó dưới dạng phân số có mẫu dương. Khi đó mẫu của phân số sẽ cho ta biết đoạn thẳng đơn vị được chia thành bao nhiêu phần bằng nhau.

Bước 2. Lấy đoạn thẳng mới làm đơn vị.

Bước 3. Số hữu tỉ dương (âm) nằm bên phải (trái) điểm 0 và cách điểm 0 một khoảng bằng giá trị tuyệt đối của số hữu tỉ đó.

Ví dụ: Biểu diễn phân số $- \frac{2}{3}$ trên trục số.

Bước 1. Chia các đoạn thẳng đơn vị làm 3 phần bằng nhau.

Bước 2. Lấy đoạn thẳng mới làm đơn vị (bằng $\frac{1}{3}$ đơn vị cũ).

Bước 3. Lấy điểm nằm bên trái điểm 0, cách điểm 0 một đoạn bằng 2 đơn vị mới.

Điểm vừa lấy là điểm phải tìm.

Ví dụ mẫu

Ví dụ 1. Biểu diễn số hữu tỉ $\frac{3}{4}$ trên trục số.

Hướng dẫn giải

Chia các đoạn thẳng đơn vị ra làm 4 phần bằng nhau.

Lấy đoạn thẳng mới làm đơn vị (bằng $\frac{1}{4}$ đơn vị cũ).

Lấy điểm nằm bên trái điểm 0, cách điểm 0 một đoạn bằng 3 đơn vị mới.

Điểm vừa lấy là điểm phải tìm.

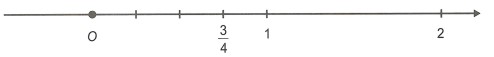
Ví dụ 2. Biểu diễn số hữu tỉ $\frac{3}{{ - 5}}$ trên trục số.

Hướng dẫn giải

Ta có: $\frac{3}{{ - 5}} = \frac{{ - 3}}{5}$

Chia các đoạn thẳng đơn vị ra làm 5 phần bằng nhau.

Lấy đoạn thẳng mới làm đơn vị (bằng $\frac{1}{5}$ đơn vị cũ).

Lấy điểm nằm bên trái điểm 0, cách điểm 0 một đoạn bằng 3 đơn vị mới.

Điểm vừa lấy là điểm phải tìm.

Bài toán 2: Biểu diễn số hữu tỉ dưới dạng các phân số bằng nhau

Phương pháp giải

Số hữu tỉ thường được biểu diễn dưới dạng phân số tối giản $\frac{a}{b}\left( {a,b \in \mathbb{Z};b \ne 0} \right)$

Ví dụ:

$\begin{gathered} \frac{1}{2} = \frac{{ - 1}}{{ - 2}} = \frac{2}{4} = \frac{3}{6} = \ldots \hfill \\ 1 = \frac{1}{1} = \frac{2}{2} = \frac{{ - 3}}{{ - 3}} = \ldots \begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ 1\frac{2}{3} = \frac{5}{3} = \frac{{10}}{6} = \ldots \hfill \\ \end{gathered}$

Ví dụ mẫu

Ví dụ. Cho các phân số sau: $\frac{{ - 6}}{{15}};\frac{4}{{ - 12}};\frac{4}{{ - 10}};\frac{{20}}{{ - 8}}$

Những phân số nào biểu diễn số hữu tỉ $\frac{2}{{ - 5}}$ ?

Hướng dẫn giải

Ta có: $\frac{2}{{ - 5}} = \frac{{ - 2}}{5}$ . Rút gọn các phân số đã cho ta được:

$\frac{{ - 6}}{{15}} = \frac{{ - 2}}{5};\frac{4}{{ - 12}} = \frac{{ - 1}}{3};\frac{4}{{ - 10}} = \frac{{ - 2}}{5};\frac{{20}}{{ - 8}} = \frac{{ - 5}}{2}$

Vậy các phân số biểu diễn số hữu tỉ $\frac{2}{{ - 5}}$ là: $\frac{{ - 6}}{{15}}$ và $\frac{4}{{ - 10}}$

Bài tập tự luyện dạng 2

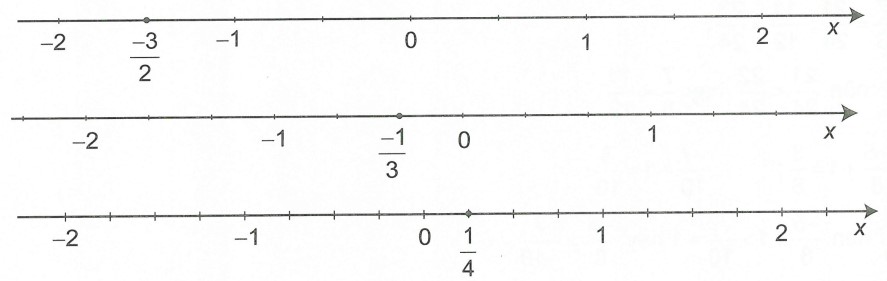
Câu 1: Biểu diễn các số hữu tỉ sau trên trục số: $\frac{{ - 3}}{2};\frac{1}{{ - 3}};\frac{1}{4}$

Hướng dẫn giải

Biểu diễn các số hữu tỉ $\frac{{ - 3}}{2};\frac{1}{{ - 3}};\frac{1}{4}$ trên trục số như sau:

Câu 2: Cho các phân số sau $\frac{{ - 9}}{6};\frac{{ - 14}}{{21}};\frac{4}{{ - 6}};\frac{{12}}{{20}}$ . Những phân số nào biểu diễn số hữu tỉ $\frac{2}{{ - 3}}$ ?

Hướng dẫn giải

Ta có: $\frac{2}{{ - 3}} = \frac{{ - 2}}{3}$

Rút gọn các phân số đã cho ta được:

$\frac{{ - 9}}{6} = \frac{{ - 3}}{2};\frac{{ - 14}}{{21}} = \frac{{ - 2}}{3};\frac{4}{{ - 6}} = \frac{{ - 2}}{3};\frac{{12}}{{ - 20}} = \frac{{ - 3}}{5}$

Vậy các phân số biểu diễn số hữu tỉ $\frac{2}{{ - 3}}$ là: $\frac{{ - 14}}{{21}};\frac{4}{{ - 6}}$

Câu 3:

a) Cho các phân số $\frac{{ - 21}}{{27}};\frac{{ - 14}}{{19}};\frac{{ - 42}}{{ - 54}};\frac{{35}}{{ - 45}};\frac{{ - 5}}{7};\frac{{ - 28}}{{36}}$ . Những phân số nào biểu diễn số hữu tỉ $\frac{{ - 7}}{9}$ ?

b) Biểu diễn số hữu tỉ $\frac{{ - 7}}{9}$ trên trục số.

Hướng dẫn giải

a) Ta có:

$\frac{{ - 21}}{{27}} = \frac{{ - 7}}{9};\frac{{ - 28}}{{36}} = \frac{{ - 7}}{9};\frac{{35}}{{ - 45}} = \frac{{ - 35}}{{45}} = \frac{{ - 7}}{9}$

Vậy các phân số biểu diễn số hữu tỉ $\frac{{ - 7}}{9}$ là $\frac{{ - 21}}{{27}};\frac{{ - 28}}{{36}};\frac{{35}}{{ - 45}}$

b) Biểu diễn các số hữu tỉ $\frac{{ - 7}}{9}$ trên trục số như sau:

Câu 4: Trong các phân số sau, phân số nào không bằng phân số $\frac{3}{5}$ ?

A $\frac{6}{{11}}$

B $\frac{9}{{15}}$

C $\frac{{ - 6}}{{ - 10}}$

D $\frac{{ - 3}}{{ - 5}}$

Hướng dẫn giải

Chọn A

Các đáp án B, C, D sau khi rút gọn ta đều được phân số $\frac{3}{5}$ .

Câu 5: Biểu diễn các số: $\frac{1}{4};0,25;\frac{{ - 25}}{{ - 100}};\frac{5}{{20}}$ bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?

A Một điểm

B Hai điểm

C Ba điểm

D Bốn điểm

Hướng dẫn giải

Chọn A

Đưa các số hữu tỉ về dạng phân số tối giản, ta có:

$\frac{1}{4};0,25 = \frac{1}{4};\frac{{ - 25}}{{ - 100}} = \frac{1}{4};\frac{5}{{20}} = \frac{1}{4}$

Vậy các số trên cùng biểu diễn bởi điểm $\frac{1}{4}$ trên trục số.

Câu 6: Trong các phân số sau có bao nhiêu phân số bằng phân số $\frac{{12}}{{13}}$ ?

$\frac{{14}}{{18}};\frac{{24}}{{26}};\frac{{26}}{{ - 28}};\frac{{ - 28}}{{30}};\frac{{72}}{{78}}$

A 1

B 2

C 3

D 4

Hướng dẫn giải

Chọn B

$\frac{{14}}{{18}} = \frac{7}{9};\frac{{24}}{{26}} = \frac{{12}}{{13}};\frac{{26}}{{ - 28}} = - \frac{{13}}{{14}};\frac{{ - 28}}{{30}} = - \frac{{14}}{{15}};\frac{{72}}{{78}} = \frac{{12}}{{13}}$

Vậy có hai phân số biểu diễn phân số $\frac{{12}}{{13}}$

Dạng 3: So sánh hai số hữu tỉ

Phương pháp giải

Để so sánh hai số hữu tỉ ta thường thực hiện các bước sau:

Bước 1. Viết số hữu tỉ dưới dạng phân số có mẫu dương.

Bước 2. Đưa các phân số ở bước một về cùng mẫu số (quy đồng).

Bước 3. So sánh các tử của các phân số ở bước hai, phân số nào có tử lớn hơn thì sẽ lớn hơn.

Ví dụ. So sánh các số hữu tỉ sau: $\frac{{ - 11}}{6}$ và $\frac{8}{{ - 9}}$

Hướng dẫn giải

$\frac{8}{{ - 9}} = \frac{{ - 8}}{9}$

Ta có: $\frac{{ - 11}}{6} = \frac{{ - 33}}{{18}};\frac{8}{{ - 9}} = \frac{{ - 8}}{9} = \frac{{ - 16}}{{18}}$

Vì –33 < –16 nên $\frac{{ - 33}}{{18}} < \frac{{ - 16}}{{18}}$ hay $\frac{{ - 11}}{6} < \frac{8}{{ - 9}}$

Ví dụ mẫu

Ví dụ 1. So sánh các số sau:

a) $\frac{{ - 25}}{{20}}$ và $\frac{{20}}{{25}}$

b) $\frac{{15}}{{21}}$ và $\frac{{21}}{{49}}$

c) $\frac{{ - 19}}{{49}}$ và $\frac{{ - 23}}{{47}}$

Hướng dẫn giải

a) Ta có: $\frac{{ - 25}}{{20}} < 0$ và $\frac{{20}}{{25}} > 0$ nên $\frac{{ - 25}}{{20}} < \frac{{20}}{{25}}$

b) Ta có: $\frac{{15}}{{21}} = \frac{5}{7};\frac{{21}}{{49}} = \frac{3}{7}$ . Vì $\frac{5}{7} > \frac{3}{7}$ nên $\frac{{15}}{{21}} > \frac{{21}}{{49}}$

c) Ta có: $\frac{{ - 19}}{{49}} > \frac{{ - 23}}{{49}}$ và $\frac{{ - 23}}{{49}} > \frac{{ - 23}}{{47}}$

Do đó: $\frac{{ - 19}}{{49}} > \frac{{ - 23}}{{47}}$

Ví dụ 2. So sánh các số hữu tỉ sau:

a) $\frac{{998}}{{555}}$ và $\frac{{999}}{{556}}$

b) $\frac{{ - 315}}{{380}}$ và $\frac{{ - 316}}{{381}}$

c) $\frac{{2020}}{{2019}}$ và $\frac{{2018}}{{2019}}$

Hướng dẫn giải

a) Ta thấy 998 – 555 = 999 – 556 = 443 nên ta so sánh hai phân số qua phần bù

Ta có: $\frac{{998}}{{555}} - 1 = \frac{{443}}{{555}};\frac{{999}}{{556}} - 1 = \frac{{443}}{{556}}$

Vì $\frac{{443}}{{556}} < \frac{{443}}{{555}}$ nên $\frac{{999}}{{556}} - 1 < \frac{{998}}{{555}} - 1$ hay $\frac{{999}}{{556}} < \frac{{998}}{{555}}$

b) Ta thấy 380 + (–315) = 381 + (–316) = 65 nên ta so sánh hai phân số bằng cách cộng thêm 1.

Ta có: $\frac{{ - 315}}{{380}} + 1 = \frac{{65}}{{380}};\frac{{ - 316}}{{381}} + 1 = \frac{{65}}{{381}}$

Vì $\frac{{65}}{{380}} > \frac{{65}}{{381}}$ nên $\frac{{ - 315}}{{380}} + 1 > \frac{{ - 316}}{{381}} + 1$ hay $\frac{{ - 315}}{{380}} > \frac{{ - 316}}{{381}}$

c) Ta có: 2020 > 2019 nên $\frac{{2020}}{{2019}} > 1$

Lại có: 2018 < 2019 nên $\frac{{2018}}{{2019}} < 1$

Do đó: $\frac{{2020}}{{2019}} > \frac{{2018}}{{2019}}$

Chú ý: Ngoài phương pháp so sánh bằng cách quy đồng mẫu số, ta có thể sử dụng các phương pháp khác như:

+) So sánh qua một phân số trung gian.

+) So sánh qua phần bù.

+) Đưa về so sánh hai phân số có cùng tử số.

Bài tập tự luyện dạng 3

Câu 1: So sánh các số hữu tỉ sau:

a) $\frac{7}{8}$ và $\frac{{11}}{{12}}$

b) $\frac{{ - 5}}{8}$ và $\frac{7}{{ - 10}}$

c) $\frac{{24}}{{35}}$ và $\frac{{19}}{{30}}$

d) $\frac{{ - 9}}{{21}}$ và $\frac{{27}}{{ - 63}}$

Hướng dẫn giải

a) Ta có: $\frac{7}{8} = \frac{{21}}{{24}};\frac{{11}}{{12}} = \frac{{22}}{{24}}$

Vì 21 < 22 nên $\frac{{21}}{{24}} < \frac{{22}}{{24}}$ hay $\frac{7}{8} < \frac{{11}}{{12}}$

b) Ta có: $\frac{{ - 5}}{8} + 1 = \frac{3}{8};\frac{{ - 7}}{{10}} + 1 = \frac{3}{{10}}$

Vì $\frac{3}{8} > \frac{3}{{10}}$ nên $\frac{{ - 5}}{8} + 1 > \frac{{ - 7}}{{10}} + 1$ hay $\frac{{ - 5}}{8} > \frac{7}{{ - 10}}$

c) Ta có: $\frac{{24}}{{35}} = 1 - \frac{{11}}{{35}};\frac{{19}}{{30}} = 1 - \frac{{11}}{{30}}$

Vì $\frac{{11}}{{35}} < \frac{{11}}{{30}}$ nên $1 - \frac{{11}}{{35}} > 1 - \frac{{11}}{{30}}$ hay $\frac{{24}}{{35}} > \frac{{19}}{{30}}$

d) Ta có: $\frac{{ - 9}}{{21}} = \frac{{ - 3}}{7};\frac{{27}}{{ - 63}} = \frac{{ - 27}}{{63}} = \frac{{ - 3}}{7}$

Suy ra: $\frac{{ - 9}}{{21}} = \frac{{27}}{{ - 63}}$

Câu 2: So sánh các số hữu tỉ sau:

a) $\frac{9}{{70}}$ và $\frac{5}{{42}}$

b) $\frac{{ - 4}}{{27}}$ và $\frac{{15}}{{ - 63}}$

c) $\frac{{13}}{{15}}$ và $\frac{9}{{11}}$

d) $\frac{{ - 9}}{{17}}$ và $\frac{{ - 20}}{{ - 21}}$

Hướng dẫn giải

a) Ta có: $\frac{9}{{70}} = \frac{{27}}{{210}};\frac{5}{{42}} = \frac{{25}}{{210}}$

Vì 27 > 25 nên $\frac{{27}}{{210}} > \frac{{25}}{{210}}$ hay $\frac{9}{{70}} > \frac{5}{{42}}$

b) Ta có: $\frac{{ - 4}}{{27}} = \frac{{ - 28}}{{189}};\frac{{15}}{{ - 63}} = \frac{{ - 15}}{{63}} = \frac{{ - 45}}{{189}}$

Vì –28 > –45 nên $\frac{{ - 28}}{{189}} > \frac{{ - 45}}{{189}}$ hay $\frac{{ - 4}}{{27}} > \frac{{15}}{{ - 63}}$

c) Ta có: $\frac{{13}}{{15}} = 1 - \frac{2}{{15}};\frac{9}{{11}} = 1 - \frac{2}{{11}}$

Vì $\frac{2}{{15}} < \frac{2}{{11}}$ nên $1 - \frac{2}{{15}} > 1 - \frac{2}{{11}}$ hay $\frac{{13}}{{15}} > \frac{9}{{11}}$

d) Ta có: $\frac{{ - 9}}{{17}} < 0;\frac{{ - 20}}{{ - 21}} = \frac{{20}}{{21}} > 0$

Suy ra: $\frac{{ - 9}}{{17}} < \frac{{ - 20}}{{ - 21}}$

Câu 3: Sắp xếp các số hữu tỉ sau theo thứ tự giảm dần:

$\frac{{ - 12}}{{19}};\frac{{ - 3}}{{19}};\frac{{ - 16}}{{19}};\frac{{ - 1}}{{19}};\frac{{ - 11}}{{19}};\frac{{ - 14}}{{19}};\frac{{ - 9}}{{19}}$

Hướng dẫn giải

Vì –16 < –14 < –12 < –11 < –9 < –3 < –1 nên

$\frac{{ - 16}}{{19}} < \frac{{ - 14}}{{19}} < \frac{{ - 12}}{{19}} < \frac{{ - 11}}{{19}} < \frac{{ - 9}}{{19}} < \frac{{ - 3}}{{19}} < \frac{{ - 1}}{{19}}$

Sắp xếp các số theo thứ tự giảm dần:

$\frac{{ - 1}}{{19}};\frac{{ - 3}}{{19}};\frac{{ - 9}}{{19}};\frac{{ - 11}}{{19}};\frac{{ - 12}}{{19}};\frac{{ - 14}}{{19}};\frac{{ - 16}}{{19}}$

Câu 4: Sắp xếp các số hữu sau theo thứ tự tăng dần:

$\frac{{ - 16}}{{27}};\frac{{ - 16}}{{29}}; - \frac{{19}}{{27}}$

Hướng dẫn giải

Có 27 < 29 nên $\frac{{16}}{{27}} > \frac{{16}}{{29}}$ . Suy ra: $\frac{{ - 16}}{{27}} < \frac{{ - 16}}{{29}}$

Lại có: –16 > –19 nên $\frac{{ - 16}}{{27}} > \frac{{ - 19}}{{29}}$

Vậy $- \frac{{19}}{{27}} < \frac{{ - 16}}{{27}} < \frac{{ - 16}}{{29}}$

Sắp xếp các số theo thứ tự tăng dần:

$- \frac{{19}}{{27}};\frac{{ - 16}}{{27}};\frac{{ - 16}}{{29}}$

Dạng 4: Tìm điều kiện để một số hữu tỉ là số âm (dương) hay số nguyên

Phương pháp giải

+) Số hữu tỉ âm là những số hữu tỉ nhỏ hơn 0.

+) Số hữu tỉ dương là những số hữu tỉ lớn hơn 0.

+) Số 0 không là số hữu tỉ âm cũng không là số hữu tỉ dương.

+) Số hữu tỉ $\frac{a}{b}$ là số hữu tỉ dương khi a, b cùng dấu.

+) Số hữu tỉ $\frac{a}{b}$ là số hữu tỉ âm khi a, b khác dấu.

+) Số hữu tỉ $\frac{a}{b}$ bằng 0 khi a = 0 và b ≠ 0.

Chú ý: Số 0 không là số âm cũng không là số dương.

+) Số hữu tỉ $\frac{a}{b}$ là số nguyên khi a ⋮ b hay b là ước của a.

Ví dụ. Cho số hữu tỉ $x = \frac{{2a - 1}}{2}$ . Với giá trị nào của a thì:

a) x là số hữu tỉ dương?

b) x là số hữu tỉ âm?

c) x không là số hữu tỉ dương cũng không là số hữu tỉ âm?

d) x là số nguyên?

Hướng dẫn giải

a) Để x là số dương thì $\frac{{2a - 1}}{2} > 0$

Mà 2 > 0 nên 2a – 1 > 0 ⇒ a > $\frac{1}{2}$

Vậy a > $\frac{1}{2}$ thì x là số hữu tỉ dương.

b) Để x là số âm thì $\frac{{2a - 1}}{2} < 0$

Mà 2 > 0 nên 2a – 1 < 0 ⇒ a < $\frac{1}{2}$

Vậy a < $\frac{1}{2}$ thì x là số hữu tỉ âm.

c) Để x không là số dương cũng không là số âm thì $\frac{{2a - 1}}{2} = 0$

Mà 2 ≠ 0 nên 2a – 1 = 0 ⇒ a = $\frac{1}{2}$

Vậy a = $\frac{1}{2}$ thì x không là số hữu tỉ dương, cũng không là số hữu tỉ âm.

d) Để x là số nguyên thì (2a – 1) ⋮ 2. Suy ra:

2a – 1 = 2k, k ∈ ℤ

⇔ 2a = 2k + 1

⇔ a = k + $\frac{1}{2}$ , k ∈ ℤ

Vậy a = k + $\frac{1}{2}$ , k ∈ ℤ thì x là số nguyên.

Ví dụ 1. Cho số hữu tỉ $x = \frac{a}{{{a^2} + 1}}$ . Với giá trị nào của a thì:

a) x là số hữu tỉ âm?

b) x không là số hữu tỉ âm, x cũng không là số hữu tỉ dương?

Hướng dẫn giải

Ta có: a² ≥ 0, ∀a nên a² + 1 ≥ 1 > 0 hay a² + 1 > 0, ∀a. Do đó:

a) x là số hữu tỉ nếu $\frac{a}{{{a^2} + 1}} < 0$ , suy ra a < 0

b) x không là số hữu tỉ âm, x cũng không là số hữu tỉ dương nếu $\frac{a}{{{a^2} + 1}} = 0$ , suy ra a = 0.

Ví dụ 2. Cho số hữu tỉ $x = \frac{7}{{a + 1}}$ . Xác định số nguyên a để x là số nguyên dương.

Hướng dẫn giải

Để x ∈ ℤ thì 7 ⋮ (a + 1) hay (a + 1) ∈ Ư(7) = {–7; –1; 1; 7}. Ta có bảng sau:

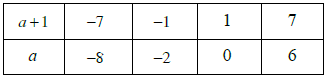
Mà x là số nguyên dương nên $\frac{7}{{a + 1}} > 0$

Mà 7 > 0 nên a + 1 > 0 ⇒ a > –1 ⇒ a ∈ {0; 6}

+) Với a = 0 ta có $x = \frac{7}{{0 + 1}} = 7$

+) Với a = 6 ta có $x = \frac{7}{{6 + 1}} = 1$

Vậy a ∈ {0; 6} thì x là số nguyên dương.

Bài tập tự luyện dạng 4

Câu 1: Cho số hữu tỉ $x = \frac{{3a + 7}}{{ - 5}}$ . Với giá trị nào của a thì

a) x là số hữu tỉ dương?

b) x là số hữu tỉ âm?

c) x không là số hữu tỉ dương và cũng không là số hữu tỉ âm?

Hướng dẫn giải

a) Để x là số hữu tỉ dương thì $\frac{{3a + 7}}{{ - 5}} > 0$ .

Mà –5 < 0 nên 3a + 7 < 0 ⇒ a < $\frac{{ - 7}}{3}$

b) Để x là số hữu tỉ âm thì $\frac{{3a + 7}}{{ - 5}} < 0$ .

Mà –5 < 0 nên 3a + 7 > 0 ⇒ a > $\frac{{ - 7}}{3}$

c) Để x không là số hữu tỉ dương cũng không là số hữu tỉ âm thì $\frac{{3a + 7}}{{ - 5}} = 0$ .

Mà –5 ≠ 0 nên 3a + 7 = 0 ⇒ a = $\frac{{ - 7}}{3}$

Câu 2: Cho số hữu tỉ $x = \frac{{3n - 1}}{4}$ . Với giá trị nào của a thì

a) x là số hữu tỉ dương?

b) x là số hữu tỉ âm?

c) x không là số hữu tỉ dương cũng không là số hữu tỉ âm?

Hướng dẫn giải

a) Để x là số hữu tỉ dương thì $\frac{{3n - 1}}{4} > 0$

Mà 4 > 0 nên 3n – 1 > 0 ⇒ n > $\frac{1}{3}$

b) Để x là số hữu tỉ âm thì $\frac{{3n - 1}}{4} < 0$

Mà 4 > 0 nên 3n – 1 < 0 ⇒ n < $\frac{1}{3}$

c) Để x không là số hữu tỉ dương cũng không là số hữu tỉ âm thì $\frac{{3n - 1}}{4} = 0$

Mà 4 ≠ 0 nên 3n – 1 = 0 ⇒ n = $\frac{1}{3}$

Câu 3: Cho số hữu tỉ $x = \frac{7}{{n - 1}}$ . Tìm số nguyên n để x nhận giá trị là số nguyên.

Hướng dẫn giải

Để $x = \frac{7}{{n - 1}} \in \mathbb{Z}$ thì n – 1 ∈ Ư(7) = {±1; ±7}

Ta lập bảng:

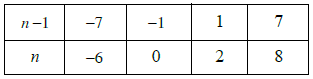
Vậy n ∈ {–6; 0; 2; 8} thì x nhận giá trị nguyên.

Thầy Tú dạy toán