Góc ở vị trí đặc biệt
Hai góc kề nhau: Hai góc kề nhau là hai góc có chung đỉnh và chung 1 cạnh, hai cạnh còn lại nằm về 2 phía của đường thẳng chứa cạnh chung đó.
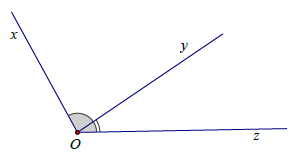
Hai góc bù nhau: hai góc bù nhau là hai góc có tổng số đo của hai góc là 180°.
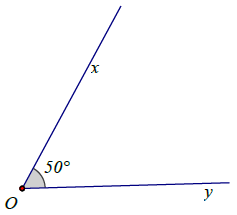
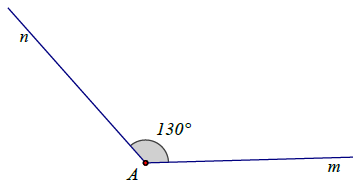
Hai góc kề bù: hai góc vừa kề vừa bù gọi là hai góc kề bù.
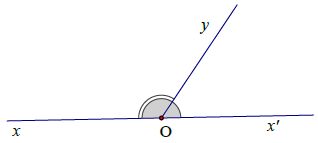
Hai góc đối đỉnh: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh góc kia.
Tính chất: Hai góc đối đỉnh thì bằng nhau. Mỗi góc chỉ có duy nhất một góc đối đỉnh với nó.
Tia phân giác của một góc
Tia phân giác của một góc: Là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.
Cách vẽ
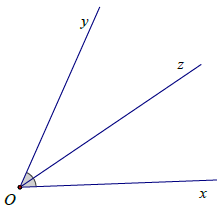
Để vẽ tia phân giác Oz của . Ta thực hiện theo 2 bước.
Bước 1: Vẽ
Bước 2: Vẽ tia Oz nằm giữa hai tia Ox, Oy sao cho hoặc
.
Đường thẳng chứa tia phân giác của một góc được gọi là đường phân giác của góc đó.
Phân dạng bài tập
Dạng 1. Góc ở vị trí đặc biệt:
Phương pháp giải
Nhận biết và tính được một số góc kề bù, đối đỉnh
Bài toán.
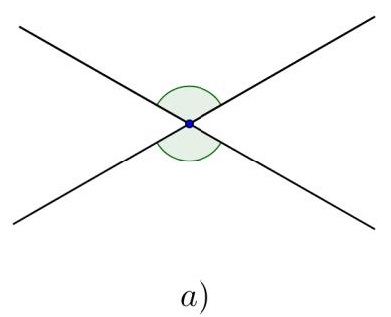
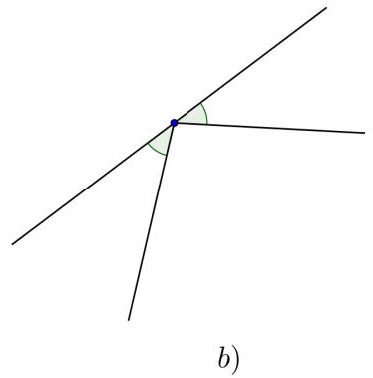
Bài 1. Trong các hình a), b), c), d) cặp góc nào đối đỉnh, cặp góc nào không đối đỉnh? Vì sao?
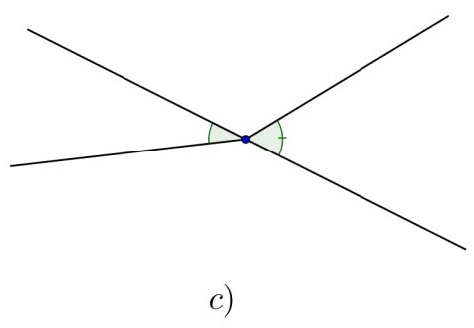
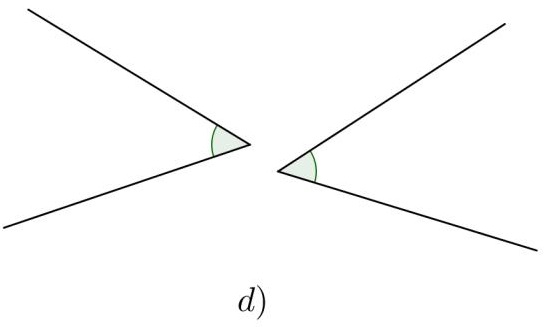
Hướng dẫn giải
Vì hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh góc kia nên chỉ có hình a) là cặp góc đối đỉnh.
Bài 2.
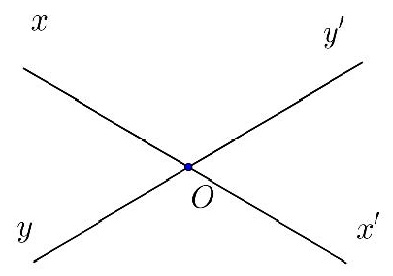
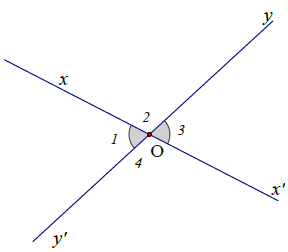
Hai đường thẳng xx’ và yy’ cắt nhau tại O như hình vẽ. Hãy điền vào chỗ trống (…) trong các phát biểu sau:
a) Góc và góc… là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox’ và cạnh Oy là… của cạnh Oy’.
b) Góc và góc
là… vì cạnh Ox là tia đối của cạnh… và cạnh…
Hướng dẫn giải
a) và
là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox’ và cạnh Oy là tia đối của cạnh Oy’.
b) và
là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox’ và cạnh Oy là tia đối của cạnh Oy’.
Bài 3. Vẽ ba đường thẳng cùng đi qua một điểm. Đặt tên cho các góc tạo thành.
a) Viết tên các cặp góc đối đỉnh. Chỉ ra các cặp góc bằng nhau
b) Viết tên các 3 cặp góc kề bù.
Hướng dẫn giải
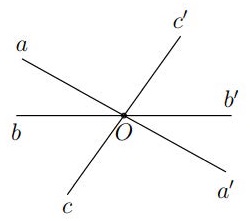
a) Các cặp góc đối đỉnh là:
và
;
và
;
và
;
và
;
và
;
và
Các cặp góc đối đỉnh thì bằng nhau.
b) Các cặp góc kề bù là: và
;
và
;
và
Bài 4. Cho có số đo bằng 60°. Vẽ góc đối đỉnh với
. Hỏi góc này có số đo bằng bao nhiêu độ?
Hướng dẫn giải
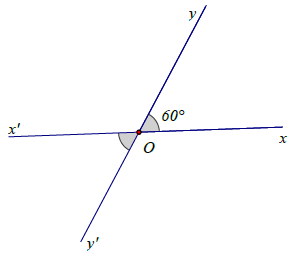
Vì hai góc đối đỉnh có số đo bằng nhau nên góc đối đỉnh với cũng có số đo bằng 60°.
Bài 5. Hai đường thẳng MN và PQ cắt nhau tại A tạo thành có số đo bằng 30°.
a) Tính số đo góc .
b) Tính số đo góc .
c) Viết tên các cặp góc đối đỉnh.
d) Viết tên các cặp góc kề bù.
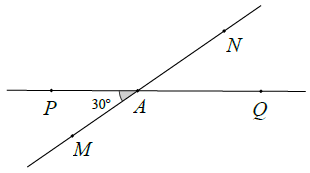
Hướng dẫn giải
a) Vì và
là hai góc đối đỉnh nên
b) Vì kề bù với
nên
c) Các cặp góc đối đỉnh: và
;
và
.
d) Các cặp góc bù nhau: và
;
và
;
và
;
và
.
Bài 6.
a) Vẽ có số đo bằng 56°.
b) Vẽ kề bù với
. Hỏi số đo của
?
c) Vẽ kề bù với
. Tính số đo
?
Hướng dẫn giải
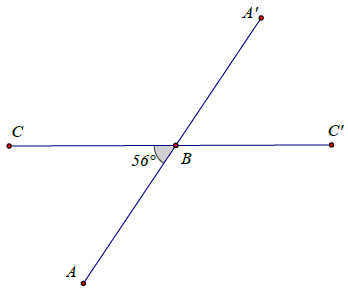
a) Xem hình vẽ.
b) Vì kề bù với
nên
c) Vì kề bù với
nên
Bài 7. Cho hai góc kề nhau .
a) Tính số đo các góc và
b) Vẽ các tia Ox’, Oy’ lần lượt là các tia đối của các tia Ox, Oy. Tính số đo các góc ,
và
Hướng dẫn giải
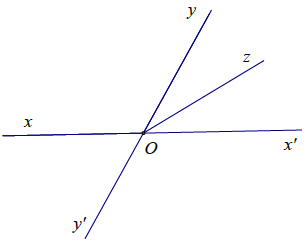
a) Ta có: . Thay vào
tìm được
b) Ta có:
Tương tự, ta tìm được
Bài 8. Vẽ hai đoạn thẳng cắt nhau sao cho trong số các góc tạo thành có một góc bằng 47°. Tính số đo các góc còn lại.
Hướng dẫn giải
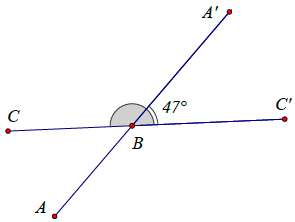
Vì và
là hai góc đối đỉnh nên
Vì kề bù
nên
suy ra
Do và
là hai góc đối đỉnh nên
Bài 9. Cho . Vẽ tia Oz là phân giác
. Vẽ Oz’ là tia đối của tia Oz. Vẽ góc kề bù
với
. Khi đó hai
và
có phải là hai góc đối đỉnh không?
Hướng dẫn giải
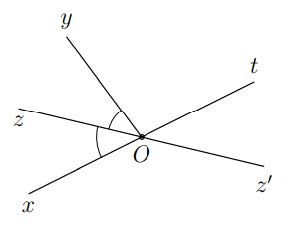
Vì kề bù với
nên Ox, Ot là hai tia đối nhau.
Theo đề bài Oz’ là tia đối của tia Oz nên và
là hai góc đối đỉnh.
Bài 10. Cho . Vẽ góc kề bù
và
. Vẽ
kề bù với
. Khi đó
và
có phải là hai góc đối đỉnh không?
Hướng dẫn giải
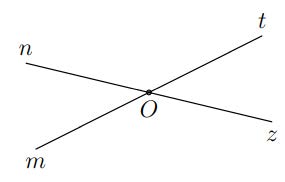
Vì kề bù với
nên Om và Ot là hai tia đối nhau;
kề bù với
nên On và Oz là hai tia đối nhau.
Do đó và
là hai góc đối đỉnh.
Bài 11. Cho . Vẽ
kề bù với
. Vẽ
kề bù với
. Vẽ On là phân giác
. Vẽ Om là phân giác
. Khi đó
và
có phải là hai góc đối đỉnh hay không?
Hướng dẫn giải
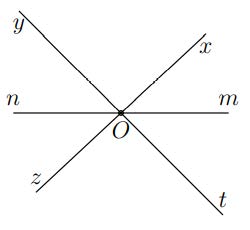
Vì kề bù với
nên Ox và Oz là hai tia đối nhau, vì
kề bù với
nên Oy và Ot là hai tia đối. Ta có:
(đối đỉnh).
Do On và Om lần lượt là phân giác và
nên
. Lại có:
Hay và
kề bù.
Từ đó suy ra Om và On là hai tia đối nhau nên và
là hai góc đối đỉnh.
Bài 12. Cho góc bẹt . Vẽ tia Oz sao cho góc
a) Tính góc .
b) Trên nửa mặt phẳng bờ Ox chứa Oz vẽ tia Ot sao cho . Chứng tỏ tia Oz là tia phân giác của
.
c) Vẽ tia Om là tia đối của tia Oz, tia On là tia đối của tia Ot. Tính góc và so sánh với
.
Hướng dẫn giải
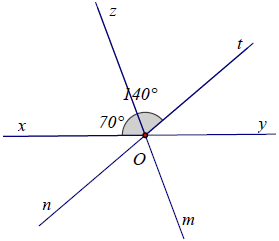
a) Vì là góc bẹt và
b) Vì ba tia Ox, Oz, Ot cùng nằm trên một nửa mặt phẳng có bờ là Ox và nên tia Oz nằm giữa hai tia Ox, Ot.
Lại có: nên tia Oz là tia phân giác của góc
.
c) Vì tia Om là tia đối của tia Oz và
Vậy
Vì tia On là tia đối của tia Ot và .
Vậy
Suy ra:
Dạng 2. Vẽ tia phân giác của một góc và áp dụng tính chất tia phân giác
Phương pháp giải
+) Bước 1: Biết vẽ góc với một số đo cho trước
+) Bước 2: Biết áp dụng vẽ tia phân giác của góc theo số đo hoặc theo cách vẽ bằng thước hai lề.
Bài toán.
Bài 1.
a) Vẽ góc có số đo 126°.
b) Vẽ tia phân giác Ot của góc ở ý trên.
Hướng dẫn giải
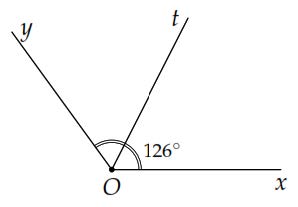
Cách vẽ
Vẽ tia Ox.
Đặt thước đo góc sao cho tâm của thước trùng với gốc O của tia Ox và tia Ox đi qua vạch 0°.
Vẽ tia Oy đi qua vạch 126° của thước. Ta vẽ được:
Vì tia Ot là tia phân giác của nên ta có:
Đặt thước đo góc sao cho tâm của thước trùng với điểm O của tia Ox và tia Ox đi qua vạch 0°.
Vẽ tia Ot đi qua vạch 63° và tia Ot nằm giữa hai tia Ox và Oy, ta được tia phân giác Ot của .
Bài 2.
a) Vẽ góc có số đo 44°.
b) Vẽ tia phân giác Ot của góc ở ý trên.
Hướng dẫn giải
Cách vẽ
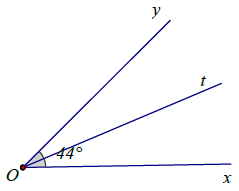
a) Vẽ tia Ox.
Đặt thước đo góc sao cho tâm của thước trùng với điểm O của tia Ox và tia Ox đi qua vạch 0°.
Vẽ tia Oy đi qua vạch 44° của thước. Ta vẽ được:
b) Vì tia Ot là tia phân giác của nên ta có:
Đặt thước đo góc sao cho tâm của thước trùng với điểm O của tia Ox và tia Ox đi qua vạch 0°.
Vẽ tia Ot đi qua vạch 22° và tia Ot nằm giữa hai tia Ox và Oy, ta được tia phân giác Ot của .
Bài 3.
a) Vẽ có số đo 90°.
b) Vẽ tia phân giác Ot của ở ý trên.
Hướng dẫn giải
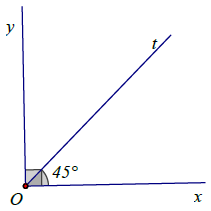
Cách vẽ
Vẽ tia Ox.
Đặt thước đo góc sao cho tâm của thước trùng với điểm O của tia Ox và tia Ox đi qua vạch 0°.
Vẽ tia Oy đi qua vạch 90° của thước. Ta vẽ được:
Vì tia Ot là tia phân giác của nên ta có:
Đặt thước đo góc sao cho tâm của thước trùng với điểm O của tia Ox và tia Ox đi qua vạch 0°.
Vẽ tia Ot đi qua vạch 45° và tia Ot nằm giữa hai tia Ox và Oy, ta được tia phân giác Ot của .
Bài 4. Vẽ tia phân giác của các góc được cho dưới đây:
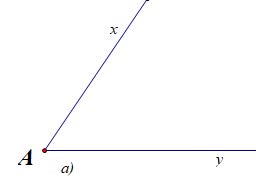
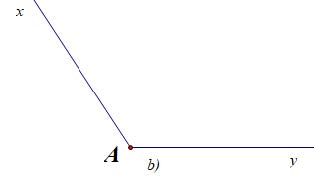
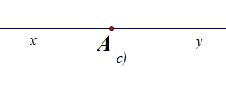
Hướng dẫn giải
Cách 1: Dùng thước kẻ hai lề vẽ tia phân giác dựa theo tính chất hình thoi có hai đường chéo là hai đường phân giác. Ta có các tia phân giác cần vẽ, riêng ý c) là góc bẹt vì vậy kẻ vuông góc ta có tia phân giác.
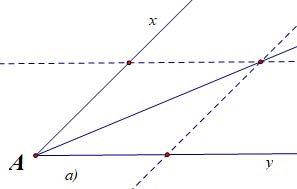
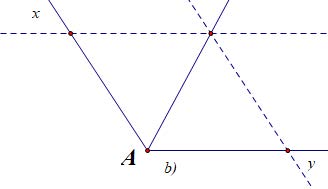
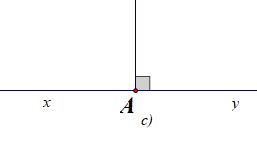
Cách 2: Dùng thước đo góc ta tiến hành đo góc cần dựng tia phân giác áp dụng tính chất chia đôi góc ta vẽ góc nhỏ có số đo bằng một nửa góc đã cho có chung 1 cạnh, riêng ý c) là góc bẹt vì vậy kẻ vuông góc ta có tia phân giác.
Bài 5. Vẽ tia phân giác của K được cho dưới đây:
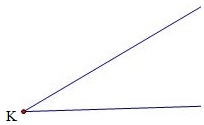
Hướng dẫn giải
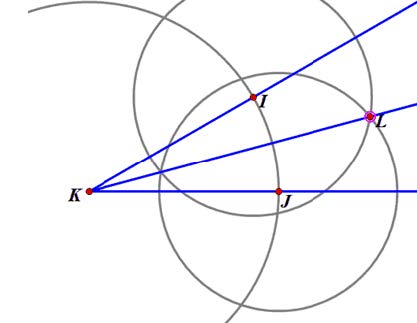
Vẽ đường tròn tâm K bán kính R cắt hai cạnh của K tại I, J.
Vẽ các đường tròn tâm I; J có cùng bán kính r cắt nhau tại L.
Vẽ tia KL
Khi đó tia phân giác của K là tia KL.
Bài 6. Cho hình vẽ. Biết O1 = O2; O3 = O4 và hai tia Ox, On đối nhau. Chỉ ra các tia phân giác trên hình bên. Tính số đo của .
Hướng dẫn giải
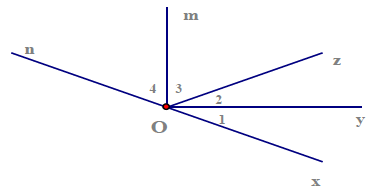
Vì O1 = O2 ⇒ Oy là tia phân giác của
O3 = O4 ⇒ Om là tia phân giác của
Ta có:
Bài 7. Cho hai góc kề bù ,
sao cho
a) Tính .
b) Gọi Ot là tia phân giác của . Chứng tỏ:
Hướng dẫn giải
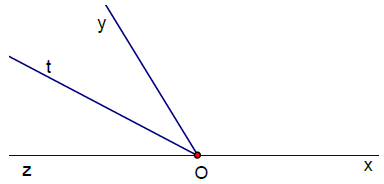
a) Vì hai ,
là hai góc kề bù
= 180° – 120° = 60°
Vậy = 60°
b) Vì Ot là tia phân giác của có:
Mà . Vậy
Bài 8. Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ hai tia Oy và Ot sao cho = 30°;
= 70°.
a) Tính ? Tia Oy có là tia phân giác của
không? Vì sao?
b) Gọi tia Om là tia đối của tia Ox. Tính số đo của ?
c) Gọi Oz là tia phân giác của . Tính số đo của
?
Hướng dẫn giải
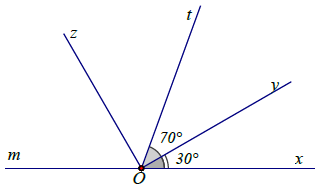
a) Vì
⇒ Tia Oy nằm giữa hai tia Ox và Ot
Vậy
Oy không là tia phân giác của vì:
b) Vì tia Om là tia đối của tia Ox nên tia Ot nằm giữa hai tia Om và Ox suy ra:
Vậy
c) Vì Oz là tia phân giác của nên
Mà tia Ot nằm giữa hai tia Oz và Oy nên ta có:
Vậy
Bài 9. Vẽ 2 góc kề bù và
, biết
= 70°. Gọi Ot là tia phân giác của
, Ot’ là tia phân giác của
. Tính
.
Hướng dẫn giải
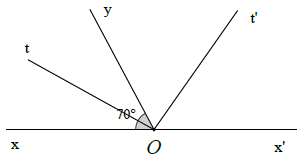
Ta có: và
là 2 góc kề bù
Vì Ot’ là tia phân giác của
Vì Ot là tia phân giác của
Vì Ox và Ox’ đối nhau ⇒ Ot và Ot’ nằm giữa Ox và Ox’
Có và
là 2 góc kề bù
Bài 10. Cho và
là hai góc kề bù. Biết
a) Tính số đo mỗi góc.
b) Gọi OD là tia phân giác của . Tính số đo
.
Hướng dẫn giải
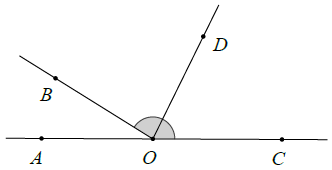
a) Vì và
là hai góc kề bù nên:
Mà . Do đó:
b) Vì OD là tia phân giác của nên
Vì và
là hai góc kề bù nên:
Do đó:
Bài 11. Cho điểm O thuộc đường thẳng xy. Trên nửa mặt phẳng bờ xy, vẽ các tia Oz và Ot sao cho
a) Tính số đo . Từ đó suy ra Ot là tia phân giác của
.
b) Tính số đo và
.
c) Tia Oz có phải tia phân giác của không? Vì sao?
Hướng dẫn giải
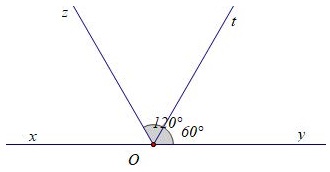
a) Ta có tia Oz và tia Ot cùng thuộc nửa mặt phẳng bờ là đường thẳng xy.
Mà
Suy ra tia Ot nằm giữa hai tia Oy và Oz (1)
Từ (1) và (2) ⇒ Ot là tia phân giác của .
b) Ta có: và
là hai góc có chung cạnh Oz, hai cạnh còn lại Ox và Oy là hai tia đối nhau
⇒ và
là hai góc kề bù.
Ta có:
Ta có: và
là hai góc có chung cạnh Ot, hai cạnh còn lại Ox và Oy là hai tia đối nhau
⇒ và
là hai góc kề bù:
c) Ta có tia Oz và tia Ot cùng thuộc nửa mặt phẳng bờ là đường thẳng xy
Mà
Suy ra tia Oz nằm giữa hai tia Ox và Ot (3)
Từ (3) và (4) ⇒ Oz là tia phân giác của .
Bài 12. Cho hai đường thẳng aa’ và bb’ cắt nhau tại O. Biết
a) Tính các góc
b) Vẽ tia phân giác Oc của góc và tia phân giác Oc’ của góc
. Hai tia Oc và Oc’ có phải là hai tia đối nhau không?
Hướng dẫn giải
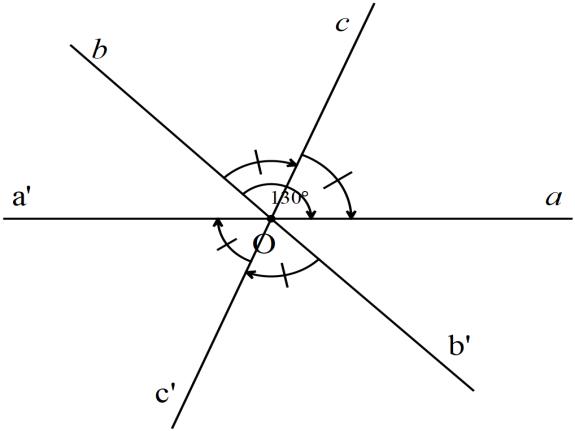
a) Ta có: (đối đỉnh)
Mặt khác ta cũng có:
(bù nhau),
Do đó:
(đối đỉnh)
b) Oc, Oc’ theo thứ tự là các tia phân giác của hai góc và
nên
Mà
Do đó:
Suy ra: góc là góc bẹt hay hai tia Oc và Oc’ là hai tia đối nhau.