Bài viết này, DanChuyenToan sẽ giúp bạn tìm hiểu phương pháp tính nguyên hàm từng phần bằng sơ đồ đường chéo. Đây là một trong những phương pháp tính nguyên hàm cực kỳ quan trọng thuộc chương trình đại số toán lớp 12, có ý nghĩa quan trọng trong phần giải tích và các bài tập thi THPTQG.

Lý thuyết nguyên hàm từng phần
Phương pháp nguyên hàm từng phần thường được sử dụng để tính tích phân bất định của các hàm số phức tạp và cần phải biến đổi. Điển hình như các hàm số vô tỉ, hàm lượng giác, hàm logarit hay hàm số mũ. Sao cho tích phân được tạo bởi công thức tích phân từng phần dễ tính toán hơn so với bản gốc. [1]Theo Hazewinkel, Tích phân từng phần – Wikipedia Tiếng Việt, cập nhật ngày 24/10/2021
Nhắc lại kiến thức
+) Công thức: ∫udv = vu – ∫vdu
+) Áp dụng với các dạng nguyên hàm: ∫p(x).eax+bdx; ∫p(x).sin(ax + b)dx
+) Cách đặt:
– Ưu tiên đặt “u” theo: logarit (ln) _ đa thức (p(x)) _ lượng giác (sin x, cos x) _ mũ (ex). Nhất “log”, nhì “đa”, tam “lượng”, tứ “mũ”
– Phần còn lại là “dv”. [2]Theo Hazewinkel, Tích phân từng phần – Wikipedia Tiếng Việt, cập nhật ngày 24/10/2021,Theo Hazewinkel, Tích phân từng phần – Wikipedia Tiếng Việt, cập nhật ngày 24/10/2021
Phương pháp đường chéo
Chia thành 2 cột
- Cột 1 (cột trái: cột u) luôn lấy đạo hàm tới 0
- Cột 2 (cột phải: cột dv) luôn lấy nguyên hàm cho tới khi tương ứng với cột 1
Nhân chéo kết quả của hai cột với nhau.
Dấu của phép nhân đầu tiên sẽ có dấu (+), sau đó đan dấu (–), (+), (–)…
Phân dạng bài tập
Dạng 1: ∫f(x).eax+bdx
Bài tập vận dụng
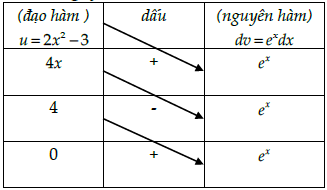
Câu 1. Tính nguyên hàm I = ∫(2x2 – 3).ex.dx
⇒ I = ex(2x2 – 3) – 4x.ex + 4ex + C = ex(2x2 – 4x + 1) + C
Câu 2. Tính nguyên hàm
Ta biến đổi đưa I về dạng thuần tuý:

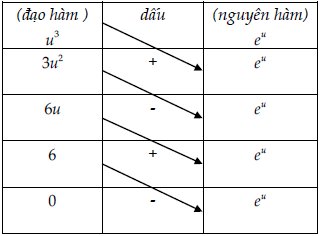
Câu 3. Tính nguyên hàm I = ∫x3.e2x+1.dx
Ta biến đổi
Dạng 2: ∫f(x).sin(ax + b).dx; ∫f(x).cos(ax + b).dx
Bài tập vận dụng
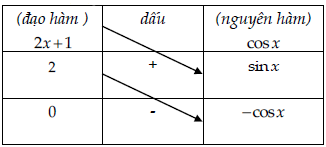
Câu 1. Tính nguyên hàm I = ∫(2x + 1).cosx.dx
⇒ I = (2x + 1)sinx – 2(–cosx) + C = (2x + 1)sinx + cosx + C
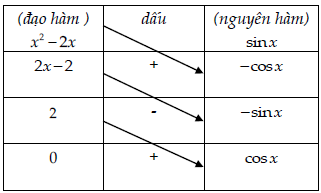
Câu 2. Tính nguyên hàm I = ∫(x2 – 2x).sinx.dx
⇒ I = (–cosx)(x2 – 2x) – (2x – 2)(–sinx) + 2cosx + C
= cosx(–x2 + 2x + 2) + (2x + 2)sinx + C
Câu 3. Tính nguyên hàm ∫I = (x7 – 2x).cos(x2).dx
Ta biến đổi

Dạng 3: ∫f(x).lnn(ax + b)dx
Bài tập vận dụng
Chú ý: Dạng ∫f(x).lnn(ax + b)dx thì ưu tiên đặt u = lnn(ax + b) vì vậy khi đạo hàm “u” sẽ không bằng 0 được, do vậy cần phải điều chỉnh hệ số rút gọn (nhân ngang → đơn giản tử mẫu) rồi sau đó mới làm tiếp
Câu 1. Tính nguyên hàm I = ∫x.lnx.dx
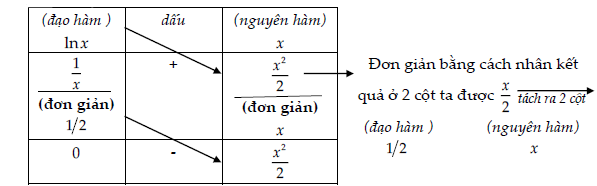
(Cách hiểu: do từ cột đạo hàm đã “nhảy” sang cột nguyên hàm để triệt tiêu với x nên
phải “nhảy” ngược lại sang cột đạo hàm để bù)
Câu 2. Tính nguyên hàm I = ∫x.ln2x.dx

Câu 3. Tính nguyên hàm I = ∫(x5 – 3)lnx.dx

Câu 4. Tính nguyên hàm I = ∫(2x + 1).ln5(3x).dx

Câu 5. Tính nguyên hàm I = ∫ln5(5x).dx
Ta biến đổi

Dạng 4. Nguyên hàm lặp (tích phân lặp)
Phương pháp giải
Nếu khi ta tính nguyên hàm (tích phân) theo sơ đồ đường chéo mà lặp lại nguyên hàm ban đầu cần tính (theo hàng ngang) thì dừng lại luôn ở hàng đó, không tính tiếp nữa.
+) Dấu hiệu khi dừng lại : nhận thấy trên cùng 1 hàng ngang tích của 2 phần tử ở 2 cột (không kể dấu và hệ số) giống nguyên hàm ban đầu cần tính.
+) Ghi kết quả (nhân theo đường chéo) như các ví dụ trên.
+) Nối 2 phần tử (ở dòng dừng lại), có thêm dấu ∫ trước kết quả và coi gạch nối là 1 đường chéo, sử dụng quy tắc đan dấu.
Bài tập vận dụng
Câu 1. Tính nguyên hàm I = ∫sinx.ex.dx
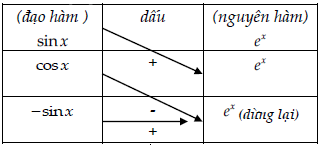
Câu 2. Tính nguyên hàm
Ta biến đổi

Nguồn tham khảo
Website chỉ sử dụng các nguồn tài liệu toán học uy tín.