Tích phân cùng với nghịch đảo của nó là vi phân đóng vai trò quan trọng trong các phép tính của giải tích. Ngoài ra, tích phân còn có ý nghĩa đặc biệt trong các ứng dụng thực tế. Bài viết này DanChuyenToan sẽ giúp bạn hiểu rõ các ứng dụng đặc trưng của tích phân trong thực tế.

Ứng dụng tính vận tốc, quãng đường
Phương pháp giải
Với bài toán chuyển động ứng dụng tích phân ta áp dụng các công thức sau đây:
Giả sử một vật chuyển động với vận tốc 𝓋t trong khoảng thời gian từ t1 đến t2 (t2 > t1) thì: 𝓋t = s’(t)
- Gia tốc tức thời của vật: a(t) = 𝓋’t = s’’t
- Quãng đường vật đi được trong khoảng thời gian từ t1 đến t2 là:
- Vận tốc tức thời của vật là:
Bài tập vận dụng
Câu 1. Cho hai quả bóng A, B di chuyển ngược chiều nhau va chạm với nhau. Sau va chạm mỗi quả bóng nảy ngược lại một đoạn thì dừng hẳn. Biết sau khi va chạm, quả bóng A nảy ngược lại với vậ+n tốc 𝓋A (t) = 8 – 2t (m/s) và quả bóng B nảy ngược lại với vận tốc 𝓋B (t) = 12 – 4t (m/s). Tính khoảng cách giữa hai quả bóng sau khi đã dừng hẳn (Giả sử hại quả bóng đều chuyển động thẳng).
A. 36 mét
B. 32 mét
C. 34 mét
D. 30 mét
Hướng dẫn giải
Thời gian quả bóng A chuyển động từ lúc va chạm đến khi dừng hẳn là:
𝓋A (t) = 0 ⇔ 8 – 2t = 0 ⇒ t = 4s
Quãng đường quả bóng A di chuyển
Thời gian quả bóng B chuyển động từ lúc va chạm đến khi dừng hẳn là:
𝓋B (t) = 0 ⇔ 12 – 4t = 0 ⇒ t = 3s
Quãng đường quả bóng B di chuyển
Vậy: Khoảng cách hai quả bóng sau khi dừng hẳn là S = SA + SB = 34m
⟹ Chọn C
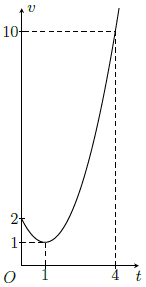
Câu 2. Một vật chuyển động trong 4 giờ với vận tốc 𝓋 (km/h) phụ thuộc thời gian t (h) có đồ thị là một phần của đường parabol có đỉnh I(1; 1) và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s mà vật di chuyển được trong 4 giờ kể từ lúc xuất phát.
A. s = 6 km
B. s = 8 km
C. s = km
D. s = km
Hướng dẫn giải
Hàm số biểu diễn vận tốc của vật là (t) = t2 – 2t + 2.
Do đó, hàm số biểu diễn quãng đường di chuyển được của vật là
Do khi bắt đầu chuyển động thì quãng đường đi được bằng 0 nên C = 0.
Vậy quãng đường vật di chuyển được trong 4 giờ kể từ lúc xuất phát là s(4) = km
⟹ Chọn D
Câu 3. Một chiếc máy bay chuyển động trên đường băng với vận tốc (t) = t2 + 10t (m/s) với t là thời gian tính theo đơn vị giây kể từ khi máy bay bắt đầu chuyển động. Biết khi máy bay đạt vận tốc 200(m/s) thì nó rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng là
A. (m)
B. 2000 (m)
C. 500 (m)
D. (m)
Hướng dẫn giải
Xét (t) = 200 ⇔ t2 + 10t – 200 = 0 ⇔ t = 10 ∨ t = –20
Vậy thời gian máy bay đạt vận tốc 200 m/s là thời điểm t = 10s sau khi bắt đầu chuyển động.
Quãng đường máy bay đã di chuyển trên đường băng là
⟹ Chọn A
Câu 4. Một ô tô đang chạy với vận tốc 20m/s thì người lái đạp phanh; từ thời điểm đó, ô tô chuyển động chậm dần đều và sau đúng 4 giây thì ô tô bắt đầu dừng hẳn. Hỏi từ lúc đạp phanh đến khi ô tô dừng hẳn, ô tô còn di chuyển được bao nhiêu mét?
A. 20
B. 50
C. 40
D. 30
Hướng dẫn giải
Từ khi người lái đạp phanh ô tô chuyển động chậm dần đều ta có 𝓋 = 20 + at với a là gia tốc của ô tô.
Sau 4 giây thì ô tô dừng hẳn nên 20 + a․4 = 0 ⇔ a = –5
Quảng đường xe đi được là
⟹ Chọn C
Câu 5. Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc (t) = 7t (m/s). Đi được 5 (s) người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc a = –35 (m/s2). Tính quãng đường của ô tô đi được tính từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.
A. 87.5 mét
B. 96.5 mét
C. 102.5 mét
D. 105 mét
Hướng dẫn giải
Quãng đường ô tô đi được trong 5 (s) đầu là
Phương trình vận tốc khi ô tô phanh là (t) = 35 – 35t, do đó quãng đường ô tô đi được từ khi phanh đến khi dừng hẳn là
Vậy quãng đường cần tính là s = s1 + s2 = 105(m).
⟹ Chọn D
Câu 6. Một ô tô đang chạy thì người lái đạp phanh, từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc (t) = –10t + 20 (m/s), trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?
A. 20 m
B. 25 m
C. 60 m
D. 15 m
Hướng dẫn giải
Khi ô tô dừng hẳn thì (t) = 0 ⇔ t = 2
Vậy đoạn đường ô–tô di chuyển được là
⟹ Chọn A
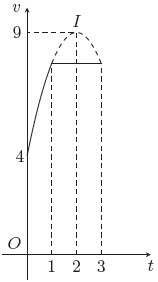
Câu 7. Một vật chuyển động trong 3 giờ với vận tốc 𝓋 (km/h) phụ thuộc vào thời gian t (h) có đồ thị của vận tốc như hình bên. Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh I(2; 9) và trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song với trục hoành. Tính quãng đường S mà vật di chuyển được trong 3 giờ đó (kết quả làm tròn đến hàng phần trăm).
A. S = 15,50 (km)
B. S = 21,58 (km)
C. S = 23,25 (km)
D. S = 13,83 (km)
Hướng dẫn giải
Gọi phương trình chuyển động của vật trong 1 giờ đầu là (t) = at2 + bt + c
Từ đồ thị ta có
Quãng đường đi được trong giờ đầu là
Tại thời điểm t = 1, vận tốc của vật là
Quãng đường vật đi được trong 2 giờ tiếp theo là
Vậy quãng đường vật di chuyển được trong 3 giờ là
⟹ Chọn B
Câu 8. Một chuyến máy bay chuyển động trên đường bằng với vận tốc (t) = t2 + 10t (m/s) với t là thời gian được tính bằng giây kể từ khi máy bay bắt đầu chuyển động. Biết khi máy bay đạt vận tốc 200 m/s thì nó rời đường băng. Tính quãng đường máy bay đã di chuyển trên đường băng.
A. m
B. 2000 m
C. 500 m
D. m
Hướng dẫn giải
Khi 𝓋 = 200, ta có
Máy bay di chuyển trên đường băng từ thời điểm t = 0 đến thời điểm t = 10, do đó quãng đường đi được trên đường băng là
⟹ Chọn A
Câu 9. Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc 𝓋1 (t) = 7t (m/s). Đi được 5s, người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc a = –70 (m/s2). Tính quãng đường S đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.
A. S = 96,25 (m)
B. S = 87,5 (m)
C. S = 94 (m)
D. S = 95,7 (m).
Hướng dẫn giải
Ta có
Quãng đường xe đi được sau 5s là
Vận tốc của xe sau 5s là 𝓋0 = 35 (m/s).
Xe chuyển động chậm dần đều với gia tốc a = –70 (m/s2) nên 𝓋2 (t)= 𝓋0 + at = 35 – 70t (m/s).
Suy ra quãng đường xe chuyển động được tính theo công thức S2(t) = 35t – 35t2 (m).
Xe dừng hẳn thì 𝓋2 = 0 ⇔ 35 – 70t = 0 ⇔
Quãng đường xe đi thêm cho tới khi dừng hẳn là
Vậy tổng quãng đường xe đi là S1 + S2 = 96,25 (m).
⟹ Chọn A
Câu 10. Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc 𝓋1 (t) = 2t (m/s). Đi được 12 giây, người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc a = –12 (m/s2). Tính quãng đường s (m) đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.
A. s = 168 m
B. s = 166 m
C. s = 144 m
D. s = 152 m
Hướng dẫn giải
Quãng đường ô tô đi được từ lúc xe lăn bánh đến khi được phanh
Vận tốc v2 (t) (m/s) của ô tô từ lúc được phanh đến khi dừng hẳn thỏa mãn
𝓋2(t) ∫(–12)dt = –12t + C, 𝓋2(12) = 𝓋1(12) = 24 ⇒ C = 168 ⇒ 𝓋2(t) = –12t + 168 (m/s)
Thời điểm xe dừng hẳn tương ứng với t thỏa mãn 𝓋2(t) = 0 ⇔ t =14 (s).
Quãng đường ô tô đi được từ lúc xe được phanh đến khi dừng hẳn
Quãng đường cần tính s = s1 + s2 = 144 + 24 = 168 (m).
⟹ Chọn A
Câu 11. Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc 𝓋1(t) = 7t (m/s). Đi được 5 (s), người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc a = –70 (m/s2). Tính quãng đường S (m) đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.
A. S = 87,50 (m)
B. S = 94,00 (m)
C. S = 95,70 (m)
D. S = 96,25 (m)
Hướng dẫn giải
Trong 5 giây đầu tiên xe đi được quãng đường
Kể từ khi phanh 𝓋2 = ∫(–70) dt = –70t +C.
Lúc xe bắt đầu phanh t = 0 thì 𝓋2 = 35 (m/s) suy ra 35 = –70․0 + C = 35.
Khi xe dừng hẳn 𝓋2 = 0 ⇒ –70t + C = 0 ⇒
Quãng đường xe đi được kể từ lúc đạp phanh
Quãng đường đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn là S = S1 + S2 = 96,25 (m).
⟹ Chọn D
Câu 12. Một học sinh đang điều khiển xe đạp điện chuyển động thẳng đều với vận tốc a m/s. Khi phát hiện có chướng ngại vật phía trước học sinh đó thực hiện phanh xe. Sau khi phanh, xe chuyển động chậm dần đều với vận tốc (t) = a – 2t m/s. Tìm giá trị lớn nhất của a để quãng đường xe đạp điện đi được sau khi phanh không vượt quá 9m.
A. a = 7
B. a = 4
C. a = 5
D. a = 6
Hướng dẫn giải
Khi . Quãng đường xe đi được kể từ lúc phanh cho đến khi dừng lại là
Để quãng đường đi được sau khi phanh không vượt quá 9m thì
⟹ Chọn D
Câu 13. Một ô tô đang đi với vận tốc lớn hơn 72 km/h, phía trước là đoạn đường chỉ cho phép chạy với tốc độ tối đa là 72 km/h, vì thế người lái xe đạp phanh để ô tô chuyển động chậm dần đều với vận tốc (t) = 30 – 2t (m/s), trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc bắt đầu đạp phanh đến lúc đạt tốc độ 72 km/h, ô tô đã di chuyển quãng đường là bao nhiêu mét?
A. 100 m
B. 150 m.
C. 175 m
D. 125 m
Hướng dẫn giải
Thời điểm t ô tô đạt tốc độ 72 km/h (tức 20 m/s) là nghiệm của 30 – 2t = 20 ⇔ t = 5 (s).
Quãng đường đi được trong khoảng thời gian 5 s là
⟹ Chọn D
Ứng dụng tích phân tính diện tích
Lý thuyết
Định lý 1: Cho hàm số y = f(x) liên tục, không âm trên [a; b]. Khi đó diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục hoành và 2 đường thẳng x = a, x = b là
Bài toán 1
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [a; b], trục hoành và 2 đường thẳng x = a, x = b được xác định:
Bài toán 2
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), y = g(x) liên tục trên đoạn [a; b] và 2 đường thẳng x = a, x = b được xác định:
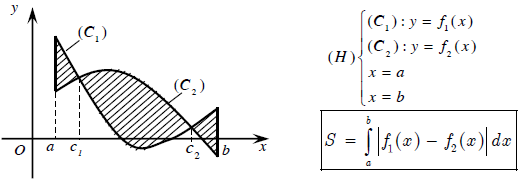
Chú ý: Nếu trên đoạn [a; b], hàm số f(x) không đổi dấu thì:
Bài toán 3
Diện tích của hình phẳng giới hạn bởi các đường x = g(y), x = h(y) và hai đường thẳng y = c, y = d được xác định: 
Bài toán 4
Diện tích hình phẳng giới hạn bởi 2 đồ thị (C1): f1(x), (C2): f2(x) là: . Trong đó x1, x2 tương ứng là nghiệm của phương trình f(x) = g(x), (x1 < x2)
Phân dạng bài tập
Dạng 1. Tính diện tích giới hạn bởi 1 đồ thị
Phương pháp 1
Xét dấu biểu thức f(x); x ∈ [a; b], phá dấu trị tuyệt đối và tính tích phân.
Phương pháp 2
Giải phương trình f(x) = 0; chọn nghiệm trong [a; b]. Giả sử các nghiệm là α; β với α < β
Áp dụng tính chất liên tục của hàm số f(x) trên [a; b], ta có:
Bài tập vận dụng
Câu 1. Tính diện tích S của hình phẳng giới hạn bởi đồ thị y = x2, trục hoành và đường thẳng x = 2.
A.
B.
C.
D.
Hướng dẫn giải
Nhận thấy rằng, để tính diện tích ta cần phải tìm được 2 cận. Để tìm thêm cận còn lại ta giải phương trình hoành độ giao điểm của đồ thị (P): y = x2 với trục hoành.
Phương trình hoành độ giao điểm của đồ thị (P): y = x2 với trục hoành: x2 = 0 ⇔ x = 0
Áp dụng công thức ta có
Nhận xét: Nếu ta vẽ đồ thị hàm số y = x2 và đường thẳng x = 2 ta dễ dàng xác định được hình phẳng giới hạn bởi các đường này. Từ đó ta dễ dàng tính được diện tích S.
⟹ Chọn D
Câu 2. Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = x2.ex, trục hoành và đường thẳng x = 1
A. e – 2
B. 2 + e
C. 2 – e
D. 1
Hướng dẫn giải
Phương trình hoành độ giao điểm x2.ex = 0 ⇔ x = 0
Ta có:
Lời bình:
Bài toán trên đã có 1 cận, ta chỉ cần tìm thêm 1 cận nữa bằng cách giải phương trình hoành độ giao điểm. Sau đó áp dụng công thức. Nếu vẽ đồ thị bài này để tìm hình phẳng giới hạn bởi các đường là không nên vì đồ thị hàm số hơi phức tạp. Việc tìm được công thức và tính tích phân này ta có thể dùng MTCT để tính và chọn Chọn.
⟹ Chọn A
Câu 3. Tính diện tích hình phẳng giới hạn bởi đồ thị và trục hoành:
A. π – 2
B.
C. 1
D.
Hướng dẫn giải
Phương trình hoành độ giao điểm của, Ox là
Khi đó, diện tích hình phẳng cần tìm là
Đặt x = sint ⇔ dx = cost.dt và
Suy ra
Lời bình:
Bài toán trên chưa có cận, ta phải giải phương trình hoành độ giao điểm để tìm cận. Sau đó áp dụng công thức. Việc tìm được công thức và tính tích phân này tương đối phức tạp, do đó ta có thể dùng MTCT để tính và chọn Chọn.
Nếu vẽ được đồ thị thì ta xác định được hình phẳng và diện tích của nó dễ dàng, đó chính là diện tích của nữa đường tròn bán kính bằng 1. Do đó:
⟹ Chọn D
Câu 4. Tính diện tích S hình phẳng giới hạn bởi các đường và trục hoành
A.
B.
C.
D.
Hướng dẫn giải
Phương trình hoành độ giao điểm của đồ thị y = lnx và trục hoành là:
⟹ Chọn A
Câu 5. Diện tích tam giác được cắt ra bởi các trục tọa độ và tiếp tuyến của đồ thị y = lnx tại giao điểm của đồ thị hàm số với trục Ox là:
A.
B.
C.
D.
Hướng dẫn giải
Phương trình hoành độ giao điểm: lnx = 0 ⇔ x = 1
Ta có:
Phương trình tiếp tuyến của đồ thị y = lnx tại giao điểm của đồ thị hàm số với trục Ox là:
y = 1(x – 1) + 0 hay y = x – 1
Đường thẳng y = x – 1 cắt Ox tại điểm A(1; 0) và cắt Oy tại điểm B(0; –1)
Tam giác vuông OAB có
⟹ Chọn D
Dạng 2. Tính diện tích giới hạn bởi 2 hai đồ thị
Phương pháp giải
Công thức tính . Tính như dạng 1.
Bài tập vận dụng
Câu 1. Tính diện tích hình phẳng giới hạn bởi đồ thị
Hướng dẫn giải
Ta có:
Trong trường hợp này nếu chọn cách xét dấu biểu thức hoặc vẽ đồ thị hàm số
là khá khó khăn.
Vì vậy ta chọn cách sau:
+) Xét phương trình:
Từ đó suy ra:
Câu 2. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
Hướng dẫn giải
Xét phương trình hoành độ giao điểm của hai đồ thị trên:
Vì vậy hình phẳng đã cho có diện tích là:
Do trên (–1; 1) phương trình vô nghiệm nên ta có:
Tính
+) Đặt
+) Đổi cận:
Thay thế vào ta được:
Câu 3. Tính diện tích hình phẳng giới hạn bởi đồ thị y = |x2 – 4x + 3| và y = 3
Hướng dẫn giải
Xét phương trình hoành độ giao điểm của hai đồ thị trên:
Khi đó:
Câu 4. Tính diện tích hình phẳng giới hạn bởi đồ thị: y = sin|x|; y = |x| – π.
Hướng dẫn giải
Xét phương trình hoành độ: sin|x| = |x| – π
Đặt |x| = t
Khi đó trở thành: sint = t – π ⇔ sint – t + π = 0
Xét hàm số f(t) = sint – t + π; t ∈ [0; +∞)
⇒ f’(t) = cost – 1 ≤ 0, ∀t ∈ [0; +∞)
BBT của hàm số f(t) như sau:
⇒ Phương trình có nghiệm duy nhất t = π
⇒ Phương trình có 2 nghiệm phân biệt: x = –π và x = π
Câu 5. Người ta cần trồng một vườn hoa theo hình giới hạn bởi một đường Parabol và nửa đường tròn có bán kính mét (phần tô trong hình vẽ). Biết rằng: để trồng mỗi m2 hoa cần ít nhất là 250.000 đồng, số tiền tối thiểu để trồng xong vườn hoa Cẩm Tú Cầu gần bằng
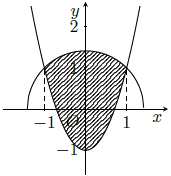
A. 893.000 đồng
B. 476.000 đồng
C. 809.000 đồng
D. 559.000 đồng
Hướng dẫn giải
Nửa đường tròn (T) có phương trình
Xét parabol (P) có trục đối xứng Oy nên có phương trình dạng: y = ax2 + c
(P) cắt Oy tại điểm (0; –1) nên ta có: c = –1
(P) cắt (T) tại điểm (1; 1) thuộc (T) nên ta được: a + c = 1 ⇒ a = 2.
Phương trình của (P) là: y = 2x2 – 1
Diện tích miền phẳng D (tô màu trong hình) là:
Xét , đặt
thì
Đổi cận: x = –1 thì , với x = 1 thì
, ta được:
Suy ra
Số tiền trồng hoa tối thiểu là: đồng
⟹ Chọn C
Câu 6. Ông Nam có một mảnh vườn hình elip có độ dài trục lớn bằng 16 m và độ dài trục bé bằng 10 m. Ông muốn trồng hoa trên một dải đất rộng 8 m và nhận trục bé của elip làm trục đối xứng (như hình vẽ). Biết kinh phí để trồng hoa là 100.000 đồng/1m2. Hỏi ông Nam cần bao nhiêu tiền để trồng hoa trên dải đất đó? (Số tiền được làm tròn đến hàng nghìn).
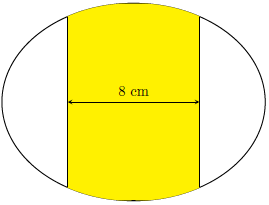
A. 7.862.000 đồng
B. 7.653.000 đồng
C. 7.128.000 đồng
D. 7.826.000 đồng
Hướng dẫn giải
Giả sử elip có phương trình , với a > b > 0.
Từ giả thiết ta có 2a = 16 ⇒ a = 8 và 2b = 10 ⇒ b = 5.
Vậy phương trình của elip là
Khi đó diện tích dải vườn được giới hạn bởi các đường (E1), (E2), x = –4, x = 4 và diện tích của dải vườn là
Khi đó số tiền là
⟹ Chọn B
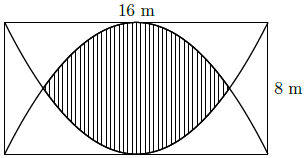
Câu 7. Một mảnh vườn toán học có dạng hình chữ nhật, chiều dài là 16 m và chiều rộng là 8 m. Các nhà toán học dùng hai đường parabol có đỉnh là trung điểm của một cạnh dài và đi qua 2 điểm đầu của cạnh đối diện, phần mảnh vườn nằm ở miền trong của cả hai parabol (phần gạch sọc như hình vẽ minh họa) được trồng hoa hồng. Biết chi phí để trồng hoa hồng là 45.000 đồng/m2. Hỏi các nhà toán học phải chi bao nhiêu tiền để trồng hoa trên phần mảnh vườn đó (số tiền được làm tròn đến hàng nghìn)?
A. 3.322.000 đồng
B. 3.476.000 đồng
C. 2.715.000 đồng
D. 2.159.000 đồng
Hướng dẫn giải
Chọn hệ trục tọa độ có gốc là tâm hình chữ nhật, các trục tọa độ song song với các cạnh của hình chữ nhật khi đó các phương trình của parabol là và
Diện tích phần trồng hoa là
Khi đó số tiền cần chi là T = 60,34 × 45.000 = 2.175.300 (đồng)
⟹ Chọn C
Câu 8. Nhà bạn Minh cần làm một cái cửa có dạng như hình vẽ, nửa dưới là hình vuông, phần phía trên (phần tô đen) là một Parabol. Biết các kích thước a = 2,5m; b = 0,5m; c = 2m. Biết số tiền để làm 1m2 cửa là 1 triệu đồng. Số tiền để làm cửa là

A. triệu đồng
B. triệu đồng
C. triệu đồng
D. triệu đồng
Hướng dẫn giải
Gọi (P): y = ax2 + bx + c là Parabol đi qua A(1; 2) và có đỉnh là B(0; 2,5).
Khi đó ta có
Vậy (P): y = –0,5x2 + 2,5
Diện tích cái cửa là
Do đó, số tiền để làm cửa là triệu đồng.
⟹ Chọn A
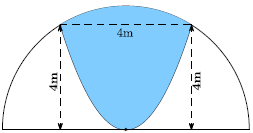
Câu 9. Một khuôn viên dạng nửa hình tròn có đường kính bằng (m). Trên đó người thiết kế hai phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm nửa hình tròn và hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu), cách nhau một khoảng bằng 4 (m), phần còn lại của khuôn viên (phần không tô màu) dành để trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ và kinh phí để trồng cỏ Nhật Bản là 100.000 đồng/m2. Hỏi cần bao nhiêu tiền để trồng cỏ Nhật Bản trên phần đất đó? (Số tiền được làm tròn đến hàng nghìn)
A. 3.895.000 (đồng)
B. 1.948.000 (đồng)
C. 2.388.000 (đồng)
D. 1.194.000 (đồng)
Hướng dẫn giải
Đặt hệ trục tọa độ như hình vẽ.
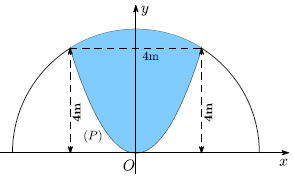
Khi đó phương trình nửa đường tròn là
Phương trình parabol (P) có đỉnh là gốc O sẽ có dạng y = ax2
Mặt khác (P) qua điểm M (2; 4) do đó 4 = a․(–2)2 ⇒ a = 1
Phần diện tích của hình phẳng giới hạn bởi (P) và nửa đường tròn (phần tô màu).
Ta có công thức
Vậy phần diện tích trồng cỏ là Strồng cỏ = Shình tròn – S1 ≈ 19,47592654
Vậy số tiền cần có là Strồng cỏ x 100.000 ≈ 1.948.000 (đồng)
⟹ Chọn B
Câu 10. Một mảnh vườn hình elip có trục lớn bằng 100m, trục nhỏ bằng 80m được chia thành 2 phần bởi một đoạn thẳng nối hai đỉnh liên tiếp của elip. Phần nhỏ hơn trồng cây con và phần lớn hơn trồng rau. Biết lợi nhuận thu được là 2000 mỗi m2 trồng cây con và 4000 mỗi m2 trồng rau. Hỏi thu nhập từ cả mảnh vườn là bao nhiêu? (Kết quả làm tròn đến hàng nghìn).
A. 31.904.000
B. 23.991.000
C. 10.566.000
D. 17.635.000
Hướng dẫn giải
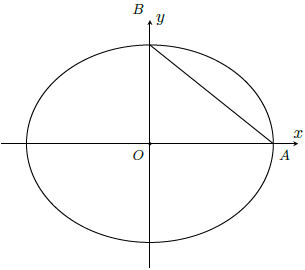
Theo giả thiết phương trình của Elip là
Diện tích của cả khu vườn là
Diện tích phần trồng cây con là
Diện tích phần trồng rau là
S2 = S – S1 = 3․500π + 1000 (m2).
Tổng thu nhập của cả mảnh vườn là
T = 2000․(500π – 1000) + 4000․(3․500π + 1000) ≈ 23.991.000.
⟹ Chọn B
Câu 11. Một sân chơi cho trẻ em hình chữ nhật có chiều dài 100m và chiều rộng là 60m người ta làm một con đường nằm trong sân (như hình vẽ). Biết rằng viền ngoài và viền trong của con đường là hai đường elip, elip của đường viền ngoài có trục lớn và trục bé lần lượt song song với các cạnh hình chữ nhật và chiều rộng của mặt đường là 2m.
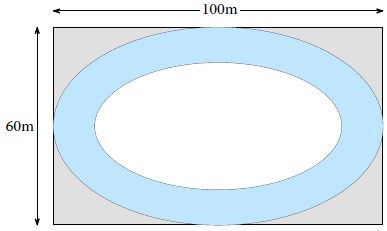
Kinh phí cho mỗi m2 làm đường 600.000 đồng. Tính tổng số tiền làm con đường đó (Số tiền được làm tròn đến hàng nghìn).
A. 293.904.000
B. 283.904.000
C. 293.804.000
D. 283.604.000
Hướng dẫn giải
Xét hệ trục tọa độ Oxy đặt gốc tọa độ O vào tâm của hình Elip.
Phương trình Elip của đường viền ngoài của con đường là . Phần đồ thị của (E1) nằm phía trên trục hoành có phương trình
Phương trình Elip của đường viền trong của con đường là . Phần đồ thị của (E2) nằm phía trên trục hoành có phương trình
Gọi S1 là diện tích của (E1) và bằng hai lần diện tích phần hình phẳng giới hạn bởi trục hoành và đồ thị hàm số y = f1(x).
Gọi S2 là diện tích của (E2) và bằng hai lần diện tích phần hình phẳng giới hạn bởi trục hoành và đồ thị hàm số y = f2(x).
Gọi S là diện tích con đường. Khi đó
Tính tích phân
Đặt t = a sint, ⇒ dx = acostdt
Đổi cận
Khi đó
Do đó S = S1 – S2 = 50․30π – 48․28π = 156π
Vậy tổng số tiền làm con đường đó là 600000․S = 600000․156π ≈ 294.053.000 (đồng)
⟹ Chọn A
Câu 12. Trong mặt phẳng tọa độ, cho hình chữ nhật (H) có một cạnh nằm trên trục hoành, và có hai đỉnh trên một đường chéo là A(–1; 0) và B(a; ), với a > 0. Biết rằng đồ thị hàm số y =
chia hình (H) thành hai phần có diện tích bằng nhau, tìm a. .
A. a = 9
B. a = 4
C. a =
D. a = 3
Hướng dẫn giải
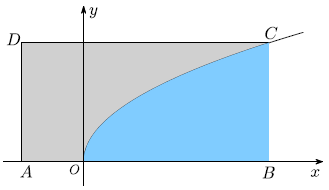
Gọi ACBD là hình chữ nhật với AC nằm trên trục Ox, A(–1; 0) và B(a; )
Nhận thấy đồ thị hàm số y = cắt trục hoành tại điểm có hoành độ bằng 0 và đi qua B(a;
)
Do đó nó chia hình chữ nhật ACBD ra làm 2 phần là có diện tích lần lượt là S1, S2.
Gọi S2 là diện tích hình phẳng giới hạn bởi các đường y = và trục Ox, x = 0, x = a và S1 là diện tích phần còn lại
Ta lần lượt tính S1, S2.
Tính diện tích
Đặt t = ⇒ t2 = x ⇒ 2tdt = dx; Khi x = 0 ⇒ t = 0; x = a ⇒ t =
Do đó
Hình chữ nhật ACBD có AC = a + 1; AD = nên
Do đồ thị hàm số y = chia hình (H) thành hai phần có diện tích bằng nhau nên
(do a > 0)
⟹ Chọn D
Câu 13. Một khuôn viên dạng nửa hình tròn, trên đó người ta thiết kế phần trồng hoa hồng có dạng một hình parabol có đỉnh trùng với tấm hình tròn và có trục đối xứng vuông góc với đường kính của nửa đường tròn, hai đầu mút của parabol nằm trên đường tròn và cách nhau một khoảng bằng 4 mét (phần gạch chéo). Phần còn lại của công viên (phần không gạch chéo) dùng để trồng hoa cúc. Biết các kích thước cho như hình vẽ. Chi phí để trồng hoa hồng và hoa cúc lần lượt là 120.000 đồng/m2 và 80.000 đồng/m2.

Hỏi chi phí trồng hoa khuôn viên đó gần nhất với số tiền nào dưới đây (làm tròn đến nghìn đồng)
A. 6.847.000 đồng
B. 6.865.000 đồng
C. 5.710.000 đồng
D. 5.700.000 đồng
Hướng dẫn giải
Chọn hệ trục tọa độ như hình vẽ
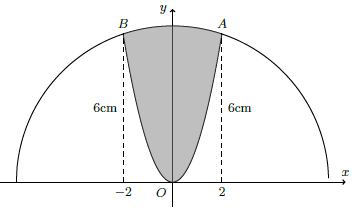
Đường tròn tâm O(0; 0) và đi qua điểm A(2; 6) có bán kính
Phương trình đường tròn có dạng: là phương trình nửa đường tròn phía trên trục hoành.
Diện tích nửa hình tròn là
Gọi parabol (P): y = ax2 + bx + c (a ≠ 0).
(P) đi qua các điểm O(0; 0); A(2; 6); B(–2; 6) suy ra
Diện tích trồng hoa hồng giới hạn bởi các đường là
Vậy chi phí cần dùng để trồng hoa trong khuôn viên là
⟹ Chọn D
Câu 14. Trong đợt hội trại “Khi tôi 18” được tổ chức tại trường THPT X, Đoàn trường có thực hiện một dự án ảnh trưng bày trên một pano có dạng parabol như hình vẽ. Biết rằng Đoàn trường sẽ yêu cầu các lớp gửi hình dự thi và dán lên khu vực hình chữ nhật ABCD, phần còn lại sẽ được trang trí hoa văn cho phù hợp. Chi phí dán hoa văn là 200.000 đồng cho một m2 bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu (làm tròn đến hàng nghìn ?

A. 900.000 (đồng)
B. 1.232.000 (đồng)
C. 902.000 (đồng)
D. 1.230.000 (đồng)
Hướng dẫn giải
Xét hệ trục tọa độ như hình vẽ.
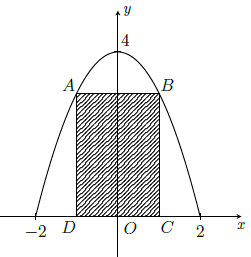
Parabol của pano có dạng y = ax2 + c với a < 0
Vì (P) cắt Oy tại điểm có tung độ 4 nên c = 4. Mà (P) đi qua điểm (2; 0) nên a = –1
Như vậy, parabol của pano là đồ thị của hàm số y = 4 – x2 trên đoạn [–2; 2]
Giả sử CD = 2x với 0 ≤ x ≤ 2, khi đó diện tích hình chữ nhật là SABCD = 2x․(4 – x2)
Diện tích phần trang trí hoa văn là
Hàm số S(x) có S’(x) = 6x2 – 8 và
Trên đoạn [–2; 2], ta có
Do đó giá trị nhỏ nhất của S(x) trên [–2; 2] là
Chi phí cho việc trang trí hoa văn lúc đó là × 200.000 ≈ 902.000 (đồng).
⟹ Chọn C
Câu 15. Một biển quảng cáo có dạng hình elip với bốn đỉnh A1, A2, B1, B2 như hình vẽ bên. Biết chi phí để sơn phần tô đậm là 200.000 đồng/m2 và phần còn lại là 100.000 đồng/m2. Hỏi số tiền để sơn theo cách trên gần nhất với số tiền nào dưới đây, biết A1A2 = 8m, B1B2 = 6m và tứ giác MNPQ là hình chữ nhật có MQ = 3m?
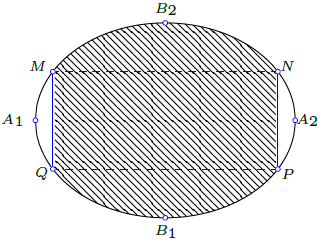
A. 7.322.000 đồng
B. 7.213.000 đồng
C. 5.526.000 đồng.
D. 5.782.000 đồng.
Hướng dẫn giải
Giả sử phương trình elip
Theo giả thiết ta có:
Suy ra
Diện tích của elip (E) là S(E) = πab = 12π (m2).
Ta có với
Khi đó, diện tích phần không tô màu là
Diện tích phần tô màu là S’ = S(E) – S = 8π +
Số tiền để sơn theo yêu cầu bài toán là
T = 100.000 × (4π – ) + 200.000 × (8π +
) ≈ 7.322.000 đồng.
⟹ Chọn A
Câu 16. Một người có mảnh đất hình tròn có bán kính 5m. Người này tính trồng cây trên mảnh đất đó, biết mỗi mét vuông trồng cây thu hoạch được 100 nghìn. Tuy nhiên, cần có khoảng trống để dựng chòi và đồ dùng nên người này cũng sợi dây 6m vào hai đầu mút dây nằm trên đường tròn xung quanh mảnh đất. Hỏi người này thu hoạch được bao nhiêu tiền? (Tính theo đơn vị nghìn đồng và bỏ số thập phân).

A. 3722
B. 7445
C. 7446
D. 3723
Hướng dẫn giải
Đưa vào hệ trục tọa độ Oxy như hình vẽ.
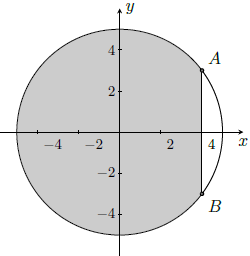
Diện tích trồng cây là
Do đó, số tiền thu được là 7445 nghìn đồng.
⟹ Chọn B
Câu 17. Ông An muốn làm cửa rào sắt có hình dạng và kích thước như hình vẽ bên, biết đường cong phía trên là một Parabol. Giá 1m2 của rào sắt là 700.000 đồng. Hỏi ông An phải trả bao nhiêu tiền để làm cái cửa sắt như vậy (làm tròn đến hàng phần nghìn).
A. 6.520.000 đồng
B. 6.320.000 đồng
C. 6.417.000 đồng
D. 6.620.000 đồng
Hướng dẫn giải
Chọn hệ trục tọa độ như hình vẽ.
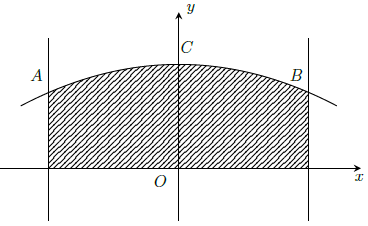
Trong đó A(–2,5; 1,5), B(2,5; 1,5), C(0; 2).
Giả sử đường cong phá trên là một Parabol có dạng y = ax2 + bx + c, với a, b, c ∈ R.
Do Parabol đi qua các điểm A(–2,5; 1,5), B(2,5; 1,5), C(0; 2) nên ta có hệ phương trình
Khi đó phương trình Parabol là
Diện tích S của cửa rào sắt là diện tích phần hình phẳng giới bởi đồ thị hàm số , trục hoành và hai đường thẳng x = –2,5; x = 2,5
Ta có
Vậy ông An phải trả số tiền để làm cái cửa sắt là
(đồng).
⟹ Chọn C
Ứng dụng tích phân trong thể tích
1. Lý thuyết về thể tích
Thể tích vật thể
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b; S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x, (a ≤ x ≤ b). Giả sử S(x) là hàm số liên tục trên đoạn [a; b].
Thể tích khối tròn xoay
Bài toán 1
Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y = f(x), trục hoành và hai đường thẳng x = a, x = b quanh trục Ox:
Bài toán 2
Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường x = g(y), trục hoành và hai đường thẳng y = c, y = d quanh trục Oy:
Bài toán 3
Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y = f(x), y = g(x) và hai đường thẳng x = a, x = b quanh trục Ox:
2. Phân dạng bài toán thể tích
Dạng 1. Tính thể tích vật thể tròn xoay dựa vào định nghĩa
Phương pháp giải
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b; S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x, (a ≤ x ≤ b)
Giả sử S(x) là hàm số liên tục trên đoạn [a; b]
Bài tập vận dụng
Câu 1. Cho phần vật thể B giới hạn bởi hai mặt phẳng có phương trình x = 0 và x = 2. Cắt phần vật thể B bởi mặt phẳng vuông góc trục Ox tại điểm có hoành độ x (0 ≤ x ≤ 2), ta được diện tích là một tam giác đều có độ dài cạnh bằng . Tính thể tích V của phần vật thể B.
Hướng dẫn giải
Một tam giác đều cạnh a có diện tích .
Do đó tam giác đều cạnh có diện tích là
.
Suy ra thể tích
Câu 2. Trong không gian Oxyz , cho vật thể nằm giữa hai mặt phẳng x = 0 và x = π, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ bằng x, (0 ≤ x ≤ π)là một tam giác đều cạnh là . Tính thể tích của vật thể đó.
Hướng dẫn giải
Một tam giác đều cạnh a có diện tích
Do đó tam giác đều cạnh có diện tích là
Suy ra thể tích
Câu 3. Một bồn trụ đang chứa dầu được đặt nằm ngang có chiều dài bồn là 5m, bán kính đáy 1m. Người ta rút dầu ra trong bồn tương ứng với 0,5m của đường kính đáy. Tính thể tích gần đúng của dầu còn lại trong bồn
Hướng dẫn giải
Thể tích cả khối trụ V1 = πR2h = π.12.5 = 5π (m3)
Tính thể tích phần khối trụ bị mất đi

+) Cách 1:
Suy ra thể tích khối trụ còn lại
+) Cách 2: Tính góc ở tâm
Câu 4. Bạn A có một cốc thủy tinh hình trụ, đường kính trong lòng đáy cốc là 6cm, chiều cao trong lòng cốc là 10cm đang đựng một lượng nước. Bạn A nghiêng cốc nước, vừa lúc khi nước chạm miệng cốc thì ở đáy mực nước trùng với đường kính đáy. Tính thể tích lượng nước trong cốc.
Hướng dẫn giải
Phân tích: Thể tích nước có hình dạng “cái nêm”; có 2 phương pháp tính thể tích này
+) Cách 1 – Chứng minh công thức bằng PP tích phân: Xét thiết diện cắt cốc thuỷ tinh tại vị trí x (–R ≤ x ≤ R) bất kỳ; ta có diện tích thiết diện là
; thể tích
+) Cách 2:
Gọi S là diện tích thiết diện do mặt phẳng có phương vuông góc với trục Ox với khối nước, mặt phẳng này cắt trục Ox tại điểm có hoành độ h ≥ x ≥ 0. Ta có:
, vì thiết diện này là nửa hình tròn bán kính r
Thể tích lượng nước chứa trong bình là.
Bài giải
+) Cách 1: Áp dụng công thức tính thể tích cái nêm biết góc giữa mặt cắt và mặt đáy bằng α là
với
ta được
+) Cách 2: Tính trực tiếp bài toán bằng PP tích phân
; thể tích
Câu 5. Cắt một khối trụ bởi một mặt phẳng ta được một khối như hình vẽ bên. Biết rằng thiết diện là một hình elip có độ dài trục lớn bằng 10, khoảng cách từ điểm thuộc thiết diện gần mặt đáy nhất và điểm thuộc thiết diện xa mặt đáy nhất lần lượt là 8 và 14. Tính thể tích của.

Hướng dẫn giải
Tính các số đo: ; suy ra bán kính khối trụ là
Cách 1: Thể tích khối bằng thể tích “khối trụ trung bình”:
Cách 2: Áp dụng công thức tính thể tích “cái nêm”: Lấy mặt phẳng (P) vuông góc với đường sinh của hình trụ và đi qua điểm A , khi đó chia khối (H) thành hai khối:
+) Khối 1: là khối trụ chiều cao h = 8, bán kính r = 4 nên thể tích V1 = πr2h = 128π
+ Khối 2: là phân nửa một khối trụ có chiều cao DE = 6 và bán kính r = 4 nên thể tích
+ Vậy V(H) = V1 + V2 = 128π + 48π = 176π (đvtt)
Dạng 2. Tính thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi 1 đồ thị
Phương pháp giải
Vật thể tròn xoay sinh bởi miền hình phẳng được giới hạn: Đồ thị y = f(x); trục Ox (y = 0); x = a, x = b; quay xung quanh Ox
+) Nếu thiếu cận thì giải phương trình f(x) = 0 để bổ sung cận
+) Tính thể tích theo công thức:
Bài tập vận dụng
Câu 1. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = 2x – x2 và trục hoành. Tính thể tích V của vật thể tròn xoay được sinh ra bởi hình phẳng đó khi nó quay quanh trục Ox .
Hướng dẫn giải
Phương trình hoành độ giao điểm
Thể tích của vật thể tròn xoay cần tìm
Câu 2. Cho miền hình phẳng giới hạn bởi: y = x.ex, Ox: x = 1 quay xung quanh Ox. Tính thể tích của vật thể tạo thành.
Hướng dẫn giải
Xét phương trình hoành độ giao điểm của đồ thị hàm số y = x.ex và trục Ox: x.ex = 0 ⇔ x = 0
Vậy vật thể tròn xoay có thể tích là:
Câu 3. Cho miền hình phẳng giới hạn bởi: y = x2 – 4x, y = 0; quay xung quanh Ox. Tính thể tích của vật thể tạo thành.
Hướng dẫn giải
Hoành độ giao điểm của đồ thị hàm số y = x2 – 4x và đường thẳng y = 0 là nghiệm của phương trình:
Vật thể tạo thành có thể tích là:
Câu 4. Gọi V là thể tích khối tròn xoay tạo thành khi quanh hình phẳng giới hạn bởi các đường ; y = 0; x = 4 và trục Ox. Đường thẳng x = a (0 < a < 4) cắt đồ thị hàm số
tại M
Gọi V1 là thể tích khối tròn xoay tạo thành khi quay tam giác MOH quanh trục Ox . Biết rằng V = 2V1. Tính a.
Hướng dẫn giải
Ta có:

Tam giác MOH quanh trục Ox tạo nên hai khối nón chung đáy. Gọi N là hình chiếu vuông góc của M trên trục Ox . Suy ra
Suy ra
Câu 5. Cho (H) là hình phẳng giới hạn bởi độ thị hàm số ; trục Ox và đường thẳng x = 1. Tính thể tích khối tròn xoay thu được khi quay quanh hình (H) xung quanh trục Ox.
Hướng dẫn giải
Phương trình hoành độ giao điểm
Theo bài toán thì thể tích của vật thể tròn xoay cần tìm
Do đó a = 4, b = 3 ⇒ a + b = 7
Dạng 3. Tính thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi 2 đồ thị
Phương pháp giải
Nếu hình phẳng D được giới hạn bởi các đường y = f(x), y = g(x), x = a, x = b thì thể tích khối tròn xoay sinh bởi khi quay D quanh trục Ox được tính bởi công thức:
Bài tập vận dụng
Câu 1. Cho hình phẳng giới hạn bởi các đường y = ax2, y =bx (a, b ≠ 0) quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:
A.
B.
C.
D.
Hướng dẫn giải
Tọa độ giao điểm của hai đường y = a.x2 và y = b.x là các điểm O(0; 0) và
Vậy thể tích của khối tròn xoay cần tính là:
⟹ Chọn D
Câu 2. Cho hình phẳng giới hạn bởi các đường quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:

A.
B.
C.
D.
Hướng dẫn giải
Tọa độ giao điểm của hai đường là các điểm
Vậy thể tích của khối tròn xoay cần tính là:
⟹ Chọn B
Cho hình phẳng giới hạn bởi các đường y = 2x2, y2 = 4x quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:
A.
B.
C.
D.
Hướng dẫn giải
Với x ∈ [0; 2] thì
Tọa độ giao điểm của đường y = 2x2 và y2 = 4x là các điểm O(0; 0) và A(1; 2).
Vậy thể tích của khối tròn xoay cần tính là:
⟹ Chọn D
Câu 4. Thể tích khối tròn xoay khi quay hình phẳng D giới hạn bởi các đường elip x2 + 9y2 = 9 quay quanh Ox bằng:
A. π
B. 2π
C. 3π
D. 4π
Hướng dẫn giải
Ta có:
⟹ Chọn D
Câu 5. Thể tích của khối tròn xoay khi quay hình phẳng D giới hạn bởi các đường quanh trục Ox bằng:
A.
B.
C.
D.
Hướng dẫn giải
Xét phương trình
Và
⟹ Chọn D
Dạng 4. Tính thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi nhiều đồ thị
Bài tập vận dụng
Câu 1. Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường , y = 0 và x = 4 quanh trục Ox. Đường thẳng x = a (0 < a < 4) cắt đồ thị hàm
tại M
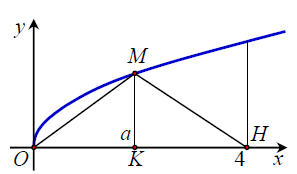
Gọi V1 là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng V = 2V1. Khi đó:
A. a = 2
B.
C.
D. a = 3
Hướng dẫn giải
Ta có . Khi đó
Ta có
Khi quay tam giác OMH quanh trục Ox tạo thành hai hình nón có chung đáy:
+) Hình nón (N1) có đỉnh là O, chiều cao h1 = OK = a, bán kính đáy
+) Hình nón (N2) thứ 2 có đỉnh là H, chiều cao h2 = HK = 4 – a, bán kính đáy
Khi đó
Theo đề bài
⟹ Chọn D
Câu 2. Cho hình thang cong giới hạn bởi các đường y = ex, y = 0, x = 0, x = ln4. Đường thẳng x = k (0 < k < ln4) chia thành hai hình phẳng là S1 và S2 như hình vẽ bên. Quay S1, S2 quanh trục Ox được khối tròn xoay có thể tích lần lượt là V1, V2. Với giá trị nào của k thì V1 = 2V2
A.
B.
C.
D.
Hướng dẫn giải
Ta có
Theo giả thiết:
⟹ Chọn B
Câu 3. Cho hình phẳng D giới hạn bởi các đường y2 = 4x và đường thẳng x = 4. Thể tích của khối tròn xoay sinh ra khi D xoay quanh trục Ox là:

A. 32π
B. 64π
C. 16π
D. 4π
Hướng dẫn giải
Giao điểm của hai đường y2 = 4x và x = 4 là D(4; –4) và E(4; 4). Phần phía trên Ox của đường y2 = 4x có phương trình . Từ hình vẽ suy ra thể tích của khối tròn xoay cần tính là:
⟹ Chọn A
Câu 4. Cho hình phẳng giới hạn bởi các đường y = 3x, y = x, x = 0, x = 1 quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:
A.
B.
C.
D.
Hướng dẫn giải
Tọa độ giao điểm của đường x = 1 với đường y = x là các điểm C(1; 1) và B(3; 1). Tọa độ giao điểm của đường y = 3x với đường y = x là O(0; 0)
Vậy thể tích của khối tròn xoay cần tính là:
⟹ Chọn A
Câu 5. Trên mặt phẳng Oxy, cho hình phẳng giới hạn bởi các đường (P): y = x2; (P’): y = 4x2; (d): y = 4. Thể tích của khối tròn xoay khi quay quanh trục Ox bằng:
A.
B.
C.
D.
Hướng dẫn giải
Đặt V là thể tích cần tìm
Xét phương trình hoành độ giao điểm của (P) và (d):
Xét phương trình hoành độ giao điểm của (P’) và (d):
VOAC là thể tích khối tròn xoay sinh bởi khi quay: quanh Ox
VOAB là thể tích khối tròn xoay sinh bởi khi quay: quanh Ox
Lúc đó:
⟹ Chọn B
Bài tập vận dụng tính thể tích vật thể
Bài tập vận dụng
Câu 1. Một bác thợ làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đường và trục Ox, khi quay quanh trục Ox. Biết đáy lọ và miệng lọ có đường kính lần lượt là 2dm và 4dm. Khi đó thể tích của lọ là
A. 8π dm3
B. dm3
C. dm3
D. dm3
Hướng dẫn giải
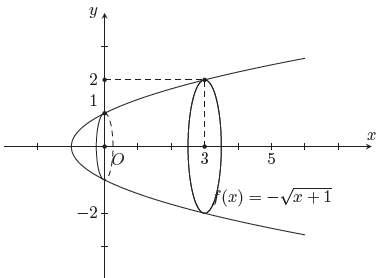
Đường kính đáy lần lượt là 2dm và 4dm nên ta có hoành độ giao điểm của mặt đáy và Ox là nghiệm của các phương trình sau
Vậy thể tích của lọ là
⟹ Chọn B
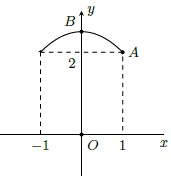
Câu 2. Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên dưới. Biết rằng OO’ = 5 cm, OA = 10 cm, OB = 20 cm, đường cong AB là một phần của parabol có đỉnh là điểm A. Thể tích của chiếc mũ bằng
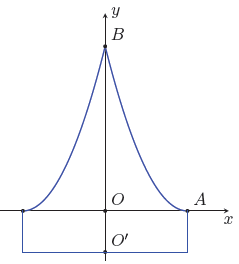
A. cm3
B. cm3
C. cm3
D. cm3
Hướng dẫn giải
Ta gọi thể tích của chiếc mũ là V.
Thể tích của khối trụ có bán kính đáy bằng OA = 10 cm và đường cao OO’ = 5 cm là V1.
Thể tích của vật thể tròn xoay khi quay hình phẳng giới hạn bởi đường cong AB và hai trục tọa độ quanh trục Oy là V2
Ta có V = V1 + V2
V1 = 5․102π = 500π (cm3).
Chọn hệ trục tọa độ như hình vẽ.
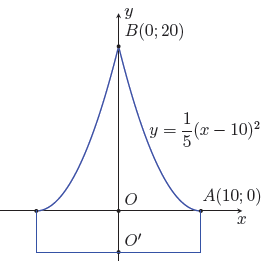
Do parabol có đỉnh A nên nó có phương trình dạng (P): y = a (x – 10)2
Vì (P) qua điểm B(0; 20) nên
Do đó (P): . Từ đó suy ra
(do x < 10).
Suy ra
Do đó
⟹ Chọn B
Câu 3. Một cái thùng đựng dầu có thiết diện ngang (mặt trong của thùng) là một đường elip có trục lớn bằng 1m, trục bé bằng 0,8m, chiều dài (mặt trong của thùng) bằng 3m. Được đặt sao cho trục bé nằm theo phương thẳng đứng (như hình bên). Biết chiều cao của dầu hiện có trong thùng (tính từ đáy thùng đến mặt dầu) là 0,6m. Tính thể tích V của dầu có trong thùng (Kết quả làm tròn đến phần trăm).
A. V = 1,52 m3
B. V = 1,31 m3
C. V = 1,27 m3
D. V = 1,19 m3
Hướng dẫn giải
Chọn hệ trục tọa độ như hình vẽ.
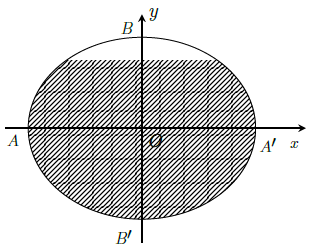
Theo đề bài ta có phương trình của Elip là
Gọi M, N lần lượt là giao điểm của dầu với elip.
Gọi S1 là diện tích của Elip ta có
Gọi S2 là diện tích của hình phẳng giới hạn bởi Elip và đường thẳng MN.
Theo đề bài chiều cao của dầu hiện có trong thùng (tính từ đáy thùng đến mặt dầu) là 0,6m nên ta có phương trình của đường thẳng MN là
Mặt khác từ phương trình ta có
Do đường thẳng cắt Elip tại hai điểm M, N có hoành độ lần lượt là
và
nên
Tính . Đặt
Khi x = thì
Khi x = thì
Khi đó
Vậy
Thể tích của dầu trong thùng là
⟹ Chọn A
Câu 4. Một cái thùng đựng dầu có thiết diện ngang (mặt trong của thùng) là một đường elip có trục lớn bằng 1m, trục bé bằng 0,8m, chiều dài (nằm trong của thùng) bằng 3m. Được đặt sao cho trục bé nằm theo phương thẳng đứng (như hình vẽ bên). Biết chiều cao của dầu trong thùng (tính từ đáy thùng đến mặt dầu) là 0,6m. Tính thể tích V của dầu có trong thùng (kết quả được làm tròn đến phần trăm).
A. V = 1,42 m3
B. V = 1,31 m3
C. V = 1,27 m3
D. V = 1,52 m3
Hướng dẫn giải
Xét một đáy của của thùng đựng dầu và gán hệ trục như hình vẽ.
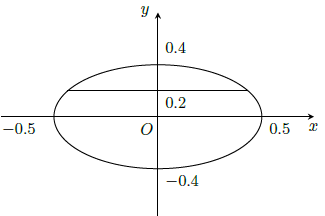
Phương trình đường elip đáy khi đó có phương trình
Khi đó chiều cao mép dầu trong thùng trùng với đường thẳng y = 0,2.
Xét phương trình
Diện tích phần mặt chứa dầu là
Do đó thể tích dầu trong thùng là V = 3․S ≈ 1,52 m3.
⟹ Chọn D
Câu 5. Một quả trứng có hình dạng khối tròn xoay, thiết diện qua trục của nó là hình elip có độ dài trục lớn bằng 6, độ dài trục bé bằng 4. Tính thể tích quả trứng đó.
A. 12π
B. 18π
C. 14π
D. 16π
Hướng dẫn giải
Chọn hệ trục tọa độ như hình vẽ.
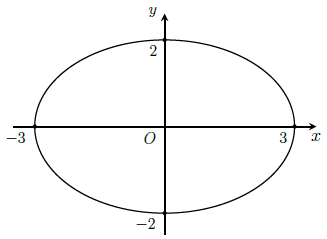
Ta có phương trình đường elip là
Suy ra
Elip cắt trục hoành tại điểm có hoành độ là 3 và –3. Do đó thể tích của quả trứng là
⟹ Chọn D
Câu 6. Cho một chiếc trống như hình vẽ, có đường sinh là nữa elip được cắt bởi trục lớn với độ dài trục lớn bằng 80 cm, độ dài trục bé bằng 60 cm và đáy trống là hình tròn có bán kính bằng 60 cm. Tính thể tích V của trống (kết quả làm tròn đến hàng đơn vị).

A. V = 344.963 cm3
B. V = 344.964 cm3
C. V = 208.347 cm3
D. V = 208.346 cm3
Hướng dẫn giải
Chọn hệ trục tọa độ Oxy như hình vẽ.
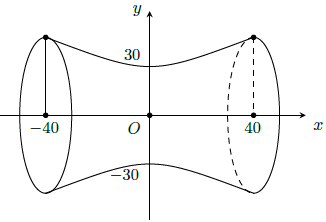
Khi đó chiếc trống là hình tròn xoay được sinh bởi một nửa elip, dưới của elip có phương trình là
Khi đó nửa đường elip dưới có phương trình
Vậy thể tích của chiếc trống là
⟹ Chọn B
Câu 7. Người ta cắt hai hình cầu có bán kính lần lượt là R = 13 cm và cm để làm hồ lô đựng rượu như hình vẽ bên. Biết đường tròn giao của hình cầu có bán kính r’ = 5 cm và nút đựng rượu là một hình trụ có bán kính đáy bằng
cm, chiều cao bằng 4 cm. Giả sử độ dày vỏ hồ lô không đáng kể. Hỏi hồ lô đựng được bao nhiêu lít rượu? (kết quả làm trong đến một chữ số thập phân sau dấu phẩy).
A. 9,5 lít
B. 8,2 lít
C. 10,2 lít
D. 11,4 lít.
Hướng dẫn giải
Xét hệ trục tọa độ Oxy như hình vẽ.
Có thể coi hồ lô được tạo thành bằng cách cho đường cong, gấp khúc quay quanh trục Ox.
Phương trình cung cong lớn là
Phương trình cung cong nhỏ là
Thể tích hồ lô là
⟹ Chọn C
Ứng dụng tích phân tính điện lượng
Phương pháp giải
Điện lượng chuyển qua tiết diện của dây dẫn của đoạn mạch trong thời gian từ t1 đến t2 là:
Bài tập vận dụng
Câu 1. Một vật chuyển động với vận tốc 10 m/s thì tăng tốc với gia tốc a(t) = 3t + t2. Tính quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc.
A. m
B. 4300m
C. 430m
D. m
Hướng dẫn giải
Hàm vận tốc
Lấy mốc thời gian lúc tăng tốc ⇒ v(0) = 10 ⇒ C = 10
Ta được
Sau 10 giây, quãng đường vật đi được là
⟹ Chọn A
Câu 2. Dòng điện xoay chiều hình sin chạy qua một đoạn mạch LC có biểu thức cường độ là . Biết i = q’ với q là điện tích tức thời ở tụ điện. Tính từ lúc t = 0, điện lượng chuyển qua tiết diện thẳng của dây dẫn của đoạn mạch đó trong thời gian từ 0 đến
là
A.
B. 0
C.
D.
Hướng dẫn giải
Điện lượng chuyển qua tiết diện của dây dẫn của đoạn mạch trong thời gian từ 0 đến H8 là
⟹ Chọn C
Ứng dụng tích phân nâng cao
Câu 1. Tính thể tích hình xuyến tạo thành do quay hình tròn (C): x2 + (y – 2)2 = 1 quanh trục Ox
Hướng dẫn giải
Hình tròn (C) có tâm I(0; 2), bán kính R = 1 là x2 + (y – 2)2 = 1
Thể tích cần tính:
Câu 2. Thành phố định xây cây cầu bắc ngang con sông dài 500m, biết rằng người ta định xây cầu có 10 nhịp cầu hình dạng parabol, mỗi nhịp cách nhau 40m, biết 2 bên đầu cầu và giữa mối nhịp nối người ta xây 1 chân trụ rộng 5m. Bề dày nhịp cầu không đổi là 20cm. Biết 1 nhịp cầu như hình vẽ. Hỏi lượng bê tông để xây các nhịp cầu là bao nhiêu
A. 20m3
B. 50m3
C. 40m3
D. 100m3
Hướng dẫn giải
Chọn hệ trục tọa độ như hình vẽ với gốc O(0; 0) là chân cầu, đỉnh I(25; 2), điểm A(50; 0)

Gọi Parabol trên có phương trình (P1): y1 = ax2 + bx + c = ax2 + bx (O ∈ (P1))
là phương trình parabol dưới
Ta có
Khi đó diện tích mỗi nhịp cầu là S = S1 với S1 là phần giới hạn bởi y1; y2 trong khoảng (0; 25)
Vì bề dày nhịp cầu không đổi nên coi thể tích là tích diện tích và bề dày V = S × 0,2 ≈ 1,98m3 ⇒ số lượng bê tông cần cho mỗi nhịp cầu ≈ 2m3
Vậy mười nhịp cầu hai bên cần ≈ 40m3 bê tông
⟹ Chọn C
Câu 3. Trong Công viên Toán học có những mảnh đất mang hình dáng khác nhau. Mỗi mảnh được trồng một loài hoa và nó được tạo thành bởi một trong những đường cong đẹp trong toán học. Ở đó có một mảnh đất mang tên Bernoulli, nó được tạo thành từ đường Lemmiscate có phương trình trong hệ tọa độ Oxy là 16y2 = x2(25 – x2) như hình vẽ bên.
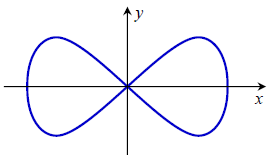
Tính diện tích S của mảnh đất Bernoulli biết rằng mỗi đơn vị trong hệ tọa độ Oxy tương ứng với chiều dài 1 mét.
A.
B.
C.
D.
Hướng dẫn giải
⟹ Chọn D
Vì tính đối xứng trụ nên diện tích của mảnh đất tương ứng với 4 lần diện tích của mảnh đất thuộc góc phần tư thứ nhất của hệ trục tọa độ Oxy .
Từ giả thuyết bài toán, ta có
Góc phần tư thứ nhất
Nên
Câu 4. Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các đường và trục Ox quay quanh trục Ox biết đáy lọ và miệng lọ có đường kính lần lượt là 2dm và 4dm, khi đó thể tích của lọ là:
A.
B.
C.
D.
Hướng dẫn giải
+) r1 = y1 = 1 ⇒ x1 = 0
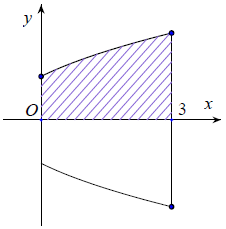
+) r2 = y2 = 2 ⇒ x2 = 3
Suy ra:
⟹ Chọn B
Câu 5. Để kéo căng một lò xo có độ dài tự nhiên từ 10cm đến 15cm cần lực 40N. Tính công (A) sinh ra khi kéo lò xo có độ dài từ 15cm đến 18cm.
A. A = 1,56 (J)
B. A = 1 (J)
C. A = 2,5 (J)
D. A = 2 (J)
Hướng dẫn giải
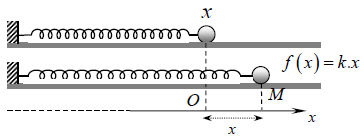
Theo Định luật Hooke, lực cần dùng để giữ lò xo giãn thêm x mét từ độ dài tự nhiên là f(x) = kx, với k (N/m) là độ cứng của lò xo. Khi lò xo được kéo giãn từ độ dài 10cm đến 15cm, lượng kéo giãn là 5cm = 0.05m . Điều này có nghĩa f (0.05) = 40, do đó:
Vậy f(x) = 800x và công cần để kéo dãn lò xo từ 15cm đến 18cm là:
Góc phần tư thứ nhất
Nên
⟹ Chọn A
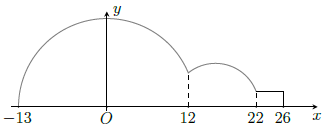
Câu 6. Trong chương trình nông thôn mới, tại một xã X có xây một cây cầu bằng bê tông như hình vẽ. Tính thể tích khối bê tông để đổ đủ cây cầu.

A. 19m3
B. 21m3
C. 18m3
D. 40m3
Hướng dẫn giải
Chọn hệ trục Oxy như hình vẽ
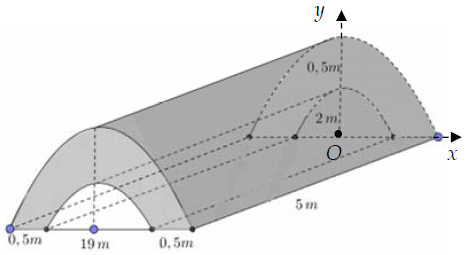
Ta có
Gọi (P1): y = ax2 + c là Parabol đi qua hai điểm
Nên ta có hệ phương trình sau:
Gọi (P2): y = ax2 + c là Parabol đi qua hai điểm
Nên ta có hệ phương trình sau:
Ta có thể tích của bê tông là:
⟹ Chọn D
Câu 7. Cho hai mặt cầu (S1) và (S2) có cùng bán kính R thỏa mãn tính chất: tâm của (S1) thuộc (S2) và ngược lại. Tính thể tích phần chung V của hai khối cầu tạo bởi (S1) và (S2).
A.
B.
C.
D.
Hướng dẫn giải
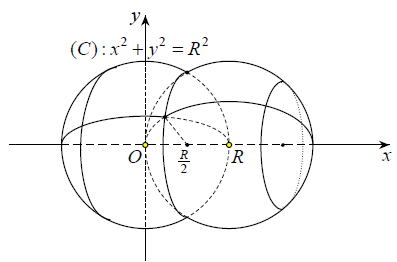
Gắn hệ trục Oxy như hình vẽ
Khối cầu S(O; R) chứa một đường tròn lớn là (C): x2 + y2 = R2
Dựa vào hình vẽ, thể tích cần tính là
⟹ Chọn C
Câu 8. Một thùng rượu có bán kính các đáy là 30cm, thiết diện vuông góc với trục và cách đều hai đáy có bán kính là 40cm, chiều cao thùng rượu là 1m. Biết rằng mặt phẳng chứa trục và cắt mặt xung quanh thùng rượu là các đường parabol, hỏi thể tích của thùng rượu là bao nhiêu?

A. 425, 2 lit
B. 425162 lit
C. 212581 lit
D. 212, 6 lit
Hướng dẫn giải
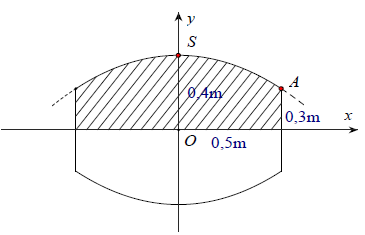
Gọi (P): y = ax2 + bx + c là parabol đi qua điểm A(0.5; 0.3) và có đỉnh S(0; 0.4). Khi đó, thể tích thùng rượu bằng thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi (P), trục hoành và hai đường thẳng x = ±0.5 quay quanh trục Ox.
Dễ dàng tìm được
Thể tích thùng rượu là:
⟹ Chọn A
Câu 9. Bác Năm làm một cái cửa nhà hình parabol có chiều cao từ mặt đất đến đỉnh là 2,25 mét, chiều rộng tiếp giáp với mặt đất là 3 mét. Giá thuê mỗi mét vuông là 1.500.000 đồng. Vậy số tiền bác Năm phải trả là:
A. 33.750.000 đồng
B. 12.750.000 đồng
C. 6.750.000 đồng
D. 3.750.000 đồng
Hướng dẫn giải
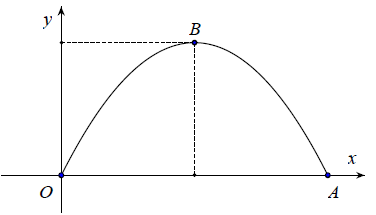
Gắn parabol (P) và hệ trục tọa độ sao cho (P) đi qua O(0; 0)
Gọi phương trình của parbol là: (P): y = ax2 + bx + c
Theo đề ra, (P) đi qua ba điểm O(0; 0), A(3; 0), B(1.5; 2.25)
Từ đó, suy ra (P): y = –x2 + 3x
Diện tích phần Bác Năm xây dựng:
Vậy số tiền bác Năm phải trả là:
⟹ Chọn C
Câu 10. Ông An có một mảnh vườn hình Elip có độ dài trục lớn bằng 16m và độ dài trục bé bằng 10m . Ông muốn trồng hoa trên một dải đất rộng 8m và nhận trục bé của elip làm trục đối xứng. Biết kinh phí để trồng hoa là 100.000 đồng/m2. Hỏi ông An cần bao nhiêu tiền để trồng hoa trên dải đất đó?
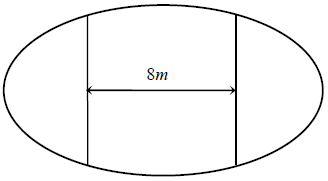
A. 7.862.000 đồng
B. 7.653.000 đồng
C. 7.128.000 đồng
D. 7.826.000 đồng
Hướng dẫn giải
Giả sử elip có phương trình
Từ giả thiết ta có 2a = 16 ⇒ a = 8 và 2b = 10 ⇒ b = 5
Vậy phương trình của elip là
Khi đó diện tích dải vườn được giới hạn bởi các đường (E1); (E2); x = –4; x = 4 và diện tích của dải vườn là
Tính tích phân này bằng phép đổi biến x = 8sint, ta được
Khi đó số tiền là
⟹ Chọn B
Câu 11. Người ta dựng một cái lều vải có dạng hình “chóp lục giác cong đều” như hình vẽ bên. Đáy của là một hình lục giác đều cạnh 3m. Chiều cao SO = 6m. Các cạnh bên của là các sợi dây c1, c2, c3, c4, c5, c6 nằm trên các đường parabol có trục đối xứng song song với SO. Giả sử giao tuyến của với mặt phẳng vuông góc với SO là một lục giác đều và khi qua trung điểm của SO thì lục giác đều có cạnh bằng 1m. Tính thể tích phần không gian nằm bên trong cái lều đó.
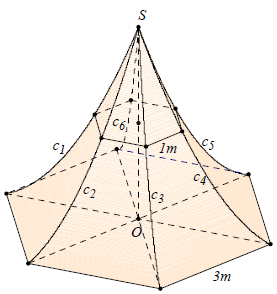
A.
B.
C.
D.
Hướng dẫn giải
Đặt hệ tọa độ như hình vẽ, ta có parabol cần tìm đi qua 3 điểm có tọa độ lần lượt là A(0; 6), B(1; 3), C(3; 0) nên có phương trình là
Theo hình vẽ ta có cạnh của thiết diện là BM
Nếu ta đặt t = OM thì
Khi đó diện tích của thiết diện lục giác:
Vậy thể tích của túp lều theo đề bài là:
⟹ Chọn D
Câu 12. Một vật có kích thước và hình dáng như hình vẽ dưới đây. Đáy là hình tròn giới hạn bởi đường tròn x2 + y2 = 16, cắt vật bởi các mặt phẳng vuông góc với trục Ox ta được thiết diện là tam giác đều. Thể tích của vật thể là:
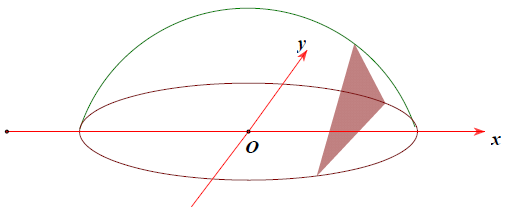
A.
B.
C.
D.
Hướng dẫn giải
Giải phương trình
Diện tích thiết diện là
Thể tích cần tìm là
⟹ Chọn B
Câu 13. Cho hàm số y = f(x) có đồ thị trên [–2; 6] như hình vẽ bên. Biết các miền A, B, x = 2 có diện tích lần lượt là 32; 2; 3. Tích phân bằng
A.
B. 41
C. 37
D.
Hướng dẫn giải
Ta có
Xét
Đặt
Đổi cận: x = –2 ⇒ t = –2; x = 2 ⇒ t = 6
Suy ra
Gọi x1, x2 là các hoành độ giao điểm của đồ thị hàm số y = f(x) với trục hoành (–2 < x1 < x2< 6). Ta có
Vậy
⟹ Chọn D
Câu 14. Cho hàm số y = f(x) đồ thị của hàm số y = f’(x) như hình bên. Đặt g(x) = 2f(x) – (x + 1)2. Mệnh đề nào dưới đây đúng?
A. g(3) > g(–3) > g(1)
B. g(–3) > g(3) > g(1)
C. g(1) > g(–3) > g(3)
D. g(1) > g(3) > g(–3)
Hướng dẫn giải
Ta có g’(x) = 2f’(x) – 2(x + 1)
g’(x) = 0 ⇔ f’(x) = x + 1. Đây là phương trình hoành độ giao điểm của đồ thị hàm số f’(x) và đường thẳng d: y = x + 1.
Dựa vào đồ thị ta thấy:
Bảng biến thiên:

Suy ra g(–3) < g(1) và g(3) < g(1)
Gọi S1, S2 lần lượt là diện tích các hình phẳng giới hạn bởi đồ thị hàm số f’(x), đường thẳng d: y = x + 1 trên các đoạn [–3; 1] và [1; 3] ta có
+) Trên đoạn [–3; 1] ta có f’(x) ≥ x + 1 nên
+) Trên đoạn [1; 3] ta có f’(x) ≤ x + 1 nên
Dựa vào đồ thị ta thấy S1 > S2 nên ta có:
Vậy g(1) > g(3) > g(–3)
Lưu ý:
+) Hoành độ giao điểm của đồ thị hàm số f’(x) và đường thẳng d: y = x + 1 chính là nghiệm của phương trình g’(x) = 0.
+) Lập bảng biến thịên ta thấy g(1) lớn hơn g(±3). Ta chỉ cần so sánh g(3) và g(–3).
+) So sánh diện tích dựa vào đồ thị.
⟹ Chọn D
Câu 15. Hình phẳng (H) được giới hạn bởi đồ thị (C) của hàm đa thức bậc ba và parabol (P) có trục đối xứng vuông góc với trục hoành. Phần tô đậm của hình vẽ có diện tích bằng
A.
B.
C.
D.
Hướng dẫn giải
Vì đồ thị hàm bậc ba và đồ thị hàm bậc hai cắt trục tung tại các điểm có tung độ lần lượt là y = 2 và y = 0 nên ta xét hai hàm số là y = ax3 + bx2 + cx + 2, y = mx2 + nx (với a, m ≠ 0)
Suy ra (C): y = f(x) = ax3 + bx2 + cx + 2 và (P): y = g(x) = mx2 + nx
Phương trình hoành độ giao điểm của (C) và (P) là
ax3 + bx2 + cx + 2 = mx2 + nx ⇔ (ax3 + bx2 + cx + 2) – (mx2 + nx) = 0
Đặt P(x) = (ax3 + bx2 + cx + 2) – (mx2 + nx)
Theo giả thiết, (C) và (P) cắt nhau tại các điểm có hoành độ lần lượt là x = –1, x = 1, x = 2 nên P(x) = a(x + 1)(x – 1)(x – 2)
Ta có P(0) = 2a
Mặt khác, ta có P(0) = f(0) – g(0) = 2 ⇒ a = 1
Vậy diện tích phần tô đậm là
⟹ Chọn A