Hệ thức Vi-et: Tổng quan lý thuyết và dạng bài tập đặc trưng

Trong bài viết này, Dân Chuyên Toán sẽ giúp bạn đọc tìm hiểu chi tiết nội dung của hệ thức Vi-et, các ứng dụng bao gồm: Nhẩm nghiệm, tìm hai số khi biết tổng tích, xác định dấu của nghiệm, … Từ đó áp dụng vào các dạng toán đặc trưng thường gặp nhất như: Giải phương trình bậc hai, tính giá trị biểu thức giữa các nghiệm của phương trình, tìm hai số khi biết tổng tích, phân tích tam thức bậc hai thành nhân tử, tìm điều kiện tham số để phương trình bậc hai có nghiệm thỏa điều kiện cho trước, …

Tổng quan lý thuyết

Hệ thức Vi-ét

– Cho phương trình bậc hai ax² + bx + c = 0 (a ≠ 0). Nếu x₁, x₂ là hai nghiệm của phương trình thì:

$S = {x_1} + {x_2} = - \frac{b}{a}$ và $P = {x_1}{x_2} = \frac{c}{a}$

– Để áp dụng hệ thức Vi-ét phải chú ý đến điều kiện phương trình là phương trình bậc hai có nghiệm $\left\{ \begin{gathered} a \ne 0 \hfill \\ \Delta \geqslant 0 \hfill \\ \end{gathered} \right.$

Ứng dụng của hệ thức Vi-ét

Nhẩm nghiệm

Xét phương trình bậc hai ax² + bx + c = 0 (a ≠ 0)

– Nếu a + b + c = 0 thì phương trình có một nghiệm là x₁ = 1, nghiệm còn lại là ${x_2} = \frac{c}{a}$

– Nếu a – b + c = 0 thì phương trình có một nghiệm là x₁ = −1, nghiệm còn lại là ${x_2} = - \frac{c}{a}$

Tìm hai số biết tổng và tích của chúng

Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình X² – SX + P = 0.

Xác định dấu của nghiệm

Phương trình ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x₁, x₂

– Nếu $P = {x_1}{x_2} = \frac{c}{a} < 0$ thì phương trình có hai nghiệm trái dấu

– Nếu $P = {x_1}{x_2} = \frac{c}{a} > 0$ và S = x₁ + x₂ > 0 thì phương trình có hai nghiệm dương

– Nếu $P = {x_1}{x_2} = \frac{c}{a} > 0$ và S = x₁ + x₂ < 0 thì phương trình có hai nghiệm âm

Phân dạng bài tập

Dạng 1. Giải phương trình bậc hai bằng cách tính nhẩm nghiệm

Phương pháp giải

Từ định lý Vi-ét ta có: Nếu phương trình bậc hai ax² + bx + c = 0 có:

– a + b + c = 0 thì phương trình có nghiệm là ${x_1} = 1,{x_2} = \frac{c}{a}$

– a – b + c = 0 thì phương trình có nghiệm là ${x_1} = - 1,{x_2} = - \frac{c}{a}$

Bài tập vận dụng

Câu 1. Giải các phương trình sau:

a) 1,5x² – 1,6x + 0,1 = 0

b) $\left( {2 - \sqrt 3 } \right){x^2} + 2\sqrt 3 x - \left( {2 + \sqrt 3 } \right) = 0$

c) $\sqrt 3 {x^2} - \left( {1 - \sqrt 3 } \right)x - 1 = 0$

d) (m – 1)x² – (2m + 3)x + m + 4 = 0 (m ≠ 1)

Hướng dẫn giải

Đa số học sinh khi gặp yêu cầu giải phương trình thường tính ngay Δ hoặc Δ’ mà không để ý đến các trường hợp đặc biệt a + b + c = 0 hoặc a – b + c = 0. Thậm chí có em khi gặp phương trình có các hệ số là số vô tỷ như phương trình b) , c) hoặc phương trình có chứa tham số như phương trình d) thì tỏ ra ái ngại. Rõ ràng nếu ta để ý sẽ thấy các phương trình trong ví dụ trên đều có dạng đặc biệt có thể nhẩm nghiệm ngay mà không phải tính Δ hoặc Δ’

a) Vì phương trình đã cho có a + b + c = 1,5 + (–1,6) + 0,1 = 0 nên phương trình có hai nghiệm là:

${x_1} = 1,{x_2} = \frac{{0,1}}{{1,5}} = \frac{1}{{15}}$

b) Vì phương trình đã cho có $a + b + c = \left( {2 - \sqrt 3 } \right) + 2\sqrt 3 + \left[ { - \left( {2 + \sqrt 3 } \right)} \right] = 0$ nên phương trình có hai nghiệm là:

$\begin{gathered} {x_1} = 1 \hfill \\ {x_2} = \frac{{ - \left( {2 + \sqrt 3 } \right)}}{{2 - \sqrt 3 }} = \frac{{ - {{\left( {2 + \sqrt 3 } \right)}^2}}}{{{2^2} - {{\left( {\sqrt 3 } \right)}^2}}} = - \left( {7 + 4\sqrt 3 } \right)\begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \hfill \\ \hfill \\ \end{gathered} \\ {} \end{array} \hfill \\ \end{gathered}$

c) Vì phương trình đã cho có $a + b + c = \sqrt 3 - \left( {1 - \sqrt 3 } \right) - 1 = 0$ nên phương trình có hai nghiệm là:

${x_1} = - 1,{x_2} = \frac{{ - \left( { - 1} \right)}}{{\sqrt 3 }} = \frac{1}{{\sqrt 3 }} = \frac{{\sqrt 3 }}{3}$

d) Vì m ≠ 1 nên phương trình đã cho là phương trình bậc hai, có a + b + c = (m – 1) – (2m + 3) + m + 4 = 0 nên phương trình có hai nghiệm là:

${x_1} = 1,{x_2} = \frac{{m + 4}}{{m - 1}}$

Trong trường hợp giải phương trình đơn giản ta cũng có thể nhẩm nghiệm dựa vào định lý Vi-ét:

Câu 2. Giải phương trình:

a) x² – 7x + 10 = 0

b) x² + 8x + 15 = 0

Hướng dẫn giải

a) Vì 2 + 5 = 7; 2⋅5 = 10 nên x₁ = 2; x₂ = 5 là nghiệm của phương trình đã cho.

b) Vì (–3) + (–5) = –8; (–3)⋅(–5) = 15 nên x₁ = –3; x₂ = –5 là nghiệm của phương trình đã cho.

Như vậy trước khi học sinh giải phương trình, giáo viên cần tạo cho học sinh thói quen nhẩm nghiệm trước khi tính theo công thức nghiệm.

Dạng 2. Tính giá trị của biểu thức giữa các nghiệm của phương trình bậc hai

Phương pháp giải

Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x₁, x₂ thì ta có thể biểu thị các biểu thức đối xứng giữa các nghiệm theo S = x₁ + x₂ và P = x₁⋅x₂.

Ví dụ:

$x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {S^2} - 2P$

${\left( {{x_1} - {x_2}} \right)^2} = {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = {S^2} - 4P$

$x_1^3 + x_2^3 = {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right) = {S^3} - 3SP$

$x_1^4 + x_2^4 = {\left( {x_1^2 + x_2^2} \right)^2} - 2x_1^2x_2^2 = {\left( {{S^2} - 2P} \right)^2} - 2{P^2}$

$\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} = \frac{{{x_1} + {x_2}}}{{{x_1}{x_2}}} = \frac{S}{P}$

$\frac{{{x_1}}}{{{x_2}}} + \frac{{{x_2}}}{{{x_1}}} = \frac{{x_1^2 + x_2^2}}{{{x_1}{x_2}}} = \frac{{{S^2} - 2P}}{P}$

$\frac{1}{{x_1^2}} + \frac{1}{{x_2^2}} = \frac{{x_1^2 + x_2^2}}{{x_1^2x_2^2}} = \frac{{{S^2} - 2P}}{{{P^2}}}$

$\left( {{x_1} - \alpha } \right)\left( {{x_2} - \alpha } \right) = {x_1}{x_2} - \alpha \left( {{x_1} + {x_2}} \right) + {\alpha ^2}$

$\frac{1}{{{x_1} - \alpha }} + \frac{1}{{{x_2} - \alpha }} = \frac{{{x_1} + {x_2} - 2\alpha }}{{\left( {{x_1} - \alpha } \right)\left( {{x_2} - \alpha } \right)}} = \frac{{S - 2\alpha }}{{P - \alpha S + {\alpha ^2}}}$

Chú ý: Khi tính giá trị của một biểu thức giữa các nghiệm thông thường ta biến đổi sao cho trong biểu thức đó xuất hiện tổng và tích các nghiệm rồi áp dụng định lý Vi-ét để giải.

Bài tập vận dụng

Câu 1. Cho x₁, x₂ là hai nghiệm của phương trình: x² – x – 1 = 0

a) Hãy tính $x_1^2 + x_2^2$

b) Chứng minh ${\text{Q}} = x_1^2 + x_2^2 + x_1^4 + x_2^4$ chia hết cho 5

Hướng dẫn giải

Phương trình đã cho có hai nghiệm phân biệt vì ac = –1 < 0

Theo định lý Vi-ét ta có: x₁ + x₂ = 1; x₁⋅x₂ = –1

a) $x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {1^2} - 2 \cdot \left( { - 1} \right) = 3$

b) ${\text{Q}} = \left( {x_1^2 + x_2^2} \right) + {\left( {x_1^2 + x_2^2} \right)^2} - 2x_1^2x_2^2$

$= 3 + {3^2} - 2 \cdot {\left( { - 1} \right)^2} = 10 \Rightarrow Q \vdots 5$

Chú ý: Ta có thể chứng minh biểu thức ${\text{M}} = x_1^{2008} + x_2^{2008} + x_1^{2010} + x_2^{2010}$ cũng chia hết cho 5.

Câu 2. Cho phương trình: x² – ax + a – 1 = 0 có hai nghiệm là x₁, x₂. Không giải phương trình hãy tính giá trị biểu thức:

${\text{M}} = \frac{{2x_1^2 - {x_1}{x_2} + 2x_2^2}}{{x_1^2{x_2} + {x_1}x_2^2}}$

Hướng dẫn giải

Trước hết ta kiểm tra xem phương trình đã cho có nghiệm hay không.

Ta có: Δ = (–a)² – 4(a – 1) = (a – 2)² ≥ 0 ⇒ Phương trình đã cho có hai nghiệm x₁, x₂.

Áp dụng định lý Vi–et ta có: x₁ + x₂ = a; x₁⋅x₂ = a – 1

$\begin{gathered} {\text{M}} = \frac{{2\left( {x_1^2 + x_2^2} \right) - {x_1}{x_2}}}{{{x_1}{x_2}\left( {{x_1} + {x_2}} \right)}} = \frac{{2{{\left( {{x_1} + {x_2}} \right)}^2} - 5{x_1}{x_2}}}{{{x_1}{x_2}\left( {{x_1} + {x_2}} \right)}} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ = \frac{{2{a^2} - 5\left( {a - 1} \right)}}{{a\left( {a - 1} \right)}} = \frac{{2{a^2} - 5a + 5}}{{a\left( {a - 1} \right)}} \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

Câu 3. Gọi x₁, x₂ là các nghiệm của phương trình: x² – 6x + 1 = 0. Ký hiệu ${S_n} = x_1^n + x_2^n$ với n là số nguyên dương.

a) Tính S₁, S₂, S₃

b) Tìm một hệ thức giữa S_n, S_n+1, S_n+2

Hướng dẫn giải

Phương trình: x² – 6x + 1 = 0 có ∆ = (–6)² – 4 = 32 > 0 nên phương trình có hai nghiệm phân biệt x₁, x₂

Theo định lý Vi-ét ta có: x₁ + x₂ = 6; x₁⋅x₂ = 1

S = x₁ + x₂ = 6

a) Ta có:

$\begin{gathered} {S_2} = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} \hfill \\ \begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \hfill \\ \hfill \\ \end{gathered} &{ = {6^2} - 2 \cdot 1 = 34} \end{array} \hfill \\ {S_3} = x_1^3 + x_2^3 = {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right) \hfill \\ \begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \hfill \\ \hfill \\ \end{gathered} &{ = {6^3} - 3 \cdot 1 \cdot 6 = 198} \end{array} \hfill \\ \end{gathered}$

b) Ta có:

$\begin{gathered} {S_{n + 2}} = x_1^{n + 2} + x_2^{n + 2} \hfill \\ \begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \hfill \\ \hfill \\ \end{gathered} &{} \end{array} = x_1^{n + 1} + x_2^{n + 1}\left( {{x_1} + {x_2}} \right) - {x_1}{x_2}\left( {x_1^n + x_2^n} \right) \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = 6{S_{n + 1}} - {S_n} \hfill \\ \end{gathered}$

Chú ý: Ta còn chứng minh được trường hợp tổng quát: phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x₁, x₂ với ${S_n} = x_1^n + x_2^n$ thì S_n, S_n+1, S_n+2 liên hệ với nhau bởi hệ thức:

a⋅S_n+2 + b⋅S_n+1 + c⋅S_n = 0

Vận dụng hệ thức trên cho ta lời giải thú vị của nhiều bài toán.

Câu 4. Cho a, b là nghiệm của phương trình 30x² – 4x = 2010 tính giá trị của biểu thức:

${\text{M}} = \frac{{30\left( {{a^{2010}} + {b^{2010}}} \right) - 4\left( {{a^{2009}} + {b^{2009}}} \right)}}{{{a^{2008}} + {b^{2008}}}}$

Hướng dẫn giải

Ta thấy phương trình đã cho có Δ > 0 nên phương trình có hai nghiêm phân biệt

x₁ = a; x₂ = b ⇒ S_n = aⁿ + bⁿ

Áp dụng hệ thức ở chú ý trên ta có:

A⋅S_n+2 + B⋅S_n+1 + C⋅S_n = 0

Ta có: S_n = a²⁰⁰⁸ + b²⁰⁰⁸

S_n+1 = a²⁰⁰⁹ + b²⁰⁰⁹

S_n+2 = a²⁰¹⁰ + b²⁰¹⁰

⇒ 30S_n+2 – 4S_n+1 – 2010S_n = 0

⇒ 30S_n+2 – 4S_n+1 = 2010S_n

⇒ ${\text{M}} = \frac{{2010{{\text{S}}_{\text{n}}}}}{{{{\text{S}}_{\text{n}}}}} = 2010$

Câu 5. Tính giá trị của các biểu thức:

${\text{A}} = {\left( {2 + 3\sqrt 2 } \right)^6} + {\left( {2 - 3\sqrt 2 } \right)^6}$

${\text{B}} = \frac{1}{{{{\left( {2 + 3\sqrt 2 } \right)}^6}}} + \frac{1}{{{{\left( {2 - 3\sqrt 2 } \right)}^6}}}$

Hướng dẫn giải

Đặt ${x_1} = 2 + 3\sqrt 2 ,{x_2} = 2 - 3\sqrt 2$ thì x₁ + x₂ = 4; x₁⋅x₂ = –14 do đó x₁, x₂ là hai nghiệm của phương trình x² – 4x – 14 = 0.

Khi đó hệ thức ở chú ý trên có dạng: S_n+2 = 4S_n+1 + 14S_n. Ta tính được:

S₁ = 4; S₂ = 44; S₃ = 4⋅44 + 14⋅4 = 232;

S₄ = 4⋅232 + 14⋅44 = 1544;

S₅ = 4⋅1544 + 14⋅232 = 9424;

⇒ A = S₆ = 4⋅9424 + 14⋅1544 = 59312

${\text{B}} = \frac{{{S^6}}}{{{{14}^6}}} = \frac{{59312}}{{16 \cdot 47059}} = \frac{{3707}}{{47059}}$

Dạng 3. Tìm hai số khi biết tổng và tích

Phương pháp giải

Áp dụng định lý Vi-ét đảo: Nếu hai số u, v có $\left\{ \begin{gathered} u + v = S \hfill \\ uv = P \hfill \\ \end{gathered} \right.$ thì u, v là nghiệm của phương trình: x² – Sx + P = 0

Điều kiện để tồn tại hai số u, v là S² ≥ 4P.

Chú ý: Các hệ phương trình $\left\{ \begin{gathered} {u^2} + {v^2} = a \hfill \\ uv = b \hfill \\ \end{gathered} \right.$ ; $\left\{ \begin{gathered} {u^2} + {v^2} = a \hfill \\ u \pm v = b \hfill \\ \end{gathered} \right.$ ; $\left\{ \begin{gathered} {u^3} + {v^3} = a \hfill \\ u \pm v = b \hfill \\ \end{gathered} \right.$ đều có thể đưa về hệ $\left\{ \begin{gathered} u + v = S \hfill \\ uv = P \hfill \\ \end{gathered} \right.$

Bài tập vận dụng

Câu 1. Tính các kích thước của hình chữ nhật ABCD. Biết diện tích và chu vi của nó theo thứ tự là 2a² và 6a.

Hướng dẫn giải

Gọi các kích thước của hình chữ nhật là x, y (x, y > 0). Theo bài ra ta có:

$\left\{ \begin{gathered} x + y = 3a \hfill \\ xy = 2{a^2} \hfill \\ \end{gathered} \right.$

Suy ra x, y là hai nghiệm của phương trình: t² – 3at + 2a² = 0

Ta có: ∆ = (–3a)² – 4⋅2a = a² ⇒ t₁ = a; t₂ = 2a

Vậy các kích thước của hình chữ nhật là a, 2a.

Câu 2. Tìm hai số u, v trong các trường hợp sau:

a) u + v = 4; uv = 19

b) u – v = 10; uv = 24

c) u²+ v² = 85; uv = 18

Hướng dẫn giải

a) Ta có: u, v là hai nghiệm của phương trình x² – 4x + 19 = 0.

Ta có: Δ’ = (–2)² – 19 = –15 < 0

⇒ Phương trình vô nghiệm

Vậy không tìm được hai số u, v.

b) Ta có: (u – v)² = (u + v)² – 4uv

⇒ (u + v)² = (u – v)² + 4uv = 100 + 4⋅24 = 196

⇒ u + v = 14 hoặc u + v = –14

Trường hợp 1: $\left\{ \begin{gathered} u + v = 14 \hfill \\ uv = 24 \hfill \\ \end{gathered} \right.$ ⇒ u, v là hai nghiệm của phương trình t² – 14t + 24 = 0

Ta có: Δ’ = (–7)² – 24 = 25 > 0

⇒ Phương trình có hai nghiệm phân biệt

t₁ = 12; t₂ = 2 ⇒ u = 12, v = 2 vì u – v = 10

Trường hợp 2: $\left\{ \begin{gathered} u + v = - 14 \hfill \\ uv = 24 \hfill \\ \end{gathered} \right.$ ⇒ u, v là hai nghiệm của phương trình t² + 14t + 24 = 0

Ta có: Δ’ = 49 – 24 = 25 > 0

⇒ Phương trình có hai nghiệm phân biệt

t₁ = –12; t₂ = –2 ⇒ u = –2, v = –12 vì u – v = 10

Vậy $\left\{ \begin{gathered} u = 12 \hfill \\ v = 2 \hfill \\ \end{gathered} \right.$ hoặc $\left\{ \begin{gathered} u = - 2 \hfill \\ v = - 12 \hfill \\ \end{gathered} \right.$

Chú ý: Ta có thể giải cách khác như sau;

Ta có: $\left\{ \begin{gathered} u - v = 10 \hfill \\ uv = 24 \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} u + \left( { - v} \right) = 10 \hfill \\ u \cdot \left( { - v} \right) = - 24 \hfill \\ \end{gathered} \right.$

⇒ u, –v là hai nghiệm của phương trình: t² – 10t – 24 = 0

Ta có: Δ’ = (–5)² – (–24) = 49 > 0

⇒ Phương trình có hai nghiệm phân biệt t₁ = –2; t₂ = 12

$\Rightarrow \left\{ \begin{gathered} u = - 2 \hfill \\ - v = 12 \hfill \\ \end{gathered} \right.$ hoặc $\left\{ \begin{gathered} u = 12 \hfill \\ - v = - 2 \hfill \\ \end{gathered} \right.$

Vậy $\left\{ \begin{gathered} u = 12 \hfill \\ v = 2 \hfill \\ \end{gathered} \right.$ hoặc $\left\{ \begin{gathered} u = - 2 \hfill \\ v = - 12 \hfill \\ \end{gathered} \right.$

c) Ta có: (u + v)² = u² + v² + 2uv = 85 + 36 = 121

⇒ u + v = 11 hoặc u + v = –11

Giải tiếp ta được $\left\{ \begin{gathered} u = 9 \hfill \\ v = 2 \hfill \\ \end{gathered} \right.$ hoặc $\left\{ \begin{gathered} u = 2 \hfill \\ v = 9 \hfill \\ \end{gathered} \right.$ hoặc $\left\{ \begin{gathered} u = - 9 \hfill \\ v = - 2 \hfill \\ \end{gathered} \right.$ hoặc $\left\{ \begin{gathered} u = - 2 \hfill \\ v = - 9 \hfill \\ \end{gathered} \right.$

Câu 3. Tìm các số p, q của phương trình x² – px + q = 0 sao cho các nghiệm x₁, x₂ của nó thỏa mãn điều kiện $\left\{ \begin{gathered} {x_1} - {x_2} = 5 \hfill \\ x_1^3 - x_2^3 = 35 \hfill \\ \end{gathered} \right.$

Hướng dẫn giải

Theo định lý Vi-ét ta có: $\left\{ \begin{gathered} {x_1} + {x_2} = - p \hfill \\ {x_1} \cdot {x_2} = q \hfill \\ \end{gathered} \right.$

${\left( {{x_1} - {x_2}} \right)^2} = {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1} \cdot {x_2} = {p^2} - 4q = 25$

Suy ra:

$\begin{gathered} x_1^3 - x_2^3 = \left( {{x_1} - {x_2}} \right)\left( {x_1^2 + {x_1} \cdot {x_2} + x_2^2} \right) \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ \hfill \\ \hfill \\ \end{gathered} \end{array}}&{ = 5\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - {x_1} \cdot {x_2}} \right] = 35} \end{array} \hfill \\ \Rightarrow {\left( {{x_1} + {x_2}} \right)^2} - {x_1} \cdot {x_2} = {p^2} - q = 7 \hfill \\ \end{gathered}$

Ta có hệ: $\left\{ \begin{gathered} {p^2} - 4q = 25 \hfill \\ {p^2} - q = 7 \hfill \\ \end{gathered} \right.$

Giải hệ trên ta được: $\left\{ \begin{gathered} p = 1 \hfill \\ q = - 6 \hfill \\ \end{gathered} \right.$ và $\left\{ \begin{gathered} p = - 1 \hfill \\ q = - 6 \hfill \\ \end{gathered} \right.$ đều thỏa mãn điều kiện Δ = p² – 4q > 0

Vậy (p; q) = (1; –6) hoặc (–1; –6)

Dạng 4. Phân tích tam thức bậc hai thành nhân tử

Phương pháp giải

Giả sử phương trình ax² + bx + c = 0 (*) (a ≠ 0) có Δ ≥ 0.

Khi đó theo Vi-ét ta có:

${x_1} + {x_2} = - \frac{b}{a};{x_1} \cdot {x_2} = \frac{c}{a}$

Do đó:

$\begin{gathered} a{x^2} + bx + c = a\left( {{x^2} + \frac{b}{a}x + \frac{c}{a}} \right) \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&\begin{gathered} \hfill \\ \hfill \\ \end{gathered} \end{array} = a\left[ {{x^2} - \left( {{x_1} + {x_2}} \right)x + {x_1} \cdot {x_2}} \right] \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&\begin{gathered} \hfill \\ \hfill \\ \end{gathered} \end{array} = a\left( {{x^2} - {x_1}x - {x_2}x + {x_1} \cdot {x_2}} \right) \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&\begin{gathered} \hfill \\ \hfill \\ \end{gathered} \end{array} = a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right) \hfill \\ \end{gathered}$

Vậy nếu phương trình bậc hai ax² + bx + c = 0 có hai nghiệm x₁, x₂ thì ta có:

ax² + bx + c = a(x – x₁)(x – x₂)

Bài tập vận dụng

Câu 1. Phân tích thành nhân tử:

a) 2x² – 5x + 3

b) 3x² + 8x + 2

Hướng dẫn giải

a) Phương trình đã cho có hai nghiệm là x₁ = 1; x₂ = $\frac{3}{2}$

Do đó ta có:

$2{x^2} - 5x + 3 = 2\left( {x - 1} \right)\left( {x - \frac{3}{2}} \right) = \left( {x - 1} \right)\left( {2x - 3} \right)$

b) Phương trình đã cho có hai nghiệm là ${x_1} = \frac{{ - 4 + \sqrt {10} }}{3};{x_2} = \frac{{ - 4 - \sqrt {10} }}{3}$

Do đó ta có:

$3{x^2} + 8x + 2 = 3\left( {x - \frac{{4 - \sqrt {10} }}{3}} \right)\left( {x + \frac{{4 + \sqrt {10} }}{3}} \right)$

Ứng dụng này học sinh rất hay sử dụng để phân tích các mẫu thành nhân tử trong các bài tập rút gọn

Dạng 5. Tìm điều kiện của tham số để phương trình bậc hai có một nghiệm x = x₁ cho trước. Tìm nghiệm thứ hai

Phương pháp giải

Tìm điều kiện để phương trình có nghiệm x = x₁ cho trước ta có thể làm như sau:

Cách 1:

– Tìm điều kiện để phương trình có hai nghiệm

Δ ≥ 0 (Δ’ ≥ 0) (*)

– Thay x = x₁ vào phương trình đã cho tìm giá trị của tham số

– Đối chiếu giá trị vừa tìm được với điều kiện (*) để kết luận

Cách 2:

– Thay x = x₁ vào phương trình đã cho tìm được giá trị của tham số

– Thay giá trị tìm được của tham số vào phương trình và giải phương trình

Nếu sau khi thay giá trị của tham số vào phương trình đã cho mà có Δ < 0 thì kết luận không có giá trị nào của tham số để phương trình có nghiệm x₁ cho trước.

Để tìm nghiệm thứ hai ta có thể làm như sau:

Cách 1: Thay giá trị của tham số tìm được vào phương trình rồi giải phương trình

Cách 2: Thay giá trị của tham số tìm được vào công thức tổng 2 nghiệm để tìm nghiệm thứ hai.

Cách 3: Thay giá trị của tham số tìm được vào công thức tích hai nghiệm để tìm nghiệm thứ hai.

Bài tập vận dụng

Câu 1. Với giá trị nào của k thì:

a) Phương trình 2x² + kx – 10 = 0 có một nghiệm x = 2. Tìm nghiệm kia?

b) Phương trình (k – 5)x² – (k – 2)x + 2k = 0 có một nghiệm x = −2. Tìm nghiệm kia?

c) Phương trình kx² – kx – 72 = 0 có một nghiệm x = −3. Tìm nghiệm kia?

Hướng dẫn giải

a) Nếu x = 2 là một nghiệm của phương trình thì:

2⋅4 + 2k – 10 = 0 ⇔ 2k = 2 ⇔ k = 1

Với k = 1 ta có: 2x² + x – 10 = 0

Cách 1: Ta có:

$\begin{gathered} \Delta = 1 + 80 = 81 \Rightarrow \sqrt \Delta = \sqrt {81} = 9 \hfill \\ \hfill \\ \Rightarrow {x_1} = \frac{{ - 1 + 9}}{4} = 2;{x_2} = \frac{{ - 1 - 9}}{4} = - 2.5 \hfill \\ \end{gathered}$

Cách 2: Theo hệ thức Vi-ét ta có:

${x_1} \cdot {x_2} = - 5 \Rightarrow {x_2} = - \frac{5}{{{x_1}}} = - \frac{5}{2} = - 2,5$

Cách 3: Theo hệ thức Vi-ét ta có;

$\begin{gathered} {x_1} + {x_2} = - \frac{k}{2} = - \frac{1}{2} \hfill \\ \hfill \\ \Rightarrow {x_2} = - \frac{1}{2} - {x_1} = - 0,5 - 2 = - 2,5 \hfill \\ \end{gathered}$

b) Tương tự câu a) ta có k = 3, nghiệm kia x₂ = 1,5

c) Tương tự câu a) ta có k = 6, nghiệm kia x₂ = 4

Dạng 6. Xác định tham số để các nghiệm của phương trình bậc hai thỏa mãn hệ một điều kiện cho trước

Phương pháp giải

“Điều kiện cho trước” ở đây có thể là các nghiệm của phương trình bậc hai thỏa mãn một đẳng thức hoặc bất đẳng thức hoặc để một biểu thức của các nghiệm của phương trình bậc hai đạt GTLN, GTNN,…

Phương pháp: –

– Xác định giá trị của tham số để phương trình bậc hai có nghiệm x₁, x₂

– Áp dụng định lý Vi-ét ta có: $\left\{ \begin{gathered} {x_1} + {x_2} = f\left( m \right) \hfill \\ {x_1} \cdot {x_2} = g\left( m \right) \hfill \\ \end{gathered} \right.{\text{ }}\left( * \right)$

– Kết hợp hệ (*) với điều kiện bài ra để suy ra điều kiện của tham số m

Chú ý: Sau khi tìm được tham số ta phải đối chiếu với điều kiện phương trình có nghiệm.

Bài tập vận dụng

Câu 1. Cho phương trình: x² – 6x + m = 0. Tính giá trị của m biết phương trình có hai nghiệm x₁, x₂ thỏa mãn điều kiện: x₁ – x₂ = 4

Hướng dẫn giải

Phương trình x² – 6x + m = 0 có ∆ = 9 – m

Phương trình có nghiệm ⇔ ∆’ ≥ 0 ⇔ 9 – m ≥ 0 ⇔ m ≤ 9 (*)

Theo định lý Vi-ét ta có: $\left\{ \begin{gathered} {x_1} + {x_2} = 6{\text{ }}\left( 1 \right) \hfill \\ {x_1} \cdot {x_2} = m{\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right.$

Theo bài ra ta có: x₁ – x₂ = 4 (3)

Từ (1) và (3) ta có: x₁ = 5; x₂ = 1. Thay vào (2) ta có m = 5 thỏa mãn điều kiện (*)

Vậy với m = 5 thì phương trình đã cho có hai nghiệm thỏa mãn x₁ – x₂ = 4

Câu 2. Cho phương trình: x²– 4x + m = 0. Tìm các giá trị của m để phương trình có hai nghiệm x₁, x₂ thỏa mãn: $x_1^3 + x_2^3 = 26$

Hướng dẫn giải

Phương trình đã cho có nghiệm khi và chỉ khi:

Δ’ = 4 – m ≥ 0 ⇔ m ≤ 4 (*)

Theo hệ thức Vi-ét ta có: $\left\{ \begin{gathered} {x_1} + {x_2} = 4 \hfill \\ {x_1} \cdot {x_2} = m \hfill \\ \end{gathered} \right.$

Theo bài ra ta có:

$\begin{gathered} x_1^3 + x_2^3 = 26 \hfill \\ \hfill \\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right) = 26 \hfill \\ \hfill \\ \Leftrightarrow {4^3} - 3m \cdot 4 = 26 \hfill \\ \hfill \\ \Leftrightarrow 64 - 12m = 26 \hfill \\ \hfill \\ \Leftrightarrow m = \frac{{19}}{6} \hfill \\ \end{gathered}$

Giá trị này của m không thỏa mãn điều kiện (*).

Vậy không có giá trị nào của m để $x_1^3 + x_2^3 = 26$

Câu 3. Cho phương trình: x² – 2(m – 2)x + (m² + 2m – 3) = 0. Tìm các giá trị của m để phương trình có hai nghiệm phân biệt x₁, x₂ thỏa mãn: $\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} = \frac{{{x_1} + {x_2}}}{5}$

Hướng dẫn giải

Ta có: Δ’ = (m – 2)² – (m² + 2m – 3) = 7 – 6m

Phương trình có hai nghiệm phân biệt

⇔ Δ’ > 0 ⇔ 7 – 6m > 0 ⇔ m < $\frac{7}{6}$ (*)

Theo định lý Vi-ét ta có:

$\left\{ \begin{gathered} {x_1} + {x_2} = 2\left( {m - 2} \right){\text{ }}\left( 1 \right) \hfill \\ {x_1} \cdot {x_2} = {m^2} + 2m - 3{\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right.$

Theo bài ra ta có:

$\begin{gathered} \frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} = \frac{{{x_1} + {x_2}}}{5} \hfill \\ \hfill \\ \Leftrightarrow \left( {{x_1} + {x_2}} \right)\left( {\frac{1}{{{x_1} \cdot {x_2}}} - 5} \right) = 0{\text{ }}\left( 3 \right) \hfill \\ \end{gathered}$

Từ (3) ta suy ra: x₁_⋅x₂ ≠ 0

⇔ m² + 2m – 3 ≠ 0

⇔ m ≠ 1 ∨ m ≠ 3 (**)

Mặt khác từ (3) suy ra

$\begin{gathered} \left[ \begin{gathered} {x_1} + {x_2} = 0 \hfill \\ {x_1} \cdot {x_2} = 5 \hfill \\ \end{gathered} \right. \Rightarrow \left[ \begin{gathered} m = 2 \hfill \\ {m^2} + 2m - 3 - 5 = 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left[ \begin{gathered} m = 2 \hfill \\ \left( {m - 2} \right)\left( {m + 4} \right) = 0 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Suy ra m = 2 (loại) hoặc m = –4 (thỏa mãn * và **)

Vậy m = – 4 thì $\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} = \frac{{{x_1} + {x_2}}}{5}$

Câu 4. Cho phương trình bậc hai tham số m: 2x² – (m + 3)x + m = 0. Gọi x₁, x₂ là hai nghiệm của phương trình. Tìm GTNN của biểu thức P = |x₁ – x₂|

Hướng dẫn giải

Phương trình đã cho có: Δ = (m + 3)² – 8m = m² – 2m + 9 = (m + 1)² + 8 > 0 với mọi m suy ra phương trình luôn có hai nghiệm phân biệt x₁, x₂ (x₁ ≠ x₂)

Theo hệ thức Vi-ét ta có:

$\left\{ \begin{gathered} {x_1} + {x_2} = \frac{{m + 3}}{2} \hfill \\ \hfill \\ {x_1} \cdot {x_2} = \frac{m}{2} \hfill \\ \end{gathered} \right.$

Theo bài ra ta có:

$\begin{gathered} {\text{P }} = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2}} = \left| {{x_1} - {x_2}} \right| \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ = \sqrt {x_1^2 + x_2^2 - 2{x_1}{x_2}} \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \hfill \\ = \sqrt {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ = \sqrt {{{\left( {\frac{{m + 3}}{2}} \right)}^2} - 4 \cdot \frac{m}{2}} \hfill \\ \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} = \sqrt {\frac{{{m^2} + 6m + 9 - 8m}}{4}} \hfill \\ \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} = \sqrt {\frac{{{m^2} - 2m + 1 + 8}}{4}} \hfill \\ \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} = \frac{{\sqrt {{{\left( {m - 1} \right)}^2} + 8} }}{2} \geqslant \frac{{\sqrt 8 }}{2} = \sqrt 2 \hfill \\ \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

Dấu ” = ” xảy ra khi và chỉ khi m = 1

Vậy GTNN của P bằng $\sqrt 2$ ⇔ m = 1

Nhận xét: Với bài toán trên học sinh có thể tính các nghiệm x₁, x₂ theo m rồi thay vào biểu thức P để giải.

Câu 5. Cho phương trình: x² – (m – 2)x – m² + 3m – 4 = 0

a) Chứng minh rằng phương trình có hai nghiệm phân biệt với mọi m.

b) Tìm m để tỷ số giữa hai nghiệm của phương trình có giá trị tuyệt đối bằng 2.

Hướng dẫn giải

a) Phương trình đã cho có:

$a \cdot c = 1 \cdot \left( { - {m^2} + 3m - 4} \right) = - {\left( {m - \frac{1}{2}} \right)^2} - \frac{7}{4} < 0$

Suy ra phương trình luôn có hai nghiệm phân biệt trái dấu với mọi m.

b) Vì phương trình có hai nghiệm phân biệt trái dấu nên x₁ = –2x₂ hoặc x₂ = –2x₁

(x₁ + 2x₂)(x₂ + 2x₁) = 0 ⇔ x₁x₂ + 2(x₁ + x₂)² = 0

Theo hệ thức Vi-ét ta có:

$\begin{gathered} \left\{ \begin{gathered} {x_1} + {x_2} = m - 2 \hfill \\ {x_1} \cdot {x_2} = - {m^2} + 3m - 4 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Rightarrow {x_1}{x_2} + 2{\left( {{x_1} + {x_2}} \right)^2} = 0 \hfill \\ \hfill \\ \Leftrightarrow - {m^2} + 3m - 4 + 2{\left( {m + 2} \right)^2} = 0 \hfill \\ \hfill \\ \Leftrightarrow {m^2} - 5m + 4 = 0 \hfill \\ \hfill \\ \Leftrightarrow \left[ \begin{gathered} m = 1 \hfill \\ m = 4 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Nhận xét:

Ở bài toán trên nếu học sinh chứng minh phương trình có hai nghiệm phân biệt bằng cách chứng minh Δ > 0 thì việc đi tìm lời giải cho câu b) sẽ rất vất vả.

Vì chứng minh được phương trình có hai nghiệm phân biệt trái dấu suy ra x₁ = –2x₂ và x₂ = –2x₁ do đó vận dụng định lý Vi-ét một cách khéo léo cho ta một lời giải đẹp.

Câu 6. Cho phương trình: 2x² + 2(m + 1)x + m² + 4m + 3 = 0. Tìm m để phương trình có hai nghiệm x₁, x₂ và A = |x₁x₂ – 2(x₁ + x₂)| đạt GTLN.

Hướng dẫn giải

Phương trình đã cho là phương trình bậc hai có:

Δ’ = (m + 1)² – 2(m² + 4m + 3)

= –m² – 6m – 5 = 4 – (m – 3)²

Phương trình đã cho có hai nghiệm x₁, x₂ khi và chỉ khi: Δ’ ≥ 0

⇔ 4 – (m – 3)² ≥ 0

⇔ (m – 3)² ≤ 4

⇔ −2 ≤ m + 3 ≤ 2

⇔ −5 ≤ m ≤ −1

Theo định lý Vi-ét ta có:

$\left\{ \begin{gathered} {x_1} + {x_2} = - \left( {m + 1} \right) \hfill \\ \hfill \\ {x_1} \cdot {x_2} = \frac{{{m^2} + 4m + 3}}{2} \hfill \\ \end{gathered} \right.$

Do đó:

$\begin{gathered} {\text{A }} = \left| {\frac{{{m^2} + 4m + 3}}{2} + 2\left( {m + 1} \right)} \right| \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ = \frac{1}{2}\left| {\left( {{m^2} + m + 3m + 3} \right) + 4\left( {m + 1} \right)} \right| \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ = \frac{1}{2}\left| {\left( {m + 1} \right)\left( {m + 3} \right) + 4\left( {m + 1} \right)} \right| \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ = \frac{1}{2}\left| {\left( {m + 1} \right)\left( {m + 7} \right)} \right| = \frac{1}{2}\left( { - m - 1} \right)\left( {m + 7} \right) \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ \leqslant \frac{1}{2}{\left( {\frac{{ - m - 1 + m + 7}}{2}} \right)^2} = \frac{9}{2} \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

(Vì –m – 1 ≥ 0; m + 7 ≥ 0 và áp dụng bất đẳng thức Cô–si)

Dấu “=” xảy ra ⇔ –m – 1 = m + 7 ⇔ m = –4 (thỏa mãn điều kiện)

Vậy Max A = $\frac{9}{2}$ ⇔ m = –4

Dạng 7. Lập phương trình bậc trình bậc hai một ẩn khi biết hai nghiệm của nó hoặc hai nghiệm có liên quan tới hai nghiệm của một phương trình đã cho

Phương pháp giải

Để lập phương trình bậc hai khi biết hai nghiệm là α và β ta cần phải tính α + β và α⋅β, áp dụng định lý Vi-ét đảo ta có phương trình cần lập là:

x² – (α + β)x + α⋅β = 0

Bài tập vận dụng

Câu 1. Lập phương trình bậc hai có hai nghiệm là hai số cho trong các trường hợp sau:

a) −5 và $\frac{1}{3}$

b) $3 - \sqrt 5$ và $3 + \sqrt 5$

Hướng dẫn giải

a) Ta có: $- 5 + \frac{1}{3} = - \frac{{14}}{3}$ và $\left( { - 5} \right) \cdot \frac{1}{3} = - \frac{5}{3}$

Vậy phương trình bậc hai nhận −5 và $\frac{1}{3}$ làm nghiệm là:

${x^2} + \frac{{14}}{3}x - \frac{5}{3} = 0 \Leftrightarrow 3{x^2} + 14x - 5 = 0$

b) Ta có: $\left( {3 - \sqrt 5 } \right) + \left( {3 + \sqrt 5 } \right) = 6$ và $\left( {3 - \sqrt 5 } \right)\left( {3 + \sqrt 5 } \right) = 4$

Vậy phương trình bậc hai nhận $3 - \sqrt 5$ và $3 + \sqrt 5$ làm nghiệm là:

x² – 6x + 4 = 0

Câu 2. Cho phương trình: x² + px – 5 = 0 có hai nghiệm x₁, x₂. Hãy lập phương trình có hai nghiệm là hai số cho trong các trường hợp sau:

a) –x₁ và –x₂

b) $\frac{1}{{{x_1}}}$ và $\frac{1}{{{x_2}}}$

Hướng dẫn giải

Vì x₁, x₂ là hai nghiệm của phương trình: x² – 6x + 4 = 0 nên ta có:

$\left\{ \begin{gathered} {x_1} + {x_2} = - p \hfill \\ {x_1} \cdot {x_2} = - 5 \hfill \\ \end{gathered} \right.$

a) Ta có: (–x₁) + (–x₂) = –(x₁ + x₂) = p

(–x₁)(–x₂) = x₁x₂ = –5

⇒ –x₁, –x₂ là nghiệm của phương trình: x² – px – 5 = 0

b) Ta có:

$\begin{gathered} \frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} = \frac{{{x_1} + {x_2}}}{{{x_1}{x_2}}} = \frac{{ - p}}{{ - 5}} = \frac{p}{5} \hfill \\ \hfill \\ \frac{1}{{{x_1}}} \cdot \frac{1}{{{x_2}}} = - \frac{1}{5} \hfill \\ \end{gathered}$

Suy ra $\frac{1}{{{x_1}}}$ và $\frac{1}{{{x_2}}}$ là nghiệm của phương trình: ${x^2} - \frac{p}{5}x - \frac{1}{5} = 0$

Câu 3. Gọi x₁, x₂ là hai nghiệm của phương trình: x² – 7x + 3 = 0. Hãy lập phương trình bậc hai có hai nghiệm là: 2x₁ – x₂ và 2x₂ – x₁.

Hướng dẫn giải

Phương trình: x² – 7x + 3 = 0 có ∆ = (–7)² – 34 = 37 > 0 suy ra phương trình có hai nghiệm phân biệt x₁, x₂. Theo hệ thức Vi-ét ta có: $\left\{ \begin{gathered} {x_1} + {x_2} = 7 \hfill \\ {x_1} \cdot {x_2} = 3 \hfill \\ \end{gathered} \right.$

Ta có: 2x₁ – x₂ + 2x₂ – x₁ = x₁ + x₂ = 7

(2x₁ – x₂)(2x₂ – x₁) = 9x₁x₂ – (x₁ + x₂)² = 9⋅3 – 2⋅7² = –71

Vậy 2x₁ – x₂ và 2x₂ – x₁ là nghiệm của phương trình bậc hai: x² – 7x – 71 = 0

Câu 4. Chứng minh rằng tồn tại một phương trình bậc hai có các hệ số hữu tỉ có một nghiệm là: $\frac{{\sqrt 2 - \sqrt 3 }}{{\sqrt 2 + \sqrt 3 }}$

Hướng dẫn giải

Cách 1: Phương trình bậc hai cần tìm có dạng x² + ax + b = 0 (a, b ∈ ℚ)

Ta có:

$\frac{{\sqrt 2 - \sqrt 3 }}{{\sqrt 2 + \sqrt 3 }} = \frac{{{{\left( {\sqrt 2 - \sqrt 3 } \right)}^2}}}{{\left( {\sqrt 2 - \sqrt 3 } \right)\left( {\sqrt 2 + \sqrt 3 } \right)}} = 2\sqrt 6 - 5$

Theo giả thiết $2\sqrt 6 - 5$ là nghiệm của phương trình cần tìm nên:

$\begin{gathered} {\left( {2\sqrt 6 - 5} \right)^2} + a\left( {2\sqrt 6 - 5} \right) + b = 0 \hfill \\ \hfill \\ \Leftrightarrow 49 - 20\sqrt 6 + 2\sqrt 6 a - 5a + b = 0 \hfill \\ \hfill \\ \Leftrightarrow \left( {49 - 5a + b} \right) + \left( {2a - 20} \right)\sqrt 6 = 0{\text{ }}\left( * \right) \hfill \\ \end{gathered}$

Nếu 2a – 20 ≠ 0 thì $\sqrt 6 = \frac{{49 - 5a + b}}{{2a - 20}} \in \mathbb{Q}$ . Vô lý vì $\sqrt 6$ là số vô tỷ

Vậy 2a – 20 = 0 ⇒ a = 10. Thay a =10 vào phương trình (*) ta được b =1.

Vậy phương trình cần tìm là: x² + 10x + 1 = 0

Cách 2: Gọi ${x_1} = \frac{{\sqrt 2 - \sqrt 3 }}{{\sqrt 2 + \sqrt 3 }} = - 2\sqrt 6 - 5$

Ta được:

$\left\{ \begin{gathered} S = {x_1} + {x_2} = - 2\sqrt 6 - 5 + 2\sqrt 6 - 5 = - 10 \hfill \\ P = {x_1} \cdot {x_2} = - \left( {2\sqrt 6 - 5} \right)\left( {2\sqrt 6 + 5} \right) = 1 \hfill \\ \end{gathered} \right.$

Vậy x₁, x₂ là nghiệm của phương trình x² + 10x + 1 = 0

Dạng 8. Tìm hệ thức liên hệ giữa hai nghiệm của phương trình bậc hai không phụ thuộc vào tham số

Phương pháp giải

Để tìm hệ thức liên hệ giữa các nghiệm không phụ thuộc vào tham số trong phương trình bậc hai ta làm như sau:

– Tìm điều kiện để phương trình có hai nghiệm x₁, x₂ là: $\left\{ \begin{gathered} a \ne 0 \hfill \\ \Delta \geqslant 0 \hfill \\ \end{gathered} \right.$

– Theo hệ thức Vi-ét ta được: $\left\{ \begin{gathered} {x_1} + {x_2} = S \hfill \\ {x_1} \cdot {x_2} = P \hfill \\ \end{gathered} \right.\left( * \right)$

– Khử tham số từ hệ (*) ta được hệ thức cần tìm (thông thường ta dùng phương pháp cộng hoặc phương pháp thế).

Bài tập vận dụng

Câu 1. Cho phương trình bậc hai (m – 1)x² – 2mx + m – 4 = 0 (m ≠ 1). Trong trường hợp phương trình có hai nghiệm x₁, x₂, hãy tìm một hệ thức liên hệ giữa các nghiệm không phụ thuộc vào m.

Hướng dẫn giải

Vì phương trình đã cho là phương trình bậc hai nên m ≠ 1

Ta có: Δ’ = m² – (m – 1)(m – 4) = 5m – 4. Phương trình đã cho có hai nghiệm x₁, x₂

$\Leftrightarrow \Delta ' \geqslant 0 \Leftrightarrow 5m - 4 \geqslant 0 \Leftrightarrow m \geqslant \frac{4}{5}$

Theo định lý Vi-ét ta có:

$\left\{ \begin{gathered} {x_1} + {x_2} = S = \frac{{2m}}{{m - 1}} = 2 + \frac{2}{{m - 1}} \hfill \\ \hfill \\ {x_1} \cdot {x_2} = P = \frac{{m - 4}}{{m - 1}} = 1 - \frac{3}{{m - 1}} \hfill \\ \end{gathered} \right.$

Do đó:

$\left\{ \begin{gathered} S = 6 + \frac{6}{{m - 1}} \hfill \\ \hfill \\ 2P = 2 - \frac{6}{{m - 1}} \hfill \\ \end{gathered} \right. \Rightarrow 3S + 2P = 8$

hay 3(x₁ + x₂) + 2x₁x₂ = 8

Chú ý: Ta có thể khử m ở ví dụ trên như sau:

Cách 2:

Từ $S = \frac{{2m}}{{m - 1}} \Rightarrow Sm - S = 2m$

$\Rightarrow m\left( {S - 2} \right) = S \Rightarrow m = \frac{S}{{S - 2}}$

Thế vào $P = \frac{{m - 4}}{{m - 1}}$ ta có:

$\frac{\begin{gathered} \hfill \\ \frac{S}{{S - 2}} - 4 \hfill \\ \end{gathered} }{\begin{gathered} \frac{S}{{S - 2}} - 1 \hfill \\ \hfill \\ \end{gathered} } \Leftrightarrow P = \frac{{ - 3S + 8}}{2} \Leftrightarrow 2P + 3S = 8$

Cách 3: Xét biểu thức aP + bS, trong đó a, b là những số phải xác định để khử tham số m ra khỏi hệ thức đó. Ta có:

$\begin{gathered} aS + bP = \frac{{2am + b\left( {m - 4} \right)}}{{m - 1}} \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array} = \frac{{\left( {2a + b} \right)m - 4m}}{{m - 1}} \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array} = \frac{{\left( {2a + b} \right)m - \left( {2a + b} \right) + 2a - 3b}}{{m - 1}} \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array} = \frac{{\left( {2a + b} \right)\left( {m - 1} \right) + 2a - 3b}}{{m - 1}} \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array} = 2a + b + \frac{{2a - 3b}}{{m - 1}} \hfill \\ \end{gathered}$

Để biểu thức aS + bP không phụ thuộc vào m thì ta phải có:

$2a - 3b = 0 \Rightarrow \left\{ \begin{gathered} a = 3 \hfill \\ b = 2 \hfill \\ \end{gathered} \right.$

Thay vào biểu thức, ta được:

3S + 2P = 2⋅3 + 2 = 8 ⇔ 3(x₁ + x₂) + 2x₁x₂ = 8

Câu 2. Cho phương trình: 8x² – 4(m – 2)x + m(m – 4) = 0. Định m để phương trình có hai nghiệm x₁, x₂. Tìm hệ thức giữa hai nghiệm độc lập với m, suy ra vị trí của các nghiệm với hai số –1 và 1.

Hướng dẫn giải

Phương trình đã cho là phương trình bậc hai có:

Δ’ = 4(m – 2)² – 8m(m – 4) = –4(m² – 4m – 4)

Phương trình có hai nghiệm x₁, x₂ khi và chỉ khi:

$\begin{gathered} \Delta ' \geqslant 0 \Leftrightarrow {m^2} - 4m - 4 \leqslant 0 \hfill \\ \hfill \\ \Leftrightarrow {m^2} - 4m + 4 \leqslant 8 \hfill \\ \hfill \\ \Leftrightarrow {\left( {m - 2} \right)^2} \leqslant 8 \hfill \\ \hfill \\ \Leftrightarrow \left| {m - 2} \right| \leqslant 2\sqrt 2 \hfill \\ \hfill \\ \Leftrightarrow - 2\sqrt 2 \leqslant m - 2 \leqslant 2\sqrt 2 \hfill \\ \hfill \\ \Leftrightarrow 2 - 2\sqrt 2 \leqslant m \leqslant 2 + 2\sqrt 2 \hfill \\ \end{gathered}$

Khi đó theo định lý Vi-ét ta có:

$\left\{ \begin{gathered} {x_1} + {x_2} = \frac{{4\left( {m - 2} \right)}}{8} = \frac{{m - 2}}{2}{\text{ }}\left( 1 \right) \hfill \\ \hfill \\ {x_1} \cdot {x_2} = \frac{{m\left( {m - 4} \right)}}{8}{\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right.$

Từ (1) ta có: m = 2(x₁ + x₂ + 1). Thay vào (2) ta được:

8x₁x₂ = 2(x₁ + x₂ + 1)[2(x₁ + x₂ + 1) – 4]

⇔ 8x₁x₂ = 2(x₁ + x₂ + 1)2(x₁ + x₂ – 1)

⇔ 8x₁x₂ = 4[(x₁ + x₂)² – 1]

⇔ (x₁ + x₂)² – 2x₁x₂ + 1 = 0

⇔ x₁² + x₂² = 1

Vậy hệ thức cần tìm là: x₁² + x₂² = 1

Từ hệ thức trên suy ra:

$\left\{ \begin{gathered} 0 \leqslant x_1^2 \leqslant 1 \hfill \\ 0 \leqslant x_2^2 \leqslant 1 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} \left| {{x_1}} \right| \leqslant 1 \hfill \\ \left| {{x_2}} \right| \leqslant 1 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} - 1 \leqslant {x_1} \leqslant 1 \hfill \\ - 1 \leqslant {x_2} \leqslant 1 \hfill \\ \end{gathered} \right.$

Dạng 9. Chứng minh hệ thức giữa các nghiệm của phương trình bậc hai hoặc hai phương trình bậc hai

Câu 1. Gọi a, b là hai nghiệm của phương trình: x² + px + 1 = 0. b, c là hai nghiệm của phương trình: x² + qx + 2 = 0. Chứng minh hệ thức: (b – c)(b – a) = pq – 6.

Hướng dẫn giải

Vì a, b là hai nghiệm của phương trình x² + px + 1 = 0 nên theo định lý Vi-ét ta có: $\left\{ \begin{gathered} a + b = - p \hfill \\ ab = 1 \hfill \\ \end{gathered} \right.$

Vì p, q là hai nghiệm của phương trình x² + qx + 2 = 0 nên theo định lý Vi-ét ta có: $\left\{ \begin{gathered} b + c = - q \hfill \\ bc = 2 \hfill \\ \end{gathered} \right.$

Ta có: (b – c)(b – a)

= b² – ab – bc + ac

= b² + ab + bc + ac – 2(ab + bc)

= b(a + b) + c(a + c) – 2(ab + bc)

= (a + b)(b + c) – 2(ab + bc)

= (–p)(–q) – 2(1 + 2) = pq – 6

Vậy ta có đpcm.

Câu 2. Chứng minh rằng nếu a₁, a₂ là các nghiệm của phương trình x² + px + 1 = 0 và b₁, b₂ là các nghiệm của phương trình x² + qx + 1 = 0 thì:

(a₁ – b₁)(a₂ – b₁)(a₁ + b₂)(a₂ + b₂) = q² – p²

Hướng dẫn giải

Vì a₁, a₂ là các nghiệm của phương trình x² + px + 1 = 0 nên theo định lý Vi-ét ta có: $\left\{ \begin{gathered} {a_1} + {a_2} = - p \hfill \\ {a_1}{a_2} = 1 \hfill \\ \end{gathered} \right.$

Vì b₁, b₂ là các nghiệm của phương trình x² + qx + 1 = 0 nên theo định lý Vi-ét ta có: $\left\{ \begin{gathered} {b_1} + {b_2} = - q \hfill \\ {b_1}{b_2} = 1 \hfill \\ \end{gathered} \right.$

Ta có: (a₁ – b₁)(a₂ – b₁)(a₁ + b₂)(a₂ + b₂)

= [(a₁ – b₁)(a₂ + b₂)][(a₂ – b₁)(a₁ + b₂)]

= (a₁a₂ + a₁b₂ – a₂b₁ – b₁b₂)(a₁a₂ + a₂b₂– a₁b₁ – b₁b₂)

= (1 +a₁b₂ – a₂b₁ – 1)(1 + a₂b₂ – a₁b₁ – 1)

= (a₁b₂ – a₂b₁)(a₂b₂ – a₁b₁)

= a₁a₂b₂² – a₁²b₁b₂ – a₂²b₁b₂ + a₁a₂b₁²

= b₂² – a₁² – a₂² + b₁²

= (b₁² + b₂² + 2) – (a₁² + a₂² + 2)

= (b₁ + b₂)² – (a₁ + a₂)²

=(–q)² – (–p)² = q² – p²

Câu 3. Cho phương trình ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x₁, x₂ thỏa mãn x₁ = x₂². Chứng minh: b³ + a²c + ac² = 3abc

Hướng dẫn giải

Xét phương trình ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x₁, x₂ thỏa mãn x₁ = x₂²

Cách 1: Theo định lý Vi-ét ta có:

$\begin{gathered} \left\{ \begin{gathered} {x_1} + {x_2} = - \frac{b}{a} \hfill \\ \hfill \\ {x_1} \cdot {x_2} = \frac{c}{a} \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} x_2^2 + {x_2} = - \frac{b}{a} \hfill \\ \hfill \\ x_2^3 = \frac{c}{a} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Rightarrow {\left( {x_2^2 + {x_2}} \right)^3} = - \frac{{{b^3}}}{{{a^3}}} \hfill \\ \hfill \\ \Rightarrow x_2^6 + x_2^3 + 3x_2^3\left( {x_2^2 + {x_2}} \right) = - \frac{{{b^3}}}{{{a^3}}} \hfill \\ \hfill \\ \Rightarrow {\left( {x_2^3} \right)^2} + x_2^3 + 3x_2^3\left( {x_2^2 + {x_2}} \right) = - \frac{{{b^3}}}{{{a^3}}} \hfill \\ \hfill \\ \Rightarrow \frac{{{c^2}}}{{{a^2}}} + \frac{c}{a} + 3 \cdot \frac{c}{a} \cdot \left( { - \frac{b}{a}} \right) = - \frac{{{b^3}}}{{{a^3}}} \hfill \\ \hfill \\ \Rightarrow a{c^2} + {a^2}c - 3abc = - {b^3} \hfill \\ \hfill \\ \Rightarrow {b^3} + {a^2}c + a{c^2} = 3abc \hfill \\ \end{gathered}$

Cách 2: Ta có:

$\begin{gathered} \left( {{x_2} - x_1^2} \right)\left( {{x_1} - x_2^2} \right) = 0 \hfill \\ \hfill \\ \Leftrightarrow {x_1}\left( {{x_2} - x_1^2} \right) + x_2^2\left( {{x_1} - x_2^2} \right) = 0 \hfill \\ \hfill \\ \Leftrightarrow {x_1}{x_2} + x_1^2x_2^2 = x_1^3 + x_2^3 \hfill \\ \hfill \\ \Leftrightarrow {x_1}{x_2} + {\left( {{x_1}{x_2}} \right)^3} = {\left( {{x_1} + {x_2}} \right)^3} - 3\left( {{x_1} + {x_2}} \right){x_1}{x_2} \hfill \\ \hfill \\ \Leftrightarrow - {\left( {{x_1} + {x_2}} \right)^3} + {x_1}{x_2} + {\left( {{x_1}{x_2}} \right)^2} = - 3\left( {{x_1} + {x_2}} \right){x_1}{x_2} \hfill \\ \hfill \\ \Leftrightarrow - {\left( { - \frac{b}{a}} \right)^3} + \frac{c}{a} + {\left( {\frac{c}{a}} \right)^2} = - 3\left( { - \frac{b}{a}} \right)\frac{c}{a}{\text{ }}\left( * \right) \hfill \\ \hfill \\ \Leftrightarrow {b^3} + {a^2}c + a{c^2} = 3abc \hfill \\ \end{gathered}$

Chú ý: Phần đảo ở (*) xảy ra khi $\left\{ \begin{gathered} {x_1} + {x_2} = - \frac{b}{a}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ {x_1} \cdot {x_2} = \frac{c}{a}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right.$ , nghĩa là với điều kiện b³ + a²c + ac² = 3abc ta phải kiểm tra điều kiện có nghiệm của phương trình được thỏa mãn.

Câu 4. Cho các phương trình:

ax² + bx + c = 0 (1)

cx² + dx + a = 0 (2)

Biết rằng phương trình (1) có các nghiệm m và n, phương trình (2) có các nghiệm p và q. Chứng minh rằng: m² + n² + p² + q² ≥ 4.

Hướng dẫn giải

Vì m, n là các nghiệm của phương trình (1) nên theo Vi-ét ta có: $m \cdot n = \frac{c}{a}$

Vì p, q là các nghiệm của phương trình (2) nên theo Vi-ét ta có: $p \cdot q = \frac{a}{c}$

Ta có:

$\begin{gathered} {m^2} + {n^2} \geqslant 2\left| {m \cdot n} \right| = 2\left| {\frac{c}{a}} \right| \hfill \\ \hfill \\ {p^2} + {q^2} \geqslant 2\left| {p \cdot q} \right| = 2\left| {\frac{a}{c}} \right| \hfill \\ \hfill \\ \Rightarrow {m^2} + {n^2} + {p^2} + {q^2} \geqslant 2\left( {\left| {\frac{c}{a}} \right| + \left| {\frac{a}{c}} \right|} \right) \geqslant 2 \cdot 2 = 4 \hfill \\ \end{gathered}$

Vậy m² + n² + p² + q² ≥ 4.

Dạng 10. Xét dấu các nghiệm của phương trình bậc hai, so sánh nghiệm của phương trình bậc hai với một số cho trước

Phương pháp giải

Dùng định lý Vi-ét ta có thể xét dấu các nghiệm của phương trình bậc hai ax² + bx + c = 0 (1) dựa trên các kết quả sau:

– Phương trình có hai nghiệm trái dấu

${x_1} < 0 < {x_2} \Leftrightarrow P = \frac{c}{a} < 0 \Leftrightarrow ac < 0$

– Phương trình có hai nghiệm cùng dấu

$\Leftrightarrow \left\{ \begin{gathered} \Delta \geqslant 0 \hfill \\ P > 0 \hfill \\ \end{gathered} \right.$

– Phương trình có hai nghiệm cùng dương

$0 < {x_1} \leqslant {x_2} \Leftrightarrow \left\{ \begin{gathered} \Delta \geqslant 0 \hfill \\ p > 0 \hfill \\ S > 0 \hfill \\ \end{gathered} \right.$

– Phương trình có hai nghiệm cùng âm

${x_1} \leqslant {x_2} < 0 \Leftrightarrow \left\{ \begin{gathered} \Delta \geqslant 0 \hfill \\ p > 0 \hfill \\ S < 0 \hfill \\ \end{gathered} \right.$

Ngoài ra áp dụng định lý Vi-ét ta có thể so sánh được nghiệm của phương trình bậc hai với một số cho trước.

Bài tập vận dụng

Câu 1. Cho phương trình: x² + 2(m – 2)x – 2m + 1 = 0

a) Tìm m để phương trình có hai nghiệm trái dấu

b) Tìm m để phương trình có hai nghiệm dương

Hướng dẫn giải

Ta có: Δ’ = (m – 2)² – (–2m + 1) = m² – 2m + 3 = (m – 1)² + 2 > 0 với mọi m, suy ra phương trình đã cho luôn có hai nghiệm phân biệt.

Theo định lý Vi-ét ta có:

$\left\{ \begin{gathered} {x_1} + {x_2} = - 2\left( {m - 2} \right) \hfill \\ {x_1} \cdot {x_2} = - 2m + 1 \hfill \\ \end{gathered} \right.$

a) Phương trình có hai nghiệm trái dấu

$\Leftrightarrow {x_1}{x_2} < 0 \Leftrightarrow - 2m + 1 < 0 \Leftrightarrow m > \frac{1}{2}$

b) Phương trình có hai nghiệm dương

$\begin{gathered} \Leftrightarrow \left\{ \begin{gathered} {x_1} + {x_2} > 0 \hfill \\ {x_1}{x_2} > 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} - 2\left( {m - 2} \right) > 0 \hfill \\ - 2m + 1 > 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m < 2 \hfill \\ m < \frac{1}{2} \hfill \\ \end{gathered} \right. \Leftrightarrow m < \frac{1}{2} \hfill \\ \end{gathered}$

Câu 2. Cho phương trình x² – (2m + 3)x + m² + 3m + 2 = 0. Tìm m để phương trình có hai nghiệm đối nhau.

Hướng dẫn giải

Ta có: Δ = (2m + 3)² – 4(m² + 3m + 2)

= 4m² + 12m + 9 – 4m² – 12m – 8 = 1

Δ > 0 với mọi m nên phương trình đã cho có hai nghiệm phân biệt.

Theo định lý Vi-ét ta có:

$\left\{ \begin{gathered} {x_1} + {x_2} = 2m + 3 \hfill \\ {x_1} \cdot {x_2} = {m^2} + 3m + 2 \hfill \\ \end{gathered} \right.$

Phương trình có hai nghiệm đối nhau

$\Leftrightarrow {x_1} + {x_2} = 0 \Leftrightarrow 2m + 3 = 0 \Leftrightarrow m = - \frac{3}{2}$

Câu 3. Cho phương trình: (m – 1)x² – 2(m – 3)x + m – 4 = 0. Xác định m để phương trình có:

a) Hai nghiệm trái dấu

b) Hai nghiệm dương

c) Hai nghiệm âm

d) Hai nghiệm bé hơn 2

Hướng dẫn giải

Phương trình đã cho là phương trình bậc hai ⇔ m – 1 ≠ 0 ⇔ m ≠ 1

Ta có: Δ’ = (m – 3)² – (m – 1)(m – 4)

= m² – 6m + 9 – (m² – 5m + 4) = 5 – m

a) Phương trình có hai nghiệm trái dấu

⇔ x₁ < 0 < x₂ ⇔ ac < 0 ⇔ (m – 1)(m – 4) < 0 ⇔ 1 < m < 4

b) Phương trình có hai nghiệm dương

$\begin{gathered} 0 < {x_1} \leqslant {x_2} \hfill \\ \Leftrightarrow \left\{ \begin{gathered} a \ne 0 \hfill \\ \Delta ' \geqslant 0 \hfill \\ P > 0 \hfill \\ S > 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m \ne 1 \hfill \\ 5 - m \geqslant 0 \hfill \\ \frac{{m - 4}}{{m - 1}} > 0 \hfill \\ \frac{{2\left( {m - 3} \right)}}{{m - 1}} > 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m \ne 1 \hfill \\ m \leqslant 5 \hfill \\ \left[ \begin{gathered} m < 1 \hfill \\ m > 4 \hfill \\ \end{gathered} \right. \hfill \\ \left[ \begin{gathered} m < 1 \hfill \\ m > 3 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \hfill \\ \Leftrightarrow \left[ \begin{gathered} m < 1 \hfill \\ 4 < m \leqslant 5 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

c) Phương trình có hai nghiệm âm

$\begin{gathered} {x_1} \leqslant {x_2} < 0 \hfill \\ \Leftrightarrow \left\{ \begin{gathered} a \ne 0 \hfill \\ \Delta ' \geqslant 0 \hfill \\ P > 0 \hfill \\ S < 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m \ne 1 \hfill \\ 5 - m \geqslant 0 \hfill \\ \frac{{m - 4}}{{m - 1}} > 0 \hfill \\ \frac{{2\left( {m - 3} \right)}}{{m - 1}} < 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m \ne 1 \hfill \\ m \leqslant 5 \hfill \\ \left[ \begin{gathered} m < 1 \hfill \\ m > 4 \hfill \\ \end{gathered} \right. \hfill \\ 1 < m < 3 \hfill \\ \end{gathered} \right. \hfill \\ \Leftrightarrow m \in \emptyset \hfill \\ \end{gathered}$

d) Phương trình có hai nghiệm nhỏ hơn

$\begin{gathered} {x_1} \leqslant {x_2} < 2 \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} a \ne 0 \hfill \\ \Delta ' \geqslant 0 \hfill \\ {x_1} - 2 < 0 \hfill \\ {x_2} - 2 < 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m \ne 1 \hfill \\ m \leqslant 5 \hfill \\ \left( {{x_1} - 2} \right)\left( {{x_2} - 2} \right) < 0 \hfill \\ \left( {{x_1} - 2} \right) + \left( {{x_2} - 2} \right) < 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} m \ne 1 \hfill \\ m \leqslant 5 \hfill \\ {x_1}{x_2} - 2\left( {{x_1} + {x_2}} \right) + 4 > 0 \hfill \\ \left( {{x_1} + {x_2}} \right) - 4 < 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} m \ne 1 \hfill \\ m \leqslant 5 \hfill \\ \frac{{m - 4}}{{m - 1}} - \frac{{4\left( {m - 3} \right)}}{{m - 1}} + 4 > 0 \hfill \\ \frac{{2\left( {m - 3} \right)}}{{m - 1}} - 4 < 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} m \ne 1 \hfill \\ m \leqslant 5 \hfill \\ \frac{{m - 4}}{{m - 1}} > 0 \hfill \\ \frac{{ - 2\left( {m + 1} \right)}}{{m - 1}} < 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m \ne 1 \hfill \\ m \leqslant 5 \hfill \\ \left[ \begin{gathered} m < - 4 \hfill \\ m > 1 \hfill \\ \end{gathered} \right. \hfill \\ \left[ \begin{gathered} m < - 1 \hfill \\ m > 1 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left[ \begin{gathered} m < - 4 \hfill \\ 1 < m \leqslant 5 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Câu 4. Cho phương trình: x² + 2(m – 1)x – (m + 1) = 0. Xác định giá trị của m để phương trình có một nghiệm nhỏ hơn 1, một nghiệm lớn hơn 1.

Hướng dẫn giải

Phương trình đã cho là phương trình bậc hai có:

$\begin{gathered} \Delta ' = {\left( {m - 1} \right)^2} + \left( {m + 1} \right) = {m^2} - m + 2 \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ = {\left( {m - \frac{1}{2}} \right)^2} + \frac{7}{4} > 0,{\text{ }}\forall m \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

⇒ Phương trình đã cho có hai nghiệm phân biệt x₁, x₂ (x₁ < x₂)

Theo định lý Vi-ét ta có:

$\left\{ \begin{gathered} {x_1} + {x_2} = - 2\left( {m - 1} \right) \hfill \\ {x_1} \cdot {x_2} = - \left( {m + 1} \right) \hfill \\ \end{gathered} \right.$

Phương trình đã cho có hai nghiệm thỏa mãn

$\begin{gathered} {x_1} < 1 < {x_2} \Leftrightarrow \left\{ \begin{gathered} {x_1} - 1 < 0 \hfill \\ {x_2} - 1 > 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left( {{x_1} - 1} \right)\left( {{x_2} - 1} \right) < 0 \hfill \\ \hfill \\ \Leftrightarrow {x_1}{x_2} - \left( {{x_1} + {x_2}} \right) + 1 < 0 \hfill \\ \hfill \\ \Leftrightarrow - \left( {m + 1} \right) + 2\left( {m - 1} \right) + 1 < 0 \hfill \\ \hfill \\ \Leftrightarrow m - 2 < 0 \Leftrightarrow m < 2 \hfill \\ \end{gathered}$

Câu 5. Cho phương trình: mx² – 2(m – 3)x + m – 4 = 0. Xác định m để phương trình có đúng một nghiệm dương.

Hướng dẫn giải

Ta xét hai trường hợp:

TH1: m = 0, phương trình đã cho có dạng: $6x = 4 \Leftrightarrow x = \frac{2}{3}$ (thỏa mãn bài ra).

TH2: m ≠ 0, phương trình đã cho là phương trình bậc hai. Để phương trình đã cho có đúng một nghiệm dương ta xét các khả năng sau:

– Phương trình có nghiệm kép dương

$\begin{gathered} \Leftrightarrow \left\{ \begin{gathered} \Delta ' = 0 \hfill \\ S > 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} {\left( {m - 3} \right)^2} - m\left( {m - 4} \right) = 0 \hfill \\ \frac{{2\left( {m - 3} \right)}}{m} > 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} - 2m + 9 = 0 \hfill \\ \left[ \begin{gathered} m < 0 \hfill \\ m > 3 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow m = \frac{9}{2} \hfill \\ \end{gathered}$

– Phương trình có một nghiệm bằng 0 còn nghiệm kia lớn hơn 0 tức là:

$\begin{gathered} {x_1} = 0 < {x_2} \hfill \\ \Leftrightarrow \left\{ \begin{gathered} \Delta ' > 0 \hfill \\ P = 0 \hfill \\ S > 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} - 2m + 9 > 0 \hfill \\ \frac{{m - 4}}{m} = 0 \hfill \\ \frac{{2\left( {m - 3} \right)}}{m} > 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m < \frac{9}{2} \hfill \\ m = 4 \hfill \\ \left[ \begin{gathered} m < 0 \hfill \\ m > 3 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \hfill \\ \Leftrightarrow m = 4 \hfill \\ \end{gathered}$

– Phương trình có hai nghiệm trái dấu

⇔ x₁ < 0 < x₂ ⇔ ac < 0 ⇔ m(m – 4) < 0 ⇔ 0 < m < 4

Vậy kết hợp lại các trường hợp ta có phương trình có đúng một nghiệm dương khi m = $\frac{9}{2}$ hoặc 0 < m ≤ 4

Dạng 11. Nghiệm chung của hai hay nhiều phương trình, hai phương trình tương đương

Câu 1. Cho phương trình: ax² + bx + c = 0 cũng có hai nghiệm dương x₁, x₂

a) Chứng minh rằng phương trình cx² + bx + a = 0 cũng có hai nghiệm dương x₃, x₄

b) Chứng minh rằng M = x₁ + x₂ + x₃ + x₄ ≥ 4

Hướng dẫn giải

a) Phương trình ax² + bx + c = 0 cũng có hai nghiệm dương x₁, x₂ nên:

$\begin{gathered} \left\{ \begin{gathered} {b^2} - 4ac \geqslant 0 \hfill \\ {x_1} + {x_2} = - \frac{b}{a} > 0 \hfill \\ {x_1} \cdot {x_2} = \frac{c}{a} > 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} c \ne 0 \hfill \\ {b^2} - 4ac \geqslant 0 \hfill \\ ab < 0 \hfill \\ ac > 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} c \ne 0 \hfill \\ {b^2} - 4ac \geqslant 0 \hfill \\ bc < 0 \hfill \\ ac > 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} c \ne 0 \hfill \\ {b^2} - 4ac \geqslant 0 \hfill \\ {x_3} + {x_4} = - \frac{b}{c} > 0 \hfill \\ {x_3} \cdot {x_4} = \frac{a}{c} > 0 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

⇔ Phương trình cx² + bx + a = 0 cũng có hai nghiệm dương x₃, x₄

b) Nếu α > 0 là nghiệm của phương trình ax² + bx + c = 0 thì aα² + bα + c = 0, khi đó:

$c \cdot {\left( {\frac{1}{\alpha }} \right)^2} + b \cdot \frac{1}{\alpha } + a = c + b\alpha + a{\alpha ^2} = 0$

Nghĩa là $\frac{1}{\alpha } > 0$ là nghiệm của phương trình cx² + bx + a = 0

Ta có:

$\begin{gathered} {\text{M }} = {x_1} + {x_2} + {x_3} + {x_4} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ = \left( {{x_1} + \frac{1}{{{x_1}}}} \right) + \left( {{x_2} + \frac{1}{{{x_2}}}} \right) \geqslant 2 + 2 = 4 \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

Câu 2. Hai phương trình x² + ax + bc = 0 và x² + bx + ac = 0 chỉ có một nghiệm chung (c ≠ 0). Chứng minh rằng hai nghiệm còn lại là nghiệm của phương trình: x² + cx + ab = 0

Hướng dẫn giải

Giả sử phương trình x² + cx + ab = 0 có nghiệm x₀, x₁ và phương trình x² + bx + ac = 0 có nghiệm x₀, x₁ (x₀ là nghiệm chung của hai phương trình nêu trên và x₁ ≠ x₂). Khi đó ta có:

$\begin{gathered} \left\{ \begin{gathered} x_0^2 + a{x_0} + bc = 0 \hfill \\ x_0^2 + b{x_0} + ac = 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Rightarrow \left( {a - b} \right){x_0} - c\left( {a - b} \right) = 0 \hfill \\ \hfill \\ \Rightarrow \left( {a - b} \right)\left( {{x_0} - c} \right) = 0 \Rightarrow {x_0} = c \hfill \\ \end{gathered}$

(giả thiết a ≠ b để x₀ là nghiệm duy nhất của hai phương trình).

Theo định lý Vi-ét ta có:

$\left\{ \begin{gathered} {x_0} + {x_1} = - a \hfill \\ {x_0} \cdot {x_1} = bc \hfill \\ \end{gathered} \right.$ và $\left\{ \begin{gathered} {x_0} + {x_2} = - b \hfill \\ {x_0} \cdot {x_2} = ac \hfill \\ \end{gathered} \right.$

Vì x₀ = c nên x₁ = b và x₂ = a. Mặt khác:

2x₀ + (x₁ + x₂) = –(a + b)

⇒ 2x + (a + b) = –(a + b)

⇒ a + b = –c

Ta có: $\left\{ \begin{gathered} S = {x_1} + {x_2} = a + b \hfill \\ P = {x_1} \cdot {x_2} = ab \hfill \\ \end{gathered} \right.$

Và S² – 4P = (–c)² – 4ac = (a + b)² – 4ac = (a – b)² > 0, do a ≠ b suy ra S² > 4P.

Do đó theo định lý đảo của định lý Vi-ét ta có x₁, x₂ là nghiệm của phương trình x² + cx + ab = 0.

Câu 3. Tìm các giá trị m và n để hai phương trình sau tương đương:

x² + (4m + 3n) – 9 = 0;

x² + (3m + 4n)x + 3n = 0

Hướng dẫn giải

Phương trình x² + (4m + 3n) – 9 = 0 có ac = –9 < 0 nên có hai nghiệm phân biệt.

Để hai phương trình đã cho tương đương thì phương trình x² + (3m + 4n)x + 3n = 0 cũng phải có

hai nghiệm phân biệt và hai phương trình phải có cùng tập nghiệm.

Gọi x₁, x₂ là nghiệm của phương trình x² + (4m + 3n) – 9 = 0 và x₃, x₄ là hai nghiệm của phương trình x² + (3m + 4n)x + 3n = 0. Khi đó:

$\begin{gathered} \left\{ \begin{gathered} {x_1} + {x_2} = {x_3} + {x_4} \hfill \\ {x_1} \cdot {x_2} = {x_3} \cdot {x_4} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} - \left( {4m + 3n} \right) = - \left( {3m + 4n} \right) \hfill \\ - 9 = 3n \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} n = - 3 \hfill \\ - m = - n \hfill \\ \end{gathered} \right. \Leftrightarrow m = n = - 3 \hfill \\ \end{gathered}$

Với m = n = −3 thì hai phương trình đã cho trở thành:

x² – 21x – 9 = 0 và x² – 21x – 9 = 0

Rõ ràng hai phương trình này tương đương.

Câu 4. Xác định m để hai phương trình sau tương đương với nhau:

x² + 2x – m = 0 (1)

2x² + mx + 1 = 0 (2)

Hướng dẫn giải

Hai phương trình đã cho đều là phương trình bậc hai. Gọi Δ’₍₁₎, Δ’₍₂₎ theo thứ tự là các biệt số của phương trình (1), (2).

Ta xét các khả năng sau:

*) Cả hai phương trình đều vô nghiệm: hai phương trình (1) và (2) vô nghiệm khi và chỉ khi:

$\begin{gathered} \left\{ \begin{gathered} {{\Delta '}_{\left( 1 \right)}} \geqslant 0 \hfill \\ {\Delta _{\left( 2 \right)}} \geqslant 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} 1 + m < 0 \hfill \\ {m^2} - 8 < 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m < - 1 \hfill \\ \left| m \right| < 2\sqrt 2 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow - 2\sqrt 2 < m < - 1{\text{ }}\left( 3 \right) \hfill \\ \end{gathered}$

**) Hai phương trình đều có cùng tập nghiệm: Hai phương trình đều có nghiệm khi và chỉ khi:

$\left\{ \begin{gathered} {{\Delta '}_{\left( 1 \right)}} \geqslant 0 \hfill \\ {\Delta _{\left( 2 \right)}} \geqslant 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m \geqslant - 1 \hfill \\ \left[ \begin{gathered} m \leqslant - 2\sqrt 2 \hfill \\ m \geqslant 2\sqrt 2 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow m \geqslant 2\sqrt 2$

Với $m \geqslant 2\sqrt 2$ , gọi x₁, x₂ là nghiệm của phương trình (1). Để hai phương trình có cùng tập nghiệm thì x₁, x₂ cũng là nghiệm của phương trình (2), khi đó ta phải có:

$\left\{ \begin{gathered} {x_1} + {x_2} = - 2 = - \frac{m}{2} \hfill \\ {x_1} \cdot {x_2} = - m = \frac{1}{2} \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m = 4 \hfill \\ m = - \frac{1}{2} \hfill \\ \end{gathered} \right. \Leftrightarrow m \in \emptyset {\text{ }}\left( 4 \right)$

Kết hợp (3) và (4) ta được $- 2\sqrt 2 < m < - 1$ là các giá trị cần tìm.

Dạng 12. Ứng dụng của định lý Vi-ét vào giải các bài toán số học

Câu 1. Giải phương trình x² – mx + n = 0 biết phương trình có hai nghiệm nguyên dương phân biệt và m, n là các số nguyên tố.

Hướng dẫn giải

Gọi x₁, x₂ là các nghiệm của phương trình đã cho. Theo định lý Vi-ét ta có:

$\left\{ \begin{gathered} {x_1} + {x_2} = m \hfill \\ {x_1} \cdot {x_2} = n \hfill \\ \end{gathered} \right.$

Do m, n là các số nguyên tố suy ra x₁ = 1, x₂ = n (giả sử x₁, x₂).

Từ x₁ + x₂ = m ⇒ 1 + n = m ⇒ m, n là hai số nguyên tố liên tiếp ⇒ n = 2, m = 3.

Ta có phương trình: x² – 3x + 2 = 0, phương trình này có hai nghiệm là 1 và 2.

Câu 2. Tìm số nguyên m sao cho phương trình mx² – 2(m + 3)x + m + 2 = 0 có hai nghiệm x₁, x₂ thỏa mãn: $F = \frac{1}{{{x_1}}} + \frac{1}{{{x_2}}}$ là số nguyên.

Hướng dẫn giải

Phương trình đã cho có hai nghiệm x₁, x₂

$\begin{gathered} \Leftrightarrow \left\{ \begin{gathered} a \ne 0 \hfill \\ \Delta \geqslant 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m \ne 0 \hfill \\ {\left( {m + 3} \right)^2} - m\left( {m + 2} \right) \geqslant 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} m \ne 0 \hfill \\ 4m + 9 \geqslant 0 \hfill \\ \end{gathered} \right. \Leftrightarrow m \geqslant - \frac{9}{4} \hfill \\ \end{gathered}$

Theo định lý Vi-ét ta có:

$\left\{ \begin{gathered} {x_1} + {x_2} = \frac{{2\left( {m + 3} \right)}}{m} \hfill \\ \hfill \\ {x_1} \cdot {x_2} = \frac{{m + 2}}{m} \hfill \\ \end{gathered} \right.$

Ta có:

$F = \frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} = \frac{{{x_1} + {x_2}}}{{{x_1}{x_2}}} = \frac{{2\left( {m + 3} \right)}}{{m + 2}} = 2 + \frac{2}{{m + 2}}$

F là số nguyên ⇔ m + 2 ∈ Ư(2)

$\Leftrightarrow \left[ \begin{gathered} m + 2 = \pm 2 \hfill \\ m + 2 = \pm 1 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} m = 0 \hfill \\ m = - 4 \hfill \\ m = - 1 \hfill \\ m = 1 \hfill \\ \end{gathered} \right.$

Vì $m \geqslant - \frac{9}{4} \Rightarrow m = 9;m = \pm 1$ là các giá trị cần tìm thỏa mãn bài toán.

Câu 3. Giả sử phương trình x² + ax + b + 1 = 0 có hai nghiệm nguyên dương. Chứng minh rằng a² + b² là hợp số.

Hướng dẫn giải

Để phương trình đã cho có hai nghiệm x₁, x₂ (x₁, x₂ ∈ ℕ*) thì ta phải có:

Δ ≥ 0 ⇔ a² – 4(b + 1) ≥ 0

Theo định lý Vi-ét ta có:

$\left\{ \begin{gathered} {x_1} + {x_2} = - a \hfill \\ {x_1}{x_2} = b + 1 \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} a = - \left( {{x_1} + {x_2}} \right) \hfill \\ b = {x_1}{x_2} - 1 \hfill \\ \end{gathered} \right.$

Ta có:

$\begin{gathered} {a^2} + {b^2} = {\left[ { - \left( {{x_1} + {x_2}} \right)} \right]^2} + {\left( {{x_1}{x_2} - 1} \right)^2} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&\begin{gathered} \hfill \\ = x_1^2 + 2{x_1}{x_2} + x_2^2 + x_1^2x_2^2 - 2{x_1}{x_2} + 1 \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&\begin{gathered} \hfill \\ = x_1^2 + x_2^2 + x_1^2x_2^2 + 1 \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&\begin{gathered} \hfill \\ = \left( {x_1^2 + 1} \right)\left( {x_2^2 + 1} \right) \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

Do x₁, x₂ ∈ ℕ* nên suy ra:

$\left\{ \begin{gathered} x_1^2 + 1 \in \mathbb{N} \hfill \\ x_1^2 + 1 \geqslant 2 \hfill \\ \end{gathered} \right.$ và $\left\{ \begin{gathered} x_2^2 + 1 \in \mathbb{N} \hfill \\ x_2^2 + 1 \geqslant 2 \hfill \\ \end{gathered} \right.$

Vậy a² + b² ∈ ℕ, a² + b² ≥ 4; a² + b² = (x₁² + 1)(x₂² + 1) ⇒ a² + b² là hợp số.

Câu 4. Tìm các số nguyên dương x, y thỏa mãn phương trình: x³ + y³ + 1 = 3xy

Hướng dẫn giải

Đặt u = x + y, v = xy

Ta có: x³ + y³ + 1 = 3xy

⇔ (x + y)³ – 3xy(x + y) + 1 – 3xy = 0

Hay u³ – 3uv + 1 – 3v = 0

⇔ (u + 1)(u² – u + 1) – 3v(u + 1) = 0

⇔ (u + 1)(u² – u + 1 – 3v) = 0

Vì x, y > 0 ⇒ u = x + y > 0 ⇒ u + 1 ≠ 0

Vậy u² – u + 1 – 3v = 0 ⇒ v = $\frac{1}{3}$ (u² – u + 1)

Ta phải tìm x, y nguyên dương sao cho:

$\left\{ \begin{gathered} x + y = u \hfill \\ xy = \frac{1}{3}\left( {{u^2} - u + 1} \right) \hfill \\ \end{gathered} \right.$

Suy ra x, y là hai nghiệm của phương trình bậc hai:

X² – uX + $\frac{1}{3}$ (u² – u + 1) = 0

Ta có: $\Delta = - \frac{1}{3}{\left( {u - 2} \right)^2} < 0$ nếu u ≠ 2. Vậy ta phải có:

$u = x + y = 2 \Rightarrow x = y = \frac{u}{2} = 1$

Câu 5. Tìm các số nguyên a để các phương trình sau có nghiệm nguyên:

a) x² – (a + 5)x + 5a + 2 = 0 (1)

b) x² + ax + 198 = a (2)

Hướng dẫn giải

a) Gọi x₁, x₂ ∈ ℤ là nghiệm của phương trình (1), theo Vi-ét ta có:

$\left\{ \begin{gathered} {x_1} + {x_2} = a + 5 \hfill \\ {x_1} \cdot {x_2} = 5a + 2 \hfill \\ \end{gathered} \right.{\text{ }}\left( * \right)$

Từ (*) ta có $\left\{ \begin{gathered} 5{x_1} + 5{x_2} = 5a + 25 \hfill \\ {x_1} \cdot {x_2} = 5a + 2 \hfill \\ \end{gathered} \right.$

$\begin{gathered} \Rightarrow \left( {{x_1} - 5} \right)\left( {{x_2} - 5} \right) = 2 = 1 \cdot 2 = 2 \cdot 1 \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&{} \end{array}}&\begin{gathered} \hfill \\ \hfill \\ \end{gathered} \end{array} = \left( { - 1} \right) \cdot \left( { - 2} \right) = \left( { - 2} \right) \cdot \left( { - 1} \right) \hfill \\ \end{gathered}$

Suy ra a = 8 hoặc a = 2

b) Ta có:

$\begin{gathered} \left\{ \begin{gathered} {x_1} + {x_2} = - a \hfill \\ {x_1}{x_2} = 198 - a \hfill \\ \end{gathered} \right. \Rightarrow {x_1} + {x_2} - {x_1}{x_2} = - 198 \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&{\begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \hfill \\ \end{gathered} &{ \Leftrightarrow \left( {{x_1} - 1} \right)\left( {{x_2} - 1} \right) = 199} \end{array}} \end{array} \hfill \\ \end{gathered}$

Do 199 là số nguyên tố nên:

(x₁ – 1)(x₂ – 1) = 1⋅199 = 199⋅1 = (–1)⋅(–199) = (–199)⋅(–1)

⇒ a = 198 hoặc a = –2

Dạng 13. Ứng dụng của định lý Vi-ét vào giải phương trình, hệ phương trình.

Câu 1. Giải phương trình: $x\left( {\frac{{5 - x}}{{x + 1}}} \right)\left( {x + \frac{{5 - x}}{{x + 1}}} \right) = 6{\text{ }}\left( 1 \right)$

Hướng dẫn giải

Ta có ĐKXĐ: x ≠ 1.

Đặt $u = x\left( {\frac{{5 - x}}{{x + 1}}} \right),v = x + \frac{{5 - x}}{{x + 1}}$

⇒ u + v = 5 (2)

Từ (1) và (2) ⇒ $\left\{ \begin{gathered} u + v = 5 \hfill \\ uv = 6 \hfill \\ \end{gathered} \right.$ ⇒ u, v là nghiệm của phương trình:

$\begin{gathered} {t^2} - 5t + 6 = 0 \Rightarrow {t_1} = 3;{t_2} = 2 \hfill \\ \hfill \\ \Rightarrow \left[ \begin{gathered} \left\{ \begin{gathered} u = 3 \hfill \\ v = 2 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} u = 2 \hfill \\ v = 3 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} x\left( {\frac{{5 - x}}{{x + 1}}} \right) = 3 \hfill \\ \hfill \\ x + \frac{{5 - x}}{{x + 1}} = 2 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} x\left( {\frac{{5 - x}}{{x + 1}}} \right) = 2 \hfill \\ \hfill \\ x + \frac{{5 - x}}{{x + 1}} = 3 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} \left[ \begin{gathered} {x^2} - 2x + 3 = 0 \hfill \\ {x^2} - 3x + 2 = 0 \hfill \\ \end{gathered} \right. \hfill \\ x \ne - 1 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} x = 1 \hfill \\ x = 2 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Vậy phương trình đã cho có nghiệm {1; 2}

Câu 2. Giải phương trình: $\sqrt {1 - x} + \sqrt {4 + x} = 3$

Hướng dẫn giải

ĐKXĐ: −4 ≤ x ≤ 1

Đặt $u = \sqrt {1 - x} ,v = \sqrt {4 + x}$ ta có:

$\left\{ \begin{gathered} u + v = 3 \hfill \\ {u^2} + {v^2} = 5 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} u + v = 3 \hfill \\ {\left( {u + v} \right)^2} - 2uv = 5 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} u + v = 3 \hfill \\ uv = 2 \hfill \\ \end{gathered} \right.$

Suy ra u, v là hai nghiệm của phương trình:

$\begin{gathered} {X^2} - 3X + 2 = 0 \Rightarrow {X_1} = 1;{X_2} = 2 \hfill \\ \hfill \\ \Rightarrow \left[ \begin{gathered} u = 1 \hfill \\ u = 2 \hfill \\ \end{gathered} \right. \Rightarrow \left[ \begin{gathered} \sqrt {1 - x} = 1 \hfill \\ \sqrt {1 - x} = 2 \hfill \\ \end{gathered} \right. \Rightarrow \left[ \begin{gathered} x = 0 \hfill \\ x = - 3 \hfill \\ \end{gathered} \right.{\text{ }}\left( {TM\rlap{--} DK} \right) \hfill \\ \end{gathered}$

Vậy phương trình đã cho có tập nghiệm S = {–3; 0}

Câu 3. Cho phương trình:

$\sqrt {3 + x} + \sqrt {6 - x} - \sqrt {\left( {3 + x} \right)\left( {6 - x} \right)} = m$

a) Giải phương trình khi m = 3

b) Tìm m để phương trình có nghiệm.

Hướng dẫn giải

ĐKXĐ: −3 ≤ x ≤ 6

Đặt $u = \sqrt {3 + x} ,v = \sqrt {6 - x}$ , ta có:

$\left\{ \begin{gathered} u + v - uv = m \hfill \\ {u^2} + {v^2} = 9 \hfill \\ u,v > 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} u + v - uv = m{\text{ }}\left( 1 \right) \hfill \\ {\left( {u + v} \right)^2} - 2uv = 9{\text{ }}\left( 2 \right) \hfill \\ u,v > 0 \hfill \\ \end{gathered} \right.$

Từ (1) suy ra: uv = (u + v) – m thay vào (2) ta có phương trình:

(u + v)² – 2(u + v) + 2m – 9 = 0 (3)

a) Với m = 3 thì từ (3) ta có: u + v = −1 (loại) hoặc u + v = 3 ⇒ uv = 0 ⇒ u, v là nghiệm của phương trình:

$\begin{gathered} {X^2} - 3X = 0 \hfill \\ \hfill \\ \Rightarrow \left[ \begin{gathered} X = 0 \hfill \\ X = 3 \hfill \\ \end{gathered} \right. \Rightarrow \left[ \begin{gathered} \sqrt {3 + x} = 0 \hfill \\ \sqrt {3 + x} = 3 \hfill \\ \end{gathered} \right. \Rightarrow \left[ \begin{gathered} x = - 3 \hfill \\ x = 6 \hfill \\ \end{gathered} \right.\left( {TM\rlap{--} DK} \right) \hfill \\ \end{gathered}$

Vậy với m = 3 thì phương trình đã cho có tập nghiệm S = {–3; 6}

b) Xét phương trình:

(u + v)² – 2(u + v) + 2m – 9 = 0 (3)

Phương trình đã cho có nghiệm khi và chỉ khi phương trình (3) có nghiệm không âm

$\begin{gathered} \Leftrightarrow \left\{ \begin{gathered} \Delta ' \geqslant 0 \hfill \\ S \geqslant 0 \hfill \\ P \geqslant 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} 10 - 2m \geqslant 0 \hfill \\ 4 > 0 \hfill \\ 2m - 9 \geqslant 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m \leqslant 5 \hfill \\ m \geqslant \frac{9}{2} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \frac{9}{2} \leqslant m \leqslant 5 \hfill \\ \end{gathered}$

Câu 4. Giải hệ phương trình:

$\left\{ \begin{gathered} \frac{1}{{x - 2y}} + x + 2y = 5 \hfill \\ \hfill \\ \frac{{x + 2y}}{{x - 2y}} = 6 \hfill \\ \end{gathered} \right.$

Hướng dẫn giải

Đặt $u = \frac{1}{{x + 2y}},v = x + 2y$ (ĐK: x ≠ ±2y).

Ta có: $\left\{ \begin{gathered} u + v = 5 \hfill \\ uv = 6 \hfill \\ \end{gathered} \right.$ ⇒ u, v là nghiệm của phương trình:

${t^2} - 5t + 6 = 0 \Rightarrow \left[ \begin{gathered} \left\{ \begin{gathered} u = 2 \hfill \\ v = 3 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} u = 3 \hfill \\ v = 2 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Rightarrow \left[ \begin{gathered} \left\{ \begin{gathered} x = \frac{7}{4} \hfill \\ y = \frac{5}{8} \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} x = \frac{7}{6} \hfill \\ y = \frac{5}{{12}} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right.{\text{ }}\left( {TM} \right)$

Câu 5. Giải hệ phương trình:

$\left\{ \begin{gathered} \sqrt x + \sqrt y = 5 \hfill \\ \sqrt {x + 5} + \sqrt {y + 5} = 8 \hfill \\ \end{gathered} \right.$

Hướng dẫn giải

ĐK: x ≥ 0; y ≥ 0

Hệ đã cho

$\begin{gathered} \Leftrightarrow \left\{ \begin{gathered} \left( {\sqrt x + \sqrt {x + 5} } \right) + \left( {\sqrt y + \sqrt {y + 5} } \right) = 13 \hfill \\ \left( {\sqrt {x + 5} - \sqrt x } \right) + \left( {\sqrt {y + 5} - \sqrt y } \right) = 3 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} \left( {\sqrt x + \sqrt {x + 5} } \right) + \left( {\sqrt y + \sqrt {y + 5} } \right) = 13 \hfill \\ \frac{5}{{\sqrt x + \sqrt {x + 5} }} + \frac{5}{{\sqrt y + \sqrt {y + 5} }} = 3 \hfill \\ \end{gathered} \right.{\text{ }}\left( 1 \right) \hfill \\ \end{gathered}$

Đặt $u = \sqrt x + \sqrt {x + 5} \geqslant \sqrt 5$ ; $v = \sqrt y + \sqrt {y + 5} \geqslant \sqrt 5$

Khi đó:

$\left( 1 \right) \Leftrightarrow \left\{ \begin{gathered} u + v = 13 \hfill \\ \frac{1}{u} + \frac{1}{v} = \frac{3}{5} \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} u + v = 13 \hfill \\ \frac{{u + v}}{{uv}} = \frac{3}{5} \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} u + v = 13 \hfill \\ uv = \frac{{65}}{3} \hfill \\ \end{gathered} \right.\left( 2 \right)$

Vậy u, v là nghiệm của phương trình:

${t^2} - 13t + \frac{{65}}{3} = 0 \Leftrightarrow {t_{1,2}} = \frac{{39 \pm \sqrt {741} }}{6}$

Do đó ta có nghiệm của hệ (2) là:

$\left\{ \begin{gathered} u = {t_1} \hfill \\ v = {t_1} \hfill \\ \end{gathered} \right.$ hay $\left\{ \begin{gathered} u = {t_2} \hfill \\ v = {t_2} \hfill \\ \end{gathered} \right.$

Do ${t_2} = \frac{{39 - \sqrt {741} }}{6} < 0$ ⇒ (2) vô nghiệm. Vậy hệ (1) vô nghiệm.

Câu 6. Giải hệ phương trình:

$\left\{ \begin{gathered} \sqrt {{x^2} + {y^2}} + \sqrt {2xy} = 8\sqrt 2 {\text{ }}\left( 1 \right) \hfill \\ \sqrt x + \sqrt y = 4{\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right.$

Hướng dẫn giải

ĐKXĐ: x ≥ 0; y ≥ 0

Đặt $S = \sqrt x + \sqrt y ;P = \sqrt x \cdot \sqrt y = \sqrt {xy}$

Theo bài ra ta có: S = 4 ⇒ x + y = 16 – 2P

Phương trình

$\begin{gathered} \left( 1 \right) \Leftrightarrow \sqrt {{{\left( {x + y} \right)}^2} - 2xy} + \sqrt 2 \cdot \sqrt {xy} = 8\sqrt 2 \hfill \\ \hfill \\ \Leftrightarrow \sqrt {{{\left( {16 - 2P} \right)}^2} - 2{P^2}} + \sqrt 2 P = 8\sqrt 2 \hfill \\ \hfill \\ \Leftrightarrow \sqrt {2\left( {{P^2} - 32P + 128} \right)} = 8\sqrt 2 - \sqrt 2 P \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} P \leqslant 8 \hfill \\ {P^2} - 32P + 128 = {\left( {8 - P} \right)^2} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow P = 4 \hfill \\ \end{gathered}$

⇒ $\sqrt x ,\sqrt y$ là nghiệm của phương trình: t² – 4t + 4 = 0 ⇒ t₁ = t₂ = 2

Vậy ta có: $\left\{ \begin{gathered} \sqrt x = 2 \hfill \\ \sqrt y = 2 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x = 4 \hfill \\ y = 4 \hfill \\ \end{gathered} \right.$ (thỏa mãn ĐKXĐ)

Vậy hệ đã cho có nghiệm (x, y) = (4; 4)

Câu 7. Giải hệ phương trình:

$\left\{ \begin{gathered} {x^2} + {y^2} + 2\left( {x + y} \right) = 23 \hfill \\ x + y + xy = 11 \hfill \\ \end{gathered} \right.$

Hướng dẫn giải

Hệ đã cho $\Leftrightarrow \left\{ \begin{gathered} {\left( {x + y} \right)^2} - 2xy + 2\left( {x + y} \right) = 23 \hfill \\ x + y + xy = 11 \hfill \\ \end{gathered} \right.$

Đặt S = x + y; P = xy hệ đã cho

$\begin{gathered} \Leftrightarrow \left\{ \begin{gathered} {S^2} - 2P + 2S = 23 \hfill \\ S + P = 11 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} {S^2} - 2P + 2S = 23 \hfill \\ 2S + 2P = 22 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Rightarrow {S^2} + 4S - 45 = 0 \hfill \\ \end{gathered}$

Ta có: $\Delta ' = 49 \Rightarrow \left[ \begin{gathered} S = - 9 \hfill \\ S = 5 \hfill \\ \end{gathered} \right. \Rightarrow \left[ \begin{gathered} P = 20 \hfill \\ P = 6 \hfill \\ \end{gathered} \right.$ (Các giá trị này đều thỏa mãn ĐK: S² ≥ 4P)

$\Rightarrow \left[ \begin{gathered} \left\{ \begin{gathered} S = - 9 \hfill \\ P = 20 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} S = 5 \hfill \\ P = 6 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} x = - 4 \hfill \\ y = - 5 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} x = - 5 \hfill \\ y = - 4 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} x = 2 \hfill \\ y = 3 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} x = 3 \hfill \\ y = 2 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right.$

Vậy hệ phương trình đã cho có nghiệm (x; y) ∈ {(–4; –5), (–5; –4), (2; 3), (3; 2)}

Nhận xét: Khi giải hệ phương trình trong đó vai trò của các ẩn trong các phương trình là như nhau và khi ta thay đổi vị trí của các ẩn trong các phương trình thì hệ không thay đổi(hệ đối xứng loại I), ta hướng dẫn học sinh đặt S = x + y, P = xy để đưa hệ về hệ phương trình của S và P, tìm S và P sau đó sử dụng định lý Vi-ét đảo để tìm x và y

Dạng 14. Ứng dụng của định lý Vi-ét vào các bài toán chứng minh đẳng thức, bất đẳng thức, tìm GTLN, GTNN

Phương pháp giải

Học sinh đã được làm quen với bất đẳng thức Cô–si, tuy nhiên ta có thể chứng minh bất đẳng thức này dựa vào định lý Vi-ét:

– Giả sử x₁ + x₂ = S không đổi, còn P = x₁x₂ thay đổi. Từ điều kiện:

$\begin{gathered} {S^2} = 4P \Rightarrow P \leqslant \frac{{{S^2}}}{4} \hfill \\ \hfill \\ \Rightarrow {\text{Max }}P = \frac{{{S^2}}}{4} \Leftrightarrow {x_1} = {x_2} = \frac{S}{2} \hfill \\ \end{gathered}$

Vậy nếu hai số có tổng không đổi thì tích hai số đó lớn nhất khi hai số đó bằng nhau.

– Giả sử x₁ > 0, x₂ > 0 và x₁x₂ = P không đổi còn x₁ + x₂ = S thay đổi. Từ điều kiện:

$\begin{gathered} {S^2} - 4P \geqslant 0 \Rightarrow \left( {S - 2\sqrt P } \right)\left( {S + 2\sqrt P } \right) \geqslant 0 \hfill \\ \hfill \\ \Rightarrow S - 2\sqrt P \geqslant 0 \Rightarrow S \geqslant 2\sqrt P \hfill \\ \end{gathered}$

Vậy ${\text{Min }}S = 2\sqrt P \Leftrightarrow {x_1} = {x_2} = \sqrt P$

Vậy hai số dương có tích không đổi thì tổng của hai số đó nhỏ nhất khi hai số đó bằng nhau.

Bài tập vận dụng

Câu 1. Cho a và b là các số thực thỏa mãn các điều kiện 6a² + 20a + 15 = 0; 15b² + 20b + 6 = 0; ab ≠ 1. Chứng minh rằng;

$\frac{{{b^3}}}{{a{b^2} - 9ab + {1^3}}} = \frac{6}{{2015}}$

Hướng dẫn giải

Ta ký hiệu các điều kiện như sau:

6a² + 20a + 15 = 0 (1);

15b² + 20b + 6 = 0 (2);

ab ≠ 1 (3).

Dễ thấy các phương trình (1) và (2) đều có hai nghiệm phân biệt.

Do (2) nên b khác 0. Chia hai vế của (2) cho b² ta được:

$6{\left( {\frac{1}{b}} \right)^2} + 20\left( {\frac{1}{b}} \right) + 15 = 0{\text{ }}\left( 4 \right)$

Từ (1), (3) và (4), suy ra a và $\frac{1}{b}$ là hai nghiệm khác nhau của phương trình

6x² + 20x + 15 = 0 (5)

Theo định lí Vi-ét:

$\left\{ \begin{gathered} a + \frac{1}{b} = - \frac{{10}}{3}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \frac{a}{b} = \frac{5}{2}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right.$

Từ đó:

$\begin{gathered} \frac{{a{b^2} - 9ab + {1^3}}}{{{b^3}}} = \frac{a}{b} - 9{\left( {a + \frac{1}{b}} \right)^3} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&\begin{gathered} \hfill \\ = \frac{5}{2} - 9{\left( { - \frac{{10}}{3}} \right)^3} = \frac{{2015}}{6} \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

Suy ra $\frac{{{b^3}}}{{a{b^2} - 9ab + {1^3}}} = \frac{6}{{2015}}$ , điều phải chứng minh.

Nhận xét: Bài toán sử dụng phép ẩn phụ hóa, đưa về các phương trình đối xứng, đồng thời kết hợp với biểu thức đồng bậc ở giả thiết để suy ra điều phải chứng minh.

Ý tưởng: Quan sát giả thiết bài toán, giữa hai phương trình bậc hai có sự đối xứng giữa các hệ số của chúng, tuy nhiên sự khác biệt nằm ở 6a² + 15 và 15b² + 6 vì thế ta sẽ đặt $t = \frac{1}{b}$ khi đó $\left\{ \begin{gathered} 6{a^2} + 20a + 15 = 0 \hfill \\ 6{t^2} + 20t + 15 = 0 \hfill \\ \end{gathered} \right.$ , vì thế ta có được a, t đều là nghiệm của phương trình 6x² + 20x + 15 = 0. Theo định lý Vi-ét ta có:

$\left\{ \begin{gathered} a + t = - \frac{{10}}{3}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ at = \frac{5}{2}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right.$ $\Rightarrow \left\{ \begin{gathered} a + \frac{1}{b} = - \frac{{10}}{3}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \frac{a}{b} = \frac{5}{2}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right.$

Khi có được điều này, ta sẽ khai thác đến biểu thức $\frac{{{b^3}}}{{a{b^2} - 9ab + {1^3}}}$ , đây là một biểu thức đồng bậc ba nên ta sẽ “chia để trị” nên chia cả tử và mẫu cho b³ ta được:

$\begin{gathered} \frac{{{b^3}}}{{a{b^2} - 9ab + {1^3}}} = \frac{1}{\begin{gathered} \frac{a}{b} - 9{\left( {a + \frac{1}{b}} \right)^3} \hfill \\ \hfill \\ \end{gathered} } \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&\begin{gathered} = \frac{1}{\begin{gathered} \frac{5}{2} - 9{\left( { - \frac{{10}}{3}} \right)^3} \hfill \\ \hfill \\ \end{gathered} } = \frac{6}{{2015}} \hfill \\ \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

Suy ra đpcm.

Câu 2. Trong các hình chữ nhật có chu vi bằng 6, tìm hình chữ nhật có diện tích lớn nhất.

Hướng dẫn giải

Gọi độ dài hai cạnh liên tiếp của hình chữ nhật là x₁, x₂ > 0. Ta có: x₁ + x₂ = 3

Đặt x₁x₂ = m là diện tích của hình chữ nhật.

Vậy x₁, x₂ là các nghiệm của phương trình: x² – 3x + m = 0

Phương trình này phải có nghiệm nên Δ = 9 – 4m ≥ 0 ⇔ m ≤ $\frac{9}{4}$ .

Vậy diện tích lớn nhất của hình chữ nhật là $\frac{9}{4}$ ⇔ x₁ = x₂ = $\frac{3}{2}$ .

Khi đó hình chữ nhật trở thành hình vuông.

Câu 3. Chứng minh rằng nếu các số a, b, c thỏa mãn: $\left\{ \begin{gathered} a + b + c = 5 \hfill \\ ab + bc + ca = 8 \hfill \\ \end{gathered} \right.$ thì:

$1 \leqslant a \leqslant \frac{7}{3};{\text{ }}1 \leqslant b \leqslant \frac{7}{3};{\text{ }}1 \leqslant c \leqslant \frac{7}{3}$

Hướng dẫn giải

Ta có: $\left\{ \begin{gathered} a + b + c = 5 \hfill \\ ab + bc + ca = 8 \hfill \\ \end{gathered} \right.$

$\Rightarrow \left\{ \begin{gathered} b + c = 5 - a \hfill \\ bc = 8 - a\left( {b + c} \right) \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} b + c = 5 - a \hfill \\ bc = 8 - a\left( {5 - a} \right) \hfill \\ \end{gathered} \right.$

Các số b, c là nghiệm của phương trình: x² – (5 – a)x + (a² – 5a + 8) = 0

Để phương trình có nghiệm ta phải có Δ ≥ 0

⇔ (5 – a)² – 4(a² – 5a + 8) ≥ 0

⇔ a² – 10a + 25 – 4a² + 20a – 32 ≥ 0

⇔ –3a² + 10a – 7 ≥ 0

⇔ (a – 1)(7 – 3a) ≥ 0

⇔ –1 ≤ a ≤ $\frac{7}{3}$

Chứng minh tương tự ta có:

1 ≤ b ≤ $\frac{7}{3}$ ; 1 ≤ c ≤ $\frac{7}{3}$

Câu 4. Biết rằng các số x, y thỏa mãn điều kiện x + y = 2. Hãy tìm GTNN của F = x³ + y³.

Hướng dẫn giải

Nhận xét: Để giải bài toán trên có rất nhiều cách giải như biến đổi biểu thức F chỉ có một biến, đổi biến số. Tuy nhiên vận dụng định lý Vi-ét cho ta một cách giải mới như sau:

Đặt $\left\{ \begin{gathered} S = x + y \hfill \\ P = xy \hfill \\ \end{gathered} \right.$ ta có:

$\left\{ \begin{gathered} x + y = 2 \hfill \\ {x^3} + {y^3} = F \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} S = 2 \hfill \\ {S^2} - 3SP = F \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} S = 2 \hfill \\ P = \frac{{8 - F}}{6} \hfill \\ \end{gathered} \right.$

Vậy x, y là nghiệm của phương trình:

${t^2} - 2t + \frac{{8 - F}}{6} = 0{\text{ }}\left( * \right)$

x, y tồn tại ⇔ (*) có nghiệm tức là

$\begin{gathered} \Delta ' \geqslant 0 \Leftrightarrow 1 - \frac{{8 - F}}{6} \geqslant 0 \Leftrightarrow F \geqslant 2 \hfill \\ \hfill \\ \Rightarrow {\text{Min }}F = 2 \Leftrightarrow x = y = 1 \hfill \\ \end{gathered}$

Câu 5. Cho các số x, y, z ≠ 0 thỏa mãn điều kiện $\left\{ \begin{gathered} x + y + z = xyz \hfill \\ {x^2} = yz \hfill \\ \end{gathered} \right.$ . Chứng minh rằng x³ ≥ 3.

Hướng dẫn giải

Ta có:

$\left\{ \begin{gathered} x + y + z = xyz \hfill \\ {x^2} = yz \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} y + x = xyz - x = {x^3} - x \hfill \\ yz = {x^2} \hfill \\ \end{gathered} \right.$

Vậy các số y, z là các nghiệm của phương trình: t² + (x³ – x)t + x² = 0 (*)

Do tồn tại x, y, z thỏa mãn điều kiện đầu bài nên phương trình (*) phải có nghiệm

Phương trình (*) có nghiệm

$\begin{gathered} \Leftrightarrow {\left( {{x^3} - x} \right)^2} - 4{x^2} \geqslant 0 \hfill \\ \hfill \\ \Leftrightarrow {x^2}\left[ {{{\left( {1 - {x^2}} \right)}^2} - 4} \right] \geqslant 0 \hfill \\ \hfill \\ \Leftrightarrow {\left( {1 - {x^2}} \right)^2} \geqslant 4 \hfill \\ \hfill \\ \Leftrightarrow \left[ \begin{gathered} 1 - {x^2} \leqslant - 2 \hfill \\ 1 - {x^2} \geqslant 2 \hfill \\ \end{gathered} \right. \Leftrightarrow {x^2} \geqslant 3 \hfill \\ \end{gathered}$

Dạng 15. Vận dụng định lý Vi-ét trong mặt phẳng tọa độ

Phương pháp giải

Vận dụng định lý Vi-ét ta có thể giải một số dạng toán trong mặt phẳng tọa độ như khảo sát hàm số, viết phương trình đường thẳng, xét vị trí tương đối của đường thẳng và Parabol.

Bài tập vận dụng

Câu 1. Cho Parabol (P): $y = \frac{1}{4}{x^2}$

a) Viết phương trình đi qua hai điểm A và B thuộc Parabol có hoành độ lần lượt là x_A = –2; x_B = 4

b) Viết phương trình tiếp tuyến với (P) tại điểm C thuộc (P) có hoành độ là 2.

Hướng dẫn giải

Nhận xét: Hầu hết học sinh và giáo viên khi gặp bài toán trên đều cho lời giải như sau:

a) $\left\{ \begin{gathered} A \in \left( P \right) \hfill \\ {x_A} = - 2 \hfill \\ \end{gathered} \right. \Rightarrow {y_A} = \frac{1}{4} \cdot {\left( { - 2} \right)^2} = 1$ . Vậy A(–2; 1)

$\left\{ \begin{gathered} B \in \left( P \right) \hfill \\ {x_B} = 4 \hfill \\ \end{gathered} \right. \Rightarrow {y_B} = \frac{1}{4} \cdot {4^2} = 4$ . Vậy B(4; 4)

Phương trình đường thẳng AB cần tìm có dạng y = ax + b nên ta có hệ:

$\left\{ \begin{gathered} 1 = - 2a + b \hfill \\ 4 = 4a + b \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} a = \frac{1}{2}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ b = 2\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right.$

Vậy phương trình đường thẳng AB là: $y = \frac{1}{2}x + 2$

b) $\left\{ \begin{gathered} C \in \left( P \right) \hfill \\ {x_C} = 2 \hfill \\ \end{gathered} \right. \Rightarrow {y_C} = \frac{1}{4} \cdot {2^2} = 1$ . Vậy C(2; 1)

Phương trình đường thẳng cần tìm có dạng y = ax + b (d)

C ∈ (d) ⇔ 1 = 2a + b ⇔ b = 1 – 2a ⇒ (d): y = ax + 1 – 2a

Phương trình hoành độ giao điểm của (P) và (d) là:

$\frac{1}{4}$ x² = ax + 1 – 2a

⇔ x² – 4ax – 4 + 8a = 0

Δ’ = 4a² + 4 – 8a = 4(a – 1)²

(d) tiếp xúc với (P)’ ⇔ Δ’ = 0 ⇔ a = 1 ⇒ b = 1 – 2⋅1 = –1

Vậy phương trình tiếp tuyến cần tìm là: y = x – 1

⨂ Nếu vận dụng định lý Vi-ét ta có lời giải đẹp như sau:

a) Phương trình đường thẳng AB cần tìm có dạng y = ax + b.

Phương trình hoành độ giao điểm của (P) và đường thẳng AB là:

$\frac{1}{4}$ x² = ax + b ⇔ x² – 4ax – 4b = 0 (*)

Ta có: x_A = –2; x_B = 4 là nghiệm của phương trình (*), theo hệ thức Vi-ét ta có:

$\left\{ \begin{gathered} {x_A} + {x_B} = 4a \hfill \\ {x_A} \cdot {x_B} = - 4b \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} a = \frac{1}{2}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ b = 2\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right.$

Vậy phương trình đường thẳng AB là: $y = \frac{1}{2}x + 2$

b) Phương trình tiếp tuyến (d) cần tìm có dạng: y = ax + b.

Phương trình hoành độ giao điểm của (d) và (P) là

$\frac{1}{4}$ x² = ax + b ⇔ x² – 4ax – 4b = 0 (*)

Vì (d) và (P) tiếp xúc với nhau nên phương trình (*) có nghiệm kép x₁ = x₂ = 2

Theo Vi-ét ta có:

$\left\{ \begin{gathered} {x_1} + {x_2} = 4a \hfill \\ {x_1} \cdot {x_2} = - 4b \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} a = 1 \hfill \\ b = - 1 \hfill \\ \end{gathered} \right.$

Vậy phương trình tiếp tuyến cần tìm là: y = x − 1

⨂ Qua ví dụ trên ta đưa ra phương pháp viết phương trình đường thẳng dựa vào định lý Vi-ét:

Loại 1: Lập phương trình đường thẳng y = ax + b (a ≠ 0) đi qua hai điểm A(x_A; y_A); B(x_B; y_B) thuộc Parabol y = mx² (m ≠ 0)

Vì đường thẳng và (P) có hai giao điểm nên hoành độ giao điểm là nghiệm của phương trình:

mx² = ax+ b ⇔ mx² – ax – b = 0

Theo Vi-ét ta có: $\left\{ \begin{gathered} {x_A} + {x_B} = \frac{a}{m}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ {x_A} \cdot {x_B} = - \frac{b}{m}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right.$ ⇒ tìm được a, b

Loại 2: Lập phương trình đường thẳng (d) tiếp xúc với (P) tại điểm M(x_M; y_M)

Do (d) và (P) có một điểm chung duy nhất nên phương trình mx² – ax – b = 0 có nghiệm kép x₁ = x₂

Theo Vi-ét ta có: $\left\{ \begin{gathered} {x_1} + {x_2} = \frac{a}{m}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ {x_1} \cdot {x_2} = - \frac{b}{m}\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ \end{gathered} \right.$ ⇒ tìm được a, b

Câu 2. Trong cùng mặt phẳng tọa độ Oxy, cho (P): y = x² và đường thẳng (D): y = mx + 1. Xác định m để (D) cắt (P) tại hai điểm phân biệt A(x_A; y_A); B(x_B; y_B) và:

a) (x_A – 1)² + (x_B – 1)² đạt GTNN

b) Độ dài AB ngắn nhất.

Hướng dẫn giải

Ta có phương trình hoành độ giao điểm của (D) và (P):

x² = mx + 1 ⇔ x² – mx – 1 = 0 (*)

Phương trình (*) có Δ = m² + 4 > 0 với mọi m nên (*) luôn có hai nghiệm phân biệt với mọi m, suy ra (D) luôn cắt (P) tại hai điểm phân biệt A(x_A; y_A); B(x_B; y_B) trong đó x_A, x_B là hai nghiệm của phương trình (*).

Theo hệ thức Vi-ét ta có: $\left\{ \begin{gathered} {x_A} + {x_B} = m \hfill \\ {x_A} \cdot {x_B} = - 1 \hfill \\ \end{gathered} \right.$

a) (x_A – 1)² + (x_B – 1)²

= x_A² – 2x_A + 1 + x_B² – 2x_B + 1

= (x_A + x_B)² – 2x_Ax_B – 2(x_A + x_B) + 2

= m² + 2 – 2m + 2

= (m – 1)² + 3 ≥ 3

Dấu “=” xảy ra khi và chỉ khi m – 1 = 0 ⇔ m = 1

Vậy Min{(x_A – 1)² + (x_B – 1)²} = 3 ⇔ m = 1

b) Do A, B ∈ (D) ⇒ y_A = mx_A + 1; y_B = mx_B + 1

$\begin{gathered} AB = \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ = \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {m{x_A} - m{x_B}} \right)}^2}} \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ = \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2}\left( {{m^2} + 1} \right)} \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ = \sqrt {\left[ {{{\left( {{x_A} - {x_B}} \right)}^2} - 4{x_A}{x_B}} \right]\left( {{m^2} + 1} \right)} \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ = \sqrt {\left( {{m^2} + 4} \right)\left( {{m^2} + 1} \right)} \geqslant \sqrt {4 \cdot 1} = 2 \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

Dấu “=” xảy ra ⇔ m = 0

Vậy độ dài đoạn thẳng AB ngắn nhất khi và chỉ khi m = 0.

Câu 3. Cho (P): y = –x² và đường thẳng (D) có hệ số góc là a đi qua điểm M(–1; –2)

a) Chứng minh rằng với mọi giá trị của a thì (D) luôn cắt (P) tại hai điểm phân biệt A và B

b) Xác định a để A, B nằm về hai phía trục tung.

Hướng dẫn giải

a) Phương trình đường thẳng (D) có hệ số góc là a và đi qua điểm M(–1; –2) là: y = ax + a – 2

Phương trình hoành độ giao điểm của (D) và (P) là:

–x² = ax + a – 2 ⇔ x² + ax + a – 2 = 0 (*)

Phương trình (*) có Δ = a² – 4a + 8 = (a – 2)² + 4 > 0 với mọi a, suy ra phương trình (*) luôn có hai nghiệm phân biệt với mọi a.

Do đó (D) luôn cắt (P) tai hai điểm phân biệt A và B.

b) Để (D) cắt (P) tại hai điểm A và B nằm về hai phía trục tung thì phương trình hoành độ giao điểm phải có hai nghiệm trái dấu ⇔ a – 2 < 0 ⇔ a < 2.

Dạng 16. Ứng dụng của định lý Vi-ét trong các bài toán hình học

Phương pháp giải

Ta đã biết một trong những phương pháp giải các bài toán hình học là “phương pháp đại số”, phương pháp này vận dụng rất có hiệu quả trong các dạng bài tập tính độ dài đoạn thẳng, một số bài toán cực trị hình học. Kết hợp với định lý Vi-ét sẽ cho ta những lời giải hay và thú vị.

Bài tập vận dụng

Câu 1. Cho ΔABC có B = 90°, đường cao BH = 3cm, AC = 7cm. Tính AB, BC.

Hướng dẫn giải

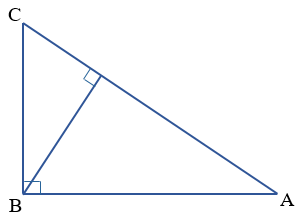
Cách 1: Ta tìm AB, BC thông qua tìm AH, HC

Ta có: $\left\{ \begin{gathered} AH + HC = AC = 7 \hfill \\ AH \cdot HC = B{H^2} = 9 \hfill \\ \end{gathered} \right.$

⇒ AH, HC là nghiệm của phương trình: x² – 7x + 9 = 0

Cách 2: Ta tìm trực tiếp AB, BC dựa vào định lý Pitago và Vi-ét

Ta có: AB² + BC² = AC²

⇔ (AB + BC)² – 2AB⋅BC

⇔ (AB + BC)² – 2AC⋅BH = 49

⇒ (AB + BC)² = 49 + 42 = 91

⇒ AB + BC = $\sqrt {91}$

Mà: AB⋅BC = AC⋅BH = 21

Suy ra: AB, BC là nghiệm của phương trình ${x^2} - \sqrt {91} x + 21 = 0$ , từ đó ta sẽ tìm được AB, BC.

Câu 2. Cho tam giác đều ABC, trên các đoạn thẳng BC, CA, AB lần lượt lấy các điểm I, J, K sao cho K không trùng với A, B và ∠IKJ = 60°. Chứng minh rằng: $AJ \cdot BI \leqslant \frac{{A{B^2}}}{4}$

Hướng dẫn giải

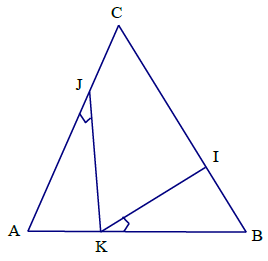
Ta có: ∠IKJ = ∠BAC +∠AJK (góc ngoài tại đỉnh Kcủa ΔAJK)

Mà ∠JKB = ∠JKI + ∠IKB (Vì ∠BAC = ∠JKB = 60°)

⇒ ∠AJK = ∠BKI

Vậy ΔBKI đồng dạng với ΔAJK

⇒ $\frac{{BI}}{{AK}} = \frac{{BK}}{{AJ}}$ hay AJ⋅BI = AK⋅BK

Đặt AK = x₁, BK = x₂ (x₁, x₂ > 0) ta có:

AB = x₁ + x₂ = a (không đổi)

Và AKBK = m (m > 0)

Do đó x₁, x₂ là nghiệm của phương trình x² – ax + m = 0

Phương trình này phải có nghiệm nên

$\Delta = {a^2} - 4m \geqslant 0 \Leftrightarrow m \leqslant \frac{{{a^2}}}{4}$

Vậy $BI \cdot AJ = AK \cdot BK \leqslant \frac{{{a^2}}}{4} = \frac{{A{B^2}}}{4}$

Dấu “=” xảy ra ⇔ ${x_1} = {x_2} = \frac{a}{2}$ tức K là trung điểm của AB.

Câu 3. Cho hình vuông ABCD có cạnh là a và hai điểm M, N theo thứ tự chuyển động trên cạnh BC và CD sao cho 0 ∠MAN = 45°. Tìm GTNN và GTLN của diện tích tam giác AMN.

Hướng dẫn giải

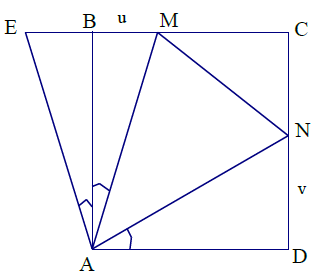
Đặt MB = u; ND = v (0 ≤ u; v ≤ a)

Ta có:

$\begin{gathered} {S_{AMN}} = {S_{ABCD}} - {S_{ABM}} - {S_{ADN}} - {S_{CMN}} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&\begin{gathered} \hfill \\ = {a^2} - \frac{1}{2}au - \frac{1}{2}av - \frac{1}{2}\left( {a - u} \right)\left( {a - v} \right) \hfill \\ \end{gathered} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&\begin{gathered} \hfill \\ = \frac{1}{2}\left( {{a^2} - uv} \right){\text{ }}\left( 1 \right) \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

Trên tia đối của tia BM lấy điểm E sao cho BE = ND = v.

Ta có: ∆ABE = ∆AND (g.g)

⇒ AE = AN và ∠EBA = ∠DAN

⇒ ∠EAM = ∠EAB + ∠BAM = ∠BAM + ∠DAN = 45° = ∠MAN

⇒ ∆AME = ∆AMN (c.g.c)

⇒ MN = ME = u + v

∆CMN có: MN² + CM² + CN²

⇔ (u + v)² = (a – u)² + (a – v)²

⇔ a(u + v) = a² – uv

Đặt t = a² – uv, từ (1) ta có ${S_{AMN}} = \frac{{at}}{2}$

Do đó tìm GTLN và GTNN của S_AMN là tìm GTLN, GTNN của t

Ta có: $\left\{ \begin{gathered} u + v = t \hfill \\ av = {a^2} - at \hfill \\ \end{gathered} \right.$

⇒ u, v là nghiệm của phương trình X² – tX + a² – at = 0 (*)

Phương trình (*) có nghiệm

$\begin{gathered} \Leftrightarrow \Delta = {t^2} + 4a{t^2} - {a^2} \geqslant 0 \hfill \\ \hfill \\ \Leftrightarrow t \geqslant 2a\left( {\sqrt 2 - 1} \right){\text{ }}\left( {{\text{do }}t \geqslant 0} \right) \hfill \\ \end{gathered}$

Khi $t = 2a\left( {\sqrt 2 - 1} \right)$ thì phương trình (*) có nghiệm kép

${t_1} = {t_2} = a\left( {\sqrt 2 - 1} \right) \Rightarrow u = v = a\left( {\sqrt 2 - 1} \right)$

Do đó: ${\text{Min }}t = 2a\left( {\sqrt 2 - 1} \right) \Leftrightarrow u = v = a\left( {\sqrt 2 - 1} \right)$

Mặt khác ta có: at = a² – uv ≤ a² (vì u, v ≥ 0) t ≤ a

Khi t = a, phương trình (*) có hai nghiệm phân biệt

${t_1} = a;{t_2} = 0 \Rightarrow \left[ \begin{gathered} {u_1} = a;{v_1} = 0 \hfill \\ {u_2} = 0;{v_2} = a \hfill \\ \end{gathered} \right.$

Vậy ${\text{Max }}t = a \Leftrightarrow {\text{Max }}{S_{AMN}} = \frac{{{a^2}}}{2}$ khi M ≡ B, N ≡ C hoặc M ≡ C, N ≡ D.

Thầy Tú dạy toán

Tổng quan lý thuyết

Hệ thức Vi-ét

Ứng dụng của hệ thức Vi-ét

Nhẩm nghiệm

Tìm hai số biết tổng và tích của chúng

Xác định dấu của nghiệm

Phân dạng bài tập

Dạng 1. Giải phương trình bậc hai bằng cách tính nhẩm nghiệm

Phương pháp giải

Bài tập vận dụng

Dạng 2. Tính giá trị của biểu thức giữa các nghiệm của phương trình bậc hai

Phương pháp giải

Bài tập vận dụng

Dạng 3. Tìm hai số khi biết tổng và tích

Phương pháp giải

Bài tập vận dụng

Dạng 4. Phân tích tam thức bậc hai thành nhân tử

Phương pháp giải

Bài tập vận dụng

Dạng 5. Tìm điều kiện của tham số để phương trình bậc hai có một nghiệm x = x1 cho trước. Tìm nghiệm thứ hai

Phương pháp giải

Bài tập vận dụng

Dạng 6. Xác định tham số để các nghiệm của phương trình bậc hai thỏa mãn hệ một điều kiện cho trước

Phương pháp giải

Bài tập vận dụng

Dạng 7. Lập phương trình bậc trình bậc hai một ẩn khi biết hai nghiệm của nó hoặc hai nghiệm có liên quan tới hai nghiệm của một phương trình đã cho

Phương pháp giải

Bài tập vận dụng

Dạng 8. Tìm hệ thức liên hệ giữa hai nghiệm của phương trình bậc hai không phụ thuộc vào tham số

Phương pháp giải

Bài tập vận dụng

Dạng 9. Chứng minh hệ thức giữa các nghiệm của phương trình bậc hai hoặc hai phương trình bậc hai

Dạng 10. Xét dấu các nghiệm của phương trình bậc hai, so sánh nghiệm của phương trình bậc hai với một số cho trước

Phương pháp giải

Bài tập vận dụng

Dạng 11. Nghiệm chung của hai hay nhiều phương trình, hai phương trình tương đương

Dạng 12. Ứng dụng của định lý Vi-ét vào giải các bài toán số học

Dạng 13. Ứng dụng của định lý Vi-ét vào giải phương trình, hệ phương trình.

Dạng 14. Ứng dụng của định lý Vi-ét vào các bài toán chứng minh đẳng thức, bất đẳng thức, tìm GTLN, GTNN

Phương pháp giải

Bài tập vận dụng

Dạng 15. Vận dụng định lý Vi-ét trong mặt phẳng tọa độ

Phương pháp giải

Bài tập vận dụng

Dạng 16. Ứng dụng của định lý Vi-ét trong các bài toán hình học

Phương pháp giải

Bài tập vận dụng

Dạng 5. Tìm điều kiện của tham số để phương trình bậc hai có một nghiệm x = x₁ cho trước. Tìm nghiệm thứ hai