Tìm m để hàm số có cực trị thỏa mãn điều kiện cho trước là một bài toàn phổ biến trong chương trình toán lớp 12 và trong kỳ thi THPT Quốc Gia. Để giúp các bạn học sinh nắm rõ dạng toán này, bài viết dưới đây sẽ trình bày hơn 10 loại bài tập hay gặp nhất và cách giải kèm tài liệu phía cuối bài viết.
Phương pháp
– Bước 1: Hàm số đạt cực đại (cực tiểu) tại điểm x0 thì f’ (x0) = 0, tìm được tham số.
– Bước 2: Với giá trị tham số tìm được, ta thế vào hàm số ban đầu để thử lại.
Phân dạng bài tập
Dạng 1: Tìm m để hàm số có 3 cực trị
Phương pháp giải
Chú ý: Đối với hàm bậc ba, ta có thể làm trắc nghiệm như sau:
– Hàm số đạt cực tiểu tại x = x0 ⇔
– Hàm số đạt cực đại tại x = x0 ⇔
Bài tập vận dụng
Câu 1. Tìm m để hàm số đạt cực đại tại điểm x = 3.
A. m = -1.
B. m = -5.
C. m = 5.
D. m = 1.
Hướng dẫn giải
Chọn C
Ta có y’ = x2 – 2mx + m2 – 4 ⇒ y’’ = 2x – 2m
Hàm số đạt cực đại tại x = 3 thì
y’ (3) = 0 ⇔ m2 – 6m + 5 = 0 ⇔ .
Với m = 1, y’’ (3) = 2.3 – 2.1 = 4 > 0 suy ra x = 3 là điểm cực tiểu.
Với m = 5, y’’ (3) = 2.3 – 2.5 = -4 < 0 suy ra x = 3 là điểm cực đại.
Câu 2. Hàm số y = ax3 + x2 – 5x + b đạt cực tiểu tại x = 1 và giá trị cực tiểu bằng 2, giá trị của H = 4a – b là
A. H = 1.
B. H = -1.
C. H = -2.
D. H = 3.
Hướng dẫn giải
Chọn B.
Ta có: y’ = 3ax2 + 2x – 5 ⇒ y’’ = 6ax + 2.
Hàm số đạt cực tiểu tại x = 1 ⇒ y’ (1) = 0 ⇔ a = 1.
Thay a = 1 ta thấy y’’ (1) = 6 + 2 = 8 > 0 nên x = 1 là điểm cực tiểu.
Mặt khác ta có: y (1) = 2 ⇔ 1 + 1 – 5 + b = 2 ⇔ b = 5
Vậy H = 4. 1 – 5 = -1.
Câu 3. Hàm số f (x) = ax3 + bx2 + cx + d đạt cực tiểu tại điểm x = 0, f (0) = 0 và đạt cực đại tại điểm x = 1, f (1) = 1. Giá trị của biểu thức T = a + 2b – 3c + d là
A. T = 2
B. T = 3
C. T = 4
D. T = 0
Hướng dẫn giải
Chọn C.
Ta có f’ (x) = 3ax2 + 2bx + c.
Do hàm số đạt cực tiểu tại điểm x = 0, f (0) = 0 và đạt cực đại tại điểm x = 1, f (1) = 1 nên ta có hệ phương trình
⇔
⇒
⇒ T = 4.
Câu 4. Giá trị của m để hàm số y = x3 + mx – 1 có cực đại và cực tiểu là
A. m ≥ 0
B. m ≤ 0
C. m > 0
D. m < 0
Hướng dẫn giải
Chọn D.
Hàm số y = x3 + mx – 1 có cực đại và cực tiểu khi và chỉ khi y’ = 0 có hai nghiệm phân biệt hay 3x2 + m = 0 có hai nghiệm phân biệt.
Do đó m < 0.
Chú ý: Do hàm bậc ba có đạo hàm là tam thức bậc hai nên có các yêu cầu sau: hàm số có cực trị, hàm số có cực đại và cực tiểu, hàm số có hai cực trị có cách làm giống nhau, tức là y’ = 0 có hai nghiệm phân biệt.
Câu 5. Với giá trị nào của m thì hàm số H10 có cực trị?
A.
B. m < 1
C.
D. m ≤ 1
Hướng dẫn giải
Chọn B.
Ta có: y’ = mx2 + 2x + 1.
Với m = 0, hàm số trở thành y = x2 + x + 7, đồ thị là một parabol nên hiển nhiên có cực trị.
Vậy m = 0 thỏa mãn yêu cầu.
Xét m # 0, để hàm số có cực trị thì y’ = 0 có hai nghiệm phân biệt ⇔ ∆’ > 0
⇔ 1 – m > 0 ⇔ m < 1.
Hợp cả hai trường hợp, khi m < 1 thì hàm số có cực trị.
Chú ý: Với bài toán hỏi “có cực trị” và hệ số của bậc ba (bậc cao nhất) có chứa tham số thì nên chia hai trường hợp: Hệ số của bậc cao nhất bằng 0 và khác 0.
Câu 6. Tìm các giá trị của m để hàm số y = mx3 – 3mx2 – (m – 1) x + 2 không có cực trị.
A.
B.
C.
D.
Hướng dẫn giải
Chọn C.
Ta có: y’ = 3mx2 – 6mx – m + 1.
Với m = 0, hàm số trở thành y = x + 2 là hàm đồng biến trên ℝ nên không có cực trị, nhận m = 0.
Xét m ≠ 0, hàm số không có cực trị khi y’ = 0 có nghiệm kép hoặc vô nghiệm
⇔ ∆’ = 9m2 – 3m (1 – m) ≤ 0 ⇔ 12m2 – 3m ≤ 0 ⇔ .
Hợp cả hai trường hợp, khi thì hàm số không có cực trị.
Câu 7. Số giá trị nguyên của tham số m ∊ [-20; 20/] để hàm số có hai điểm cực trị trái dấu là
A. 18
B. 17
C. 19
D. 16
Hướng dẫn giải
Chọn A.
y’ = (m – 1) x2 + 2(m2 – 4) x + (m2 – 9).
Hàm số có hai điểm cực trị trái dấu khi y’ = 0 có hai nghiệm trái dấu
⇔ (m – 1)(m2 – 9) < 0 ⇔ .
Vậy m ∊ {-20; -19; …; -4; 2}, có 18 giá trị của m.
Câu 8. Có bao nhiêu giá trị nguyên của m để hàm số y = mx3 + m (m – 1) x2 – (m + 1) x -1 có hai điểm cực trị đối nhau?
A. 0
B. 2
C. 1
D. 3
Hướng dẫn giải
Chọn C.
Ta có: y’= 3mx2 + 2m (m – 1) x – (m + 1).
Hàm số có hai điểm cực trị đối nhau ⇔ y’ = 0 có hai nghiệm đối nhau
⇔ ⇔
⇔ m = 1.
Câu 9. Giá trị của m để đồ thị hàm số có hai điểm cực trị có hoành độ dương là
A .
B.
C. m < 0
D.
Hướng dẫn giải
Chọn B.
Ta có: y’ = mx2 + 2 (m – 1) x + m + 2.
Đồ thị hàm số có hai điểm cực trị có hoành độ dương ⇔ y’ = 0 có hai nghiệm phân biệt dương
⇔ ⇔
⇔
⇔
.
Câu 10. Cho hàm số y = x3 + (1 – 2m) x2 + (2 – m) x +m + 2. Các giá trị của m để đồ thì của hàm số có điểm cực đại, cực tiểu, đồng thời hoành độ của điểm cực tiểu nhỏ hơn 1 là
A.
B.
C.
D.
Hướng dẫn giải
Chọn A.
Ta có: y’ = 3x2 + 2 (1 – 2m) x + 2 – m.
Đồ thị hàm số có điểm cực đại, cực tiểu khi phương trình y’ = 0 có hai nghiệm phân biệt
⇔ ∆’ = (1 – 2m)2 – 3 (2 – m) > 0 ⇔ 4m2 – m – 5 > 0 ⇔ .
Khi đó, giả sử x1, x2 (với x1 < x2) là hai nghiệm của phương trình y’ = 0.
Bảng biến thiên
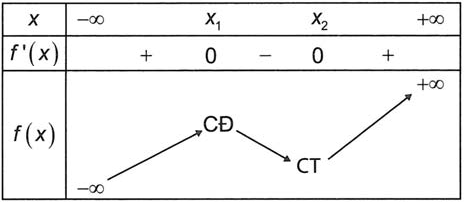
Khi đó, yêu càu bài toán trở thành:
x2 < 1 ⇔ ⇔
.
⇔ ⇔
⇔
.
Kết hợp điều kiện có cực trị thì m < -1 và thỏa mãn yêu cầu.
Chú ý: Có thể dùng Vi-ét để lời giải đơn giản hơn như sau:
Xét x1 < x2 < 1
⇔
⇔
⇔ ⇔
.
Câu 11. Tìm các giá trị thực của tham số m sao cho điểm cực tiểu của đồ thị hàm số y = x3 + x2 + mx – 1 nằm bên phải trục tung.
A. m < 0
B.
C.
D. Không tồn tại
Hướng dẫn giải
Chọn A.
Ta có: y’ = 3x2 + 2x + m.
Đồ thị hàm số có điểm cực tiểu khi phương trình y’ = 0 có hai nghiệm phân biệt
⇔ ∆’ = 1 – 3m > 0 ⇔ (1).
Khi đó, giả sử x1, x2 (với x1 < x2) là nghiệm của phương trình y’ = 0 thì
.
Bảng biến thiên
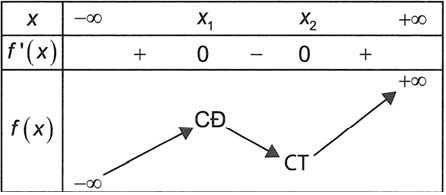
Do nên điểm cực tiểu của đồ thị hàm số y = x3 + x2 + mx – 1 nằm bên phải trục tung
⇔ x1 x2 < 0 ⇔ ⇔ m < 0 (2).
Từ (1), (2) ta có m < 0.
Câu 12. Giá trị của m để hàm số có hai điểm cực trị x1, x2 thỏa mãn yêu cầu x1 < -2 < x2 là
A. m < 2
B. m < 2 hoặc m > 6
C. hoặc m > 6
D.
Hướng dẫn giải
Chọn D
Ta có: y’ = x2 – 2 (m – 2) x + (4m – 8).
Yêu cầu bài toán trở thành
(x1 + 2) (x2+2) < 0 ⇔ (4m – 8) + 4 (m – 2) + 4 < 0 ⇔ .
Câu 13. Gọi S là tập các giá trị thực của tham số m để hàm số y = (x – m) (x2 – 2x – m – 1) có hai điểm cực trị x1, x2 thỏa mãn . Tổng tất cả các phần tử của S bằng
A. 2
B. -2
C. 4
D. 0
Hướng dẫn giải
Chọn A
Ta có: y’ = 3x2 – 2 (m + 2) x + m – 1.
Hàm số có hai điểm cực trị khi y’ = 0 có hai nghiệm phân biệt
⇔ ∆’ = m2 + m + 7 > 0 (luôn đúng).
Theo định lí Vi-ét ta có:
⇒
⇔
⇔
.
Vậy tổng cần tìm bằng 4 + (-2) = 2.
Dạng 2: Tìm m để hàm bậc 4 trùng phương có cực trị
Phương pháp giải
Xét hàm số y = ax4 + bx2 + c, (a ≠ 0), có đạo hàm là y’ = 4ax3 + 2bx = 2x (2ax2 + b).
– Đồ thị hàm số có ba điểm cực trị khi và chỉ khi y’ = 0 có đúng một nghiệm ⇔ ab ≥ 0.
– Đồ thị hàm số có đúng một điểm cực trị hoặc có ba điểm cực trị, và luôn có một điểm cực trị nằm trên trục tung.
Đồ thị hàm số có ba cực trị:
– Nếu a > 0 hàm số có hai điểm cực tiểu và một điểm cực đại;
– Nếu a < 0 hàm số có hai điểm cực đại và một điểm cực tiểu.
Chú ý rằng ba điểm cực trị của đồ thị hàm số luôn tạo thành một tam giác cân.
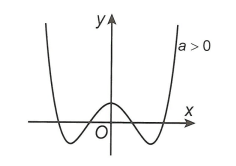
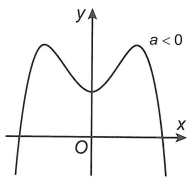
Khi hàm số có một cưc trị:
– a > 0 thì điểm cực trị là điểm cực tiểu;
– a < 0 thì điểm cực trị là điểm cực đại.
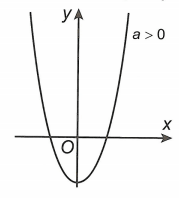
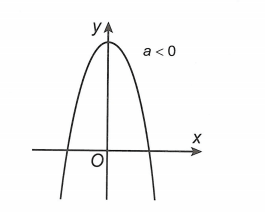
Đồ thị hàm số có nhiều điểm cực trị nhất (bảy cực trị) khi đò thị hàm số f(x) = ax4 + bx2 + c có ba điểm cực trị và đồ thị của nó cắt trục hoành tại bốn điểm phân biệt.
Đồ thị hàm số có ít điểm cực trị nhất (một cực trị) khi đồ thị hàm số f(x) = ax4 + bx2 + c có một điểm cực trị và đồ thị của nó không có điểm chung hoặc chỉ tiếp xúc với trục hoành.
Bài tập vận dụng
Câu 1. Có bao nhiêu số nguyên m ∊ [-20; 20/] để đồ thị hàm số y = mx4 + (m2 – 9) x2 + 1 có ba điểm cực trị?
A. 20
B. 19
C. 18
D. 17
Hướng dẫn giải
Chọn B.
Ta có: y’ = 4mx3 + 2 (m2 – 9) x = .
y’ = 0 ⇔ (1).
Hàm số có ba điểm cực trị khi và chỉ khi y’ = 0 có ba nghiệm phân biệt hay (1) có hai nghiệm phân biệt khác 0 ⇔ 2m (m2 – 9) < 0 ⇔ .
Vậy có 19 giá trị của m thỏa mãn đề bài.
Câu 2. Tập hợp các giá trị của tham số m để đồ thị hàm số y = x4 + 3mx2 – 4 có ba điểm cực trị phân biệt và hoành độ của chúng trong khoảng (-2; 2) là
A.
B.
C.
D.
Hướng dẫn giải
Chọn A.
Ta có y’ = 4x3 + 6mx. Cho y’ = 0 ⇔ (2).
Để thỏa mãn đề bài phương trình (2) có hai nghiệm phân biệt khác 0 và thuộc khoảng (-2; 2) ⇔ ⇔
.
Câu 3. Biết rằng hàm số y = x4 – 2 (m2 + 1) x2 + 2 có điểm cực tiểu. Giá trị lớn nhất của cực tiểu là
A. 1
B. -1
C. 0
D. 2
Hướng dẫn giải
y’ = 4x3 – 4 (m2 + 1) x ⇒ y’ = 0 ⇔ .
Rõ ràng phương trình y’ = 0 luôn có ba nghiệm phân biệt.
Lập bảng biến thiên, dễ thấy là các điểm cực tiểu của đồ thị hàm số.
Giá trị cực tiểu là yCT = 2 – (m2 + 1) = 1 – (m4 + 2m2) ≤ 1 (dấu “=” xảy ra khi m = 0).
Câu 4. Với giá trị nào của k thi hàm số y = kx4 + (k – 1) x2 + 1 – 2k chỉ có một cực trị?
A. 0 < k ≤ 1
B. 0 ≤ k ≤ 1
C.
D.
Hướng dẫn giải
Chọn D.
Với k = 0, hàm số trở thành y = -x2 + 1 có đồ thị là một parabol nên có đúng một cực trị. Do đó
k = 0 thỏa mãn đề bài
Với k ≠ 0. Ta có y’ = 4kx3 + 2(k – 1) x=2x (2kx2 + k – 1).
Để thỏa mãn yêu cầu đề bài thì phương trình 2kx2 + k – 1 = 0 vô nghiệm hoặc có nghiệm
x = 0 ⇔ k (k -1) ≥ 0 ⇔ .
Kết hộ hai trường hợp ta được các giá trị cần tìm là k ≥ 1 hoặc k ≤ 0.
Chú ý: x=0 là nghiệm của phương trình 2kx2 + k – 1 = 0.
Câu 5. Giá trị của m để hàm số y = (m + 1) x4 – 2mx2 + 2m + m4 đạt cực đại tại x = 2 lá
A.
B.
C.
D. ∅
Hướng dẫn giải
Chọn B.
Ta có: y’ = 4(m + 1) x3 – 4mx ⇒ y’’ = 12(m + 1) x2 – 4m.
Để hàm số đạt cực đại tại x = 2 thì y’ (2) = 0 ⇒ 32(m + 1) – 8m = 0 ⇒ .
Với thì y’’ (2) =
, suy ra x = 2 là điểm cực đại.
Chú ý: Nếu f’(x0) = f’’(x0) = 0 thì ta lập bảng biến thiên hoặc bảng xét dấu đạo hàm để kiểm tra.
Bài tập 6. Cho hàm số là một điểm cực trị. Tổng các giá trị của m là
A. 1
B.
C. -1
D.
Hướng dẫn giải
Chọn D.
y’ = 2x3 – 3mx + 1 ⇒ y’’ = 6x2 – 3m
Hàm số đạt cực trị tại điểm x = m ⇒ y’(m) = 0 ⇔ .
Với m = 1, ta có: y’’ (1) = 6 – 3 > 0 x = 1 là điểm cực tiểu (cực trị) nên m = 1 thỏa mãn.
Với , ta có:
là điểm cực tiểu (cực trị) nên
thỏa mãn.
Vậy tổng các giá trị của m thỏa mãn điều kiện trên là .
Bài tập 7: Biết đồ thị hàm số y = ax4 + bx2 + c có hai điểm cực trị là A(0;2 ), B (2; -14 ). Giá trị của y (1) là
A. y (1) = -5
B. y (1) = -4
C. y (1) = -2
D. y (1) = 0
Hướng dẫn giải
Chọn A.
Ta có: y’ = 4ax3 + 2bx.
Các điểm A(0; 2), B(2; -14) thuộc đồ thị hàm số nên (1).
Mặt khác, hàm số đạt cực trị tại điểm x = 2, suy ra 32a + 4b = 0 (2).
Từ (1); (2) ta có y = x4 – 8x2 + 2.
Dễ thấy hàm số có các điểm cực trị là A(0; 2); B(2; -14) nên y = x4 – 8x2 + 2 là hàm số cần tìm.
Khi đó y (1) = -5.
Câu 6. Biết rằng đồ thị hàm số y = x4 – 2 (m – 1) x2 + 3m có A là điểm cực đại và B, C là hai điểm cực điểm. Giá trị nhỏ nhất của biểu thức là
A. 9
B. 8
C. 12
D. 15
Hướng dẫn giải
Chọn C.
Ta có: y’ = 4x3 – 4 (m – 1) x. Cho y’ = 0 ⇔ .
Hàm số có ba điểm cực trị nên m > 1.
Khi đó tọa độ ba điểm cực trị là A (0; 3m), và
. Suy ra OA = 3m,
.
Ta có: =
≥
.
Dấu “=” xảy ra khi 3 (m – 1) = ⇔ m = 2.
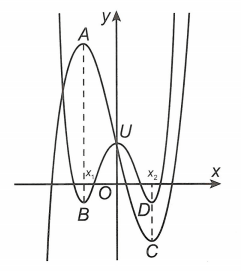
Câu 7. Cho đồ thị hàm số (C1): y = f(x) = x4 + ax2 + b và đồ thị hàm số (C2): y = g(x) = x3 + mx2 + nx + p như hình vẽ dưới. Gọi B, D là hai điểm cực tiểu của (C1) và A, C lần lượt là điểm cực đại và điểm cực tiểu của (C2) (A, C đối xứng nhau qua ⋃ ∊ Oy). Biết hoành độ của A, B bằng nhau và hoành độ của C, D bằng nhau. Có bao nhiêu giá trị nguyên của a để AB ≤ 3?
A. 1
B. 2
C. 3
D. 4
Phân tích: dựa vào đồ thị ta có b = p và m = 0. Khi đó: (C2): y = x3 + nx + b.
Ta cần tìm tung độ của điểm A và B (theo a).
Hướng dẫn giải
Chọn B.
f’(x) = 0 ⇔ và g’(x) = 0 ⇔
.
Theo đề bài ta có a, n < 0 và ⇔
.
Khi đó:
;
.
trong đó
.
Xét AB ≤ 3 ⇔ t4 + 2t3 ≤ 3 ⇔ t ≤ 1 ⇒ ⇔ a ≥ -2.
Do a < 0 nên a ∊ {-2; -1 }.
Câu 8. Cho hai hàm đa thức y = f(x) = g(x) có đồ thị là hai đường cong như hình vẽ. Biết rằng đồ thị hàm số y = f(x) có đúng một điểm cực trị là A, đồ thị hàm số y = g(x) có đúng một điểm cực trị là B (với xA = xB) và . Có bao nhiêu giá trị nguyên của m ∊ (-10; 10) để hàm số
có đúng bảy điểm cực trị?
A. 5
B. 6
C. 3
D. 4
Hướng dẫn giải
Chọn C.
Gọi x1, x2 với x1 < x2 là hoành độ giao điểm của đồ thị y = f(x) và y = g(x) (dựa vào đồ thị đã cho, hai đồ thị chỉ có hai giao điểm đã kể trên, tức là
f(x) – g(x) = 0 ⇔ .
Xét
Ta có: .
Cho h’(x) = 0 ⇔ x = xA = xB. Ta có bảng biến thiên của h(x) như sau
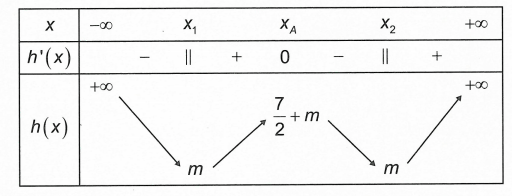
Dựa vào bảng biến thiên của h(x), yêu cầu bài toán trở thành .
Do m nguyên và m ∊ (-10; 10) nên m ∊{-3; -2; -1 }.
Dạng 3. Tìm m để hàm hàm phân thức có cực trị thỏa mãn
Phương pháp giải
Xét . Ta có
.
Gọi M (x0; y0) là điểm cực trị. Khi đó y’(x0) = 0.
Suy ra u’(x0). v (x0) – v’(x0). u(x0) = 0 ⇒ .
Đường cong qua các điểm cực trị (nếu có) của đồ thị hàm số là
.
Nói riêng, đường thẳng qua các điểm cực trị (nếu có) của đồ thị hàm số là
.
Chú ý:
=
=
.
Bài tập vận dụng
Câu 1. Giá trị của m để hàm số có cực trị là:
A.
B.
C.
D.
Hướng dẫn giải
Chọn A.
Điều kiện x ≠ 0. Ta có: .
Hàm số có cực trị khi x2 – 3m +1 = 0 có hai nghiệm phân biệt khác 0
⇔ 3m – 1 > 0 ⇔ .
Câu 2. Giá trị của m để hàm số đạt cực đại tại x = 1 là
A. m = 2
B. m = -1
C. m = -2
D. m = 1
Hướng dẫn giải
Chọn C.
Điều kiện: x ≠ -m.
Ta có: ; y’ = 0 ⇔
.
Bảng biến thiên
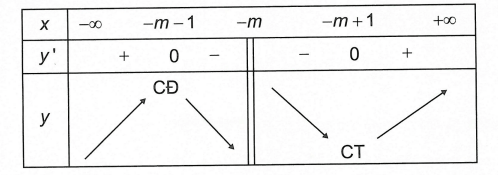
Dựa vào bảng biến thiên, hàm số cực đại tại x = 1 ⇔ -m – 1 = 1. ⇔ m = -2.
Câu 3. Cho hàm số (với p, q là tham số thực). Biết hàm số đạt cực đại tại x = -2, giá trị cực đại bằng -2. Tổng S = p + 2q bằng
A. S = 2
B. S = 0
C. S = 1
D. S = 3
Hướng dẫn giải
Chọn D.
Điều kiện x ≠ 1.
Ta có: .
Hàm số đạt cực đại tại điểm x = -2, giá trị cực đại bằng -2 nên
⇔
.
Thử lại p = q = 1 thỏa mãn nên S = 1 + 2 = 3.
Câu 4. Giá trị của m để khoảng cách giữa hai điểm cực trị của đồ thị hàm số bằng 10 là
A. m = 10
B. m = 8
C. m = 4
D. m = 2
Lời giải
Điều kiện: x ≠ 1.
Ta có: .
Hàm số có hai cực trị khi -x2 + 2x + m = 0 có hai nghiệm phân biệt x1, x2 khác
⇔ ⇔ m > -1.
Khi đó theo định lý Vi-ét ta có .
Đường thẳng qua hai điểm cực trị của đồ thị là (d): y = -2x – m.
Tọa độ hai điểm cực trị của đồ thị A (x1, -2x1 – m), B (x2, -2x2 – m)
⇒ .
Theo yêu cầu của đề bài ta có
(x1 – x2)2 + 4 (x1 – x2)2 = 100 ⇔ (x1 + x2)2 – 4x1x2 = 20
⇔ 4 + 4m = 20 ⇔ m = 4.
B
Câu 5. Có bao nhiêu giá trị nguyên của m để đồ thị hàm số có hai điểm cực trị và tất cả các điểm cực trị đều thuộc hình tròn tâm O, bán kính 6?
A. 10
B. 8
C. 9
D. 7
Hướng dẫn giải
Chọn B.
Điều kiện: x ≠ 0. Ta có: .
Hàm số có hai điểm cực trị khi m > 0. Khi đó y’ = 0 ⇔ .
Tọa độ hai điểm cực trị của đồ thị là ,
.
Theo đề bài ta có OA2 = OB2 = ⇔ 4m2 – 36m + 1 ≤ 0.
Do m ∊ ℤ, m > 0 nên m ∊ {1; 2; 3…; 8}.
Vậy có 8 giá trị nguyên của m thỏa mãn.
Câu 6. Có bao nhiêu giá trị của m để đồ thị hàm số có hai điểm cực trị A, B và ba điểm A, B, C(4; 2) phân biệt thẳng hàng?
A. 0
B. 2
C. 3
D. 1
Hướng dẫn giải
Chọn A.
Điều kiện: x ≠ |m|.
Ta có: .
Cho y’ = 0 ⇔ (x – |m|)2 – 4 = 0 ⇔ .
Do |m| + 2 ≠ |m| – 2, ∀m nên y’ = 0 luôn có hai nghiệm phân biệt.
Do đó đồ thị hàm số luôn có hai điểm cực trị. Khi đó đường thẳng qua hai điểm cực trị là (AB): y = 2x – |m|. Ba điểm A, B, C (4; 2) phân biệt thẳng hàng khi và chỉ khi
⇔
.
Suy ra không có giá trị nào của m thỏa mãn đề bài.
Câu 7. Cho hàm số . Có bao nhiêu giá trị thực của m để đồ thị hàm số (C) có điểm cực đại, cực tiểu A, B sao cho tam giác OAB vuông?
A. 4
B. 2
C. 3
D. 1
Hướng dẫn giải
Ta có: x ≠ 2. Ta có: .
Ta có x2 + 4x + 4 – m2 = 0 ⇔ .
Hàm số có điểm cực đại, cực tiểu khi chỉ và khi m ≠ 0.
Tọa độ các điểm cực trị của đồ thị là
A (-m – 2; -2), B (m – 2; 4m – 2) ⇒ .
Dễ thấy .
Trường hợp 1: Tam giác OAB vuông tại O.
⇔ ⇔ -m2 – 8m + 8 = 0 ⇔
(thỏa mãn)
Trường hợp 2: Tam giác OAB vuông tại A ⇔
⇔ 2m (-m – 2) – 2.4m = 0 ⇔ -m – 2 – 4 = 0 ⇔ m = -6 (thỏa mãn).
Trường hợp 3: Tam giác OAB vuông tại B ⇔
⇔ 2m (m – 2) + (4m – 2) 4m = 0 ⇔ m – 2 + 2 (4m – 2) = 0 ⇔ (thỏa mãn).
Vậy có bốn giá trị thực của m thỏa mãn đề bài.
Câu 8. Cho hàm số (C): với m là tham số. Giá trị thực của m để đồ thị hàm số (C) có hai điểm cực trị A, B sao cho đường thẳng (AB) đi qua hai điểm M (-1; 2) là
A. m = 8
B. m= 6
C. m = 4
D. m = 2
Hướng dẫn giải
Chọn B.
Tập xác định: D = ℝ. Ta có: .
Hàm số có hai điểm cực trị khi và chỉ khi mx2 + 4x – m = 0 có hai nghiệm phân biệt
⇔ ⇔ m ≠ 0.
Đường cong qua hai điểm cực trị có phương trình là .
Ta viết phương trình đường cong dưới dạng .
Ta chọn k sao cho nghiệm của mẫu là nghiệm của tử để có thể rút gọn thành hàm số bậc nhất. Vì x = 0 là nghiệm của mẫu, nên thế x = 0 vào tử ta được -m + k (-m) = 0 ⇒ k = -1.
Với k = -1: ⇒
.
Điểm M (-1; 2) ∊ (AB) ⇒ ⇔ m = 6 (thỏa mãn).
Dạng 4: Tìm m để cực trị của hàm chứa căn thỏa mãn điều kiện
Câu 1. Có bao nhiêu giá trị nguyên của m ∊ [-10; 10/] để hàm số có cực tiểu?
A. 7
B. 16
C. 8
D. 14
Hướng dẫn giải
Chọn C.
Hàm số xác định trên ℝ.
Ta có: và
.
y’ = 0 ⇔ ⇔
(1).
Hàm số có cực tiểu khi và chỉ khi (1) có nghiệm ⇒ m2 – 4 > 0 ⇔ .
Khi đó, (1) có hai nghiệm phân biệt là .
Với m > 2, thì thỏa mãn y’(x1) = 0 và y’’(x1) > 0, suy ra x1 là điểm cực tiểu, nhận m > 2.
Với m < -2, thì thỏa mãn y’(x2) = 0 và y’’(x2) < 0, suy ra x2 là điểm cực đại, loại, do m < -2
Do m nguyên, m > 2 và m ∊ [-10; 10/] nên m ∊ {3; 4; …; 9; 10}.
Chú ý: Để làm trắc nghiệm ta có thể làm như sau: Hàm số đạt cực tiểu khi hệ sau có nghiệm:
⇔
⇒ .
Câu 2. Có bao nhiêu gia trị nguyên của tham số m để đồ thị hàm số có điểm cực trị và tất cả các điểm cực trị thuộc hình tròn tâm O, bán kính
?
A. 4
B. 2
C. 3
D. 1
Hướng dẫn giải
Chọn A.
Tập xác định: D = ℝ.
Ta có: .
Cho y’ = 0 ⇔ , (x ≠ 0).
Xét ⇒
, ∀ x ≠ 0.
Ta có .
Bảng biến thiên
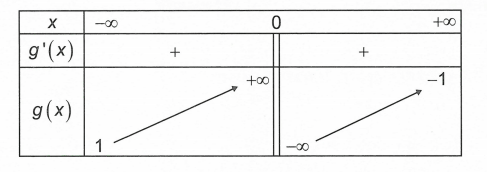
Hàm số có cực trị khi m ∊ ℝ\ [-1; 1/].
Gọi A (a; b) là điểm cực trị của đồ thị hàm số.
Khi đó và
.
Ta có: .
Vậy .
Kết hợp với các điều kiện m ∊ ℤ, m ∊ ℝ\ [-1; 1/] ta được m ∊ {-3; -2; 2; 3}.
Câu 3. Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số có điểm cực trị và tất cả các điểm cực trị thuộc hình tròn tâm O, bán kính
?
A. 16
B. 10
C. 12
D. 4
Hướng dẫn giải
Chọn C.
Tập xác định: D = ℝ
Ta có: , ∀x ∊ ℝ
y’ = 0 ⇔ .
Hàm số có cực trị khi và chỉ khi .
Gọi A (a; b) (a ≠ 0) là điểm cực trị của đồ thị hàm số, khi đó:
và
.
Theo đề bài ta có ⇔
⇔ a2 ≤ 4.
Ta có:
0 < a2 ≤ 4 ⇔ .
Vì m ∊ ℤ và nên m ∊ {-14; -13; …; -4; -3}.
Vậy có 12 giá trị của tham số m thỏa mãn đề bài.
Chú ý: Hàm số không thể đạt cực trị tại điểm x = 0
Dạng 5: Cực trị của hàm bậc cao và hàm lượng giác
Câu 1. Biết rằng tồn tại các số thực a, b, c sao cho hàm số f(x) = x6 + ax4 + bx2 +3x +c đạt cực trị tại điểm x = 2. Hệ số góc tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = -2 là
A. 0
B. -3
C. 3
D. 6
Hướng dẫn giải
Chọn D.
Ta có: f’(x) = 6x5 +4ax3 + 2bx + 3.
Hàm số đạt cực trị tại điểm x = 2 nên f’ (2) = 0 ⇒ 6.25 + 4. a. 23 + 4b + 3 = 0.
Hệ số góc tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = -2 là
f’ (-2) = 0 ⇒ -6. 25 – 4. a. 23 – 4b + 3 = 3 – (6. 25 + 4. A. 23 + 4b) = 6.
Câu 2. Biết rằng tồn tại các số thực a, b, c sao cho hàm số f(x) = a. sin2x – b. cos3x + x + c đạt cực trị tại điểm . Hệ số góc tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ
là
A. 0
B. -1
C. 2
D. -2
Hướng dẫn giải
Chọn C.
Ta có: f’(x) = a. sin2x + 3b. sin3x + 1.
Hàm số đạt cực trị tại điểm , suy ra
.
Hệ số góc tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ là
.
Câu 3. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x8 + (m – 4) x5 – (m2 – 16) x4 + 1 đạt cực tiểu tại điểm x = 0?
A. 8
B. Vô số
C. 7
D. 9
Hướng dẫn giải
Chọn A.
Ta có: y’ = 8x7 + 5 (m – 4) x4 – 4 (m2 – 16) x3 = x3 [8x4 + 5 (m – 4) x – 4 (m2 – 16)/] = x3. g(x)
Với g(x) = 8x4 + 5 (m – 4) x – 4 (m2 – 16). Ta xét các trường hợp sau:
Nếu m2 – 16 = 0 ⇔ m = ± 4.
Khi m = 4 ta có y’ = 8x7 ⇒ x = 0 là điểm cực tiểu.
Khi m = -4 ta có y’ = x4 (8x3 – 40) ⇒ x = 0 không là điểm cực tiểu.
Nếu m2 – 16 ≠ 0 ⇔ m ≠ ± 4 ⇒ g (0) ≠ 0.
Hàm số đạt cực tiểu tại điểm x = 0.
⇔ Đạo hàm đổi dấu từ âm sang dương khi đi qua điểm x = 0.
⇔ .
⇔ -4 (m2 – 16) > 0 ⇔ m2 – 16 < 0 ⇔ -4 < m < 4 ⇒ m ∊ {-3; -2; -1; 0; 1; 2; 3}.
Tổng hợp các trường hợp ta có: m ∊ {-3; -2; -1; 0; 1; 2; 3;4}.
Vậy có tám giá trị nguyên của m thỏa mãn yêu cầu.
Câu 4. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x8 + (m – 2) x5 – (m2 – 4) x4 + 1 đạt cực tiểu x = 0?
A. 3
B. 5
C. 4
D. Vô số
Hướng dẫn giải
Chọn C.
Ta có: y’ = 8x7 + 5 (m – 2) x4 – 4 (m2 – 4) x3 = x3. h(x) với h(x) = 8x4 + 5 (m – 2) x – 4 (m2 – 4).
Ta xét các trường hợp sau:
Nếu m2 – 4 = 0 ⇔ m = ±2.
Khi m = 2 thì y’ = 8x7 ⇒ x = 0 là điểm cực tiểu nên m = 2 thỏa mãn.
Khi m = -2 thì y’ = x4 (8x3 – 20) ⇒ x = 0 không là điểm cực tiểu.
Nếu m2 – 4 ≠ 0 ⇔ m ≠ ±2 ⇒ h (0) ≠ 0.
Hàm số đạt cực tiểu tại điểm x = 0 khi và chỉ khi giá trị đạo hàm đổi dấu từ âm sang dương khi đi qua điểm x = 0.
Do đó
⇒ -4 (m2 – 4) > 0 ⇔ -2 < m < 2 ⇒ m ∊ {-1; 0; 1}.
Tổng hợp các trường hợp ta có m ∊ {-1; 0; 1; 2}.
Vậy có bốn giá trị nguyên của m thỏa mãn yêu cầu.
Dạng 6: Tìm cực trị của hàm số chứa trị tuyệt đối
Phương pháp giải
Bước 1. Tập xác định và tính đạo hàm
Đạo hàm hàm chứa trị tuyệt đối với công thức:
.
Chú ý: .
Bước 2. Giải phương trình đạo hàm bằng 0 và tìm những điểm làm cho đạo hàm không xác định (nhưng hàm số xác định tại những điểm đó).
Bước 3. Lập bảng biến thiên hoặc bảng xét dấu đạo hàm.
Bài tập vận dụng
Câu 1. Số điểm cực đại của hàm số là
A. 1
B. 3
C. 2
D. 0
Hướng dẫn giải
Chọn C.
Hàm số liên tục trên ℝ có .
Hàm số không có đạo hàm tại điểm x = 0.
Khi x < 0 ta có
f’(x) = 0 ⇔ .
Khi x > 0 ta có
f’(x) = 0 ⇔ .
Bảng xét dấu y’:

Vậy hàm số có hai điểm cực đại.
Câu 2. Số điểm cực trị của hàm số y = (x +1) |x – 2| là
A. 1
B. 4
C. 2
D. 3
Hướng dẫn giải
Chọn C.
Ta có đồ thị của hàm số y = (x + 1) (x – 2) như sau.
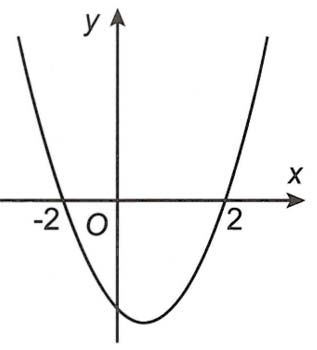
Vì y = (x + 1) |x – 2| =
Nên để vẽ đồ thị hàm số đã cho, ta giữ nguyên đồ
thị y = (x +1) (x – 2) khi x ≥ 2 và lấy đối xứng qua
trục hoành phần đồ thị y = (x + 1) (x – 2) ứng với
x < 2.
Dễ thấy hàm số y = (x + 1) |x – 2| có hai điểm cực trị (xem hình vẽ dưới đây):
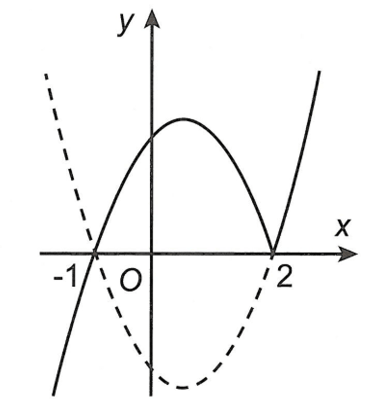
Dạng 7: Định tham số để hàm số chứa dấu trị tuyệt đối có n điểm cực trị
Phương pháp giải
Xét bài toán: Định tham số để đồ thị hàm số y = f(|x|) hoặc y = |f(|x|)| có n điểm cực trị.
– Bước 1. Lập bảng biến thiên của hàm số y = f(x)
– Bước 2: Dựa vào bảng biến thiên, suy ra tham số thỏa mãn yêu cầu đề bài
Bài tập vận dụng
Câu 1. Có bao nhiêu giá trị nguyên của m ∊ [-5; 5/] để hàm số y = |x3 – 6x2 + (9 – m) x + 2m – 2| có 5 điểm cực trị?
A. 6
B. 8
C. 5
D. 7
Hướng dẫn giải
Chọn B
Xét f(x) = x3 – 6x2 + (9 – m) x + 2m – 2
Cho f(x) = 0 ⇔ x3 – 6x2 + (9 – m) x + 2m – 2 = 0
⇔ x3 – 6x2 + 9x – 2 – mx + 2m = 0
⇔ (x – 2) (x2 – 4x + 1 – m) = 0
⇔ .
Hàm số y = |x3 – 6x2 + (9 – m) x+ 2m – 2| có 5 điểm cực trị khi f(x) = 0 có 3 nghiệm phân biệt và chỉ khi x2 – 4x +1 – m = 0 có 2 nghiệm phân biệt khác 2.
⇔ .
Do m nguyên m ∊ [-5; 5/] nên m ∊ { -2; -1; 0; 1; 2; 3; 4; 5}.
Vậy có 8 giá trị của m thỏa mãn đề bài.
Lời bình: Ta có thể nhìn rõ những kết luận này từ việc biến đổi đồ thị.
Từ đồ thị y = f(x) suy ra đồ thị y = |f(x)|
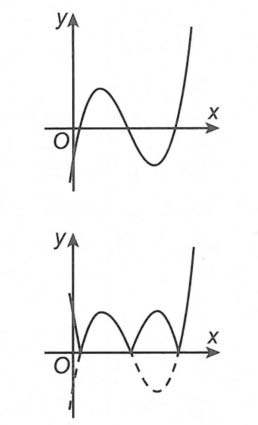
Câu 2. Có bao nhiêu giá trị của m để hàm số y = |x|3 – (2m + 1) x2 + 3m|x| – 5 có 5 điểm cực trị
A.
B.
C.
D.
Hướng dẫn giải
Chọn B.
Xét f(x) = y = x3 – (2m + 1) x2 + 3mx – 5.
Suy ra f’(x) = 3x2 – 2 (2m +1) x + 3m.
Hàm số y = |x|3 – (2m + 1) x2 + 3m|x| – 5 có 5 điểm cực trị khi và chỉ khi hàm số y = f(x) có hai điểm cực trị dương ⇔ f’(x) = 0 có hai nghiệm phân biệt dương
⇔ .
Lời bình: Ta có thể nhìn rõ những kết luận này từ việc biến đổi đồ thị.
Từ đồ thị y = f(x) suy ra đồ thị y = f(|x|)
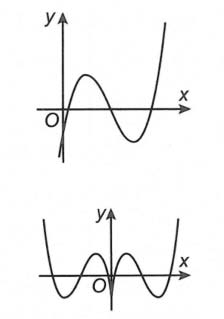
Câu 3. Có bao nhiêu số nguyên của tham số m ∊ (-2021; 2020) để hàm số f(x) = x2 – 2m |x – m + 2020| + 2021 có 3 điểm cực trị?
A. 1009
B. 2020
C. 2019
D. 1008
Hướng dẫn giải
Chọn A.
f’(x) = =
.
Dễ thấy hàm số không có đạo hàm tại điểm x = m – 2020.
Ta có: f’(x) = 0 ⇔ .
⇔ .
Nếu m ≤ 1010 thì f’(x) = 0 ⇔ x = m và không có đạo hàm tại điểm x = m – 2020 nên không có đủ 3 điểm cực trị. Do đó loại trường hợp này.
Nếu m > 1010, ta có bảng xét dấu đạo hàm như sau

Vậy hàm số có 3 điểm cực trị với m > 1010.
Mà m ∊ (-2021; 2020) nên m ∊ {1011; 1012; …; 2019}.
Vậy có 1009 số thỏa mãn đề bài.
Dạng 8: Cho bảng biến thiên, định giá trị tham số để hàm số trị tuyệt đối có n điểm cực trị
Phương pháp giải
Bài toán: Cho bảng biến thiên của hàm số y = f(x) hoặc cho bảng biến thiên, bảng xét dấu của f’(x).
Yêu cầu tìm giá trị của tham số m để hàm số g (x, m) có n điểm cực trị.
Đưa hàm số g (x, m) về hàm số đơn giản hơn (nếu có thể). Sau đó sử dụng các phép biến đổi đồ thị hàm trị tuyệt đối.
Bài tập vận dụng
Câu 1. Cho hàm số y = f(x) liên tục trên ℝ\ {1}, có đạo hàm trên ℝ\ {1} và có bảng biến thiên của hàm số y = f’(x) như sau
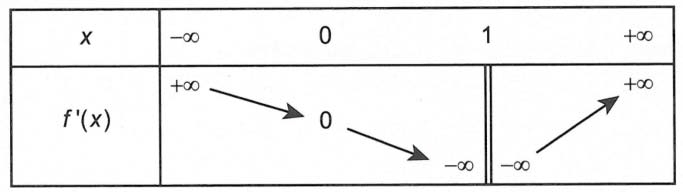
Có bao nhiêu giá trị nguyên của tham số m ∊ [-20; 20/] để hàm số co nhiều điểm cực trị nhất?
A. 21
B. 19
C. 22
D. 20
Hướng dẫn giải
Chọn D.
Số điểm cực trị của bằng với số điểm cực trị của hàm số h(x) = f (|x| – m).
Ta có .
Hiển nhiên hàm số không có đạo hàm tại điểm x = 0.
Cho h’(x) = 0 ⇔ .
Hàm số h(x) = f (|x| – m) có nhiều điểm cực trị nhất khi và chỉ khi h’(x) = 0 có nhiều nghiệm dương nhất hay 0 < m.
Do m nguyên và m ∊ [-20; 20/] nên m ∊ {1; 2; 3; …; 20}.
Câu 2. Cho hàm số y = f(x) có đạo hàm trên ℝ và có bảng biến thiên của hàm số y = f’(x) như sau:
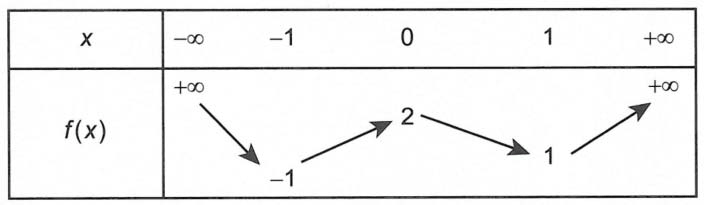
Số giá trị nguyên của tham số m để hàm số g(x) = f (|x4 – 4x2 +m|) có nhiều điểm cực trị nhất?
A. 2
B. 4
C. 3
D. 5
Hướng dẫn giải
Chọn C.
Ta có
Ta có |x4 – 4x2 + m| ≥ 0.
Dựa vào bảng biến thiên, suy ra f’(|x4 – 4x2 +m|) = 0 vô nghiệm (*).
Hàm số g(x) có nhiều điểm cực trị nhất khi g’(x) = 0 có nhiều nghiệm phân biệt nhất.
Kết hợp với (*), ta có hệ phương trình có nhiều nghiệm phân biệt nhất ⇔ x4 – 4x2 + m = 0 có nhiều nghiệm nhất và tất cả các nghiệm đều khác 0 và khác
(vì 4x3 – 8x = 0 luôn có ba nghiệm phân biệt là 0;
) ⇔ m = -x4 + 4x2 có nhiều nghiệm nhất và tất cả các nghiệm đều khác 0 và khác
(**).
Lập bảng biến thiên y = -x4 + 4x2 ta có:
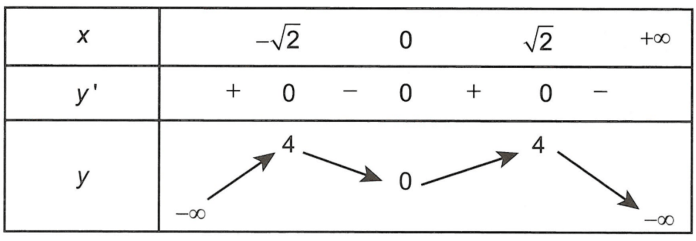
Do đó (**) ⇔ 0 < m < 4.
Vậy có ba giá trị nguyên là m ∊ {1; 2; 3}.
Dạng 9: Cho đồ thị, định tham số để có hàm số có n điểm cực trị
Phương pháp giải
Bước 1. Tìm hàm số đơn giản hơn có cùng số điểm cực trị với hàm số ban đầu
Bước 2. Dựa vào đồ thị, xác định số cực trị của hàm số đơn giản ở bước 1.
Bài tập vận dụng
Câu 1. Cho đường cong như hình vẽ là đồ thị của hàm số y = f(x). Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = (|x + 3|) có 5 điểm cực trị.
A.
B.
C.
D.
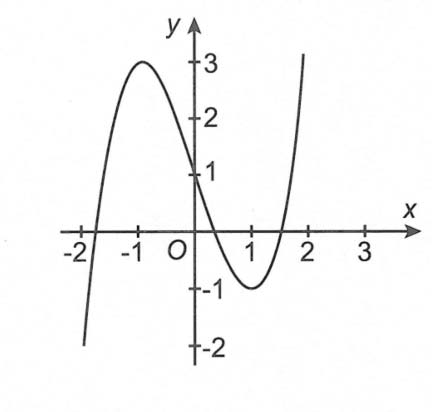
Hướng dẫn giải
Chọn D.
Số điểm cực trị của hàm số y = (|x + 3|) bằng với số điểm cực trị của hàm số g(x) = f (|x| +m).
Ta có .
Dựa vào đồ thị, ta có g’(x) = 0 ⇔ .
(chú ý rằng hàm số g(x) không có đạo hàm tại điểm x = 0).
Hàm số y = (|x + 3|) có 5 điểm cực trị ⇔ g(x) = f (|x| +m) có 5 điểm cực trị ⇔ (*) có 4 nghiệm phân biệt ⇔ -1 – m > 0 ⇔ m < -1.
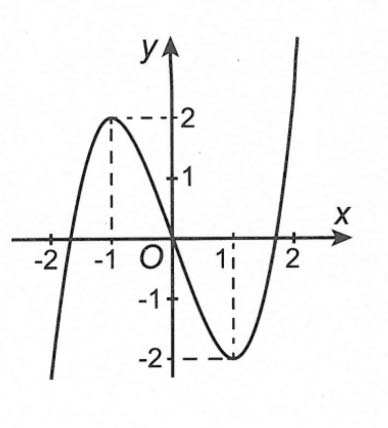
Câu 2. Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình vẽ. Tìm tất cả các giá trị của tham số m để hàm số y = |f(x) + m| có nhiều điểm cực trị nhất.
A. m ∊ (-2; 2)
B. m ∊ [-2; 2/]
C. m ∊ (-1; 1)
D. m ∊ [-1; 1/]
Hướng dẫn giải
Chọn A.
Đồ thị hàm số y = |f(x) + m| có nhiều điểm cực trị nhất khi và chỉ khi y = f(x) + m cắt trục hoành tại nhiều điểm nhất ⇔ -2 < m < 2.
Câu 3. Cho hàm số y = f(x) có đồ thị như hình vẽ.
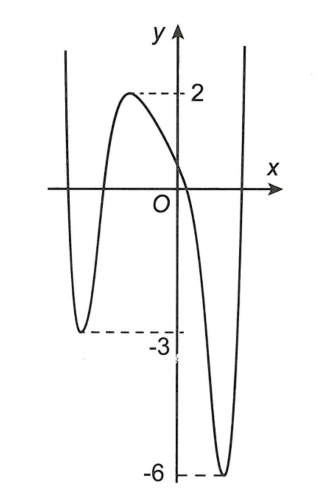
Gọi S là tập hợp các số nguyên dương của m để hàm số có 5 điểm cực trị. Tổng tất cả các phần tử của S là
A. 5
B. 10
C. 6
D. 7
Hướng dẫn giải
Chọn D.
Ta có số điểm cực trị của hàm bằng số điểm cực trị của hàm
.
Xét hàm số .
Dựa vào đồ thị ta có số điểm cực trị của hàm g(x) bằng số điểm cực trị của hàm f(x) và bằng 3.
Suy ra hàm số có 5 điểm cực trị thì số giao điểm của g(x) với trục Ox (không kể các điểm tiếp xúc) là 2.
⇔ .
Do m nguyên dương nên m ∊ {3; 4}.
Vậy tổng các giá trị là 7.
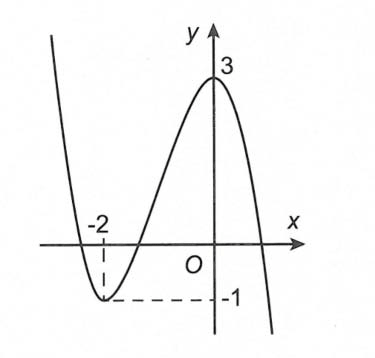
Câu 4. Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới. Số giá trị nguyên của tham số m để đồ thị hàm số g(x) = |f 3(x) – 3f(x) + m| có đúng 9 điểm cực trị là
A. 16
B. 17
C. 15
D. 18
Hướng dẫn giải
Chọn A.
Xét h(x) = f’(x) – 3 f(x) + m.
Suy ra h’(x) = 0 ⇔ 3 f’(x) [f 2 (x) – 1/] = 0.
Dựa vào đồ thị, ta có f’(x) = 0 ⇔ .
f(x) = 1 ⇔ (đạo hàm đều đổi dấu khi qua cả ba nghiệm đều là nghiệm đơn và khác 2 nghiệm trên).
f(x) = -1 ⇔ (trong đó x = x4 là nghiệm đơn x = -2 là nghiệm kép).
Ta tính các giá trị: h(x1) = h(x2) = h(x3) = m – 2.
h(x4) = h (-2) = m + 2 và h (0) = m + 18
Bảng biến thiên h(x):
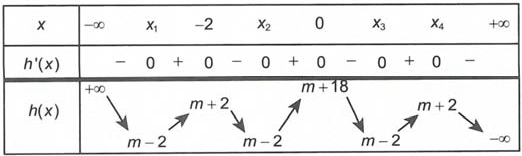
Suy ra hàm số h(x) luôn có 6 điểm cực trị.
Đồ thị hàm số g(x) = |f 3(x) – 3f(x) + m| có đúng 9 điểm cực trị tương đương đồ thị y = h(x) cắt trục hoành tại đúng 3 điểm (không kể những điểm tiếp xúc) ⇔ m + 2 ≤ 0 < 18 + m ⇔ -18 < m ≤ -2.
Vậy m ∊ {-17; -16; …; -2} hay có 16 giá trị nguyên của m.