Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số thuộc chương trình toán lớp 12. Bài viết này chúng ta sẽ điểm qua 3 dạng đồ thị cơ bản nhất gồm: Hàm số bậc 3, hàm phân thức, hàm trùng phương. Mỗi dạng hàm số sẽ đều có ví dụ và bài tập tự luyện cơ bản.

Lý thuyết
Hàm số y = ax3 + bx2 + cx + d
Tập xác định
– D = ℝ
– Tính y’ và cho y’ = 0 ⇒ các nghiệm (nếu có)
– Tính các giới hạn:
Lập bảng biến thiên
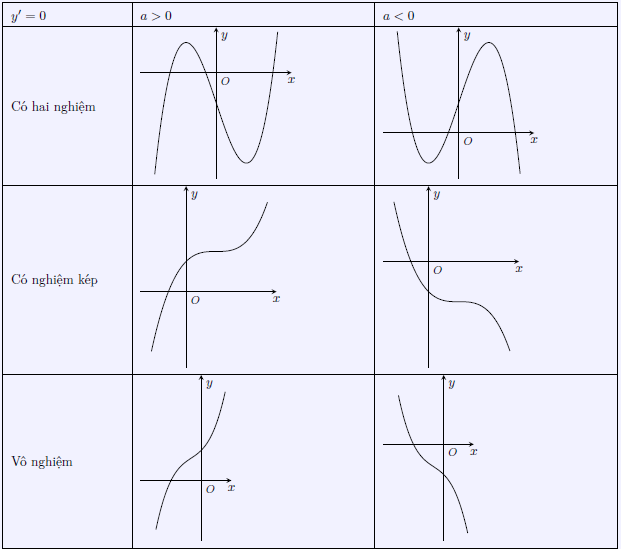
– Nếu y’ = 0 có hai nghiệm thì dấu của y’ là: “trong trái ngoài cùng”
– Nếu y’ = 0 có nghiệm kép thì dấu của y’ là: “luôn cùng dấu với a” ngoại trừ tại nghiệm kép.
– Nếu y’ = 0 vô nghiệm thì dấu của y’ là: “luôn cùng dấu với a”
Kết luận
– Tính chất đơn điệu.
– Cực trị hàm số.
– Chọn vài điểm đặc biệt vẽ đồ thị hàm số. Đồ thị có 6 dạng như sau:
Hàm số y = ax4 + bx2 + c
Tập xác định
– D = ℝ
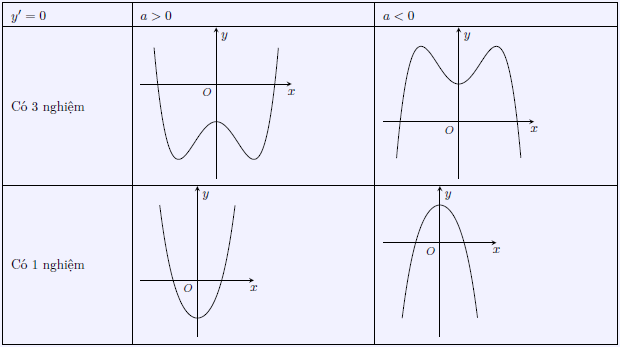
– Tính y’ và cho y’ = 0 (có 3 có nghiệm hoặc có 1 nghiệm và luôn có 1 nghiệm x = 0).
– Tính giới hạn:
– Lập bảng biến thiên: “Bên phải bảng biến thiên, dấu y’ luôn cùng dấu với a”.
Kết luận
– Tính chất đơn điệu.
– Cực trị hàm số.
– Giới hạn của hàm số.
Vẽ đồ thị
– Chọn vài điểm đặc biệt vẽ đồ thị hàm số
– Đồ thị hàm số có 4 dạng sau:
Hàm số 
Tập xác định
Tính (y’ hoặc dương hoặc âm ∀ x ∈ D)
Đường tiệm cận
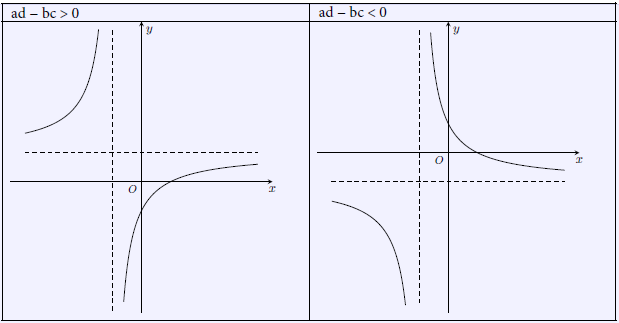
– Tiệm cận đứng: vì
và
– Tiệm cận ngang: vì
– Lập bảng biến thiên: Khi x → ±∞, thì
Kết luận
– Hàm số luôn đồng biến trên từng khoảng xác định hoặc luôn nghịch biến trên từng khoảng xác định.
– Vẽ đồ thị: Đồ thị có 2 dạng và luôn luôn nhận giao điểm của hai đường tiệm cận là tâm đối xứng.
– Vẽ đồ thị: Lấy thêm vài điểm đặc biệt.
– Đồ thị có 2 dạng sau:
Phân dạng bài tập
Dạng 1. Khảo sát sự biến thiên hàm số y = ax3 + bx2 + cx + d
Câu 1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = x3 − 3x + 1.
Hướng dẫn giải
Tập xác định: D = ℝ; y’ = 3x2 − 3
– y’ = 0 ⇔
Bảng biến thiên

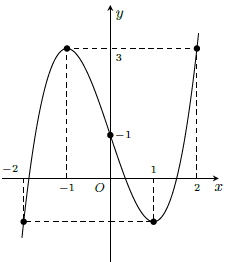
– Hàm số đồng biến trên các khoảng (-∞; -1) và (1; +∞), nghịch biến trên khoảng (-1; 1)
– Hàm số đạt cực đại tại x = -1; yCĐ = 3, hàm số đạt cực tiểu tại x = 1; yCĐ = -1.
– Đồ thị hàm số đi qua các điểm: (-2; -1), (-1; 3), (0; 1), (1; -1), (2; 3)
Dạng 2. Khảo sát sự biến thiên và vẽ đồ thị hàm số y = ax4 + bx2 + c
Câu 1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Hướng dẫn giải
Tập xác định: D = ℝ
y’ = x3 − x;
y’ = 0 ⇔
Bảng biến thiên

– Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞), nghịch biến trên các khoảng (-∞; -1) và (0; 1).
– Hàm số đạt cực đại tại x = 0 và yCĐ = , đạt cực tiểu tại x = ±1 và yCT = -1.
– Đồ thị hàm số đi qua các điểm

Dạng 3. Khảo sát sự biến thiên và vẽ đồ thị hàm số 
Câu 1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Hướng dẫn giải
Tập xác định: D = ℝ \{-1}
, ∀ x ∈ D.
Bảng biến thiên

– Hàm số đồng biến trên các khoảng (-∞; -1) và (-1; +∞) và không có cực trị.
– Đồ thị: Đồ thị hàm số qua các điểm (0; -1), và nhận I(-1; 2) làm tâm đối xứng.
