Bài viết này sẽ giúp bạn đọc tìm hiểu khái niệm hình trụ, công thức tính diện tích xung quanh, diện tích toàn phần, thể tích và ứng dụng vào các bài toán liên hệ thực tế.
Khái niệm hình trụ
Định nghĩa
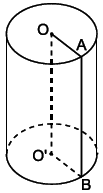
Khi quay hình chữ nhật ABO’O một vòng quanh cạnh OO’ cố định ta được một hình trụ.
– Hai đáy là hai hình tròn (O) và (O’) bằng nhau và nằm trong hai mặt phẳng song song.
– Đường thẳng OO’ gọi là trục của hình trụ.
– AB là một đường sinh. Đường sinh vuông góc với hai
mặt phẳng đáy. Độ dài đường sinh là chiều cao của hình trụ.
Cắt hình trụ
– Cắt hình trụ bởi một mặt phẳng song song với đáy thì mặt cắt là một hình tròn bằng hình tròn đáy.
– Cắt hình trụ bởi một mặt phẳng song song với trục thì mặt cắt là một hình chữ nhật.
Diện tích xung quanh của hình trụ
– Diện tích xung quanh hình trụ được tính bằng chu vi đường tròn đáy nhân với chiều cao. Công thức tổng quát là: Sxq = 2πrh;
– Diện tích toàn phần hình trụ được tính bằng diện tích xung quanh cộng với diện tích của 2 đáy. Công thức tổng quát là: Stp=2πrh + 2r2 hay Stp = 2πR(h + r) với r là bán kính đáy; h là chiều cao
Thể tích hình trụ
– Thể tích hình trụ được tính bằng chiều cao nhân với bình phương độ dài bán kính hình tròn mặt đáy hình trụ và số pi. Công thức tổng quát là: V = S⋅h = πr2h
Bài tập vận dụng
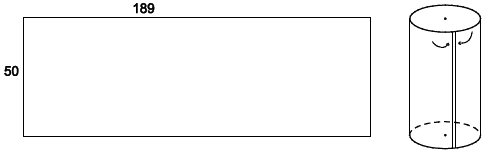
Câu 1. Từ một tấm tôn hình chữ nhật, kích thước 50 cm × 189 cm người ta cuộn tròn lại thành mặt xung quanh của một hình trụ cao 50 cm. Hãy tính:
a) Diện tích tôn để làm hai đáy;
b) Thể tích của hình trụ được tạo thành.
Hướng dẫn giải
a) Vì chiều cao của hình trụ là 50 cm nên chu vi hình tròn đáy là C = 189 cm.
Ta có: ![\[C = 2\pi R \Rightarrow R = \frac{C}{{2\pi }} = \frac{{189}}{{2\pi }} \approx 30\left( {cm} \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-1.svg)
Vậy bán kính hình tròn đáy là 30 cm.
Diện tích tôn để làm hai đáy là:
S = 2πR2 = 2 ⋅ π ⋅ 302 = 1800π (cm2)
b) Thể tích hình trụ là:
V = πR2h = π ⋅ 302 ⋅ 50 = 45000π (cm3).
Nhận xét: Để trả lời hai câu hỏi của bài toán, ta cần biết bán kính của đường tròn đáy. Muốn vậy, phải xác định cạnh nào của tấm tôn cần giữ nguyên để làm chiều cao của hình trụ, cạnh nào phải cuộn lại. Từ công thức tìm chu vi của hình tròn suy ra cách tìm bán kính.
Câu 2. Một hình trụ có chiều cao là 25 cm và diện tích toàn phần là 1200π cm2. Tính thể tích của hình trụ đó.
Hướng dẫn giải
Gọi bán kính đáy hình trụ là R, chiều cao hình trụ là h.
Vì diện tích toàn phần của hình trụ là 1200π cm2 nên 2πR(h + R) = 1200π
Suy ra: R⋅(25 + R) = 600 ⇔ R2 + 25R – 600 = 0
Phương trình có hai nghiệm: R1 = 15 (chọn); R2 = –40 (loại).
Vậy bán kính đáy hình trụ là 15 cm.
Thể tích hình trụ là: V = πR2h = π ⋅ 152 ⋅ 25 = 5625π (cm3).
Nhận xét: Ta đã biết chiều cao nên muốn tính thể tích hình trụ chỉ cần tìm bán kính đáy. Do đó ta tìm bán kính đáy từ công thức tính diện tích toàn phần của hình trụ.
Câu 3. Một hình trụ với ABCD là một mặt cắt song song với trục. Diện tích mặt cắt là 96 cm2, AB = 8 cm. Biết tâm O cách AB là 3 cm. Tính diện tích xung quanh và thể tích của hình trụ.
Hướng dẫn giải
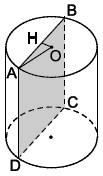
Mặt cắt ABCD là một hình chữ nhật. Diện tích mặt cắt là 96 cm2 nên AB⋅AD = 96 cm2.
Suy ra: ![\[AD = \frac{{96}}{{AB}} = \frac{{96}}{8} = 12\left( {cm} \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-2.svg)
Vậy chiều cao của hình trụ là 12 cm.
Trong mặt phẳng đáy, vẽ OH ⊥ AB.
Ta có HA = HB = 8 : 2 = 4 (cm).
Xét △AOH vuông tại H có:
OA2 = OH2 + AH2 = 32 + 42 = 25
Suy ra: OA = 5 cm. Vậy bán kính đáy là 5 cm.
Diện tích xung quanh của hình trụ là:
Sxq = 2πRh = 2 ⋅ π ⋅ 5 ⋅ 12 = 120π (cm2)
Thể tích của hình trụ là:
V = πR2h = π ⋅ 52 ⋅ 12 = 300π (cm3).
Nhận xét: Để xác định đúng chiều cao và bán kính đáy của hình trụ trong ví dụ này, ta dựa vào mặt cắt ABCD. Từ số đo diện tích là 96 cm2 và AB = 8 cm, ta tìm ra chiều cao. Từ khoảng cách OH = 3 cm ta tìm được bán kính nhờ định lí Py-ta-go.
Câu 4. Một hình trụ có diện tích toàn phần bằng 432π cm2 và chiều cao bằng 5 lần bán kính đáy. Chứng minh rằng diện tích xung quanh bằng 10 lần diện tích đáy.
Hướng dẫn giải
Gọi bán kính đáy và chiều cao hình trụ lần lượt là R và h.
Vì chiều cao bằng 5 lần bán kính đáy và diện tích toàn phần bằng 432π cm2 nên ta có hệ phương trình:
![\[\left\{ \begin{gathered} h = 5R{\text{ }}\left( 1 \right) \hfill \\ 2\pi R\left( {h + R} \right) = 432\pi {\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right.\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-3.svg)
Giải hệ này bằng phương pháp thế:
Thế h = 5R vào phương trình (2) ta được:
2πR(5R + R) = 432π ⇔ R2 = 36 ⇔ R = ±6
Giá trị R = –6 bị loại
Vậy R = 6; h = 30
Diện tích xung quanh của hình trụ là:
Sxq = 2πRh = 2 ⋅ π ⋅ 6 ⋅ 30 = 360π (cm2)
Diện tích đáy của hình trụ là:
S = πR2 = π⋅62 = 36π (cm2)
Ta thấy: ![\[\frac{{{S_{xq}}}}{S} = \frac{{360\pi }}{{36\pi }} = 10\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-4.svg)
(lần)
Do đó diện tích xung quanh gấp 10 lần diện tích đáy.
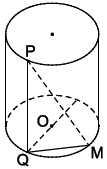
Câu 5. Cho hình trụ có bán kính đáy là 10 cm và diện tích xung quanh là 420π cm2. Vẽ một đường sinh PQ cố định. Lấy điểm M trên đường tròn đáy, có chứa điểm Q. Xác định vị trí của điểm M để PM lớn nhất. Tính giá trị lớn nhất đó.
Hướng dẫn giải
Gọi bán kính hình trụ là R và chiều cao hình trụ là h.
Ta có: Sxq = 2πRh
Suy ra: ![\[h = \frac{{{S_{xq}}}}{{2\pi R}} = \frac{{420\pi }}{{2\pi \cdot 10}} = 21\left( {cm} \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-5.svg)
Ta có PQ là đường sinh nên PQ = 21 cm và PQ vuông góc với mặt phẳng đáy.
Suy ra PQ ⊥ QM.
Xét △PQM vuông tại Q, ta có:
PM2 = PQ2 + QM2 = 441 + QM2.
Do đó PM lớn nhất ⇔ QM lớn nhất
⇔ QM là đường kính ⇔ QM = 20 cm.
Vậy ![\[\max PM = \sqrt {441 + 400} = \sqrt {841} = 29\left( {cm} \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-6.svg)
khi QM là đường kính của đường tròn đáy.
Lưu ý: Trong hình trụ, đường sinh vuông góc với đáy nên vuông góc với mọi đường thẳng nằm trong đáy, do đó PQ ⊥ QM.
Câu 6. Một hình trụ có thể tích là V (m3) và diện tích toàn phần là S (m2). Gọi R là bán kính đáy hình trụ và h là chiều cao của nó. Biết thương ![\[\frac{V}{S}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-7.svg)
bằng ![\[\frac{1}{2}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-8.svg)
chứng minh rằng: ![\[\frac{1}{h} + \frac{1}{R} = 1\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-9.svg)
Hướng dẫn giải
Ta có: V = πR2h; S = 2πR(h + R). Theo đề bài ta có: ![\[\frac{V}{S} = \frac{1}{2}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-10.svg)
Suy ra: ![\[\frac{{\pi {R^2}h}}{{2\pi R\left( {h + R} \right)}} = \frac{1}{2}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-11.svg)
![\[\begin{gathered} \Leftrightarrow Rh = R + h \hfill \\ \Leftrightarrow 1 = \frac{{R + h}}{{Rh}} \Leftrightarrow \frac{1}{h} + \frac{1}{R} = 1\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array} \hfill \\ \end{gathered} \]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-12.svg)
Câu 7. Một hình trụ có bán kính đáy bằng ![\[\frac{2}{5}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-13.svg)
chiều cao. Cắt hình trụ này bằng một mặt phẳng chứa trục ta được một mặt cắt có diện tích là 80 cm2. Tính diện tích toàn phần của hình trụ.
Hướng dẫn giải
Gọi bán kính đáy và chiều cao của hình trụ lần lượt là R và h.
Mặt cắt chứa trục là một hình chữ nhật có một cạnh là 2R và cạnh kề là h.
Theo các điều kiện trong đề bài ta có:
![\[\left\{ \begin{gathered} R = \frac{2}{5}h{\text{ }}\left( 1 \right)\begin{array}{*{20}{c}} {} \\ {} \end{array} \hfill \\ 2R \cdot h = 80{\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right.\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-14.svg)
Thế R từ (1) vào (2) ta được:
2 ⋅ ⋅ h ⋅ h = 80 hay 4h2 = 400 ⇒ h = ±10.
Giá trị h = −10 bị loại. Vậy chiều cao của hình trụ là 10 cm.
Bán kính đáy là: R = 10 ⋅ = 4 (cm)
Diện tích toàn phần của hình trụ là:
Stp = 2πR(h + R) = 2 ⋅ π ⋅ 4(10 + 4) = 112π (cm2).
Câu 8. Một hình trụ có chiều cao bằng ![\[\frac{3}{4}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-15.svg)
đường kính đáy. Biết thể tích của nó là 768π cm3. Tính diện tích xung quanh của hình trụ.
Hướng dẫn giải
Gọi bán kính đáy và chiều cao hình trụ lần lượt là R và h.
Vì chiều cao bằng đường kính nên chiều cao bằng ![\[\frac{3}{2}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-16.svg)
bán kính đáy. Vậy h = R
Ta có: V = πR2h mà h = R nên
V = πR2⋅ R = πR3
Theo đề bài ta có:
![\[\frac{3}{2}\pi {R^3} = 786 \Rightarrow {R^3} = 512 \Rightarrow R = 8\left( {cm} \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-17.svg)
Vậy h = 8 ⋅ = 12 (cm)
Do đó diện tích xung quanh của hình trụ là:
Sxq = 2πRh = 2π ⋅ 8 ⋅ 12 = 192π (cm2)
Câu 9. Một hộp bánh hình trụ có chiều cao nhỏ hơn bán kính đáy là 1,5 cm. Biết thể tích của hộp là 850π cm3, tính diện tích vỏ hộp.
Hướng dẫn giải
⨂ Tìm hướng giải
Diện tích vỏ hộp chính là diện tích toàn phần của hình trụ. Tìm được bán kính đáy sẽ tìm được chiều cao do đó sẽ tìm được diện tích toàn phần.
⨂ Trình bày lời giải
Gọi R và h lần lượt là bán kính đáy và chiều cao của hộp bánh hình trụ.
Ta có: h = R – 1,5
Vì thể tích của hộp là 850π cm3 nên:
πR2h = 850π
Suy ra: R2(R – 1,5) = 850
⇔ R3 – 1,5R2 – 850 = 0
⇔ 2R3 – 3R2 – 1700 = 0
⇔ 2R3 – 20R2 + 17R2 – 170R + 170R – 1700 = 0
⇔ 2R2(R – 10) + 17R(R – 10) + 170(R – 10) = 0
⇔ (R – 10)(2R2 + 17R + 170) = 0
⇔ R – 10 = 0 (1) ∨ 2R2 + 17R + 170 = 0 (2)
Phương trình (1) có nghiệm R = 10 (thoả mãn).
Phương trình (2) vô nghiệm.
Vậy bán kính đáy hộp là 10 cm.
Chiều cao của hộp là: 10 – 1,5 = 8,5 (cm).
Diện tích vỏ hộp là:
S = 2pR(h + R) = 2 ⋅ π ⋅ 10 ⋅ (8,5 + 10) = 370π (cm2)
Câu 10. Một hình trụ có diện tích toàn phần gấp hai lần diện tích xung quanh. Biết bán kính đáy hình trụ là 6 cm. Tính thể tích hình trụ.
Hướng dẫn giải
Gọi bán kính đáy hình trụ là R và chiều cao hình trụ đó là h.
Vì diện tích toàn phần bằng hai lần diện tích xung quanh nên
2πRh + 2πR2 = 4πRh
Suy ra: 2πR2 = 2πRh ⇒ R = h = 6 cm
Thể tích của hình trụ là:
V = πR2h = π ⋅ 62 ⋅ 6 = 216π (cm3).
Câu 11. Một chậu hình trụ cao 20 cm. Diện tích đáy bằng nửa diện tích xung quanh. Trong chậu có nước cao đến 15 cm. Hỏi phải thêm bao nhiêu nước vào chậu để nước vừa đầy chậu?
Hướng dẫn giải
Gọi R là bán kính đáy chậu và h là chiều cao của chậu.
Vì diện tích đáy bằng nửa diện tích xung quanh nên
πR2 = H8 ⋅2πRh ⇒ R = h = 20 cm
Thể tích của chậu là:
V = πR2h = π ⋅ 202 ⋅ 20 = 8000π (cm3)
Thể tích nước trong chậu là:
V1 = π ⋅ 202 ⋅ 15 = 6000π (cm3)
Thể tích nước phải thêm vào chậu là:
V2 = V – V1 = 8000π – 6000π = 2000π (cm3)
Câu 12. Một hình trụ có thể tích là 200 cm3. Giảm bán kính đáy đi hai lần và tăng chiều cao lên hai lần ta được một hình trụ mới. Tính thể tích của hình trụ này.
Hướng dẫn giải
Gọi bán kính đáy và chiều cao hình trụ lần lượt là R và h.
Thể tích của hình trụ này là: V1 = πR2h (cm3)
Nếu giảm bán kính đáy đi hai lần và tăng chiều cao lên hai lần thì bán kính đáy là ![\[\frac{R}{2}\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-18.svg)
và chiều cao là 2h.
Thể tích hình trụ về sau là:
![\[{V_2} = \pi {\left( {\frac{R}{2}} \right)^2} \cdot 2h = \frac{{\pi {R^2}h}}{2} = \frac{{200}}{2} = 100\left( {c{m^3}} \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-19.svg)
Câu 13. Một viên than tổ ong có dạng hình trụ, đường kính đáy là 114 mm, chiều cao là 100 mm. Viên than này có 19 lỗ “tổ ong” hình trụ có trục song song với trục của viên than, mỗi lỗ có đường kính 12 mm. Tính thể tích nhiên liệu đã được nén của mỗi viên than (làm tròn đến cm3).
Hướng dẫn giải
Thể tích viên than (kể cả 19 lỗ) là:
V1 = πR12h = π ⋅ 572 ⋅ 100 ≈ 1020186 (mm3) ≈ 1020 (cm3)
Thể tích 19 lỗ “tổ ong” là:
V2 = 19πR22h = 19 ⋅ π ⋅ 62 ⋅ 100 ≈ 214776 (mm3) ≈ 215 (cm3)
Thể tích nhiên liệu đã được nén của mỗi viên than là:
V = V1 – V2 = 1020 – 215 = 805 (cm3).
Câu 14. Một cây gỗ hình trụ có đường kính đáy là 4 dm và dài 5 m. Từ cây gỗ này người ta xẻ thành một cây cột hình lăng trụ đứng có đáy là hình vuông lớn nhất. Tính thể tích phần gỗ bị loại bỏ đi.
Hướng dẫn giải
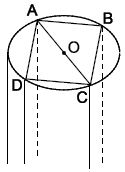
Thể tích cây gỗ hình trụ là:
V1 = πR12h ≈ 3,14 ⋅ 22 ⋅ 50 ≈ 628 (dm3)
Diện tích đáy hình vuông của hình lăng trụ đứng là:
![\[S = A{B^2} = \frac{{A{C^2}}}{2} = \frac{{{4^2}}}{2} = 8\left( {d{m^2}} \right)\]](https://danchuyentoan.com/wp-content/uploads/2023/10/dien-tich-xung-quanh-va-the-tich-hinh-tru-20.svg)
Thể tích hình lăng trụ đứng là:
V2 = S⋅h = 8 ⋅ 50 = 400 (dm3).
Thể tích phần gỗ bị loại bỏ đi là:
V = V1 – V2 = 628 – 400 = 228 (dm3).
Câu 15. Hai mặt của một cổng vòm thành cổ có dạng hình chữ nhật, phía trên là một nửa hình tròn có đường kính bằng chiều rộng của cổng. Biết chiều rộng của cổng là 3,2 m, chiều cao của cổng (phần hình chữ nhật) bằng 2,8 m và chiều sâu của cổng bằng 3,0 m. Tính thể tích phần không gian bên trong cổng (làm tròn đến phần mười m3).
Hướng dẫn giải
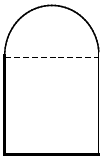
Phần không gian bên trong cổng gồm một hình hộp chữ nhật và một nửa hình trụ.
Thể tích phần hình hộp chữ nhật là:
V1 = 3,2 ⋅ 2,8 ⋅ 3,0 = 26,9 (m3).
Thể tích phần nửa hình trụ là:
V2 = H8 πR2h = H8 ⋅ 3,14 ⋅ (1,6)2 ⋅ 3,0 = 12,1 (m3)
Thể tích phần không gian bên trong cổng là:
V = V1 + V2 = 26,9 + 12,1 = 39,0 (m3).
Câu 16. Một hình trụ có thể tích bằng 125π cm3. Biết diện tích xung quanh bằng hai lần diện tích đáy. Tính bán kính đáy và chiều cao của hình trụ này.
Hướng dẫn giải
Gọi R và h lần lượt là bán kính đáy và chiều cao của hình trụ.
Vì diện tích xung quanh bằng hai lần diện tích đáy nên ta có:
2πRh = 2πR2 ⇒ h = R
Theo đề bài, thể tích hình trụ bằng 125π cm3 nên
πR2h = 125π
Suy ra: πR3 = 125π (vì h = R)
Do đó: R3 = 125 ⇒ R = 5 cm
Vậy h = 5 cm.
