Công thức tính Diện tích hình cầu và thể tích hình cầu

Bài viết này sẽ giúp bạn đọc tìm hiểu chi tiết công thức tính diện tích hình cầu, thể tích hình cầu và ứng dụng giải các bài tập tính toán liên quan đến hình cầu.

Lý thuyết hình cầu

Định nghĩa

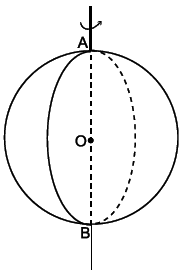
– Khi quay nửa hình tròn (O; R) một vòng quanh đường kính AB cố định thì được một hình cầu tâm O, bán kính R.

– Nửa đường tròn khi quay tạo nên mặt cầu.

Cắt hình cầu

– Khi cắt hình cầu bởi một mặt phẳng thì mặt cắt là một hình tròn;

– Khi cắt mặt cầu bán kính R bởi một mặt phẳng ta được một đường tròn:

⋄ Có bán kính R (gọi là đường kính lớn) nếu mặt cắt đi qua tâm;

⋄ Có bán kính nhỏ hơn R nếu mặt cắt không đi qua tâm.

Diện tích mặt cầu

Diện tích mặt cầu được tính bằng công thức S = 4πR² hay S = πd² .Trong đó R là bán kính; d là đường kính mặt cầu và số π=3.14159265359…

Thể tích hình cầu

Thể tích hình cầu được tính bằng công thức: V = 4/3 πR³, trong đó R là bán kính, số π=3.14159265359…

Bài tập vận dụng

Bài 1. Hai hình cầu có hiệu các bán kính bằng 3 cm và hiệu các thể tích bằng 1332π cm³. Tính hiệu các diện tích của hai mặt cầu.

Hướng dẫn giải

– Tìm hướng giải

Để tính được hiệu diện tích của hai mặt cầu ta cần biết các bán kính của hai mặt cầu.

– Trình bày lời giải

Gọi bán kính của hình cầu lớn là R và bán kính của hình cầu nhỏ là r.

Ta có: R – r = 3 hay R = r + 3

Thể tích hình cầu lớn là:

V₁ = $\frac{4}{3}$ πR³

Thể tích hình cầu nhỏ là: 3

V₂ = $\frac{4}{3}$ πr³

Vì V₁ – V₂ = 1332π (cm³) nên

$\frac{4}{3}$ π(R³ – r³) = 1332π ⇔ R³ – r³ = 999

Do đó: (r + 3)³ – r³ = 999 ⇔ r² + 3r – 108 = 0

Giải ra được r₁ = –12 (loại); r₂ = 9 (chọn).

Vậy bán kính hình cầu nhỏ là 9 cm. Bán kính hình cầu lớn là 12 cm.

Diện tích mặt cầu lớn là:

S₁ = 4πR² = 4 ⋅ π ⋅ 12² = 576π (cm²)

Diện tích mặt cầu nhỏ là:

S₂ = 4πr² = 4 ⋅ π ⋅ 9² = 324π (cm²)

Hiệu các diện tích của hai mặt cầu là:

S = S₁ – S₂ = 576π – 324π = 252π (cm²).

Bài 2. Một hình cầu nội tiếp một hình nón bán kính đáy bằng 6 cm và đường sinh bằng 10 cm. Chứng minh rằng diện tích đáy hình nón bằng diện tích mặt cầu.

Hướng dẫn giải

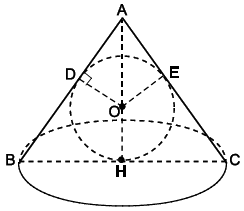
Vì hình cầu nội tiếp hình nón nên OH ⊥ BC, OD ⊥ AB. Ta có:

$AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{{10}^2} - {6^2}} = 8\left( {cm} \right)$

Gọi bán kính đáy hình nón là R, bán kính hình cầu là r.

Ta có BH = BD = R = 6 cm; OH = OD = r.

AD = AB – BD = 10 – 6 = 4 cm.

△AOD ∼ △ABH (g.g)

$\Rightarrow \frac{{OD}}{{BH}} = \frac{{AD}}{{AH}}$

Do đó: $\frac{r}{6} = \frac{4}{8} \Rightarrow r = 3\left( {cm} \right)$

Diện tích đáy hình nón là:

S₁ = πR² = π ⋅ 6² = 36π (cm²).

Diện tích mặt cầu là:

S₂ = 4πr² = 4 ⋅ π ⋅ 3² = 36π (cm²).

Vậy diện tích đáy hình nón bằng diện tích mặt cầu.

Bài 3. Cho tam giác ABC cân tại A nội tiếp đường tròn đường kính AD. Gọi H là giao điểm của AD và BC. Quay hình vẽ một vòng quanh đường kính AD cố định ta được hai hình nón nội tiếp một hình cầu. Biết AH = 24 cm; DH = 6 cm, hãy tính:

a) Thể tích của hình cầu được tạo thành;

b) Thể tích hình nón đỉnh A đáy là hình tròn đường kính BC.

Hướng dẫn giải

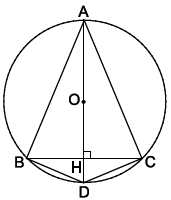
a) Tam giác ABC cân tại A, AD là đường kính nên AD ⊥ BC

Ta có: $\widehat {ABD} = 90^\circ$ (vì AD là đường kính).

Xét △ABD vuông tại B ta có:

BH² = HA⋅HD = 24 ⋅ 6 = 144 ⇒ BH = 12(cm).

Bán kính của đường tròn ngoại tiếp △ABC là:

R = (24 + 6) : 2 = 15 (cm)

Thể tích của hình cầu tạo thành là:

V₁ = $\frac{4}{3}$ πR³ = $\frac{4}{3}$ ⋅ π ⋅ 15³ = 4500π (cm³)

b) Thể tích của hình nón đỉnh A là:

V₂ = $\frac{1}{3}$ πr²h = $\frac{1}{3}$ ⋅ π ⋅ 12² ⋅ 24 = 1152π (cm³)

Bài 4. Cho một hình cầu nội tiếp một hình trụ. Chứng minh rằng:

a) Thể tích hình cầu bằng $\frac{2}{3}$ thể tích hình trụ;

b) Diện tích mặt cầu bằng $\frac{2}{3}$ diện tích toàn phần hình trụ.

Hướng dẫn giải

– Tìm hướng giải

Cần tìm mối quan hệ giữa bán kính hình cầu với bán kính đáy hình trụ và chiều cao hình trụ.

– Trình bày lời giải

Gọi bán kính hình cầu là R thì bán kính đáy hình trụ là R và chiều cao của hình trụ là 2R.

a) Thể tích hình cầu là: V₁ = $\frac{4}{3}$ πR³

Thể tích hình trụ là: V₂ = πR²h = 2πR³

Ta có: $\frac{{{V_1}}}{{{V_2}}} = \frac{\begin{gathered} \hfill \\ \frac{4}{3}\pi {R^3} \hfill \\ \end{gathered} }{{2\pi {R^3}}} = \frac{2}{3}$

b) Diện tích mặt cầu là: S₁ = 4πR²

Diện tích hình trụ là:

S₂ = 2πR (h + R) = 2πR (2R+ R) = 6πR³

Ta có: $\frac{{{S_1}}}{{{S_2}}} = \frac{{4\pi {R^2}}}{{6\pi {R^2}}} = \frac{2}{3}$

Bài 5. Cho đoạn thẳng AB = 24 cm. Lấy điểm C nằm giữa A và B. Vẽ về cùng một phía của AB ba nửa đường tròn đường kính AB, AC và BC. Quay toàn bộ hình vẽ một vòng quanh đường kính AB cố định ta được ba hình cầu. Tìm thể tích lớn nhất của phần không gian được giới hạn bởi ba hình cầu.

Hướng dẫn giải

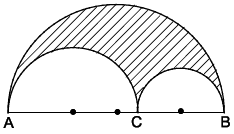
– Tìm hướng giải

Cần tìm mối quan hệ giữa các bán kính của ba nửa hình tròn, từ đó tìm được quan hệ giữa thể tích của ba hình cầu.

– Trình bày lời giải

Đặt AC = 2x thì BC = 24 – 2x.

Bán kính của nửa đường tròn đường kính AB là 12 cm.

Bán kính của nửa đường tròn đường kính AC là x.

Bán kính của nửa đường tròn đường kính BC là 12 – x.

Thể tích của ba hình cầu đường kính AB, AC và BC lần lượt là:

$\frac{4}{3}$ π12³; $\frac{4}{3}$ πx³ và $\frac{4}{3}$ π (12 – x)³

Thể tích phần không gian giới hạn bởi ba hình cầu là:

V = 2304π – $\frac{4}{3}$ π [x³ + (12 – x)³]

= 2304π – $\frac{4}{3}$ π (x³ + 1728 – 432x + 36x² – x³)

= 2304π – 48π (x² – 12x + 48)

V_max = (x² – 12x + 48)_min

⇔ [(x – 6)² + 12]_min

⇔ x = 6

Khi đó max V = 1728π cm³ khi AC = 12 cm hay khi C là trung điểm của AB.

Bài 6: Cắt hình cầu tâm O bởi một mặt phẳng ta được một hình tròn tâm K, đường kính AB. Biết OK = 9 cm và diện tích hình tròn tâm K bằng 16% diện tích mặt cầu. Tính diện tích mặt cầu.

Hướng dẫn giải

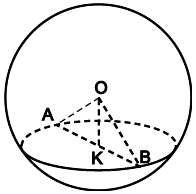
Xét △AOB cân tại O có KA = KB nên OK ⊥ AB.

Gọi R là bán kính hình cầu, r là bán kính hình tròn (K).

Xét △KOA vuông tại K ta có:

r² = R² – OK² = R² – 81

Diện tích hình tròn (K) là:

S₁ = πr² = π (R² – 81)

Diện tích mặt cầu là:

S₂ = 4πR²

Vì S₁ =16% S₂ nên π (R² – 81) = $\frac{{16}}{{100}}$ ⋅ 4πR²

Thu gọn phương trình này ta được:

36R² = 8100

Suy ra: R² = 225. Do đó diện tích mặt cầu là S = 4πR² = 900π (cm²).

Bài 7: Người ta cắt một quả địa cầu cũ bằng một mặt phẳng theo một vĩ tuyến và được một phần có dạng hình chảo, đường kính miệng chảo là 24 cm và độ sâu nhất của chảo là 8 cm. Tính diện tích bề mặt của quả địa cầu.

Hướng dẫn giải

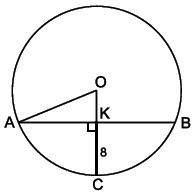
Mặt cắt qua tâm là hình tròn tâm O với AB là đường kính miệng chảo.

Vẽ bán kính OC ⊥ AB tại K.

Ta có: KA = KB = 24 : 2 = 12 (cm)

Gọi R là bán kính quả địa cầu.

Xét △KOA vuông tại K ta có:

OA² = OK² + AK²

⇒ R² = (R – 8)² + 12²

⇒ R² = R² – 16R + 64 + 144

⇒ 16R = 208

⇒ R = 13 (cm).

Diện tích bề mặt quả địa cầu là:

S = 4πR² = 4 ⋅ π ⋅ 13² = 676π (cm²).

Bài 8: Một hình cầu nội tiếp một hình lập phương cạnh 12 cm. Tính thể tích phần không gian bên ngoài hình cầu và bên trong hình lập phương.

Hướng dẫn giải

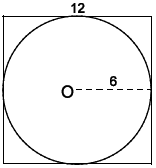
Vì độ dài cạnh của hình lập phương là 12 cm nên bán kính hình cầu nội tiếp là 6 cm.

Thể tích hình lập phương là:

V₁ = 12³ = 1728 (cm³).

Thể tích của hình cầu là:

V2 = $\frac{4}{3}$ ⋅ π ⋅ 6³ = 288π (cm³)

Thể tích phần không gian bên ngoài hình cầu và bên trong hình lập phương là:

V = V₁ – V₂ = 1728 – 288π ≈ 824 (cm³).

Nhận xét: Ta có: $\frac{{{V_1}}}{{{V_2}}} = \frac{{288\pi }}{{1728}} = \frac{\pi }{6}$

Tổng quát, ta có thể chứng minh được rằng nếu một hình cầu nội tiếp một hình lập phương thì tỉ số thể tích của chúng là $\frac{\pi }{6}$

Bài 9: Một hình cầu có bán kính bằng bán kính đáy của một hình nón. Biết đường sinh của hình nón bằng 12 cm và diện tích xung quanh của hình nón bằng diện tích mặt cầu. Tính thể tích hình cầu.

Hướng dẫn giải

Gọi bán kính hình cầu cũng như bán kính đáy hình nón là R.

Diện tích xung quanh hình nón là:

πRl = 12πR

Diện tích mặt cầu là: 4πR²

Vì diện tích xung quanh hình nón bằng diện tích mặt cầu nên:

12πR = 4πR² ⇒ R = 3 (cm).

Thể tích hình cầu là:

V = $\frac{4}{3}$ πR³ = $\frac{4}{3}$ ⋅ π ⋅ 3³ = 36π (cm³).

Bài 10: Một hình cầu nội tiếp một hình trụ. Biết diện tích toàn phần hình trụ là 384π cm². Tính thể tích hình cầu.

Hướng dẫn giải

Gọi bán kính hình cầu là R thì bán kính đáy hình trụ là R và chiều cao hình trụ là 2R. Vì diện tích toàn phần hình trụ là 384π cm² nên ta có:

2πR (2R + R) = 384π

⇒ 6πR² = 384π ⇒ R = 8 (cm).

Thể tích hình cầu là:

V = $\frac{4}{3}$ πR³ = $\frac{4}{3}$ ⋅ π ⋅ 8³ = $\frac{{2048}}{3}$ π (cm³)

Bài 11. Một chiếc thuyền thúng có dạng nửa hình cầu, có khối lượng 45 kg, người chèo thuyền khối lượng 65 kg. Biết đường kính của thuyền là 1,2 m và trên thuyền có thêm 2,4 tạ cá, hỏi nước có ngập đến mép thuyền không? Biết khối lượng riêng của nước là 1 kg/dm³.

Hướng dẫn giải

Bán kính của thuyền thúng là:

1,2 : 2 = 0,6 (m) = 6 (dm).

Thể tích của thuyền là:

V = $\frac{1}{2}$ ⋅ $\frac{4}{3}$ ⋅ πR³= $\frac{1}{2}$ ⋅ $\frac{4}{3}$ ⋅ π ⋅ 6³

= 144π (dm³) ≈ 425 dm³

Tổng khối lượng của thuyền, người và cá là:

45 + 65 + 240 = 350 (kg)

Khối lượng riêng của thuyền là:

350 : 452 = 0,8 (kg/dm³)

Khối lượng riêng của nước là: 1 kg/dm³

Vậy khối lượng riêng của thuyền nhỏ hơn khối lượng riêng của nước nên nước không ngập đến mép thuyền.

Nhận xét: Học sinh cần ghi nhớ công thức $d = \frac{m}{V}$ (m là khối lượng riêng, m khối lượng, V là thể tích)

Bài 12. Cho hình cầu tâm O, bán kính cm. Cắt mặt cầu bởi một mặt $OA = 10\sqrt 3 cm$ phẳng vuông góc với OA tại trung điểm M của OA ta được một đường tròn. Tính độ dài của đường tròn này.

Hướng dẫn giải

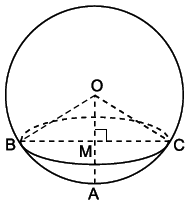
Xét △OBC có OB = OC và OM ⊥ BC nên MB = MC. Ta có:

$M{C^2} = O{C^2} - O{M^2} = {\left( {10\sqrt 3 } \right)^2} - {\left( {5\sqrt 3 } \right)^2} = 225$

Suy ra: MC = 15 (cm).

Độ dài của đường tròn (M) là: 2π ⋅ 15 = 30π (cm).

Bài 13. Một bình thuỷ tinh hình trụ chứa nước. Trong bình có một vật rắn hình cầu ngập hoàn toàn trong nước. Khi người ta lấy vật rắn đó ra khỏi bình thì mực nước trong bình giảm đi 48,6 mm. Biết đường kính bên trong của đáy bình là 50 mm, tính bán kính của vật hình cầu.

Hướng dẫn giải

Gọi r là bán kính của vật hình cầu. Thể tích của vật hình cầu là:

V₁ = $\frac{4}{3}$ πr³

Thể tích khối nước rút xuống là:

V₂ = π ⋅ 50² ⋅ 48,6 = 121500π (mm³)

Ta có phương trình:

$\frac{4}{3}$ πr³ = 121500π ⇒ r³ = 91125

Do đó: $r = \sqrt[3]{{91125}} = 45\left( {mm} \right)$

Bài 14. Vĩ độ của Thanh Hoá là 20° Bắc. Tính độ dài vĩ tuyến qua Thanh Hoá biết bán kính Trái Đất là 6370km.

Hướng dẫn giải

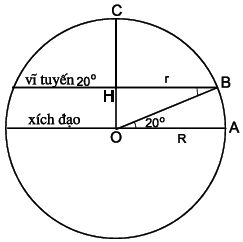
Gọi R là bán kính Trái Đất, gọi r là bán kính của r là bán kính của vĩ tuyến 20° qua Thanh Hoá.

Ta có: $\widehat {HBO} = \widehat {AOB} = 20^\circ$

Xét △HBO vuông tại H có:

r = HB = OB⋅cos 20° = R⋅cos 20°

Do đó độ dài của vĩ tuyến 20° là:

2πr = 2πR ⋅ cos 20° = 2π ⋅ 6370 ⋅ cos 20° ≈ 37590 (km)

Bài 15. Một hình cầu có số đo thể tích (tính bằng m³) bằng số đo diện tích mặt cầu (tính bằng m²). Tính độ dài của đường tròn lớn.

Hướng dẫn giải

Gọi bán kính của hình cầu là R. Vì số đo thể tích bằng số đo diện tích mặt cầu nên ta có:

$\frac{4}{3}$ πR³ = 4πR² ⇒ R = 3 (m).

Độ dài của đường tròn lớn là:

C = 2πR = 2π ⋅ 3 = 6π (m).

Bài tập tổng hợp

Bài 1. Tính diện tích toàn phần của hình nón có chiều cao h = 16 cm và bán kính đường tròn đáy r = 12 cm.

Hướng dẫn giải

Độ dài đường sinh của hình nón:

$l = \sqrt {{h^2} + {r^2}} = \sqrt {{{16}^2} + {{12}^2}} = \sqrt {400} = 20\left( {cm} \right)$

Diện tích toàn phần của hình nón:

S_tp = πrl + πr² = π ⋅ 12 ⋅ 20 + π ⋅ 12² = 384π (cm²)

Bài 2. Cho tam giác vuông ABC ( $\widehat A = 90^\circ$ ); AB = 4 cm; AC = 3 cm. Quay tam giác vuông ABC một vòng xung quanh cạnh AB cố định. Tính thể tích của hình nón được tạo thành?

Hướng dẫn giải

Theo công thức tính thể tích của hình nón V = $\frac{1}{3}$ πR²h

Trong đó: R = 3 (cm); h = 4 (cm)

Vậy: V = πR²h = π ⋅ 3² ⋅ 4 = 12π (cm³)

Bài 3. Một hình trụ có thể tích là 20π dm³, chiều cao bằng 5 dm. Tính diện tích xung quanh của hình trụ đó.

Hướng dẫn giải

Hình trụ có thể tích là V = 20π dm³, chiều cao h = 5 dm nên ta có: V = πr²h = 20π

Hay πr² ⋅ 5 = 20π ⇒ r² = 4 ⇒ r = 2

Do đó: S_xq = 2πrh = 2π ⋅ 2 ⋅ 5 = 20π (dm²)

Vậy diện tích xung quanh của hình trụ là 20π (dm²)

Bài 4. Một hình trụ có chiều cao bằng đường kính đáy, Nếu bán kính đáy bằng 6 cm. Hỏi diện tích xung quanh của hình trụ là bao nhiêu cm²?

Hướng dẫn giải

Ta có: R = 6 cm mà h = d = 12 cm

Khi đó: S_xq = 2πRh = 2π ⋅ 6 ⋅ 12 = 144π (cm²)

Bài 5. Một hình trụ có diện tích xung quanh là 40 m² và chiều cao của hình trụ bằng 5 m. Thể tích của hình trụ đó bằng bao nhiêu?

Hướng dẫn giải

Ta có:

${S_{xq}} = 2\pi Rh \Rightarrow 40 = 2\pi R \cdot 5 \Rightarrow R = \frac{4}{\pi }$

Thể tích của hình trụ đó là:

$V = \pi {R^2}h = \pi {\left( {\frac{4}{\pi }} \right)^2} \cdot 5 = \frac{{80}}{\pi }\left( {{m^3}} \right)$

Bài 6. Cho ΔABC vuông tại A. Cạnh AB = 3 cm; AC= 4 cm. Quay ΔABC một vòng quanh cạnh AC. Vẽ hình, tính diện tích xung quanh và thể tích của hình được sinh ra?

Hướng dẫn giải

Vẽ đúng hình: Hình sinh ra là hình nón

Tính được: BC = 5 cm

Tính được:

S_xq = πrl = π ⋅ 3 ⋅ 5 = 15π ≈ 47,1 (cm²)

Tính được:

V = $\frac{1}{3}$ ⋅ π ⋅ 3² ⋅ 4 = 12π ≈ 37,68 (cm³)

Bài 7. Cho hình nón có đỉnh S, đường kính 2R chiều cao SH = R $\sqrt 3$ . Tích thể tích của hình nón.

Hướng dẫn giải

Theo đề bài chiều cao của hình nón SH = R $\sqrt 3$ , đường kính 2R

⇒ Bán kính đáy là R

Thể tích hình nón

$V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {R^2} \cdot R\sqrt 3 = \frac{{\pi {r^2}\sqrt 3 }}{3}$

Bài 8. Cho hình chữ nhật ABCD có AB = 4 cm, BC = 5 cm. Quay hình chữ nhật đó một vòng quanh cạnh AB được một hình trụ. Tính thể tích hình trụ.

Hướng dẫn giải

Hình trụ nhận được có bán kính đáy là BC = 5(cm), chiều cao AB = 4 (cm)

Thể tích hình trụ: V = π⋅AB⋅BC² = 100π cm³

Bài 9. Một hình cầu có thể tích bằng 972π cm³. Tính diện diện tích của mặt cầu đó?

Hướng dẫn giải

Bán kính của mặt cầu đó là:

$\frac{4}{3}$ πR³ = 972π ⇒ R = 9 cm

Diện tích của mặt cầu đó là:

S = 4πR² = 324π cm²

Thầy Tú dạy toán