Tính đơn điệu của hàm số: Lý thuyết và dạng bài tập đặc trưng

Tìm hiểu lý thuyết tính đơn điệu của hàm số, dạng bài tìm khoảng đơn điệu dựa vào hàm số – đồ thị và các dạng biện luận m để hàm đơn điệu. Các định nghĩa, định lý về tính đơn điệu của hàm số trong bài viết này sẽ giúp các bạn học sinh nắm chắc hơn trong việc khảo sát hàm số cũng như các dạng toán trong phần giải tích toán 12. Là nền tảng kiến thức đóng vai trò quan trọng trong các kỳ thi trên trường cũng như ôn thi THPT quốc gia.

Lý thuyết

Tính đơn điệu của hàm số là cách gọi chung cho tính đồng biến (tăng) và tính nghịch biến (giảm). Thông thường để xác định tính chất đơn điệu của hàm số ta thường tìm đạo hàm của nó. Xét trong khoảng bất kỳ, nếu đạo hàm dương trong khoảng nào thì hàm số đồng biến trong khoảng đó và ngược lại với đạo hàm âm. ^{[1]Wikipedia, Hàm số đơn điệu, 25/04/2022}

Định nghĩa đồng biến, nghịch biến

Cho hàm số y = f(x) xác định trên K , trong đó K là một khoảng, đoạn hoặc nữa khoảng.

a) Hàm số y = f(x) đồng biến trên K nếu mọi x₁, x₂ ∊ K, x₁ < x₂ ⇒ f(x₁) < f(x₂).

b) Hàm số y = f(x) nghịch biến trên K nếu mọi x₁, x₂ ∊ K, x₁ < x₂ ⇒ f(x₁) > f(x₂). ^{[2]Phan Đức Chinh, Toán lớp 9 Tập 1 Trang 44, 2011}

Định lí cơ bản

Cho hàm số y = f(x) có đạo hàm trên K .

a) Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.

b) Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.

c) Nếu f’(x) = 0 với mọi x thuộc K thì hàm số f(x) không đổi trên K. ^{[3]Trần Văn Hạo và đồng nghiệp, Giải tích 12 Trang 6 – Định lí thừa nhận}

Chú ý: Nếu hàm số f liên tục trên đoạn [a;b] và có đạo hàm f’(x) > 0 trên khoảng (a;b) thì hàm số f đồng biến trên đoạn [a;b]. Nếu hàm số f liên tục trên đoạn [a;b] và có đạo hàm f’(x) < 0 trên khoảng (a;b) thì hàm số f nghịch biến trên đoạn [a;b].

Định lí mở rộng

Cho hàm số y = f(x) có đạo hàm trên K.

a) Nếu f’(x) ≥ 0 với mọi x thuộc K và f’(x) = 0 xảy ra tại một số hữu hạn điểm của K thì hàm số f(x) đồng biến trên K.

b) Nếu f’(x) ≤ 0 với mọi x thuộc K và f’(x) = 0 xảy ra tại một số hữu hạn điểm của K thì hàm số f(x) nghịch biến trên K.

Qui tắc xét tính đơn điệu của hàm số

– Bước 1: Tìm tập xác định.

– Bước 2: Tính đạo hàm f’(x). Tìm các điểm xᵢ (i = 1, 2, …,n) mà tại đó đạo hàm bằng 0 hoặc không xác định.

– Bước 3: Sắp xếp các điểm xᵢ theo thứ tự tăng dần và lập bảng biến thiên.

– Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

Phân dạng bài tập

Dạng 1. Tìm khoảng đồng biến, nghịch biến của hàm số bất kì

Phương pháp giải

Cho hàm số y = f(x)

+) f’(x) > 0 ở đâu thì hàm số đồng biến ở đấy.

+) f’(x) < 0 ở đâu thì hàm số nghịch biến ở đấy.

Quy tắc

+) Tính f’(x), giải phương trình f’(x) = 0 tìm nghiệm.

+) Lập bảng xét dấu f’(x).

+) Dựa vào bảng xét dấu và kết luận.

Bài tập vận dụng

Câu 1. Xét tính đơn điệu của mỗi hàm số sau

a. y = x³ – 3x² + 2

b. y = -x³ + 3x² -3x + 2

c. y = x³ + 2x

Hướng dẫn giải

a. y = x³ – 3x² + 2.

Hàm số xác định với mọi x ∊ R

Ta có: y’ = 3x² – 6x, cho y’ = 0 ⇒ 3x² – 6x = 0 ⇔ x = 0, x = 2

Bảng biến thiên

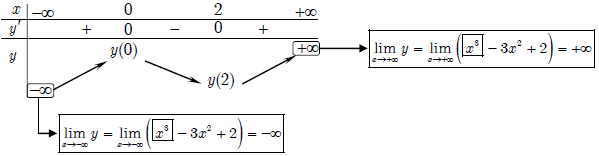
Dựa vào bảng biến thiên suy ra:

– Hàm số đồng biến trên các khoảng (-∞;0) và (2;+∞).

– Hàm số nghịch biến trên khoảng (0;2)

Chú ý: Không được kết luận: “Hàm số đồng biến trên khoảng (-∞;0) ∪ (2;+∞)”

b. y = -x³ + 3x² -3x + 2

Hàm số xác định với mọi x ∊ R

Ta có: y’ = -3x² + 6x – 3, cho y’ = 0 ⇒ -3x² + 6x – 3 = 0 ⇔ x = 1 (nghiệm kép)

⇒ y’ ≤ 0, ∀ x ∊ R ⇒ hàm số luôn nghịch biến trên tập xác định R

c. y = x³ + 2x

Hàm số xác định với mọi x ∊ R

y’ = 3x² + 2, cho y’ = 0 ⇒ 3x² + 2 = 0 (vô nghiệm)

⇒ y’ > 0, ∀ x ∊ R ⇒ hàm số luôn đồng biến trên tập xác định R

Câu 2. Xét tính đơn điệu của mỗi hàm số sau:

a. y = x⁴ – 2x² + 1

b. y = -x⁴ + x² – 2

c. y= ¼ x⁴ + 2x² – 1

Hướng dẫn giải

a. y = x⁴ – 2x² + 1

Hàm số xác định với mọi x ∊ R

y’ = 4x³ – 4x = 4x (x² – 1), cho y’ = 0 ⇒ 4x (x² – 1) = 0 ⇔ x = 0 hoặc x = -1 hoặc x = 1

Bảng biến thiên

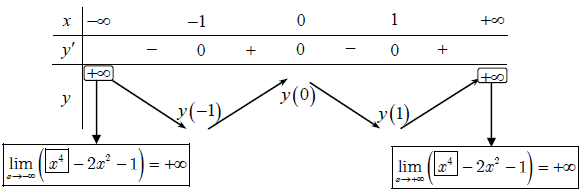
Dựa vào bảng biến thiên suy ra:

• Hàm số đồng biến trên các khoảng (-1;0) và (1;+∞)
• Hàm số nghịch biến trên các khoảng (-∞;-1) và (0;1)

b. y = -x⁴ + x² – 2

Hàm số xác định với mọi x ∊ R

y’ = -4x³ + 2x = 2x (-2x² + 1)

Cho y’ = 0 ⇒ 2x (-2x² + 1) = 0

⇔ x = 0 hoặc

Bảng biến thiên

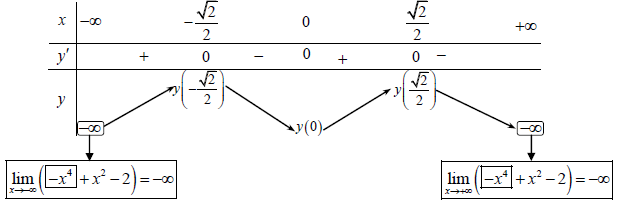
Dựa vào bảng biến thiên suy ra:

– Hàm số đồng biến trên các khoảng:

– Hàm số nghịch biến trên các khoảng:

c. y= ¼ x⁴ + 2x² – 1

Hàm số xác định với mọi x ∊ R

y’ = x³ + 4x = x (x² + 4), cho y’ = 0 ⇒ x (x² + 4) = 0 ⇔ x = 0 (do x² + 4 vô nghiệm)

Bảng biến thiên

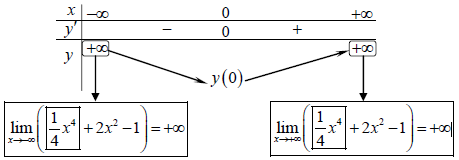
Từ bảng biến thiên suy ra: Hàm số đồng biến trên khoảng (0; +∞) và nghịch biến trên các khoảng (-∞; 0).

Dạng 2. Đọc khoảng đơn điệu của hàm số bằng hình ảnh đồ thị cho trước

Phương pháp giải

Nếu đề bài cho đồ thị y = f(x), ta chỉ việc nhìn các khoảng mà đồ thị “đi lên” hoặc “đi xuống”.

• Khoảng mà đồ thị “đi lên”: hàm đồng biến;
• Khoảng mà đồ thị “đi xuống”: hàm nghịch biến.

Nếu đề bài cho đồ thị y = f’(x). Ta tiến hành lập bảng biến thiên của hàm y = f(x) theo các bước:

• Tìm nghiệm của f’(x) = 0 (hoành độ giao điểm với trục hoành);
• Xét dấu f’(x) (phần trên Ox mang dấu dương; phần dưới Ox mang dấu âm);
• Lập bảng biến thiên của y = f(x), suy ra kết quả tương ứng.

Bài tập vận dụng

Câu 1. Cho hàm số y = f(x) có bảng biến thiên như sau

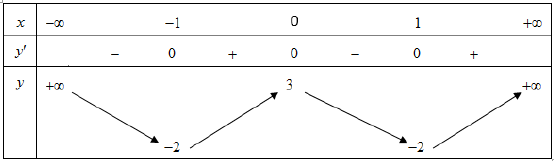
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. (-1;0)

B. (-∞;0)

C. (1;+∞)

D. (0;1)

Hướng dẫn giải

Dựa vào bảng biến thiên ta có hàm số đã cho nghịch biến trên các khoảng (0;1) và (-∞;-1)

⟹ Chọn D

Dạng 3. Tìm m để hàm số đơn điệu trên từng khoảng xác định

Phương pháp giải

Tính

– Hàm số đồng biến trên từng khoảng xác định của nó ⇔ y’ > 0 ⇔ ad − cb > 0.

– Hàm số nghịch biến trên từng khoảng xác định của nó ⇔ y’ < 0 ⇔ ad − cb < 0.

Bài tập vận dụng

Câu 1. Có bao nhiêu giá trị nguyên của tham số m để hàm số đồng biến trên khoảng (-∞;-6)

A. 2

B. 6

C. Vô số

D. 1

Hướng dẫn giải

Tập xác định: D = (-∞;-3m) ∪ (-3m; +∞)

Ta có

Hàm số đổng biến trên khoảng

Mà m nguyên nên m ∊ {1; 2}

⟹ Chọn A

Câu 2. Có bao nhiêu giá trị nguyên của tham số m để hàm số nghịch biến trên khoảng (6;+∞)

A. 0

B. 6

C. 3

D. Vô số

Hướng dẫn giải

Tập xác định D = ℝ\{-3m};

Hàm số nghịch biến trên khoảng (6;+∞) khi và chỉ khi:

Vì m ∊ ℤ ⇒ m ∊ {-2; -1; 0}

⟹ Chọn C

Dạng 4. Tìm m để hàm số bậc 3 (y = ax³ + bx² + cx + d) đơn điệu trên ℝ

Phương pháp giải

– Hàm số đồng biến trên ℝ thì y’ ≥ 0, ∀ x ∊ ℝ ⇔ hoặc suy biến

– Hàm số nghịch biến trên ℝ thì y’ ≤ 0, ∀ x ∊ ℝ ⇔ hoặc suy biến

Bài tập vận dụng

Câu 1. Hỏi có bao nhiêu số nguyên m để hàm số y = (m² – 1) x³ + (m – 1) x² – x + 4 nghịch biến trên khoảng (-∞;+∞)

A. 0

B. 3

C. 2

D. 1

Hướng dẫn giải

TH1: m = 1. Ta có: y = – x + 4 là phương trình của một đường thẳng có hệ số góc âm nên hàm số luôn nghịch biến trên ℝ. Do đó nhận m = 1.

TH2: m = -1. Ta có: y = -2x² – x + 4 là phương trình của một đường Parabol nên hàm số không thể nghịch biến trên ℝ. Do đó loại m = -1.

TH3: m ≠ 1. Khi đó hàm số nghịch biến trên khoảng (-∞;+∞) ⇔ y’ ≤ 0 ∀ x ∊ ℝ, dấu “=” chỉ xảy ra ở hữu hạn điểm trên ℝ.

⇔ 3(m² – 1) x² + 2(m – 1) x – 1 ≤ 0, ∀ x ∊ ℝ

Vì m ∊ ℤ nên m = 0

Vậy có 2 giá trị m nguyên cần tìm là m = 0 hoặc m = 1.

⟹ Chọn C

Câu 2. Cho hàm số y = -x³ – mx² + (4m + 9) x + 5 , với m là tham số. Hỏi có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng (-∞;+∞)

A. 5

B. 4

C. 6

D. 7

Hướng dẫn giải

Ta có:

TXĐ: D = ℝ

y’ = -3x² – 2mx + 4m + 9

Hàm số nghịch biến trên (-∞;+∞) khi y’ ≤ 0, ∀ x ∊ (-∞;+∞)

⇒ Có 7 giá trị nguyên của m thỏa mãn.

⟹ Chọn D

Câu 3. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số đồng biến trên khoảng (-∞;+∞)?

A. 4

B. 5

C. 3

D. 0

Hướng dẫn giải

y’ = (m² – m) x² + 4mx + 3

Hàm số đã cho đồng biến trên khoảng (-∞;+∞) ⇔ y’ ≥ 0, ∀ x ∊ ℝ

Với m = 0 ta có y’ = 3 > 0 với ∀ x ∊ ℝ ⇒ Hàm số đồng biến trên khoảng (-∞;+∞).

Với m = 1 ta có y’ = 4x + 3 > 0 ⇔ x > -¾ ⇒ m = 1 không thỏa mãn.

Với ta có y’ ≥ 0, ∀ x ∊ ℝ

Tổng hợp các trường hợp ta được -3 ≤ m ≤ 0.

Vì m ∊ ℤ ⇒ m ∊ {-3; -2; -1; 0}.

Vậy có 4 giá trị nguyên của m thỏa mãn bài ra.

⟹ Chọn A

Dạng 5. Tìm m để hàm số lượng giác đơn điệu trên khoảng cho trước.

Để tìm hiểu chi tiết dạng toán này. Chúng ta có thể xem xét các ví dụ dưới đây:

Câu 1. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đồng biến trên khoảng

A. m ≤ 0 hoặc 1 ≤ m < 2

B. m ≤ 0

C. 1 ≤ m < 2

D. m ≥ 2

Hướng dẫn giải

Đặt t = tan x , vì x ∊ ⇒ t ∊ {0; 1}

Xét hàm số . Tập xác định: D = ℝ\{m}

Ta có

Ta thấy hàm số t(x) = tan x đồng biến trên khoảng . Nên để hàm số đồng biến trên khoảng khi và chỉ khi: f’(t) > 0, ∀ t ∊ {0; 1}

⟹ Chọn A

Câu 2. Tìm tất cả các giá trị thực của tham số để hàm số nghịch biến trên khoảng

A.

B.

C. m ≤ 3

D. m < 3

Hướng dẫn giải

Điều kiện: cos x ≠ m. Ta có:

Vì x ∊ ⇒ sin x > 0, (cos x – m)2 > 0, ∀ x ∊ ; cos x ≠ m

Để hàm số nghịch biến trên khoảng ⇔ y’ < 0 ∀ x ∊

Chú ý: Tập giá trị của hàm số y = cos x, ∀ x ∊ là (-1; 0)

⟹ Chọn A

Dạng 6. Tìm khoảng đơn điệu khi biết đồ thị hàm f’(x)

Phương pháp giải

Loại 1. Cho đồ thị y = f’(x), hỏi tính đơn điệu của hàm y = f(x).

– Tìm nghiệm của f’(x) = 0 (hoành độ giao điểm với trục hoành);

– Xét dấu f’(x) (phần trên Ox mang dấu dương; phần dưới Ox mang dấu âm);

– Lập bảng biến thiên của y = f(x), suy ra kết quả tương ứng.

Loại 2. Cho đồ thị y = f’(x), hỏi tính đơn điệu của hàm hợp y = f(u).

– Tính y’ = u’ ‧ f’(u);

– Giải phương trình f’(u) = 0 (Nhìn đồ thị, suy ra nghiệm);

– Lập bảng biến thiên của y = f(u), suy ra kết quả tương ứng.

Loại 3. Cho đồ thị y = f’(x), hỏi tính đơn điệu của hàm hợp y = g(x), trong đó g(x) có liên hệ với f(x).

– Tính y’ = g’(x);

– Giải phương trình g’(x) = 0 (thường dẫn đến việc giải phương trình liên quan đến f’(x). Loại này ra nhìn hình để suy ra nghiệm);

– Lập bảng biến thiên của y = g(x), suy ra kết quả tương ứng.

Bài tập vận dụng

Câu 1. Cho hàm số y = f(x). Hàm số y = f'(x) có đồ thị như hình bên. Hàm số y = f(2-x) đồng biến trên khoảng

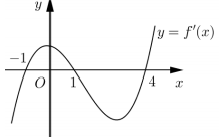
A. (2;+∞)

B. (-2; 1)

C. (-∞; -2)

D. (1; 3)

Hướng dẫn giải

Cách 1:

Ta thấy f’(x) < 0 với nên f(x) nghịch biến trên (1; 4) và (-∞; -1) suy ra g(x) = f(-x) đồng biến trên (-4; -1) và (1; +∞). Khi đó f (2 – x) đồng biến trên khoảng (-2; 1) và (3; +∞)

Cách 2:

Dựa vào đồ thị của hàm số y = f’(x) ta có f’(x) < 0

Ta có (f (2 – x))’ = (2 – x)’. f’(2 – x) = – f’(2 – x)

Để hàm số y = f (2 – x) đồng biến thì (f (2 – x))’ > 0 ⇔ f’(2 – x) < 0

⟹ Chọn B

Câu 2. Cho hàm số f(x), bảng xét dấu của f’(x) như sau:

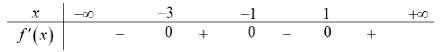
Hàm số y = f (5 – 2x) đồng biến trên khoảng nào dưới đây?

A. (3; 4)

B. (1; 3)

C. (-∞; -3)

D. (4; 5)

Hướng dẫn giải

Ta có y’ = f’(5 – 2x) = -2f’(5 – 2x)

Bảng biến thiên

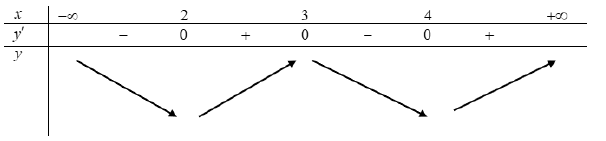
Dựa vào bảng biến thiên hàm số y = f (5 – 2x) đồng biến trên khoảng (4; 5)

⟹ Chọn D

Dạng 7. Biện luận đơn điệu của hàm đa thức trên khoảng con của tập ℝ

Phương pháp giải

Loại 1: Tìm điều kiện của tham số để hàm số y = ax3 + bx2 + cx + d đơn điệu trên toàn miền xác định ℝ

– Đồng biến trên hoặc suy biến

– Nghịch biến trên ℝ thì hoặc suy biến

Loại 2: Tìm điều kiện của tham số để hàm số y = ax³ + bx² + cx + d đơn điệu trên khoảng con của tập ℝ

Ta thường gặp hai trường hợp:

– Nếu phương trình y’ = 0 giải được nghiệm “đẹp”: Ta thiết lập bảng xét dấu y’ theo các nghiệm vừa tìm (xét hết các khả năng nghiệm trùng, nghiệm phân biệt). Từ đó “ép” khoảng mà dấu y’ không thỏa mãn ra khỏi khoảng đề bài yêu cầu.

– Nếu phương trình y’ = 0 có nghiệm “xấu” : Ta sử dụng 1 trong 2 cách sau

• Cách 1. Dùng định lý về so sánh nghiệm (sẽ nói rõ hơn qua bài giải cụ thể).
• Cách 2. Cô lập tham số m, dùng đồ thị (cách này xét sau).

Loại 3: Tìm điều kiện của tham số để hàm số y = ax⁴ + bx² + c đơn điệu trên khoảng con của tập ℝ

– Giải phương trình y’ = 0, tìm nghiệm.

– Biện luận các trường hợp nghiệm (nghiệm trùng, nghiệm phân biệt). Từ đó “ép” khoảng mà dấu y’ không thỏa mãn ra khỏi khoảng đề bài yêu cầu.

Bài tập vận dụng

Câu 1. Cho hàm số với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S.

A. 4

B. Vô số

C. 3

D. 5

Hướng dẫn giải

D = ℝ \ {m};

Hàm số nghịch biến trên các khoảng xác định khi y’ < 0, ∀ x ∊ D ⇔ m² – 4m < 0 ⇔ 0 < m < 4

Mà m ∊ ℤ nên có 3 giá trị thỏa mãn.

⟹ Chọn D

Câu 2. Có bao nhiêu giá trị nguyên của tham số m để hàm số nghịch biến trên khoảng (10; +∞)?

A. Vô số

B. 4

C. 5

D. 3

Hướng dẫn giải

Tập xác định D = ℝ \ {-5m}

Hàm số nghịch biến trên (10; +∞) khi và chỉ khi

Mà m ∊ ℤ nên m ∊ {-2; -1; 0; 1}

⟹ Chọn B

Tài liệu tham khảo

Thầy Tú dạy toán